2018-2019学年度七年级数学上册 第2章 有理数的运算 2.4 有理数的除法同步练习 (新版)浙教版
七年级数学上册 第2章 有理数及其运算 2.9 有理数的乘方(第2课时)有理数乘方的运算教案(新版)

三:
开放
训练
体现
应用
【应用举例】
例计算:(1)102,103,104,105;
(2)(-10)2,(-10)3,(-10)4,(-10)5.
处理方式:先给学生1分钟时间观察例3两式的特点,再分别口述解题过程,教师板书.教师点评归纳10的正整数次幂的规律性.
变式
1.计算:(1)- ;(2)-(- )2;(3)-52;(4)- .
第2课时 有理数乘方的应用
课题
第2课时 有理数乘方的应用
授课人
教
学
目
标
知识技能
1.进一步理解有理数乘方的意义并能解决一些相关的数学问题.
2.经历有理数乘方的符号法则的探究过程,通过实际计算发现底数为10的幂的特点.
数学思考
利用有理数的乘方运算解决一些简单实际问题,使学生初步了解转化、类比、归纳的数学思想方法.
A.-1B.1
C.3D.无法确定
通过例题和变式训练体会有理数的乘方的符号法则,进一步加深对有理数乘方意义的理解.
活动
三:
开放
训练
体现
应用
,第1次截去一半,第2次又截去剩下的一半,如此下去,第7次后剩下的木棒有多长?如果木棒原长为3.2米呢?
图2-9-
4.如图2-9-,将一个边长为1的正方形分割成7部分,其中部分①是边长为1的正方形面积的一半,部分②是部分①的一半,部分③是部分②的一半,…以此类推.
2.判断下列各式的符号:
(1)(-5)2;(2)(-5)5;(3)-(-5)6;(4)-(-5)7.
【拓展提升】
1.已知21=2,22=4,23=8,24=16,…,根据上述规律,请你猜想211的末尾数字是( )
七年级数学上册第2章有理数的运算2.5有理数的乘方有理数的乘方

第一课时(kèshí) 有理数的乘方
2021/12/11
第一页,共十八页。
1.(2分)计算(-1)3的值等于(děngyú)( A )
A.-1
B.1
C.-2
D.2
2.(2分)对于乘积(-3)×(-3)×(-3)×(-3),记法正确的是( )
C
A.-34
B.-(+3)4
C.(-3)4
D.(-3)×4
3.(2分)计算-24=(
A.8 C.16
) D B.-8
D.-16
2021/12/11
第二页,共十八页。
4.(2分)下列(xiàliè)各组数互为相反数的是( B)
A.32与-23
B.32与-32
C.32与(-3)2
D.(-2)3与-23
5.(2分)-53表示(
A.3个-5的积
No 多少。(3)国王应给这位大臣(264-1)粒米。81
Image
12/11/2021
第十八页,共十八页。
)B
B.3个5相乘的相反数
C.5个3相乘的相反数 D.5个-3的积
2021/12/11
第三页,共十八页。
2021/12/11
C C
第四页,共十八页。
2021/12/11
A
D
B
第五页,共十八页。
11.(3分)在(-2)8中,底数是____,指-数2是____,运算(y8ùn suàn)结果是____;2在56-28
20.(4分)一个数的平方等于它本身,则这个数是_____;
1或0
一个数的立方等于它本身,则这个数是_______.
±1或0
2021/12/11
2018_2019学年七年级数学上册第2章有理数的运算2.7近似数作业设计新版浙教版

2.7 近似数(1)1.数学课上老师给出了下面的数据,精确的是()A.某战争每月耗费10亿美元B.地球上煤储量为5万亿吨以上C.人的大脑约有1×1010个细胞D.七年级某班有51个人2.近似数1.40所表示的准确数a的范围是()A.1.395≤a<1.405 B.1.35≤a<1.45C.1.30<a<1.50 D.1.400≤a<1.4053.下列说法中正确的是()A.近似数1.70与近似数1.7的精确度相同B.近似数5百与近似数500的精确度相同C.近似数4.70×104是精确到百位的数D.近似数24.30是精确到十分位的数4.如果a是b的近似值,那么我们把b叫做a的真值.若用四舍五入法得到的近似数是85,则下列各数不可能是其真值的是()A.85.01 B.84.51C.84.99 D.84.495.近似数91.60万精确到()A.百位B.千位C.百分位D.千分位6.由四舍五入得到的近似数14.85,下面的数中,不可能是其真值的是()A.14.8549 B.14.8461C.14.8512 D.14.85597.填空:下列叙述中,哪些数是准确数?哪些数是近似数?(1)我们班里有18位女同学,“18”是数;(2)小红体重约38 kg,“38”是数;(3)我国科盲达5亿之多,5亿是数;(4)某机场年起降各类飞机159307架次,“159307”是数.8.我国古代数学家祖冲之算出了圆周率的范围是 3.1415926<π<3.1415927,对于3.1415926:(1)取近似值3.14,是精确到位;(2)取近似值3.142,是精确到位;(3)精确到个位时,π的近似数为;(4)精确到万分位时,π的近似数为.9.(1)近似数4.20×105精确到__ __位;(2)近似数50元与50.00元的精确度相同吗?请说明理由.10.按括号内的要求,用四舍五入法对下列各数取近似值.(1)82.150(精确到个位);(2)0.123000(精确到万分位);(3)59.9952(精确到0.01).11.世界上最大的沙漠——非洲的撒哈拉沙漠可以粗略地看成是一个长方形,撒哈拉沙漠的长度大约是5149900 m,沙层的深度大约是366 cm.已知撒哈拉沙漠中沙的体积约为33345 km3.请分别按下列要求取近似数.(1)将撒哈拉沙漠的长度用科学记数法表示;(2)将撒哈拉沙漠中沙层的深度四舍五入到10 cm;(3)将撒哈拉沙漠中沙的体积精确到1000 km3.12.1公顷生长茂盛的树林每天大约可以吸收二氧化碳1 t,成人每小时平均呼出二氧化碳38 g.如果要通过森林吸收10000人一天呼出的二氧化碳,那么至少需要多少公顷的树林(1公顷=10000 m2,结果精确到0.1公顷)?13.车间接受了加工2根轴的任务,车间马主任交给小明去完成,小明拿来图纸一看,轴长要求为2.60 m,他用了3天的时间完成任务.他把轴交给马主任验收,马主任与小明当场量了这两根轴的长度,一根为2.57 m,另一根为2.63m.小明很高兴,他说:“两根轴都合格.”而马主任阴沉着脸说:“两根轴都不合格,都要报废.”请问:小明加工的这两根轴到底是否合格?为什么?参考答案1.D2.A3.C4.D5.A6.D7.(1)准确;(2)近似;(3)近似;(4)准确8.(1)百分;(2)千分;(3)3;(4)3.14169.【解】(1)千;(2)不相同.因为50元精确到元,50.00元精确到分.10.【解】(1)82.150≈82.(2)0.123000≈0.1230.(3)59.9952≈60.00.11.【解】(1)撒哈拉沙漠的长度大约是5149900 m=5.1499×106 m.(2)沙层的深度大约是366 cm≈3.7×102 cm.(3)撒哈拉沙漠中沙的体积约为33345 km3≈3.3×104 km3.12.【解】10000×38×241000000=9.12≈9.1(公顷).13.【解】不合格.因为轴长要求为2.60 m,则实际轴长的范围需大于或等于2.595 m且小于2.605 m才合格,显然,小明加工的轴长不在合格范围内.2.7 近似数(2)1.用计算器计算124×115,按键的顺序为( ) A.12y x 4×1ab/c 1ab/c 5= B.124yx ×1ab/c 1ab/c 5= C.12x 24×1ab/c 1ab/c 5=D.124x 2×1ab/c 1ab/c 5 =2.用计算器计算230,按键顺序正确的是( )A.230=B.2×30=C.230y xD.2y x 30=3.用计算器计算20-4×(-5)显示:__ _.4.根据如图所示的程序计算,若输入x 的值为1,则输出y 的值为__ __.(第4题)5.用计算器计算:(1)0.84÷4+(-0.79)×2;(2)49.75÷0.252;(3)12×(5.63-3.31)×112-25.6.(1)用计算器计算下列各式,将结果写在横线上:999×21= ;999×22= ;999×23= ;999×24= ;…;(2)不用计算器,你能直接写出999×29的结果吗?7.利用计算器探究: (1)计算0.22,22,202,2002,….观察计算结果,底数的小数点向左(右)移动一位时,平方数的小数点的移动规律是 (直接写结论);(2)计算0.23,23,203,2003,….观察计算结果,底数的小数点向左(右)移动一位时,立方数的小数点的移动规律是 (直接写结论);(3)计算0.24,24,204,2004,….观察计算结果,底数的小数点向左(右)移动一位时,四次方数的小数点有什么移动规律(写出探索过程)?(4)由此,根据0.2n ,2n ,20n ,200n,…的计算结果,猜想底数的小数点与n 次方数的小数点有怎样的移动规律(直接写结论)?参考答案1.A 2.D 3.40 4.45.【解】 (1)0.84÷4+(-0.79)×2=-1.37.(2)49.75÷0.252=796.(3)12×(5.63-3.31)×112-25=108.36. 6. 【解】(1)20979; 21978; 22977; 23976;(2)能,999×29=28971.7.【解】(1)向左(右)移动两位;(2)向左(右)移动三位;(3)∵0.24=0.0016,24=16,204=160000,∴底数的小数点向左(右)移动一位时,四次方数的小数点的移动规律是:向左(右)移动四位.(4)规律:底数的小数点向左(右)移动一位时,n次方数的小数点向左(右)移动n位.。
2018-2019学年度七年级数学上册第2章有理数的运算2.1有理数的加法同步练习(新版)

2.1有理数的加法学校: ____________ 姓名: ____________ 班级: ____________一 •选择题(共12小题) 1.如图,现有3X 3的方格,每个小方格内均有不同的数字,要求方格内每一行.每一列以及每一条对角线上的三个数字之和均相等,图中给出了部分数字,则 P 处对应的数字是( )L M Ur □ i E □ □A. 7B. 5C. 4D. 12.下列各式运算正确的是()B. (— 2) + ( +2) =- 4C.( +6) + (- 11) =- 5D. (- 5) + (+3) =-83.计算:| - 5+3|的结果是( )A. - 8B. 8C. - 2D. 2田L 口 2 吗 7眄陽如砌A. a 1+a 2+a 3+a 7+a 8+a 9=2 (a 4+a 5+a 6)B. a 1+a 4+a 7+a 3+a 6+a 9=2 (a 2+a 5+a 8)C. a 1+a 2+a 3+a 4+a 5+a 6+a 7+a s +a 9=9a 5D.( a 3+a 6+a 9)— ( a 计a 4+a ?) = (a 2+a 5+a 8)5. 下面说法中正确的是( )A. 两数之和为负,则两数均为负B. 两数之和为正,则两数均为正C. 两数之和- -定大 于每一个加数D. 两数之和为0,则这两数互为相反数 6.计算| - 5+2|的结果是( )A. (- 3) + (+7) =- 4 4.如图,在3X 3的正方形,则里面九个数不满足的关系式是(A. 3B. 2C. - 3D. - 27. 小林家冰箱冷冻室的温度为-5C,调高6C后的温度为()A. - 1C B . O C C. 1C D. 11C& 已知|x|=5 , |y|=3,且x > y,则x+y 的值为()A. 8B. 2C. - 8 或-2 D . 8 或29.下列说法中,正确的是()A.符号不同的两个数互为相反数B.两个有理数和- -定大于每一个加数C.有理数分为正数和负数D.所有的有理数都能用数轴上的点来表示10 .下列语句:①不带“-”号的数都是正数;②不存在既不是正数,也不是负数的数;③0表示没有;④一个有理数不是正数就是分数;⑤符号相反的两个数互为相反数;⑥若两个有理数的和为正数,则这两个数都是正数.正确的有()A. 0个B. 1个C. 2个D. 3个11.如图,在一个由6个圆圈组成的三角形里,把11〜16这6个数分别填入图的圆圈中,要求三角形的每一条边上的三个数的和S都相等,那么S的最大值是()A. 39B. 40C. 42D. 4312 .计算3+5+7+9+…+195+197+199 的值是()A. 9699B. 9999C. 9899D. 9799二 .填空题(共8小题)13 .若|a+1|+|a - 2|=5 , |b - 2|+|b+3|=7 ,贝卩a+b= _______14 .若|x|=5 , |y|=3,且|x - y|= - x+y,则x+y= ________ .15 .在进行异号的两个有理数加法运算时,用到下面的一些操作:①将绝对值较大的有理数的符号作为结果的符号并记住②将记住的符号和绝对值的差一起作为最终的计算结果③用较大的绝对值减去较小的绝对值④求两个有理数的绝对值⑤比较两个绝对值的大小其中操作顺序正确的步骤是 ________ (填序号)16•若a是最小的正整数,b是绝对值最小的数,c是相反数等于它本身的数,d是到原点的距离等于2的负数,e是最大的负整数,则a+b+c+d+e= __________ •17. _________________________________________________________________________ 从1,4, 7……295, 298 (隔3的自然数)中任选两个数相加,和的不同值有________________ 个.18. 【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”(图1所示),是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”(图2所示).【规律总结】观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是 _______________ ;若图3,是一个“幻方”,则a= __________ .19. (- 2) +4+ (- 6) +8+…+ (- 98) +100= __________20. 观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+仁25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1= ______ .三.解答题(共4小题)21. 在一个3X 3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3X 3的方格称为一个三阶幻方.(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.图:22.用“〉”或“v”填空:(1 ) 如果a> 0,b>0,那么a+b0 ;(2) 如果a v 0,b v 0,那么a+b0 ;(3) 如果a> 0,b v 0,|a| > |b|,那么a+b0(4) 如果a> 0,b v 0,|a| v |b|,那么a+b023. 某邮局检修队沿公路检修线路,规定前进为正,后退为负,某天自A点出发到收工时所走路程为(单位:千米) +10,- 3, +4,- 8, +13,- 2, +7, +5,- 5,- 2.(1 )求收工时,检修队距A点多远?(2)若每千米耗油0.3千克,问从A点出发到收工,共耗油多少千克?24. ( 1)比较下列各式的大小:|5|+|3| ______ |5+3| , | - 5|+| - 3| _________ | (- 5) + (-3) | ,| - 5|+|3| _______ | (- 5) +3| , |0|+| - 5| ______ |0+ (- 5) |…(2)通过(1)的比较、观察,请你猜想归纳:当a、b 为有理数时,|a|+|b| _________ |a+b| •(填入“》”、*”、“>” 或“v”)(3)根据(2)中你得出的结论,求当|x|+| - 2|=|x - 2|时,直接写出x的取值范围.参考答案与试题解析一•选择题(共12小题)1.8+x,【解答】解:设下面中间的数为x,则三个数字之和为8- 3=5,8+x - 3 - 6=x - 1,8+x- 2 -( x - 1) =7,5+6+7 - 7- 3=8,如图所示:E□0H□□aP+6+8=7+6+5,解得P=4.故选:C.2.【解答】解:A、(- 3) + (+7) =4,此选项错误;B ( - 2) + (+2) =0,此选项错误;C( +6) + (- 11) =- 5,此选项正确;D ( - 5) + (+3) =- 2,此选项错误;故选:C.3.【解答】解:原式=| - 2|=2 ,故选:D.4.【解答】解:A、a i+a2+a3+a7+a8+a9= (a4+a5+a6)—21+ (a4+a?+a6)+21=2 (a4+a5+a6),正确,不符合题意;B、a1+a4+a7+a3+a6+a9=a1 +a3+a4+a6+a7+a9=2 ( a 2+ a5+ a 8) ,正确,不符合题意;C、a i+a2+a3+a4+a5+a6+a7+a8+a9=9a5,正确,不符合题意D、( a3+a6+a9)-( a计a4+a7)=6,错误,符合题意.故选:D.5.【解答】解:A、两数之和为负,两数均为负数,也可能一正一负,故A错误;B两数之和为正,两数均为正数,也可能一正一负,故B错误C两数之和一定不大于每一个加数,故C错误;D、两数之和为0,则这两数互为相反数,故D正确.故选:D.6.【解答】解:| - 5+2|=| - 3|=3 ,故选:A.7.【解答】解:-5+6=1 (C).故选:C.8.【解答】解:T |x|=5 , |y|=3 ,x= ± 5, y= ± 3;••• x > y,. x=5, y=± 3.当x=5,y=- 3 时,x+y=2;当x=5,y=3 时,x+y=8.故选:D.9.【解答】解:A、+2与-1符号不同,但不是互为相反数,错误;B两个负有理数的和小于每一个加数,错误;C有理数分为正有理数、负有理数和0,错误;D所有的有理数都能用数轴上的点来表示,正确.故选:D.10.【解答】解:0不含“-”号也不是正数,故①错误;0即不是正数也不是负数,故②错误;0有时表示没有,但表示温度时,0表示的是冰水混合物的温度,表示海拔时,0表示的是一个高度,故③错误;一个有理数不是整数就是分数,一个有理数不是正数,也可能是负整数,不一定是分数,故④错误;+3和-2虽然符号相反,但他们不是相反数,故⑤错误;3+(- 2) =1,虽然和为正数,但这两个数不都是正数,故⑥错误.综上正确的0个.故选:A.11.【解答】解:11 + 12+13+14+15+16=81 , 81 - 3=27,14+15+16=45, 45- 3=15,27+15=42.故选:C.12.【解答】解:•••都是连续奇数,99+2=101,•••共有(199+1)- 2 -仁99个数,即:共有49对202和正中间的•••原式=202X 49+10仁9999 .故选:B.二.填空题(共8 小题)13.【解答】解:当a w - 1时,-a- 1+2- a=5,解得a=- 2;当-1v x v 2 时,a+1+2- a=3工5,舍去;当a> 2 时,a+1+a- 2=5,解得a=3;当b w- 3 时,2- b- b- 3=7,解得b=- 4;当-3v b v 2 时,-b - 3+b- 2=- 5 工7,舍去;当b>2 时,b- 2+b+3=7,解得b=3;综上a=- 2 或a=3, b=- 4 或b=3;当a=- 2、b=- 4 时,a+b=- 6;当a=- 2、b=3 时,a+b=1;当a=3、b=- 4 时,a+b=- 1;当a=3、b=3 时,a+b=6;即a+b=± 1 或± 6;故答案为:± 1 或± 6 .14.【解答】解:T |x|=5 , |y|=3 ,•x= ±5,y=±3,••• |x - y|= -( x- y),•x- y w 0,•x= - 5, y=±3,当x=- 5、y=- 3 时, x+y= - 5- 3=- 8;当x= - 5、y=3 时,x+y= - 5+3= - 2;故答案为:-8或-215.【解答】解;在进行异号的两个有理数加法运算时,应先求两个有理数的绝对值,然后比较两个绝对值的大小,接下来将绝对值较大的有理数的符号作为结果的符号并记住,然后用较大的绝对值减去较小的绝对值,最后将记住的符号和绝对值的差一起作为最终的计算结果,故正确的顺序是④⑤①③②.故答案为:④⑤①③②.16.【解答】解:••• a是最小的正整数,b是绝对值最小的数,c是相反数等于它本身的数,d 是到原点的距离等于 2 的负数, e 是最大的负整数,••• a=1, b=0, c=0, d=- 2, e= - 1,/• a+b+c+d+e=1+0+0 - 2 - 1 = - 2.故答案为:- 2.17.【解答】解:1+4=5,295+298=593 ,和是隔 3 的自然数,n= (593- 5)- 3+1=588- 3+1=197.故答案为:197.18.【解答】解:【阅读材料】“九宫图”源于我国古代夏禹时期的“洛书”(图 1 所示),是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”(图 2 所示).【规律总结】观察图 1 、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是每一行、每一列和每条对角线上各个数之和都相等;若图3,是一个“幻方”,则4+1+ (- 2) =4+2+a,即a=-3,故答案为:每一行、每一列和每条对角线上各个数之和都相等;- 319.【解答】解:(-2) +4+ (- 6) +8+…+ (- 98) +100=25X 2=50.20.【解答】解:根据观察可得规律:结果等于中间数的平方. ••• 1+2+3+ …+99+100+99+…+3+2+1=100^=10000.三.解答题(共 4 小题)21.【解答】解:( 1 ) 2+3+4=9,9- 6- 4=- 1 ,9- 6- 2=1,9- 2- 7=0,9- 4- 0=5,如图所示:(2)- 3+1- 4=- 6,-6+1 -(- 3) =- 2,-2+1+4=3,如图所示:x=3- 4-(- 6) =5,y=3- 1 -(- 6) =8,x+y=5+8=13.16137450图I 图222.【解答】解:同号两数相加,取相同的符号,所以(1)中两数的和为正;(2)中两数的和为负;异号两数相加,取绝对值较大的加数的符号,所以(3)中两数的符号为正;(4)中两数的符号为负.故答案为:(1)>,( 2)<,( 3)>,( 4)V.23.【解答】解:(1)( +10) + (- 3) + ( +4) + (- 8) + (+13) + (- 2) + (+7) + (+5) + (-5) + (-2) =19 千米.故检修队离A点19千米.(2) |+10|+| - 3|+|+4|+| - 8|+|+13|+| - 2|+|+7|+|+5|+| - 5|+| - 2|=59 ,0.3 X 59=17.7 .故共耗油17.7千克.24.【解答】解:(1))比较下列各式的大小:|5|+|3|=|5+3| - 5|+| - 3|=| (- 5) + (- 3) | ,| - 5|+|3| > | (- 5) +3| , |0|+| - 5|=|0+ (- 5) | …(2)通过(1)的比较、观察,请你猜想归纳:当a、b 为有理数时,|a|+|b| > |a+b| .(填入"》”、"w”、">” 或"v”)(3)根据(2)中你得出的结论,当|x|+| - 2|=|x - 2|时,x的取值范围x<0. 故答案为:(1)=; =;>; = (2) >。
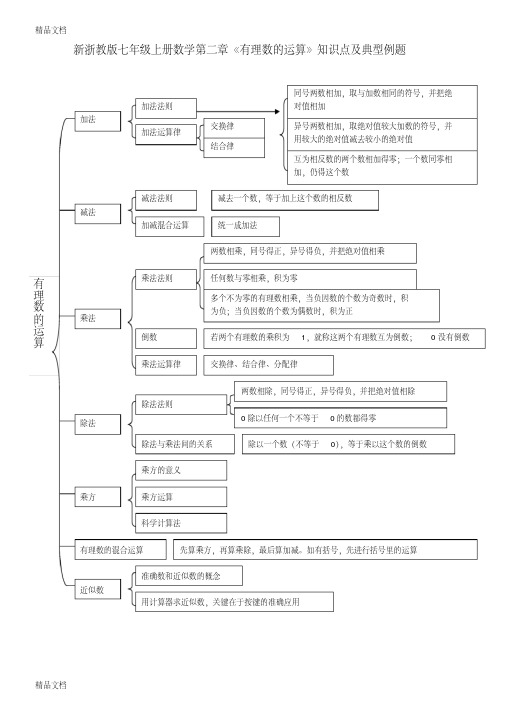
最新新浙教版七年级上册数学第二章《有理数的运算》知识点及典型例题
精品文档
精品文档
将考点与相应习题联系起来
考点一、 有理数的加减乘除乘方运算
2
2 1、 (-3) 3÷ 2 1 × (- 2 )2 –4-23×( -
)
43
3
2、 -32+(-2) 3 –(0.1)2 × (-10) 3
3、 -0.5- ( -3 1 ) +2.75+( -7 1 )
4
2
4、( -23) -( -5) +(-64) -( -12)
27 的
A.26.48
B.26.53
C.26.99
D.27.02
16. 小华和小丽最近测了自己的身高,小华量得自己约
高的说法正确的是
()
1.6m ,小丽测得自己的身高约为 1.60m,下列关于她俩身
A. 小华和小丽一样高 二、填空题
B.小华比小丽高
C.小华比小丽低
D.无法确定谁高
1.若规定 a※ b=5a+2b-1 ,则 (-4) ※ 6 的值为 _________
24,用四种方
2、四张牌为: -12 、-1 、 12、3 将这四个数(每个数只用一次)进行加减乘除乘方运算,使其结果为 方法表示。
24,用三种
3、四张牌为: -1 、2、-2 、3 将这四个数(每个数只用一次)进行加减乘除乘方运算,使其结果为 法表示。
24,用三种方
考点九 、乘方在生活中的实际应用
1
称为
a
a 的差.倒.数.. 如:
3 的差倒数是
1
3
1
增减量
-5 +7 -3 +4 +9 -8 -25
( 1)本周六生产了多少辆? ( 2)产量最多的一天比产量最少的一天多生产了多少辆? ( 3)用简便方法算出本周实际总产量
浙教版2019-2020学年度七年级数学上册第2章有理数的运算2.4有理数的除法(有答案)

浙江版2019-2020学年度七年级数学上册第2章有理数的运算2.4有理数的除法【知识清单】1、有理数的除法法则:两数相除,同号得正,异号得负,并把绝对值相除;0除以任何一个不为0的数都得0. 2、有理数的除法与乘法的转换:除以一个数(不等于0),等于乘以这个数的倒数.且0不能作除数,否则无意义. 3、解决含有除法的题目一般步骤:(1)先将除法转化乘法;(2)再根据乘法法则和运算律进行计算. 【经典例题】例题1、等式[(-7.5) -□]÷(-221)=0中,□表示的数是 . 【考点】有理数的除法,简单方程.【分析】根据有理数的除法,可得答案. 【解答】 [(-7.5)-□]÷(-221)=0,得 (-7.5) -□=0, 解得□=-7.5, 故答案为:-7.5.【点评】本题考查了有理数的除法,零除以任何非零的数都得零. 例题2、计算:(-15)÷(-5)×51= . A .4 B .10 C .12 D .20 【考点】有理数的除法.【分析】先把除法转化为乘法,再根据有理数的乘法运算法则进行计算即可得解. 【解答】(-15)÷(-5)×51 =(﹣15)×(﹣51)×51 =15×51×51 =53. 故答案为:53.【点评】本题考查了有理数的除法,有理数的乘法,是基础题,要注意按照从左到右的顺序依次进行计算,不能随意简化. 【夯实基础】1、711-的倒数与7的相反数的商为( )A .-8个B .8C .81- D .812、下列运算中,正确的是( )A .-21÷(-3) =-7B .-6÷)65(-=5 C .(-0.375)÷(-3)=81 D .-5÷)51(-=1 3、若两个有理数的和除以这两个有理数的积,其商为0,则这两个数为( )A .互为倒数B .互为相反数C .都为0D .互为相反数且都不为4、在算式647□-÷中“□”的所在的位置,填入下列运算符号,计算出来的值最小的是( )A. +B. -C. ×D. ÷5、若a ,b ,c 为非零有理数,则acacb b aa ++可能为 . 6、有理数a 、b 在数轴上是位置如图所示,则ba ab- 0. 7、若a +5没有倒数,则a = ;在计算24÷a 时,误将“÷”看成“+”,结果得16,而24÷a 的正确结果是________ 8、计算:(1)-7÷(-1121)×76×(-612)÷11;(2)-15÷)517()65()65(-÷⎥⎦⎤⎢⎣⎡-⨯-);(3)1251-÷)216132(-+ ; (4)-3÷(83-)+15÷(65-).9、有若干数,第一个数记作a 1,第二个数记作a 2, 第三个数记作a 3,…,第n 个数记作a n , 若a 1=-32,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”. 第6题图(1)试计算a 2= , a 3= ; (2)求a 2019的值.【提优特训】10、下列四个算式中,误用分配律的是( ) A .-24×(-81+61-41)=24×81-24×61+24×41B .(-81+61-41)×(-48)=81×48-61×48+41×48 C .-24÷(-81+61-41)=24÷81-24÷61+24÷41D .(-81+61-41)÷(-24)=81÷24-61÷24+41÷24 11、若a +b <0,ba<0,则a ,b 为 ( ) A .异号0 B .都小于0 C .异号,且正的绝对值大 D .异号,且负的绝对值大 12、已知a 是负整数,则a ,-a ,a1的大小关系为( ) A .-a >a 1>a B .-a >a 1≥a C .a >a 1>-a D . a1>a >-a 13、若a ,b 是互为相反数且都不等于零,则(a -3+b )×(ba+3) A .6 B .3 C .0 D .-614、已知两个数的积为-31,若其中一个因数为615-,则另一个数为 . 15、若b a 36122-++=0,则ba ab+的值为 . 16、在11.2与它的倒数之间有a 个整数,在11.2与它的相反数之间有b 个整数.求(a -b )÷(a +b )+17、若a 、b 互为相反数(a 、b 均不为0),c 、d 互为倒数,且032=+m ,求mcd bam b a 63299-++ 的值.18、计算:(1))202011()411()311()211(1-÷⋅⋅⋅÷-÷-÷-÷;(2) (-2161+-43125+)÷(121-)19、阅读下列材料,然后解决问题:计算:(481-)÷(3281-61+43-).解法一:原式=(481-)÷32-(481-)÷81+(481-)÷61-(481-)÷43 =-321+6181-+361=28811; 解法二:原式=(481-)÷[(3261+)+(81-43-)]=(481-)÷(6587-)=481-×(-24)=21;解法三:原式的倒数为(3281-61+43-)÷(481-)=(3281-61+43-)×(-48)=-32+6-8+36=2, 故原式=21. 解决问题:上述三种解法得出的结果不同,肯定有错误的,你认为哪种解法是错误的,在正确的解法中,你认为哪种解法比较简捷? 然后请你解答下列问题: 计算:(361-)÷(61-125+94-41+).20、(1)判断[])9()27(36-÷-+-与)9()27()9()36(-÷-+-÷-的结果是否相等? (2)计算(-72)÷(-24-8)与(-72)÷(-24)+(-72)÷(-8),观察其结果是否相等? (3)总结(1)、(2)的规律,我们得到(a +b )÷c _____,a ÷c + b ÷c ;c ÷(a +b ) _______ c ÷a + c ÷b (填入“=”或“≠”),其中(2)的计算结果说明:除法的分配律_____(填入“成立”或“不成立”).21、已知a =201820182018201920192019+⨯⨯-, b =201920192019202020202020+⨯⨯-, c =202020202020202120212021+⨯⨯-,求(a +b +c )÷abc 的值.【中考链接】22.(2018•株洲)如图,52的倒数在数轴上表示的点位于下列两个点之间( ) A. 点E 和点FB. 点F 和点GC. 点F 和点GD. 点G 和点H 23、(2019•山东省聊城市•3分)计算:(2131--)÷54= . 24、(2019•浙江嘉兴•4分)数轴上有两个实数a ,b ,且a >0,b <0,a +b <0,则四个数a ,b ,-a ,-b 的大小关系为 (用“<”号连接).第22题图参考答案1、D2、C3、D4、C5、3或1或-16、<7、-5,-3 10、C 11、D 12、B 13、D 14、6 15、-3 22、D 23、32- 24、b <-a <a <-b 8、计算:(1)-7÷(-1121)×76×(-612)÷11;(2)-15÷)517()65()65(-÷⎥⎦⎤⎢⎣⎡-⨯-);(3)1251-÷)216132(-+ ; (4)-3÷(83-)+15÷(65-). 解:(1)原式=-7×1311×76×613×111=-1; (2)原式=15×3652536⨯=3; (3)原式=1217-÷)636164(-+ =1217-÷31=-441;(4)原式=3×38+15×(56-) =8-18=-10.9、有若干数,第一个数记作a 1,第二个数记作a 2, 第三个数记作a 3,…,第n 个数记作a n , 若a 1=-32,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”.(1)试计算a 2= 53 , a 3= 25; (2)求a 2019的值.解:由题意得:a 1=-32,a 2不难发现-32,53,25,这三个数反复出现. ∵2019÷3=673,其余数为0, 16、在11.2与它的倒数之间有a 个整数,在11.2与它的相反数之间有b 个整数.求(a -b )÷(a+b )+∴a =11,∵11.2的相反数为-11.2,之间的整数有-11~11共23个, ∴b =23, ∴(a-b )÷(a +b=(1117、若a 、b 互为相反数(a 、b 均不为0),c 、d 互为倒数,且032=+m ,求mcd bam b a 63299-++ 的值. 解:∵a 、b 互为相反数,且a 、b 均不为0,∴a +b =0,∵c 、d 互为倒数, ∴cd =1,03=+m , ∴2m+3=0,即2m=-3. mcd ba63-+=cd m bam b a )2(332)(9⨯-++ =0-3-3×(-3)×1 =-3+9=6. 18、计算:(1))202011()411()311()211(1-÷⋅⋅⋅÷-÷-÷-÷;(2) (-2161+-43125+)÷(121-) 解:(1)原式=202020194332211÷⋅⋅⋅÷÷÷÷=202020192020342321=⨯⋅⋅⋅⨯⨯⨯⨯. (2)原式=(-2161+-43125+)⨯(-12) =(-21)⨯(-12)61+⨯(-12)-43⨯(-12)125+⨯(-12) =6-2+9-5=8.19、阅读下列材料,然后解决问题:计算:(481-)÷(3281-61+43-).解法一:原式=(481-)÷32-(481-)÷81+(481-)÷61-(481-)÷43 =-321+6181-+361=28811; 解法二:原式=(481-)÷[(3261+)+(81-43-)]=(481-)÷(6587-)=481-×(-24)=21;解法三:原式的倒数为(3281-61+43-)÷(481-)=(3281-61+43-)×(-48)=-32+6-8+36=2, 故原式=21. 解决问题:上述三种解法得出的结果不同,肯定有错误的,你认为哪种解法是错误的,在正确的解法中,你认为哪种解法比较简捷? 然后请你解答下列问题:计算:(361-)÷(61-125+94-41+). 解:解法一是错误的.在正确的解法中,解法三比较简捷. 原式的倒数为(61-125+94-41+)÷(361-) =(61-125+94-41+)×(-36) =6-15+16-9=-2. 故原式=21-. 20、(1)判断[])9()27(36-÷-+-与)9()27()9()36(-÷-+-÷-的结果是否相等? (2)计算(-72)÷(-24-8)与(-72)÷(-24)+(-72)÷(-8),观察其结果是否相等? (3)总结(1)、(2)的规律,我们得到(a +b )÷c _____,a ÷c + b ÷c ;c ÷(a +b ) _______ c ÷a + c ÷b (填入“=”或“≠”),其中(2)的计算结果说明:除法的分配律_____(填入“成立”或“不成立”). (1)相等,其结果均为7. (2)不相等. (-72)÷(-24-8)=49;(-72)÷(-24)+(-72)÷(-8)=12. 49≠12. (3)=;≠;不成立. 21、已知a =201820182018201920192019+⨯⨯-, b =201920192019202020202020+⨯⨯-, c =202020202020202120212021+⨯⨯-,求(a +b +c )÷abc 的值. 解:a =201820182018201920192019+⨯⨯-=12019201820182019-=⨯⨯-,b =201920192019202020202020+⨯⨯-=12020201920192020-=⨯⨯-,c =202020202020202120212021+⨯⨯-=12021202020202021-=⨯⨯-.∴ (a +b +c )÷abc =(-1-1-1)÷(-1)⨯(-1)⨯(-1) =-3÷(-1)=3.学海迷津:数学学习十大方法1、配方法所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。
2024年新人教版七年级数学上册《第2章有理数的运算 小结与复习》教学课件
0.030
练一练 4. (奉贤期中) 近似数 2.74×105 精确到__千____位.
5. (银川期中) 四舍五入法把 4.036 精确到 0.01 的 近似值是_4_._0_4__,把 5.049 精确到十分位的近似值 是_5_._0___.
一、有理数的运算
1. 有理数的加法
(1) 加法法则
加法的交换律
(2) 加法的运算律 加法的结合律
2. 有理数的减法
减法法则:减去一个数,等于加上这个数的相反数.
3. 有理数的乘法
(1) 乘法法则
乘法的交换律
(2) 乘法的运算律 乘法的结合律
乘法的分配律
4. 有理数的除法
除法法则:除以一个数,等于乘这个数的倒数.
= 21 - 27 + 30 - 10 = 14.
注意符号问题
= -2×12×12 = -288.
先确定商的符号, 再把绝对值相除
注意:1. 底数或因数 是带分数时,要先将 带分数化成假分数; 2. 区分 -24 与 (-2)4.
练一练
1. 计算:(1) -3 + 8 - 7 - 15; (2) 23 - 6×(-3) + 2×(-4);
分析:15200 - 14700 = 500 万千米
500×104 千 米
5×106 千米
练一练
3. (湖南中考) 某年,长沙市全年地区生产总值约为
1 400 000 000 000 元,比上年增长 4.5%,其中数据
1 400 000 000 000 用科学记数法表示为( A )
A. 1.4×1012
义务教育(2024年)新人教版 七年级数学上册
《第2章 有理数的运算》 系列教学课件
数学 第二单元 有理数及其运算 知识点汇总
七年级-上册
七年级上册-第二章 有理数及其运算
七年级上册-第二章 有理数及其运算
1.有理数 2.数轴 3.绝对值 4.有理数的加法 5.有理数的减法 6.有理数的加减混合运算 7.水位的变化 8.有理数的乘法 9.有理数的除法 10.有理数的乘方 11.科学记数法
七年级上册-第二章 有理数及其运算
思维导图
七年级上册-第二章 有理数及其运算
正数和负数的概念
⒈正数和负数的概念 负数:比 0 小的数 正数:比 0 大的数 0 既不是正数,也不是负数。 注意: ①字母 a 可以表示任意数,当 a 表示正数时,-a 是负数;当 a 表示负数时,-a 是正数;当 a 表示 0 时,-a 仍是 0。 (如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a, -a 就不能做出简单判断) ②正数有时也可以在前面加“+”,有时“+”省略不写。所以省略“+”的正数的符号是正号。 2. 具有相反意义的量 若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量, 比如:零上 8℃表示为: +8℃; 零下 8℃表示为: -8℃ 3. 0 表示的意义 ⑴0 表示“ 没有”,如教室里有 0 个人,就是说教室里没有人; ⑵0 是正数和负数的分界线,0 既不是正数,也不是负数。
七年级数学上册 第二章 有理数及其运算 4 有理数的加法课件上册数学课件
初中数学(北师大版)
七年级 上册
第二章 有理数及其运算
知识点一 有理数的加法法则
1.加法法则
同号取相同的符号,并把绝对值相加 异号绝 绝 符对 对 号,值 值并相 不用等 等较 大的 和 取绝 为 绝对 0对值 值减 较去 大较 的小 加的 数的 一个数 绝与对0相 值加仍得这个数
8
=7 .
8
(2)原式= +137[(-3.36)11+74(+7.36)] =1+4
314(0.25)
=5.
(3)原式=[(+1)+(-2)]+…+[(+99)+(-100)]
=(-1)+(-1)+…+(-1)
=-50.
12/6/2021
4.某仓库存储钢材,5天内进出钢材的吨数如下(“+”表示进库,“-”表 示出库):+20、-25、-13、+28、-16. (1)经过这5天,仓库里的钢材增加或减少了多少吨? (2)如果进出仓库的钢材装卸费都是每吨15元,那么这5天要付多少元装 卸费?
12/6/2021
2.若m、n互为相反数,则m+8+n=
7,则a+b+c+(-d)=
.
;已知a+c=-2 016,b+(-d)=2 01
答案 8;1 解析 因为m、n互为相反数,所以m+n=0,所以m+8+n=(m+n)+8=0+8=8. 因为a+c=-2 016,b+(-d)=2 017,所以a+b+c+(-d)=(a+c)+[b+(-d)]=(-2 016)+ 2 017=1.
七年级上册第二章有理数的运算2-3有理数的乘方第1课时乘方新版新人教版
题 型 5 利用乘方的意义进行循环规律探究
例 10 探索规律:31=3,个位数字是3;32=9,个位数字是 9;33=27,个位数字是7;34=81,个位数字是1;35 =243,个位数字是3;36=729,个位数字是9;则37 的个位数字是________,32024的个位数字是________.
思路引导 解:因为|x+1|+(y-12)2=0,|x+1|≥0,(y-12)2≥0,所 以x+1=0,y-12=0,解得x=-1,y=12.当输入x=-1, y=12时,输出的值为[(-1)2+(2×12+1)]÷2=[1+2]÷2= 32,故输出的结果为32.
技巧点拨 任何数的偶次幂都是非负数,即a2n≥0(n为正整数);
加与减是第一级运算; ••• 乘与除是第二级运算; ••• 乘• 方• 与• 开• 方• 是第三级运算.
知3-讲
2. 有理数混合运算的顺序 (1)先算高级运算,再算低级运算,即:先乘方,再乘除,
最后加减; (2)同级运算,按从左到右的顺序进行; (3)若有括号,先做括号内的运算,一般按小括号、中括号、
思路引导
解:由题意可知,对于3的正整数幂,个位数字只出现3, 9,7,1,且按这一顺序每4个一循环,因此,求37,32024的 个位数字是多少,关键看共有几个循环,余数是几. 因为 7÷4=1……3,所以37的个位数字是7. 因为2 024÷4=506 ,所以32024的个位数字是1.
答案:7;1
思路点拨 关于循环规律的探究,先根据特殊数探究出循环的规
律,关键是看清几个一循环,然后利用余数与循环规律 相比较,找出对应的结果.
易 错 点 不理解乘方中底数的括号意义而出错
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.4 有理数的除法
学校:___________姓名:___________班级:___________
一.选择题(共12小题)
1.8的倒数是()
A.﹣8 B.8 C.﹣ D.
2.若a与﹣3互为倒数,则a等于()
A.B.C.3 D.﹣3
3.一个数和它的倒数相等,则这个数是()
A.1 B.﹣1 C.±1 D.±1和0
4.下列说法正确的是()
A.负数没有倒数 B.正数的倒数比自身小
C.任何有理数都有倒数D.﹣1的倒数是﹣1
5.下列说法中①相反数等于本身的数是0,②绝对值等于本身的是正数,③倒数等于本身的数是±1,正确的个数为()
A.3个B.2个C.1个D.0个
6.下列各对数中,互为倒数的一对是()
A.4和﹣4 B.﹣2和﹣C.﹣3和D.0和0
7.若﹣的倒数与m+4互为相反数,那么m的值是()
A.m=1 B.m=﹣1 C.m=2 D.m=﹣2
8.计算(﹣18)÷9的值是()
A.﹣27 B.﹣9 C.﹣2 D.2
9.如果a+b>0,且ab<0,那么()
A.a>0,b>0
B.a<0,b<0
C.a、b异号且正数的绝对值较大
D.a,b异号且正数的绝对值较小
10.计算:的结果是()
A.±2 B.0 C.±2或0 D.2
11.在下列各题中,结论正确的是()
A.若a>0,b<0,则>0 B.若a>b,则a﹣b>0
C.若 a<0,b<0,则ab<0 D.若a>b,a<0,则<0 12.下列说法:
①若|a|=a,则a=0;
②若a,b互为相反数,且ab≠0,则=﹣1;
③若a2=b2,则a=b;
④若a<0,b<0,则|ab﹣a|=ab﹣a.
其中正确的个数有()
A.1个B.2个C.3个D.4个
二.填空题(共10小题)
13.﹣的倒数= .
14.若a≠b,且a、b互为相反数,则= .
15.若a、b是互为倒数,则2ab﹣5= .
16.已知﹣的倒数是p,且m、n互为相反数,则p+m+n= .17.如果一个数的倒数是3,那么这个数的相反数是.
18.计算:﹣9÷×= .
19.被除数是﹣5,除数是﹣,则商是.
20.有理数的除法法则,除以一个数等于乘以这个数的.
21.若=2, =6,则= .
22.若a,b互为倒数,则a2b﹣(a﹣2017)值为.
三.解答题(共4小题)
23.计算:
(1)100÷×(﹣8);
(2).
24.小华在课外书中看到这样一道题:
计算:()+().
她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,她顺利地解答了这道题
(1)前后两部分之间存在着什么关系?
(2)先计算哪部分比较简便?并请计算比较简便的那部分.
(3)利用(1)中的关系,直接写出另一部分的结果.
(4)根据以上分析,求出原式的结果.
25.如图,小明有4张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题.
(1)从中取出2张卡片,使这2张卡片上数字的乘积最大,如何抽取?最大值是多少?(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?
26.若a、b、c都不等于0,且++的最大值是m,最小值是n,求m+n的值.
参考答案与试题解析
一.选择题(共12小题)
1.
【解答】解:8的倒数是,
故选:D.
2.
【解答】解:﹣与﹣3互为倒数,
∴a=﹣.
故选:B.
3.
【解答】解:∵1×1=1,(﹣1)×(﹣1)=1,
∴一个数和它的倒数相等的数是±1.
故选:C.
4.
【解答】解:A、负数有倒数,例如﹣1的倒数是﹣1,选项错误;
B、正数的倒数不一定比自身小,例如0.5的倒数是2,选项错误;
C、0没有倒数,选项错误;
D、﹣1的倒数是﹣1,正确.
故选:D.
5.
【解答】解:①相反数等于本身的数是0,故①符合题意,
②绝对值等于本身的是非负数,故②不符合题意,
③倒数等于本身的数是±1,故③符合题意,
故选:B.
6.
【解答】解:A、4和﹣4互为相反数,此选项不符合题意;
B、﹣2和﹣互为倒数,此选项符合题意;
C、﹣3和不是互为倒数,此选项不符合题意;
D、0没有倒数,此选项不符合题意;
故选:B.
7.
【解答】解:﹣的倒数与m+4互为相反数,得
m+4=2,
解得m=﹣2,
故选:D.
8.
【解答】解:(﹣18)÷9=﹣2.
故选:C.
9.
【解答】解:根据题意,ab<0,则a、b异号,
a+b>0可得,正数的绝对值较大,
但无法确定a、b哪个为正,哪个为负,
故选:C.
10.
【解答】解:当a>0,b>0时, +=+=2,
当a>0,b<0时, +=+=0,
当a<0,b<0时, +=+=﹣2,
当a<0,b>0时, +=+=0,
故选:C.
11.
【解答】解:A、两数相除,异号得负,故选项错误;
B、大数减小数,一定大于0,故选项正确;
C、两数相乘,同号得正,故选项错误;
D、若a>b,a<0,则>0,故选项错误.
故选:B.
12.
【解答】解:①若|a|=a,则a=0或a为正数,错误;
②若a,b互为相反数,且ab≠0,则=﹣1,正确;
③若a2=b2,则a=b或a=﹣b,错误;
④若a<0,b<0,所以ab﹣a>0,
则|ab﹣a|=ab﹣a,正确;
故选:B.
二.填空题(共10小题)
13.
【解答】解:﹣的倒数是:﹣5.
故答案为:﹣5.
14.
【解答】解:∵a、b互为相反数,
∴a=﹣b.
∴.
故答案为:﹣1.
15.
【解答】解:∵a、b是互为倒数,
∴ab=1,
∴2ab﹣5=﹣3.
故答案为:﹣3.
16.
【解答】解:依题意的:p=﹣,m+n=0,
所以p+m+n=﹣.
故答案是:﹣.
17.
【解答】解:的倒数是3,
的相反数是﹣.
故答案为:﹣.
18.
【解答】解:原式=﹣9××=﹣4,
故答案为:﹣4.
19.
【解答】解:﹣5=﹣×(﹣)=6,故答案为:6.
20.
【解答】解:有理数的除法法则,除以一个数等于乘以这个数的倒数,故答案为:倒数
21.
【解答】解:∵=2, =6,
∴a=2b,c=,
∴=12,
故答案为12.
22.
【解答】解:∵a,b互为倒数,
∴ab=1,
∴a2b﹣(a﹣2017)
=ab•a﹣(a﹣2017)
=a﹣a+2017
=2017.
故答案为:2017.
三.解答题(共4小题)
23.
【解答】解:(1)100÷×(﹣8)
=100×8×(﹣8)
=800×(﹣8)
=﹣6400
(2)
=﹣16×(20﹣)
=﹣320+1
=﹣319
24.
【解答】解:(1)前后两部分互为倒数;
(2)先计算后一部分比较方便.
()=()×36=9+3﹣14﹣1=﹣3;
(3)因为前后两部分互为倒数,所以()=﹣;
(4)根据以上分析,可知原式==﹣3.
25.
【解答】解:(1)抽﹣3和﹣5,
最大值为:﹣3×(﹣5)=15;
(2)抽1和﹣5,
最小值为:(﹣5)÷1=﹣5;
26.
【解答】解:由题知,,
依次计算++可知m=3,n=﹣3,
所以m+n=3+(﹣3)=3﹣3=0.。
