2010年上海市松江区中考数学二模卷及答案
2010年上海市中考数学二模卷及答案

中考数学一.选择题(本大题共10个小题,每小题4分,共40分)1.-2的相反数是 ( ) (A )1/2 (B )-1/2 (C )-2 (D )22.如果t>0,那么a+t 与a 的大小关系是 ( )(A )a+t >a (B )a+t <a (C )a+t ≥a (D )不能确定 3.若∠A =34°,则∠A 的余角的度数为 ( )(A )54° (B )56° (C )146° (D )66° 4.下列交通标志图中,属于轴对称图形的是 ( )5.△ABC 中,∠C =90°,BC =5,AB =13,则sin A 的值是 ( )(A )135 (B )1312 (C )125 (D )5126.如果两圆的半径长分别为2cm 和5cm ,圆心距为8cm ,那么这两个圆的位置关系是( )(A )内切 (B )外切 (C )相交 (D )外离7.下列调查,比较容易用普查方式的是 ( ) (A )了解嘉兴市居民年人均收入 (B )了解嘉兴市初中生体育中考的成绩 (C )了解嘉兴市中小学生的近视率 (D )了解某一天离开嘉兴市的人口流量8.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( ) (A )小明的影子比小强的影子长 (B )小明的影长比小强的影子短 (C )小明的影子和小强的影子一样长 (D )无法判断谁的影子长9.图1所示的电路的总电阻为10Ω,若R 1=2R 2,则R 1,R 2( )(A)R 1=30Ω,R 2=15Ω (B )R 1=203Ω,R 2=103Ω(C )R 1=15Ω,R 2=30Ω (D )R 1=103Ω,R 2=203Ω10.若用(1)、(2)、(3)、(4)四幅图象分别表示变量之间的关系, ( )(1) (2) (3) (4) 请按图象所给顺序,将下面的(a )、(b )、(c )、(d )对应排序 (a )小车从光滑的斜面上滑下(小车的速度与时间的关系)(b )一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物的重量的关系) (c )运动员推出去的铅球(铅球的高度与时间的关系)(d )小杨从A 到B 后,停留一段时间,然后按原速度返回(路程与时间的关系)正确的顺序是 ( ). A.(c )(d )(b )(a ) B.(a )(b )(c )(d ) C.(b )(c )(a )(d ) D.(d )(a )(c )(b )图1二.填空题(每小题5分,共30分)11.函数y=3-x 中自变量x 的取值范围是 。
2010上海各区中考二模数学压轴25题解析

2010上海各区二模数学压轴25题解析1、(松江)解:1(1)∵90=Ð=ÐFEB DEC ,∴BEC DEF Ð=Ð…………11分∵90=Ð+Ð=Ð+ÐDCP BCE DCP EDF ,…………………………,…………………………11分∴BCE EDF Ð=Ð,∴△DEF ∽△CEB ……………………………………………………………………11分(2)∵PDC Rt D 中,CP DE ^,∴90=Ð=ÐCED CDP ∴△DEC ∽△PDC ,∴DC PDECDE=………………………………………………………………………………11分∵△DEF ∽△CEB ,∴DCDF CBDF ECDE ==……………………………………………………………………11分∴DCDF DCPD =,∴DF PD =………………………………………………………………………………………………11分∵AP =x ,DF =y ,∴,1x PD -=∴x y -=1…………………………………………………………11分)10(<<x ……………………………………………………………………………………………………………………………………11分(3)∵△DEF ∽△CEB ,∴22CBDF S S CEBDEF =D D (1)……………………………………………………11分∵CFDF S S CEFDEF =D D (2),∴(1)¸(2)得2CBCF DF S S CEBcEF ×=D D …………………………11分又∵EFC BECS SD D =4,∴412=×=D D CB CFDF S S CEBcEF …………………………………………………………11分当P 点在边DA 上时,有411)1(=×-xx ,解得21=x ………………………………………………………………………………………………22分当P 点在边DA 的延长线上时,411)1(=×+xx ,解得212-=x …………………………………………………………………………………………11分2、(浦东)解:(1)在矩形ABCD 中,中,∵AD ∥BC ,∴∠APB =∠DAP .又由题意,得∠QAD =∠DAP ,∴∠APB =∠QAD .∵∠B =∠ADQ =90°,∴△ADQ ∽△PBA .………………………………(1分)∴BPAD ABDQ =,即443+=x y .∴412+=x y .………………………………………………………………(1分)定义域为0>x .……………………………………………………………(1分)(2)不发生变化.…………………………………………………………………(1分) 证明如下:证明如下:∵∠QAD =∠DAP ,∠ADE =∠ADQ =90°,AD =AD , ∴△ADE ≌△ADQ .∴DE =DQ =y .………………………………………………………………(1分)∴124124482121=+++=×+×=+=D D x x x PC QE AD QE S S S PQE AQE .…(3分)(3)过点Q 作QF ⊥AP 于点F .∵以4为半径的⊙Q 与直线AP 相切,∴QF =4.…………………………(1分) ∵12=S ,∴AP =6.………………………………………………………(1分)分) 在Rt △ABP 中,中,∵AB =3,∴∠BPA =30°.…………………………………………………(1分) ∴∠PAQ =60°.°. ∴AQ =338.………………………………………………………………(1分)分)设⊙A 的半径为r .∵⊙A 与⊙Q 相切,∴⊙A 与⊙Q 外切或内切.外切或内切.(i )当⊙A 与⊙Q 外切时,AQ =r +4,即338=r +4.∴r =4338-.………………………………………………………………(1分)(ii )当⊙A 与⊙Q 内切时,AQ =r -4,即338=r -4.∴r =4338+.………………………………………………………………(1分)综上所述,⊙A 的半径为4338-或4338+.3、(长宁)(1)由题意知由题意知 ∠COB = 90°B(8,0) OB=8 在Rt △OBC 中tan ∠ABC = 21OBOC = OC= O B ×tan tan∠∠ABC = 8ABC = 8××21=4 =4 ∴∴C(0,4) …1分 8OC AB 21S ABC =×=D ∴AB = 4 A(4,0)………………………1分 把A 、B 、C 三点的坐标带入)0(2>++=a c bx ax y 得 ïîïíì==++=++408640416c c b a c b a解得解得ïîïíì=-==42381c b a ……………………………………….2分 所以抛物线的解析式为423812+-=x x y 。
2010年上海数学各区二模试卷填空选择部分答案

2010年上海各区二模试卷答案填空选择部分 奉贤区:一 、选择题:(本大题共8题,满分24分)1.D ; 2.B ; 3.A ; 4.B ; 5.D ; 6.D ; 二、填空题:(本大题共12题,满分48分)7.2±; 8.)2)(22-+m m (1; 9.4; 10.0=x ; 11.3-; 12.1=y ; 13.201; 14.面ABFE 和面DCGH ; 15.1︰4; 16.21; 17.6; 18.10或310; 虹口区:一、选择题:(本大题共6题,满分24分)1.C ; 2.C ; 3.D ; 4.B ; 5.D ;6.D . 二、填空题:(本大题共12题,满分48分)7.21x - ; 8.1; 9.2x =-; 10.1x ≠;11.增大; 12.(1,2)--; 13.23200(1)2500x -=; 14.13; 15.70°; 16.1:2; 17.24; 18.25或23.黄浦区:一、选择题1、D ;2、B ;3、D ;4、C ;5、B ;6、A .二、填空题7、1-x ; 8、x ≤-1<2; 9、()()11-+++y x y x ; 10、2±;11、21; 12、()7,2-; 13、0,12; 14、2-; 15、132; 16、3232+; 17、6; 18、0.8.金山区:一.选择题:(本大题共6题,满分24分)1. B ; 2.B ; 3.C ; 4.A ; 5.C ; 6.D . 二.填空题:(本大题共12题,满分48分)7.()2x x -; 8.3a =-; 9.略; 10.1x ≠; 11.6a b -;12.18; 13.8; 14.110°; 15.1∶16;16. 17.略; 18.1。
静安区:一、选择题:(本大题共6题,每题4分,满分24分) 1.C ; 2.B ; 3.D ; 4.D ; 5.A ; 6.A . 二.填空题:(本大题共12题,满分48分) 7.2; 8.253+; 9.2=x ; 10.43,43-=-=-y x y x ; 11.32≤a ; 12.x y 45=; 13.94; 14.BF ; 15.163; 16.2--; 17.31; 18.37π. 卢湾区:一、选择题(本大题共6题,每题4分,满分24分)1. C ; 2. A ; 3.B ; 4.D ; 5.B ; 6.C .二、填空题(本大题共12题,每题4分,满分48分)7. 2-; 8.9.49; 10.22(1)x -;11. 321y y-=;12. 4; 13.24y x =--; 14.232y x =-+;15.13a b + ; 16; 17.15 ; 18. 15或105.闵行区:一、选择题:(共6题,每题4分,满分24分) 1.B ; 2.C ; 3.D ; 4.A ; 5.B ; 6.C .二、填空题:(共12题,每题4分,满分48分) 7.69a ; 8.32x >; 9.x = 4; 10.2; 11.-2; 12.-5; 13.下降; 14.13;15.b a -; 16.24; 17.AD = BC 或AB // CD 或∠A =∠C 等,正确即可;18.3.浦东新区:一、选择题:(本大题共6题,每题4分,满分24分) 1.B ; 2.D ; 3.C ; 4.C ; 5.A ; 6.D .二、填空题:(本大题共12题,每题4分,满分48分)7.4; 8.()()222+-x x ; 9.1-=x ; 10.12-; 11.41≤m ; 12.23-; 13.30 %; 14.a m -2; 15.33 ; 16.6; 17.4; 18.(2-,6).普陀区:1.(A) ; 2.(B) ; 3.(C); 4.(D) ; 5.(C) ; 6.(B) .二、填空题:(本大题共12题,每题4分,满分48分)7. 45a ; 8. 34.310-⨯; 9. 1; 10. 25x -<<; 11. c =0; 12. ;13.2x ≠; 14.23y x =+; 15. 30; 16.AB =CD 等; 17.5 ; 18. 9.青浦区:一、选择题:(本大题共6题,每题4分,满分24分) 1.(B );2.(C );3.(D );4.(C );5.(B );6.(B ). 二、填空题:(本大题共12题,每题4分,满分48分)7.2-π;8.2≤x ;9.1->x ;10.2=x ;11.)1)(2(-+a a a ;12.1<k 且0≠k ; 13.二;14.21;15.4.2:1;16.-3;17.10;18. 65或25. 松江区:一、选择题1、D ;2、C ;3、B ;4、D ;5、A ;6、A 二、填空题7、1-; 8、3≥x ; 9、)1)(1(-+x x x ; 10、5=x ; 11、x y 2-=; 12、a 64.0; 13、51; 14、5; 15、8; 16、4; 17、3132+; 18、52 徐汇区:一、选择题1.B; 2.C; 3.D; 4.C ; 5.A; 6.B . 二、填空题7.)2)(2(-+a a a ; 8.4=x ; 9.9<a ; 10.)3,1(; 11.①③④;12.15)1(5.122=+x ; 13.43; 14.)(21→→-a b ; 15.161; 16.623π-;17.216; 18.5144。
2010年上海市普陀区中考数学二模卷及答案(无水印)

2009学年度第二学期普陀区初三质量调研数学试卷2010.4(时间:100分钟,满分:150分)考生注意:所有答案务必按照规定在答题纸上完成,写在试卷上不给分一、单项选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上] 1 ).(A)(B) ; (C) ; (D) .2. 两条对角线互相垂直平分的四边形是………………………………………………( ).(A) 等腰梯形; (B) 菱形; (C) 矩形; (D) 平行四边形.3.下列条件中,能判定两个等腰三角形相似的是……………………………………( ). (A )都含有一个30°的内角; (B )都含有一个45°的内角; (C )都含有一个60°的内角; (D )都含有一个80°的内角. 4.如果一元二次方程220x x k -+=有两个不相等的实数根,那么k 的取值范围是( ).(A) 1k ≥; (B) 1k ≤; (C) 1k >; (D) 1k <.5.如右图,△ABC 中,D 是边BC 的中点,BA a = ,AD b = ,那么BC等于…( ).(A )a +b ; (B )12(a +b );(C )2(a +b ); (D )—(a +b).6. 气象台预报“本市明天降水概率是80%”,对此消息,下面几种说法正确的是…( ).(A) 本市明天将有80%的地区降水; (B) 明天降水的可能性比较大; (C) 本市明天降有80%的时间降水; (D) 明天肯定下雨.二、填空题:(本大题共12题,每题4分,满分48分)[请将结果直接填入答题纸的相应位置] 7.计算:23(2)a a ⋅= .8.生物学家发现一种病毒的长度约为0.0043mm ,用科学记数法表示为 = mm . 9.当a=2时,1a -= .AD B 第5题10.不等式组24,50x x >-⎧⎨-<⎩的解集是 .11.一元二次方程20(0)ax bx c a ++=≠有一根为零的条件是 . 12.将图形(右)绕中心旋转180°后的图形是 (画出图形). 13.函数y =的定义域是 . 14. 已知一次函数3y kx =+的图像与直线2y x =平行,那么此一次函数的解析式为 . 15.梯形ABCD 中,AD ∥BC ,如果∠A=5∠B ,那么∠B= 度.16. 在四边形ABCD 中,如果AB ∥CD ,AB=BC ,要使四边形ABCD 是菱形,还需添加一个条件,这个条件可以是 .17.如果一斜坡的坡度为i =110米,那么物体升高了米.18.中心角是40°的正多边形的边数是 .三、解答题(本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分, 满分78分) 19.化简:1(1)11a a a -÷++.20.解方程组:2224,2 1.x y x xy y +=⎧⎨-+=⎩第12题第21题21.如图,在平行四边形ABCD 中,点G 是BC 延长线上一点,AG 与BD 交于点E ,与DC 交于点F ,如果AB=m ,CG =12BC , 求:(1)DF 的长度;(2)三角形ABE 与三角形FDE 的面积之比.22. 如图所示,已知在△ABC 中,AB=AC ,AD 是∠BAC的平分线,交BC 于点D ,AN 是△ABC 外角∠CAM 的平分线,CE ⊥AN ,垂足为点E , (1)求证:四边形ADCE 是矩形;(2)当△ABC 满足什么条件时,四边形ADCE 是一个 正方形?请加以证明.23. 为了引导学生树立正确的消费观,某机构随机调查了一所小学100名学生寒假中使用零花钱的情况(钱数取整数元),根据调查制成了频率分布表,如下: (1) 补全频率分布表;(2) 使用零化钱钱数的中位数在第 组; (3) 此机构认为,应对消费200元以上的学生提出 勤俭节约的建议,那么应对该校800名学生中约 名学生提出此项建议.A B C D E MN 第22题24. 如图,在平面直角坐标系中,点O为原点,已知点A的坐标为(2,2),点B、C在x轴上,BC=8,AB=AC,直线AC与y轴相交于点D.1)求点C、D的坐标;2)求图象经过B、D、A三点的二次函数解析式及它的顶点坐标.25.如图,已知Sin∠ABC=13,⊙O的半径为2,圆心O在射线BC上,⊙O与射线BA相交于E、F两点,EF=(1)求BO的长;(2)点P在射线BC上,以点P为圆心作圆,使得⊙P同时与⊙O和射线BA相切,求所有满足条件的⊙P的半径.BC上D CFA B O第25题EG2009学年度第二学期普陀区九年级质量调研数学试卷参考答案及评分说明一、单项选择题:(本大题共6题,每题4分,满分24分)1.(A) ; 2.(B) ; 3.(C); 4.(D) ; 5.(C) ; 6.(B) .二、填空题:(本大题共12题,每题4分,满分48分)7. 45a ; 8. 34.310-⨯; 9. 1; 10. 25x -<<; 11. c =0; 12. ;13.2x ≠; 14.23y x =+; 15. 30; 16.AB =CD 等; 17.5 ; 18. 9. 三、解答题(本大题共7题,其中第19---22题每题10分,第23、24题每题12分,第25题14分,满分78分) 19.解: 原式=1()(1)11a a a a a +-+++ …………………………………………………………4′(各2分) =(1)a a -+ …………………………………………………………………………………2′ =1a a -- ……………………………………………………………………………………2′=1-. ………………………………………………………………………………………2′ 20.2224,(1)2 1.(2)x y x xy y +=⎧⎨-+=⎩解: 由(2)式得到:2()1x y -=,…………………………………………………………………………1′ 再得到 1x y -=或者1x y -=-,……………………………………………………………1′与(1)式组成方程组:24,1.x y x y +=⎧⎨-=⎩或24,1.x y x y +=⎧⎨-=-⎩……………………………………………3′解得:112,1.x y =⎧⎨=⎩,222,35.3x y ⎧=⎪⎪⎨⎪=⎪⎩……………………………………………………………………4′经检验,原方程组的解是:112,1.x y =⎧⎨=⎩,222,35.3x y ⎧=⎪⎪⎨⎪=⎪⎩……………………………………………1′21.解:(1)∵四边形ABCD 是平行四边形,∴AB=CD=m ,AB ∥CD . ………………………………2′∵CG =12BC , ∴CG =13BG ,………………………………………………1′∵AB ∥CD ,∴CF CGAB BG=.…………………………………………………………………………………1′ ∴13CF m =, …………………………………………………………………………………1′∴23DF m =.…………………………………………………………………………………1′(2)∵AB ∥CD ,∴△ABE ∽△FDE ,………………………………………………………………………………2′ ∴239()24ABE FDE S S ∆∆==. …………………………………………………………………………2′ ∴ 三角形ABE 与三角形FDE 的面积之比为9∶4.22.证明:(1) ∵AB=AC ,AD 是∠BAC 的平分线,∴AD ⊥BC , ………………………………………1′ ∴∠ADC =90°.∵AD 是∠BAC 的平分线,∴∠1=12∠BAC ,…………………………………1′ 同理:∠2=12∠MAC .…………………………………1′∵∠BAC +∠MAC=180°. ∴∠1+∠2=90°.即∠EAD =90°. …………………………………1′∵CE ⊥AN , ∴∠AEC =90°. …………………………………1′ ∴四边形ADCE 是矩形.…………………………1′(2)当△ABC 是等腰直角三角形时,四边形ADCE 是一个正方形.……………………………1′ 证明:∵∠BAC =90°,AB=AC ,AD 是∠BAC 的平分线,∴AD 是斜边BC 上的中线,∴AD=DC .……………………………………………………………………………………1′∵四边形ADCE 是矩形, …………………………………………………………………1′∴四边形ADCE 是正方形.…………………………………………………………………1′23.解:(1)见右,每个数1分,共8分;A B CD EM N第22题12(2) 3;…………………………………………2′ (3)120.…………………………………………2′24.解:(1)过点A 作AE ⊥x 轴,垂足为点E .…………1′∵点A 的坐标为(2,2), ∴点E 的坐标为(2,0).……………………1′ ∵AB=AC ,BC =8,∴BE=CE , ……………………………………1′ 点B 的坐标为(-2,0), ……………………1′ 点C 的坐标为(6,0).………………………1′ 设直线AC 的解析式为:y kx b =+(0k ≠),将点A 、C 的坐标代入解析式,得到: 132y x =-+.………………………1′ ∴点D 的坐标为(0,3). …………………1′(2)设二次函数解析式为:2y ax bx c =++(0a ≠), ∵ 图象经过B 、D 、A 三点,∴4230,423 2.a b a b -+=⎧⎨++=⎩…………………………………………………………………………2′解得:1,21.2a b ⎧=-⎪⎪⎨⎪=⎪⎩…………………………………………………………………………1′∴此二次函数解析式为:211322y x x =-++. …………………………………………1′ 顶点坐标为(12,138). ……………………………………………………………………1′25.(1)解:联接EO ,过点O 作OH ⊥BA 于点H . ………………2′∵EF=EH………………………………1′∵⊙O的半径为2,即EO=2,∴OH=1.…………………………………………………1′在Rt△BOH中,∵Sin∠ABC=13,………………………………………1′∴BO=3.…………………………………………………1′(2)当⊙P与直线相切时,过点P的半径垂直此直线.…………………………………………1′(a)当⊙P与⊙O外切时,①⊙P与⊙O切于点D时,⊙P与射线BA相切,…………………………………………………1′Sin∠ABC=113PPrr=-,得到:14Pr=;………………………………………………………1′②⊙P与⊙O切于点G时,⊙P与射线BA相切,Sin∠ABC =133PPrr=+,得到:52Pr=. ……………………………………………………1′(b) 当⊙P与⊙O内切时,①⊙P与⊙O切于点D时,⊙P与射线BA相切,…………………………………………………1′Sin∠ABC =113PPrr=+,得到:12Pr=;…………………………………………………1′②⊙P与⊙O切于点G时,⊙P与射线BA相切,Sin∠ABC =153PPrr=-,得到:54Pr=. ………………………………………………………1′综上所述:满足条件的⊙P的半径为14、52、12、54.……………………………………………1′。
上海市松江区中考数学二模试卷(含解析)

2016年上海市松江区中考数学二模试卷一、选择题1.下列各数是无理数的是()A.B.C.D.162.下列式子中,属于最简二次根式的是()A.B.C.D.3.在平面直角坐标系中,直线y=x﹣1经过()A.第一、二、三象限 B.第一、二、四象限C.第一、三、四象限 D.第二、三、四象限4.某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是()A.27,25 B.25,27 C.27,27 D.27,305.如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是()A.AC⊥BD B.AB=AC C.∠ABC=90°D.AC=BD6.已知⊙O1的半径r1=6,⊙O2的半径为r2,圆心距O1O2=3,如图⊙O1与⊙O2有交点,那么r2的取值范围是()A.r2≥3 B.r2≤9 C.3<r2<9 D.3≤r2≤9二、填空题7.因式分解:2a2﹣3a=______.8.函数的定义域是______.9.计算:2(﹣)+3=______.10.关于x的一元二次方程x2﹣2x+m=0有两个实数根,则m的取值范围是______.11.不等式组:的解集为______.12.将抛物线y=x2﹣2向左平移3个单位长度,再向上平移2个单位长度,所得的抛物线的解析式为______.13.反比例函数y=的图象经过点(﹣1,2),A(x1,y1),B(x2,y2)是图象上另两点,其中x1<x2<0,则y1、y2的大小关系是______.14.用换元法解分式方程时,如果设,将原方程化为关于y的整式方程,那么这个整式方程是______.15.某服装厂从20万件同类产品中随机抽取了100件进行质检,发现其中有2件不合格,那么你估计该厂这20万件产品中合格品约为______万件.16.从1到10的十个自然数中,随意取出一个数,该数为3的倍数的概率是______.17.某商品原价289元,经连续两次降价后售价为256元,设平均每次降价的百分率为x,那么根据题意可列关于x的方程是______.18.如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE 沿着直线CE翻折,点B恰好与D点重合,则BE=______.三、解答题19.计算:()﹣2+(π﹣3.14)0+.20.解方程组:.21.已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示﹣40℃与﹣40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐.(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)当华氏温度为104℉时,温度表上摄氏温度为多少?22.如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于D,O为AD上一点,以O为圆心,OA 为半径的圆交AB于G,交BC于E、F.且AG=AD.(1)求EF的长;(2)求tan∠BDG的值.23.如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.(1)求证:∠CAD=∠ECB;(2)点F是AC的中点,连结DF,求证:BD2=FC?BE.24.如图,平面直角坐标系xOy中,已知B(﹣1,0),一次函数y=﹣x+5的图象与x轴、y 轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B.(1)求这个二次函数的解析式;(2)点P是该二次函数图象的顶点,求△APC的面积;(3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标.25.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上.(1)求线段CF的长;(2)如图2,当点M在线段FE上,且AM⊥MN,设FM?cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域;(3)如果△AMN为等腰直角三角形,求线段FM的长.2016年上海市松江区中考数学二模试卷参考答案与试题解析一、选择题1.下列各数是无理数的是()A.B.C.D.16【考点】无理数.【分析】根据无理数是无限不循环小数,可得答案.【解答】解:A、是有理数,故A错误;B、是无理数,故B正确;C、是有理数,故C错误;D、16是有理数,故D错误;故选:B.2.下列式子中,属于最简二次根式的是()A.B.C.D.【考点】最简二次根式.【分析】根据最简二次根式是被开方数不含分母,被开方数不含开的尽的因数或因式,可得答案.【解答】解:A、被开方数含分母,故A错误;B、被开方数含开的尽的因数,故B错误;C、被开方数含开的尽的因数,故C错误;D、被开方数不含分母,被开方数不含开的尽的因数或因式,故D正确;故选:D.3.在平面直角坐标系中,直线y=x﹣1经过()A.第一、二、三象限 B.第一、二、四象限C.第一、三、四象限 D.第二、三、四象限【考点】一次函数图象与系数的关系.【分析】根据k,b的符号判断直线所经过的象限.【解答】解:由已知,得:k=1>0,b=﹣1<0,故图象经过第一、三、四象限.故选C.4.某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是()A.27,25 B.25,27 C.27,27 D.27,30【考点】众数;中位数.【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.【解答】解:在这一组数据中27是出现次数最多的,故众数是27;将这组数据从小到大的顺序排列后,处于中间位置的那个数是27,这组数据的中位数是27.故选C5.如图,已知四边形ABCD是平行四边形,要使它成为菱形,那么需要添加的条件可以是()A.AC⊥BD B.AB=AC C.∠ABC=90°D.AC=BD【考点】菱形的判定.【分析】根据菱形的判定方法有四种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形,④对角线平分对角,作出选择即可.【解答】解:A、∵四边形ABCD是平行四边形,AC⊥BD,∴平行四边形ABCD是菱形,故本选项正确;B、∵四边形ABCD是平行四边形,AB=AC≠BC,∴平行四边形ABCD不是,故本选项错误;C、∵四边形ABCD是平行四边形,∠ABC=90°,∴四边形ABCD是矩形,不能推出,平行四边形ABCD是菱形,故本选项错误;D、∵四边形ABCD是平行四边形,AC=BD∴四边形ABCD是矩形,不是菱形.故选:A.6.已知⊙O1的半径r1=6,⊙O2的半径为r2,圆心距O1O2=3,如图⊙O1与⊙O2有交点,那么r2的取值范围是()A.r2≥3 B.r2≤9 C.3<r2<9 D.3≤r2≤9【考点】圆与圆的位置关系.【分析】由⊙O1的半径r1=6,⊙O2的半径为r2,圆心距O1O2=3,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系,可求得内切时,r2的值,继而求得答案.【解答】解:∵⊙O1的半径r1=6,⊙O2的半径为r2,圆心距O1O2=3,∴若⊙O1与⊙O2内切,则r2=3或r2=9,∵⊙O1与⊙O2有交点,∴r2的取值范围是:3≤r2≤9.故选D.二、填空题7.因式分解:2a2﹣3a= a(2a﹣3).【考点】因式分解-提公因式法.【分析】直接找出公因式a,提取公因式得出答案.【解答】解:2a2﹣3a=a(2a﹣3).故答案为:a(2a﹣3).8.函数的定义域是x≠1 .【考点】函数自变量的取值范围.【分析】根据分式有意义的条件是分母不为0;分析原函数式可得关系式x﹣1≠0,解可得自变量x的取值范围.【解答】解:根据题意,有x﹣1≠0,解可得x≠1.故答案为x≠1.9.计算:2(﹣)+3= .【考点】*平面向量.【分析】先去括号,然后进行向量的加减即可.【解答】解:2(﹣)+3=2﹣2+3=2+.故答案为:2+.10.关于x的一元二次方程x2﹣2x+m=0有两个实数根,则m的取值范围是m≤1 .【考点】根的判别式.【分析】根据方程有实数根,得出△≥0,建立关于m的不等式,求出m的取值范围即可.【解答】解:由题意知,△=4﹣4m≥0,∴m≤1,故答案为:m≤1.11.不等式组:的解集为x>2 .【考点】解一元一次不等式组.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式﹣x≤0,得:x≥0,解不等式2x﹣4>0,得:x>2,则不等式组的解集为:x>2,故答案为:x>2.12.将抛物线y=x2﹣2向左平移3个单位长度,再向上平移2个单位长度,所得的抛物线的解析式为y=(x+3)2.【考点】二次函数图象与几何变换.【分析】先利用二次函数的性质得到抛物线y=x2﹣2的顶点坐标为(0,﹣2),再根据点平移的规律得到点(0,﹣2)平移后所得对应点的坐标为(﹣3,0),然后根据顶点式写出平移后的抛物线的解析式.【解答】解:抛物线y=x2﹣2的顶点坐标为(0,﹣2),点(0,﹣2)向左平移3个单位长度,再向上平移2个单位长度所得对应点的坐标为(﹣3,0),所以平移后的抛物线的解析式为y=(x+3)2.故答案为y=(x+3)2.13.反比例函数y=的图象经过点(﹣1,2),A(x1,y1),B(x2,y2)是图象上另两点,其中x1<x2<0,则y1、y2的大小关系是y1<y2.【考点】反比例函数图象上点的坐标特征.【分析】先代入点(﹣1,2)求得k的值,根据k的值判断此函数图象所在的象限,再根据x1<x2<0判断出A(x1,y1)、B(x2,y2)所在的象限,根据此函数的增减性即可解答.【解答】解:∵反比例函数y=的图象经过点(﹣1,2),∴k=﹣2,∴此函数的图象在二、四象限,在每一象限内y随x的增大而增大,∵x1<x2<0,∴A(x1,y1)、B(x2,y2)两点均位于第二象限,∴y1<y2.故答案为:y1<y2.14.用换元法解分式方程时,如果设,将原方程化为关于y的整式方程,那么这个整式方程是y2+y﹣3=0 .【考点】换元法解分式方程.【分析】根据题意,设=y,则=,代入分式方程,整理可得整式方程.【解答】解:由题意,设=y,则=,∴原方程化为:y﹣+1=0,∴整理得:y2+y﹣3=0.故答案为y2+y﹣3=0.15.某服装厂从20万件同类产品中随机抽取了100件进行质检,发现其中有2件不合格,那么你估计该厂这20万件产品中合格品约为19.6 万件.【考点】用样本估计总体.【分析】抽取的100件进行质检,发现其中有2件不合格,那么合格的有98件,由此即可求出这类产品的合格率是98%,然后利用样本估计总体的思想,即可知道合格率是98%,即可求出该厂这20万件产品中合格品的件数.【解答】解:∵某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有2件不合格,∴合格的有98件,∴合格率为98÷100=98%,∴估计该厂这20万件产品中合格品约为20×98%=19.6万件.故答案为:19.6.16.从1到10的十个自然数中,随意取出一个数,该数为3的倍数的概率是.【考点】概率公式.【分析】由从1到10的十个自然数中,是3的倍数的有3,6,9,直接利用概率公式求解即可求得答案.【解答】解:∵从1到10的十个自然数中,是3的倍数的有3,6,9,∴随意取出一个数,该数为3的倍数的概率是:.故答案为:.17.某商品原价289元,经连续两次降价后售价为256元,设平均每次降价的百分率为x,那么根据题意可列关于x的方程是289(1﹣x)2=256 .【考点】由实际问题抽象出一元二次方程.【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),本题可参照增长率问题进行计算,如果设平均每次降价的百分率为x,可以用x表示两次降价后的售价,然后根据已知条件列出方程.【解答】解:根据题意可得两次降价后售价为289(1﹣x)2,即方程为289(1﹣x)2=256.故答案为:289(1﹣x)2=256.18.如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE 沿着直线CE翻折,点B恰好与D点重合,则BE= .【考点】翻折变换(折叠问题);梯形.【分析】如图作DM⊥BC于M,先证明四边形ABMD是矩形,在RT△DMC中求出DM,再在△AED 中利用勾股定理即可解决问题.【解答】解:如图作DM⊥BC于M.∵∠A=∠B=∠DMB=90°,∴四边形ABMD是矩形,∴AD=BM=2,AB=DM,∵BC=CD=5,在RT△DMC中,∵CM=BC﹣BM=3,CD=5,∴DM=AB===4,设BE=DE=x,在RT△AED中,∵AE2+AD2=ED2,∴(4﹣x)2+22=x2,∴x=,∴BE=,故答案为.三、解答题19.计算:()﹣2+(π﹣3.14)0+.【考点】实数的运算;零指数幂;负整数指数幂.【分析】根据实数的运算顺序,首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.【解答】解:()﹣2+(π﹣3.14)0+=9﹣(﹣1)+1+×2=9+1+1+=11.20.解方程组:.【考点】高次方程.【分析】首先把第二个方程左边分解因式,即可转化为两个一次方程,分别与第一个方程,即可组成方程组,即可求解.【解答】解:由(2)得(x﹣y)(x﹣2y)=0.∴x﹣y=0或x﹣2y=0.原方程组可化为解这两个方程组,得原方程组的解为另解:由(1)得x=12﹣2y.(3)把(3)代入(2),得(12﹣2y)2﹣3(12﹣2y)y+2y2=0.整理,得y2﹣7y+12=0.解得y1=4,y2=3.分别代入(3),得x1=4,x2=6.∴原方程组的解为21.已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示﹣40℃与﹣40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐.(1)求y关于x的函数关系式(不需要写出函数的定义域);(2)当华氏温度为104℉时,温度表上摄氏温度为多少?【考点】一次函数的应用.【分析】(1)设y关于x的函数关系式为y=kx+b,根据给定两组数据得出关于k和b的二元一次方程组,解方程组即可得出结论;(2)将y=104带入(1)得出的函数关系式中,得出关于x的一元一次方程,解方程即可得出结论.【解答】解:(1)设y关于x的函数关系式为y=kx+b,由已知得:,解得:.故y关于x的函数关系式为y=x+32.(2)令y=104,则有x+32=104,解得:x=40.故当华氏温度为104℉时,温度表上摄氏温度为40℃.22.如图,在△ABC中,AB=AC=10,BC=12,AD⊥BC于D,O为AD上一点,以O为圆心,OA 为半径的圆交AB于G,交BC于E、F.且AG=AD.(1)求EF的长;(2)求tan∠BDG的值.【考点】相似三角形的判定与性质;勾股定理;圆周角定理;解直角三角形.【分析】(1)连接AF,GE,根据等腰三角形的性质得到BD=CD=BC=6,由勾股定理得到AG=AD==8,根据相似三角形的性质列方程即可得到结论;(2)作GH⊥BC于H,推出AD∥GH,由相似三角形的性质得到,根据三角形函数的定义即可得到结论.【解答】解:(1)连接AF,GE,∵AD⊥BC,AB=AC,圆心在AD上,∴BD=CD=BC=6,ED=FD,∴BE=CF,∴AG=AD==8,BG=AB﹣AD=2,设BE=CF=x,则BF=BC﹣BE=12﹣x,∵四边形AGEF内接于⊙O,∴∠BEG=∠BAF,∠BGE=∠BFA,∴△BEG∽△BAF,∴,∴x(12﹣x)=20,∴x=2,x=10(不合题意舍去),∴EF=BC﹣2x=8;(2)作GH⊥BC于H,∵D⊥BC,GH⊥BC,∴AD∥GH,∴△BGH∽△BAD,∴,∴tan∠BDG═.23.如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.(1)求证:∠CAD=∠ECB;(2)点F是AC的中点,连结DF,求证:BD2=FC?BE.【考点】相似三角形的判定与性质;等腰三角形的性质.【分析】(1)由三线合一定理可证得∠BAD=∠CAD,由CE⊥AB,得到∠ECB=∠BAD,由等量代换可得结论;(2)根据等腰三角形的性质得到BD=CD,∠B=∠ACD,根据直角三角形斜边上的中线定理证得FD=FC,BD=ED,于是有∠B=∠BED=∠ACD=∠CDF,从而证得△BDE∽△CFD,由相似三角形的性质即可证得结论.【解答】证明:(1)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵CE⊥AB,∴∠ECB=∠BAD=90°﹣∠B,∴∠CAD=∠ECB;(2)∵AB=AC,AD⊥BC,∴BD=CD,∠B=∠ACD,∵CE⊥AB,∴BD=FD,∵F是AC的中点,∴FD=FC,∴∠B=∠BED,∴∠B=∠BED=∠ACD=∠CDF,∴△BDE∽△CFD,∴,∴BD?CD=BE?FC,∴BD2=FC?BE.24.如图,平面直角坐标系xOy中,已知B(﹣1,0),一次函数y=﹣x+5的图象与x轴、y 轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B.(1)求这个二次函数的解析式;(2)点P是该二次函数图象的顶点,求△APC的面积;(3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标.【考点】二次函数综合题.【分析】(1)由一次函数的解析式求出A、C两点坐标,再根据A、B两点坐标求出b、c即可确定二次函数解析式;(2)根据二次函数的解析式求出P点坐标,然后计算三角形APC的面积;(3)分两种情况讨论:①△ABC∽△AOQ,②△ABC∽△AQO.【解答】解:(1)∵一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点,∴A(5,0),C(0,5),∵二次函数y=﹣x2+bx+c的图象经过点A、点B,∴b=4,c=5,∴二次函数的解析式为:y=﹣x2+4x+5.(2)∵y=﹣x2+4x+5=﹣(x﹣2)2+9,∴P(2,9),过点P作PD∥y轴交AC于点D,如图,则D(2,3),∴=15;(3)①若△ABC∽△AOQ,如图,此时,OQ∥BC,由B、C两点坐标可求得BC的解析式为:y=5x+5,∴OQ的解析式为:y=5x,由解得:,∴Q(,);②若△ABC∽△AQO,如图,此时,,∵AB=6,AO=5,AC=,∴AQ=3,∴Q(2,3).综上所述,满足要求的Q点坐标为:Q(,)或Q(2,3).25.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上.(1)求线段CF的长;(2)如图2,当点M在线段FE上,且AM⊥MN,设FM?cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域;(3)如果△AMN为等腰直角三角形,求线段FM的长.【考点】四边形综合题.【分析】(1)过A作AH⊥BC,于是得到AH=CD=6,解直角三角形即可得到结论;(2)过M作MP⊥CD于P,MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,解直角三角形求得MK=2x=PC,NP=y﹣2x,MP=CK=5﹣x=QD,于是得到AQ=8﹣(5﹣x)=3+x,QM=6﹣2x,推出△AMQ∽△PMN,根据相似三角形的性质列方程即可得到结论;(3)①当M在线段EF上时,根据全等三角形的性质和等量代换得到QM=MP,列方程得到6﹣2x=5﹣x,解方程即可得到结论;②当M在FE的延长线上时,根据已知条件得到△AQM≌△MNH,由全等三角形的性质得到AQ=MH,由(2)知FK=x,CK=5﹣x=MH,MK=2x=CH,列方程即可得到结论.【解答】解:(1)过A作AH⊥BC,∴AH=CD=6,∵tan∠ABC=2,∴,∴BH=3,∴CH=AD=8,∴AE=,∴CF=5;(2)过M作MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,在Rt△FMK中,FM?cos∠EFC=FK=x,∵∠EFC=∠B,∴tan∠EFC=2,∴MK=2x=PC,NP=y﹣2x,MP=CK=5﹣x=QD,∴AQ=8﹣(5﹣x)=3+x,QM=6﹣2x,∵∠AMN=90°,∵∠AMQ=∠PMN,∠AQM=∠MPN=90°,∴△AMQ∽△PMN,∴,解得:y=(0≤x≤1);(3)①当M在线段EF上时,∵AM=MN,△AMQ≌△NMP,∴△AMQ≌△NMP,∴QM=MP,∴6﹣2x=5﹣x,∴x=1,∴FM=,②当M在FE的延长线上时,∵∠AMN=90°,∴∠AMQ+∠NMH=∠NMH+∠MNH=90°,∴∠AMQ=∠MNH,在△AMQ与△NMH中,,∴△AQM≌△MNH,∴AQ=MH,由(2)知FK=x,CK=5﹣x=MH,MK=2x,=CH,∴AQ=DH=2x﹣6,∴2x﹣6=5﹣x,∴,∴FM==,。
2010年上海市部分区县中考数学二模答案

2010年松江区初中毕业学业模拟考试数学参考答案及评分标准2010.4一、选择题1、D ;2、C ;3、B ;4、D ;5、A ;6、A 二、填空题7、1-; 8、3≥x ; 9、)1)(1(-+x x x ; 10、5=x ; 11、x y 2-=; 12、a 64.0; 13、51; 14、5; 15、8; 16、4; 17、b a 3132+; 18、52 三、解答题19.解:原式=13133)32(322-++---………………………………5分 =734-……………………………………………………………………5分 20.解:方程两边同乘以)3)(3(-+x x 得:………………………………………1分)3(2)3(2942--++-=x x x x …………………………………………2分整理得:0342=+-x x …………………………………………………2分解得:11=x ,32=x ………………………………………………………3分 经检验:32=x 是原方程的增根;……………………………………………1分 所以,原方程的解为1=x . …………………………………………………1分 21.解:连接AF ,∵AD=AB ,F 是BD 的中点∴AF ⊥BC ,∴︒=∠90AFC …………………………………………………2分 在AFC Rt ∆中,︒=∠90AFC ∵E 是AC 的中点,∴421==AC EF ………………………………………3分 又∵FE ⊥AC ,∴24==CF AF …………………………………………2分 在AFB Rt ∆中,︒=∠90AFB∵2tan ==∠BFAFB ,∴22=BF ,∴102=AB ……………………3分 22.(1)160;0.4;40……3分(2)图略;……2分(3)90~80.……………2分(4)5000………………3分23.(1)证明:∵CE 平分∠BCD 、CF 平分∠GCD∴GCF DCF DCE BCE ∠=∠∠=∠,……………………………………1分∵EF ∥BC ,∴GCF EFC FEC BCE ∠=∠∠=∠,………………………1分 ∴DCF EFC FEC DCE ∠=∠∠=∠,………………………………………1分 ∴OE=OC ,OF=OC ,∴OE=OF ……………………………………………2分 (2)∵点O 为CD 的中点,∴OD=OC ,又OE=OF∴四边形DECF 是平行四边形………………………………………………2分∵CE 平分∠BCD 、CF 平分∠GCD∴DCG DCF BCD DCE ∠=∠∠=∠21,21 ………………………………2分 ∴︒=∠+∠=∠+∠90)21(21DCG BCD DCF DCE ………………………2分即︒=∠90ECF ,∴四边形DECF 是矩形 ………………………………1分24.解:(1)因为直线343+-=x y 分别与x 轴、y 轴交于点A 和点B .由,0=x 得3=y ,0=y ,得4=x , 所以)0,4(A )3,0(B ……………1分 把)0,1(-C )3,0(B 代入c ax ax y +-=42中,得⎩⎨⎧=++=043c a a c , 解得⎪⎩⎪⎨⎧-==533a c …………………………………2分 ∴这个二次函数的解析式为3512532++-=x x y ……………………………1分 527)2(532+--=x y ,P 点坐标为P )527,2( ………………………………1分(2)设二次函数图象的对称轴与直线343+-=x y 交于E 点,与x 轴交于F 点把2-=x 代入343+-=x y 得,23=y , ∴)23,2(E ,∴103923527=-=PE …………………………1分∵PE//OB ,OF=AF , ∴AE BE =∵AD ∥BP ,∴DE PE =,5392==PE PD ……………………………2分(3)∵)23,2(E , ∴25494=+=OE ,∴OE ED > 设圆O 的半径为r ,以PD 为直径的圆与圆O 相切时,只有外切,………1分 ∴251039=-r , 解得:5321=r ,572=r ……………………………3分 即圆O 的半径为532或5725.解:1(1)∵90=∠=∠FEB DEC ,∴BEC DEF ∠=∠……………1分∵90=∠+∠=∠+∠DCP BCE DCP EDF ,…………………………1分 ∴BCE EDF ∠=∠,∴△DEF ∽△CEB …………………………………1分(2)∵PDC Rt ∆中,CP DE ⊥,∴90=∠=∠CED CDP∴△DEC ∽△PDC ,∴DCPDEC DE = ………………………………………1分 ∵△DEF ∽△CEB ,∴DCDFCB DF EC DE ==…………………………………1分 ∴DCDFDC PD =,∴DF PD =………………………………………………1分 ∵AP =x ,DF =y ,∴,1x PD -= ∴x y -=1 ……………………………1分)10(<<x …………………………………………………………………1分(3)∵△DEF ∽△CEB ,∴22CB DF S S CE B DE F =∆∆ (1) …………………………1分 ∵CF DF S S CE F DE F =∆∆(2),∴(1)÷(2)得2CBCFDF S S CE B cE F ⋅=∆∆ ……………1分 又∵E F C B E C S S ∆∆=4,∴412=⋅=∆∆CB CF DF S S CE B cE F ……………………………1分 当P 点在边DA 上时, 有411)1(=⋅-x x ,解得21=x ………………………………………………2分 当P 点在边DA 的延长线上时,411)1(=⋅+x x ,解得212-=x ……………………………………………1分长宁一、选择题(本大题共6题,每题4分,满分24分.) 1.D 2.C 3.A 4.B 5.C 6.D二、填空题(本大题共12题,每题4分,满分48分.填对得4分,填错或不填、多填均得0分) 7. 2 8.1 9.x 5 10. 1 11. b a - 12. 3±≠x 13. 2321+=x y 14. △OAF ,△OED 15.0120-22=+x x (或()12112=+x ,()12111=+++x x x )16.31 17. ()b a +43(或b a 4343+) 18. 30三、解答题:(本大题共7题,满分78分)19.(本题10分)解:︒︒-︒+︒60sin 30sin 260sin 30sin 22=()260sin 30sin ︒-︒ ………4分=22321⎪⎪⎭⎫⎝⎛-=2321- ……………… 4分 =213-(或2123-) …… 2分 20.(本题10分)解:整理(1)\(2)得⎪⎩⎪⎨⎧+>+->335211x x x (2)()()⎪⎩⎪⎨⎧->-+-+>22212121x x⎩⎨⎧<+->22)21(x x …………… 2分⎩⎨⎧<-->121x x …… …….2分∴ 121<<--x …… ……..1分∴不等式组的整数解为-2,-1,0 …….. 3分21.(本题10分)(1)80;…… ………..2分(2)0.05 ;…… …...2分 (3)84;…… ……..3分(4)不合理,初三年级学生的随机样本不能代表该校全体学生。
2010松江初三数学模拟试题答案

2010年松江区初中毕业学业模拟考试数学参考答案及评分标准2010.4一、选择题1、D ;2、C ;3、B ;4、D ;5、A ;6、A二、填空题7、1-; 8、3≥x ; 9、)1)(1(-+x x x ; 10、5=x ; 11、x y 2-=; 12、a 64.0;13、51; 14、5; 15、8; 16、4; 17、b a 3132+; 18、52 三、解答题 19.解:原式=13133)32(322-++---………………………………5分 =734-……………………………………………………………………5分20.解:方程两边同乘以)3)(3(-+x x 得:………………………………………1分 )3(2)3(2942--++-=x x x x …………………………………………2分 整理得:0342=+-x x …………………………………………………2分解得:11=x ,32=x ………………………………………………………3分经检验:32=x 是原方程的增根;……………………………………………1分所以,原方程的解为1=x . …………………………………………………1分21.解:连接AF ,∵AD=AB ,F 是BD 的中点∴AF ⊥BC ,∴︒=∠90AFC …………………………………………………2分 在AFC Rt ∆中,︒=∠90AFC∵E 是AC 的中点,∴421==AC EF ………………………………………3分 又∵FE ⊥AC ,∴24==CF AF …………………………………………2分 在AFB Rt ∆中,︒=∠90AFB ∵2tan ==∠BFAF B ,∴22=BF ,∴102=AB ……………………3分 22.(1)160;0.4;40……3分(2)图略;……2分(3)90~80.……………2分 (4)5000………………3分23.(1)证明:∵CE 平分∠BCD 、CF 平分∠GCD∴GCF DCF DCE BCE ∠=∠∠=∠,……………………………………1分∵EF ∥BC ,∴GCF EFC FEC BCE ∠=∠∠=∠,………………………1分 ∴DCF EFC FEC DCE ∠=∠∠=∠,………………………………………1分 ∴OE=OC ,OF=OC ,∴OE=OF ……………………………………………2分(2)∵点O 为CD 的中点,∴OD=OC ,又OE=OF∴四边形DECF 是平行四边形………………………………………………2分∵CE 平分∠BCD 、CF 平分∠GCD∴DCG DCF BCD DCE ∠=∠∠=∠21,21 ………………………………2分 ∴︒=∠+∠=∠+∠90)21(21DCG BCD DCF DCE ………………………2分 即︒=∠90ECF ,∴四边形DECF 是矩形 ………………………………1分24.解:(1)因为直线343+-=x y 分别与x 轴、y 轴交于点A 和点B . 由,0=x 得3=y ,0=y ,得4=x , 所以)0,4(A )3,0(B ……………1分 把)0,1(-C )3,0(B 代入c ax ax y +-=42中,得 ⎩⎨⎧=++=043c a a c , 解得⎪⎩⎪⎨⎧-==533a c …………………………………2分 ∴这个二次函数的解析式为3512532++-=x x y ……………………………1分 527)2(532+--=x y ,P 点坐标为P )527,2( ………………………………1分 (2)设二次函数图象的对称轴与直线343+-=x y 交于E 点,与x 轴交于F 点 把2-=x 代入343+-=x y 得, 23=y , ∴)23,2(E ,∴103923527=-=PE …………………………1分 ∵PE//OB ,OF=AF , ∴AE BE =∵AD ∥BP ,∴DE PE =,5392==PE PD ……………………………2分 (3)∵)23,2(E , ∴25494=+=OE ,∴OE ED >设圆O 的半径为r ,以PD 为直径的圆与圆O 相切时,只有外切,………1分 ∴251039=-r , 解得:5321=r ,572=r ……………………………3分 即圆O 的半径为532或57 25.解:1(1)∵ 90=∠=∠FEB DEC ,∴BEC DEF ∠=∠……………1分∵90=∠+∠=∠+∠DCP BCE DCP EDF ,…………………………1分 ∴BCE EDF ∠=∠,∴△DEF ∽△CEB …………………………………1分(2)∵PDC Rt ∆中,CP DE ⊥,∴ 90=∠=∠CED CDP ∴△DEC ∽△PDC ,∴DCPD EC DE = ………………………………………1分 ∵△DEF ∽△CEB ,∴DCDF CB DF EC DE ==…………………………………1分 ∴DC DF DC PD =,∴DF PD =………………………………………………1分 ∵AP =x ,DF =y ,∴,1x PD -= ∴x y -=1 ……………………………1分 )10(<<x …………………………………………………………………1分(3)∵△DEF ∽△CEB ,∴22CBDF S S CE B DE F =∆∆ (1) …………………………1分 ∵CF DF S S CE F DE F =∆∆(2),∴(1)÷(2)得2CB CF DF S S CE B cE F ⋅=∆∆ ……………1分 又∵E F C B E C S S ∆∆=4,∴412=⋅=∆∆CB CF DF S S CE B cE F ……………………………1分 当P 点在边DA 上时, 有411)1(=⋅-x x ,解得21=x ………………………………………………2分 当P 点在边DA 的延长线上时,411)1(=⋅+x x ,解得212-=x ……………………………………………1分。
2010上海中考二模真题综合复习一
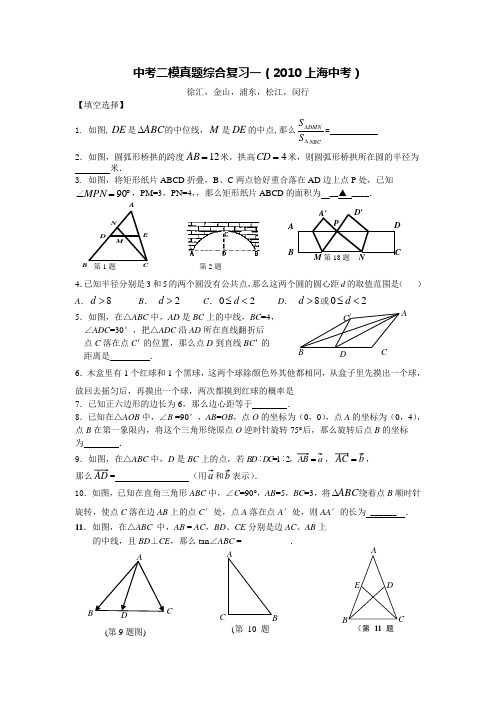
中考二模真题综合复习一(2010上海中考)徐汇,金山,浦东,松江,闵行【填空选择】1. 如图,DE 是ABC ∆的中位线,M 是DE 的中点,那么NBCDMNS S ∆∆= ______2.如图,圆弧形桥拱的跨度12=AB 米,拱高4=CD 米,则圆弧形桥拱所在圆的半径为 米.3. 如图,将矩形纸片ABCD 折叠,B 、C 两点恰好重合落在AD 边上点P 处,已知︒=∠90MPN ,PM=3,PN=4,,那么矩形纸片ABCD 的面积为 __▲ ____.4.已知半径分别是3和5的两个圆没有公共点,那么这两个圆的圆心距d 的取值范围是( ) A .8d > B . 2d > C .02d ≤< D . 8d >或02d ≤< 5.如图,在△ABC 中,AD 是BC 上的中线,BC =4, ∠ADC =30°,把△ADC 沿AD 所在直线翻折后 点C 落在点C ′ 的位置,那么点D 到直线BC ′ 的 距离是 .6.木盒里有1个红球和1个黑球,这两个球除颜色外其他都相同,从盒子里先摸出一个球,放回去摇匀后,再摸出一个球,两次都摸到红球的概率是___________ 7.已知正六边形的边长为6,那么边心距等于 . 8.已知在△AOB 中,∠B =90°,AB =OB ,点O 的坐标为(0,0),点A 的坐标为(0,4),点B 在第一象限内,将这个三角形绕原点O 逆时针旋转75°后,那么旋转后点B 的坐标 为 .9.如图,在△ABC 中,D 是BC 上的点,若B D ︰D C =1︰2,a AB =,b AC =, 那么AD = _____________ (用a 和b 表示).10.如图,已知在直角三角形ABC 中,∠C =90°,AB =5,BC =3,将ABC ∆绕着点B 顺时针旋转,使点C 落在边AB 上的点C ′处,点A 落在点A ′处,则AA ′的长为 ______ . 11.如图,在△ABC 中,AB = AC ,BD 、CE 分别是边AC 、AB 上的中线,且BD ⊥CE ,那么tan ∠ABC =___________.MN E DCB A 第1题第18题D CB A N M P D'A'第2题C /BDCAABCD (第9题图)ABC(第10题ABCDE(第11题【解答题(函数)】 1.(本题满分12分,第(1)、(2)、(3)题各4分)已知:如图,在平面直角坐标系中,点B 在x 轴上,以3为半径的⊙B 与y 轴相切,直线l 过点()2,0A -,且和⊙B 相切,与y 轴相交于点C . (1)求直线l 的解析式;(2)若抛物线2(0)y ax bx c a =++>经过点O 和B,顶点在⊙B 上,求抛物线的解析式; (3) 若点E 在直线l 上,且以A 为圆心,AE 为半径的圆与⊙B 相切,求点E 的坐标.2.(本题满分12分,每小题满分各6分)在直角坐标平面内,O 为原点,二次函数2y x bx c =-++的图像经过A (-1,0)和点B (0,3),顶点为P 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年松江区初中毕业生学业模拟考试数学试卷(满分150分,完卷时间100分钟) 2010.4考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列计算中,正确的是(A )532a a a =+; (B )632a a a =⋅; (C )532)(a a =; (D )222532a a a =+. 2.在方程x 2+xx 312-=3x -4中,如果设y =x 2-3x ,那么原方程可化为关于y 的整式方程是(A )0142=-+y y ; (B )0142=+-y y ;(C )0142=++y y ;(D )0142=--y y .3.如果反比例函数x k y 12-=的图像在每个象限内y 随x 的增大而增大,那么k 的取值范围是 (A )21>k ; (B )21<k ; (C )0>k ; (D )0<k .4.如果将二次函数12-=x y 的图像向左平移2个单位,那么所得到二次函数的图像的解析式是(A )12+=x y ;(B )32-=x y ; (C )1)2(2--=x y ; (D )1)2(2-+=x y .5.下列命题中,正确的是(A )正多边形都是轴对称图形; (B )正多边形都是中心对称图形;(C )每个内角都相等的多边形是正多边形; (D )正多边形的每个内角等于中心角. 6.下列各式错误的是(A )033=-a a ; (B )a a 9)3(3=⨯; (C )a a a 633=+; (D )b a b a 33)(3+=+. 二、填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7.计算:111---x x x =__▲_.8.函数3-=x y 的定义域是__▲__ .9.因式分解:=-x x 3 ▲ . 10.方程21=-x 的解是___▲___ .11.已知正比例函数的图像经过点(2-,4),则正比例函数的解析式是 ▲ . 12.某商品原价a 元,连续两次降价%20后的售价为 ▲ 元.13.在不大于20的正整数中任意取一个正整数能被5整除的概率为 ▲ . 14.在半径为13的圆中,弦AB 的长为24,则弦AB 的弦心距为 ▲ .15.在梯形ABCD 中,AD // BC ,E 、F 分别是两腰AB 、CD 的中点,如果AD = 4,EF = 6,那么BC = __▲__.16.已知一斜坡的坡比3:1=i ,坡面垂直高度为2米,那么斜坡长是 ▲ 米. 17.如图,在△ABC 中,D 是BC 上的点,若BD ︰D C =1︰2,a AB =,b AC =, 那么AD = ▲ (用a 和b 表示).18.如图,已知在直角三角形ABC 中,∠C =90°,AB =5,BC =3,将ABC ∆绕着点B 顺时针旋转,使点C 落在边AB 上的点C ′处,点A 落在点A ′处,则AA ′的长为 ▲ .三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 计算:31)33(27323212021-+++-+--.C(第17题图)ABC(第18题图)20.(本题满分10分)解方程:32321942+--+=-x x x x .21.(本题满分10分)已知:如图,在△ABC 中,D 是BC 上的点,AD=AB ,E 、F 分别是AC 、BD 的中点, 且FE ⊥AC ,若AC=8,2tan =∠B ,求EF 和AB 的长.22.(本题满分10分,第(1)题3分,第(2)题2分,第(3)题2分,第(4)题3分)有关部门想了解本区20000名初中生对世博知识掌握情况,对全区初中生进行世博知识统一测试,在测试结果中随机抽取了400名学生的成绩进行分析,并将分析结果(分数取整数)绘制了如下的频数分布表和频数分布直方图.频数分布表F EDCBA(第21题图)根据以上提供的信息,解答下列问题: (1)补全频数分布表;(2)补全频数分布直方图;(3)样本中学生成绩的中位数位于频数分布表中 ▲ 分数段内; (4)若90分及以上为优秀,请你估计该区有 ▲ 名学生测试成绩为优秀. 23.(本题满分12分,第(1)题5分,第(2)题7分)已知:如图,在四边形ABCD中,点G 在边BC 的延长线上,CE 平分∠BCD 、 CF 平分∠GCD , EF ∥BC 交CD 于点O . (1)求证:OE=OF ; (2)若点O 为CD 的中点,求证:四边形DECF 是矩形.24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(2)小题5分)如图,在平面直角坐标系中,直线343+-=x y 分别与x 轴、y 轴交于点A 和点B .二次函数c ax ax y +-=42的图象经过点B 和点C (-1,0),顶点为P . (1)求这个二次函数的解析式,并求出P 点坐标;(2)若点D 在二次函数图象的对称轴上,且AD ∥BP ,求PD 的长; 为直径的圆与圆O 相切,求圆O 的半径.(第23题图)C40 80 120 160 200 (分)(频数分布直方图25.(本题满分14分,第(1)小题①4分,第(1)小题②5分,第(2)小题5分) 如图,正方形ABCD 中, AB =1,点P 是射线DA 上的一动点, DE ⊥CP ,垂足为E , EF ⊥BE 与射线DC 交于点F .(1)若点P 在边DA 上(与点D 、点A 不重合). ①求证:△DEF ∽△CEB ;②设AP =x ,DF =y ,求y 与x 的函数关系式,并写出函数定义域; (2)当EFC BECS S ∆∆=4时,求AP 的长.2010年松江区初中毕业学业模拟考试数学参考答案及评分标准C2010.4一、选择题1、D ;2、C ;3、B ;4、D ;5、A ;6、A 二、填空题7、1-; 8、3≥x ; 9、)1)(1(-+x x x ; 10、5=x ; 11、x y 2-=; 12、a 64.0; 13、51; 14、5; 15、8; 16、4; 17、b a 3132+; 18、52三、解答题19.解:原式=13133)32(322-++---………………………………5分=734-……………………………………………………………………5分 20.解:方程两边同乘以)3)(3(-+x x 得:………………………………………1分)3(2)3(2942--++-=x x x x …………………………………………2分 整理得:0342=+-x x …………………………………………………2分 解得:11=x ,32=x ………………………………………………………3分 经检验:32=x 是原方程的增根;……………………………………………1分 所以,原方程的解为1=x . …………………………………………………1分 21.解:连接AF ,∵AD=AB ,F 是BD 的中点∴AF ⊥BC ,∴︒=∠90AFC …………………………………………………2分 在AFC Rt ∆中,︒=∠90AFC ∵E 是AC 的中点,∴421==AC EF ………………………………………3分又∵FE ⊥AC ,∴24==CF AF …………………………………………2分 在AFB Rt ∆中,︒=∠90AFB ∵2tan ==∠BFAF B ,∴22=BF ,∴102=AB ……………………3分22.(1)160;0.4;40……3分(2)图略;……2分(3)90~80.……………2分 (4)5000………………3分23.(1)证明:∵CE 平分∠BCD 、CF 平分∠GCD∴GCF DCF DCE BCE ∠=∠∠=∠,……………………………………1分∵EF ∥BC ,∴GCF EFC FEC BCE ∠=∠∠=∠,………………………1分∴DCF EFC FEC DCE ∠=∠∠=∠,………………………………………1分 ∴OE=OC ,OF=OC ,∴OE=OF ……………………………………………2分 (2)∵点O 为CD 的中点,∴OD=OC ,又OE=OF∴四边形DECF 是平行四边形………………………………………………2分∵CE 平分∠BCD 、CF 平分∠GCD ∴DCG DCF BCD DCE ∠=∠∠=∠21,21 ………………………………2分 ∴︒=∠+∠=∠+∠90)21(21DCG BCD DCF DCE ………………………2分即︒=∠90ECF ,∴四边形DECF 是矩形 ………………………………1分 24.解:(1)因为直线343+-=x y 分别与x 轴、y 轴交于点A 和点B .由,0=x 得3=y ,0=y ,得4=x , 所以)0,4(A )3,0(B ……………1分 把)0,1(-C )3,0(B 代入c ax ax y +-=42中,得⎩⎨⎧=++=043c a a c , 解得⎪⎩⎪⎨⎧-==533a c …………………………………2分 ∴这个二次函数的解析式为3512532++-=x x y ……………………………1分 527)2(532+--=x y ,P 点坐标为P )527,2( ………………………………1分 (2)设二次函数图象的对称轴与直线343+-=x y 交于E 点,与x 轴交于F 点把2-=x 代入343+-=x y 得,23=y , ∴)23,2(E ,∴103923527=-=PE …………………………1分∵PE//OB ,OF=AF , ∴AE BE =∵AD ∥BP ,∴DE PE =,5392==PE PD ……………………………2分(3)∵)23,2(E , ∴25494=+=OE ,∴OE ED >设圆O 的半径为r ,以PD 为直径的圆与圆O 相切时,只有外切,………1分 ∴251039=-r , 解得:5321=r ,572=r ……………………………3分即圆O 的半径为532或5725.解:1(1)∵ 90=∠=∠FEB DEC ,∴BEC DEF ∠=∠……………1分∵ 90=∠+∠=∠+∠DCP BCE DCP EDF ,…………………………1分 ∴BCE EDF ∠=∠,∴△DEF ∽△CEB …………………………………1分 (2)∵PDC Rt ∆中,CP DE ⊥,∴ 90=∠=∠CED CDP∴△DEC ∽△PDC ,∴DC PD EC DE = ………………………………………1分∵△DEF ∽△CEB ,∴DCDF CBDF ECDE ==…………………………………1分∴DCDF DCPD =,∴DF PD =………………………………………………1分∵AP =x ,DF =y ,∴,1x PD -= ∴x y -=1 ……………………………1分)10(<<x …………………………………………………………………1分(3)∵△DEF ∽△CEB ,∴22CBDF S S CEBDEF =∆∆ (1) …………………………1分∵CFDF S S CEFDEF =∆∆(2),∴(1)÷(2)得2CBCF DF S S CEBcEF ⋅=∆∆ ……………1分又∵EFC BECS S∆∆=4,∴412=⋅=∆∆CBCF DF S S CEBcEF ……………………………1分当P 点在边DA 上时, 有411)1(=⋅-xx ,解得21=x ………………………………………………2分当P 点在边DA 的延长线上时,411)1(=⋅+xx ,解得212-=x ……………………………………………1分。
