机组组合问题的模型与优化方法综述
电力系统机组组合问题研究综述

2 机 组 组 合 数 学 模 型
2 . 1 目标 函数
机组 组合 问题 在不 同的社会 发展 阶段具有 不 同 的 数学 表达 模 型 , 传统 模 式下 , 机组 组合 问题 的优 化 目标 通常 是系 统成 本最 小 , 包括 发 电机组 的开 、 停机 成本 和
Ke y wo r ds: u n i t c o mb i n a t i o n; h e u i r s t i c a p p r o a c h; o p t i ma l a l o g r i t h m o f ma t h s ; i n t e l l i g e n t o p t i ma l lo a g r i t h m
摘 要: 机 组 组合 问题 是 电力 系统优 化 运行 的重要 组 成部 分 , 一直是 电力 系统研 究 中的 热点和 难 点。 总结 了传统
机组组合数学模型及经典求解方法, 并在此基础上介绍 了近年来基f f - - q  ̄、 节能等因素用于机组组合问题 求解的
新 型智 能优化 算 法 , 综述 了机 组组合 问题 的发展 和应 用现 状 , 并展 望 了未 来有待 进 一步研 究的 内容 。 关键 词 : 机 组 组合 ; 启 发 式算 法 ; 数 学优 化算 法 ; 智 能优化 算 法
《电气开关》 ( 2 0 1 5 . N o . 3 )
5
文 章编 号 : 1 0 0 4— 2 8 9 X( 2 0 1 5 ) o 3—0 0 0 5— 0 5
电 力 系统 机 组 组 合 问题 研 究 综 述
刘艳芳 , 夏 昌浩
( 三峡 大学电气与新能 源学院 , 湖 北 宜 昌 4 4 3 0 0 0 )
电力系统机组组合问题的研究

电力系统机组组合问题的研究1. 本文概述电力系统机组组合问题是电力系统运行和规划中的一个重要议题。
在这篇文章中,我们将深入探讨如何通过优化算法和决策支持系统来提高电力系统的经济性、可靠性和可持续性。
本文首先介绍了电力系统机组组合问题的研究背景和意义,阐述了在当前能源转型和电力市场改革的大背景下,如何通过科学合理的机组组合来实现电力系统的高效运行。
接着,文章将回顾相关领域的研究进展,包括传统的优化方法和近年来兴起的智能优化算法,以及它们在电力系统机组组合问题中的应用情况。
本文还将讨论电力系统机组组合问题面临的挑战和未来的研究方向,特别是在考虑环境保护和可再生能源融入的情况下,如何实现电力系统的绿色、低碳转型。
文章将介绍本文的研究方法和主要内容安排,为读者提供一个清晰的研究框架和阅读指南。
通过本文的研究,我们期望能够为电力系统的运行和规划提供有价值的参考和指导,为实现能源的可持续发展贡献力量。
2. 电力系统机组组合问题的理论基础电力系统机组组合问题(Unit Commitment Problem, UCP)是电力系统运行中的一个核心优化问题,旨在确定在未来某个时间段内,哪些发电机组应该开启或关闭,以及它们的出力水平应该是多少,从而满足预期的电力需求,同时优化运行成本和其他相关指标。
UCP是一个复杂的组合优化问题,涉及到大量的决策变量和约束条件,其理论基础涉及多个学科领域的知识。
UCP的理论基础包括电力系统的基本运行原理。
电力系统由多个发电机组、输电网和配电网组成,这些组成部分之间的相互作用和相互影响构成了电力系统运行的基础。
发电机组的出力、电网的传输容量以及负荷的变化等因素都会影响到电力系统的稳定运行。
在解决UCP时,必须充分考虑这些因素,确保电力系统的安全、稳定和经济运行。
UCP的理论基础还包括优化理论和算法。
由于UCP是一个复杂的组合优化问题,传统的数学方法往往难以直接求解。
需要借助优化理论和算法来寻找问题的最优解。
发电机机组最优组合数学模型
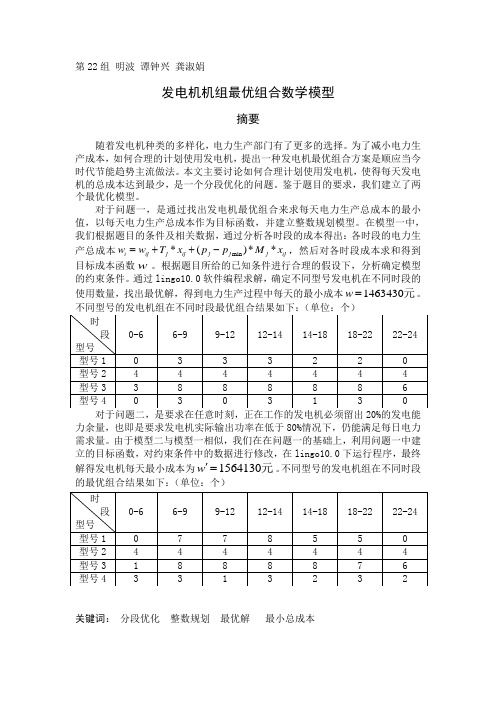
第22组 明波 谭钟兴 龚淑娟发电机机组最优组合数学模型摘要随着发电机种类的多样化,电力生产部门有了更多的选择。
为了减小电力生产成本,如何合理的计划使用发电机,提出一种发电机最优组合方案是顺应当今时代节能趋势主流做法。
本文主要讨论如何合理计划使用发电机,使得每天发电机的总成本达到最少,是一个分段优化的问题。
鉴于题目的要求,我们建立了两个最优化模型。
对于问题一,是通过找出发电机最优组合来求每天电力生产总成本的最小值,以每天电力生产总成本作为目标函数,并建立整数规划模型。
在模型一中,我们根据题目的条件及相关数据,通过分析各时段的成本得出:各时段的电力生产总成本min *()**i ij j ij j j j ij w w T x p p M x =++-,然后对各时段成本求和得到目标成本函数w 。
根据题目所给的已知条件进行合理的假设下,分析确定模型的约束条件。
通过lingo10.0软件编程求解,确定不同型号发电机在不同时段的使用数量,找出最优解,得到电力生产过程中每天的最小成本1463430w =元。
力余量,也即是要求发电机实际输出功率在低于80%情况下,仍能满足每日电力需求量。
由于模型二与模型一相似,我们在在问题一的基础上,利用问题一中建 立的目标函数,对约束条件中的数据进行修改,在lingo10.0下运行程序,最终解得发电机每天最小成本为1564130w '=元。
不同型号的发电机组在不同时段的最优组合结果如下:(单位:个)关键词: 分段优化 整数规划 最优解 最小总成本1. 问题重述为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。
每日电力需求如下表1。
每种发电机都有一个最大发电能力,当接入电网时,其输出功率不应低于某一最小输出功率。
所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
组合优化问题的模型分析与求解

组合优化问题的模型分析与求解在当今复杂多变的世界中,组合优化问题无处不在。
从物流运输的最佳路径规划,到生产线上的资源分配,从网络拓扑的设计,到金融投资组合的选择,我们都在不断地寻求最优的解决方案。
组合优化问题的核心在于从众多可能的组合中找出最优的那一个,以实现某种目标,例如最小化成本、最大化利润或者最小化时间消耗等。
组合优化问题通常具有离散的决策变量和复杂的约束条件。
以旅行商问题(Travelling Salesman Problem,TSP)为例,假设有一个旅行商要访问若干个城市,每个城市只能访问一次,最后回到出发地,目标是找到一条总路程最短的路径。
在这个问题中,城市的选择就是离散的决策变量,而每个城市只能访问一次就是一个约束条件。
为了有效地分析和解决组合优化问题,我们需要建立合适的数学模型。
数学模型是对实际问题的抽象和简化,它能够帮助我们清晰地理解问题的结构和本质。
常见的组合优化问题模型包括整数规划模型、线性规划模型、动态规划模型等。
整数规划模型适用于决策变量只能取整数值的情况。
例如,在一个资源分配问题中,如果我们要决定分配给不同项目的设备数量,设备数量必然是整数,这时就可以建立整数规划模型。
线性规划模型则是在目标函数和约束条件都是线性的情况下使用。
比如,在生产计划中,要确定不同产品的产量以使总利润最大,同时满足原材料和人力等资源的限制,就可以构建线性规划模型。
动态规划模型适用于具有重叠子问题和最优子结构性质的问题。
以求解最短路径问题为例,从起点到终点的最短路径可以通过逐步求解从起点到中间节点的最短路径来得到,这就是动态规划的基本思想。
然而,建立了模型只是第一步,求解这些模型往往具有很大的挑战性。
由于组合优化问题的搜索空间通常非常大,直接枚举所有可能的组合往往是不现实的。
因此,人们开发了各种各样的求解算法。
贪心算法是一种常见的启发式算法。
它在每一步都做出当前看起来最优的选择,希望最终能得到全局最优解。
数学建模优秀论文--基于遗传算法的机组组合问题的建模与求解

数学建模优秀论文--基于遗传算法的机组组合问题的建模与求解摘要本文针对当前科技水平不足以有效存储电力的情况下产生的发电机机组组合的问题,考虑负荷平衡、输电线传输容量限制等实际情况产生的约束条件,建立机组组合优化模型,追求发电成本最小。
同时采用矩阵实数编码遗传算法(MRCGA)和穷举搜索算法,利用MATLAB 7.0.1和C++编程,分别对模型进行求解,并对所得结果进行分析比较,以此来帮助电力部门制定机组启停计划。
首先,建立发电成本最小目标函数和各项约束条件的数学表达式。
其中机组空载成本和增量成本之和随该机组发电出力增长呈折线关系,在分析计算时为了简便,本文采用一条平滑的二次曲线来近似代替。
对于问题1,选取相应的约束条件对目标函数进行约束,从而给出优化模型Ⅰ。
由于问题1的求解规模很小,所以采用穷举搜索算法,利用C++编程求解,得到了3母线系统4小时的最优机组组合计划(见表一)。
对于问题2,在优化模型Ⅰ的基础上,增加最小稳定运行出力约束、机组启动和停运时的出力约束以及机组最小运行时间和最小停运时间约束这三个约束条件,建立了优化模型II。
同时采用遗传算法和穷举搜索算法,利用MATLAB和C++编程,分别对模型进行求解,部分结果如下:发电总成本(单位:元)矩阵实数编码遗传算法6780穷举搜索算法6820在对所得结果进行了分析比较,重新制定了3母线系统4小时最优机组组合计划(见表三)。
对于问题3,用IEEE118系统对优化模型II进行测试。
由于求解规模巨大,同样采用遗传算法和穷举搜索算法,利用MATLAB和C++编程,分别对模型进行求解,部分结果如下:发电总成本(单位:百万)矩阵实数编码遗传算法 2.034穷举搜索算法 2.135在对所得结果进行比较时发现对于大规模问题,遗传算法优势明显,将其求解结果作为24小时的最优机组组合计划(见附录)。
最后,我们就模型存在的不足之处提出了改进方案,并对优缺点进行了分析。
机组组合问题的优化方法综述

机组组合问题的优化方法综述陈皓勇 王锡凡(西安交通大学电力工程系 710049 西安)摘 要 机组组合问题是编制短期发电计划首先要解决的问题,合理的开停机方案将带来很大的经济效益,由于问题十分复杂,很难找出理论上的最优解,文中介绍了机组组合问题的数学模型,分类综述了从60年代起该问题的主要解法,比较了各种方法的优缺点,并提出了尚待研究的问题。
关键词 发电计划 机组组合 优化方法分类号 TM 7321998205215收稿。
国家教委博士点基金资助项目。
0 引言电力系统经济调度的目的是在满足系统安全约束、电能质量要求的条件下尽可能提高运行的经济性。
经济调度的效益很大,根据国外资料和华北、东北等电网的实际测算,节省能源可达总耗量的015%~115%[1]。
经济调度是一个十分复杂的系统优化问题,从总体上解决,难度非常大,常分解为一系列的子问题分别处理。
从短期发电计划来看,可分为机组组合、火电计划、水电计划、交换计划、燃料计划等子问题。
其中机组的优化组合是编制短期发电计划首先要解决的问题,它的经济效益一般大于负荷经济分配的效益。
文献[2,3]中介绍了电力系统经济调度和机组组合问题的数学模型和基本方法。
机组组合问题是一个高维数、非凸的、离散的、非线性的优化问题,很难找出理论上的最优解,但由于它能够带来显著的经济效益,人们一直在积极研究,提出各种方法来解决这个问题,如启发式方法、优先顺序法、动态规划法、整数规划和混合整数规划法、分支定界法、拉格朗日松弛法、专家系统法、人工神经网络法、模拟退火算法、遗传算法等,文献[4,5]介绍了历年来机组组合问题的各种解法和相关参考文献。
本文对机组组合问题的主要解法进行了更深入的探讨,并加以分类综述,比较了各种方法的优缺点,提出了尚待研究的问题。
1 机组组合问题的数学模型根据实际系统不同的要求,对于机组组合问题可以建立不同的模型。
在一般情况下,应以系统各发电机组的开停机状态和出力为控制变量,在满足系统负荷和备用要求、线路潮流限制及机组爬坡速率(ram p rate ,即功率变化速率)、最小开停机时间、燃料总量等约束条件下,使开停机费用和运行费用之和最小。
机组组合问题的优化方法综述2

机组组合问题的优化方法综述陈皓勇 王锡凡(西安交通大学电力工程系 710049 西安)1998205215收稿。
国家教委博士点基金资助项目。
(上接本刊1999年第4期第56页)5 拉格朗日松弛法电力系统是一个非常典型的大系统,是大系统优化和控制理论的一个重要应用领域[42]。
大系统的分解协调思想最早见于D an tzig 和W o lfe 对于线性规划问题的分解[43],而用于机组组合问题的主要是拉格朗日松弛(L agrangian relaxati on )法[44~47],该方法产生于70年代,是解决复杂整数和组合优化问题的一类优化算法,它建立在下述思想的基础上:许多困难的整数规划问题可看成是由一些边界约束条件联系在一起的一系列相对容易的子问题组成,利用这个特点,把约束条件被破坏的量和它们各自的对偶变量的乘积加在目标函数上作为惩罚项,形成拉格朗日问题。
拉格朗日问题相对容易解决,对于最大(小)化问题,它的优化值是原问题优化值的上(下)界,因此在分支定界法中,它能够取代线性规划法以提供下界。
下面以最大化问题为例来说明这种方法:Z =m ax X{c TX AX ≤b ,D X ≤e ,X ≥0且是整数向量}其中 X 是n 维向量;b ,c ,e 分别为m 维、n 维、k 维向量;A ,D 分别为m ×n ,k ×n 的矩阵。
假设问题的约束条件可以分为两组,即AX ≤b 和D X ≤e ,并且如果去掉约束AX ≤b ,问题会变得相对容易解决。
因此可以构造拉格朗日问题:Z D (u )=m ax X{c T X +u T(b -AX ) D X ≤e ,X ≥0且是整数向量} 对偶变量u 的值应该通过解对偶问题Z D =m in u{Z D (u ) u ≥0}来得到。
由于Z D (u )对u 是不可微的,通常用次梯度法来求解,从初始点u 0开始,应用公式u k +1=m ax{0,u k -t k (b -AX k )}迭代求解。
组合优化问题的线性规划建模与求解方法

组合优化问题的线性规划建模与求解方法组合优化问题是指在给定的一组元素中,通过选择和排列这些元素,使得满足一定的约束条件下,所得到的组合具有最优的性质或目标值。
这类问题广泛应用于各个领域,例如物流配送、生产调度、项目管理等。
线性规划是一种数学优化方法,其目标是在一组线性约束条件下,找到满足某个目标函数的最佳线性解。
线性规划在组合优化问题中的应用非常广泛,通过建立合适的线性规划模型,可以有效地求解各种组合优化问题。
在组合优化问题中,线性规划建模的关键是确定决策变量、目标函数和约束条件。
决策变量表示需要选择或排列的元素,目标函数则衡量所得到的组合的质量或性能指标,约束条件则限制决策变量的取值范围。
以下是一些常见的组合优化问题及其线性规划建模与求解方法:1. 装箱问题(Bin Packing Problem):将一组物品装入容量有限的容器中,要求最小化使用的容器数量。
该问题可以使用整数线性规划进行建模。
决策变量可以表示物品是否被装入某个容器,目标函数可以表示使用的容器数量,约束条件包括容器的容量限制以及每个物品被装入一个容器的限制。
2. 旅行商问题(Traveling Salesman Problem):给定一组城市和各城市之间的距离,求解一条最短路径,使得每个城市恰好被访问一次,并回到起始城市。
该问题可以使用混合整数线性规划进行建模。
决策变量可以表示城市之间的连接关系,目标函数可以表示路径的总长度,约束条件包括每个城市的进出度限制以及避免子循环的限制。
3. 生产调度问题(Production Scheduling Problem):给定一组任务和可用资源,求解最优的任务分配和调度方案,使得总体生产时间最短。
该问题可以使用整数线性规划进行建模。
决策变量可以表示任务的开始时间和资源的分配情况,目标函数可以表示生产完成时间,约束条件包括资源的可用性和任务之间的时间限制。
4. 资源分配问题(Resource Allocation Problem):给定一组资源和一组需求,求解最优的资源分配方案,使得满足所有需求的同时最小化资源的使用量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机组组合问题的模型与优化方法综
述
机组组合问题是指求解在一定的发电量要求下,使得总成本最低的最优机组组合。
机组组合问题可以被分解成多种不同的子问题,如调度问题、发电量优化问题和投资决策问题。
在这些子问题的基础上,机组组合问题的模型可以根据具体的问题细分为多种不同的模型,比如单目标机组组合模型、多目标机组组合模型、碳排放机组组合模型等。
对于机组组合问题,常用的优化方法主要有模糊数学方法、遗传算法、粒子群算法、模拟退火算法等。
模糊数学方法能够通过模糊因子来提供模糊结果,而遗传算法、粒子群算法和模拟退火算法则能够快速搜索最优解。
此外,还有一些其他的优化方法,如混合数学规划、模式识别、空间搜索算法等。
