静电场的高斯定理复习题
浙江农林大学静电场中的导体和电介质有介质时的高斯定理习题

四解答题1、如图所示,一导体球半径为&,外罩一半径为冬的同心薄导体球壳,外球壳所带总电荷 为0,而内球的电势为匕,求导体球和球壳之间的电势差 ___________ (填写A 、B. C 或D. 从下而的选项中选取)°答案:A 解设导体球所带电荷为因静电平衡,电荷q 分布在导体球的外表面。
这样一来,就可以把体系看成是两个半径分别为&和电荷分别为q 和Q 的带电球壳。
由电势叠加原理,导体球的电势为一^―+ — = %解出4亦°7?] 4亦()尺2q = 4亦店岭)因此 导体球和球壳之间的电势差为久,=%-仝0=(1-色||匕——0-4码)忌 R?人 4亦。
/?2丿2、如图所示,在一半径为/?i=6.0cm 的金属球A 外而套有一个同心的金属球壳B 。
已知球 壳内,夕卜半径分别为/?2=8.0cnn /?3=10.0cnio 设A 球带有总电^Q A =3x\0^C 9球壳B带有总电量0〃=2xlO*C 。
(1)求球壳B 内表而上带有的电量 ___________ 外表而上带有的 电屋 ________ 以及球A 的电势 _______ 球壳B 的电势 _______A. 5xlO 」CB. -3xlO^C C 、5.6xlO 3VD 、4.5xlO 3V 答案:B, A, C, D(2)将球壳B 接地然后断开,再把球A 接地。
求球A 带有的电量 _______ 球壳B 内表而上带有的电量 ________ 外表面上带有的电量 ________ 以及球A 的电势和球壳B 的电势 ______ o1 / 21 A 、B 、A —Q 1 <心丿1 4碣鸟丿R 2L 4矶尼丿 C. V oQ D 、 岭Q 4矶R? < 4碣尼丿A. -3xlO^C B 、2.1xlO^C C 、—2・lxlO*CD 、-0.9xl0^CE 、8.1xlO 2VF 、0答案:B, C, D, F, E解(l )由高斯泄理可知,B 球壳内表而带的电量等于金属球A 带的电量Qi 的负值,即 缢=-2=-3"0弋因电荷守恒,则B 球壳外表面所带电量为Q Bcxt =Q R + Q A =5xlO-8C= 9.0X 10^X (^ + ^122 + ^)=5.6X 10V 0.06 0.08 0.10球壳B 的电势为^=_L^L = 9.0X 1094亦o 尺3 (2)球壳B 接地后电势(p B =0 ,因此Q^{ = 0 o B 接地断开后总电量变为 Q B =Q B :M =-3xlO-8Co 然后球A 接地,则吩=°。
大学物理复习题

图1-9 1-9(1-121、静电场的高斯定理描述了它是 场。
2、在点电荷+q 的电场中,若取图1-2中P 点处电势为零点,则M 点的电势为: 。
3、如图1-3电路中两个电容器1和2,串联以后接上电动势恒定的电源充电。
在电源保持联接的情况下,若把电介质充入电容器2中,则电容器1上的电势差 电容器1极板上的电量 ;电容器2上的电势差 电容器2极板上的电量 。
(填增大、减小、不变) 5、载有电流为I 的无限长导线,弯成如图1-5所示形状,其中有一部分为半径为R 的半圆弧,则其圆心O 点的磁感应强度的大小为 ,方向为 。
6、闭合导体回路电阻R =5 ,回路所包围面积为0.08m 2,均匀磁场垂直于线圈平面。
欲使电路中有一稳定的感应电流i = 0.08 A ,则磁感应强度的变化率为:d B /d t = T/s 。
7、产生动生电动势和感生电动势的非静电力分别为 、 。
8、磁场能量密度为: ,电场能量密度为: 。
一个电容器加了电压之后储存的电场的能量为: 。
一个自感回路,其中通有电流时,其周围空间磁场的能量为: 。
9、如图1-9,一个矩形线圈与通有相同大小电流的平行直导线在同一平面,而且处在两导线的中央,如图(1-9)所示。
(1)两电流同向且随时间均匀增大时,线圈中有无感应电流 。
(2)两电流反向且随时间均匀增大时,线圈中有无感应电流 。
10、真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d 1/d 2 =1/2,当它们通以相同电流时,两螺线管贮存的磁能之比为W 1/W 2= 。
11、杨氏双缝干涉实验时,用红光和绿光分别做实验时,红光的干涉条纹间距比绿光图1-3图1-5 图1-2的 。
(填:宽 或 窄)。
12、获得相干光常用的方法有两种是: , 。
13、波长为 的单色光垂直照射到宽a 的单缝上,单缝后面放置一个凸透镜, 在凸透镜的焦平面上放置一个屏幕,用以观测衍射条纹,今测得屏幕上中央明条纹两侧第二级暗纹之间的距离为 d ,则透镜的焦距 f 为: 。
第11章(高斯定理及安培环路定理)习题答案

ò ×
S
ò
S
= 0. ”这个推理正确吗? [ B 不一定要等于零 ] 答:不正确, B d S 各自有不同的方向,B 不一定要等于零 116 如图,在一圆形电流 I 所在的平面内,选取一个同心圆形闭合回路 L,则由安培 环路定理可知 (A) (B) I L O 思考题 116 图
q 1 1 ( - ) ] 4 pe 0 r R
解;
U 1 =
q 4 peo r
+
Q 4 peo R
U 2 =
q + Q 4 peo R
U1-U2 =
q 1 1 ( - ) 4 pe 0 r R
117 [
已 知 某 静 电 场 的 电 势 分 布 为 U = 8x + 12x2 y - 20y2 (SI) , 求 场 强 分 布 E .
B r r U C = U C - U B = ò E × d l = C
ò 4 pe r
o
2
115 两块面积均为 S 的金属平板 A 和 B 彼此平行放置,板间距离为 d(d 远小于板的 线度) , 设 A 板带有电荷 q1, B 板带有电荷 q2, 求 AB 两板间的电势差 UAB. [
(1)dq =
q dl 2 L
U = ò dU = ò
dq q q x + L = ò dl = ln 4pe o ( x - l ) 4pe o 2 L ( x - l ) 8pL e o x - L
(2)E= -
¶u q 1 1 1 q r = ( ) = i 2 ¶x 8p L e o x - L x + L 4 pe 0 x 2 - L
大学物理静电场答案

大学物理静电场答案【篇一:大学物理静电场试题库】txt>1、下列关于高斯定理的说法正确的是(a) a如果高斯面上e处处为零,则面内未必无电荷。
b如果高斯面上e处处不为零,则面内必有静电荷。
c如果高斯面内无电荷,则高斯面上e处处为零。
d如果高斯面内有净电荷,则高斯面上e处处不为零。
2、以下说法哪一种是正确的(b)a电场中某点电场强度的方向,就是试验电荷在该点所受的电场力方向 b电场中某点电场强度的方向可由e?fq0确定,其中q0为试验电荷的电荷量,q0可正可负,f为试验电荷所受的电场力c在以点电荷为中心的球面上,由该点电荷所产生的电场强度处处相同 d以上说法都不正确3、如图所示,有两个电2、下列说法正确的是(d)a电场强度为零处,电势一定为零。
电势为零处,电场强度一定为零。
b电势较高处电场强度一定较大,电场强度较小处电势一定较低。
c带正电的物体电势一定为正,带负电的物体电势一定为负。
d 静电场中任一导体上电势一定处处相等。
3、点电荷q位于金属球壳中心,球壳内外半径分别为试判断下r1,r2,所带静电荷为零a,b为球壳内外两点,说法的正误(c)a移去球壳, b点电场强度变大b移去球壳,a点电场强度变大 c移去球壳,a点电势升高 d移去球壳,b点电势升高4、下列说法正确的是(d)列a场强相等的区域,电势也处处相等 b场强为零处,电势也一定为零 c电势为零处,场强也一定为零 d场强大处,电势不一定高a 5、如图所示,一个点电荷q位于立方体一顶点a上,则通过abcdq6?0q12?0q24?0q36?0a b cd6、如图所示,在电场强度e的均匀电场中,有一半径为r的半球面,场强e的方向与半球面的对称抽平行,穿过此半球面的电通量为(c) a 2?r2e b22?re c ?red212?re27、如图所示两块无限大的铅直平行平面a和b,均匀带电,其电荷密度均为?(??0c?m?2),在如图所示的a、b、c三处的电场强度分别为(d) a 0,8、如图所示为一具有球对称性分布的静电场的e~r关系曲线.请指出该静电场是由下列哪种带电体产生的.(b)a 半径为r的均匀带电球面. b半径为r的均匀带电球体.c半径为r的、电荷体密度为??ar(a为常数)的非均匀带电球体 d半径为r的、电荷体密度为??a/r(a为常数)的非均匀带电球体9、设无穷远处电势为零,则半径为r的均匀带电球体产生的电场的电势分布规律为(图中的u0和b皆为常量):(c)??,0,0 b 0,?2?,0,0c?2?0?0?0,?,?d??0,0,??010、如图所示,在半径为r的“无限长”均匀带电圆筒的静电场中,各点的电场强度e的大小与距轴线的距离r 关系曲线为(a)ee or r orrorror r(a)(b) (c)(d)11、下列说法正确的是( d)(a)闭合曲面上各点电场强度都为零时,曲面内一定没有电荷(b)闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零(c)闭合曲面的电通量为零时,曲面上各点的电场强度必定为零。
(整理)浙江省大学物理试题库302-静电场的高斯定理

题号:30232014
分值:2分
难度系数等级:2
一闭合面包围着一个电偶极子,则通过此闭合面的电场强度通量 _________________。
答案:
题号:30232015
分值:2分
难度系数等级:2
一点电荷 处在球形高斯面的中心,当将另一个点电荷置于高斯球面外附近时,穿过此高斯面的 通量是否会发生变化?_________________。
如图所示,真空中有两个点电荷,带电量分别为 和 ,相距 。若以负电荷所在处 点为中心,以 为半径作高斯球面 ,则通过该球面的电场强度通量 。
答案:
题号:30233005
分值:2分
难度系数等级:3
一均匀静电场,电场强度 ,则电场通过阴影表面的电场强度通量是______(正方体边长为 )。
答案:
题号:30233006
答案:
题号:30233020
分值:2分
难度系数等级:3
一均匀带电球面,半径是 ,电荷面密度为 。球面上面元 带有 的电荷,该电荷在球心处产生的电场强度为____________。
答案:
四计算题
题号:30242001
分值:10分
难度系数等级:2
一边长为 的立方体置于直角坐标系中,如图所示。现空间中有一非均匀电场 , 、 为常量,求:电场对立方体各表面的电场强度通量。
; ; ; 。〔〕
答案:
题号:30211011
分值:3分
难度系数等级:1
一点电荷,放在球形高斯面的中心处。下列哪一种情况,通过高斯面的电场强度通量发生变化:
将另一点电荷放在高斯面外; 将另一点电荷放进高斯面内;
将球心处的点电荷移开,但仍在高斯面内; 将高斯面半径缩小。
静电场复习题(包含答案)

______________________________________________________________________________________________________________精品资料练习一 库仑定律 电场强度σ,球面内电场强度处处为零(原因是场强叠加原理),球面上面元d S 的一个电量为σd S 的电荷元在球面内各点产生的电场强度(C)(面元相当于点电荷)(A) 电荷电量大,受的电场力可能小; (B) 电荷电量小,受的电场力可能大;(C) 电场为零的点,任何点电荷在此受的电场力为零; (D) 电荷在某点受的电场力与该点电场方向一致.边长为a 的正方形的四个顶点上放置如图2.1所示的点电荷,则中心O 处场强(C) (用点电荷的场强叠加原理计算,注意是矢量叠加,有方向性)(A) 大小为零.(B) 大小为q/(2πε0a 2), 方向沿x 轴正向.图2.12(C) 大小为()2022a q πε, 方向沿y 轴正向. (D) 大小为()2022a q πε, 方向沿y 轴负向.二、填空题1.4所示,带电量均为+q 的两个点电荷,分别位于x的+a 和-a 位置.则y 轴上各点场强表达式 为E = ,场强最大值的位置在y = .( 2qy j /[4πε0 (a 2+y 2)3/2] , ±a/21/2.) (也是用点电荷的场强叠加原理计算)三、计算题1.用绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正点荷Q , 试求圆心O 处的电场强度. (此题的计算尽量掌握,涉及连续带电体的电场强度计算,可与书上总结部分的例子进行比较对应)解. 取园弧微元 d q=λd l=[Q/(πR )]R d θ=Q d θ/πd E =d q/(4πε0r 2)=Q d θ/(4π2ε0R 2) d E x =d E cos(θ+π)=-d E cos θ d E y =d E sin(θ+π)=-d E sin θ E x =()⎰⎰-=2/32/2024d cos d ππεπθθR Q E x =Q/(2π2ε0R 2)E y =⎰d E y ()⎰-2/32/2024d sin ππεπθθR Q =0图1.4______________________________________________________________________________________________________________精品资料故 E=E x =()2022R Q επ方向沿x 轴正向.练习二 高斯定理一、选择题如图3.1所示.有一电场强度E 平行于x 轴正向的均匀电场,则通过图中一半径为R 的半球面的电场强度通量为(D)(此题注意场强的方向,联系场线穿入与穿出)(A) πR 2E . (B) πR 2E /2 . (C) 2πR2E . (D) 0 . 关于高斯定理,以下说法正确的是:(A)(A) 高斯定理是普遍适用的,但用它计算电场强度时要求电荷分布具有某种对称性;(实际是要求场具有对称性)(B) 高斯定理对非对称性的电场是不正确的;(C) 高斯定理一定可以用于计算电荷分布具有对称性的电场的电场强度;(D) 高斯定理一定不可以用于计算非对称性电荷分布的电场的电场强度.3.3所示为一球对称性静电场的E ~ r 关系曲线,请指出该电场是由哪种带电体产生的(E 表示电场强度的大小,r 表示离对称中心的距离) . (C) (如果是均匀带电球体,其E ~ r 又该如何画)图3.1图3.34(A) 点电荷.(B) 半径为R 的均匀带电球体. (C) 半径为R 的均匀带电球面.(D) 内外半径分别为r 和R 的同心均匀带球壳.如图3.4所示,一个带电量为q 的点电荷位于一边长为l 的 正方形abcd 的中心线上,q 距正方形l/2(这一点很关键),则 通过该正方形的电场强度通量大小等于: (B) (要学会如何化解,考查对高斯定理通量的理解 (A)02εq . (B) 06εq .(C) 012εq .(D) 024εq .3.5, 两块“无限大”的带电平行平板,其电荷面密度分别为-σ (σ > 0 )及2σ.试写出各区域的电场强度.Ⅰ区E 的大小 ,方向 . Ⅱ区E 的大小 ,方向 . Ⅲ区E 的大小 ,方向 .σ/(2ε0),向左;3σ/(2ε0),向左;σ/(2ε0),向右.(考查对连续带电体场强叠加原理的理解。
(整理)浙江农林大学静电场的高斯定理习题

四、计算题1、 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场两面间 , 1σ面外 , 2σ面外 . (填写A 、B 、C 或D ,从下面的选项中选取)A 、n E )(21210σσε-=B 、1201()E n σσε=+C 、n E)(21210σσε+-= D 、n E)(21210σσε+= 答案:A ,C ,D解: 如图所示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+=n:垂直于两平面由1σ面指为2σ面.2、一无限长带电直线,电荷线密度为λ,傍边有长为a , 宽为b 的一矩形平面, 矩形平面中心线形平面电通量的大小.. (填写A 、B 、C 或D A 、()0arctan 22a b c λπε⎡⎤⎣⎦ B 、()0arctan 2a b c λπε⎡⎤⎣⎦ C 、()0arctan 24a b c λπε⎡⎤⎣⎦D 、()02arctan 2a b c λπε⎡⎤⎣⎦ 答案:B λ解:取窄条面元adx ds =,该处电场强度为rE 02πελ=过面元的电通量为()220022cos xc acdxadx r s d E d e +=⨯=⋅=Φπελπεθλ ()⎰⎰-+=Φ=Φ2/2/2202b b e e xc acdxd πελ2/2/0arctan 12b b cxc ac -⋅=πελ()[]02arctan πελc b a =3、 如图所示,在x -y 平面内有与y 轴平行、位于x=a / 2和x =-a / 2处的两条“无限长”平行的均匀带电细线,电荷线密度分别为+λ和-λ.求z 轴上任一点的电场强度.. . (填写A 、B 、C 或D ,从下面的选项中选取)A 、()2204a i a z λπε-+B 、()22024a i a z λπε-+ C 、()22024a i a z λπε-+ D 、()22044a i a z λπε-+ 答案:C解:过z 轴上任一点(0 , 0 , z )分别以两条带电细线为轴作单位长度的圆柱形高斯面,如图所示.按高斯定理求出两带电直线分别在该处产生的场强大小为 ()r E 02/ελπ=± 场强方向如图所示. 按场强叠加原理,该处合场强的大小为r a r E E 2/c o s 20⋅π==+ελθ ()22042z a a +π=ελ方向如图所示. 或用矢量表示 ()iz a a E 22042+π-=ελ4、均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C·m -3求距球心5cm 的场强 ,8cm 的场强 ,12cm 的场强 . (填写A 、B 、C 或D ,从下面的选项中选取).A 、43.4810⨯1C N -⋅, 方向沿半径向外 B 、44.1010⨯1C N -⋅ ,沿半径向外C 、44.1010⨯1C N -⋅,方向沿半径向外D 、 0 答案: D, A ,B解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm 时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=rr r E ερ内外 1C N -⋅ 沿半径向外.5、有两个半径分别为1R 、2R 的同心球壳,带电分别为1Q 、2Q ,试求空间电场分布。
静电场的高斯定理
r
E1
dS
S
E1 4
r
2
R
面内电量 qi 0
用高斯定理求解:
E1 4 r2 0 E1 0
E
高斯面
44
2) r R
Φe S E2 dS
r
E2
dS
S
E2
4
r2
qi q
E2 4r 2 q 0
E
E2
q
40r 2
q
40 R2
O
R
E
1 r2
r
45
例题 求均匀带电球体的电场。(已知 q、R)
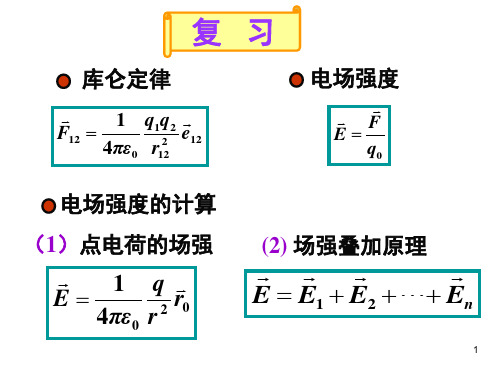
复习
库仑定律
F12
1 4πε0
q1q2 r122
e12
电场强度
F
E
q0
电场强度的计算
(1)点电荷的场强
E
1 4πε0
q r2
r0
(2) 场强叠加原理
E E1 E2 En
1
(3) 电荷连续分布的带电体的电场
E
dE
(q)
dq (q)4πε0r 2
r0
电荷分布
dq ρdV (体 分 布) dq σdS (面 分 布)
其余三个面上直接计算困难
考虑用 8 个这样的立方体 将点电荷拥在中心
其外表面上的通量为
Φ'e
E
S
由对称性
dS
q
03
e 24
q
0
•
39
4. 高 斯 定 理 的 应 用
Applications of Gauss’ Law
Φe
E dS
1
S
ε0
qi (内)
高斯定理的一个重要应用是:计算带电体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 选择题1.关于高斯定理的理解有下面几种说法,其中正确的是:()A 如果高斯面上E处处为零,则该面内必无电荷;()B 如果高斯面内无电荷,则高斯面上E处处为零;()C 如果高斯面上E处处不为零,则高斯面内必有电荷;()D 如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零。
〔 〕 答案:()D2.如在边长为a 的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为 ()A 0/q ; ()B 0/2q ; ()C 0/4q ; ()D 0/6q 。
〔 〕 答案:()D3.在电场强度为E Ej v v的匀强电场中,有一如图所示的三棱柱,取表面的法线向外,设过面AA'CO ,面B'BOC ,面ABB'A'的电通量为1 ,2 ,3 ,则()A 1230Ebc Ebc ; ()B 1230Eac Eac ;()C 22123Eac Ec a b Ebc ;()D 22123Eac Ec a b Ebc 。
〔 〕 答案:()B4.已知一高斯面所包围的体积内电荷代数和0iq,则可肯定:()A 高斯面上各点场强均为零。
()B 穿过高斯面上每一面元的电通量均为零。
()C 穿过整个高斯面的电通量为零。
()D 以上说法都不对。
〔 〕答案:()C5.有两个点电荷电量都是q ,相距为2a ,今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面。
在球面上取两块相等的小面积1S 和2S ,其位置如图所示。
设通过1S 和2S 的电场强度通量分别为1 和2 ,通过整个球面的电场强度通量为 ,则()A 120,/q ; ()B 120,2/q ;()C 120,/q ; ()D 120,/q 。
〔 〕 答案:()D6.一点电荷,放在球形高斯面的中心处。
下列哪一种情况,通过高斯面的电场强度通量发生变化: ()A 将另一点电荷放在高斯面外; ()B 将另一点电荷放进高斯面内; ()C 将球心处的点电荷移开,但仍在高斯面内; ()D 将高斯面半径缩小。
答案:()B7.A 和B 为两个均匀带电球体,A 带电荷q ,B 带电荷q ,作一与A 同心的球面S 为高斯面,如图所示。
则()A 通过S 面的电场强度通量为零,S 面上各点的场强为零;()B 通过S 面的电场强度通量为0/q ,S 面上场强的大小为x yza bcEOAABBCx O qq a2aS 1 S 2A S+qr -qB20π4rq E;()C 通过S 面的电场强度通量为 0()/q ,S 面上场强的大小为20π4r q E;()D 通过S 面的电场强度通量为0/q ,但S 面上各点的场强不能直接由高斯定理求出。
〔 〕 答案:()D8.若穿过球形高斯面的电场强度通量为零,则 ()A 高斯面内一定无电荷; ()B 高斯面内无电荷或正负电荷的代数和为零;()C 高斯面上场强一定处处为零; ()D 以上说法均不正确。
〔 〕 答案:()B9.如果把一点电荷Q 放在某一立方体的一个顶点,则()A 穿过每一表面的电通量都等于Q6; ()B 穿过每一表面的电通量都等于Q 60()C 穿过每一表面的电通量都等于Q 30;()D 穿过每一表面的电通量都等于024Q〔 〕答案:()D 10.高斯定理nti dqS E S()A 适用于任何静电场。
()B 只适用于真空中的静电场。
()C 只适用于具有球对称性、轴对称性和平面对称性的静电场。
()D 只适用于虽然不具有()C 中所述的对称性,但可以找到合适的高斯面的静电场。
〔 〕 答案:()A11.半径为R 的均匀带电球面,若其电荷面密度为 ,则在距离球面R 处的电场强度大小为:()A 0; ()B 02 ; ()C 04 ; ()D 08。
〔 〕答案:()C12.同一束电场线穿过大小不等的两个平面,如图所示。
则两个平面的E 通量和场强关系是:()A 12 ?21E E ; ?()B ??12 ?21E E ;()C 12 ?21E E ; ?()D ? 12 ?21E E 。
〔 〕 答案:()D13.在静电场中,一闭合曲面外的电荷的代数和为q ,则下列等式不成立的是: 〔 〕 答案:()C二 填空题1.如图所示,在场强为E 的均匀电场中取一半球面,其半径为R ,电场强度的方向与半球面的对称轴平行。
则通过这个半球面的电通量为 。
答案:2E R2.如图所示,在场强为E 的均匀电场中取一半球面,其半径为R ,电场强度的方EEOxy向与半球面的对称轴垂直。
则通过这个半球面的电通量为 。
答案:03.反映静电场性质的高斯定理表明静电场是___ ___场。
答案:有源场4.如图所示, 真空中有两个点电荷, 带电量分别为Q 和Q , 相距2R 。
若以负电荷所在处O 点为中心, 以R 为半径作高斯球面S , 则通过该球面的电场强度通量e 。
答案:0/Q5.电荷1q 、2q 、3q 和4q 在真空中的分布如图所示, 其中2q 是半径为R 的均匀带电球体,S 为闭合曲面,则通过闭合曲面S 的电通量SS Ed 。
答案:120()q q6.一面积为S 的平面,放在场强为E 的均匀电场中,已知E与平面法线的夹角为)2(,则通过该平面的电场强度通量的数值e ________________。
答案:||cos E S v7.有一个球形的橡皮膜气球,电荷q 均匀地分布在球面上,在此气球被吹大的过程中,被气球表面掠过的点(该点与球中心距离为r ),其电场强度的大小将由 变为0。
答案:204qR8.把一个均匀带电量Q 的球形肥皂泡由半径1r 吹胀到2r ,则半径为R (12r R r )的高斯球面上任一点的场强大小E 由204qR 变为______________。
答案:09.在匀强电场E v 中,取一半径为R 的圆,圆面的法线 n v 与E v成060角,如图所示,则通过以该圆周为边线的如图所示的任意曲面S 的电通量 Se S E Φd 。
答案:212E R10.均匀电场E v垂直于以R 为半径的的圆面,以该圆周为边线作两个曲面1S 和2S ,1S 和2S 构成闭合曲面,如图所示。
则通过1S 、2S 的电通量1Φ和2 分别为 和 。
答案:22E RE R11.一点电荷q 处在球形高斯面的中心,当将另一个点电荷置于高斯球面外附近时,穿过此高斯面的E 通量是否会发生变化? _________________。
答案:不变化12.一点电荷q 处在球形高斯面的中心,当将另一个点电荷置于高斯球面外附近时,此高斯面上任意点的电场强度是否会发生变化?________________。
答案:变化13.把一个均匀带有电荷Q 的球形肥皂泡由半径1r 吹胀到2r ,则半径为R (12r R r )的高斯球面上任一点的场强大小E 是否变化:________________。
答案:变化14.一均匀带电球面,半径是R ,电荷面密度为 。
球面上面元d S 带有d S 的电荷,该电荷在球心处产生SQ+Qb a2RROq 1q 3 q 4Sq 2的电场强度为____________。
答案:20d 4S R三计算题1.一半径为R 的带电球体,其电荷体密度分布为()Arr R ,0()r R ,A 为大于零的常量。
试求球体内外的场强分布及其方向。
答案:在球内取半径为r 、厚为d r 的薄球壳,该壳内所包含的电荷为 在半径为r 的球面内包含的总电荷为以该球面为高斯面,按高斯定理有 0421/4 Ar r E 得到0214/ Ar E , (r ≤R )方向沿径向向外在球体外作一半径为r 的同心高斯球面,按高斯定理有 得到20424/rAR E , ()r R方向沿径向向外2.如图所示,有一带电球壳,内、外半径分别为a 、b ,电荷体密度为r A ,在球心处有一点电荷Q 。
求:(1)在a r b 区域的电场强度;(2)当A 取何值时,球壳区域内电场强度E的大小与半径r 无关。
答案: 在a r b 区域,用高斯定理求球壳内场强:而 r r A r r r A V rV r a d 4d 4d 02 222a r A故: 2220202414a r A rr Q E 即: 202020224rAa A r Q E 要使E的大小与r 无关,则应有 :即22aQ A 3.有两个同心的均匀带电球面,半径分别为1R 、2R )(21R R ,若大球面的面电荷密度为 ,且大球面外的电场强度为零,求:(1)小球面上的面电荷密度;(2)大球面内各点的电场强度。
答案: (1)设小球面上的电荷密度为 ,在大球面外作同心的球面为高斯面, 由高斯定理:'1220int 4'4d R R q S E S∵大球面外0 E ∴ 2221440R R解得: 221()R R(2) 大球面内各点的场强两个均匀带电球面场强的迭加:内部场强为零,外部相当点电荷 在1r R 区域: 00021 E E E在12R r R 区域: 2112204'04R E E E r 220r R 4.如图所示,一个均匀分布带电球层,电荷体密度为 ,球层内表面半径为R ,外表面为2R ,求:电场分布。
答案: 本题的电荷分布具有球对称性,因而电场分布也具有对称性,作同心球面为r Q a b高斯面,由高斯定理 0intdqS E S由对称性可以得到E r S E S24d对于不同的高斯面,电荷是不同的,结果如下 因而场强分布为5.均匀带电球壳内半径16cm R ,外半径210cm R ,电荷体密度为5-3210C m 。
求:距球心15cm r 、28cm r 、312cm r 各点的场强及方向(真空介电常数122-1-208.8510C N m )。
答案: 由高斯定理:0intdqS E S,得:int204πqE r当5cm r 时,int0q故: 0 E8cm r 时, int q 4π33(r 31)R ∴ 331204π34πr R E r41048.3 1C N , 方向沿半径向外 12cm r 时,int 4π3q32(R 31R ) ∴ 33214204π3 4.10104πR R E r1C N 沿半径向外. 6.两个均匀带电的同心球面,半径分别为1R 和2R ,带电量分别为1q 和2q 。
求(1)场强的分布;(2)当12q q q 时,场强的分布。
答案: (1)选择高斯面:选与带电球面同心的球面作为高斯面。
由高斯定理:intdqS E S,得:int24πq E r当2r R 时, int12qq q解得 12204q q E r当12R r R 时, int1qq解出 2014r q ES 1O1R 2R 3S 2S 1S当1r R 时,int0q解得0E(2)当12q q q 时,由上面计算的结果,得场强的分布为。
