不规则图形体积计算公式
不规则图形体积计算公式
实用标准文案
a,b,c-半轴
梯 形 体
图形 正方形
长方形
三角形
平行四 边形
任意四 边形
实用标准文案
常用图形求面积公式
尺寸符号
面积(F) 表面积(S)
正多边 形
精彩文档
菱形
梯形 圆形 椭圆形 扇形 弓形 圆环
精彩文档
实用标准文案
a·b-主轴
F= (π/4) a·b
部分圆 环
新月形
L d/10 P 0.40 抛物线 形
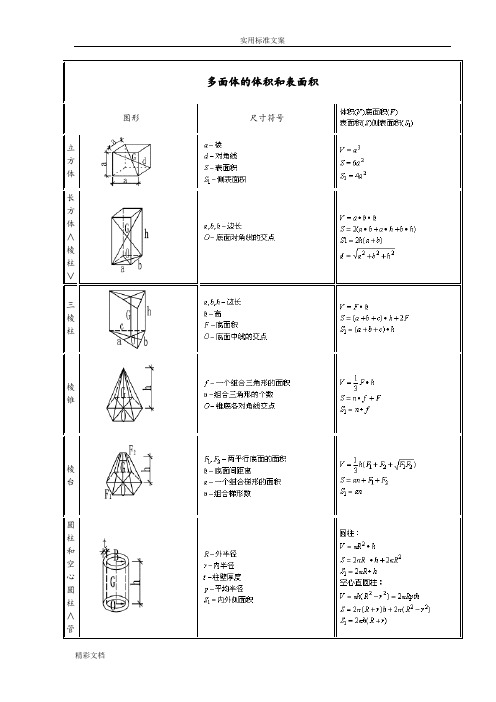
图形
立 方 体
长 方 体 ∧ 棱 柱 ∨
三 棱 柱
棱 锥
棱 台
圆 柱 和 空 心 圆 柱 ∧ 管
精彩文档
实用标准文案
多面体的体积和表面积
尺寸符号
∨
斜 线 直 圆 柱
直 圆 锥
圆 台
球 球 扇 形 ∧ 球 楔 ∨
精彩文档
实用标准文案
球 缺
圆 环 体 ∧ 胎 ∨
球 带 体
桶 形
椭 球 体
交 叉 圆 柱 体
等多边 形
实用标准文案
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55
精彩文档
立体几何中的体积与面积计算方法总结

立体几何中的体积与面积计算方法总结立体几何是数学中的一个重要分支,它研究的是三维空间中的物体的形状、大小以及相互关系。
在立体几何中,体积和面积是两个常见且重要的概念。
本文将总结一些常见的体积和面积计算方法,帮助读者更好地理解和应用这些概念。
一、体积计算方法1. 直接计算法:对于一些简单的几何体,如长方体、正方体、圆柱体等,可以直接通过公式计算其体积。
例如,长方体的体积公式为V = l × w × h,其中l、w、h分别表示长方体的长度、宽度和高度。
2. 分割求和法:对于一些复杂的几何体,可以通过将其分割成若干个简单的几何体,然后计算每个简单几何体的体积,最后将它们求和得到整个几何体的体积。
这种方法常用于计算不规则体的体积,如棱柱、棱锥等。
3. 旋转体积法:对于一些具有旋转对称性的几何体,可以通过旋转这个几何体得到一个旋转体,然后计算旋转体的体积,并乘以旋转角度的比例系数得到原几何体的体积。
这种方法常用于计算圆锥、圆台等几何体的体积。
二、面积计算方法1. 直接计算法:对于一些简单的几何形状,如矩形、正方形、圆形等,可以直接通过公式计算其面积。
例如,矩形的面积公式为A = l × w,其中l和w分别表示矩形的长度和宽度。
2. 分割求和法:对于一些复杂的几何形状,可以通过将其分割成若干个简单的几何形状,然后计算每个简单形状的面积,最后将它们求和得到整个几何形状的面积。
这种方法常用于计算不规则图形的面积,如多边形、曲线图形等。
3. 面积积分法:对于一些无法通过简单的公式计算的几何形状,可以利用面积积分的方法进行计算。
面积积分是将几何形状分割成无穷小的面元,然后对每个面元的面积进行积分得到整个几何形状的面积。
这种方法常用于计算曲面的面积。
三、应用举例1. 体积计算应用:在建筑工程中,需要计算房间的体积,以确定所需的建材数量。
在制造业中,需要计算产品的体积,以确定运输和储存的空间需求。
不规则梯形体积

不规则梯形体积
不规则梯形体积是指一个梯形的两个底面不在同一平面上的立
体图形。
计算不规则梯形体积的方法与计算普通梯形体积的方法类似,需要先求出底面积,然后再乘以高度。
不规则梯形的底面积可以通过将其分解为若干个简单的几何形
状来计算,例如将其分解为一个矩形和若干个三角形。
对于每个三角形,可以通过已知的两个边长和它们之间的夹角来计算其面积,然后将所有的面积相加即可得到整个底面积。
高度可以通过垂直于底面的距离来测量。
计算不规则梯形体积的公式为:
体积 = 底面积×高度
其中,底面积可以通过上述方法计算得到,高度则需要通过测量获得。
计算出来的体积单位通常为立方米或立方厘米,具体取决于所使用的单位。
- 1 -。
不规则多边形体积计算公式

不规则多边形体积计算公式
不规则多边形体积计算公式可以通过将多边形分解为三角形并计算各个
三角形的体积之和来求得。
在计算之前,我们需要先确定多边形的顶点坐标。
假设我们有一个不规则多边形,其中的顶点坐标分别为(x₁, y₁), (x₂,
y₂), (x₃, y₃), ..., (xₙ, yₙ)。
我们可以将其分解为由同一个顶点 (x₁, y₁) 和
相邻的两个顶点 (xᵢ, yᵢ)、(xᵢ₊₁, yᵢ₊₁) 组成的三角形。
这样,不规则多边形
的体积就可以通过计算所有三角形的体积之和得到。
三角形的体积可以使用以下公式来计算:
V = (1/6) * |(x₁y₂ + x₂y₃ + ... + xₙy₁) - (x₂y₁ + x₃y₂ + ... + x₁yₙ)|
其中 "|" 表示取绝对值。
按照上述方法,我们可以将不规则多边形的体积计算公式总结为如下步骤:
1. 确定多边形的顶点坐标 (x₁, y₁), (x₂, y₂), (x₃, y₃), ..., (xₙ, yₙ)。
2. 将多边形分解为由同一个顶点 (x₁, y₁) 和相邻的两个顶点 (xᵢ, yᵢ)、
(xᵢ₊₁, yᵢ₊₁) 组成的三角形。
3. 对于每个三角形,使用三角形的体积计算公式 V = (1/6) * |(x₁y₂ +
x₂y₃ + ... + xₙy₁) - (x₂y₁ + x₃y₂ + ... + x₁yₙ)| 计算其体积。
4. 将所有三角形的体积相加,得到不规则多边形的体积。
通过以上步骤,我们可以计算出不规则多边形的体积,无需使用任何网
址链接或涉及政治方面的内容。
不规则球体体积计算公式

不规则球体体积计算公式咱来聊聊不规则球体体积的计算公式哈,这可是个挺有趣的事儿。
不知道大家有没有过这样的经历,比如说去玩那种投球的游戏,球的形状怪怪的,这时候你会不会好奇,这要是想知道它的体积该咋算呢?要说不规则球体体积的计算,那可不是像算普通球体那么简单。
咱们先来说说普通球体的体积公式,V = 4/3 × π × r³ ,这大家应该都熟悉。
但不规则球体可就没这么直接了。
那咋办呢?这时候就得靠一些巧妙的方法啦。
有一种方法叫排水法,就是把这个不规则的球体放到一个装满水的容器里,看看排出来多少水,排出来水的体积就约等于这个不规则球体的体积。
我记得有一次,我带着一群小朋友做这个实验。
有个小家伙特别着急,还没准备好就把球扔进去了,结果水溅得到处都是,大家都哈哈大笑。
还有一种方法是用微积分的知识。
这听起来好像很高深,其实简单来说,就是把这个不规则的球体切成无数个超级薄的小块,每一小块都近似看成一个规则的形状,然后把这些小块的体积加起来。
比如说,想象一下一个长得像歪瓜裂枣的球体,咱们从不同的角度去切它。
横着切一刀,竖着切一刀,斜着再切一刀。
每一刀下去形成的截面,我们都尽量去找到它的规律,然后通过计算这些截面的面积,再乘以厚度,一点点地累加起来,就能算出这个不规则球体的大概体积啦。
在实际生活中,很多东西其实都不是完美的规则形状。
像有些水果,比如长得奇形怪状的芒果,或者是一些手工做出来的陶土球,它们的形状都不规则。
这时候,如果我们想要知道它们的体积,就得用上这些计算方法。
总之,计算不规则球体体积虽然有点复杂,但只要咱们掌握了合适的方法,再加上一点点耐心和细心,就能搞定啦。
就像解决生活中其他难题一样,只要咱们肯琢磨,办法总比困难多!希望大家以后再遇到不规则球体体积计算的问题时,都能轻松应对,说不定还能发现更有趣的计算方法呢!。
各种形状的体积和面积计算公式

各种形状的体积和面积计算公式在几何学中,我们经常需要计算各种形状的体积和面积。
这些计算公式可以帮助我们在设计、建造和解决各种问题中准确地计算出所需要的数值。
以下是一些常见形状的体积和面积计算公式。
1. 矩形(Rectangle)矩形是最简单的平面形状之一,由两对相等的直角边组成。
- 面积(Area)= 底边(length) * 高(width)- 周长(Perimeter)= 2 * (底边 + 高)2. 正方形(Square)正方形是一种特殊的矩形,四个边相等,四个角是直角。
- 面积(Area)= 边长(length)^2- 周长(Perimeter)= 4 * 边长3. 圆(Circle)圆是一个不规则形状,由一个圆心和等长的半径组成。
- 周长(Circumference)= 2 * π * 半径4. 椭圆(Ellipse)椭圆是由两个焦点之间距离总和等于定值的点的轨迹组成。
- 面积(Area)= π * 长轴半径(major axis radius) * 短轴半径(minor axis radius)- 周长(Circumference)≈ 2 * π * √((长轴半径^2 + 短轴半径^2) / 2)5. 三角形(Triangle)三角形是由三条线段组成的平面图形。
- 面积(Area)= (底边 * 高) / 2- 周长(Perimeter)= 边1 + 边2 + 边36. 梯形(Trapezoid)梯形是由一对平行边和两个非平行边组成的四边形。
- 面积(Area)= (上底 + 下底) * 高 / 2- 周长(Perimeter)= 上底 + 下底 + 边1 + 边27. 圆柱体(Cylinder)圆柱体是由两个平行且等大的圆形底面以及围绕这些圆形底面生成的侧面组成。
- 体积(Volume)= π * 半径^2 * 高- 曲面积(Curved Surface Area)= 2 * π * 半径 * 高- 表面积(Total Surface Area)= 2 * π * 半径 * (半径 + 高)8. 球体(Sphere)球体是由所有与球心距离相等的点组成的集合。
不规则图形体积计算公式

实用标准文案
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55
精彩文档
图形
立 方 体
长 方 体 ∧ 棱 柱 ∨
三 棱 柱
棱 锥
实用标准文案
多面体的体积和表面积
尺寸符号
棱 台
圆 柱 和 空 心 圆 柱 ∧ 管
精彩文档
∨
斜 线 直 圆 柱
直 圆 锥
圆 台
球 球 扇 形 ∧ 球 楔 ∨
精彩文档
实用标准文案
球 缺
圆 环 体 ∧ 胎 ∨
球 带 体
桶 形
椭 球 体
交 叉 圆 柱 体
精彩文档
实用标准文案
a,b,c-半轴
梯 形 体
正方 形
长方 形
三角 形
平行 四边
形
任意 四边
形
图形
实用标准文案
正多 边形
精彩文档
菱 形
梯形 圆形 椭圆
形 扇形
弓形
圆环
精彩文档
实用标准文案
a·b-主轴
F= (π/4) a·b
部分 圆环
新月 形
L d/10 P 0.40 抛物 线形
不规则物体体积计算

谢谢观赏
2分米=20厘米 h=V÷ab =20×20×20÷〔50×40〕 =8000 ÷ 2000 =4〔厘米〕
答:水面会上升4厘米。
学以致用
土豆 13cm
5L 土豆
13cm=1.3dm 5L=5dm3
土豆和水的体积:
2 × 2 × 1.3=5.2(dm3)
土豆的体积:
5.2-5=0.2〔dm3〕 水深13厘米 dm3。
64-48=16〔dm3)=16(L)
答:缸里的水会溢出16L。
拓展应用
〔24-12〕÷3 =12÷3 =4(ml)
12-4 =8(ml)
答:大圆球的体积是8ml。
4、 一个长方体容器内装满水,现在有大、 中、小三个石块。第一次把小石块沉入水中, 溢出了5ml水;第二次把小石块拉出来,把中 石块沉入水中,溢出的水是第一次的3倍;第 三次把中石块拉出来,把大石块沉入水中, 溢出的水是第一次的2倍。中石块和大石块的 体积各是多少cm3?
不规则物体体积计算你总Fra bibliotek出一般规律了吗?
不规那么物体的体积=
( 升水法 ) 上升那局部水的体积
物
( 降水法 ) 下降那局部水的体积
体 必
〔或=底面积×上升(或下降)的高度〕
须 完
( 溢水法) 溢出那局部水的体积
全 浸 没
V物 = V(水+物)-V水
注意:不是所有不规那么物体都能用排水法
测体积。有些物体放入水中,会浮在水面或
写出列式
50 ×40 ×3
解决问题 1、把一个铁球漂浮在长分米, 宽分米的长方体容器里,水面由 分米上升到6分米,你能求出这 个铁球的体积是多少吗?
V=abh ×1.2×〔6-〕
