点的坐标变换及在MATHCAD中的实现方法
mathcad函数运算

第四章
1
MathCAD 函数运算
基本数学函数运算 离散数值变换 微分方程函数 方程的求解和优化 其他函数运算
2
3
4
6 5
基本数学函数运算
三角函数和反三角函数 sin(z) cos(z) tan(z) cot(z) sec(z) 正弦函数 余弦函数 正切函数 余切函数 正割函数 asin(z) acos(z) atan(z) acot(z) asec(z) 反正弦函数 反余弦函数 反正切函数 反余切函数 反正割函数
csch(z)
余割函数
acsch(z) 反余割函数
基本数学函数运算
对数和指数函数 exp(z) Ln(z) log(z,b) 返回e的z次幂 返回z的自然对数(z≠0) 返回z的以b为基地对数(z≠0, b≠0),省略b返回以10为基地对数
基本数学函数运算
复数函数
Re(Z) 返回 Z 的实数部分
Im(Z) arg(z)
csgn(z)
返回 Z 的虚数部分 返回 z 的主值辐角,在 −π —— π 之间
返回复数的符号,在 Re(z) > 0 或 (Re(z) = 0 且 Im(z) > 0) 时返回 1,其他情况下 仍返回 1。
返回单位向量,在 z = 0 时将返回 x,其他 signum(z, [x]) 情况下则返回 z/|z|。如果省略 x,则 z = 0 时将返回 1。 在 x = 0 时将返回 0,在 x > 0 时返回 1 sign(x) ,其他情况下仍返回 −1。
Trunc(z, y)
返回 y ≥ z 的最小倍数 通过去掉 z 的小数部分,返回其整数部分。
返回 trunc(z / y) · y。
mathcad教程Mathcad是一款用于科学、工程和数学领域的符号计算软件,

mathcad教程Mathcad是一款用于科学、工程和数学领域的
符号计算软件,
Mathcad是一款用于科学、工程和数学领域的符号计算软件,其主要功能是通过标准公式的输入,实现科学计算和数据分析等操作。
一个Mathcad的基础教程。
1. 界面介绍
打开Mathcad软件,可以看到主界面分为多个区域,包括公式编辑区、工具栏、浏览器等。
了解Mathcad界面组件的作用和使用方法对于学习该软件非常重要。
2. 基本操作
在Mathcad中输入公式可以实现各种数学运算。
可以使用Mathcad中的符号、函数和运算符来输入公式,还可以设置变量和常量。
输入完成后,可以进行计算和结果显示操作。
3. 分析和优化
在Mathcad中,可以使用多种先进工具来分析和优化输出结果。
例如,可以使用方程求解器来解决方程组,使用非线性规划器解决优化问题,使用数值积分符号来计算积分等。
4. 绘图
Mathcad提供了丰富的绘图工具和选项,可以绘制各种二维和三
维数据图表、函数图形等。
这些图表可以通过设置坐标轴、标注和标题等方式来形成高质量的图表。
5. 建模和仿真
利用Mathcad,可以进行各种建模和仿真操作。
通过数学建模和仿真,可以更好地理解系统和过程的运行,提高分析速度和准确性。
总的来说,Mathcad是一款非常实用的科学计算软件,初学者需要通过多次练习和实践来掌握其基本使用方法和技巧。
学习过程中,可以参考Mathcad的官方网站提供的教程资料及其各种工具和功能。
Mathcad操作方法

Mathcad一.一.MathCAD简介MathCAD是美国Mathsoft公司推出的一个交互式的数学软件。
该软件定位于向广大教师、学生、工程人员提供一个兼备文字处理、数学和图形能力的集成工作环境,使他们能方便地准备教案、完成作业和准备科学分析报告。
在输入一个数学公式、方程组、矩阵之后,计算机能直接给出结果,而无须去考虑中间计算过程。
在加入软件包自带的Maple插件后能直接支持符号运算。
你可以在计算机上输入数学公式、符号和等式等,很容易地算出代数、积分、三角以及很多科技领域中的复杂表达式的值,并可显示数学表格和图形,通过对图形结果的分析,使我们对问题的理解更加形象。
二.二.特点1. 1.与数学书写习惯非常接近;2. 2.动态的所见即所得(WYSIWYG)界面;例:a:=3 a+4=7 当a的值改变时后a+4的值自动更新。
3. 3.任意位置输入You can place equations, text, and graphics anywhere(不受行的限制)。
三.三.操作环境的设置(一)(一)显示/关闭工具栏1.1.常用工具栏:“View”菜单——Toolbar2.2.格式工具栏:“View”菜单——Format bar3.3.数学工具栏:“View”菜单——Math Palatte(二)(二)对象域RegionMathcad 文档是一个式子、文字、图形等对象的集合。
创建每一个对象时就生成了一个不可见矩形包围的对象域Region.显示/关闭对象域Region:“View”菜单——Regions四.四.文档编辑(MATHCAD WORKSHEET)(三)(一)常用数学符号的输入4. 1.键盘输入字母,Ctrl+G 希腊字母:例:a,Ctrl+G →αp,Ctrl-G→πD,Ctrl-G→Δ* 乘号multiplication or inner (dot) product/ 分数division^ 指数exponentiation。
MathCAD介绍

Presenter
议程
Mathcad介绍 Mathcad简介 Mathcad功能简述 Mathcad的优势 案例分享
Mathcad介绍
Mathsoft成立于1985 总部设于Cambridge, MA 2006年4月PTC收购Mathsoft公司
在工程计算领域20年的领先地位
客户大多是来自工业领域的佼佼者,其中90%为世界财 富1000 250K商业用户使用Mathcad进行工程计算和优化 全球近2000所大学,500K学生用户和老师使用Mathcad 进行学习和学术研究
网络分析,回馈饲服,稳定性分 析Conduct network analysis, feedback controls, and circuit stability analysis
工程应用:信号处理
14.0
Mathcad应用
1D信号分析Analyze 1D signals from sound, sonar, radar, etc.
Windchill PDMLink 能够提供内容
和过程管理功能,并能 管理物料列表和产品配
置
Arbortext发行 引擎能够为下游 读者自动汇编组 件并发行产品档
购通
工程规范 用户/培训手册
制造文件 法规档 维护档 营销材料 产品目录
Arbortext IsoView 提供交互功能 浏览嵌入式 MCAD和ECAD
资料分析Perform data analysis: Parametric fitting, quality of regression, etc.
工程设计应用:微波电路设计
Mathcad可用于: 分析从电路板输出的电磁辐射级别 分析电磁干涉(EMI) 执行传导线路分析
MATHCAD中建模方法及工程应用
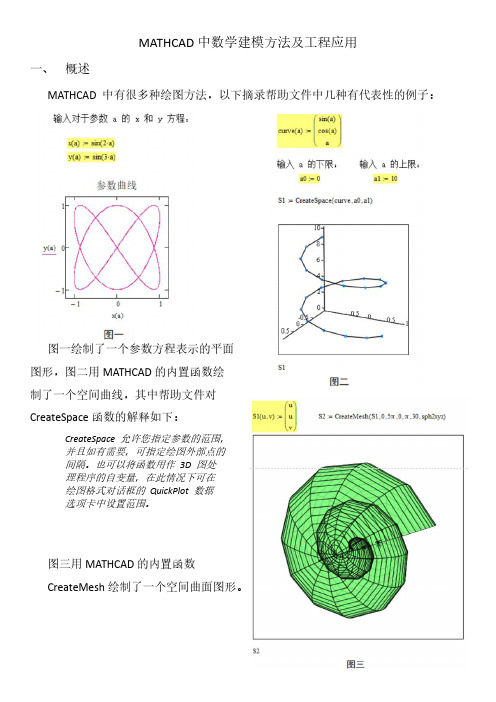
MATHCAD中数学建模方法及工程应用一、概述MATHCAD中有很多种绘图方法,以下摘录帮助文件中几种有代表性的例子:图一绘制了一个参数方程表示的平面图形,图二用MATHCAD的内置函数绘制了一个空间曲线,其中帮助文件对CreateSpace函数的解释如下:CreateSpace允许您指定参数的范围,并且如有需要,可指定绘图外部点的间隔。
也可以将函数用作3D图处理程序的自变量,在此情况下可在绘图格式对话框的QuickPlot数据选项卡中设置范围。
图三用MATHCAD的内置函数CreateMesh绘制了一个空间曲面图形。
MC中也可以读取外部数据绘制图形,如下:二、MATHCAD的绘图方法浅析看以上绘图方法能感觉到MATHCAD是个不错的软件,但同时结合自己的数学知识及工作中的问题,想作一些图形或者进一步分析时会发现好像自己仍然还是不清楚如何把自己想要的图形绘制出来,这应该也是部分人认为MATHCAD只适合教学、做一些简单数学计算的原因。
个人认为这是低估了MATHCAD的能力,深入研究及尝试会发现自己想要的图形都可以在MATHCAD中表现出来,只是相关的资料较少或者MATHCAD的研发人员的实现思路和自己固有的想法不同而已。
MATHCAD绘图时使用比较多的是嵌套矩阵,即矩阵的元素也是矩阵。
而且同一个矩阵的元素的数据格式可以不同,这使矩阵的使用比较灵活。
如果有编程经验的话应该对“面向对象的编程方法”并不陌生,MC中的矩阵也可以理解为封装“对象”的一个容器,具体保存何种数据取决于你想分析什么问题、需要什么数据。
通常实际的工程项目中的数据或者函数能象如上例子中可以用解析方式表达的情况并不多见,多数情况只能用数值的方法表达,比如实验数据、模型的空间结构尺寸数据等。
以下对MC的绘图方法做一些初步的探讨并列举几种常用的绘图方式。
1.等高线图的绘图解析(以图四为例)a)矩阵M的数据结构利用MC中的内置函数,可对M中的数据结构进行分析如下:从矩阵M的数据及三维图可看出MC中对数据表绘制三维图的定义如下所示:图五由此可知,MC 在通过二维图表数据绘制三维图时把数据表(或矩阵)的行数、列数作为数据的X,Y 坐标来看待,而其中的数据即是Z 值。
坐标变换的方法

坐标变换的方法
哇塞,坐标变换的方法啊,这可真是个超有趣的话题呢!
坐标变换呢,简单来说就是把一个坐标系中的点转换到另一个坐标系中。
步骤其实不难理解啦,首先要确定原始坐标系和目标坐标系之间的关系,比如平移、旋转或者缩放的参数啥的。
然后呢,根据这些参数,利用相应的数学公式来计算每个点在新坐标系中的位置。
这里可一定要小心哦,参数可不能搞错,不然结果就全乱套啦!注意事项也不少呢,比如说要仔细检查坐标系的定义和方向,确保变换的准确性呀。
在这个过程中,安全性和稳定性那可是相当重要的呀!想象一下,如果在变换过程中出了差错,那后果可能不堪设想呢!就像盖房子,根基没打好,那房子还不得摇摇欲坠呀!所以必须要保证数据的准确性和计算的稳定性,这样才能让我们放心大胆地进行坐标变换呀。
坐标变换的应用场景那可太多啦!比如在计算机图形学中,让图像能够自由地旋转、缩放和平移,呈现出各种酷炫的效果。
在机器人领域,能帮助机器人准确地定位和移动。
优势也是显而易见的呀,它让我们能够更灵活地处理和分析数据,就像给我们的思维装上了翅膀,能自由翱翔在数据的天空中呢!
我给你说个实际案例哈,在虚拟现实游戏中,坐标变换就发挥了巨大的作用呢!玩家在虚拟世界中自由移动,看到的场景也会随之变化,这背后就是坐标变换在默默地工作呀。
玩家可以尽情享受游戏的乐趣,感受身临其境的体验,这效果简直太棒啦!
坐标变换真的是超级神奇又超级有用的方法呀!它就像一把神奇的钥匙,能打开无数知识和技术的大门,让我们的世界变得更加丰富多彩呢!。
MathCAD计算说明书

点击vector 的Matrix Palette 按翎(或选择Insert 菜单中的Matrix ) ,在弹出的对话框中输入相应的行列数,在这电我们取3 x3 然后键入数字
进行可逆运算,只要输入
要计算行列式的值,利用vectorand Matrix、Palette上的按钮
7.解方程
开始先猜测一个根
函数按钮
插入函数对话框中列出了许多您可以插入您的工作表中的函数。
您也能直接用键盘输入任一个内建的函数,下面是一些内建函数的例子。
Trig and Logs
Lesson3 :输入数学和文本
输入数字
在空白处点击一下,出现一个红色的小叉,现在您可以输入数学了:
输入1+
屏幕上可见
输入加号之后,您看到有一个黑色的小方框,还有蓝色的编辑线,在Mathcad 中,这个框称为占位符。如果您继续输入,您所输入的都会出现在这个占位符中,例如,您输入2 ,然后输入等于符号,然后回车,结果如下:
比如,在一个程序语言中,等式输入应该是这样:
x = (-B + SQRT ( B * * 2-4 * A * C ) ) / ( 2 * A )
在Mathcad中,输入同样的等式就同您在参考书中看到的一样:
v=
唯一的区别在于Mathcad 中的等式和图表是活的。改变其中的任意一个数据、变量或者等式,Mathcad 就立到重新计算这些数学公式和画图。在Mathcad 的帮助下,您可以解决许多的技术问题― 从简单的到非常复杂的数值或符号运算。您可以利用兰维或三维图形使等式和数据显性化。利用Mathcad 电子书,您也可以得到许多数学知识和相关的参考资料,并且都可以在您的工作表中直接使用的。最重要的是,Mathcad 的强大的功能可以帮助您完成您的工作。利用M athcad ,您可以钻研问题、形成新的概念、工作表、分析数据和模型并检验备选方案以作出最好的选择,而且可以记录、显示和交流这些结果。利用Mathcad 连接到因特网,您还可以把您的工作表和您的同事以及其它的专家共享。这就意味着您和您同事之间的沟通交流非常容易,而且您可以利用丰富且强大的数学语言进行工作。
MathCAD的用法
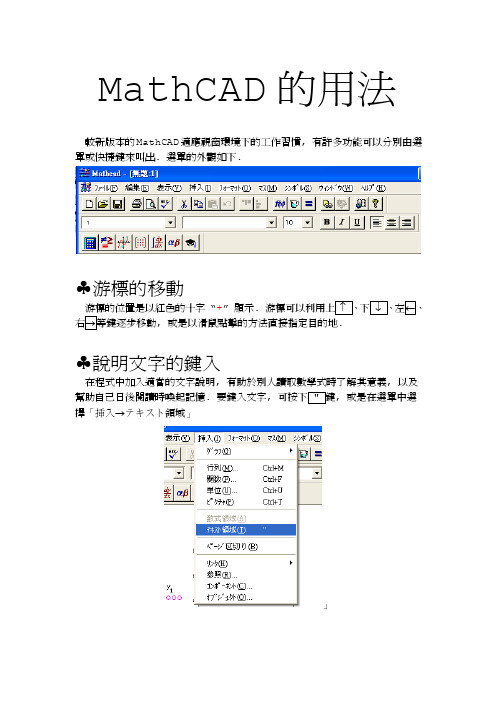
MathCAD的用法較新版本的MathCAD適應視窗環境下的工作習慣, 有許多功能可以分別由選單或快捷鍵來叫出. 選單的外觀如下.♣游標的移動游標的位置是以紅色的十字“+” 顯示., 或是以滑鼠點擊的方法直接指定目的地.♣說明文字的鍵入在程式中加入適當的文字說明, 有助於別人讀取數學式時了解其意義, 以及幫助自己日後閱讀時喚起記憶. 要鍵入文字, , 或是在選單中選擇「挿入→テキスト領域」」之後會出現, 在其中可以鍵入文字. 例如鍵入「這是李遠哲的自由落體實驗數據」, 畫面顯示♣方程式計算執行的順序方程式的計算執行順序是由左而右, 由上而下.♣虛數單位“i” 或“j”在程式中, i或j用法相同. 虛部與i之間不要加上乘號, 例如12+34i與12+34j是相同的. 注意程式硬性規定虛部是1時要鍵入1i, 不能只鍵入i, 否則會被視為變數i, 出現錯誤. 在游標移走之後, 1i的1會自動被隱藏起來, 看起來像是i. 以下是將變數i指定為3的例子.♣常數“π”這個變數名稱“π” 被保留給圓周率用. 要輸入希臘字母“π”, 除了同外, 也可用滑鼠點選鍵, 在跳出的字母盤中選取即可.♣常數 “e”自然對數的基底.e lne log e 1==.♣四則運算 ”♠範例: 詴計算78 kg 12 m 34 m (56 m)90 kg ⎛⎫+- ⎪⎝⎭.鍵入1 2 m + 3 4 m – 5 6 m * 7 8 k g / 9 0 k g = 畫面顯示.♣括號 ,♠範例: 詴計算(2 m + 3 m)(5 kg). 鍵入 ( 2 m + 3 m ) * 5 k g = 畫面顯示.另一種產生括號的方法, .用滑鼠選擇要放入括號的部份, 然後按, 即可在被選的部份外側產生一對括號.♣次方 ”♠範例: 計算(2 m). 鍵入( 2 m ) ^ 3 = 畫面顯示.♣科學記數法注意! 不能像Excel 那樣使用 “E”, 必需使用 “10^” ♠範例: 鍵入561.23410 m -⨯.鍵入畫面顯示.鍵入2. 若不向右移動2次, 無法正確輸入單位, 會產生錯誤訊息., 並以紅色顯示輸入有誤的部份, 如下.♣根號”♠範例:鍵入 \ 9 m ^ 2 =畫面顯示.♣常用的符號及函數一些常用的符號及函數, 除了用快捷鍵之外, 也可用滑鼠點出來. 用滑鼠點擊, 會跳出一個有各式符號及函數的視窗以供選擇.更多的函數可按. 但在中文環境下, 函數的日文詳細說明可能會看不到.♣單位的變更內部定義好的單位可按.♠範例1: 將1.23 m以in單位表示.鍵入 1 . 2 3 m =畫面顯示,次, 將游標移至黑色方塊的區域後, 鍵入in及畫面顯示.另外, 常數也可以當成單位的一部份.♠範例2: 將1.23 Hz改以π s-1單位表示.鍵入畫面顯示.♠範例3: 將1.23改以百分數來表示鍵入畫面顯示.♣定義新單位程式內建有常用的SI單位, cgs單位及英制單位. 若要使用其他沒有被內建的單位, 可以自行定義.♠範例: 定義公寸dm ≡ 0.1 m.鍵入 d m ~ 0 . 1 m畫面顯示.♣改變顯示的小數位數將游標移至要改變小數位數的結果上, 在選單上選取「フォーマット(O)→数値(N)」之後, 在跳出的視窗裡修改表示精度的數值, 再按下「OK」即可.♣指定變數的值注意! 變數名稱可以由1個以上的字母所組成, 除了第1個字母外, 中間或最後可以穿插數字. 因此在程式中, 變數之間的乘號不能省略. 另外注意變數的值經指定之後, 仍然可以變更.♠範例1:如果要變數看起來有下標註解的樣子, 可以用小數點“.”♠範例2: star bucks := 3 cm⋅s-1鍵入s t a r . b u c k s : = 3 c m * s ^ - 1畫面顯示.♣定義函數注意! 函數名稱可以由1個以上的字母所組成, 除了第1個字母外, 中間或最後可以穿插數字. 函數的形式經指定之後, 仍然可以變更.♠範例: 指定apple3banana(x) = x3.鍵入a p p l e 3 b a n a n a ( x ) : x ^ 3畫面顯示定義好之後, 計算apple3banana(5),鍵入a p p l e 3 b a n a n a ( 5 ) =畫面顯示♣一維數據統計♠範例1: 用矩陣的形式輸入先鍵入r a d i u s :還不要按Enter, 畫面顯示接下來按Ctrl-m, 或是由選單選「挿入(I)→行列(M)」會跳出對話視窗, 在其中輸入矩陣的大小. 注意! 在日文中行是row, 列是column, 恰好與台灣中文的習慣相反.在row輸入5, column輸入1之後按OK, 則畫面上出現5⨯1的矩陣(即5個元素的縱向量).依序在每個黑格子中輸入資料, 再以Tab鍵或滑鼠依序移至下1個位置上. 最後用右鍵移至矩陣右方, 鍵入單位. 例如:求平均值, 鍵入m e a n ( r a d i u s ) =畫面顯示求取樣標準偏差, 鍵入S t d e v ( r a d i u s / m ) m =(程式有小缺陷, 不接受有單位的數據. 另外注意開頭的S是大寫.) 畫面顯示*求群數標準偏差, 鍵入s t d e v ( r a d i u s ) =(開頭的s是小寫). 畫面顯示求平均標準偏差, 鍵入Stdev(radius/m)m/\length(radius)(注意開頭的S是大寫). 畫面顯示其中length()函數會傳回radius向量中的元素個數, 即5個.回顧一下, 整個計算看起來像這樣:♠範例2: 用表格的形式輸入為了符合一般人的習慣, 將註腳起點定為1, 必需先鍵入畫面顯示先定義駐腳變數. 如果有5個數據點, 則鍵入畫面顯示.接下來輸入數據, 鍵入畫面顯示求平均值, 鍵入m e a n ( x ) =畫面顯示求取樣標準偏差, 鍵入S t d e v ( x / m ) m =(程式有小缺陷, 不接受有單位的數據. 另外注意開頭的S是大寫.) 畫面顯示*求群數標準偏差, 鍵入s t d e v ( x ) =(開頭的s是小寫). 畫面顯示求平均標準偏差, 鍵入Stdev(x/m)m/\length(x)= (注意開頭的S是大寫). 畫面顯示回顧一下, 整個計算看起來像這樣:♣繪二維數據圖♠範例:先定義駐腳變數. 如果有5個數據點, 則鍵入畫面顯示.接下來輸入橫座標, 鍵入畫面顯示之後再輸入縱座標, 鍵入畫面顯示或者從選單上面選「挿入(I)→グラフ(G)→プロット@」畫面上會出現空的XY圖利用; 也可用滑鼠直接點擊目的地. 在橫軸上鍵入得到由於普物實驗經常並不需要數據間的連線, 因此我們將連線取消, 在圖上用滑鼠雙擊, 或是從選單中選擇「フォーマット(O)→グラフ(G)→X-Yプロット」之後會出現在「種類(T)」該欄中選擇第2項(在中文環境下有時日文字會看不見),即可將接線消去, 如下圖因為點太小了會看不清楚, 可將數據點加上記號. 在記號欄「(S)」中可以選擇.「(S)」由上到下各項所代的符號分別為., ⨯, +, □, ◊, ○.在「色(C)」欄中可以選擇不同的顏色. 若有繪接線時, 「線(N)」可以用來選擇各種不同的虛線. 而「種類(T)」則是選擇各種不同的圖形種類, 如階梯圖, 棒狀圖等.修改所顯示數據的範圍, 可將橫軸變數及縱軸變數2端的數字修正. 例如強制程式將原點表示出來, 可將橫軸左端的1.5改成0, 縱軸下端的2.5改成0, 則圖形變成最後, 為了使圖的意義清楚, 可在圖上加上說明. 在圖上以滑鼠雙擊, 選取「ラベル」這個分頁, 分別在各欄中填入圖的名稱, x軸名稱, y軸名稱, 並勾選「表示(S)」.圖形上出現各個說明.♣二維數據的線性迴歸♠範例先分別輸入自變數與因變數的數據, 可以用矩陣輸入形式或列表形式的其中任何一種. 接下來計算相關係數迴歸斜率以及迴歸截距利用線性迴歸計算後, 將迴歸直線加在圖形上的例子:注意! “m”這個變數名稱已經用來當作長度單位, 因此不宜再使用. 在做線性迴歸圖形時, 2組數據名稱之間以逗號“,”隔開.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图所示,求空间任一点 P3 绕任一轴(以线段 P1P2 表示)转动θ角所得 P 点的坐标。
设点(P1,P2,P3)的坐标:
由高等数学知识可知,通过 P3 且垂直于直线(P1,P2)的平面的方程为: (1)
设该平面和直线(P1,P2)的交点为 P4。 直线(P1,P2)的参数方程:
(2)
由联立方程组(1)(2)可解出:
如图二所示: 在直角坐标系 XOY 中任一点的坐标 可由如下参数方程定义:
则有:
(1)
由(1)(2)得:
(2) (3)
b) 向量分析 如图二所示: P2 的坐标可以由向量 OP2 来表达
向量 r2 可对 r1 作旋转变换由公式(3) 求出。 3.MATHCAD 中实现二维变换
a) 关于坐标原点的旋转平移变换公式
( ) w2 + 1 − w2 ⋅ cos(θ) r2z
则 P3 在局部坐标系(X0,Y0,Z0)中绕 直线(P1,P2)的转轴公式以齐次坐标 表示如下:
在整体坐标系中向量: 至此即求出 P 点坐标。 如考虑平移及转动叠加,2 ⋅ cos(θ)
u ⋅ v ⋅ (1 − cos(θ)) − w ⋅ sin(θ) u ⋅ w ⋅ (1 − cos(θ)) + v ⋅ sin(θ) px r20
( ) w2 + 1 − w2 ⋅ cos(θ)
pz r22
0
0
0
1 1
其中(Px Py Pz)表证了平移量。
2. MATHCAD 实现过程 MATHCAD 是一款优秀的数学工具软件,合理运用将能节省研发人员、工
程设计人员、在校师生等大量的计算时间,如下是解题过程:
① 解析运算 ② 定义函数
③ 使用函数
由此可见,MATHCAD 是一款所见即所得的数学软件,其解题过程和人们 惯用的手写计算书非常类似,会省去很多繁琐的数学推导和数值计算,对解 决实际的问题带来不少便利。
附: MATHCAD 中旋转曲面生成示意图
代入(2)即可得到交点 P4 的坐标。
图五 如图五所示,以 P4 为原点的局部坐标系(X0,Y0,Z0)中:
设向量 r5 的齐次坐标为:
单位向量:
向量:
r2=P3-P4
根据罗德里格旋转公式:设 V 是一个三维空间向量,K 是旋转轴的单位向
量,则 V 在右手螺旋定义下绕 K 轴旋转角度θ得到的向量可以由以下公式定
义:
Vrot V ⋅ cos(θ) + (K × V) ⋅ sin(θ) + K ⋅ (K ⋅ V) ⋅ (1 − cos(θ))
图六(罗德里格旋转公式详解)
u
设:
K
v
w
代入上述公式可得:
r2x
V
r2y
r2z
( ) u2 + 1 − u2 ⋅ cos(θ)
u ⋅ v ⋅ (1 − cos(θ)) − w ⋅ sin(θ) u ⋅ w ⋅ (1 − cos(θ)) + v ⋅ sin(θ) r2x
注:T 代表转置矩阵 以上是以齐次坐标表示的点(x,y)关于坐标原点的旋转平移变换,U,V 代表平 移量。 注意到以下公式:
由此可知,齐次坐标表达对于左乘和右乘公式是有区别的。
b) 定义二维变换函数
如上函数计算 P1 绕 P0 逆时针旋转θ角所得点的坐标值,以向量表达。 使用函数示例: 二、三维坐标变换 1.计算原理
Vrot
u ⋅ v ⋅ (1 − cos(θ)) + w ⋅ sin(θ)
( ) v2 + 1 − v2 ⋅ cos(θ)
u
⋅
w
⋅
(1
−
cos(θ))
−
u
⋅
sin(θ)
⋅
r2y
u ⋅ w ⋅ (1 − cos(θ)) − v ⋅ sin(θ) u ⋅ w ⋅ (1 − cos(θ)) + u ⋅ sin(θ)
r5 u ⋅ v ⋅ (1 − cos(θ)) + w ⋅ sin(θ)
( ) v2 + 1 − v2 ⋅ cos(θ)
u ⋅ w ⋅ (1 − cos(θ)) − u ⋅ sin(θ)
py
⋅
r21
u ⋅ w ⋅ (1 − cos(θ)) − v ⋅ sin(θ) u ⋅ w ⋅ (1 − cos(θ)) + u ⋅ sin(θ)
点的坐标变换及在 MATHCAD 中的实现方法 一、 二维坐标变换
1. 求解目标 如图一所示,在直角坐标系 XOY 中
设:点 P1 的坐标为 (X1,Y1),P1 绕 点 P0 (X0,Y0)逆时针旋转θ角所得坐标点 为 P2:(X2,Y2)。 求:P2:(X2,Y2) 2. 计算原理 此问题的求解可分步骤如下: a) 任一点绕坐标原点旋转的计算:
