甲醇_甲缩醛_甲醛_水四元系的汽液平衡
甲醇_甲缩醛_甲醛_水四元系的汽液平衡_(1)

收稿日期:1998-11-26基金项目:江西省自然科学基金资助项目(982004)第18卷 第1期1999年3月南昌水专学报Journal of Nanchang College of Water Conservancy and Hydroelectric Power Vol.18 No.1Mar.1999文章编号:1006-4869(1999)-01-0005-03甲醇-甲缩醛-甲醛-水四元系的汽液平衡(Ⅱ)邱祖民1,倪柳芳2,章国荣3,刘建华4(11南昌大学 化工系,江西 南昌 330029;21上饶地区工业学校,江西 上饶 334000;31南吉化学工业公司,江西 南昌 330077;41深圳市燃气工程监理有限公司,广东 深圳 518001)摘 要:本文推算了甲醛液相组成为10%和20%时的甲醇-甲缩醛-甲醛-水四元系汽液平衡,给出了X F =10%、X F =20%时的等Y W 、Y M 和等温图1关键词:汽液平衡;热力学模型;甲醇;甲醛;甲缩醛中图分类号:O64214 文献标识码:A0 引 言文献〔1〕建立了甲醇-甲缩醛-甲醛-水四元系的汽液平衡热力学模型,文献〔2〕进一步研究了该四元系的汽液平衡,文献〔3〕验证了该模型的准确性,本文旨在预测该四元系在X F 为10%和20%时的汽液平衡行为,供工程研究及设计时参考11 热力学模型〔1〕针对以往含甲醛多元系热力学模型的不足,需考虑甲醛的溶剂化反应,因而模型复杂,计算工作量大,且由于甲醛溶剂化反应的平衡常数很缺乏,需作某些假设或进行近似计算1实际上,由于甲醛与活性组分间的溶剂化反应,使得单体甲醛甚少,生成难挥发的甲醛水合物或甲醛聚合物,这在宏观上表现为影响了甲醛的饱和蒸汽压,使其远远偏离真实的甲醛饱和蒸汽压,而表现为虚拟的饱和蒸汽压1因此只要拟合出甲醛在活性溶剂中的虚拟饱和蒸汽压,即可对含甲醛多元系在虚拟组分上进行计算,可不必考虑其溶液中的真实组分,也不必考虑甲醛的溶剂化反应,因而模型易建易算,详细的描述参阅文献〔1〕1相平衡方程P S i f S i X i exp 〔V L mi (P -P S i )/R/T 〕r i =P Y i f iP S ′F f S F X F exp 〔V L mF (P -P S ′F )/R/T 〕r F =P Y F f F 式中P S ′F =P c F exp (4.5+4.5/T r -11.91/T 2r )甲醇-甲缩醛-甲醛-水四元系所含二元系的Wilson 模型参数如附表所示1附表 二元系的Wilson 模型参数表系统水-甲醇甲缩醛-水水-甲醛甲醇-甲缩醛甲醇-甲醛甲醛-甲缩醛参数225.3 444.1629.1 2271.70.5 875-65.9 903.8-345 0.23050 7152 模型预测用该模型推算了甲醛液相组成为10%和20%时的甲醇-甲缩醛-甲醛-水四元系汽液平衡,推测结果分别示于图1~图61图1 X F =10%时的甲缩醛-甲醇-甲醛-水四元系VL E 等温图 1-44.2℃;2-4415℃;3-46℃; 4-55℃;5-65℃ 图2 X F =10%时的甲缩醛-甲醇-甲醛-水四元系VL E 等Y W 图 1-2%;2-5%;3-7%;4-8%;5-9%; 6-10%;7-20%图3 X F =10%时的甲缩醛-甲醇-甲醛-水四元系VL E 等Y M 图 1-10%;2-20%;3-30%;4-40%;5-50%; 6-60%;7-70% 图4 X F =20%时的甲缩醛-甲醇-甲醛-水四元系VL E 等Y M 图 1-47℃;2-48℃;3-49℃;4-50℃; 5-55℃;6-7215℃ 6南昌水专学报1999年第1期图5 X F =20%时的甲缩醛-甲醇-甲醛-水四元系VL E 等Y W 图 1-2%;2-5%;3-7%;4-815%; 5-10%;6-20% 图6 X F =20%时的甲缩醛-甲醇-甲醛-水四元系VL E 等Y M 图 1-5%;2-10%;3-20%;4-30%; 5-40%;6-50% 3 结 论本文推算了甲醛液相组成为10%和20%时的甲醇-甲缩醛-甲醛-水四元系汽液平衡,给出了X F =10%、X F =20%时的等Y W 、Y M 和等温图,可供工程研究及设计时参考1〔参考文献〕1 邱祖民,骆赞椿,胡英1甲缩醛-甲醇-甲醛-水四元系的汽液平衡〔J 〕1高校化学工程学报,1998,12(1):61.2 邱祖民,骆赞椿,胡英1甲缩醛-甲醇-甲醛-水四元系的汽液平衡(Ⅰ)〔J 〕1南昌大学学报,1998,20(4).3 邱祖民,柳雪芳,倪柳芳等1甲醇-甲缩醛-甲醛-水四元系的汽液平衡〔J 〕1南昌水专学报,1998,17(3):10.V apor Liquid Equilibria of theMethanol -Methylal -Formaldehyde -W ater System(Ⅱ)Q IU Zu -min 1,N I Liu -fang 2,ZHAN G Guo -rong 3,L IU Jian -hua 4 (1.Department of Chemical Engineering ,Nanchang University ,Nanchang 330029China ;2.Shangrao Supervisory Office of Technicality ,Shangrao 334000China ;3.PPG Nanchang Chemical Industry Ltd.,Nanchang 330077China ;4.Shen Zhen G as Engineering Supervision Company ,Shenzhen ,518001China )Abstract :The vapor -liquid equilibria (VL E )of the methanol -methylal -formaldehyde -water system was predicted ,and the isothermal figures ,the isograms of Y W and Y M were depicted at X F =10%and 20%in this paper.K ey w ords :VL E ;Thermodynamic model ;methanol ;formaldehyde ;methylal 7第1期邱祖民:甲醇-甲缩醛-甲醛-水四元系的汽液平衡(Ⅱ)。
甲醇水汽液平衡
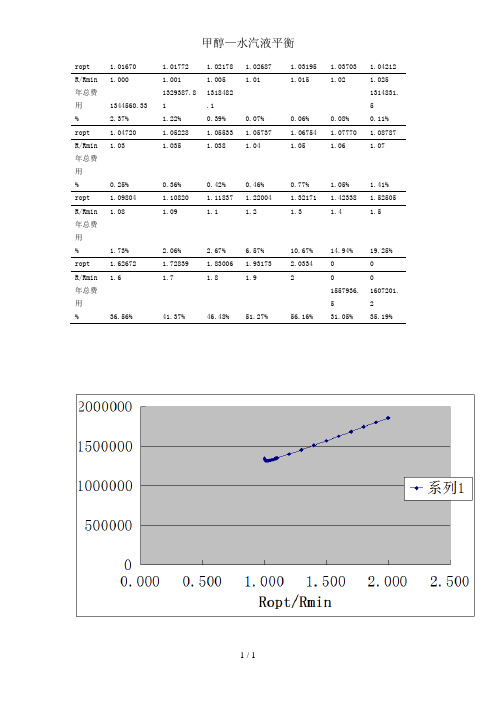
ropt 1.01670 1.01772 1.02178 1.02687 1.03195 1.03703 1.04212 R/Rmin 1.000 1.001 1.005 1.01 1.015 1.02 1.025年总费用1344560.33 1329387.811318482.11314831.5% 2.37% 1.22% 0.39% 0.07% 0.06% 0.08% 0.11% ropt 1.04720 1.05228 1.05533 1.05737 1.06754 1.07770 1.08787 R/Rmin 1.03 1.035 1.038 1.04 1.05 1.06 1.07年总费用% 0.25% 0.36% 0.42% 0.46% 0.77% 1.05% 1.41% ropt 1.09804 1.10820 1.11837 1.22004 1.32171 1.42338 1.52505 R/Rmin 1.08 1.09 1.1 1.2 1.3 1.4 1.5年总费用% 1.73% 2.06% 2.67% 6.57% 10.67% 14.94% 19.25% ropt 1.62672 1.72839 1.83006 1.93173 2.0334 0 0R/Rmin 1.6 1.7 1.8 1.9 2 0 0年总费用1557936.51607201.2% 36.56% 41.37% 46.48% 51.27% 56.16% 31.05% 35.19%附录二甲醇—水汽液平衡数据(摩尔组成)t x y t x y100.00 0.00 0.000 75.30 0.40 0.729 96.40 0.02 0.134 73.10 0.50 0.779 93.50 0.04 0.234 71.20 0.60 0.825 91.20 0.06 0.304 69.30 0.70 0.870 89.30 0.08 0.365 67.60 0.80 0.915 87.70 0.10 0.418 66.00 0.90 0.958 84.40 0.15 0.517 65.00 0.95 0.979 81.70 0.20 0.579 64.50 1.00 1.000 78.00 0.30 0.665附录一甲醇—水系统的主要物理性质附录三优化设计程序源代码优化程序'定义全局变量Dim J1#, J2#, J3#, J4#, JJ#Dim N#, R#, Ropt#Dim lilunbanshu#, jinliaoweizhi%, tajing#, chukouwendu#, chuanremianji#, zongtagao#, tiliuduanbanshu#, jinliuduanbanshu#Dim XF#, F#, q#, XD#, D#, td#, rD#, po#, u#, Rmin#, t1#, Cw#, Cp#, SI#, HETP#Dim Co#, HA#, f1#, f2#, a#, b#, FL#, θ#, ρ#, bo#, Fc#'优化所需参数Public Sub Form_Load()XF = 0.3151: F = 402.34: q = 1XD = 0.982: D = 128.97: td = 64.93: rD = 35373.48: po = 101.3u = 5.4464: Rmin = 1.0167t1 = 20: Cw = 0.0002: Cp = 4.1875: Co = 0.03: cpa = 15674.4HETP = 0.462: HA = 6f1 = 1: f2 = 6.5: a = 487: b = 0.72: SI = 3.73FL = 6.22: θ= 7200: ρ= 7860: bo = 0.005: Fc = 0.125Text1.Text = 402.34Text2.Text = 0.3151Text3.Text = 128.97Text4.Text = 0.982Text5.Text = 35373.48Text6.Text = 64.93Text7.Text = 1Text8.Text = 1.0167Text9.Text = 7200Text10.Text = 3.73Text11.Text = 0.125Text12.Text = 6.22Text13.Text = 0.005Text14.Text = 7860Text15.Text = 5.4464Text16.Text = 0.462Text17.Text = 6Text18.Text = 15674.4Text19.Text = 0.0002Text20.Text = 4.1875Text21.Text = 20Text22.Text = 2000Text23.Text = 1Text24.Text = 6.5Text25.Text = 487Text26.Text = 0.72Text27.Text = 0.03Text28.Text = 1.01Text29.Text = 2Text30.Text = 0.0001Text31.Text = " "Text32.Text = " "Text33.Text = " "Text34.Text = " "Text35.Text = " "Text36.Text = " "Text37.Text = " "Text38.Text = " "Text39.Text = " "Text40.Text = " "Text41.Text = " "Text42.Text = " "Text43.Text = " "Text44.Text = " "Text45.Text = " "Text46.Text = " "Text47.Text = " "End Sub'主程序Private Sub Command1_Click() '菲波拿契法求RoptDim Aa#, Bb#, W#(1 To 50), i%, K%, N#, M%, R1#, R2#, ε# Dim JJ1#, JJ2#Aa = 1.01 * Rmin: Bb = 2 * Rmin '搜索区间[Aa,Bb]W(1) = 1: W(2) = 2: W(3) = 3: i = 1: ε= 0.0001Do While W(i + 2) <= ((Bb - Aa) / ε)i = i + 1W(i + 2) = W(i) + W(i + 1)LoopR1 = Aa + (Bb - Aa) * W(i) / W(i + 2): JJ1 = j(R1)N = i + 2: K = 1: M = 0Do While K <> N - 1If M = 0 ThenR2 = Aa + (Bb - Aa) * W(N - K) / W(N - K + 1)JJ2 = j(R2)ElseR1 = Aa + (Bb - Aa) * W(N - K - 1) / W(N - K + 1)JJ1 = j(R1)End IfIf JJ1 < JJ2 ThenBb = R2: R2 = R1: JJ2 = JJ1: M = 1ElseAa = R1: R1 = R2: JJ1 = JJ2: M = 0End IfK = K + 1LoopR = (Aa + Bb) / 2Ropt = RJJ = j(R)Text31.Text = RoptText32.Text = RminText45.Text = Ropt / RminText33.Text = lilunbanshuText34.Text = zongtagaoText40.Text = J1Text41.Text = J2Text42.Text = J3Text43.Text = J4Text44.Text = JJText37.Text = tajingText38.Text = chukouwenduText39.Text = chuanremianjiText46.Text = Ropt * DText47.Text = (Ropt + 1) * DText35.Text = tiliuduanbanshu * HETPText36.Text = jinliuduanbanshu * HETPEnd Sub'J函数Public Function j(R#) As DoubleCall jjj1(R#, J1#)Call jjj2(R#, J2#)Call jjj3(R#, J3#)Call jjj4(R#, J4#)j = J1 + J2 + J3 + J4End Function'求J1Public Sub jjj1(R#, J1#)Dim DT#, H#, Ws#, CH#Call tabanshu(R#, N#)DT = Sqr((R + 1) * D * 22.4 / (3600 * 0.785 * u) * (273 + td) / 273 * 101.3 / po)H = N * HETP + HAWs = 3.14 * DT * (H + 0.8116 * DT) * bo * ρ'ρ为碳钢的密度CH = FL * Exp(6.95 + 0.1808 * Log(Ws) + 0.02468 * (Log(Ws)) ^ 2 + 0.0158 * H / DT)J1 = SI * (Fc + 0.06) * CHtajing = DTzongtagao = HEnd Sub'求J2Public Sub jjj2(R#, J2#)Dim xx1#, xx0#, CD#, ff#, df#, t2#, AD#, KD#KD = 2000: xx1 = 70Do '牛顿迭代法求冷却水最佳出口温度t2xx0 = xx1CD = 1.3 * SI * a * b * f1 * f2 * Fc * ((R + 1) * D * rD / (td - t1)) ^ (b - 1) / KD ^ bff = -Cw * θ/ Cp + CD * ((xx0 - 1) / xx0 / Log(xx0)) ^ (1 - b) * (xx0 - 1 - Log(xx0))df = CD * ((xx0 - 1) / xx0 / Log(xx0)) ^ (2 - b) * ((b - 1) * (xx0 - 1 - Log(xx0)) ^ 2 / (xx0 - 1) ^ 2 + Log(xx0))xx1 = xx0 - ff / dfLoop Until Abs(xx1 - xx0) < 0.000001t2 = td - (td - t1) / xx1 't2optchukouwendu = t2AD = (R + 1) * D * rD * Log((td - t1) / (td - t2)) / KD / (t2 - t1) '传热面积chuanremianji = ADJ2 = Cw * θ* (R + 1) * D * rD / Cp / (t2 - t1) + 1.3 * SI * Fc * f1 * f2 * a * AD ^ bEnd Sub'求J3Public Sub jjj3(R#, J3#)Dim Z#, Cz#Cz = 0.03Z = ((R + 1) * D - (1 - q) * F) * 18J3 = Z * Cz * θEnd Sub'求J4Public Sub jjj4(R#, J4#)Dim ho#, cpa!, HETP!cpa = 15674.4: HETP = 0.462Call tabanshu(R#, N#)ho = N * HETPDT = Sqr((R + 1) * D * 22.4 / (3600 * 0.785 * u) * (273 + td) / 273 * 101.3 / po)J4 = 3.14 / 4 * DT ^ 2 * ho * cpa * FcEnd Sub'塔板数的计算Public Sub tabanshu(R#, N#)Dim ye#, XW#Dim X!(100), Y!(100), xx!(100), i%, n1#td = 64.93: F = 402.34: XD = 0.982: XF = 0.3151: ηd = 0.999: D = 128.97: Rmin = 1.0167V = (R + 1) * D: W = F + V - D: XW = (F * XF - D * XD) / Wi = 1: Y(1) = 0.982: X(1) = 0.9702DoIf X(i) > XF ThenY(i + 1) = R * X(i) / (R + 1) + XD / (R + 1)n1 = i + 1 + (X(i) - XF) / (X(i) - X(i + 1))ElseY(i + 1) = W * (X(i) - XW) / VIf X(i) < XW Then Exit DoEnd Ifi = i + 1xx(i) = (Y(i) / (3.3874 * (1 - Y(i)))) ^ (1 / 0.7977)X(i) = xx(i) / (1 + xx(i))LoopN = i - 1 + (X(i - 1) - XW) / (X(i - 1) - X(i))lilunbanshu = Ntiliuduanbanshu = n1jinliuduanbanshu = N - n1End Sub调整ROPT程序:'定义全局变量Dim J1#, J2#, J3#, J4#, JJ#Dim N#, R#, Ropt#Dim lilunbanshu#, jinliaoweizhi%, tajing#, chukouwendu#, chuanremianji#, zongtagao#, tiliuduanbanshu#, jinliuduanbanshu#Dim XF#, F#, q#, XD#, D#, td#, rD#, po#, u#, Rmin#, t1#, Cw#, Cp#, SI#, HETP#Dim Co#, HA#, f1#, f2#, a#, b#, FL#, θ#, ρ#, bo#, Fc#'优化所需参数Public Sub Form_Load()XF = 0.3151: F = 402.34: q = 1XD = 0.982: D = 128.97: td = 64.93: rD = 35373.48: po = 101.3u = 5.4464: Rmin = 1.0167t1 = 20: Cw = 0.0002: Cp = 4.1875: Co = 0.03: cpa = 15674.4HETP = 0.462: HA = 6f1 = 1: f2 = 6.5: a = 487: b = 0.72: SI = 3.73FL = 6.22: θ= 7200: ρ= 7860: bo = 0.005: Fc = 0.125Text1.Text = 402.34 Text2.Text = 0.3151 Text3.Text = 128.97 Text4.Text = 0.982 Text5.Text = 35373.48 Text6.Text = 64.93 Text7.Text = 1Text8.Text = 1.0167 Text9.Text = 7200 Text10.Text = 3.73 Text11.Text = 0.125 Text12.Text = 6.22 Text13.Text = 0.005 Text14.Text = 7860 Text15.Text = 5.4464 Text16.Text = 0.462 Text17.Text = 6Text18.Text = 15674.4 Text19.Text = 0.0002 Text20.Text = 4.1875 Text21.Text = 20 Text22.Text = 2000 Text23.Text = 1Text24.Text = 6.5 Text25.Text = 487 Text26.Text = 0.72 Text27.Text = 0.03 Text28.Text = 1.01 Text29.Text = 2Text30.Text = 0.0001 Text31.Text = " " Text32.Text = " " Text33.Text = " " Text34.Text = " " Text35.Text = " " Text36.Text = " " Text37.Text = " " Text38.Text = " " Text39.Text = " " Text40.Text = " " Text41.Text = " " Text42.Text = " " Text43.Text = " " Text44.Text = " "Text45.Text = " "Text46.Text = " "Text47.Text = " "End Sub'主程序Private Sub Command1_Click() '菲波拿契法求Ropt R = Text31.TextRopt = RJJ = j(R)Text32.Text = RminText45.Text = Ropt / RminText33.Text = lilunbanshuText34.Text = zongtagaoText40.Text = J1Text41.Text = J2Text42.Text = J3Text43.Text = J4Text44.Text = JJText37.Text = tajingText38.Text = chukouwenduText39.Text = chuanremianjiText46.Text = Ropt * DText47.Text = (Ropt + 1) * DText35.Text = tiliuduanbanshu * HETPText36.Text = jinliuduanbanshu * HETPEnd Sub'J函数Public Function j(R#) As DoubleCall jjj1(R#, J1#)Call jjj2(R#, J2#)Call jjj3(R#, J3#)Call jjj4(R#, J4#)j = J1 + J2 + J3 + J4End Function'求J1Public Sub jjj1(R#, J1#)Dim DT#, H#, Ws#, CH#Call tabanshu(R#, N#)DT = Sqr((R + 1) * D * 22.4 / (3600 * 0.785 * u) * (273 + td) / 273 * 101.3 / po)If DT < 1 ThenDT = Int(DT * 10 + 1) / 10ElseDT = Int(DT * 5 + 1) * 0.2End IfH = N * HETP + HAWs = 3.14 * DT * (H + 0.8116 * DT) * bo * ρ'ρ为碳钢的密度CH = FL * Exp(6.95 + 0.1808 * Log(Ws) + 0.02468 * (Log(Ws)) ^ 2 + 0.0158 * H / DT)J1 = SI * (Fc + 0.06) * CHtajing = DTzongtagao = HEnd Sub'求J2Public Sub jjj2(R#, J2#)Dim xx1#, xx0#, CD#, ff#, df#, t2#, AD#, KD#KD = 2000: xx1 = 70Do '牛顿迭代法求冷却水最佳出口温度t2xx0 = xx1CD = 1.3 * SI * a * b * f1 * f2 * Fc * ((R + 1) * D * rD / (td - t1)) ^ (b - 1) / KD ^ bff = -Cw * θ/ Cp + CD * ((xx0 - 1) / xx0 / Log(xx0)) ^ (1 - b) * (xx0 - 1 - Log(xx0))df = CD * ((xx0 - 1) / xx0 / Log(xx0)) ^ (2 - b) * ((b - 1) * (xx0 - 1 - Log(xx0)) ^ 2 / (xx0 - 1) ^ 2 + Log(xx0))xx1 = xx0 - ff / dfLoop Until Abs(xx1 - xx0) < 0.000001t2 = td - (td - t1) / xx1 't2optchukouwendu = t2AD = (R + 1) * D * rD * Log((td - t1) / (td - t2)) / KD / (t2 - t1) '传热面积chuanremianji = ADJ2 = Cw * θ* (R + 1) * D * rD / Cp / (t2 - t1) + 1.3 * SI * Fc * f1 * f2 * a * AD ^ bEnd Sub'求J3Public Sub jjj3(R#, J3#)Dim Z#, Cz#Cz = 0.03Z = ((R + 1) * D - (1 - q) * F) * 18J3 = Z * Cz * θEnd Sub'求J4Public Sub jjj4(R#, J4#)Dim ho#, cpa!, HETP!cpa = 15674.4: HETP = 0.462Call tabanshu(R#, N#)ho = N * HETPDT = Sqr((R + 1) * D * 22.4 / (3600 * 0.785 * u) * (273 + td) / 273 * 101.3 / po)J4 = 3.14 / 4 * DT ^ 2 * ho * cpa * FcEnd Sub'塔板数的计算Public Sub tabanshu(R#, N#)Dim ye#, XW#Dim X!(100), Y!(100), xx!(100), i%, n1#td = 64.93: F = 402.34: XD = 0.982: XF = 0.3151: ηd = 0.999: D = 128.97: Rmin = 1.0167 V = (R + 1) * D: W = F + V - D: XW = (F * XF - D * XD) / Wi = 1: Y(1) = 0.982: X(1) = 0.9702DoIf X(i) > XF ThenY(i + 1) = R * X(i) / (R + 1) + XD / (R + 1)n1 = i + 1 + (X(i) - XF) / (X(i) - X(i + 1))ElseY(i + 1) = W * (X(i) - XW) / VIf X(i) < XW Then Exit DoEnd Ifi = i + 1xx(i) = (Y(i) / (3.3874 * (1 - Y(i)))) ^ (1 / 0.7977) X(i) = xx(i) / (1 + xx(i))LoopN = i - 1 + (X(i - 1) - XW) / (X(i - 1) - X(i))lilunbanshu = Ntiliuduanbanshu = n1jinliuduanbanshu = N - n1End Sub目录1 前言------------------------------------------------------------------------------------------------12 方案论证2.1 精馏塔类型----------------------------------------------------------------------------------1 2.2 精馏压力-------------------------------------------------------------------------------------1 2.3 进料方式-------------------------------------------------------------------------------------1 2.4 填料类型-------------------------------------------------------------------------------------2 2.5 加热方式-------------------------------------------------------------------------------------22.6 塔材料类型----------------------------------------------------------------------------------23 数学模型的建立3.1 精馏塔塔体年投资折旧费及维修费用-------------------------------------------------3 3.2 冷凝器年运转费用-------------------------------------------------------------------------4 3.3 直接蒸汽加热费用-------------------------------------------------------------------------53.4 填料年折旧费-------------------------------------------------- --54 数学模型的求解4.1 数学模型决策变量分析-------------------------------------------------------------------5 4.2 主要工艺参数的求解----------------------------------------------------------------------54.2.1 塔径的计算-----------------------------------------------------------------------------54.2.2 塔板数的计算-------------------------------------------------------------------------64.2.2.1 相平衡关系的表示--------------------------------------------------------------64.2.2.2 N的计算--------------------------------------------------------------------------64.2.3 冷凝器年运转费用的计算------------------ ----------------------- ----------------74.2.3.1 冷却水用量及冷凝器传热面积的计算- -------------------------------------74.2.3.2 冷凝器冷却水最佳出口温度的确定-----------------------------------------74.2.4 直接加热蒸气费用的计算----------------------------------------------------------8 4.3 数学模型的求解------------------------------------------------------- --------------------84.3.1 单变量最优化方法--------------------------------------------- ----------------------84.3.2 优化设计程序框图-------------------------------------------- -----------------------84.3.2.1 函数调用关系--------------------------------------------------------------------95 优化设计计算5.1 数据预处理---------------------------------------------------------------------------------105.1.1 进塔物料的计算----------------------------------------------------------------------105.1.2 塔顶蒸气温度的计算----------------------------------------------------------------105.1.3 等板高度的计算----------------------------------------------------------------------10Ⅰ5.1.4 产品汽化潜热的计算----------------------------------------------------------------115.1.5 最小回流比的确定-------------------------------------------------------------------115.1.6 填料单价的计算----------------------------------------------------------------------115.2. 塔径的计算---------------------------------------------------------------------------------13 5.3 填料层高度的计算-------------------------------------------------------------------------13 5.4 精馏塔塔体年投资折旧费及维修费用的计算-----------------------------------------13 5.5 冷凝器年运转费用的计算----------------------------------------------------------------145.5.1 冷凝器冷却水最佳出口温度的确定----------------------------------------------145.5.2 冷却水用量及冷凝器传热面积的计算-------------------------------------------145.5.3 精馏塔塔体年投资折旧费及维修费用的计算----------------------------------15 5.6 再沸器年运转费用的计算----------------------------------------------------------------15 5.7 填料年折旧费用的计算-------------------------------------------------------------------15 5.8 汽液负荷-------------------------------------------------------------------------------------155.8.1 气相负荷-------------------------------------------------------------------------------155.8.2 液相负荷-------------------------------------------------------------------------------155.9 年总费用与回流比的关系--------------------------------------------------------------156 填料塔水力学性能校核6.1 泛点率校核--------------------------------------------------------------------------------- 17 6.2 径比校核-------------------------------------------------------------------------------------17 6.3 喷淋密度校核-------------------------------------------------------------------------------176.4 填料塔压降----------------------------------------------------------------------------------177 附属设备的设计与选型7.1 塔顶冷凝器--------------------------------------------------------------------------------- 187.1.1 冷凝器传热量-------------------------------------------------------------------------187.1.2 冷凝器传热推动力-------------------------------------------------------------------187.1.3 初估冷凝器传热面积----------------------------------------------------------------197.1.4 冷凝器传热系数的校核-------------------------------------------------------------197.1.5 冷凝器传热面积的校核-------------------------------------------------------------227.1.6 冷凝器壳程、管程流动阻力-------------------------------------------------------22 7.2 接管选型------------------------------------------------------------------------------------ 247.2.1 进料口接管的选型-------------------------------------------------------------------247.2.2 冷却水接管的选型-------------------------------------------------------------------257.2.3 塔顶蒸气接管选型------------------------------------------------------------------ 25Ⅱ7.2.4 塔顶产品接管选型-------------------------------------------------------------------257.2.5 塔底产品接管选型-------------------------------------------------------------------267.2.6 塔顶产品回流接管选型-------------------------------------------------------------267.2.7 塔底加热蒸气接管选型------------------------------------------------------------- 26 7.3 冷却水输送泵7.3.1 塔高的计算---------------------------------------------------------------------------277.3.2 冷却水输送泵选型------------------------------------------------------------------27 7.4 填料支承结构-------------------------------------------------------------------------------28 7.5 液体分布装置-------------------------------------------------------------------------------287.7 液体收集再分布装置----------------------------------------------------------------------298 设计结果汇总------------------------------------------------------------------------------------299 设计心得------------------------------------------------------------------------------------------31 参考文献---------------------------------------------------------------------------------------------- 31 附录一甲醇和水部分物性参数-----------------------------------------------------------------32 附录二甲醇—水汽液平衡数据(摩尔组成)-------------------------------------------------33 附录三优化设计程序源代码--------------------------------------------------------------------34化工原理课程设计学生姓名:黄圣楠学号:081000115专业班级:10级生工(1)班____指导教师:张星___2013年1月24日。
甲醇 乙醇 水 汽液平衡

This article was downloaded by: [Dalhousie University]On: 15 January 2013, At: 07:11Publisher: Taylor & FrancisInforma Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37-41 Mortimer Street, London W1T 3JH, UKPhysics and Chemistry of Liquids: AnInternational JournalPublication details, including instructions for authors andsubscription information:/loi/gpch20Phase equilibria of binary mixturescontaining methyl acetate, water,methanol or ethanol at 101.3 k PaV.H. Álvarez a , S. Mattedi b , M. Iglesias c , R. Gonzalez-Olmos c &J.M. Resa da Chemical Engineering School, State University of Campinas, P.O.Box 6066, Campinas-SP 13081-970, Brazilb Chemical Engineering Department, Polytechnic School, FederalUniversity of Bahia, Rua Aristides Novis, 2 Federação, 40210-630Salvador-BA, Brazilc PF&PT Research T eam, Department of Chemical Engineering,T echnical High School of Engineering, University of Santiago deCompostela, Rúa Lope Gómez de Marzoa, 15782 Santiago deCompostela, Españad Departamento de Ingeniería Química, Universidad del PaísVasco, Apartado 450, 01006 Vitoria, EspañaVersion of record first published: 27 Jan 2011.PLEASE SCROLL DOWN FOR ARTICLEsources. The publisher shall not be liable for any loss, actions, claims, proceedings,demand, or costs or damages whatsoever or howsoever caused arising directly or indirectly in connection with or arising out of the use of this material.D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013Physics and Chemistry of Liquids Vol.49,No.1,January 2011,52–71Phase equilibria of binary mixtures containing methyl acetate,water,methanol or ethanol at 101.3kPaV.H.Alvarez a ,S.Mattedi b *,M.Iglesias c ,R.Gonzalez-Olmos c and J.M.Resa d aChemical Engineering School,State University of Campinas,P.O.Box 6066,Campinas-SP 13081-970,Brazil;b Chemical Engineering Department,Polytechnic School,Federal University of Bahia,Rua Aristides Novis,2Federac ¸a ˜o,40210-630Salvador-BA,Brazil;cPF&PT Research Team,Department of Chemical Engineering,Technical High School of Engineering,University of Santiago de Compostela,Ru´a Lope Go ´mez de Marzoa,15782Santiago de Compostela,Espan ˜a;dDepartamento de Ingenierı´aQuı´m ica,Universidad del Paı´s Vasco,Apartado 450,01006Vitoria,Espan ˜a(Received 3April 2009;final version received 1May 2009)Isobaric vapor–liquid equilibria data at 101.3kPa were reported for the binary mixtures (methyl acetate þ(water or methanol or ethanol),methanol þ(water or ethanol)and (ethanol þwater)).The experimental data were tested for thermodynamic consistency by means of the Wisniak method and were demonstrated to be consistent.The experimental data were correlated using Wilson,NRTL and UNIQUAC models for the activity coefficients and predicted using the UNIFAC and PSRK equation of state for testing theirs capability.The results show that the obtained data for the studied binary systems are more reliable than other published data.Keywords:phase equilibria;associating binary mixture;correlation,modelling errors1.IntroductionThermodynamic measurements and phase equilibria of ethanol,water and the different flavour components (alcohols,aldehydes and acetates,so-called congeners)in distillated alcoholic beverages are of practical interest to the food industry since industrial procedures applied are closely related to their temperature and pressure dependence in order to obtain a high quality final product.In the last few years,published studies have highlighted a clear need for accurate information about these types of mixtures,in order to develop and optimise industrial techniques.Despite the considerable effort invested in the field of thermodynamic properties,a great scarcity of data is observed in the available literature for mixtures of components present in commercial distillated alcoholic beverages.Such properties are strongly dependent on hydrogen bond potency of hydroxyl or polar groups,chain length,isomeric structures and molecular package.After decades of study,there is still much room for improvement in our ability to understand the behavior of these systems and add accurate data to the available literature.Simulation and optimisation are not used in*Corresponding author.Email:silvana@ufba.brISSN 0031–9104print/ISSN 1029–0451online ß2011Taylor &FrancisDOI:10.1080/00319100903012403D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013the right manner in this matter,with an overestimation of equipment size or high energy-consuming conditions being usually applied due to inaccurate calculations.The difficulties of simulation in these types of processes,as well as possible errors derived from that,have been commented upon previously [1].As a continuation of previous work related to alcoholic beverages [2–4],this work is part of a research project whose objective is to measure thermodynamic properties and vapour–liquid equilibrium (VLE)data for different systems involved in most distillation processes to benefit subsequent studies of modelling and simulation.In this work,the VLE at 101.3kPa was determined for binary systems:methyl acetate þwater,methyl acetate þmethanol,methyl acetate þethanol,methanol þwater,methanol þethanol and ethanol þwater.These mixtures also have some special characteristics.The concentration of the solute in the vapor phase is small and shows molecular association.Thermodynamic consistency was achieved to validate the new experimental data.In this way,data obtained have lower deviations when compared with previously published data;thereby,the information of available literature was improvement.The –’approximation was used to fit the experimental data and obtain the UNIFAC Dortmund model [5],which was used for VLE prediction.Also,the predictive Soave–Redlich–Kwong (PSRK)model proposed by Holderbaum and Gmehling [6]was used in the ’–’approximation.2.Experimental sectionAll chemicals were Lichrosolv quality (Merck Farma y Quımica S.A.).The pure components were recently acquired and kept in an inert argon atmosphere after the bottles were opened.The materials were degassed ultrasonically and dried over molecular sieves Type 4A or 3A,1/16in.Chromatographic (GLC)analysis gave purities of 0.998for methyl acetate,methanol and ethanol,with maximum water contents of 6.8Â10À3, 1.5Â10À2and 2.2Â10À2mass%(Metrohm 737KF coulometer),respectively.Water was millipore quality with organic total mass 55ppb and resistivity of 18.2M cm.The densities and refractive indices at 298.15K,as well as normal boiling points,were within recommended values and are shown in Table 1.Table 1.Observed physical properties of pure compounds and literature data (densities ( ),refractive indices (n D )at 298.15K,and normal boiling points (T b )).Mw (kg kmol À1)(kg m À3)n DT b (K)Obs.Lit.Obs.Lit.Obs.Lit.Methyl acetate 74.080a 0.926740.9273b 1.35850 1.3589b 329.82330.4a 0.9279c 1.3614c 330.09d Water 18.015a 0.99700.99705c 1.33250 1.33250c 373.15373.15a Methanol 32.042a 0.786650.78664b 1.32645 1.32652b 337.86337.7a 0.78664c 1.32652c 337.85d Ethanol46.069a0.785020.78509b 1.359221.35941b 352.07351.4a 0.78504c1.35941c351.44dNote:a See [7];b See [8];c See [9];d See [10].Physics and Chemistry of Liquids 53D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013The system used to measure VLE data was a dynamic recirculating apparatusdescribed previously [11,12].The equilibrium temperature was measured with a digital platinum 100resistance thermometer with an accuracy of Æ0.1K.For the pressure measurement,a digital manometer regulator (Divatronic DT1model),manufactured by Leybold with an accuracy of Æ0.1kPa,was used.Both vapour and liquid phase compositions for the systems were determined by measurements of physical properties (density and refractive index)and application of mathematical correlations,published earlier by the authors [13–16].The accuracy of the composition measurements on each phase was estimated as better than Æ0.001in molar fraction for each mixture.The VLE experimental data at 101.3kPa of the studied binary systems are compiled in Table 2.Table 2.Observed vapour-liquid equilibrium data for different binary systems.x 1y 1T (K)1 2 1 2 s 1 s 2Methyl acetate (1)þwater (2)0.0020.14095.6423.732 1.0090.9790.9910.9350.9930.0050.29590.3923.206 1.2260.9780.9920.9410.9940.0140.57777.8121.348 2.0150.9770.9950.9550.9960.0220.68271.2719.808 2.6560.9770.9970.9610.9970.0290.73966.9018.413 3.2160.9770.9990.9650.9970.0420.79461.9016.207 4.0320.977 1.0010.9690.9980.7120.83557.45 1.158 4.9640.978 1.0030.9720.9980.8000.86156.99 1.080 5.0790.978 1.0040.9730.9980.8730.89456.67 1.041 5.1640.979 1.0060.9730.9980.8730.89556.67 1.041 5.1640.979 1.0060.9730.9980.9300.93356.54 1.024 5.2070.981 1.0080.9730.9980.9910.98956.621.0205.2030.983 1.0110.9730.998Methyl acetate (1)þmethanol (2)0.0090.02764.00 2.417 1.0090.9750.9830.9670.9830.0540.14561.90 2.259 1.0960.9750.9830.9690.9840.0740.18661.14 2.194 1.1300.9750.9830.9690.9840.1030.24060.12 2.101 1.1770.9740.9830.9700.9850.1040.24260.09 2.097 1.1780.9740.9830.9700.9850.1210.26959.58 2.048 1.2030.9740.9830.9710.9850.1230.27259.52 2.042 1.2060.9740.9830.9710.9850.1450.30658.88 1.978 1.2380.9740.9840.9710.9860.1480.30958.82 1.971 1.2410.9740.9840.9710.9860.1650.33258.39 1.924 1.2630.9750.9840.9720.9860.1990.37357.63 1.834 1.3040.9750.9850.9720.9860.2160.39157.30 1.794 1.3220.9750.9850.9720.9860.2660.43856.45 1.680 1.3700.9750.9860.9730.9870.2950.46256.05 1.621 1.3930.9760.9860.9730.9870.3270.48655.65 1.558 1.4170.9760.9870.9730.9870.3540.50555.36 1.509 1.4350.9760.9880.9740.9870.3710.51655.19 1.480 1.4460.9760.9880.9740.9870.4190.54554.80 1.406 1.4710.9770.9890.9740.9870.4400.55754.65 1.375 1.4800.9770.9890.9740.9870.4850.58254.37 1.3151.4990.9780.9900.9740.988(Continued )54V.H.A´lvarez et al.D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013Table 2.Continued.x 1y 1T (K) 1 2 1 2 s 1 s 20.5190.59954.21 1.274 1.5100.9780.9900.9740.9880.5370.60954.13 1.254 1.5160.9780.9910.9750.9880.6320.65853.87 1.164 1.5350.9790.9930.9750.9880.6360.66053.86 1.160 1.5360.9790.9930.9750.9880.6730.68053.83 1.132 1.5390.9800.9930.9750.9880.6960.69353.83 1.116 1.5400.9800.9940.9750.9880.7190.70753.84 1.102 1.5400.9810.9950.9750.9880.7420.72153.87 1.089 1.5390.9810.9950.9750.9880.7950.75754.02 1.063 1.5320.9830.9970.9750.9880.8850.83754.65 1.035 1.4980.986 1.0010.9740.9870.9240.88155.12 1.030 1.4730.988 1.0030.9740.9870.9810.96556.191.029 1.4160.992 1.0080.9730.987Methyl acetate (1)þethanol (2)0.0110.05076.972.541 1.0110.9790.9790.9560.9800.0390.16574.47 2.420 1.1160.9780.9780.9580.9810.0890.31070.97 2.231 1.2870.9790.9790.9610.9830.1210.37869.19 2.121 1.3850.9790.9800.9630.9840.1740.46566.77 1.955 1.5350.9800.9810.9650.9850.2570.55864.02 1.734 1.7290.9820.9830.9670.9870.2670.56663.75 1.711 1.7490.9820.9830.9670.9870.2920.58763.11 1.653 1.7990.9820.9840.9680.9870.3160.60562.58 1.604 1.8420.9830.9840.9680.9870.3250.61162.39 1.585 1.8580.9830.9840.9680.9870.3360.61962.17 1.563 1.8760.9830.9850.9690.9870.3690.63961.55 1.502 1.9280.9840.9850.9690.9880.3740.64261.46 1.493 1.9360.9840.9850.9690.9880.4370.67660.48 1.392 2.0240.9850.9870.9700.9880.5340.72259.28 1.266 2.1380.9860.9880.9710.9890.5510.73059.10 1.248 2.1560.9860.9890.9710.9890.5760.74058.85 1.223 2.1810.9870.9890.9710.9890.6360.76758.30 1.169 2.2380.9880.9900.9720.9890.6370.76758.29 1.168 2.2390.9880.9900.9720.9890.6610.77858.09 1.150 2.2600.9880.9910.9720.9890.6920.79257.84 1.128 2.2870.9890.9910.9720.9890.6990.79657.79 1.124 2.2920.9890.9920.9720.9890.7520.82157.42 1.094 2.3340.9900.9930.9720.9890.7600.82557.37 1.089 2.3400.9900.9930.9720.9890.7650.82857.34 1.087 2.3430.9910.9930.9720.9890.7680.83057.32 1.085 2.3450.9910.9930.9720.9890.8080.85157.09 1.069 2.3730.9920.9940.9720.9900.8160.85657.04 1.066 2.3790.9920.9950.9730.9900.8610.88456.84 1.052 2.4040.9930.9960.9730.9900.8620.88456.83 1.052 2.4050.9930.9960.9730.9900.8820.89856.75 1.047 2.4160.9940.9970.9730.9900.9240.93056.64 1.040 2.4330.9960.9990.9730.990Methanol (1)þwater (2)0.00010.00199.65 2.425 1.0130.9860.9920.9560.9920.0010.00999.46 2.384 1.0190.9860.9920.9560.9920.0100.07597.79 2.313 1.0820.9850.9920.9580.9920.0640.32190.812.0171.4000.9850.9930.9640.994(Continued )Physics and Chemistry of Liquids55D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013Table 2.Continued.x 1y 1T (K) 1 2 1 2 s 1 s 20.1030.42587.38 1.8511.5960.9850.9940.9670.9940.2170.59681.04 1.5162.0520.9860.9960.9720.9950.3060.67277.93 1.355 2.3310.9870.9970.9740.9960.3160.67977.62 1.340 2.3610.9870.9980.9750.9960.3830.72275.80 1.256 2.5470.9880.9990.9760.9960.4430.75774.35 1.198 2.7080.988 1.0000.9770.9960.4440.75774.32 1.197 2.7120.988 1.0000.9770.9960.5320.80272.44 1.133 2.9390.989 1.0010.9780.9970.6320.84770.52 1.0843.1950.990 1.0020.9790.9970.6760.86769.73 1.068 3.3070.991 1.0030.9800.9970.6890.87269.49 1.064 3.3430.991 1.0030.9800.9970.6960.87569.37 1.062 3.3600.991 1.0030.9800.9970.7680.90668.12 1.044 3.5520.992 1.0040.9810.9970.7700.90668.11 1.043 3.5530.992 1.0040.9810.9970.8270.93067.16 1.034 3.7080.992 1.0050.9810.9970.8960.95866.05 1.026 3.8980.993 1.0060.9820.9970.9140.96665.75 1.025 3.9520.993 1.0070.9820.9970.9330.97365.46 1.0244.0040.993 1.0070.9820.9970.9370.97565.40 1.024 4.0150.993 1.0070.9820.9970.9720.98964.86 1.023 4.1150.994 1.0080.9830.9970.9770.99164.78 1.023 4.1300.994 1.0080.9830.9970.9770.99164.771.023 4.1320.994 1.0080.9830.997Methanol (1)þethanol (2)0.0180.03477.71 1.152 1.0060.9850.9790.9750.9790.0960.16776.08 1.139 1.0730.9860.9790.9760.9800.1710.27774.65 1.127 1.1360.9870.9790.9770.9810.1790.28974.49 1.126 1.1430.9870.9790.9770.9810.1820.29374.44 1.125 1.1450.9870.9790.9770.9810.2460.37673.31 1.115 1.1990.9880.9800.9780.9820.2750.41172.83 1.110 1.2230.9890.9800.9780.9820.2870.42672.62 1.108 1.2340.9890.9800.9780.9820.2940.43472.51 1.107 1.2390.9890.9800.9780.9820.3120.45572.22 1.104 1.2540.9900.9810.9780.9820.3260.46972.01 1.102 1.2650.9900.9810.9780.9830.4000.54770.90 1.090 1.3250.9910.9820.9790.9830.4230.56970.57 1.087 1.3440.9920.9820.9790.9830.4420.58770.31 1.084 1.3590.9920.9830.9790.9830.4590.60270.09 1.081 1.3710.9930.9830.9800.9840.5340.66769.12 1.070 1.4290.9950.9840.9800.9840.5690.69668.69 1.065 1.4560.9950.9850.9800.9840.5800.70568.56 1.063 1.4640.9960.9850.9800.9840.5980.71968.35 1.061 1.4780.9960.9850.9810.9850.5990.72068.34 1.060 1.4780.9960.9850.9810.9850.6820.78267.42 1.050 1.5390.9980.9870.9810.9850.7260.81366.98 1.044 1.5690.9990.9880.9810.9850.7610.83866.63 1.041 1.593 1.0000.9890.9820.9850.7630.83966.61 1.041 1.595 1.0000.9890.9820.9850.8760.91665.57 1.032 1.671 1.0040.9910.9820.9860.9410.95965.041.030 1.712 1.0060.9930.9820.986Ethanol (1)þwater (2)0.0150.17095.99 5.8380.9740.9810.9910.9650.9930.0320.27692.695.1331.0990.9800.9920.9680.993(Continued )56V.H.A´lvarez et al.D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 20133.Data treatment3.1.VLE consistency dataPhase equilibrium data should be tested in order to assure and guarantee an acceptable quality and reliability of VLE data.Available literature offers different procedures to test the thermodynamic consistency of a set of data for isothermal or isobaric condition.The thermodynamic consistency of the measured VLE data have been tested with the Wisniak method [17]to reject possible inconsistent equilibrium points from the experimental determined collection.According to this test,two experimental points (a)and (b)are thermodynamically consistent when:D 5D maxð1ÞTable 2.Continued.x 1y 1T (K) 1 2 1 2 s 1 s 20.0460.33690.68 4.624 1.1860.9800.9920.9690.9940.0680.39888.50 3.978 1.2880.9800.9920.9710.9940.0790.42087.72 3.717 1.3280.9800.9920.9720.9940.1190.47385.80 2.991 1.4300.9790.9930.9730.9950.1630.50884.54 2.454 1.5030.9790.9930.9740.9950.1900.52483.99 2.215 1.5360.9790.9940.9750.9950.2060.53283.72 2.094 1.5530.9790.9940.9750.9950.2320.54483.33 1.933 1.5770.9790.9940.9750.9950.2360.54683.27 1.908 1.5810.9790.9940.9750.9950.2390.54783.23 1.896 1.5840.9790.9940.9750.9950.2810.56582.70 1.698 1.6180.9790.9940.9760.9950.2860.56782.64 1.675 1.6220.9790.9940.9760.9950.2910.56982.59 1.658 1.6250.9790.9940.9760.9950.3030.57482.45 1.614 1.6340.9790.9950.9760.9950.3440.59082.01 1.486 1.6630.9790.9950.9760.9950.3670.59981.79 1.427 1.6780.9790.9950.9760.9950.3800.60581.66 1.396 1.6870.9790.9950.9760.9950.3920.61081.55 1.371 1.6950.9790.9950.9760.9950.3970.61281.50 1.360 1.6980.9790.9950.9770.9950.4100.61781.38 1.336 1.7070.9790.9950.9770.9950.4120.61881.36 1.332 1.7080.9790.9950.9770.9950.4810.64880.76 1.224 1.7510.9800.9960.9770.9950.5270.66980.40 1.171 1.7770.9800.9960.9770.9950.6170.71579.77 1.094 1.8250.9800.9980.9780.9960.6880.75479.36 1.053 1.8570.9810.9990.9780.9960.7220.77579.19 1.037 1.8710.9810.9990.9780.9960.7570.79779.04 1.023 1.8840.982 1.0000.9780.9960.8510.86278.770.997 1.9090.983 1.0020.9780.9960.8980.89978.720.988 1.9150.984 1.0030.9780.9960.9080.90878.720.987 1.9160.984 1.0040.9780.9960.9310.92878.730.984 1.9160.984 1.0040.9780.9960.9440.94178.750.983 1.9160.985 1.0050.9780.9960.9470.94378.750.983 1.9160.985 1.0050.9780.9960.9670.96378.790.9821.9140.9851.0060.9780.996x 1,Liquid-phase mole fraction;y 1,vapour-phase mole fraction;T ,boiling temperature; 1and2,activity coefficients; 1and 2,fugacity coefficients; s 1and s2,fugacity coefficients at saturation at 101.3kPaPhysics and Chemistry of Liquids57D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013where D max is the maximum deviation with a value of 3,D is the local deviation,which is expressed as:D ¼100L ÀW L þW,ð2Þwhere L and W are each side temperature function integrals on liquid compositionfor the Wisniak test [13].The correlations for heat of vapourisation (J kmol À1)and density liquid (kmol m À3)used are:D vap H ¼A 1ÀT r ðÞðB þCT r þDT 2r Þð3Þ ¼AB 1þð1ÀT =C ÞDðÞ,ð4Þwhere,T is the temperature in K,T r is the reduced temperature and the constants A ,B ,C and D are shown in Table 3.The physical properties used were taken from Diadem Public v1.2[10],and the activity coefficients were calculated as shown in the next section.Table 4shows the values for the integrals L and W calculated for the thermodynamic consistent test and the values for the deviation D .Also,this table shows that the condition D 5D max satisfies all systems.Therefore,the thermo-dynamic consistency of the binary VLE data reported in this work is confirmed.Table 3.Coefficients for heat of vapourisation and density liquid,Equations (3)and (4).Compound D T (K)A B C D Ethanol 159–514a557890000.3124500159–514b 1.62880.274695140.23178Methanol 175–512a 504510000.3359400175–512b 2.32670.27073512.50.24713Methyl acetate 175–506a 449200000.368500175–506b 1.130.2593506.550.2764Water273–647a 520530000.31990À0.2120.25795300–380b,c5.77830.3124462.25450.05977aInterval for heat vapourisation,b interval for liquid density,c calculated from [14].Table 4.Results of the thermodynamic consistency test;L,W and D are variables defined in Equation (2).System (1)þ(2)L W D Methyl acetate þwater 19.8420.30 1.15Methyl acetate þmethanol 5.10 5.00 1.05Methyl acetate þethanol 6.59 6.81 1.61Methanol þwater 7.527.560.30Methanol þethanol 1.48 1.470.18Ethanol þwater7.217.260.3758V.H.A´lvarez et al.D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 20133.2.Equilibrium equation and activity coefficientsThe activity coefficients ( i )of the components were calculated from the following equation:i ¼y i Èi Px i P o i,ð5Þwere x i and y i are the liquid and vapor mole fractions in equilibrium,Èi is the vaporphase correction factor,P is the total pressure and P o i is the vapour pressure of pure component i .These vapour pressures were calculated from the Antoine equation:log P ¼A i ÀB ii,ð6Þwhere,P is the vapor pressure in mmHg,T is temperature in C and the constants A i.,B i and C i are reported in Table 5.The value constants for the pure compounds were obtained in literature by Riddick et al .[9].The vapour phase correction factor is given by:Èi ¼ i sat i exp ÀV i ðP ÀP o iÞRT !,ð7Þwhere i is the fugacity coefficient of component i in the mixture, sat iis the fugacity coefficient at saturation condition and V i is the molar volume of component i in the liquid phase calculated using the correlation of the liquid density.Fugacity coefficients were calculated with PSRK model,where the expression proposed by Mathias and Copeman [18]is used to evaluate (T )in the PSRK model:ðT Þ¼1þc 1ð1ÀT 0:5r Þþc 2ð1ÀT 0:5r Þ2þc 3ð1ÀT 0:5r Þ3ÂÃ2for T r 51,ð8Þwhere,T r is the reduced temperature and T c is the critical temperature,while c 1,c 2and c 3are empirical parameters.These parameters for the pure compounds were calculated in this work and are shown in Table 5.The physical properties for the pure components used in the PSRK model were taken from [10]and shown in Table 6.The calculated fugacity and activity coefficients are shown in Table 2for all data points.Table 5.Antoine and Mathias and Copeman pound A i a B i a C i a D T (K)b C 1c c 2c C 3cEthanol 8.3221718.10237.52296.9–463.2 1.4125300.287222À1.496099Methanol7.8981474.08229.13292.0–461.3 1.433991À0.7681150.226212Methyl acetate 7.0651157.622219.724277.1–462.7 1.069537À0.759819 1.492479Water8.0121695.167230.41276.6–590.91.093544À0.6730560.699288aSee [19];b see [18];c calculated in this work.Physics and Chemistry of Liquids59D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 20133.3.Modelling –Correlation modelThe VLE data were correlated in the –’approximation,where the PSRK equation of state was used to evaluate the fugacity coefficients,as the thermodynamic model in a bubble-point calculation.The description of the models applied here (Wilson,NRTL,and UNIQUAC)is freely available in the literature [7]and hence it is not discussed here.In the ’approximation,the Wilson,NRTL and UNIQUAC models were used instead of the UNIFAC model to calculate the excess Gibbs energy in the PSRK model.Theoretically,the range for the parameters A ij (Wilson,NRTL and UNIQUAC)is defined as (À104,104)J mol À1.Since this is a very wide range based on physical considerations,it is extremely likely that it will contain the globally optimal parameter values.Renon and Prausnitz [18]explain that the range for ij with theoretical bases can have values from 0.2to 0.55.To evaluate these parameters,the regression was performed using a genetic algorithm code,implemented and fully explained in the study by Alvarez et al .[19],with the minimisation of the overall objective function (Q ).Q ¼X N j ¼1½y exp 1jÀy cal 1j = y2þX N j ¼1½T cal ÀT exp = T ÀÁ2,ð9Þwhere y is the accuracy in the vapour mole fraction (10À3), T is the accuracy in the temperature (10À1),N is the number of data sets,y i is the molar fraction of the component i and the superscript ‘exp’and ‘cal’are the experimental and calculated values,respectively.The fitting parameters of these models and deviations are shown Table 7,the relative percent deviations in temperature and vapour phase compositions are calculated by Valderrama and Alvarez [20]:D T j j %¼100N XN i ¼1T cali ÀT exp i T expi ð10ÞD y %¼100N X N i ¼1y cal i Ày exp i y exp i,ð11Þwhere N is the number of data sets,T is the temperature,y i is the vapour molarfraction of the component i and the superscript ‘exp’and ‘cal’are the experimental and calculated values,respectively.Also,this table shows that all models present similar deviations in temperature and concentration in vapour phase,with a slightly better performance of the UNIQUAC model.The modelling of VLE data areTable 6.Physical properties for components:T c,critical temperature;P c,critical pressure;!,acentric factor;and uniquac parameters r and q .Compound T c (K)P c (bar)!r q Ethanol 514.061.50.644 2.11 1.97Methanol512.581.00.566 1.43 1.43Methyl acetate 506.647.50.331 2.80 2.58Water647.1221.20.3450.921.4D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013presented in T Àx 1Ày 1diagrams shown in Figures 1–6.In Figure 7,comparisons between models desviations using Equation (11)are shown for all binary systems,it is easy to observe that UNIQUAC model has a good agreement between experimental and calculated composition vapor phase.Table 7.Correlation parameters for activity coefficients and average deviation for the studied systems.ModelA 12(KJ mol À1)A 21(KJ mol À1)j D T j %(K)j D y 1j %j D y 2j %Methyl acetate (1)þwater (2)Wilson3249.1878660.5650.27 2.9512.96NRTL ( 12¼0.415)3276.9667494.2400.050.73 2.36UNIQUAC c 2216.998959.0940.100.42 1.46UNIFAC ––0.060.75 2.08PSRK––0.39 3.25 6.52Methyl acetate (1)þmethanol (2)Wilson À75.0113815.6350.020.190.47NRTL ( 12¼0.534)1927.7051181.4910.020.190.50UNIQUAC c 2922.085À594.6130.020.220.43UNIFAC ––0.020.310.52PSRK ––0.16 2.63 1.86Methyl acetate (1)þethanol (2)Wilson 467.4572721.9650.020.230.95NRTL ( 12¼0.550)1772.0651504.5650.020.25 1.00UNIQUAC c1667.680À178.6690.030.36 1.03UNIFAC ––0.060.61 1.30PSRK ––0.23 1.93 2.24Methanol (1)þwater (2)Wilson 173.8432373.1030.040.54 3.87NRTL ( 12¼0.550)75.5062425.8120.04 1.01 3.08UNIQUAC c À1289.7642072.2820.050.35 2.12UNIFAC ––0.080.45 1.39PSRK ––0.070.530.77Methanol (1)þethanol (2)Wilson À309.2071565.2990.030.230.66NRTL ( 12¼0.200)4229.869À2822.0700.020.260.60UNIQUACc1412.023À763.4080.030.230.64UNIFAC ––0.020.380.97PSRK ––0.020.440.71Ethanol (1)+water (2)Wilson2083.97763953.53670.250.39 1.16NRTL ( 12¼0.550)734.705007.820.180.92 1.46UNIQUAC c À495.04021988.10910.210.75 1.58UNIFAC ––0.220.330.82PSRK ––0.09 1.84 2.46Mean Wilson 0.100.76 3.34NRTL0.060.56 1.50UNIQUAC 0.070.39 1.21UNIFAC 0.080.47 1.18PSRK0.161.772.43D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013Figure 1.T Àx 1Ày 1diagram for methyl acetate (1)þwater (2)at 101.3kPa:(.)experimentalliquid phase;( )experimental vapour phase;(—)UNIQUAC correlation;(---)UNIFACprediction.Figure 2.T Àx 1Ày 1diagram for methyl acetate (1)þmethanol (2)at 101.3kPa:(.)experimental liquid phase;( )experimental vapour phase;(—)UNIQUAC correlation;(---)UNIFAC prediction.D o w n l o a d e d b y [D a l h o u s i e U n i v e r s i t y ] a t 07:11 15 J a n u a r y 2013。
常压下甲醇-聚甲氧基二甲醚二元体系汽液平衡

常压下甲醇-聚甲氧基二甲醚二元体系汽液平衡王丰阳;梁欢欢;周彩荣【摘要】At 101.3 kPa constant pressure, the VLE data of methanol-DMM3 (polyoxymethylene dimethyl ethers with degree of polymerization of n, i.e., DMMn) system were determined by using an improved Rose still. Thermodynamic consistency of the obtained vapor liquid equilibrium data were examined. The results were satisfied with Gibbs-Duhenm’s thermodynamic consistency. The VLE data were correlated by Wilson, NRTL and UNIQUAC activity coefficient model by Aspen Plus v7.1. The objective function was optimized by the maximum likelihood method and the corresponding model parameters were returned. Compared with the experimental results, the average absolute deviations for temperature and the composition in the vapor phase were less than 0.65 K and 0.0065, respectively. This work provides the important engineering data for an engineering design and further study in the multicomponent system containing methanol and DMM3.%在101.3 kPa 恒定压力下,采用改进的Rose 汽液平衡釜测定了甲醇-DMM3(聚甲氧基二甲醚,聚合度为 n,即 DMMn)二元体系汽液平衡数据,并对汽液平衡数据进行热力学一致性检验,结果表明所测定数据符合Gibbs-Duhenm 的热力学一致性。
甲醇分离方法的研究进展

第1期杨振钰:甲醇分离方法的研究进展•101 +甲醇分离方法的研究进展杨振枉(中石化催化剂有限公司工程技术研究院,北京100029)摘要:甲醇的来源和应用都非常广泛,但是由于高浓甲醇在工业中难以获取,需要从混合物中分离出高浓甲醇。
目前分离甲醇混合物的方法有许多,包括萃取精馏法、膜分离法、共沸蒸馏法等,主要探讨各种含甲醇混合物的不同分离方法。
关键词:甲醇%水%分离中图分类号!T Q028文献标识码!A文章编号:1008-021X(2021)0卜0101-021甲醇的发展现状甲醇在实际化工生产过程中起着重要的作用。
在医药、染 料、合成纤维、塑料等有机工业中都是重要的化工原料[1]。
同时,甲醇也可以作为重要的原料用来制作敌百虫、甲基对磷酸、多菌灵等农药产品。
近些年来,甲醇汽油也是一个研究热点,甲醇俗称“木醇’’或“木精’’,甲醇主要是由煤经过汽化加氢而生成,性能与汽油 接近[2]。
甲醇汽油是一种新型的环保燃料,甲醇燃烧充分、热 能利用率高、耗量低、排放的颗粒物非常少,并且甲醇汽油较常 规汽油来说更便宜,来源范围更广。
总体来说,因甲醇有清洁、高效、节能等特点,甲醇汽油的相关研究被国家列为节能减排 的重点项目,各个省市也在积极推动甲醇汽油。
甲醇也可作为重要化工原料来生产甲醛、醋酸、乙二醇等,其中,30%~40%的甲醇用于生产甲醛。
甲醇一般是由合成气在 473~573 K、5~10 M P a的条件下合成[3],此外,甲醇还可通过生 物质(如玉米、甘蔗、高粱和微藻)发酵生产。
因甲醇作为燃料使 用时,具有稳定性、清洁性和运输方便性,因此在国家战略和环保 政策的双重推动下,我国对甲醇的需求量预计将加快。
2甲醇-水体系的分离目前分离醇-水体系国内外研究的方法主要有膜分离法、共沸精馏法、分子筛吸附法和萃取精馏法。
这些方法具有操作 简单、投资少、分离能力强等优点,因而具有广泛的工业应用前景[4]。
于清野等人[5]研究了低温甲醇洗甲醇-水分离系统,对工 业实际生产过程进行模拟计算,在原工艺基础上进行改造优 化,使其达到甲醇-水分离塔所要达到的分离标准。
实验三 甲醇-水二元体系汽液相平衡数据测定

在稳定运行时对EC(平衡室)作物料衡算得:
}
(1)
又因沸点仪可视为封闭系统,故运行前后物料总量不变,所以,
}
(2)
由式(1)和(2)可推得:
(3)
(4)
式中,
:为回流比;
:为滞液量因子;
:为组分的平衡常数。
式(3)和(4)将可测量的非分析量与平衡浓度联系起来,即为沸
点仪在稳定运行时各浓度间函数关系式。
四、实验方法
1. 实验前的准备工作 (1) 试剂的提纯
按照实验要求预先清洗精馏所用的仪器并且充分干燥,待用。精馏 装置主要由电炉、电加热套、可调式变压器、三口烧瓶、精馏柱和分馏 头组成。从下往上依次接好实验仪器,接好循环冷却水。由三口烧瓶加 入待精馏物质,密封后接通电源开始加热。首先可适当提高加热功率, 三口烧瓶中加玻璃珠,待液体沸腾后再控制调压器缓慢加热,防止爆 沸。在收集的过程中,必须先去掉初馏分,再收集沸点恒定的中间馏 分,馏分经气相色谱检测无杂质峰。试剂的提纯是一项复杂、耗时的工
数量级之间,若此时汽液平衡能够保持,我们称之为拟静态。对值不是
很大的体系,由于拟静态法是汽液回流比趋于零并能保持稳定沸点的循
环状态,所以从理论上说,拟静态是沸点仪测定汽液相平衡的最佳条
件。
三、实验装置
1. 设备装置 采用泵式沸点仪,在拟静态条件下,在101.325下测定了液相组成
与沸点的关系。压力控制采用二级自动控制系统,其压力波动不大于3 水柱。压力控制系统由恒压仪、电磁阀及继电器组成。大气压由福丁式 (Fortin)气压计测定,系统压力由U型压差计测出,U型压差计中装 水,计入水的密度校正。为了保证系统温度的稳定性,整个沸点仪用水
的特例。在动态法中,对于上式(3)中给定的,与的相对偏差非但不
化工热力学第五章作业讲解

第五章 例题一、填空题1. 指出下列物系的自由度数目,(1)水的三相点 0 ,(2)液体水与水蒸汽处于汽液平衡状态 1 ,(3)甲醇和水的二元汽液平衡状态 2 ,(4)戊醇和水的二元汽-液-液三相平衡状态 1 。
2. 说出下列汽液平衡关系适用的条件(1) l i v i f f ˆˆ= ______无限制条件__________; (2)i l i i v i x y ϕϕˆˆ= ______无限制条件____________; (3)i i s i i x P Py γ= _________低压条件下的非理想液相__________。
3. 丙酮(1)-甲醇(2)二元体系在98.66KPa 时,恒沸组成x 1=y 1=0.796,恒沸温度为327.6K ,已知此温度下的06.65,39.9521==s s P P kPa 则 van Laar 方程常数是A 12=______0.587_____,A 21=____0.717____(已知van Laar 方程为 221112212112x A x A x x A A RT G E+=)4. 在101.3kPa 下四氯化碳(1)-乙醇(2)体系的恒沸点是x 1=0.613和64.95℃,该温度下两组分的饱和蒸汽压分别是73.45和59.84kPa ,恒沸体系中液相的活度系数693.1,38.121==γγ。
1. 组成为x 1=0.2,x 2=0.8,温度为300K 的二元液体的泡点组成y 1的为(已知液相的3733,1866),/(75212121==+=s s E t P P n n n n G Pa) ___0.334____________。
2. 若用EOS +γ法来处理300K 时的甲烷(1)-正戊烷(2)体系的汽液平衡时,主要困难是MPa P s4.251=饱和蒸气压太高,不易简化;( EOS+γ法对于高压体系需矫正)。
3. EOS 法则计算混合物的汽液平衡时,需要输入的主要物性数据是ij Ci Ci Ci k P T ,,,ω,通常如何得到相互作用参数的值?_从混合物的实验数据拟合得到。
甲醇—水,甲缩醛—甲醇和甲缩醛—水系统的汽液平衡

甲醇—水,甲缩醛—甲醇和甲缩醛—水系统的汽液平衡
邱祖民;骆赞椿
【期刊名称】《高校化学工程学报》
【年(卷),期】1994(008)002
【摘要】用泵式沸点仪测定了常压下甲醇-水、甲缩醛-甲醇、甲缩醛-水三个
二元系在不同液相组成时的沸点,并用间接法由TPx推算了与之平衡的汽相组成。
用最小二乘法求出了三个二元系的液相活度系数模型参数,由模型参数推算的三个二元系的泡点与实验值能很好的吻合。
【总页数】5页(P106-110)
【作者】邱祖民;骆赞椿
【作者单位】不详;不详
【正文语种】中文
【中图分类】O642.42
【相关文献】
1.甲醇-甲缩醛-甲醛-水四元系的汽液平衡(Ⅱ) [J], 邱祖民;倪柳芳;章国荣;刘建华
2.甲缩醛—甲醇—甲醛—水四元系的汽液平衡 [J], 邱祖民;骆赞椿
3.甲缩醛—甲醇—水三元系的汽液平衡 [J], 邱祖民;骆赞椿
4.甲醇—甲缩醛—甲醛—水四元系的汽液平衡 [J], 邱祖民;柳雪芳
5.甲缩醛—甲醇—甲醛—水四元系的汽液平衡研究 [J], 邱谊民;倪柳芳
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17卷第3期1998年9月
南昌水专学报
Journal of Nanchang College of Water Conservancy and Hydroelectric Pow er
Vol.17No.3
S ep.1998
甲醇)甲缩醛)甲醛)水四元系的汽液平衡*
邱祖民(南昌大学南昌330029)
柳雪芳(上饶地区工业学校上饶334000)
倪柳芳(上饶地区技术监督局上饶334000)
屈芸(南昌大学南昌330029)
摘要检验了文献[1]热力学模型的准确性,并用该模型推算了难于测定的甲醇)甲醛、甲缩醛)甲醛及甲醇)甲缩醛)甲醛的汽液平衡.
关键词汽液平衡;热力学模型;甲醇;甲醛;甲缩醛
中图分类号O642.4
0引言
针对含甲醛多元系汽液平衡数据难于测准,相应的热力学模型难建且求解困难的特点,笔者采用泵式沸点计建立起来的一套测试装置能较准确地用于含甲醛多元系汽液平衡数据的测定[2].采用甲醛虚拟饱和蒸汽压[3]的方法能方便地建立起含甲醛多元系汽液平衡的热力学模型,且该模型易解,适合于工程计算.文献[1]研究了甲醇)甲缩醛)甲醛)水四元系的汽液平衡行为,使用泵式沸点计测试,甲醛虚拟饱和蒸汽压法处理,建立了该四元系的热力学模型,本文旨在进一步验证该模型的准确性,预测一些不易获取的甲醛多元系汽液平衡数据.
1热力学模型[1]
相平衡方程:P S i f S i X i exp[V L mi(P-P S i)/R/T]r i=P Y i f^i
P S F c f S F X F exp[V L mF(P-P S F c)/R/T]r F=P Y F f^F
式中P S F c=P C F exp[4.5+4.5/T r-11.91/T2r][2]
甲醇)甲缩醛)甲醛)水四元系所含二元系的Wilson模型参数如表1所示.
表1二元系的W ilson模型参数表
系统水)))甲醇甲缩醛)))水水)))甲醛甲醇)))甲缩醛甲醇)))甲醛甲醛)))甲缩醛参数225.3144.1629.12271.70.5875-65.9903.8-3450.23050715
*江西省自然科学基金资助项目
收稿日期:1998-04-30
2模型检验
用该四元系模型可推测所含二元系及三元系的汽液平衡行为.推测结果与文献值比较示于表21
表2011013M Pa下含甲醇、甲缩醛、甲醛、水体系的模型推测值与文献[4~7]值的比较体系文献页n d l d ml d Y W dm Y W d Y M dm Y M d Y D d m Y D d Y F d m Y F F-W4290.220.530.00660.01320.00660.0132 F-W49100.781.660.01640.03430.01440.0343 F-W410160.972.010.02100.03670.02100.0367 M-W440160.611.220.03080.07340.03080.0734
M-W447170.320.640.00400.01530.00400.0153
M-W453150.350.730.00780.02020.00780.0202
D-W425212.985.330.02490.06240.02490.0624
M-F-W4474280.621.900.01260.03800.03630.08900.04260.0850 M-F-W4475300.621.790.01290.03050.02050.06230.02530.0673 M-F-W4554280.621.900.01160.03800.03670.08920.04010.0817
M-W5210.110.41
D-W5221.032.01
F-W3250.351.23
M-D5210.160.44
M-D-W6190.411.85
M-F-W7131.051.95
由表2可见除甲缩醛-水体系的沸点模型推测值与文献值差异较大外,其它尚可.
图10.1013M Pa下甲醇)甲醛二元系的VLE图
)计算的X
M )计算的Y
M
3模型预测
由于难制得纯甲醛用于甲醛多元系的汽
液相平衡测定,而上述模型检验说明根据文献
[1]建立起来的甲醇)甲缩醛)甲醛)水四元
系的热力学模型具有较高的准确性,因此可用
该模型预测甲醇)甲醛、甲缩醛)甲醛二元
系、甲醇)甲缩醛)甲醛三元系的汽液平衡行
为.预测结果分别示于图1~图5.
4结论
模型检验说明该四元系模型无论是用于
其所含组分的二元系还是三元系汽液平衡行为描绘,其准确度皆较高.11
第3期邱祖民、柳雪芳、倪柳芳、屈芸:甲醇)甲缩醛)甲醛)水四元系的汽液平衡
图20.1013M Pa下甲缩醛)甲醛二元系的VLE图)计算的X D)计算的Y
D 图30.1013M Pa下甲醇)甲缩醛)甲醛三元系的VL
E 等温图1-44e;2-46e;3-47e;4-50e;
5-55e;6-60
e
图40.1013M Pa下甲醇)甲缩醛)甲醛三元系的
VLE等Y D图1-30%;2-50%;3-60%;
4-70%;5-80%;6-90%;7-95
%
图50.1013M Pa下甲醇)甲缩醛)甲醛三元系的
VLE等Y M图1-5%;2-10%;3-20%;
4-30%;5-40%;6-50%本文推测了甲醇)甲醛、甲缩醛)甲醛、甲醇)甲缩醛)甲醛的汽液平衡,可供工程研究及设计时参考.
符号说明
d)绝对平均偏差上标:
D)甲缩醛C)临界态
d m)最大绝对偏差L)液相
f)汽相逸度系数s)饱和态
f^)汽相分逸度系数s c)虚拟态
F)甲醛下标:
M)甲醇b)泡点
n)实验点数cal)计算值
12南昌水专学报1998年第3期
P )压力,M Pa D )甲缩醛r )活度系数
exp )实验值R )气体常数,J.mol -1.K -1F )甲醛
t,T )温度,e ,K i )除甲醛外的组分V )体积m )摩尔量W )))水
M )甲醇X )液相组成,mol %r )对比Y )汽相组成,mol %
W )水
参考文献
1 邱祖民、骆赞椿、胡英.甲缩醛)甲醇)甲醛)水四元系的汽液平衡.高校化学工程学报,1998,12(1):61
2 邱祖民、骆赞椿、胡英.泵式沸点仪.高校化学工程学报,1997,11(1):74
3 邱祖民、骆赞椿、胡英.含甲醛多元系汽)液平衡的模型化.高校化学工程学报,1996,10(3):61
4 Gmehling J 、Onken U 、Arlt W.V apor -L iquit Equilibrium Data Collection,Vol.1,DECHEM A(1981)
5 邱祖民、骆赞椿、胡英.甲醇)))水、甲缩醛)))甲醇和甲缩醛)))水系统的汽液平衡.高校化学工程学
报.1994,8(2):106
6 邱祖民、骆赞椿、胡英.甲缩醛)))甲醇)))水三元系的汽液平衡.高校化学工程学报,1997,11(2):189
7 邱祖民、骆赞椿、胡英.甲缩醛)))甲醇)))水三元系的汽液平衡.南昌大学学报(工科版),1996,18(4):42
Vapor Liquid Equilibria of the Methylal
Methanol -Formaldehyde-Water System
Qiu Zumin Qu Yun
(Nanchang University Nanchang 330029)
Liu Xuefang
(Shangrao Industry School Shangrao 334000)
Ni Liufang
(Shangrao Supervisory Office of Technicality Shangrao 334000)
Abstract The thermodynamic model accuracy in the literature[1]w as testified in this paper.T he vapor -liquit equilibria (VLE)of the methylal -formaldehyde,the methanol -formaldehyde,and the methylal-methanol-formaldehyde w as predicted w ith the model,w hich is difficult to determine.
Key words VLE;thermodynamic model;methanol;formaldehyde;methylal
13
第3期 邱祖民、柳雪芳、倪柳芳、屈芸:甲醇)甲缩醛)甲醛)水四元系的汽液平衡。
