化学动力学计算题
化学反应动力学计算题

化学反应动力学计算题化学反应动力学是研究化学反应速率的科学,它探究反应速率和反应物浓度的关系以及反应的机理。
在这个计算题中,我们将通过给定的反应速率常数和初始浓度来计算反应的速率常数和反应物浓度随时间的变化。
首先,我们假设一个一级反应的情况,反应方程式为A → 产物。
在一级反应中,反应速率与反应物的浓度成正比,表达式为r = k[A]。
我们已知反应速率常数k为0.05 s^-1,初始浓度[A]为0.1 mol/L。
我们需要计算出在反应时间t=10 s时,反应物浓度[A]的值。
首先,我们可以使用一级反应速率方程来计算出反应物在任意时间t的浓度:[A] = [A₀] * e^(-kt)其中,[A]为时间t时的反应物浓度,[A₀]为初始浓度,k为反应速率常数,e为自然对数的底数。
代入已知的值,我们可以计算出:[A] = 0.1 * e^(-0.05*10)通过计算,我们得到[A] ≈ 0.0364 mol/L。
接下来,我们将计算该反应在10秒内的平均反应速率。
平均反应速率可以通过反应物浓度的变化量与反应时间的比值来计算。
平均反应速率= Δ[A] / Δt我们已知初始浓度[A₀]为0.1 mol/L,在10s内,反应物浓度减少为0.0364 mol/L。
因此,变化量Δ[A]为0.1 - 0.0364 = 0.0636 mol/L。
反应时间Δt为10s。
代入已知的值,我们可以计算出:平均反应速率= 0.0636 mol/L / 10 s ≈ 0.00636 mol/(L·s)因此,在10s内,该反应的平均反应速率为0.00636 mol/(L·s)。
通过这个计算题,我们可以看到一级反应速率与反应物浓度的关系,以及如何计算出反应物浓度随时间变化和反应的平均反应速率。
请注意,在实际的化学反应动力学中,反应物的浓度变化通常是非线性的,我们需要使用更复杂的方程模型来描述这些反应。
此计算题仅仅是一个简单的示例,用于理解基本的反应动力学原理。
(整理)第11章动力学练习题

第十一章动力学练习题一、是非题(对的画√错的画×)1、反应速率系数k A 与反应物A 的浓度有关。
( )2、反应级数不可能为负值。
( )3、一级反应肯定是单分子反应。
( )4、对二级反应来说,反应物转化为同一百分数时,若反应物的初始浓度越低,则所需时间越短。
( )5、对同一反应,活化能一定,则反应的起始温度愈低,反应的速率系数对温度的变化愈敏感。
( )6、阿累尼乌斯活化能的定义是dTkd RT Ea ln 2=。
( ) 7、对于元反应,反应速率系数部随温度的升高而增大。
( ) 8、若反应A →Y ,对A 为零级,则A 的半衰期 AA k C t 20,21=.。
( )9、设对行反应正方向是放热的,并假定正逆都是元反应,则升高温度更利于增大正反应的速率系数。
( )10、连串反应的速率由其中最慢的一步决定,因此速率控制步骤的级数就是总反应的级数。
( ) 11、鞍点是反应的最低能量途径上的最高点,但它不是势能面上的最高点,也不是势能面上的最低点。
( )12、过渡态理论中的活化络合物就是一般反应历程中的活化分子。
( ) 13、催化剂只能加快反应速率,而不有改变化学反应的标准平衡常数。
( )14、复杂反应是由若干个基元反应组成的,所以复杂反应的分子数是基元反应的分子数之和.。
( )15、质量作用定律只适用于元反应。
( )16、某反应,若其反应速率方程式为υA =κA B ,则当c B,0>>c A,0时,反应速率方程可约化为假二级反应。
( )17、若反应+Z 的速率方程为 υ= kc A c B , 则该反应是二级反应,且肯定是双分子反应。
( )18、对于反应 2NO + Cl 2 −→− 2NOCl ,只有其速率方程为:υ=k {c (NO)}2c (Cl 2),该反应才有可能为元反应。
其他的任何形式,都表明该反应不是元反应。
( )19、 知道了反应物和产物可写出化学反应方程式, 但不能由配平的化学反应式直接写出反应级数和反应分子数。
化学动力学(一)练习与答案08级

化学动力学练习(一)一、选择题1. 对于反应 2NO2= 2NO + O2,当选用不同的反应物和产物来表示反应速率时,其相互关系为:( )(A) -2d[NO2]/d t = 2d[NO]/d t = d[O2]/d t(B) - d[NO2]/2d t = d[NO]/2d t = d[O2]/d t = d/d t(C) - d[NO2]/d t = d[NO]/d t = d[O2]/d t(D) - d[NO2]/2d t = d[NO]/2d t = d[O2]/d t = 1/V d/d t2. 理想气体反应A + BC[ABC]≠ 产物,若设E a为阿累尼乌斯活化能,≠Hm表示活化络合物与反应物在标准状态下的焓差,则( )(A) E a= ≠Hm+ RT(B) E a= ≠Hm+ 2RT(C) E a= ≠Hm+ 3RT(D) E a= ≠Hm- 2RT3. 均相反应 A + B k1C +D , A + Bk2E +F 在反应过程中具有[C]/[E] = k1/k2的关系,[C],[E] 为反应前后的浓差,k1,k2是反应 (1),(2)的速率常数。
下述哪个是其充要条件?( )(A) (1),(2) 都符合质量作用定律(B) 反应前 C,E 浓度为零(C) (1),(2) 的反应物同是 A,B(D) (1),(2) 反应总级数相等4. 400 K 时,某气相反应的速率常数k p= 10-3(kPa)-1·s-1,如速率常数用k C表示,则k C应为:( )(A) 3.326 (mol·dm-3)-1·s-1(B) 3.0×10-4 (mol·dm-3)-1·s-1(C) 3326 (mol·dm-3)-1·s-1(D) 3.0×10-7 (mol·dm-3)-1·s-15. 在反应 A k1Bk2C,Ak3D 中,活化能E1> E2> E3,C 是所需要的产物,从动力学角度考虑,为了提高 C 的产量,选择反应温度时,应选择: ( )(A) 较高反应温度 (B) 较低反应温度(C) 适中反应温度(D) 任意反应温度6. 如果某反应的 △r H m = 100kJ ·mol -1,那么活化能 E a 将: ( )(A) E a ≠ 100kJ ·mol -1 (B) E a ≥ 100kJ ·mol -1 (C) E a ≤ 100kJ ·mol -1 (D) 都可以7. 某反应物起始浓度相等的二级反应,k = 0.1 dm 3·mol -1·s -1,c 0= 0.1 mol ·dm -3,当反应率降低9倍所需时间为:( )(A) 200 s (B) 100 s (C) 30 s (D) 3.3 s8. 过渡态理论的速率常数的公式为()()()k k T h q q q E RT =≠-B AB//exp /∆0,下述说法正确的(A) q ≠不是过渡态的全配分函数 (B) q A , q B 是任意体积中分子的配分函数(C) q A , q B , q ≠均是分子在基态时的配分函数(D) ()k T h B /是过渡态M ≠中任一个振动自由度配分函数9. 1-1 级对峙反应 12AB k k 由纯 A 开始反应,当进行到 A 和 B 浓度相等的时间为: (正、逆向反应速率常数分别为 k 1 ,k 2) ( ) (A) t = ln12k k (B) t =11221ln kk k k -(C) t =1121212ln k k k k k +-(D) 112121ln k t k k k k =+-10. 在温度 T 时,实验测得某化合物在溶液中分解的数据如下: 初浓度 c 0/mol ·dm -3 0.50 1.10 2.48 半衰期 t 12/ s -1 4280 885 174则该化合物分解反应的级数为:( )(A) 零级 (B) 一级反应(C) 二级反应 (D) 三级反应11. 两个活化能不相同的反应,如 E 2> E 1,且都在相同的升温度区间内升温, 则:( )(A)21d ln d ln d d k k T T >(B) 21d ln d ln d d k k T T<(C )21d ln d ln d d k k T T=(D)21d d d d k k T T>12. 下表列出反应 A + B → C 的初始浓度和初速:此反应的速率方程为:( )(A) r = k c B (B) r = k c A c B (C) r = k c A (c B )2 (D) r = k c A13. 实验测得反应 3H 2+ N 2→ 2NH 3 的数据如下:由此可推知该反应的速率方程 d p (NH 3)/2d t 等于: ( )(A) kp H 23 p N 2 (B) kp H 22p N 2(C) kpH2pN2(D) kpH2pN2214. 如果臭氧 (O3) 分解反应 2O3→ 3O2的反应机理是:O3→ O + O2(1)O + O3→ 2O2(2)请你指出这个反应对O3而言可能是:( )(A) 0 级反应(B) 1 级反应(C) 2 级反应(D) 1.5 级反应15. 对于气相基元反应,按过渡态理论,不正确的关系式是:( )(A)E a=≠Um +RT (B)E a=≠Hm+nRT(C)E a=E0+ RT (D)E a=E0+mRT16. 单原子分子A与双原子分子B生成非线性过渡态时,据A(TST)=(k B T/h)[q≠/(qA qB )]计算A时,q≠为( )(A) f t3f r2f v3 (B) f t3f r2f v4(C) f t3f r3f v3 (D) f t3f r3f v217. 气相反应 A + 2B ─→ 2C,A 和 B 的初始压力分别为p A和p B,反应开始时并无C,若p为体系的总压力,当时间为t时,A 的分压为:( )(A) p A- p B(B) p - 2p A(C) p - p B(D) 2(p - p A) - p B18. 基元反应 A + B - C → A - B + C 的摩尔反应焓r Hm< 0, B - C 键的键能为BC, A 为自由基,则反应活化能等于:( )(A) 0.30BC (B) 0.05BC(C) 0.05BC+ H m (D) 0.05 BC - H m19. 反应 A →产物为一级反应,2B →产物为二级反应,t12(A) 和t12(B) 分别表示两反应的半衰期,设 A 和 B 的初始浓度相等,当两反应分别进行的时间为t = 2t12(A) 和t = 2t12(B) 时,A,B 物质的浓度c A,c B的大小关系为:( )(A) c A> c B(B) c A= c B(C) c A< c B(D) 两者无一定关系20. 一个反应的活化能是33 kJ·mol-1, 当T = 300 K 时,温度每增加 1K,反应速率常数增加的百分数约是:( )(A) 4.5%(B) 90%(C) 11%(D) 50%二、计算题 21.1,3-二氯丙醇在NaOH 存在条件下, 发生环化作用,生成环氧氯丙烷反应, 反应为二级(对1,3-二氯丙醇及NaOH 均为一级)。
第5章 化学动力学习题

第5章化学动力学习题一、思考题1.化学反应速率是如何定义的?反应速率方程如何表达?2.影响反应速率的因素有哪些?3.如何加快均相和多相反应的反应速率?4.质量作用定律适用于什么样的反应?5.能否根据反应方程式直接写出反应速率方程式?为什么?6.速率常数受哪些因素的影响?浓度和压力会影响速率常数吗?7.什么是反应级数?零级反应和一级反应各有什么特征?8.一个反应的活化能为180 kJ·mol-1,另一个反应的活化能为48 kJ·mol-1。
在相似的条件下,这两个反应中哪一个进行较快些?为什么?9.为什么说使用催化剂不会改变体系的热力学性能?10.为什么不同的反应升高相同的温度,反应速率提高的程度不同?11.是不是对于所有的化学反应,增加任意一个反应物的浓度都会提高反应速率?为什么?12.碰撞理论和过渡态理论的基本要点是什么?两者有什么区别?13.何为反应机理?你认为要想了解反应机理,最关键是要怎么做?14.试解释浓度、压力、温度和催化剂加快反应的原因。
15.总压力与浓度的改变对反应速率以及平衡移动的影响有哪些相似之处?有哪些不同之处?举例说明。
16.比较“温度与平衡常数的关系式”同“温度与反应速率常数的关系式”,有哪些相似之处?有哪些不同之处?举例说明。
17.反应2NO(g)+2H2(g)=== N2(g)+2H2O(g)的速率方程是r = k c2(NO)c(H2)试讨论以下各种条件变化时对反应速率的影响(1)NO的浓度增加1倍;(2)有催化剂参加;(3)升高温度;(4)反应容器的体积增大1倍18.对于下列平衡体系:C (s) + H2O (g) = CO (g) + H2(g),q为正值。
(1) 欲使平衡向右移动,可采取哪些措施?(2) 欲使(正)反应进行得较快(平衡向右移动)的适宜条件如何?这些措施对K及k(正)、k(逆)的影响各如何?二、是非题(对的在括号内填“√”号,错的填“×”号)1.反应速率常数仅与温度有关,与浓度、催化剂等均无关系。
物理化学-动力学练习题及参考答案

动力学1A一、选择题1. 连串反应A k1B k2 C 其中k1= 0.1 min-1,k2= 0.2 min-1,假定反应开始时只有A,且浓度为1 mol·dm-3,则B 浓度达最大的时间为:( )(A) 0.3 min (B) 5.0 min(C) 6.93 min (D) ∞2. 平行反应A k1 B (1);A k2 D (2),其反应(1)和(2)的指前因子相同而活化能不同,E1为120 kJ·mol-1,E2为80 kJ·mol-1,则当在1000K 进行时,两个反应速率常数的比是:( )(A) k1/k2= 8.138×10-3(B) k1/k2= 1.228×102(C) k1/k2= 1.55×10-5(D) k1/k2= 6.47×1043. 如果臭氧(O3) 分解反应2O3→3O2的反应机理是:O3→O + O2(1)O + O3→2O2(2)请你指出这个反应对O3而言可能是:( )(A) 0 级反应(B) 1 级反应(C) 2 级反应(D) 1.5 级反应4. 化学反应速率常数的Arrhenius 关系式能成立的范围是:( )(A) 对任何反应在任何温度范围内(B) 对某些反应在任何温度范围内(C) 对任何反应在一定温度范围内(D) 对某些反应在一定温度范围内5. 如果反应2A + B =2D 的速率可表示为:r = -12d c A /d t = - d c B /d t = 12d c D /d t 则其反应分子数为: ( )(A) 单分子 (B) 双分子(C) 三分子 (D) 不能确定6. 实验测得反应 3H 2+ N 2→ 2NH 3 的数据如下:由此可推知该反应的速率方程 d p (NH 3)/2d t 等于: ( )(A) kp H 23 p N 2(B) kp H 22p N 2 (C) kp H 2 p N 2 (D) kp H 2 p N 227. 在反应 A k 1B k 2C ,A k 3 D 中,活化能 E 1> E 2> E 3,C 是所需要的产物,从动力学角度考虑,为了提高 C 的产量,选择反应温度时,应选择: ( )(A) 较高反应温度(B) 较低反应温度 (C) 适中反应温度(D) 任意反应温度 8. [X]0 [Y]0 [Z] 增加 0.0050 mol ·dm -3 所需的时间/ s0.10 mol ·dm -3 0.10 mol ·dm -3 720.20 mol ·dm -3 0.10 mol ·dm -3 180.20 mol·dm-30.05 mol·dm-336对于反应X + 2Y →3Z,[Z] 增加的初始速率为:( )(A) 对X 和Y 均为一级(B) 对X 一级,对Y 零级(C) 对X 二级,对Y 为一级(D) 对X 四级,对Y 为二级9. 一级反应,反应物反应掉1/n所需要的时间是:( )(A) -0.6932/k(B) (2.303/k) lg[n/(n-1)](C) (2.303/k) lg n(D) (2.303/k) lg(1/n)10. 关于反应速率理论中概率因子P的有关描述,不正确的是:( )(A) P与≠S m有关(B) P体现空间位置对反应速率的影响(C) P与反应物分子间相对碰撞能有关(D) P值大多数<1,但也有>1的二、填空题12. 60Co广泛用于癌症治疗, 其半衰期为5.26 a (年), 则其蜕变速率常数为:_________________, 某医院购得该同位素20 mg, 10 a后剩余______________ mg。
化学动力学习题参考答案

第六章 化学动力学习题答案1. 某放射性元素经14天后,活性降低了%。
试求:(1)该放射性元素的半衰期;(2)若要分解掉90%,需经多长时间解:放射性元素的衰变符合一级反应规律。
设反应开始时,其活性组分为100%,14天后,剩余的活性组分为100%%,则:A,031A,011100ln ln 5.0710d 14100 6.85c k t c x --===⨯--312ln 2/ln 2/(5.0710)136.7d t k -==⨯=A,03A,0A,0111ln ln 454.2d 0.9 5.071010.9c t k c c -===-⨯-2.已知某药物在体内的代谢过程为某简单级数反应,给某病人在上午8时注射该药物,然后分别经过不同时刻t 测定药物在血液中的浓度c (以mmol?L -1表示),得到如下数据:t / h 4 8 12 16 c/(mmol?L -1)如何确定该药物在体内代谢过程的反应级数该反应的速率常数和半衰期分别是多少解:此题可用尝试法求解反应级数。
先求出不同时刻的ln c :t / h 4 8 12 16 ln c ? ? ? ?以ln c 对t 作图,得一直线,相关系数为,所以此为一级反应,即n=1。
直线的斜率为?,则有此反应的速率常数为;半衰期1/2ln 27.24h t k==。
3.蔗糖在酸催化的条件下,水解转化为果糖和葡萄糖,经实验测定对蔗糖呈一级反应的特征: 122211261266126HC H O H O C H O C H O ++−−→+蔗糖(右旋) 果糖(右旋) 葡萄糖(左旋)这种实验一般不分析浓度,而是用旋光仪测定反应过程中溶液的旋光角。
反应开始时,测得旋光角0 6.60α=o 。
在t=8min 时,测得旋光角 3.71t α=o 。
到t ∞时,即蔗糖已水解完毕,这时旋光角 1.98α∞=-o 。
由于葡萄糖的左旋大于果糖的右旋,所以最后溶液是左旋的。
化学动力学 (3)

• • • • •
不定积分: 定积分:
2 半衰期: k2的单位: (浓度)-2· (时间)-1 引伸: t1/2 :t3/4 :t7/8 = 1 :5 :21
t1
3 2 k3 a 2
3. 三级反应特点总结
1.速率系数 k 的单位为(浓度)-2(时间)-1 2.半衰期
t1/ 2
1 3. 2 与t 呈线性关系 (a x)
t1/ 2 a ' t '1/ 2 a
n 1
4. 气相反应(等容条件下)中,用压力代替物质的量浓度表示时的速率常数 (a) 对气相一级反应,用压力表示时的速率常数与用物质的量浓度表示时的 速率常数相同。 (b) 对气相二级反应,用压力表示时的速率常数与用物质的量浓度表示时的速 率常数有差别。
2A → r=-
P +
· · · · · ·
A2 =1 k2d[A]
k 1 k1
•
N2O2 + O2
k2
2NO2 (慢)
• 五. 零级反应 所谓零级反应就是反应速率与参与反应的物质的浓度无关的反应 零级反应主要是一些表面催化反应和酶催化反应。这时反应物总是过量的, 反应速率决定于固体催化剂的有效表面活性位的浓度,或酶的浓度。
A→P
r = k0
1. 零级反应的微分和积分式及半衰期
示式等一般形式。这里 n 不等于1。
nA → P
r = k[A]n
n级反应的微分式,积分式及半衰期 nA → P t =0 a 0 t =t a-x x/n (3)半衰期的一般式: (1)速率的微分式:
r=dx/dt=k(a-x)n (2)速率的定积分式:(n≠1) x t dx 0 (a x)n 0 kdt
化学动力学计算题
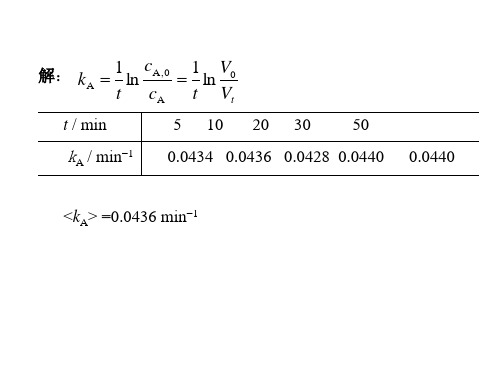
解: (1) 由
1 ln
1 xA
(k1 k2 )t
代入已知条件:k1(400 K) = 0.1 s-1; k2(400 K) = 0.01 s -1
则
ln 1 0.1s1 0.01s1 10s
1 xA
解得:
xA = 0.667
因为 cY / cZ = k1 / k2,cY + cZ = cA,0xA
kA/104s1
4.43 4.37 4.46
3155 4.50
kA =4.44×104 s1
t1/2 =ln2 /kA =1.56×103 s 。
8-2-1 均相反应2A+B
3Y+Z在一定温度体积下进行,
测得动力学数据如下:
实验编号
12 3
4
反应温度T/K
300 300 300 320
cA,0/molm3 cB,0/molm3
从实验1,2,3可以计算出300 K时,kA(300K)的平均值。 kA(300K)=1.5×107 m6·mol2·s1
(2) 把(1)的结果代入Arrhenius方程,得
ln
kA kA
320 K 300 K
Ea R
1 320 K
1 300
K
解得: Ea=200 kJ·mol1
8-2-2 某反应在15.05℃时的反应速率系(常) 数为34.40×103 dm3·mol1·s1,在40.13℃时的 反应速率系(常)数为189.9×103 dm3·mol1·s1。求反应的活化能,并计算 25.00℃时的反应速率系(常)数。
t / s 0 390 777 1587 3155 p/kPa 41.3 54.4 65.1 83.2 103.9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 化学动力学计算题1.放射性同位素的蜕变速率符合一级反应的规律(蜕变速率与放射性同位素的数量成正比)。
210Po 经α蜕变生成稳定的206Pb :210Po → 206Pb + 4He 。
实验测得14 d 后放射性降低了6.85%,试求210Po 的蜕变速率常数和半衰期,并计算它蜕变掉90%时所需要的时间。
解:2.双分子反应2A(g)−→−kB(g) + D(g), 在623 K 、初始浓度为0.400 mol·dm -3时,半衰期为105 s, 求出: (1) 反应速率常数k ; (2) A(g)反应掉90%所需时间为多少? (3) 若反应的活化能为140 kJ/mol, 573 K 时的最大反应速率为多少?解:(1) 由基元反应得: v = k [A]2那么: t 1/2= 1/(2k [A]0), k = 1/(2t 1/2[A]0)=1/(2×105×0.400) dm 3·mol -1·s -1=0.0120 dm 3·mol -1·s -1(2) 由1/[A] – 1/[A]0 =2kt得: 1/0.1[A]0 – 1/[A]0 =2kt1/0.0400 – 1/0.400 = 2×0.0120×t所以: t = 945 s(3) 由ln(k/k ')=(E a /R )×(1/T '-1/T )得: ln(0.012/k ')=(140000/8.314)×(1/573-1/623)k ' = 0.00223 dm 3·mol -1·s -1,因此, 最大反应速率v max = k '[A]02= 0.00223×(0.400)2 mol·dm -3·s -1=3.6×10-4 mol·dm -3·s -113d 1007.50685.011ln d 14111ln 1--⨯=-=-=A A x t k d 137d 1007.52ln 2ln 132/1=⨯==--A k t d 45490.011ln d 1007.5111ln 113=-⨯=-=--A A x k t3.蔗糖在稀溶液中,按照下式水解:C 12H 22O 11 + H 2O → C 6H 12O 6(葡萄糖) + C 6H 12O 6(果糖)当温度与酸的浓度一定时,反应速率与蔗糖的浓度成正比。
今有一溶液,1 dm 3溶液中含有0.300 mol C 12H 22O 11及0.1 mol HCl ,在48 ℃时20 min 内有32%的蔗糖水解。
求: (1) 计算反应速率常数; (2) 计算反应开始时(t =0)及20 min 时的反应速率; (3) 问40 min 后有多少蔗糖水解; (4) 若60%的蔗糖发生水解,需多少时间? (5) 反应40 min 要得到6 kg 葡萄糖,求反应器的有效容积。
解:(2) 当t=0时, v A =k A c A,0=0.0193×0.300 mol·dm -3·min -1=5.80×10-3 mol·dm -3·min -1当t=20 min 时, v A =k A c A,0(1- x A )=0.0193×0.300×(1-0.32) mol·dm -3·min -1=3.94×10-3 mol·dm -3·min -1(3) ln(1-x A )= -k A t= -0.0193×40= -0.772因此: x A =0.54=54%(4) (5) 由(3)得:c p =0.54×0.300 mol·dm -3n p =m/M= 6/0.1802 mol因此有: V = n p /c p =6/(0.1802×0.54×0.300) dm 3=206 dm 34.在294.2 K 时,一级反应A → C ,直接进行时A 的半衰期为1000分钟,温度升高45.76 K ,则反应开始0.1分钟后,A 的浓度降到初始浓度的1/1024,若改变反应条件,使反应分两步进行:C B A 21−→−−→−kk ,巳知两步的活化能E 1 = 105.52 kJ·mol -1,E 2 = 167.36 kJ·mol -1,问500 K 时,该反应是直接进行快,还是分步进行速率快(假定频率因子不变)?两者比值是多少?解:直接进行:T 1 = 294.2 K k 1 = 0.693/1000 min -1= 6.93 × 10-4 min -1T 2 = 294.2 + 45.76 = 339.96 K 11min 0193.0min 32.011ln 20111ln 1 )1(--=-=-=A A x t k min 4760.011ln min 0193.0111ln 11=-=-=-A A x k t 1 2 min 3 . 69 1024 ln 1 . 01 ln 1 - = ⨯ = ⎪ ⎭ ⎫ ⎝ ⎛ ⋅ = c x A t k)102.209exp(mol kJ 2.209ln 31-121221a RT A k k k T T T RT E ⨯-=⋅=⎪⎪⎭⎫ ⎝⎛⋅-=, 两步进行:∵ E 1 < E 2 ∴ 反应速率由第二步决定⎪⎪⎭⎫ ⎝⎛⨯-=⎪⎭⎫ ⎝⎛=RT A RT E A k 321036.167exp 'exp '',假定A 与A '相等, k '/k = exp(-167.36 × 103/RT )/exp(-209.2 × 103/RT ) = exp(10) = 2.2 × 104所以,分两步进行的速率快,快 2.2 × 104 倍.5.某化合物的分解为一级反应,今测得50 ℃、60 ℃时分解反应速率常数分别是7.08×10-4 h -1与1.7×10-3 h -1,计算该反应的活化能;若此化合物分解30%则无效,求温度为25 ℃时此化合物的有效期。
解: 根据Arrhenius 方程式:ln(k 2/k 1) = E (T 2 - T 1)/RT 1T 2E a = RT 1T 2/(T 2 - T 1)ln(k 2/k 1)= [8.314 × 323 × 333/(333 - 323)]·ln(1.7 × 10-3/7.08 × 10-4)= 78.33 kJ/mol设25 ℃时的速率常数为k 3,明显T 3 = 298 Kln(k 1/k 3) = 78.33 × 103(323 - 298)/(8.314 × 323 × 298) = 2.447k 1/k 3 = 11.554 k 3 = 7.08 × 10-4/11.554 = 6.13 × 10-5 h -1对一级反应有:ln[1/(1 - x A )] = k 1t , x A = 0.30t = 1/k 3·ln[1/(1 - x A )] = 1/6.13 × 10-5·ln[1/(1 - 0.3)]= 5813 h= 242.2 d6.对于以下平行反应,生成B 和C 的速率常数分别为k 1和k 2,所需的活化能分别为E 1和E 2:试推导总反应的活化能E '与E 1、E 2的关系为:C212211k k E k E k E ++='证明:总速率: - d[A]/d t = k 1[A] + k 2[A]= (k 1 + k 2)[A]= k '[A] (其中k ' = (k 1 + k 2) = Ae x p(-E '/RT ), ∵2'd 'ln d RT E T k = 又∵Tk k k k T k k T k d )d(1d )dln(d 'ln d 212121+⋅+=+= ⎪⎪⎭⎫ ⎝⎛+⨯+=⎪⎭⎫ ⎝⎛+⨯+=T k k k T k k k k k T k T k k k d d d d 1d d d d 1222111212121 ⎪⎭⎫ ⎝⎛+⨯+=⎪⎭⎫ ⎝⎛+⨯+=222211212211211d ln d d ln d 1RT E k RT E k k k T k k T k k k k 21221121k k E k E k RT ++⨯= 所以212211'k k E k E k E ++=7.试用稳态近似法导出下面气相反应历程的速率方程:A B , B + C D 23并证明该反应在高压下呈一级反应,在低压下呈二级反应。
证明:达稳态时,d[B]/d t = k 1[A] - k 2[B] - k 3[B][C] = 0,[B] = k 1[A]/(k 2 + k 3[C])所以: d[D]/d t = k 3[B][C] = k 1k 3[A][C]/(k 2 + k 3[C])高压时,k 3[C] >> k 2所以d[D]/d t = k 1[A],呈一级反应低压时,k 2 >> k 3[C]所以 d[D]/d t = k 1k 3[A][C]/k 2,故呈二级反应8.设乙醛热分解CH 3CHO → CH 4 + CO 是按下列历程进行的:CH 3CHO −→−1kCH 3· + CHO CH 3· + CH 3CHO −→−2k CH 4 + CH 3CO·(放热反应)CH 3CO·−→−3kCH 3· + CO CH 3· + CH 3·−→−4k C 2H 6 (1) 用稳态近似法求出该反应的速率方程:d[CH 4]/d t = ?(2) 巳知键焓εC -C = 355.64 kJ·mol -1,εC -H = 422.58 kJ·mol -1,求该反应的表观活化能。
解:(1) v = d[CH 4]/d t = k 2[CH 3·][CH 3CHO] (1)d[CH 3·]/d t = k 1[CH 3HO]-k 2[CH 3·][CH 3CHO]+k 3[CH 3CO·]-k 4[CH 3·]2 = 0 (2) d[CH 3CO·]/d t = k 2[CH 3·][CH 3CHO]-k 3[CH 3CO·] = 0 (3)(2)式+ (3)式: k 1[CH 3CHO] = k 4[CH 3·]2即:[CH 3·] = (k 1/k 4)1/2[CH 3CHO]1/2,代入(1)式得:v = k 2(k 1/k 4)1/2[CH 3CHO]3/2 = k a [CH 3CHO]3/2,其中 k a = k 2(k 1/k 4)1/2(2) E a = E 2 + 1/2(E 1 - E 4)E 1 = εC -C = 355.64 kJ·mol -1 ,E 2 = 0.05×εC -H =0.05 × 422.58 kJ·mol -1= 21.13 kJ·mol -1E 4 = 0所以E a = 21.13 + 1/2 (355.64-0) = 198.95 kJ·mol -19.对于加成反应A + B → P ,在一定时间Δt 范围内有下列关系:[P]/[A] = k r [A]m -1[B]n Δt ,其中k r 为此反应的实验速率常数,进一步实验表明:[P]/[A]与[A]无关;[P]/[B]与[B]有关,当Δt = 100h 时:[B](p ) 10 5[P]/[B] 0.04 0.01(A) 此反应对于每个反应物来说,级数各为若干?(B) 有人认为上述反应机理可能是:2B − → −1 k B2 ,k (平衡常数),快 (1)B + A − → −2 k 络合物,k 2(平衡常数),快 (2) B 2 + 络合物−→−3kP + B ,k 3(速率常数),慢 (3) 导出其速率方程,并说明此机理有无道理。
