2011年全国大学生数学建模竞赛D题及评阅参考
2011年高教杯数学建模竞赛D题获奖论文 无锡职业技术学院

min y
S.T.
n
j 1
a ij
b j x ij
i 1
m
1 m pk 且, m N , k 1,2,3. 88 .5 a11 x11 a12 x12 a1n x1n 89 .5 88 .5 a 21 x21 a 22 x22 a 2 n x2 n 89 .5 88 .5 a m1 xm1 a m 2 xm 2 a mn xmn 89 .5 d k 1 xi j d k , i 1,2,3, , m.
应用 LINGO 计算结果,经过验证 m 37 时,模型有最优解 ymin 428 ,即 规格二的最大成品捆数为 37,具体搭配方案如下表 4(求解程序见附录 6.2) : 表 4 规格二的搭配方案
单位长度 捆数
7
75
9
9. 5 0 0 1 3 0 0 0 1 2 0 0
3
7 6 34 7 10 21
8 6.5 21 8 10.5 18
三
根数 序号 长度 根数 序号 长度 根数
35 9 18 50 17 22 12
29 10 18.5 64 18 22.5 2
30 11 19 52 19 23 0
42 12 19.5 63 20 23.5 6
28 13 20 49 21 24 0
4.5 1 1 0 0 0 0 3 2 5 0 0 0 10
5 0 0 7 0 0 0 0 6 0 14 0 0 0
5.5 0 1 0 1 0 13 0 0 3 0 0 1 3
6 0 5 0 9 2 0 7 0 0 0 0 10 0
2011年大学生数学建模竞赛试题(全套)

2011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?B题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
2011高教社杯全国大学生数学建模竞赛ABCD4题评阅要点

2021高教社杯全国大学生数学建模比赛A题评阅要点[说明]本要点仅供参考, 各赛区评阅组应根据对题目的理解及学生的解答, 自主地进行评阅。
本问题的数据来源于某城市对土壤环境的实地监测。
评阅时, 应着重注意数学模型的建立、计算方法(或所选软件的程序语句) 及挑选该方法的理由。
(1) 可用插值拟合的方法获得. 各重金属污染物浓度的空间分布。
再参考由背景值确定的阈值, 定量分析城区各区域的污染程度。
由于空间数据是不规则的 , 较好的方法是用散乱数据插值, 例如Kriging插值、 Shepard插值等。
也可以用其他方法插值拟合, 但应明确所使用的方法, 并作出分析, 不能只简单套用软件。
各个污染元素浓度的最大值与插值后浓度的最大值距离不会太远。
(2) 分析污染产生的原因, 必须有充分的数据分析以及明确的结论。
例如, 可以根据各区域的污染浓度信息进行聚类, 考察污染物出现的相关性, 发现某些污染物结伴出现(如Cr与Ni, Cd与Pb的相关性较高) , 这与污染物产生的原因是密切相关的 , 由此可大致确定出产生这些污染的原因。
(3) 本小题可以在不同的假定下建立相应的模型, 但必须有合理的假定、建立明确的数学模型, 并根据模型和所给的数据进行数值计算。
例如, 由于雨水的作用是重金属在土壤表层中传播的主要原因之一, 可以假定传播以对流形式为主, 由此建立对流方程, 并以给出的重金属污染物浓度数据作为初始值(实际上是终值) , 从而得. 到偏微分方程的定解问题。
类似于(1) ,采纳插值拟合的方法, 可以得. 到地形高度函数。
利用特征线法, 可以得. 到各区域在各个时间点上的重金属污染物浓度数据,从而可以得. 到各时间的污染范围, 由此确定出污染源的位置。
(4) 本问题只给出一个时间点上的数据, 信息量明显不足, 需要补充更多的信息。
加入学生考虑到多个时间点上的采样信息, 给出更好的演化模式, 应予以鼓励。
2021高教社杯全国大学生数学建模比赛B题评阅要点[说明]本要点仅供参考, 各赛区评阅组应根据对题目的理解及学生的解答, 自主地进行评阅。
全国大学生数学建模竞赛2011D题评阅要点

2011高教社杯全国大学生数学建模竞赛D题评阅要点[说明]本要点仅供参考,各赛区评阅组应根据对题目的理解及学生的解答,自主地进行评阅。
本题主要有两种解法。
方法一,主要思路为首先求出三种规格成品的最大捆数,然后求出每捆成品不同长度肠衣的搭配方式。
具体做法为:
1,以现有三种规格对应原料长度和根数为约束,分别建立求三种规格成品捆数最大的整数规划模型,利用软件求解。
2,建立组合或优化模型,计算步骤1得到的各种规格成品每捆中不同原料的搭配方式。
3,根据适当规则调整步骤2得到的各种规格成品每捆中不同原料的搭配方式,使最短长度最长的捆数最多。
上述三步骤应完整,模型应清晰,算法应合理实用。
方法二,主要思路为首先计算三种规格成品的所有可能的不同的原料搭配方式,然后用捆数最大作为目标,同时求出成品的最大捆数和每捆成品的捆扎方式。
具体做法为:
1,用组合方法计算每种成品对应的所有可能的原料搭配方式。
组合模型要明确并体现原料根数和总长度的约束和允许的误差,算法的合理性和可实现性也是重要的。
2,对各种规格成品建立并求解各种搭配的最优组合使成品捆数最多的整数规划模型。
要注意模型中体现原料根数的约束条件的正确性。
在上述两种方法中均应首先考虑原料最长的成品(第三种规格)的捆扎,剩余的材料降级后参与次长的成品的捆扎,再有剩余部分降级参与最短成品的捆扎。
全国大学生数学建模竞赛D题解析

汇报人:
CONTENTS
PRT ONE
PRT TWO
竞赛名称:全国大学生数学建模竞 赛
竞赛目的:培养大学生数学建模能 力提高解决实际问题的能力
添加标题
添加标题
竞赛级别:国家级
添加标题
添加标题
竞赛影响:促进大学生数学建模技 术的发展选拔优秀人才
竞赛起始于XXXX年 每年举办一次 参赛对象为全国大学生 竞赛目的是提高大学生数学建模能力和科技创新能力
组建合适的团队分工明确
制定详细的计划合理安排时间
充分准备所需的知识和技能
准备阶段:研究 题目收集资料建 立模型
实施阶段:编程 实现模拟实验优 化模型
总结阶段:撰写 论文整理思路提 炼经验
反思阶段:总结 得失分析原因改 进策略
赛题分析:对竞赛题目进行深入剖析明确解题思路和要点 经验教训:总结竞赛过程中遇到的问题和不足提出改进措施 团队协作:评估团队成员在竞赛中的表现和贡献提出优化建议 未来规划:根据竞赛经验和教训制定个人和团队未来的学习和发展计划
模型验证:通过对比实际数据和模型预测结果对模型的准确性和可靠性进行评估和改进
数据清洗:去除异常值、缺失值和重复值 数据筛选:根据需求筛选有效数据 数据转换:对数据进行必要的转换以适应分析需求 数据可视化:通过图表、图像等形式直观展示数据
确定问题类型和目 标函数
确定算法的输入和 输出
设计算法的流程图 和伪代码
培养团队协作精神 提升大学生数学应用能力
促进学科交叉融合
为国家和社会培养创新型人 才
PRT THREE
题目背景:全国大学生数学建模竞赛D题 题目要求:分析D题所涉及的数学建模方法和技巧 题目内容:对D题进行解析包括问题分析、模型建立、求解过程等 题目难度:对D题的难度进行评估并给出解题建议
2011全国数学建模D题分析思路及讲解

申明:这不是标准答案,这只是我的一点小思路,希望能帮到各位,有兴趣的加我q:454679703 ,q群:32890089一起谈论。
第一问:(线性规划)
设X1,X2,X3……X46为46档长度肠衣分别的数,N成品捆数。
则 Max Z=M1+M2+M3(成品捆数越多越好)
3X1+3.5X2+……+6.5X8=89
7X9+7.5X10+……+13.5X22=89
14X23+14.5X24+……+25.5X46=89
X1+X2+……+X8=20N
X9+X10+……+X22=8N
X23+X24+……+X46=5N
0<=X1N1<=43 (n是正整数,下同)
0<=X2N1<=59
……
0<=X8N1<=21
0<=X9N2<=24
0<=X10N2<=24
……
0<=X22N2<=25
0<=X23N3<=35
……
0<=X46N3<=1
一:问题分析
1.根据题目附表所给信息,可知天然肠衣每根的最大长度没有超过26米,题目所给天然肠衣规格的信息中只有第三个产品的最大长度可达到任意,而其余两个产品的最大长度都没有达到原料所给长度的最大值,即无论何种方案,最合理的方案也一定有第三种规格的产品;同理可以看到只有第一种规格的产品的最短长度能容纳下长度为3~6.9的产品;第二种规格的产品也是必须的。
所以,综上所述:三种规格的产品缺一不可,现在最主要的问题就是解决如何分配。
欢迎大家一起讨论,。
全国大学生数学建模竞赛赛题综合评析
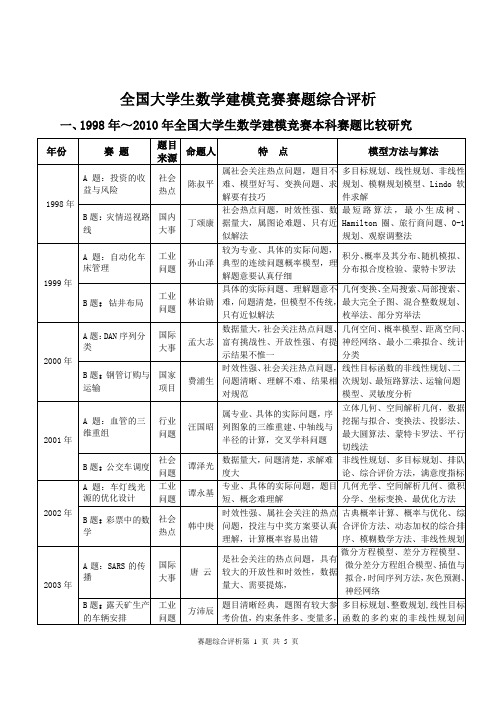
社会热点
叶其孝、周义仓
开放性强、社会关注性强,突出数据来源的可靠性、结论解释的合理性
数据收集与处理、问题的分析与假设,初等数学方法、一般统计方法、多目标规划、回归分析、综合评价方法、灰色预测
2009年
A题:制动器试验台的控制方法分析
工业问题
方沛辰、刘笑羽
问题具体、专业性强,要花时间读懂、理解清楚问题
出版社的资源配置
孟大志
艾滋病疗法的评价及疗效的预测
边馥萍
易拉罐形状和尺寸的最优设计(C题)
叶其孝
煤矿瓦斯和煤尘的监测与控制(D题)
韩中庚
2007年
中国人口增长预测
唐云
乘公交,看奥运
方沛辰、吴孟达
手机“套餐”优惠几何(C题)
韩中庚
体能测试时间安排(D题)
刘雨林
2008年
数码相机定位
谭永基
高等教育学费标准探讨
叶其孝、周义仓
地面搜索(C题)
肖华勇
NBA赛程的分析与评价(D题)
姜启源
2009年
制动器试验台的控制方法分析
方沛辰、刘笑羽
眼科病床的合理安排
吴孟达、毛紫阳
卫星和飞船的跟踪测控(C题)
周义仓
会议筹备(D题)
王宏健
2010年
储油罐的变位识别与罐容表标定
韩中庚
2010年上海世博会影响力的定量评估
杨力平
输油管的布置(C题)
1
6
8
付鹂
重庆大学
1
6
9
姜启源
清华大学
4
3
10
陈叔平
浙江大学、贵州大学
2
5
11
2011年全国数模竞赛浙江赛区D题评定结果
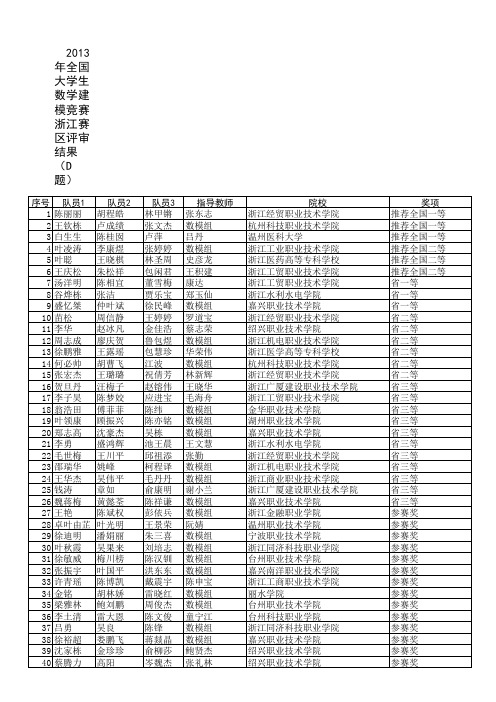
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 队员1 陈丽丽 王钦栋 白生生 叶凌涛 叶聪 王庆松 汤洋明 谷烨栋 盛忆桀 苗松 李华 周志成 徐鹏雅 何必帅 张宏杰 贺旦丹 李子昊 翁浩田 叶领康 郑志高 李勇 毛世梅 邵瑞华 王华杰 钱涛 魏蒋梅 王艳 卓叶由芷 徐迪明 叶秋霞 徐敏威 张振宇 许青瑶 金铭 梁雅林 李土清 吕勇 徐裕超 沈家栋 蔡腾力 朱建文 童珍 俞政 丁彦方 章学文 吴文亮 冯士杰 王教鼎 郑武伟 姜升杰 潘潮辉 许丰寿 应家伟 队员2 胡程皓 卢成绩 陈桂囡 李康煜 王晓棋 朱松祥 陈相宜 张洁 仲叶斌 周信静 赵冰凡 廖庆贺 王露瑶 胡曹飞 王璐璐 汪梅子 陈梦姣 傅菲菲 顾振兴 沈豪杰 盛鸿辉 王川平 姚峰 吴伟平 章如 黄懿荃 陈斌权 叶光明 潘娟丽 吴果来 梅川榜 叶国平 陈博凯 胡林娇 鲍刘鹏 雷大恩 吴良 娄鹏飞 金珍珍 高阳 蒋聪卓 黄秀慧 余晓 陈霞 王梦琪 陈正格 赵顺 余丹丹 姜丽荣 俞莉丽 邹翔 杨智彬 金苗萍 队员3 林甲锵 张文杰 卢萍 张婷婷 林圣周 包闲君 董雪梅 贾乐宝 徐民峰 王婷婷 金佳浩 鲁包煜 包慧珍 江波 祝倩芳 赵镕伟 应进宝 陈纬 陈亦铭 吴栋 池王晨 邱祖添 柯程译 毛丹丹 俞康明 陈祥谦 彭依兵 王景荣 朱三喜 刘培志 陈汉钏 洪东东 戴震宇 雷晓红 周俊杰 陈文俊 陈锋 蒋燚晶 俞柳莎 岑魏杰 郑宇 朱佳雯 谢聪聪 赵聪 戴埏埏 苏韩清 陆忆玮 张佩蓓 张怡萍 陈雯 石贞扬 黄雄毅 章凯 指导教师 张东志 数模组 吕丹 数模组 史彦龙 王积建 康达 郑玉仙 数模组 罗道宝 蔡志荣 数模组 华荣伟 数模组 林新辉 王晓华 毛海舟 数模组 数模组 数模组 王文慧 张勤 数模组 数模组 谢小兰 数模组 数模组 阮婧 数模组 数模组 数模组 数模组 陈申宝 数模组 数模组 童宁江 数模组 数模组 鲍贤杰 张礼林 数模组 数模组 茹永梅 数模组 吴伟国 童宁江 数模组 数模组 数模组 数模组 数模组 数模组 张礼林 院校 浙江经贸职业技术学院 杭州科技职业技术学院 温州医科大学 浙江工业职业技术学院 浙江医药高等专科学校 浙江工贸职业技术学院 浙江工贸职业技术学院 浙江水利水电学院 嘉兴职业技术学院 浙江经贸职业技术学院 绍兴职业技术学院 浙江机电职业技术学院 浙江医学高等专科学校 杭州科技职业技术学院 浙江经贸职业技术学院 浙江广厦建设职业技术学院 浙江工贸职业技术学院 金华职业技术学院 湖州职业技术学院 嘉兴职业技术学院 浙江水利水电学院 浙江经贸职业技术学院 浙江机电职业技术学院 浙江商业职业技术学院 浙江广厦建设职业技术学院 嘉兴职业技术学院 浙江金融职业学院 温州职业技术学院 宁波职业技术学院 浙江同济科技职业学院 台州职业技术学院 嘉兴南洋职业技术学院 浙江工商职业技术学院 丽水学院 台州职业技术学院 台州科技职业学院 浙江同济科技职业学院 嘉兴职业技术学院 绍兴职业技术学院 绍兴职业技术学院 嘉兴职业技术学院 丽水学院 浙江工贸职业技术学院 浙江商业职业技术学院 浙江工商职业技术学院 台州科技职业学院 浙江机电职业技术学院 浙江商业职业技术学院 浙江商业职业技术学院 宁波城市职业技术学院 浙江机电职业技术学院 浙江机电职业技术学院 绍兴职业技术学院 奖项 推荐全国一等 推荐全国一等 推荐全国一等 推荐全国二等 推荐全国二等 推荐全国二等 省一等 省一等 省一等 省二等 省二等 省二等 省二等 省二等 省二等 省三等 省三等 省三等 省三等 省三等 省三等 省三等 省三等 省三等 省三等 省三等 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖 参赛奖
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年全国大学生数学建模竞赛D题及评阅参考
来源:吕梁学院数学系发布时间:2011-09-27 查看次数:1092
D题天然肠衣搭配问题
天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业,出口量占世界首位。
肠衣经过清洗整理后被分割成长度不等的小段(原料),进入组装工序。
传统的生产方式依靠人工,边丈量原料长度边心算,将原材料按指定根数和总长度组装出成品(捆)。
原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米-3.9米按3.5米计算,其余的依此类推。
表1是几种常见成品的规格,长度单位为米,∞表示没有上限,但实际长度小于26米。
表1 成品规格表
为了提高生产效率,公司计划改变组装工艺,先丈量所有原料,建立一个原料表。
表2为某批次原料描述。
表2 原料描述表
根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。
公司对搭配方案有以下具体要求:
(1) 对于给定的一批原料,装出的成品捆数越多越好;
(2) 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好;
(3) 为提高原料使用率,总长度允许有±0.5米的误差,总根数允许比标准少1根;
(4) 某种规格对应原料如果出现剩余,可以降级使用。
如长度为14米的原料可以和长度介于7 -13.5米的进行捆扎,成品属于7-13.5米的规格;
(5) 为了食品保鲜,要求在30分钟内产生方案。
请建立上述问题的数学模型,给出求解方法,并对表1、表2给出的实际数据进行求解,给出搭配方案。
