1-3 线性规划-单纯形法表、计算步骤与矩阵描述(1)

合集下载

运筹学课件

12/3 4
z
1 2
x4
x5 42
x3
2 3
x4
1 3
x5
4
新典式
主元化为1，主元所在
x2
1 2
x4
6
列的其余元素
x1
2 3
x4
1 3
x5
4
化为0
观察最后一个典式，所有检验数均为非负，故其对应的基本可行解为最优解，即
X * 4,6,6,0,0T z* 42
去掉引入变量，得原问题的最优解为：
运筹学课件
目录
运筹学概论第一章线性规划基础第二章单纯形法第三章 LP对偶理论第四章灵敏度分析第五章运输问题第六章整数规划第七章动态规划第八章网络分析
第二章单纯形法
(SM-Simplex Method)
1947年，美国运筹学家Dantzig提出，原理是代数迭代。
单纯形法中的单纯形的这个术语，与该方法毫无关系，它源于求解方法的早期阶段所研究的一个特殊问题，并延用下来。
CB B1b B1b
z
CB B1N CN X N X B B1NX N
CB B1b B1b
上述方程组的矩阵形式为
10
0 I
CB
B1N B1N
CN
z XB XN
CB B1b B1b
上式的系数增广阵称为对应于基B的单纯形表：
T(B)
CB B1b B1b
0 I
CB
B1N B1N
CN
形式的LP问题，必须解决三个问题： ⑴初始基本可行解的确定； ⑵解的最优性检验； ⑶基本可行解的转移规则。这里先放一下⑴，研究⑵和⑶，为此，

单纯形法求解过程

单纯形法求解过程单纯形法是一种经典的线性规划求解方法，它是由乔治·达竞士等人在1947年提出的。

该方法的基本思想是，通过在单纯形空间内不断移动顶点的位置来寻找最优解。

单纯形法是目前广泛应用的线性规划求解方法之一，它求解线性规划问题可大大地简化计算过程。

单纯形法的求解过程包括以下几个步骤：1. 将线性规划问题转化为标准形式线性规划问题的标准形式为：$ \max_{x} \ \ c^T x $$s.t. \ Ax=b$$x\geq 0$其中，$x$是要求解的向量；$b$是一个常数向量；$A$是一个$m\times n$的矩阵；$c$是一个常数向量。

2. 初始化单纯形表因为单纯形法是通过移动顶点来寻找最优解的方法，因此需要初始化单纯形表。

单纯形表是将原始的约束条件表示为不等式形式时形成的。

例如，对于一个带有3个变量的线性规划问题，其单纯形表的形式如下：CB | X1 | X2 | X3 | X4 | RHS----|-----|-----|-----|-----|----0 | a11| a12| a13| 0 | b10 | a21| a22| a23| 0 | b20 | a31| a32| a33| 0 | b31 | z1 | z2 | z3 | 0 | 0其中，CB代表成本系数，X1、X2、X3、X4分别代表变量。

a11、a12、a13等代表矩阵A中的元素，b1、b2、b3代表矩阵b中的元素。

3. 选择进入变量和离开变量在单纯形表中，规定最后一列为等式右边的常数（RHS），即b。

在单纯形法的求解过程中，首先需要选择一个“进入变量”，即在单纯形表的第一行中，寻找一个系数为正的变量，使得将其加入目标函数后，目标函数值可以上升。

这里以X1为例，X1为进入变量。

接着，需要选择一个“离开变量”，即在单纯形表中，寻找一个使得添加X1变量后，约束条件不改变且取得约束条件中系数最小的一个变量离开。

第四节单纯形法的计算步骤

上表中由于所有σ 上表中由于所有 j>0 ，表明已求得最优解 x1=4， x2=2， x3=0， x4=0， x5=0， x6=4，，，，，，， Z=14。。当确定x 为换入变量计算θ值时值时， ◆当确定 6为换入变量计算值时，有两个相同的最小值：同的最小值：2/0.5=4，8/2=4。任选其中一，。个作为换出变量时，个作为换出变量时，则下面表中另一基变量的值将等于0，这种现象称为退化退化。量的值将等于，这种现象称为退化。含有一个或多个基变量为0的基可行解称为的基可行解称为退化一个或多个基变量为的基可行解称为退化的基可行解。的基可行解。
18
迭代
xB
次数
cB
x1
x2
x3
x4
x5 bi
θi
50
x1
100
0
0
0
50 0 100
1 0 0
0
0 0 1
0
1 -2 0
- 50
0 1 0
0
-1 1 1
- 50
50 50 250 -27500
2
x4 x2
σj
2010年8月
管理工程学院
18
《运筹学》运筹学》
19
所有的检验数 σ j ≤ 0, 此基本可行解：此基本可行解：
2010年8月
管理工程学院
5
《运筹学》运筹学》
6
c1 … cl b b1´
⋮
c j→ cB c1
⋮
… cm … xm …0 …⋮ 0 …1 …
⋮
…cj …xj …a1j´ …⋮ a2j´ …⋮ amj´
… ck … cn … xk …xn …0 …⋮ 1 …0

管理学线性规划的图解法与单纯形解法

n
z z0 (c j z j )x j j m1
最优性检验和解的判别
再令
j c j z j j m 1, , n
称为检验数。
n
z z0 j x j j m1
在线性规划模型中，可以用检验数 j替代目标函数中的价值系数cj。
最优解的判别定理
定理1 最优解的判别定理
若 X (0) b1,b2,L ,bm ,0,L ,0T 为对应于基 B 的一个基可行解，
仍取值为 0。令
x(1) mk
x(1) j
0
( j m 1,L , n, 但j m k)
x(1) i
bi ai,mk
i 1, 2,L m
X (1)
x(1) 1
,
x2(1），L
，xl(1)
,L
,
x(1) m
,
0,L
,
0,
x(1) mk
,
0,
L
,0T
新解必须满足非负约束，从而必须
x(1) i
对于一切 j=m+1,…,n,有检验数 j≤0,则 X(0)为最优解。
定理2 有无穷多最优解的判别定理
若 X (0) b1,b2,L ,bm ,0,L ,0T 为对应于基 B 的一个基可行解，
对于一切 j=m+1,…,n,有检验数 j≤0, 且存在某个非基变量对应的检验数 m+k=0, 则该线性规划问题有无穷多个最优解。
当检验某个基可行解不是最优、也非无界，那么就应该从该顶点（基可行解）处出发，寻找一个新的能使目标函数值改进的相邻顶点（基可行解）。注：称两个基可行解为相邻的，是指它们之间变换且仅变换一个基变量。
具体的方法是：在基变量中，选出一个，让它变为非基变量；同时，从非基变量中，选出一个，让它变为基变量，从而构造一个新基。

单纯形法的计算步骤

运筹学基础及应用
解：化标准型
max
z 2 x1 x2 0 x3 0 x4 0 x5 5 x2 x3 15 6 x 2 x x4 24 1 2 x5 5 x1 x2 x1 , , x5 0
运筹学基础及应用
表1：列初始单纯形表（单位矩阵对应的变量为基变量）
运筹学基础及应用
单纯形表
- Z x1基变量 x 2 ... xm XB 0 1 1E 0 单位阵 ....... 0 1 1 c c 0... c 1 2 m xm xNn 非基变量 1 .... X a1m 1 ...a1n a 2 m 1N...a 2 n
非基阵 ......
在上一节单纯形法迭代原理中可知，每一次迭代计算只要表示出当前的约束方程组及目标函数即可。
a1m 1 xm 1 ..... a1n xn b1 x1 x a2 m 1 xm 1 ..... a2 n xn b2 2 .......... .......... .......... ..... xm amm 1 xm 1 ..... amn xn bm Z c1 x1 ... cm xm cm 1 xm 1 ... cn xn 0
3
0 1 5/4 -15/2 1*3/2 0 0 1/4 -1/2 +0*15/2 检验数<=0 1 0 -1/4 3/2
cj z j
8.5
0
0
-1/4
-1/2
最优解为X=(7/2,3/2,15/2,0,0) 目标函数值Z=8.5
cj
CB
0 0 0
2
1
0最小的值对应 0 0

线性规划-讲义-3

4)、解的几种情况： 4)、解的几种情况：唯一解无穷多解－最优表中非基变量检验数有为0者。无穷多解－最优表中非基变量检验数有为0 无界解 max, σ j > 0 但Pj ≤ 0 min, σ j < 0 但Pj ≤ 0 无可行解－最优表中人工变量在基中，无可行解－最优表中人工变量在基中，且＝0。建模有问题 5)、 5)、退化解问题
表2 -2
-1/3 -1/3
两阶段法步骤 n 原问题 max S=Σ Cj xj n j=1 Σ aij xj =bi ( i=1,2, …,m) xj ≥ 0 m 作辅助问题 min W=Σ yi n i=1 Σ aij xj + yi =bi ( i=1,2, …,m) Xj ， yi ≥ 0 阶段：解辅助问题，第1阶段：解辅助问题，当进行到最优表时 ①、若W=0, 则得到原问题的一个基本可行转入第2阶段阶段。解，转入第阶段。 ②、若W>0, 则判定原问题无可行解阶段：第2阶段：用求出的初始基可行解求最优解。阶段用求出的初始基可行解求最优解。
人工变量： x6 , x7 人工变量：
cj
XB b*
0
x1
0
x2
0
x3
0
x4
0
x5
-1
x6
-1
x7
x4 11 3 x6 x7 1 - W’ 0
XB b*
1 -4 -2
0
x1
-2 1 0
0
x2
1 2 1
0
x3
1 0 0
0
x4
0 -1 0
0
x5
0 1 0
-1
x6
0 0 1
-1
x7

单纯形法表的解题步骤

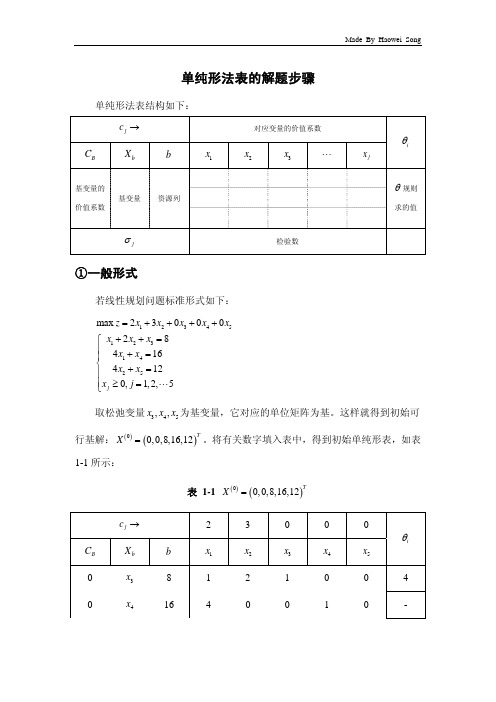
单纯形法表的解题步骤单纯形法表结构如下：j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下：123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量，它对应的单位矩阵为基。

这样就得到初始可行基解：()()00,0,8,16,12TX =。

将有关数字填入表中，得到初始单纯形表，如表1-1所示：表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0，则对上表进行调整。

选择上表中检验数最大的列，该列对应的非变量为入基变量；再应用θ规则该列对应的各基变量对应的θ值，选出其中最小的一行，该行对应的基变量为出基变量。

修改单纯形表，对各行进行初等变换，确保基变量组成的矩阵为单为矩阵。

修改后的单纯形表如表1-2所示：表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>，则进行继续调整，调整后的单纯形法表如表1-3所示：表 1-3 ()()22,3,0,8,0TX =表1-3中， 50σ>，则继续进行调整，调整结果如表1-4所示：表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤，这表示目标函数值已不可能再增大，于是得到最优解：()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题：12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解，在约束条件中加入松弛变量4x ，剩余变量5x ，人工变量6x ，7x 得到：1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中，M 是一个任意大的正数。

第01-03章线性规划(2)

三、建立线性规划模型的步骤：
确定决策变量；确定决策变量；明确约束条件并用决策变量的线性等式或不等式表示；式表示；用决策变量的线性函数表示目标，用决策变量的线性函数表示目标，并确定是求极大（Max）还是极小（Min）极大（Max）还是极小（Min）；根据决策变量的物理性质研究变量是否有非负性
方案1 方案2 方案3 方案4 方案5 方案6 方案7 方案8 2.9 m 1 2 0 1 0 1 0 0 2.1 m 0 0 2 2 1 1 3 0 1.5 m 3 1 2 0 3 1 0 4 7.4 7.3 7.2 7.1 6.6 6.5 6.3 6.0 合计 0 0.1 0.2 0.3 0.8 0.9 1.1 1.4 剩料余头
2.LP问题的典式 2.LP问题的典式 Z=CX → Z= CBXB+CNXN AX=b → BXB+NXN=b X≥0 XB=B-1b - B-1NXN Z= CB(B-1b- B-1NXN)+CNXN = CB B-1b+ (CN- CB B-1N)XN IXB + B-1NXN = B-1b
cj→ cB XB x2 x5 x6 cj － zj
。。。。
3 b 8/3 x1 2/3 -4/3 5/3 -1/3
5 x2 1 0 0 0
4 x3 0 5 4 4 ……….
0 x4 1/3 -2/3 -2/3 -5/3
0 x5 0 1 0 0
0 x6 0 0 1 0
14/3 20/3
x2 x3 x1 cj － zj
1 0 0 0
0 1 0 0
15/41 -6/41 -2/41 -45/41
8/41 5/41 -12/41 -24/41

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

CB XB 检验数
CB XB I 0
CN XN B N CN-CBB N
8
-1
B b
-1
-1
例：用单纯形表求解
max z 2 x1 3 x2 2 x1 x2 4 s.t. x1 2 x2 5 x , x 0 1 2
画初始单纯形表：
max z 2 x1 3 x2 4 2 x1 x2 x3 s.t. x1 2 x2 x4 5 x , x , x , x 0 1 2 3 4
School of Business ECUST
3.3.2 单纯形表结构
z c1b1 c2b ... cmbm m 1 c2 a2, m 1 ... cm am , m 1 xm 1 cm 1 c1a1, m 2 c2 a2, m 2 ... cm am , m 2 xm 2 cm 2 c1a1, ... n c2 a2 n ... cm amn xn cn c1a1
1-3 线性规划单纯形表、计算步骤与矩阵描述
1
3.3 单纯形法 3.3.1 单纯形法的一般思路+例子 3.3.2 单纯形表结构+例子 3.3.3 单纯形法的计算步骤 3.3.4 单纯形法的矩阵描述 3.4 大M法 3.5 两阶段法 4 几种特殊情况 4.1 无可行解 4.2 无界解 4.3 多重最优解 4.4 进基变量的相持 4.5 出基变量的相持
40 x2 25/8 1 5/8 35/4
0 x3 1 0 0 0
0 x4 0 1 0 0
0 x5 RHS 比值 -3/8 75/2 12 0 20 20 1/8 75/2 60 -25/4
当前基本可行解：(75/2, 0, 75/2, 20, 0) , Z=1875
16
40 0 50
x2 x4 x1 检验数

_ 3/1 8/2 4/1 -
j
1
1 0
2
0 1
0
1 0
0
0 1
0
0 0
0
0 2 1
j
x5
x3 x2 x1
1
1 0 0 1 0
0
0 0 1 0 0
T
0
0 1 0 0 0
-2
-2 2 1 -2 0
1
0 -1 0 1 -1
2
2 3 2
2/1
2/2 3/1 -
j
X 2,3, 2, 0, 0
假定：(1) 该线性规划问题的可行域不为空集； (2) 所有的可行解不退化； (3) 已找到一个初始可行基B(由A的前m个列向量构成)。
School of Business ECUST
B
N
T
A P , P ,..., P , P ,...., P 1 2 m m 1 n
X x , x ,..., x , x ,..., x 1 2 m m 1 n XB XN
minZ=-x1 -2x 2 x3 4 x1 x2 x4 3 x5 8 x1 2x 2 x j 0 ，j 1,2,3,4,5
解：本题的目标函数是求极小化的线性函数，可以令则
Z' = -Z = x1 +2x 2
minZ=-x1 -2x 2 max Z ' x1 +2x 2
b 4 5
cj
CB 0 0 XB x3 x4
2 x1 2 1
3 x2 1 2
0 x3 1 0
0 x4 0 1

4/1 5/2
j
0 3 x3 x2
2
3/2 1/2 1/2 1 0
3
0 1 0 0 1
0
1 0 0 2/3 -1/3
0
-1/2 1/2 -3/2 -1/3 2/3 1 2 3/2 5/2 1 5
（1）找出初始可行基，给出初始基本可行解，建立初始单纯形表。（2）检验各非基变量的检验数，如果所有检验数都大于等于0，则已得到最优解；否则，转下一步。（3）负检验数最小对应的变量作为换入变量；极小比值准则决定换出变量；迭代运算。
（4）重复（2）（3）直到得到最优解。
22
练习：求解下列线性规划问题
这两个线性规划问题具有相同的可行域和最优解，
只是目标函数相差一个符号而已。
School of Business ECUST
C CB 0 0 0 0 2 XB x3 x4 x5 x3 x2
1 x1 1 0 1
2 x2 0 1 2
0 x3 1 0 0
0 x4 0 1 0
0 x5 0 0 1 b 4 3 8 4 3
i 1 m
School of Business ECUST
单纯形原理
设标准的线性规划问题为 max z= s.t. CX AX=b X0 矩阵A可以分块记为A=[B，N] 相应地，向量X和C可以记为
XB X , C C B XN CN
6
AX=b可以写成 BXB+NXN=b 即 XB=B-1b-B-1NXN 对于一个确定的基B，目标函数z可以写成
min z x1 2 x2 x1 x2 3 x 2 1 s.t. 3x1 2 x2 1 x1 , x2 0
School of Business ECUST
3.3.4 单纯形法的矩阵描述
考虑标准形式的线性规划问题：
max z CX AX b s.t. X0
maxZ' =8 or minZ=-8
School of Business ECUST
因为非基变量x4的检验数σ4=0，由无穷多最优解判别定理，本例的线性规划问题存在无穷多最优解。事实上若以x4为换入变量，以x3为换出变量，再进行一次迭代，可得一下单纯形表：
C CB 0 2 1 XB x4 x2 x1 1 x1 0 0 1 0
x1 x2 : z CX c1, c 2,..., c m, c m 1,..., c n xm C B, C N x CB CN m 1 : xn

50 x1 0 0 1 0
40 x2 1 0 0 0
0 x3 8/25 -8/25 -5/25 -14/5
0 x4 0 1 0 0
0 x5 RHS 比值 -3/25 12 3/25 8 5/25 30 -26/5
当前基本可行解：(30, 12, 0, 8, 0) , Z=1980
17
例: 用单纯形表方法求解线性规划问题
j
2 3 x1 x2
j
0
0
-1/3
-4/3
最优解：x1=1,x2=2,x3=0,x4=0
School of Business ECUST
3.3.3 单纯形法的计算步骤（max）
（1）将线性规划问题转化为标准型，找出初始可行基，给出初始基本可行解，建立初始单纯形表。（2）检验各非基变量的检验数，如果所有检验数都小于等于0，则已得到最优解；否则，转下一步。（3）正检验数最大对应的变量作为换入变量；极小比值准则决定换出变量；迭代运算。
（4）重复（2）（3）直到得到最优解。
11
习题
max s.t.
z=
50x1 3x1
+40x2 +5x2 x2 ≤150 ≤ 20
8x1
x1,
+5x2
x2
≤300
≥ 0
12
Байду номын сангаас
X2 60 50 40 30 20 10
A
X1=0
E
X5=0
D C
X4=0 X3=0
B
(2)
X2=0 50
(3) (1)
10
T
2 x2 0 1 0 0
0 x3 1/2 -1/2 1 0
0 x4 1 0 0 0
0 x5 -1/2 1/2 0 -1
b 1 2 4 8

j
最优解 X 4, 2, 0,1, 0 最优解的一般表示式

最优值
T
maxZ' =8 or minZ=-8
T
X (2,3, 2, 0, 0) (1 ) 4, 2, 0,1, 0 , 0 1.
i 1
School of Business ECUST
m
, j 1,2,..., n j c j ci aij
i 1
m
c1 c2 … cm cm+1 … cn
c1 c2 ... cm
m 1 ... a1 n 1 0 ... 0 a1, m 1 ... a2 n 0 1 ... 0 a2, ...... , m 1 ... amn 0 0 ... 1 am
0 0 … 0
cm 1
m i 1
j
….
cn
m i 1
ci ai, m 1 c a i i,n
School of Business ECUST
单纯形表 cj
CB XB
c1
x1
c2 … cm
x2 … xm
cm+1 … cn
xm+1 … xn
b
b1 b2 ... bm
20
30
40
X1
13
标准化
max z= s.t.
50x1 3x1
+40x2 +5x2 x2 ＋x3 +x4 +x5 x3, x4, x5 =150 = 20 =300 ≥ 0 (1) (2) (3)