电磁场与微波技术第一二三章课后习题及部分答案
电磁场与微波_毕刚课后习题答案

4 2π 2 ⃗ ⃗ =∯ ⃗ ⃗⃗⃗z − ∯ ⃗ ⃗⃗⃗z + ∯ ⃗ ⃗⃗⃗⃗ ∯ A ∙ dS A ∙ dS A ∙ dS A ∙ dS ∫ (ρ ρ ⃗ + 2zz ) ∙ ρ ⃗ ρdφdz| φ =∫ S S S S 0 0
−Φ ⃗ y
∂ ∂y
∂Aₓ ∂Φ + ∂x Ay ∂y
−
∂Φ Aₓ) z ∂y
∂ΦA = ( ∂y z −
∂ΦAy ∂z
)x ⃗ +
⃗ x (
∂ΦAₓ ∂z
z
∂ ∂z
−
∂ΦAz ∂x
)y ⃗ +(
∂ΦAy ∂x
−
∂ΦAₓ ∂y
)z = |
∂ ∂x
⃗ )=Φ∙ | = 左边,所以∇ × (ΦA
ΦAₓ ΦAy
ΦAz
(∇ × ⃗ A) + ∇ ∙ Φ × ⃗ A。 1-27 已知矢量⃗ A 、⃗ B分别为⃗ A = z²sinφρ ⃗ + z²cosφφ ⃗⃗ + 2zρsinφz 和⃗ B = (3y 2 − 2x)x ⃗ + x²y ⃗ + 2zz,求 (1)哪个矢量可以由一个标量的梯度表示; (2)哪个矢量可以由一个矢量的旋度表示; (3)它们的源分布。 ⃗ = 0,∇ × B ⃗ = 2(x − 3y)z,∇ ∙ A = 2ρsinφ,∇ ∙ B = 0。 解:∇ × A ⃗ 可以由一个标量的梯度表示; (1)A ⃗ 可以由一个矢量的旋度表示; (2)B ⃗ 有散场无旋场,B ⃗ 无散场由旋场。 (3)A 第二章 2-1 半径为a的无限薄带电圆盘上面电荷密度为ρ = r 2,r为圆盘上任意点到圆心的距离,求 圆盘上的总电量。 解:Q = ∬ ρ ∙ dφdr = ∫ r 3 ∙ dr ∙ ∫ dφ = S 0 0
电磁场与电磁波部分课后答案_郭辉萍版1-6章

(2) 电磁波垂直入射到理想导体上
(3)空气中合成波的电场
磁场
(4) 空气中离导体表面最近的第一个波腹点的位置为
6.8自由空间中一均匀平面电场波垂直入射到半无限大无耗介质平面上,已知自由空间与介质分界面上的反射系数为0.5,且分界面为电场波腹点,介质内透射波的波长是自由空间波长的 ,求介质的相对磁导率和相对介电常数。
(2)导体外:a <+
=I,所以 , ,
4.5在下面的矢量中,哪些可能是磁通密度B?如果是,与它相应的电流密度J为多少?
(1)
解: = =2 0所以 不是磁通密度
(2) =- y+ x
解: . = + =0所以F是磁通密度
= =| =2 所以 =
(3) = x— y
. =0 是磁通密度
= =| =0所以 =0
3.6
两无限大接地平行板电极,距离为 ,电位分别为0和 ,板间充满电荷密度为 的电荷,如题3.6图所示。求极板间的电位分布和极板上的电荷密度。
3.8
一个沿z方向的长且中空的金属管,其横截面为矩形,金属管的三边保持零电位,而第四边的电位为U,如题3.8图所示。求:
(1)当 时,管内的电位分布;
(2)当 时,管内的电位分布。
解:设自由空间 ,无耗介质
由得:
6.15在无线电装置中常配有电磁屏蔽罩,屏蔽罩由铜制成,要求铜的厚度至少为5个趋肤深度,为防止200kHz~3GHz的无线电干扰,求铜的厚度;若要屏蔽10kHz~3GHz的电磁干扰,铜的厚度又是多少?
解:铜的电导率为
趋肤深度
(1)
(2)
6.17一均匀平面波从空间(媒质1)沿+z方向垂直入射到 、 (媒质2)的理想介质表面上,电磁波的频率为100MHz,入射波电场的振幅为 、极化为+x方向。
《电磁场与电磁波》习题参考答案

《电磁场与电磁波》知识点及参考答案第1章 矢量分析1、如果矢量场F 的散度处处为0,即0F∇⋅≡,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S 的通量等于0。
2、如果矢量场F 的旋度处处为0,即0F ∇⨯≡,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C 的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分别是:散度(高斯)定理:SVFdV F dS ∇⋅=⋅⎰⎰和斯托克斯定理:sCF dS F dl∇⨯⋅=⋅⎰⎰。
4、在有限空间V 中,矢量场的性质由其散度、旋度和V 边界上所满足的条件唯一的确定。
( √ )5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
( √ )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
( √ )7、梯度的方向是等值面的切线方向。
(× )8、标量场梯度的旋度恒等于0。
( √ ) 9、习题1.12, 1.16。
第2章 电磁场的基本规律(电场部分)1、静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
3、静电系统在真空中的基本方程的积分形式是:V V sD d S d V Q ρ⋅==⎰⎰和0lE dl ⋅=⎰。
4、静电系统在真空中的基本方程的微分形式是:V D ρ∇⋅=和0E∇⨯=。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
6、在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量B 1n -B 2n =0。
7、在介电常数为e 的均匀各向同性介质中,电位函数为 2211522x y z ϕ=+-,则电场强度E=5x y zxe ye e --+。
8、静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。
微波技术课后习题答案-第二章习题参考答案11
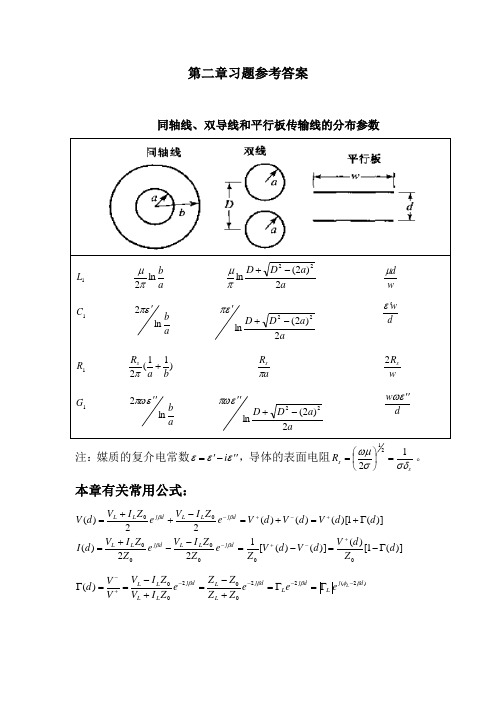
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注:媒质的复介电常数εεε''-'=i ,导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。
本章有关常用公式:)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗:aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=,间距cm D 10=,周围介质为空气(1=r ε),所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗:ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=,内导体的外直径2mm a 10=,中间填充空气(1=r ε):特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε):特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11,所以可求出相速度v k C L v p =====μεωβω1111,等于电磁波的传播速度。
微波技术习题解答

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。
根据给出的已知数据,分别写出传输线上电压、电流的复数和瞬时形式的表达式:(1) R L= 100 (),I L = e j0(mA);(2) R L = 50(),V L = 100e j0(mV);(3) V L = 200e j0 (mV),I L = 0(mA)。
解:本题应用到下列公式:(1)(2)(3)(1) 根据已知条件,可得:V L = I L R L = 100(mV),复数表达式为:瞬时表达式为:(2) 根据已知条件,可得:复数表达式为:瞬时表达式为:(3) 根据已知条件,可得:复数表达式为:瞬时表达式为:1.2 无耗传输线的特性阻抗Z0 = 100(),负载电流I L = j(A),负载阻抗Z L = j100()。
试求:(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式;(2) 利用欧拉公式改写成纯驻波的形式。
解:根据已知条件,可得:V L = I L Z L = j(j100) = 100(V),1.3 无耗传输线的特性阻抗Z0 = 75(),传输线上电压、电流分布表达式分别为试求:(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式;(2) 计算负载电压V L、电流I L和阻抗Z L;(3) 把(1)的结果改写成瞬时值形式。
解:根据已知条件求负载电压和电流:电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75,I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50(),已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。
试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z);(2) 利用负载反射系数 L计算负载阻抗Z L;(3) 通过等效阻抗Z(z)计算负载阻抗Z L。
电磁场理论与微波技术答案

z=a
= ex
A sin πct
μ0c
a
2-2 设在一载有稳恒电流i的长直导线附近,有一矩形闭合 回路,边长为a和b,其中b边平行于长导线。当回路在 包含长导线的平面内以匀速v离长导线而运动时,求回 路中的感应电动势。
解:在矩形线圈内,B的方向与线圈平面的法线方向一 致,所以有:
∫ ∫ ∫ Φ =
又 μ r =1
∴ Ei − Er =
结合两式得到
Qω = 2πf
1+
2
σ
Ei = Et
(1− j)
2ωε 0
σ 2ωε 0
(1 −
j )Et
z 导体
∴
σ= 2ωε 0
5.8 ×107
4π ×109 × 8.854 ×10−12
≈ 22832
∴ Et
≈
2
22832(1 −
j) Ei
=
1 16145
Ei
1-1试证明两个空间矢量r1(r1,θ1,ϕ1) 和矢量r2 (r2 ,θ 2 ,ϕ 2 ) 之
间的夹角Θ 的余弦为 cosΘ = cosθ1cosθ2 + sinθ1sinθ2cos(ϕ1 − ϕ2 )
解:矢量 r1{r1sinθ1cosϕ1 , r1sinθ1sinϕ1 , r1cosθ1} ,
y′)
e
y
+
1 2
2(z − R
z′)
ez
=
R R
∇
1 R
=−1 2
2(
x− R3
x
′)
e
x
−
1 2
2( y − R3
y′) e y −
1 2
电磁场习题答案

1-8 参照例图 1.1,设有标量 f ( R) ,求证:以 p ′( x ′, y ′, z ′) 为动点时的梯度 ∇ ′f ( R) 间与
以 p ( x, y, z ) 为 动 点 的 梯 度 ∇f ( R ) 间 满 足 关 系 : ∇ ′f ( R ) = −∇f ( R ) 。 其 中
R = r − r′ 。
∇• (AR) 。
答案: ∇ ? R = ; ∇ × R = 0; ∇ × ( R R ) = 0; ∇ ? AR ) = 3 A 。
( )
1-12 证明: ∇ • ( A × B) = B • (∇ × A) − A • (∇ × B) 。 1-13 证明旋度定理(1.47) 。
2 2 1-14 在圆球坐标系中, 已知 A = (sin θ R )a R + R sin θa θ + R sin θ cos ϕa ϕ , 求∇ • A 。
2
坐标原点一侧空间中的电场强度。 答案: E = 8.34( ax − 3a y + 6az ) 2—5
V m。
一点电荷 Q = 50 nC ,位于直角坐标系的原点,求点 (2,, 4 − 5) 处的电通量密度。
答案: D = 2—6
5 (2ax + 4a y − 5az ) 。 54π
两种理想电介质的相对介电常数分别为 ε r1 = 2.5和ε r 2 = 5 ,其分界面为 z = 0 的平 面。若已知介质 1 中的电场强度 E = 3a x + 4 a y + 6 a z ,求:① 介质 2 一侧的电场强 度 E2 和电位移矢量 D2 ;② E2 和 D2 是介质 2 中任意点处的场量表达式吗?为什 么? 答案:① E2 = 3ax + 4a y + 3az ; D2 = ε 0 (15ax + 20a y + 15az ) 。
电磁场与微波技术(第2版)黄玉兰-习题答案

第一章1.3证:941(6)(6)50=0A B A B A B A B =⨯+⨯-+-⨯=∴⨯∴和相互垂直和相互平行1.11 (1)22220.50.50.522220.50.50.52272(2)(2272)124sAx Ay AzA divA x y z x x y x y z Ads Ad dz dy x x y x y z dzττ---∂∂∂∇==++∂∂∂=++=∇=++=⎰⎰⎰⎰⎰ 由高斯散度定理有1.18(1) 因为闭合路径在xoy 平面内, 故有:222()()8(2)(22)()2()8x y z x y x z x sA dl e x e x e y z e dx e dy xdx x dy A dl S XOY A ds e yz e x e dxdy xdxdy A ds →→→→∙=+++=+∴∙=∇∙=+=∇∙=∴⎰⎰ 因为在面内, 所以,定理成立。
1.21(1) 由梯度公式(2,1,3)|410410x y z x y zx y z u u u u e e e x y ze e e e e e ∂∂∂∇=++∂∂∂=++=++1方向:()(2)最小值为0, 与梯度垂直1.26 证明00u A ∇⨯∇=∇∇=书上p10 1.25 第二章 2.13343sin 3sin 4qa V e wr qwr J V e aρρρπθθρπ===∙=2.3''2'3222,40=l lldl d R Er R ez z ea aez z ea aEr rPez z ea aE dz aeaπρραϕραϕπε= ==--==-=+⎰用圆柱坐标系进行求解场点坐标为P(0,0,z).线电荷元可以视为点电荷,其到场点的距离矢量得所以点的电场强度为()2'''3222cos sin020lzex ey ea dzE ez aπϕϕϕραε+∴=∴=+⎰()2.82235222023522322225052(1)4()()44()35=044()=()0351()=()0352r>b 4()8()4152()=401srs sbr b E d s r E r b r r Eq b r r dr EqE d s b r r r E r b r rE r E d s r E r Eq b r r dr bEq bE r r πππεππεεππππε≤==-=--∴-==-==⎰⎰⎰⎰⎰ 时由高斯定理有即()时由高斯定理有250r ε2.11222122212212221,22()2(2)121122(2r r r r r r b l Eb r l b e a e Eb Ea b e a e E Eb Ea r l Eb r l r e Eb a e Ea E επρπερρεερεεπρπερερερε∑∴=∴==∴=-=-∑∴===∴=⎰⎰000000当r1>b 则,E=Eb-EaqEb ds=同理:r1r2r1r2对于r1<b 且在空腔外,E=Eb-EaqEb ds=,而r22211212121)(3)112,2212(12)222r r r r r r r r a e r e r b r e r e Ea r e r e E Eb Ea r e r e ερρεερρρεεε--<∑∴=∴=-=-=-⎰00000r2且在空腔内 E=Eb-Ea qE ds=,Eb=2.14222200(1)0()cos ()sin (2)2cos r a E A a A a AA A r rA aϕϕϕϕφρεεϕ<=-∇∅=-∇∅=-∇∙--+-∂==-∂2r s 时,a r>a 时 E=(r-)cos r=e e 圆柱是由导体制成的表面电荷2.20能求出边界处即z=0处的E2 根据D 的法向量分量连续12(5)103r r Z Z z E E εε⇒+=⇒=2.28(1) 2ln22,ln ln66ln(2)62ln lne e l rbl a l rr sr s E e rbu E dl a u uE e bb r a au J E e b r aJ ds I ug e ds b b uuu r a aρρρπερπεπερπδ=====∴======⎰⎰⎰ 设内外导体单位长度带电量分别为+和-,利用高斯定理可以求得导体介质的电场为:得到2.34(1)=0=000,2=00B B er arB a B J H μμ∇∴∇=≠∇=∇⨯=取圆柱坐标系,若为磁场,根据磁场连续性方程,有所以不是磁场()取直角坐标,所以是磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
αcos 、βcos 、γcos 分别是l 方向的方向余弦。
422==∂∂MMxz xu,04==∂∂M Mzy y u,1223222=+=∂∂M M y z x z u 令:84222422294)3()()2(zy x x z xy x ++=++=∆则:542cos =∆=M Mx α,0cos 2=∆-=MMxy β,53cos -=Mγ,45360516cos cos cos -=-+=∂∂+∂∂+∂∂=∂∂M MM M z u y u x u t u γβα 5、 求标量场z y x xy z y x u 62332222--++++=在点M (0,0,0) 、点M (1,1,1)处的梯度,并找出场中梯度为0的点。
解:由梯度定义:z zu y y u x x u u ˆˆˆ∂∂+∂∂+∂∂=∇ 则:z z y x y xy x z z u y y u x x u u ˆ)66(ˆ)24(ˆ)32(ˆˆˆ-+-++++=∂∂+∂∂+∂∂=∇z y x u ˆ6ˆ2ˆ3)0,0,0(--=∇ y xu ˆ3ˆ6)1,1,1(+=∇ 若要梯度为零,则需使得梯度中各项分量为零,即:032=++y x 024=-+x y066=-z解之,得到:1,1,2==-=z y x即,在点(-2,1,1)处,标量场的梯度为零。
6、 设z z y y xx r ˆˆˆ++=,r r =,n 为正整数。
求r ∇、n r ∇、()r f ∇。
解:根据题意及梯度定义:rr z z y y x x r z z y y x x r z y x z y x z y x r =++=++=++∇++=++∇=∇-)ˆˆˆ(1)ˆ2ˆ2ˆ2(121)()(21)(22221222222 r nr r r nr rnr r n n n n 211---==∇=∇ rrr f rr f r f )(')(')(=∇=∇ 7、 求矢量场z z y y xx A ˆˆˆ333++=在点M (1,0,-1)处的散度。
解:由题意及散度定义: 222333z y x A ++=⋅∇,将M(1,0,-1)代入:得到:6303=++=⋅∇MA8、 设a为常矢量,z z y y xx r ˆˆˆ++= ,r r =,求()a r ⋅∇、()a r 2⋅∇、()a r n ⋅∇,证明a r a =⋅∇)( 解:由散度运算公式:1)()ra r r a r r ar a r a r⋅=⋅+⋅=⋅∇+⋅∇=⋅∇0 2)()ar r a r r r ar a r a r⋅=⋅+⋅=⋅∇+⋅∇=⋅∇20222223)()ar nr a r r nr r a r nr ar a r a r n n n n n n n⋅=⋅=⋅+⋅∇=⋅∇+⋅∇=⋅∇---21104)证明: 因为:zy x z y x za ya xa z y y y x x z a y a x a r a ++=++⋅++=⋅)ˆˆˆ()ˆˆˆ(且:xa ,y a ,z a 均为常数,所以有:a z a y a xa r a z y x =++=⋅∇ˆˆˆ)( 得证。
9、 设无限长细直导线与z 轴重合,其上有沿正z 轴方向流动的电流I ,导线周围的磁场()()y x xy yx IH ˆˆ222+-+=π计算H⋅∇。
解:由题意及散度的定义:()()y x xy yx IH ˆˆ222+-+⋅∇=⋅∇π22222)(/2-+=∂⎪⎪⎭⎫ ⎝⎛+∂-=∂∂y x xy Ix y x yIx H x ππ22222)(/2-+-=∂⎪⎪⎭⎫ ⎝⎛+∂=∂∂y x xy Iy y x x I y H y ππ∴=∂∂+∂∂=⋅∇y H x H H y x 10、已知xy y x u 222+-=,求u 2∇。
解:由题意及散度运算性质:)(2u u ∇⋅∇=∇y y x xy x z z uy y u x x u u ˆ)22(ˆ)22(ˆˆˆ-++=∂∂+∂∂+∂∂=∇22)ˆ)22(ˆ)22(()(=-=-++⋅∇=∇⋅∇y y x xy x u所以:02=∇u11、计算下列矢量场的旋度:(1)()()z xyz y xz y xz y x A ˆ2ˆˆ3232+-++=; (2)z xy y zx x yz A ˆˆˆ222++=; 解:由矢量场旋度定义式,可得:1)()()()()()z x z y yz xxz z x z y yz x xz xz z y A x A y x A z A x z A y A A A A z y x z y x A x y z x y z zyxˆ3ˆ21ˆ4 ˆ3ˆ21ˆ22 ˆˆˆˆˆˆrot 2222+--+=--+-++=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=2)()()()z z xz y y yz xx xy z y A x A y x A z A x z A y A A A A z y x zy x A x y z x y z zy x ˆ2ˆ2ˆ2 ˆˆˆˆˆˆrot 222-+-+-=⎪⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=∂∂∂∂∂∂=12、已知x e u =,z y y x xz A ˆˆˆ222++=,计算()A u⨯∇。
解:由题意及矢量的旋度运算公式:())ˆ)2(ˆ)2(ˆ2()ˆ2ˆ2ˆ2ˆˆ()ˆ2ˆ2ˆ2(ˆ2222z x x y y z xy e z x y z x y z x yy e z x y z x y e A xe Au A u A u x xx x ++-+=++++-=+++⨯=⨯∇+⨯∇=⨯∇13、已知z z y y xx r ˆˆˆ++= ,r r =,a 为常矢量,求r ⨯∇、()[]r f r ⨯∇、()[]r f a ⨯∇。
解:1)z ˆ)-(yˆ)-(x ˆ)-(r =∂∂∂∂+∂∂∂∂+∂∂∂∂=⨯∇y x x y xz z z x z yy z2)()[]0)(')(')()()(r f r =⨯=⨯∇=⨯∇=⨯∇+⨯∇=⨯∇rrr r f r r r f rr f rr f r r f3)()[]a r r f rar r r f a r r f ar f ar f a r f r f a⨯=⨯=⨯∇=⨯∇=⨯∇+⨯∇=⨯∇)('1)(')(')()()(14、已知z xy y z xy A ˆˆ2ˆ32++= ,z x x B ˆ4ˆ2-=,求()B A ⨯⨯∇。
解:由题意及运算规则,先求出B A⨯,再求旋度:ˆˆˆxy z xy zxy z A B A A A B B B ⨯= 22ˆˆˆ 3204x y z y z xy x =-ˆˆˆ ()()()y z z y z x x z x y y x A B A B xA B A B y A B A B z =-+-+- 2322ˆˆˆ =8(12)2z x x y y y x z z -++- ()A B ∇⨯⨯2322ˆˆˆ(8(12)2)z xx y y y x z z =∇⨯-++- 22322232(2)(12)(8)(2)(12)(8)ˆˆˆx z x y y z x z x y y z x y z y z z x x y ⎡⎤⎡⎤⎡⎤∂-∂+∂-∂-∂+∂-=-+-+-⎢⎥⎢⎥⎢⎥∂∂∂∂∂∂⎣⎦⎣⎦⎣⎦22ˆˆ(416)3xz z yx yz =-+ 15、已知位于坐标原点处电量为q 的点电荷产生的电位移矢量D 为34r r q D π =,其中z z y y xx r ˆˆˆ++=,r r=,计算D ⨯∇和D ⋅∇。
解:由题意:1)34qrD ()πr ∇⨯=∇⨯ 33r 44q q()r πr πr =∇⨯+∇⨯31()4q r πr =∇⨯4 (3)4qr r r π-=-∇⨯43 4q rr πr r-=⨯0=2)34qrD ()πr ∇⋅=∇⋅3 ()4qr r π-=∇⋅ 33 ()()4q r r r r π--⎡⎤=∇⋅+∇⋅⎣⎦ 43334q r r r r π--⎡⎤=-∇⋅+⎣⎦ 43 334q r r r r πr --⋅⎡⎤=-+⎢⎥⎣⎦33 334q r r π--⎡⎤=-+⎣⎦ 0(0)r =≠在r=0处,D 无意义,D⋅∇不存在。
16、证明()0=∇⨯∇u ,()0=⨯∇⋅∇A。
证明: 1)由标量场梯度的定义式:z z u y y u x x u u z z y y x x u ˆˆˆˆˆˆ∂∂+∂∂+∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂=∇ ())ˆˆˆ(z zuy y u x x u u ∂∂+∂∂+∂∂⨯∇=∇⨯∇ 由z y A x A y x A zA x z A y A A x y z x y z ˆˆˆ⎪⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=⨯∇ 令:z zuy y u x x u A ˆˆˆ∂∂+∂∂+∂∂= 则:()0ˆˆˆ)ˆˆˆ(222222=⎪⎪⎭⎫⎝⎛∂∂∂-∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂-∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂-∂∂∂=∂∂+∂∂+∂∂⨯∇=∇⨯∇zy x u x y u y z x u x z u x y z u z y u z zuy y u x x u u 由此得证。
