《大学物理学》机械波练习题
大学物理机械波习题附答案
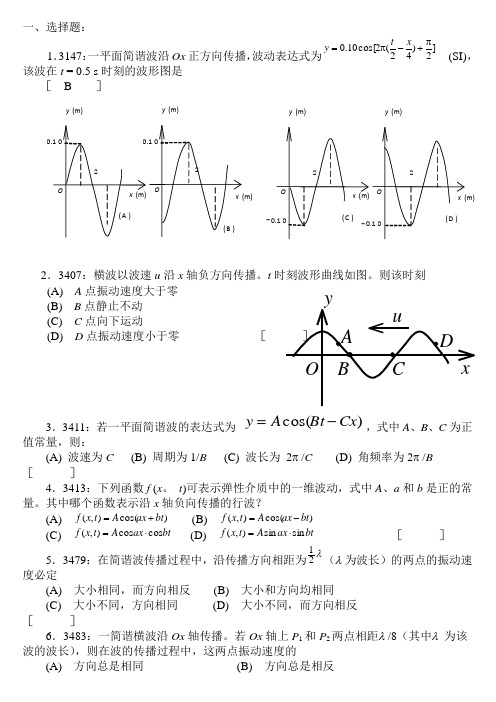
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C)大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
机械波试题(含答案)
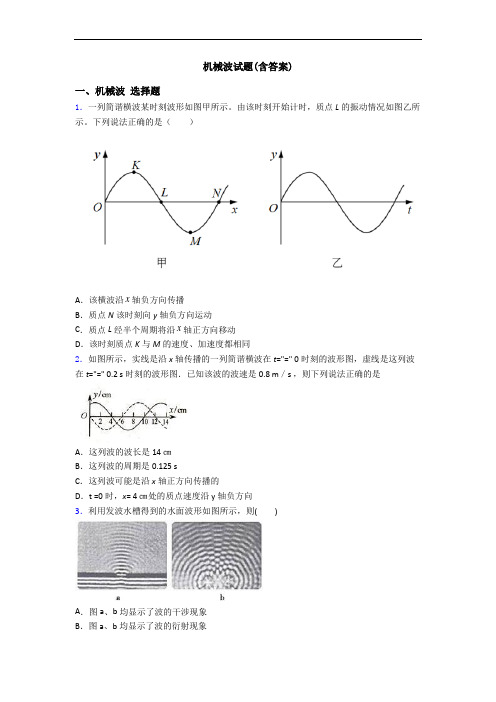
机械波试题(含答案)一、机械波选择题1.一列简谐横波某时刻波形如图甲所示。
由该时刻开始计时,质点L的振动情况如图乙所示。
下列说法正确的是()A.该横波沿x轴负方向传播B.质点N该时刻向y轴负方向运动C.质点L经半个周期将沿x轴正方向移动D.该时刻质点K与M的速度、加速度都相同2.如图所示,实线是沿x轴传播的一列简谐横波在t="=" 0时刻的波形图,虚线是这列波在t="=" 0.2 s时刻的波形图.已知该波的波速是0.8 m/s ,则下列说法正确的是A.这列波的波长是14 ㎝B.这列波的周期是0.125 sC.这列波可能是沿x轴正方向传播的D.t =0时,x= 4 ㎝处的质点速度沿y轴负方向3.利用发波水槽得到的水面波形如图所示,则()A.图a、b均显示了波的干涉现象B.图a、b均显示了波的衍射现象C .图a 显示了波的干涉现象,图b 显示了波的衍射现象D .图a 显示了波的衍射现象,图b 显示了波的干涉现象4.甲、乙两列横波在同一介质中分别从波源M 、N 两点沿x 轴相向传播,波速为2m/s ,振幅相同,某时刻的图像如图所示,则( )A .甲乙两波的起振方向相同B .甲乙两波的频率之比为3∶2C .再经过3s 时,平衡位置在x =7m 处的质点振动方向向上D .再经过3s 时,平衡位置在x =2m 处的质点将向右运动到x =8m 处的位置。
E.再经过3s 时,平衡位置在x =1m 处的质点将第二次出现在波峰5.如图所示,两列简谐横波分别沿x 轴正方向和负方向传播。
已知两波源分别位于0.2m x =-和 1.0m x =处,振幅均为0.5cm A =,波速均为0.2m/s v =。
0t =时刻,平衡位置处于0.2m x =和0.6m x =的P 、Q 两质点刚开始振动。
质点M 的平衡位置处于0.4m x =处,以下说法正确的是( )A .0t =时,质点P 、Q 振动方向分别是向下和向上B .01s ~内,质点P 的运动路程为0.2mC . 1.5s t =时,平衡位置处于0.3m 0.5m ~之间的质点位移均为0D .2s t =时,0.3m x =处质点的位移为0.5cm -E.两列波相遇分开后,各自的振幅、周期均保持不变6.一列简谐横波沿x 轴传播,在x =0和x =0.6m 处的两个质点A 、B 的振动图象如图所示。
《大学物理》习题册题目及答案第16单元 机械波

第16单元 机械波(一)学号 姓名 专业、班级 课程班序号一 选择题[ C ]1.在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同 (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后 (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前[ A ]2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI),则(A) 其波长为0.5 m (B) 波速为5 m ⋅s -1(C) 波速为25 m ⋅s -1 (D)频率为2 Hz[ C ]3. 一简谐波沿x 轴负方向传播,圆频率为ω,波速为u 。
设t = T /4时刻的波形如图所示,则该波的表达式为: (A) )/(cos u x t A y -=ω (B) ]2/)/([cos πω+-=u x t A y (C) )/(cos u x t A y +=ω (D) ])/([cos πω++=u x t A y[ D ]4. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
若振动以余弦函数表示,且此题各点振动的初相取π-到π之间的值,则 (A) 0点的初位相为00=ϕ(B) 1点的初位相为 21πϕ-=(C) 2点的初位相为 πϕ=2(D) 3点的初位相为 23πϕ-=[ D ]5. 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成势能。
(B) 它的势能转换成动能。
(C) 它从相邻的一段质元获得能量其能量逐渐增大。
(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小。
二 填空题1.频率为100Hz 的波,其波速为250m/s ,在同一条波线上,相距为0.5m 的两点的相位差为52π. 2. 一简谐波沿x 轴正向传播。
1x 和2x 两点处的振动曲线分别如图(a)和(b)所示。
《大学物理》习题库试题及答案___05_机械波习题

一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是 [ b ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零[ d ]3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B[ c ]u=λ/T C=ϖ/u4.3413:下列函数f (x 。
t)可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播-的行波?(A) )A(bt),tf-=cos(xaxax(bt),Atf+xcos(=(B) )(C) bttAaxxf sin(⋅),sin==(D) btt(⋅axxA),cosf cos[a]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反(B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反[ a ]6.3483:一简谐横波沿Ox轴传播。
若Ox轴上P1和P2两点相距λ /8(其中λ为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同(B) 方向总是相反(C) 方向有时相同,有时相反(D) 大小总是不相等[ c ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大(D) 振动频率越低,波速越大[ B ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
《大学物理学》机械波练习题

《大学物理学》机械波部分自主学习材料(解答)一、选择题10-1.图(a )表示0t =时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线,则图(a )中所表示的0x =处质点振动的初相位与图(b )所表示的振动的初相位分别为( C ) (A )均为2π; (B )均为π-; (C )π与π-; (D )2π-与2π。
【提示:图(b )为振动曲线,用旋转矢量考虑初相角为2π-,图(a )为波形图,可画出过一点时间的辅助波形,可见0x =处质点的振动为由平衡位置跑向负方向,则初相角为2π】10-2.机械波的表达式为0.05cos(60.06)y t x ππ=+,式中使用国际单位制,则( C ) (A )波长为5m ; (B )波速为110m s -⋅;(C )周期为13秒; (D )波沿x 正方向传播。
【提示:利用2k πλ=知波长为1003λ=m ,利用u k ω=知波速为1100u m s -=⋅,利用2T πω=知周期为13T =秒,机械波的表达式中的“+”号知波沿x 负方向传播】10-3.一平面简谐波沿x 轴负方向传播,角频率为ω,波速为u ,设4Tt =时刻的波形如图所示,则该波的表达式为( D )(A )cos[()]xy A t u ωπ=-+; (B )cos[()]2x y A t u πω=--;(C )cos[()]2x y A t u πω=+-;(D )cos[()]xy A t uωπ=++。
【提示:可画出过一点时间的辅助波形,可见在4Tt =时刻,0x =处质点的振动为由平衡位置向正方向振动,相位为2π-,那么回溯在0t=的时刻,相位应为π】10-4.如图所示,波长为λ的两相干平面简谐波在P 点相遇,波在点1S 振动的初相是1ϕ,到P 点的距离是1r 。
波在点2S 振动的初相是2ϕ,到P 点的距离是2r 。
以k 代表零或正、负整数,则点P 是干涉极大的条件为( D )OO1S 2S r(A )21r r k π-=; (B )212k ϕϕπ-=; (C )212122r r k ϕϕππλ--+=;(D )122122r r k ϕϕππλ--+=。
大学物理三习题机械波

1. 一平面简谐波,波速u = 5 m/s,t = 3 s时波形曲线如图, 则x = 0处质点的振动方程为 y (m)
1 1 2 y 2 10 cos( πt π) 2 2
u O x (m) 5 10 15 20 25 -2×10 2
y 2 102 cos( πt π)
X1处0时刻位移为零 ¼ 周期后 正向最大值
4. 已知波源的振动周期为 4.00 10 秒, 波的传播速度为 300m/s,波沿 x 轴正向 传播,则位于 x1 10.0 m 和 x2 16.0 m 的两质点振动位相差为_______________
2
6m 0.02s ½ 周期
5. 如图,一平面波在介质中以波速 u = 20 m/s 沿 x 轴负方向传播,已知 A 点的振动方程 为
(2) 因波速与传播方向相反,先设波动方程为 y A cos2 因为以 x 为原点,则表达形式应该为
t x , T
t x t x y A cos2 A cos[ 2 ( ) ] T T
2A/ 2
O -A 100
P x (m)
T=1/250=0.004 w=2π/0.004
1. 如图所示,两列波长为 的相干波在P点相遇.波在S1点振 动的初相是 1,S1到P点的距离是r1;波在S2点的初相是 2, S2到P点的距离是r2,以k代表零或正、负整数,则P点是干涉 极大的条件为:
r2 r1 k
S1 S2
r1 r2
P
2 1 2kπ
2 1 2π(r2 r1 ) / 2kπ
2 1 2π(r1 r2 ) / 2kπ
《大学物理学》(网工)机械波练习题(解答)

合肥学院《大学物理 B》(网工)自主学习材料
4.一列机械波沿 x 轴正向传播, t =0 时的波形如图所示,
已知波速为10 m/s,波长为2m,求: (1)波动方程;
(2) P 点的振动方程及振动曲线; (3) P 点的坐标; (4) P 点回到平衡位置所需的最短时间
(D)
53
53
(A) y 4sin 2 ( t x) ; (B) y 4sin 2 ( t x) ;
22
22
53
53
(C) x 4sin 2 ( t y) ; (D) x 4sin 2 ( t y) 。
22
22
【提示:找出正好方向相反的那个波】
拓展题:平面简谐波 y 4 cos(5 t 3 x) 与下面哪列波相干可形成驻波?
由波速 5m/s 知: ku 5 ,
由于是 y-t 图,可直接作旋转矢量知
2 波动方程为: y 0.1cos(5 t x ) 22
(2)将 x=0.5 代入波动方程,有:
3 y0.5 0.1cos(5 t 4 ) 则 t =0 时的波形图
2 x
4.一驻波的表达式为 y 2A cos( ) cos 2 t ,两个相邻的波腹之间的距离为
。
【提示:驻波相邻两波腹之间的距离为半个波长,即为 / 2 】
三、计算题
1.沿绳子传播的平面简谐波的波动方程为 y 0.05cos(10 t 4 x) ,求:(1)绳子上各质点振动时
6-7.某时刻驻波波形曲线如图所示,则 a,b 两点位相差是 (A)π; (B)π/2 ; (C)5π/4; (D) 0。
【提示:驻波波节两边的相位相反,两波节之间各点的振动相位相同】
物理机械波试题及答案

物理机械波试题及答案一、选择题(每题2分,共10分)1. 机械波的传播速度取决于:A. 波源的振动速度B. 介质的密度C. 介质的弹性模量D. 波源的振动频率答案:C2. 以下哪种波不属于机械波?A. 声波B. 光波C. 地震波D. 电磁波答案:D3. 机械波的波长与频率的关系是:A. 波长与频率成正比B. 波长与频率成反比C. 波长与频率无关D. 波长与频率的乘积为常数答案:B4. 波的干涉现象中,两个波源发出的波在空间某点相遇时,若该点的振动加强,则该点的振动幅度:A. 增加B. 减小C. 保持不变D. 无法确定答案:A5. 波的衍射现象发生在:A. 波遇到障碍物时B. 波遇到比波长大得多的障碍物时C. 波遇到比波长小得多的障碍物时D. 波遇到与波长相近的障碍物时答案:D二、填空题(每题2分,共10分)1. 机械波的传播需要______,而电磁波的传播不需要。
答案:介质2. 波的反射现象中,反射波的频率与入射波的频率______。
答案:相同3. 波的折射现象中,折射角与入射角的关系取决于______。
答案:介质的折射率4. 波的多普勒效应是指波源与观察者之间存在相对运动时,观察者接收到的波的频率与波源发出的频率______。
答案:不同5. 波的干涉现象中,当两个波的相位差为______时,会发生相长干涉。
答案:0度或整数倍的360度三、简答题(每题10分,共20分)1. 请简述机械波的传播过程。
答案:机械波的传播过程是指波源振动时,通过介质中的分子或原子的相互作用,使振动能量从一个分子传递到另一个分子,从而形成波动。
波源的振动使得介质中的分子或原子产生周期性的位移,这些位移又通过介质中的弹性力和惯性力传递给相邻的分子或原子,形成连续的波动。
波的传播速度取决于介质的性质,如密度和弹性模量。
2. 什么是波的衍射现象?请举例说明。
答案:波的衍射现象是指波在遇到障碍物或通过狭缝时,波的传播方向发生偏离直线传播的现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理学》机械波部分自主学习材料(解答)一、选择题10-1.图(a )表示0t =时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线,则图(a )中所表示的0x =处质点振动的初相位与图(b )所表示的振动的初相位分别为( C ) (A )均为2π; (B )均为π-; (C )π与π-; (D )2π-与2π。
【提示:图(b)为振动曲线,用旋转矢量考虑初相角为2π-,图(a )为波形图,可画出过一点时间的辅助波形,可见0x =处质点的振动为由平衡位置跑向负方向,则初相角为2π】10-2.机械波的表达式为0.05cos(60.06)y t x ππ=+,式中使用国际单位制,则( C ) (A )波长为5m ; (B )波速为110m s -⋅;(C )周期为13秒; (D )波沿x 正方向传播。
【提示:利用2k πλ=知波长为1003λ=m ,利用u k ω=知波速为1100u m s -=⋅,利用2T πω=知周期为13T =秒,机械波的表达式中的“+”号知波沿x 负方向传播】10-3.一平面简谐波沿x 轴负方向传播,角频率为ω,波速为u ,设4Tt =时刻的波形如图所示,则该波的表达式为( D )(A )cos[()]xy A t u ωπ=-+; (B )cos[()]2x y A t u πω=--;(C )cos[()]2x y A t u πω=+-;(D )cos[()]xy A t uωπ=++。
【提示:可画出过一点时间的辅助波形,可见在4Tt =时刻,0x =处质点的振动为由平衡位置向正方向振动,相位为2π-,那么回溯在0t=的时刻,相位应为π】OO10-4.如图所示,波长为λ的两相干平面简谐波在P 点相遇,波在点1S 振动的初相是1ϕ,到P 点的距离是1r 。
波在点2S 振动的初相是2ϕ,到P 点的距离是2r 。
以k 代表零或正、负整数,则点P 是干涉极大的条件为( D ) (A )21r r k π-=; (B )212k ϕϕπ-=; (C )212122r r k ϕϕππλ--+=; (D )122122r r k ϕϕππλ--+=。
【提示:书上P62页原公式为212122r r k ϕϕππλ---=】10-5.在驻波中,两个相邻波节间各质点的振动( B )(A )振幅相同,相位相同; (B )振幅不同,相位相同; (C )振幅相同,相位不同; (D )振幅不同,相位不同。
【提示:由书上P67页驻波两波节间各点振动相位相同】10--1.如图所示,有一横波在时刻t 沿Ox 轴负方向传播,则在该时刻( C ) (A )质点A 沿Oy 轴负方向运动;(B )质点B 沿Ox 轴负方向运动; (C )质点C 沿Oy 轴负方向运动; (D )质点D 沿Oy 轴正方向运动。
【提示:可画辅助波形来判断】10--2.设有两相干波,在同一介质中沿同一方向传播,其波源相距32λ,如图所示,当A 在波峰时,B 恰在波谷,两波的振幅分别为A 1和A 2,若介质不吸收波的能量,则两列波在图示的点P 相遇时,该处质点的振幅为( A ) (A )12A A +; (B )12A A -; (C; (D。
【提示:利用书上P62页公式为:212123222r r πλϕϕπππλλ---=-⋅=-,加强】8.如图所示,两相干平面简谐波沿不同方向传播,波速均为s m u /40.0=,其中一列波在A 点引起的振动方程为11cos(2)2y A t ππ=-,另一列波在B 点引起的振动方程为22cos(2)2y A t ππ=+,它们在P 点相遇,m AP 80.0=,m BP 00.1=,则两波在P 点的相位差为: ( A ) (A )0; (B )π/2; (C )π; (D )3π/2。
【同上题提示】10--3.当波在弹性介质中传播时,介质中质元的最大变形发生在( D )(A )质元离开其平衡位置最大位移处; (B )质元离开其平衡位置A /2处; (C)质元离开其平衡位置/A 处; (D )质元在其平衡位置处。
(A 为振幅)【书P56页:体积元的动能和势能具有相同的相位,在平衡位置处动能和势能都达最大值】AB1S 2S r•••32λP Buu10.一个平面简谐波沿x 轴负方向传播,波速u=10m/s 。
x =0处,质点振动曲线如图所示,则该波的表式为B ) (A ))2202cos(2πππ++=x t y m ;(B ))2202cos(2πππ-+=x t y m ;(C ))2202sin(2πππ++=x t y m ;(D ))2202sin(2πππ-+=x t y m 。
【提示:给出的是y -t 图,图中可定出振幅和周期、初相位,波数k 可由ukω=得出】11.一个平面简谐波沿x 轴正方向传播,波速为u =160m/s ,t =0时刻的波形图如图所示,则该波的表式为 (A )3cos(40)42y t x πππ=+-m ;(B )3cos(40)42y t x πππ=++m ; (C )3cos(40)42y t x πππ=--m ; (D )3cos(40)42y t x πππ=-+m 。
【提示:给出的是y -x 图,图中可定出振幅和波长,圆频率ω可由ukω=得出,初相位可用辅助波形判断,本题可判断出x =0处,质点的振动是从平衡位置向正方向,则初相位为2π-】12.一个平面简谐波在弹性媒质中传播,媒质质元从最大位置回到平衡位置的过程中( C ) (A )它的势能转化成动能; (B )它的动能转化成势能;(C )它从相邻的媒质质元获得能量,其能量逐渐增加;(D )把自己的能量传给相邻的媒质质元,其能量逐渐减小。
【同9题提示】13.一平面简谐波在弹性媒质中传播时,在传播方向上某质元在某一时刻处于最大位移处,则它的 ( B ) (A )动能为零,势能最大; (B )动能为零,势能也为零; (C )动能最大,势能也最大;(D )动能最大,势能为零。
【同9题提示】14. 电磁波在自由空间传播时,电场强度E 与磁场强度H( C )(A )在垂直于传播方向上的同一条直线上;(B )朝互相垂直的两个方向传播; (C )互相垂直,且都垂直于传播方向; (D )有相位差π/2。
【提示:参看电磁波示意图】15. 在同一媒质中两列相干的平面简谐波强度之比是4:21=I I ,则两列波的振幅之比21:A A 为 ( B )(A ) 4; (B ) 2; (C ) 16; (D ) 1/4。
【提示:强度定义为振幅的平方】16. 在下面几种说法中,正确的是:( C )(A )波源不动时,波源的振动周期与波动的周期在数值上是不同的; (B )波源振动的速度与波速相同;-)-(C )在波传播方向上,任一质点的振动相位总是比波源的相位滞后; (D )在波传播方向上,任一质点的振动相位总是比波源的相位超前。
【中学问题】17.两个相干波源的相位相同,它们发出的波叠加后,在下列哪条线上总是加强的?( A ) (A )两波源连线的垂直平分线上; (B )以两波源连线为直径的圆周上; (C )以两波源为焦点的任意一条椭圆上; (D )以两波源为焦点的任意一条双曲线上。
【提示:找出距离相同的那些点】18.平面简谐波4sin(53)x t y ππ=+与下面哪列波相干可形成驻波?( D )(A ))2325(2sin 4x t y +=π; (B ))2325(2sin 4x t y -=π;(C ))2325(2sin 4y t x +=π; (D ))2325(2sin 4y t x -=π。
【提示:找出正好方向相反的那个波】19.设声波在媒质中的传播速度为u ,声源的频率为S ν,若声源S 不动,而接收器R 相对于媒质以速度R υ沿S 、R 连线向着声源S 运动,则接收器R 接收到的信号频率为:( B ) (A )S ν; (B )R S u u υν+; (C )RS u uυν-; (D )S R u u νυ-。
【提示:书中P71页,多普勒效应中,迎着静止波源运动频率高,公式为0'u uυνν+=,远离静止波源运动频率低,公式为0'u uυνν-=】20.两列完全相同的平面简谐波相向而行形成驻波。
以下哪种说法为驻波所特有的特征:( C )(A )有些质元总是静止不动; (B )迭加后各质点振动相位依次落后; (C )波节两侧的质元振动相位相反; (D )质元振动的动能与势能之和不守恒。
【提示:书中P67页,驻波波节两边的相位相反,两波节之间各点的振动相位相同】 二、填空题10-7.一横波在沿绳子传播时的为0.20cos(2.50)y t x ππ=-,采用国际单位制,则(1)此横波沿x 的正向传播,波的振幅为0.20m 、频率为1.25Hz 、波长为2m 、波传播的波速为2.5/m s ;(2)绳上的各质点振动时的最大速度为0.5/m s π。
【提示:波动方程中的负号表明波沿x 的正向传播,利用波动标准方程cos()y A t k x ωϕ=-+比较可知振幅为0.20m 、频率为1.25Hz 、波长为2m 、波传播的波速为/k υω=,得2.5/m s ;振动速度不同于波速,应该用波动方程对时间求导,得最大速度为0.5/m s π。
】10--4.图示中实线表示t =0时的波形图,虚线表示t =0.1秒时的波形图。
由图可知该波的角频率ω=2.51s π-;周期T =0.8 s ;波速u =0.2 /m s ;波函数为y =250.03cos(2.5)22t x πππ-+【提示:注意图中标的是厘米,图中可见波长为16厘米,可求出波数252k π=;0.1秒波形向右跑了2厘米,可求出波速0.2u=,利用u kω=知 2.5ωπ=,0.8T =;初相位看O 位置,O 位置在t =0和t =0.1秒时间内从平衡位置向下振动,旋转矢量初相位是2πϕ=】10-10.一周期为0.02秒,波速为100/m s 的平面简谐波沿ox 轴正向传播,0t =时,波源处的质点经平衡位置向正方向运动,则其波动方程为 ,距离波源15m 处的M 点的振动方程为 ,距离波源5m 处的N 点的振动方程为 。
【提示:∵0.02T =,∴2100Tπωπ==,利用k uω=知波数k π=,由旋转矢量法知初相位2πϕ=-,故波动方程为cos(100)2y A t x πππ=--;将15x =代入,有cos(100)2M y A t ππ=+,将5x =代入,有cos(100)2N y A t ππ=+】4.一平面简谐波的周期为2.0s ,在波的传播路径上有相距为2.0cm 的M 、N 两点,如果N 点的相位比M 点相位落后π/6,那么该波的波长为 ,波速为 。
