大学物理《波动篇·机械波》复习题及答案
(完整版)高考物理机械波练习题及答案
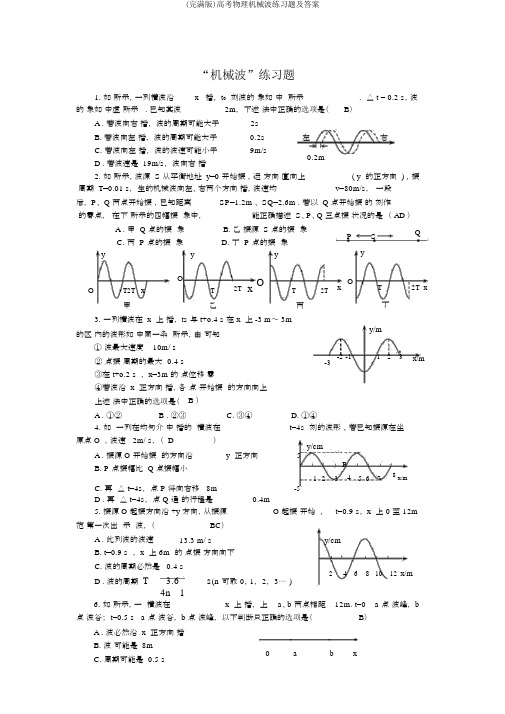
“机械波”练习题1. 如所示,一列横波沿x 播, t0刻波的象如中所示. △ t = 0.2 s,波的象如中虚所示 . 已知其波2m,下述法中正确的选项是(B)A . 若波向右播,波的周期可能大于2sB. 若波向左播,波的周期可能大于0.2s 左右C. 若波向左播,波的波速可能小于9m/s0.2mD . 若波速是 19m/s,波向右播2. 如所示,波源 S 从平衡地址 y=0 开始振,运方向直向上( y 的正方向 ) ,振周期 T=0.01 s,生的机械波向左、右两个方向播,波速均v=80m/s,一段后, P、 Q 两点开始振,已知距离SP=1.2m 、 SQ=2.6m . 若以 Q 点开始振的刻作的零点,在下所示的四幅振象中,能正确描述 S、P、Q 三点振状况的是( AD )A . 甲 Q 点的振象 B. 乙振源 S 点的振象C. 丙 P 点的振象D. 丁 P 点的振象y y yOOT 2T xOT 2T T2T x甲乙丙3.一列横波在 x 上播, ts 与 t+o.4 s 在 x 上 -3 m~ 3m的区内的波形如中同一条所示,由可知① 波最大速度 10m/ s② 点振周期的最大0.4 s -3③在 t+o.2 s , x=3m 的点位移零④若波沿 x 正方向播,各点开始振的方向向上上述法中正确的选项是( B )P S QyxOT 2T x丁y/m-2 -1 1 2 3x/mA . ①②B . ②③ C. ③④ D. ①④4. 如一列在均匀介中播的横波在t=4s 刻的波形,若已知振源在坐原点 O ,波速 2m/ s,( D )y/cmA . 振源 O 开始振的方向沿y 正方向 5PB. P 点振幅比 Q 点振幅小61 2 3 4 5 7 8 x/mC. 再△ t=4s,点 P 将向右移 8m -5D . 再△ t=4s,点 Q 通的行程是0.4m5. 振源 O 起振方向沿 +y 方向,从振源O 起振开始,t=0.9 s, x 上 0 至 12m 范第一次出示波,(BC)A . 此列波的波速13.3 m/ s y/cmB. t=0.9 s , x 上 6m 的点振方向向下C. 波的周期必然是 0.4 s2 4 6 8 10 12 x/mD . 波的周期T 3.6 s(n可取0,1,2,3⋯⋯)4n 16. 如所示,一横波在x 上播,上a、b 两点相距12m. t=0 a 点波峰, b 点波谷; t=0.5 s a 点波谷, b 点波峰,以下判断只正确的选项是(B)A . 波必然沿 x 正方向播B. 波可能是 8m0 a b xC. 周期可能是 0.5 sD. 波速必然是 24m/ s1)( n=0,1, 2, 3,⋯)剖析 : 由波的周期性可知 : 12m (n①1)T20.5s (k( n=0, 1, 2, 3⋯) ②2∴波的 播方向不确定. 由①式得 :24 m ,当 n=1 ,λ =8m.2n 1 1由②式得 Ts , T ≠0.5 s2k1由公式 v 知波速不确定 . 故正确 B.T7. 一 横波在 中 x 上 播, 和虚 分 是t 1 刻和 t 2 刻的波形 ,已知t 2- t 1=1.0 s. 由 判断以下哪一个波速y/cm是不可以能的( D )A .1 m/sB .3 m/s -2 -1O 1 2 3 4 5x/mC.5 m/sD . 10m/s剖析 : 据 可知波 λ =4m ,因 不知道波的 播方向,因此有两种可能,因此波的周期:T 14 s 或 T 24 s ( n=0, 1, 2, 3,⋯)4n 4n13波速 v 1T 1( 4n 1) m / s ,( n=0, 1,2, 3,⋯),可能 1, 5, 9,⋯v 2(4n 3)m / s ,( n=0, 1, 2, 3,⋯),可能 3,7, 11,⋯T 2波速不可以能10m/s ,故正确 D.8. 一列横波的波形如 所示, 表示 t 1=0 刻的波形 ,虚 表示t 2=0.005s 刻的波形 ,求:(1) 若 2T> t 2-t 1>T ,波速可能 多大?( T 周期)(2) 若 T< t 2-t 1,并且波速 3600m/s , 波向哪个方向 播? y/cm52468 10 12 x/m- 5解 :(1)Ot=0.005s 内波 播的距离x=10m , 波由 象可知:若波向右 播, 在△速 x 10v 1m smst /2000/0.005若 波 向 左播 ,在 △ t=0.005s内 波播 的 距 离x=14m ,波 速v 2x 14m / s 2800m / st0.005(2) 由 象可知 : 波 λ =8m在△ t=0.005s 内波 播的距离x=v △ t=3600 ×0.005 m=18m18 1,因此波向右流传 .则 x 28 4x2 y 2y/cm9. 以下列图,在双曲线 1 的两个焦点 F1和 F2 上放16 9C置两个频率相同的波源,它们激起的波的波长为4cm.就图中 A 、B、AC、 D 四个质点的振动,下面说法中正确的选项是( B ) F 1 O F2 x/cmA . 若 A 、B 振动加强,则C、 D 振动必然减弱 D BB. 若 A 、B 振动加强,则C、 D 必然振动加强C.A 、 B、 C、D 必然振动加强D . A 、 B、 C、 D 必然振动减弱10. 以下列图,声源S 和观察者 A 都沿 x 轴正方向运动,有关于地面的速度分别为v S和v A,空气中声音流传的速率为v P,设 v S<v P, v A<v P,空气有关于地面没有流动.(1) 若声源接踵发出两个声音信号,时间间隔为△t. 请依照发出的这两个声信号从声源流传到观察者的过程,确定观察者接收到这两个声音信号的时间间隔△t′;(2)利用 (1) 的结果,推导此状况下观察者接收到的声波频率和声源放出的声波频率间的关系式 .v S v A 解 :(1) 设声源发出第一个声音信号时声源与观察者间的S A x 距离为 L ,第一个声音信号放出后经过△t1的时间被观察者接收到,则:v P△ t1– v A△ t1 = L ①设第二个声音信号发出后经过△t2 的时间被观察者接收到,则 :v P△ t2– v A△ t2 = L - (v S - v A)△ t ②则观察者接收到这两个声音信号的时间间隔△t′=( △t +△t2 ) - △ t1 ③由①②③式得 : t v P v St v P v A(2) 设声源放出的声波的周期和频率分别为T 和 f,观察者接收到的声音的周期和频率分别为 T′和 f′,则 : T t v P vA . 因此,f T f vPvA f.T t v P v S T v P v S11. 以下列图,有四列简谐波同时沿x 轴正方向流传,波速分别是v、 2v、 3v 和 4v, a、b 是 x 轴上所给定的两点,且ab=l. 在 t 时辰 a、b 两点间的 4 列波的波形分别以下列图,则由该时辰起 a 点出现波峰的先后序次依次是图BDCA ;频率由高到低的先后序次依次是DBCA . vb a 2va 3vb a4va b bx x x xA B C Ds,如图12. 在均匀介质中,各质点的平衡地址在同素来线上,相邻两质点的距离均为甲所示,振动从质点 1 开始向右流传,质点 1 开始运动时的速度方向向上,经过时间t,前13 个质点第一次形成如图乙所示的波形,关于这列波的周期和波速以下说法正确的选项是( BD )A . 这列波的周期为T=2t/3 1 2 3 4 5 6 7 8 9 10 11 12 13 甲B. 这列波的周期为T=t/2C. 这列波的流传速度v=12s/ t 乙D. 这列波的流传速度v=16s/ t13. 一列沿 x 轴正方向流传的机械波,周期为0.50 s. 某一时辰,走开平衡地址的位移都相等的各元依次P1、 P2、 P3 、⋯ . 已知 P1 和 P2 之的距离20cm, P2 和 P3之的距离 80cm, P1的振到 P2所需的( C)A . 0.50 sB . 0.13 s C. 0.10 s D. 0.20 s14. 一列波沿x 的正方向播,在t=0 刻的波形如所示,已知列波的P 点最少再 0.3 s 才能到达波峰,以下法正确的选项是(D)① 列波的波是5my/cm② 列波的波速是10m/ s③ 点 Q 要0.7 s 才能第一次到达波峰O ?? ? ? ?x/m④ 点 Q 到达波峰点P 也恰好到达波峰 1 3 5 9A . 只有①、②B . 只有②、③C. 只有②、④ D . 只有②、③、④15.如所示,沿 x 正方向播的一列横波在某刻的波形一正弦曲,其波速 200m/s,以下法中不正确的是( A )...y/cmA . 示刻点 b 的加速度正在减小20 aB . 从示刻开始,0.01s,点 a 通的行程0.4m 01 35 x/mC. 若此波遇到另一波并生定干涉象,波-20 b所遇到的波的率 50HzD. 若生明衍射象,波所遇到的阻挡物或孔的尺寸必然小于4m16. 如 3 所示,振源 S 在垂直于 x 的方向振,并形成沿x 正、方向播的横波,波的率50Hz,波速 20m/s,x 上有 P、Q 两点, SP= 2.9m,SQ= 2.7m,足的今后,当点S 正通平衡地址向上振( A )3A .点 P 正于波谷B.点 Q 正于波谷C.点 P、 Q 都于波峰 D .点 P、Q 都于平衡地址17. 如所示,在xOy 平面内有一沿x 正方向播的横波,波速1m/s,振幅4cm,率 2.5H Z.在 t=0 刻( P、Q 两点均已振) P 点位于其平衡地址上方最大位移,距 P 点0.2m 的 Q 点( BC )A . 在 0.1s 的位移是4cmB. 在 0.1s 的速度最大C. 在 0.1s 的速度方向向上D. 在 0 到 0.1s 内的行程是8cm18.一横波正沿 x 的正方向在性上播,振源的周期0 .4 s,波的振幅 0.4 m.在 t0刻波形如所示,在 t0+0.3 s ( BD )A . 点 P 正于波谷B. 点 Q 正平衡地址向上运C. 点 Q 通的行程 1.2 mD. 点 M 正于波谷19. 如所示,是一列横波在某刻的波形. 若此元 P 正于加速运程中,此 ( D)y/mQ PO x/mNA . 质元 Q 和质元 N 均处于加速运动过程中 B. 质元 Q 和质元 N 均处于减速运动过程中C. 质元 Q 处于加速运动过程中,质元 N 处于减速运动过程中D. 质元 Q 处于减速运动过程中,质元 N 处于加速运动过程中20. 以下列图,是一列沿 x 轴正向流传的简谐横波在 t 时辰的图象。
《大学物理》习题库试题及答案___05_机械波习题

一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是 [ b ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零[ d ]3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B[ c ]u=λ/T C=ϖ/u4.3413:下列函数f (x 。
t)可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播-的行波?(A) )A(bt),tf-=cos(xaxax(bt),Atf+xcos(=(B) )(C) bttAaxxf sin(⋅),sin==(D) btt(⋅axxA),cosf cos[a]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反(B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反[ a ]6.3483:一简谐横波沿Ox轴传播。
若Ox轴上P1和P2两点相距λ /8(其中λ为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同(B) 方向总是相反(C) 方向有时相同,有时相反(D) 大小总是不相等[ c ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大(D) 振动频率越低,波速越大[ B ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
《大学物理学》(网工)机械波练习题(解答)

合肥学院《大学物理 B》(网工)自主学习材料
4.一列机械波沿 x 轴正向传播, t =0 时的波形如图所示,
已知波速为10 m/s,波长为2m,求: (1)波动方程;
(2) P 点的振动方程及振动曲线; (3) P 点的坐标; (4) P 点回到平衡位置所需的最短时间
(D)
53
53
(A) y 4sin 2 ( t x) ; (B) y 4sin 2 ( t x) ;
22
22
53
53
(C) x 4sin 2 ( t y) ; (D) x 4sin 2 ( t y) 。
22
22
【提示:找出正好方向相反的那个波】
拓展题:平面简谐波 y 4 cos(5 t 3 x) 与下面哪列波相干可形成驻波?
由波速 5m/s 知: ku 5 ,
由于是 y-t 图,可直接作旋转矢量知
2 波动方程为: y 0.1cos(5 t x ) 22
(2)将 x=0.5 代入波动方程,有:
3 y0.5 0.1cos(5 t 4 ) 则 t =0 时的波形图
2 x
4.一驻波的表达式为 y 2A cos( ) cos 2 t ,两个相邻的波腹之间的距离为
。
【提示:驻波相邻两波腹之间的距离为半个波长,即为 / 2 】
三、计算题
1.沿绳子传播的平面简谐波的波动方程为 y 0.05cos(10 t 4 x) ,求:(1)绳子上各质点振动时
6-7.某时刻驻波波形曲线如图所示,则 a,b 两点位相差是 (A)π; (B)π/2 ; (C)5π/4; (D) 0。
【提示:驻波波节两边的相位相反,两波节之间各点的振动相位相同】
大学物理波动篇机械波复习题及答案课件

种不同的媒质中传播, 在分界面上的 P 点
相遇, 频率n = 200Hz, 振幅A1=A2=2.00 10-
2m, S2 的位相比 S1 落后 /2。在媒质1中
波速 u1= 800 m s-1, 在媒质2中波速 u2=
1000 m s-1 , S1P=r1=4.00m,
静止的点。求两波的波长和两波源间最 小位相差。
o
S1
S2
x
d
29
解: 设S1 和 S2的振动初位相分别为 1 和 2在 x1点两波引起的振动位相差
2 2 d x1/ 1 2 x1 / 2k 1
2 1 2 d 2 x1/ 2k 1 (1)
在x2点两波引起的振动位相差
2 2 d x2/ 1 2 x2 / 2k 3
波分别通过图中的 o1和 o2 点,通过 o1 点 的简谐波在 M1M2 平面反射后,与通过 o2 点的简谐波在 P 点相遇,假定波在M1M2平 面反射时有半波损失,o1 和 o2 两点的振动
方程为,y10=Acos(2t) 和 y20=Acos(2t) , 且 o1m+mp=16,o2P = 6 (为波长) 求:
(A)波速为C/B; (B)周期为 1/B;
(C)波长为C/2 ; (D)圆频率为 B。
[]
5
5.一平面简谐波沿正方相传播, t=0 时刻的
波形如图所示, 则 P 处质点的振动在 t=0 时
刻的旋转矢量图是
y
u
A
x
o
P
( A)
o
x
A
(B)
o
x
A
(C ) A o
x
A
(D)
《大学物理》习题训练与详细解答四(机械波)

2 2 u Tu
x 2 的 振 动 方 程 为 : y A c o s ( t ) A c o s ( t . ) 8 u 2 8 2 y A c o s ( t ) 4 3 x 2 3 x 的 振 动 方 程 为 : y A c o s ( t ) A c o s ( t . ) 8 u 2 8 2 y A c o s ( t ) 4
答案为:(A)
4
4.图2所示,一平面简谐波沿OX轴正向传播,波长为 A c o s ( 2 v t ) ,则P2点 若P1点处质点的振动方程为 y 1 处质点的振动方程为
与P1点处质点振动状态相同的那些点的位置是
L L y c o s [2 ( t 1 2) ] 2 A x L k (k 1 , 2 ......) 1
( 2 )试以 A 点 距 5 cm 处的 B 点 (A 在 的左边)为坐标 出 原 波 点写
A c o s ( t ) 解:(1)对照振动方程的标准形式 y 0 可得 A 0 . 0 3 m ,, 0 = 4 0
c20 m /s ,沿x轴正向传播的波的波 以A为坐标原点、 动方程 y Acos[ (t x) ] 0 u x y 0.03cos4 (t ) (m ) 注意单位转换 20
t x y Acos[2 ( ) 0 ] T x y 0.1cos[4 (t ) 0 ] 20
15
又t 0 , y A c o s A , 0 0 0
x y 0 . 1 cos 4 ( t ) ( m ) ( x 0 ) 20 (2)由波动方程求t0时刻的波形方程,只须令波动方程 的t为常数t0. 则所求t=T/4时刻的波形方程为
大学物理机械波知识点及试题带答案

机械波一、基本要求1、掌握描述平面简谐波的各物理量及各量之间的关系。
2、理解机械波产生的条件,掌握由已知质点的简谐振动方程得出平面简谐波的波动方程的方法及波动方程的物理意义。
理解波形图,了解波的能量、能流、能量密度。
3、理解惠更斯原理,波的相干条件,能应用相位差和波程差分析、确定相干波叠加后振幅加强和减弱的条件。
4、了解驻波及其形成条件,了解半波损失。
5、了解多普勒效应及其产生的原因。
二、主要内容1、波长、频率与波速的关系 /u T λ= u λν=2、平面简谐波的波动方程])(2cos[ϕλπ+-=xT t A y 或 ])(cos[ϕω+-=ux t A y 当0ϕ=时上式变为)(2cos λπx T t A y -= 或 )(cos uxt A y -=ω3、波的能量、能量密度,波的吸收(1)平均能量密度:2212A ϖρω= (2)平均能流密度:2212I A u u ρωϖ==(3)波的吸收:0x I I e α-=4、惠更斯原理介质中波动传播到的各点都可以看作是发射子波的波源,而在其后任意时刻,这些子波的包络就是新的波前。
5、波的叠加原理(1)几列波相遇之后,仍然保持它们各自原有的特征(频率、波长、振幅、振动方向等)不变, 并按照原来的方向继续前进, 好象没有遇到过其他波一样.(独立性) (2)在相遇区域内任一点的振动,为各列波单独存在时在该点所引起的振动位移的矢量和.(叠加性)6、波的干涉121220,1,221)0,1,2k k A A A k k A A A ϕπϕπ∆=±==+⎧⎪⎨∆=±+==-⎪⎩,… (干涉相长)(,… (干涉相消) 12120,1,2(21)0,1,22k k A A A k k A A A δλλδ=±==+⎧⎪⎨=±+==-⎪⎩,… (干涉相长),… (干涉相消) 7、驻波两列频率、振动方向和振幅都相同而传播方向相反的简谐波叠加形成驻波,其表达式为22coscos xY A t πωλ=8、多普勒效应(1)波源静止,观测者运动 00(1)V u υυ=+ (2)观测者静止,波源运动 0'suuu V υυλ==- (3)观测者和波源都运动 000'xu V u V u V υυλ++==- 三、习题与解答1、振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做的往复运动,系统离开平衡位置的位移是时间的周期性函数,即可表示为)(t f y =;波动是振动在连续介质中的传播过程,此时介质中所有质元都在各自的平衡位置附近作振动,因此介质中任一质元离开平衡位置的位移既是坐标位置x ,又是时间t 的函数,即),(t x f y =. (2)在谐振动方程)(t f y =中只有一个独立的变量时间t,它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律;平面谐波方程),(t x f y =中有两个独立变量,即坐标位置x 和时间t ,它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律. 当谐波方程)(cos ux t A y -=ω中的坐标位置给定后,即可得到该点的振动方程,而波源持续不断地振动又是产生波动的必要条件之一.(3)振动曲线)(t f y =描述的是一个质点的位移随时间变化的规律,因此,其纵轴为y ,横轴为t ;波动曲线),(t x f y =描述的是介质中所有质元的位移随位置,随时间变化的规律,其纵轴为y ,横轴为x .每一幅图只能给出某一时刻质元的位移随坐标位置x 变化的规律,即只能给出某一时刻的波形图,不同时刻的波动曲线就是不同时刻的波形图.2、波动方程0cos x y A t u ωϕ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦中的xu表示什么?如果改写为0cos x y A t u ωωϕ⎛⎫=-+ ⎪⎝⎭,x u ω又是什么意思?如果t 和x 均增加,但相应的0x t u ωϕ⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦的值不变,由此能从波动方程说明什么?解: 波动方程中的u x /表示了介质中坐标位置为x 的质元的振动落后于原点的时间;uxω则表示x 处质元比原点落后的振动位相;设t 时刻的波动方程为)cos(0ϕωω+-=ux t A y t 则t t ∆+时刻的波动方程为])()(cos[0ϕωω+∆+-∆+=∆+ux x t t A y t t其表示在时刻t ,位置x 处的振动状态,经过t ∆后传播到t u x ∆+处.所以在)(uxt ωω-中,当t ,x 均增加时,)(uxt ωω-的值不会变化,而这正好说明了经过时间t ∆,波形即向前传播了t u x ∆=∆的距离,说明)cos(0ϕωω+-=uxt A y 描述的是一列行进中的波,故谓之行波方程.3、在驻波的两相邻波节间的同一半波长上,描述各质点振动的什么物理量不同,什么物理量相同?解: 取驻波方程为vt x A y απλπcos 2cos2=,则可知,在相邻两波节中的同一半波长上,描述各质点的振幅是不相同的,各质点的振幅是随位置按余弦规律变化的,即振幅变化规律可表示为x A λπ2cos2.而在这同一半波长上,各质点的振动位相则是相同的,即以相邻两波节的介质为一段,同一段介质内各质点都有相同的振动位相,而相邻两段介质内的质点振动位相则相反.4、已知波源在原点的一列平面简谐波,波动方程为y =A cos (Bt -Cx ),其中A ,B ,C 为正值恒量.求:(1)波的振幅、波速、频率、周期与波长;(2)写出传播方向上距离波源为l 处一点的振动方程;(3)任一时刻,在波的传播方向上相距为d 的两点的位相差. 解: (1)已知平面简谐波的波动方程)cos(Cx Bt A y -= (0≥x )将上式与波动方程的标准形式)22cos(λππυxt A y -=比较,可知: 波振幅为A ,频率πυ2B =, 波长C πλ2=,波速CB u ==λυ, 波动周期BT πυ21==.(2)将l x =代入波动方程即可得到该点的振动方程)cos(Cl Bt A y -=(3)因任一时刻t 同一波线上两点之间的位相差为 )(212x x -=∆λπϕ将d x x =-12,及Cπλ2=代入上式,即得 Cd =∆ϕ.5、图示为一平面简谐波在t =0时的波形图,求:(1)该波的波函数;(2)P 处质点的振动方程。
机械波标准答案
机械波标准答案一、单选题:本大题共54小题,从第1小题到第4小题每题3分小计12分;从第5小题到第54小题每题4分小计200分;共计212分。
1、◆标准答案:B★ 试题提示:冲击波向四面八方传播,能量向四周传输,振幅是决定振动能量的物理量,说明振幅越来越小,我们听到的声音也是越远处越弱.但振动周期不变.2、◆标准答案:D3、◆标准答案:C★ 试题提示:S1、S2连线的垂直平分线上所有的点都是振动加强的点.虽然相邻两圆弧间的距离都相等,但ab≠bc,目前处于平衡位置的点也不是ab和bc的中点.4、◆标准答案:C★ 试题提示:已知波长为2l/3,A.b两点相距恰为1.5个波长,这两点称为“反相”,它们的振动正好相反,当a点经过平衡位置向上运动时,b点经过平衡位置向下运动,选项C正确.5、◆标准答案:B6、◆标准答案:C7、◆标准答案:D8、◆标准答案:D9、◆标准答案:B10、◆标准答案:D11、◆标准答案:C12、◆标准答案:C13、◆标准答案:C14、◆标准答案:D★ 试题提示:15、◆标准答案:B16、◆标准答案:B17、◆标准答案:D18、◆标准答案:B19、◆标准答案:C20、◆标准答案:B21、◆标准答案:D22、◆标准答案:B23、◆标准答案:B24、◆标准答案:A25、◆标准答案:B26、◆标准答案:C27、◆标准答案:C28、◆标准答案:C29、◆标准答案:D30、◆标准答案:A31、◆标准答案:B32、◆标准答案:B★ 试题详解:解析:如图所示33、◆标准答案:B34、◆标准答案:D35、◆标准答案:B36、◆标准答案:B37、◆标准答案:B38、◆标准答案:C★ 试题提示:39、◆标准答案:C40、◆标准答案:A41、◆标准答案:C42、◆标准答案:B43、◆标准答案:B44、◆标准答案:B45、◆标准答案:D46、◆标准答案:A47、◆标准答案:A48、◆标准答案:D49、◆标准答案:A50、◆标准答案:C★ 试题提示:提示:由题意可判断出此波一定向右传播,且T=0.4s.51、◆标准答案:A52、◆标准答案:B53、◆标准答案:B★ 试题提示:54、◆标准答案:C二、填空题:本大题共56小题,从第55小题到第58小题每题2分小计8分;从第59小题到第71小题每题3分小计39分;从第72小题到第93小题每题4分小计88分;从第94小题到第103小题每题5分小计50分;从第104小题到第110小题每题6分小计42分;共计227分。
机械波试题(含答案)
机械波试题(含答案)一、机械波选择题1.一简谐横波沿x轴正向传播,图1示t=0时刻的波形图,图2是介质中某质点的振动图象,则该质点的x坐标值合理的是()A.0.5m B.1.5m C.2.5m D.3.5m2.一列简谐横波沿x轴正方向传播,频率为5Hz,某时刻的波形如图所示,介质中质点A 在距原点8cm处,质点B在距原点16cm处,从图象对应时刻算起,质点A的运动状态与图示时刻质点B的运动状态相同需要的最短时间为()A.0.08s B.0.12s C.0.14s D.0.16s3.一列简谐波某时刻的波形如图中实线所示。
经过0.5s后的波形如图中的虚线所示。
已知波的周期为T,且0.25s<T<0.5s,则()A.不论波向x轴哪一方向传播,在这0.5s内,x=1m处的质点M通过的路程都相等B.当波向+x方向传播时,波速等于10m/sC.当波沿+x方向传播时,x=1m处的质点M和x=2.5m处的质点N在这0.5s内通过的路程相等D.当波沿﹣x方向传播时,经过0.1s时,质点M的位移一定为零4.一列波长大于3m的横波沿着x轴正方向传播,处在和的两质点A、B 的振动图象如图所示,由此可知()A.波长为4mB.波速为2m/sC.3s末A、B两质点的位移相同D.1s末A点的速度大于B点的速度5.一根长20m的软绳拉直后放置在光滑水平地板上,以绳中点为坐标原点,以绳上各质点的平衡位置为x轴建立图示坐标系。
两人在绳端P、Q沿y轴方向不断有节奏地抖动,形成两列振幅分别为10cm、20cm的相向传播的机械波。
已知P的波速为2m/s,t=0时刻的波形如图所示。
下列判断正确的有()A.两波源的起振方向相反B.两列波的频率均为2Hz,叠加区域有稳定干涉图样C.t=6s时,两波源间(不含波源)有5个质点的位移为-10cmD.叠加稳定时两波源间(不含波源)有10个质点的振幅为30cm6.一列简谐横波沿直线传播,该直线上的a、b两点相距4.42m。
大学物理机械波习题附答案
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理机械波习题附答案
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 [ 3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 C (D) 角频率为B [ ]4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f coscos ),(⋅= (D) bt ax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(为波长)的两点的振动速度必定y (m) y (m) - y (m)y (m)(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距 /8(其中 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长 (C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ]8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
A
(D)
o
x []
• 机械振动选择题答案:C(BC)CD(BD)
6.某质点做简谐振动,周期为 2s,振幅为 0.06m,开始计时 (t=0),质点恰好处在A/2 处且向负方向运动,求:
(1)该质点的振动方程; (2)此振动以速度 u = 2m/s 沿 x 轴正方 向传播时,形成的平面简谐波的波动方程;
解: (1)P W / t 2.70 10-3 J S-1
( 2 )I P / S 9.00 10-2 J S-1 m -2
(3)I wu
w I / u 2.56 10-4 J m-3
9.如图所示为一平面简谐在 t=0 时刻的波 形图,设此简谐波的频率为 250Hz,若波 沿 x 负方向传播。 (1)该波的波动方程; (2)画出 t =T /8 时刻的波形图; (3)距原点 o 为 100m 处质点的振动方程 与振动速度表达式。
大学物理《波动篇·机械波》 复习题及答案
1.在下面几种说法中,正确的说法是:
(A)波源不动时,波源的振动频率与波 动的频率在数值上是不同的; (B)波源振动的速度与波速相同; (C)在波传播方向上的任一质点的振动 位相总是比波源的位相滞后; (D)在波传播方向上的任一质点的振动 位相总是比波源的位相超前。
y(m )
2A 2
O
-A
P 100 m
x(m )
解:(1)对原点 o 处质点,t=0 时
2A / 2 A cos , v0 -A sin 0 所以 / 4
则 o 点的振动方程为
y0 A cos( 500 t / 4) (SI )
y
2A 2
O
-A
P 100 m
x(m )
波动方程为
t 时刻波形图为
y
y
y
o -A
[A]
A
B
o
P
x
y
C
A
o
( A) (C )
P
A
x
O
y
PA
x
O
x
P
(B)
x
(D)
点右方 18 米处。
(1)若取x轴方向向左并以 A 为坐标原点,
试写出波动方程,并求出 D 点的振动方程。
(2)若取 x 轴方向向右以 A 点左方 10m 处
的 o 点为 x 坐标原点,重新写出波动方程
及 D 点的振动方程。
yu
yu
x
oA D
o AD x
解:(1)任取一点P,可得波动方程为
y 3 cos4t x / 5 - (SI )
3 cos4t - 23 / 5 (SI)
y x
c
A PD x
8.一平面简谐波,波速为 340m·s-1,频率为 300Hz,在横截面积为 3.00 10-2m2的管内 的空气中传播,若在10内通过截面的能量 为 2.70 10-2J,求: (1)通过截面的平均能流; (2)波的平均能流密度; (3)波的平均能量密度。
y 0.06 cos t - x / u / 3 0.06 cos t - x / 2 / 3 (SI )
(3)波长 uT 4m
7.一平面简谐波在介质中以速度 u = 20 m/s
自左向右传播。已知在波线上的某点A的振
动方程为 y=3cos(4t- ) (SI) 另一点 D在 A
[]
2.一简谐波沿X轴正方向传播,图中所示为
t =T /4 时的波形曲线。若振动以余弦函数
表示,且次提各点振动的初相取 - 到 之
间的值,则:
(A)0点的初位相为 0= 0; (B)1点的初位相为 1= - /2; (C)2点的初位相为 2= (D)3点的初位相为 3= - /2;
y
u
0 1 234
y A cos2 (250 t x / 200 ) / 4 (SI )
( 2 )t T / 8 1 /(8 ) 1/ 2000
代如上式得波形方程
y A cos2 250 1 / 2000 x / 200 / 4
-A sin x / 100 (SI)
由此画出波形图如图所示
x
[]
3.一平面简谐波的波动方程为
y=0.1cos(3t-x+) (SI) ,
t =0 时的波形曲线如图所示,则:
(A)a点的振幅为 -0.1m; (B)波长为 4m;
(C)两点间位相差为 /2;
(D)波速为 6 m·s-1。
y(m )
u
0.1
0 ab - 0.1
x(m )
[]
4.若一平面间谐波的波方程为
沿相反方向传播叠加形成的驻波中,各处
的振幅是:
(A) 2A
(B) | 2 A cos 2t |
(C) 2 A cos 2x /
(D) | 2 A cos 2x / |
[D]
11.入图所示,为一向右传播的简谐波在 t
时刻的波形图,当波从波疏介质入射到波
密介质表面 BC,在 P 点反射时,反射波在
x D -18m 代如上式有
yD 3 cos4t x / 5 -
3 cos4t - 23 / 5 (SI)
y x
xP
A
c
D
(2)任取一点P,可得波动方程为
y
cos
4
ቤተ መጻሕፍቲ ባይዱ
t
-
x
- 10 20
-
3 cos4t - x / 5 - (SI)
x D 28 m 代如上式有
yD 3 cos( 4t - 28 / 5 )
y=Acos(Bt-Cx),式中A,B,C为正值恒量,
则 (A)波速为C/B; (B)周期为 1/B;
(C)波长为C/2 ; (D)圆频率为 B。
[]
5.一平面简谐波沿正方相传播,t=0 时刻的
波形如图所示,则 P 处质点的振动在 t=0
时刻的旋转矢量图是
y
u
A
x
o
P
( A)
o
x
A
(B)
o
x
A
(C ) A o
(3)该波的波长。
解:
(1 ) 2
T
s-1 ,
A 0.06
t 0时, x0 0.03 0.06 cos ,
v0 -0.06 sin 0
/3
振动方程 y0 0.06 cost / 3 (SI )
(2)波动方程,以该质点的平衡位置为坐 标原点,振动的传播速度方向为坐标轴正 方向。
或 t T / 8 时,
y(m )
波形向左传播
/ 8 25 m 的距离
O
-A
x(m )
(3)处质点振动方程时:
y1 A cos500 t 5 / 4 (SI)
振动速度表达式是:
v -500 A sin 500 t 5 / 4 (SI)
10.两列相干波,其波动方程为
y1=Acos2(t-x/)和y2=Acos2(t+x/) ,
