超静定结构的位移计算
超静定结构的受力分析及特性

超静定结构的受力分析及特性一、超静定结构的特征及超静定次数超静定结构的静力特征是仅由静力平衡条件不能唯一地确定全部未知反力和内力。
结构的多余约束数或用静力平衡条件计算全部未知反力和内力时所缺少的方程数称为结构的超静定次数。
通常采用去除多余约束的方法来确定结构的超静定次数。
即去除结构的全部多余约束,使之成为无多余约束的几何不变体系,这时所去除的约束数就是结构的超静定次数。
去除约束的方法有以下几种:(一)切断一根两端铰接的直杆(或支座链杆),相当于去除一个约束。
(二)切断一根两端刚接的杆件,相当于去除三个约束。
(三)切断——个单铰(或支座固定铰),相当于去除二个约束;切断一个复铰(连接n根杆件的铰),相当于去除2(n—1)个约束。
(四)将单刚结点改为单铰节点,相当于去除一个约束;将连接n个杆件的复刚节点改为复铰节点,相当于去除n—1个约束。
去除一个超静定结构多余约束的方法可能有几种,但不管采用哪种方法,所得超静定次数一定相同。
去除图4—1a所示超静定结构的多余约束的方法之一如图4—1b所示,去除六个多余约束后,就成为静定结构,故为超静定六次。
再用其他去除多余约束的方案确定其超静定次数,结果是相同的。
二、力法的基本原理(一)力法基本结构和基本体系去除超静定结构的多余约束,代以相应的未知力Xi (i=1、2、…、n),Xi 称为多余未知力或基本未知力,其方向可以任意假定。
去除多余约束后的结构称为力法基本结构。
力法基本结构在各多余未知力、外荷载(有时还有温度变化、支座位移等)共同作用下的体系称为力法基本体系,它是用力法计算超静定结构的基础。
选取力法基本结构应注意下面两点:1.基本结构一般为静定结构,即无多余约束的几何不变体系。
有时当简单超静定结构的解为已知时,也可以将它作为复杂超静定结构的基本结构,以简化计算。
2.选取的基本结构应使力法典型方程中的系数和自由项的计算尽可能简便,并尽量使较多的副系数和自由项等于零。
结构力学_11超静定结构-位移法

§11.3 位移法的基本未知量和基本体系
1、结点角位移数:
结构上可动刚结点数即为位移法计算的结点角位移数。
2、结构独立线位移:
每个结点有两个线位移,为了减少未知量,引入与实际相符的两个假设:
(1)忽略轴向力产生的轴向变形 (2)变形后的曲杆长度与其弦等长。
C
C
D
D
A
B
线位移数也可以用几何方法确定。 将结构中所有刚结点和固定支座,代之以铰结点和铰支座,分析新体系的
基本方法 (手算)
机算
力法
位移法
矩阵 力法
力矩分配法
矩阵 位移法
力法几次9超次静定?
位移法几1次次超静定?
§11.1
P C θA
θA
位移法的基本概念
B
A
附加
刚臂 C
P B
附加刚臂限制结
点位移,荷载作
A 用下附加刚臂上
产生附加力矩
C θA
B
θA
施加力偶使结点产 生的角位移,以实
A 现结点位移状态的
一致性。
D
2
C
F22
A
D
A
D
Fk1111
2i B
1 =1
i
A
C
kF2211
Fk122
B
i
D
A
建立基本方程
F11+F12+F1P=0………………(1a) F21+F22+F2P=0………………(2a)
k111 + k122 +F1P =0………..(1) k211 + k222 +F2P =0………..(2)
结构力学 超静定结构的位移计算
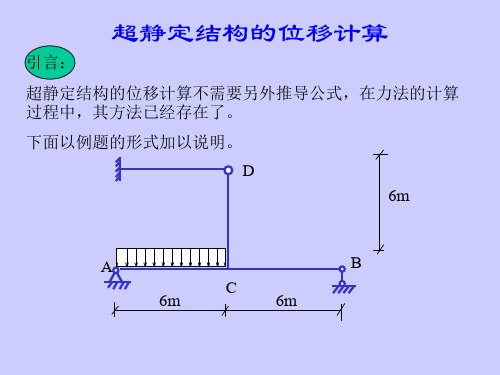
3a 3 12 21 4 EI
17 Pa 3 48EI
16 P X2 44
X1
3P 44
EI
p EI
6Pa/44 3Pa/44 3Pa/44 8Pa/44
2EI
16 P X2 44
M图
1
P=1
1 A EI
6 Pa 1 Pa 1 1 a 1 a 1 2 44 2 4 2 EI
6 150
30
90
M
P=1
MP
结构的 弯矩图
超静定结构的位移计算
4) M图与M P图图乘,
CV 1800 EI
小结:超静定结构的位移计算: 图 1)选基本体系作出超静定结构的弯矩图,作为MP
2)任选该超静定结构的一种基本结构,在拟求位移 M 的位置作用单位力,作出 图
3)
M图与M P图图乘结果就是所求的位移。
2)原结构等价于基本体系,则原结构在C点竖向位移,就 等价于求基本结构在X1 ,X2 及分布荷载q共同作用下C点竖 向位移。即,问题转化为求静定结构的位移问题。 150
q
- 5 kN
75 kN C
30
90
求此结构体系的位移, 3个荷载作用
结构的 弯矩图
超静定结构的位移计算
3)为求C处的竖向位移,在C处 作用P=1,与MP图图乘即可。
3Pa 7 Pa 2 1 1 a 44 176 EI 2
超静定结构的位移计算
计算实例
图示结构,各杆长都是 L,梁截面为矩形,截面高度h 数为 。求(1)绘弯矩图(2)求杆 A 端转角
L 10
,线膨胀系
-150 -150 A +250
结构力学 位移法计算超静定结构

情景一 位移法的基本原理和典型方程 知识链接
(2)等截面直杆的转角位移方程 常见的单跨超静定梁根据支座情况的不同,可分为如图 3 – 45 所示三种。
情景一 位移法的基本原理和典型方程
知识链接
下面介绍常见的单跨超静定梁在杆端的位移和荷载作用下杆端弯矩的计 算公式,即等截面直杆的转角位移方程。为方便计算,可参照表 3 – 2 和表 3 – 3 查出杆端位移所引起的杆端弯矩及荷载作用下引起的杆端弯 矩进行叠加计算。 ① 两端固定。超静定结构中,凡两端与刚结点或固定支座(固定端) 连接的杆件,均可看作是两端固定梁。
2.位移法的基本未知量和基本结构的确定 位移法的基本未知量为结点角位移和独立结点线位移。结点角位移未知量
的数目等于刚结点的数目。确定独立结点线位移未知量的数目时,假定受弯 直杆两端之间的距离在变形后仍保持不变,具体方法是“铰化结点,增设链 杆”,即将结构各刚性结点改为铰结点,并将固定支座改为固定铰支座,使 原结构变成铰结体系,使该铰结体系成为几何不变体系,所需增加的最少链 杆数就等于原结构独立结点线位移数目。位移法的基本未知量确定后,在每 个结点角位移处加入附加刚臂,沿每个独立结点线位移方向加入附加链杆, 所形成的单跨超静定梁的组合体即为位移法的基本结构。
计算:
① 单位位移 Δ1=1 单独作用于基本结构引起相应的约束反力为 k11 和 k21, 其相应弯矩图为M1 图(图 3 – 43a)。
② 单位位移 Δ2=1 单独作用于基本结构引起相应的约束反力为 k12 和 k22, 其相应弯矩图为M2 图(图 3 – 43b)。 ③ 荷载单独作用于基本结构引起相应的约束反力为 F1P 和 F2P,其相应弯 矩图为 MP 图(图3 – 43c)。
情景一 位移法的基本原理和典型方程
超静定结构两类解法

第六章位移法超静定结构两类解法:力法:思路及步骤,适用于所有静定结构计算。
结合位移法例题中需要用到的例子。
有时太繁,例。
别的角度:内力和位移之间的关系随外因的确定而确定。
→位移法,E,超静定梁和刚架。
于是,开始有人讨论:有没有别的方法来求解或换一个角度来分析…,what?我们知道,当结构所受外因(外荷载、支座位移、温度变化等)一定⇒内力一定⇒变形一定⇒位移一定,也就是结构的内力和位移之间有确定的关系(这也可以从位移的公式反映出来)。
力法:内力⇒位移,以多余力为基本未知量…,能否反过来,也就是先求位移⇒内力,即以结构的某些位移为基本未知量,先想办法求出这些位移,再求出内力。
这就出现了位移法。
目前通用的位移法有两种:英国的、俄罗斯的,两者的实质是相同的。
以结构的某些结点位移作为基本未知量,由静力平衡条件先求出他们,再据以求出结构的内力和其它位移。
这种方法可以用于求解一些超静定梁和刚架,十分方便。
例:上面的例子,用位移法求解,只有结点转角一个未知量。
下面,我们通过一个简单的例子来说明位移法的解题思路和步骤:一个两跨连续梁,一次超静定,等截面EI=常数,右跨作用有均布荷载q,(当然可以用力法求解),在荷载q作用下,结构会发生变形,无N,无轴向变形,B点无竖向位移,只有转角ϕB。
且B点是一个刚结点传递M;变形时各杆端不能发生相对转动和移动,刚结点所连接的杆件之间角度受力以后不变。
也就是AB、BC杆在结点B处的转角是相同的。
原结构的受力和变形情况和b是等价的。
B当作固定端又产生转角ϕB。
a(原结构)AB:BC:b如果把转角ϕB 当作支座位移这一外因看,则原结构的计算就可以变成两个单跨超静定梁来计算。
显然,只要知道ϕB ,两个单跨静定梁的计算可以用力法求解出全部反力和内力,现在的未知量是ϕB (位移法的基本未知量)。
关键:如何求ϕB ?求出ϕB 后又如何求梁的内力?又如何把a ⇒b 来计算? 我们采用了这样的方法:假定在刚结点B 附加一刚臂(▼),限制B 点转角,B ⇒固定端(无线位移,无转动)(略轴向变形)原结构就变成了AB 、BC 两个单跨超静定梁的组合体:AB : ,BC :但现在和原结构的变形不符,ϕB ,所以为保持和原结构等效,人为使B 结点发生与实际情况相同的转角ϕB (以Z 1表示,统一)。
超静定结构的位移计算

建筑力学
谢谢观看!
最后需要说明的是,在计算超静定结构的过 程中,经过的计算步骤和数学运算较多,比较容 易发生错误。为保证最后结果的正确性,校核工 作是十分重要的。最后内力图的校核,应从平衡 条件和变形条件两个方面进行:
正确的内力图首先要满足平衡条件。平衡条 件的校核 出结构的一部分都应满足平衡条件。
建筑力学
超静定结构的位移 计算
超静定结构的位移计算
超静定结构的位移计算和静定结构的位移计 算方法相同,即采用单位荷载法。由力法计算可 知,当多余未知力解出后,静定的基本结构在多 余未知力和荷载共同作用下的内力和变形是与原 结构的受力与变形完全一致的。因此,超静定结 构的位移计算问题可以转化为基本结构的位移计 算问题,即静定结构的位移计算问题。
正确的内力图还应该满足变形条件。因为计算 超静定结构内力时,除平衡条件外,还应用了变形 条件。特别是在力法中,多余未知力是由变形条件 求得的,因此,校核工作应以变形条件为重点。校 核变形条件的一般作法是,任意选取基本结构,任 意选取一个多余未知力Xi,然后根据最后的内力图 算出沿Xi方向的位移△i,并检查△i是否与原结构 中的相应位移(给定值)相等。
(a)
【解】 1)用力法求解,作出最后弯矩图如
图(b)所示。
2) 选取悬臂刚架为基本结构,将单位力施加
在基本结构上,绘出
M
图如图(c)所示。
1
(b)M图(kN m)
(c) M1图
3)按图乘法求结构的位移。
由M图与
M
图相乘,可得
1
1
11
21
ΔDV
EI
(10 2
2 2
10 2 2
3
2
2
20 4 2
自考结构力学_超静定结构的内力和位移
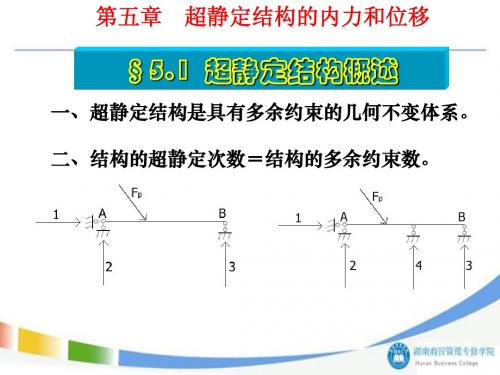
取C结点,如图6.12c所示,由∑y=0 得: 4 NCA = QCB = ql 7
取结点B,由∑X=0 ,已知 3 得 NBC = ql 7
3 x2 = ql 7
图6.12 求各杆轴力及剪力
三、力法典型方程
支座移动时的计算
X1
d11 X 1 d12 X 2 D1c = 0 h d 21 X 1 d 22 X 2 D 2c =
1、力法基本未知量 结构的多余约束中产生的多余未知力(简称多 余力)。
2、力法基本体系 力法基本结构,是原结构拆除多余约束后得到的 静定结构;力法基本体系,是原结构拆除多余约束 后得到的基本结构在荷载(原有各种因素)和多余 力共同作用的体系。
3、力法基本方程 力法基本体系在多余力位置及方向与原结构位移 一致的条件。 方程中的系数和自由项均是静定结构的位移计算 问题,显然,超静定转化为静定问题。
1 (d 11 ) k 25 X 1 = ql ( ) 32 5 X 1 = ql ( ) (c) 4
?
基 本 体 系
M图由M = M1 X1 M P 作出:
温度内力的计算
画出 M 1 , M 2 , N1 , N 2 图 计算
t1 t1 t2 t1 X1
t1 t2
梁刚架: 系 数 桁 架:
d d
d
M i yi = i ds= ii EI EI j yi Mi M j ds = ij = EI EI 2 N l = i ii EA
2
自由项
梁刚架:
桁 架:
d ij = EA M M ds D iP = EI
Ni N jl
d11 X1 d12 X 2 D1P = 0 d 21 X1 d 22 X 2 D2 P = 0
超静定结构-力法位移计算

M
3. 支座位移:
MMC EI
ds
FRCR
综合:
MM EI
ds
t0 SFN
t h
S M
FRCR
其中M为超静定结构在各种因素作用下产生的弯矩
详见教学视频“6.16荷载作用下超静定结构位移计算”
例1:求梁中点竖向位移ΔCV,EI为常数
q
ql2 12
第 六 章 力法
§6-8* 超静定结构位移计算
可取任意静定结构做为基本结构来计算超静定结构位移
施加单位荷载,计算单位荷载作用下的内力图 (M , FQ , FN )
1. 荷载作用:
MM EI
F
ds
2. 温度改变:
MMt EI
ds
t0SFN
t h
S
A
C
B
A
l/2
l/2
原结构
ql2 12
B
ql2 24
M图
CV
ql 4 384EI
()
例2:求图示刚架D结点水平位移ΔDH,各杆EI如图示。
C
D
/m
2EI
2EI 6m
31.5
A
B
6m
57.6
30.6
M图(kN m)
基本结构1
基本结构2
基本结构3
基本结构4
单位荷载施加在哪个基本结构更加简单?
EI l
线刚度
A
i
qA
B
2.等截面梁的载常数 荷载引起的杆端内力称为载常数(表7-1)
A
B
A
BA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
EI=常数
C
D L
A
L
E L
超静定结构的位移计算
计算实例
图示结构,各杆长都是 L,梁截面为矩形,截面高度h
。求(1)绘弯矩图(2)求杆 A 端转角 数为
L 10
,线膨胀系
-150 -150 +250
A
超静定结构的位移计算
计算实例 -150 -150 +250 X1 X2 基本体系
3750EI 解得: X 1 7 L2 218 .75EI X2 7 L2
EI
L
M
MP
1 1 EI EI 1 A L 535.17 535.17 317.14 L 694.29EI EI 2 l L 2
作出弯矩图。并求A点的竖向位移。画出变形图
P
C
B EI A L EI EI
D
4 EI KN 3 L
EI1
E L
L
P
1)取基本体系
X
EI EI
EI
4 EI KN 3 L
EI1
2)作M P、M1,求R1P , 11
P PL MP PL
4 EI KN 3 L
P
L
作M1图
L
4 EI KN 3 L
4 L3 11 3EI
1P 0
4)解力法方程
X=1
M
0
X=0
P PL MP
PL
4 EI KN 3 L
P
5)作M图 6)取基本结构 在A点作用PK=1 右两图图乘:
P PL
PL
KN
4 EI L3
P
1 1 2 1 7 PL3 AV L PL L P 1 EI 2 3 KN 12EI
L
4 EI KN 3 L
3)为求C处的竖向位移,在C处作用P=1
150
q
30 90
- 5 kN
MP
图乘
75 kN
6
P=1
M
P=1
不同基本体系时的位移计算
150
x1 x2
30 90
=
MP
P=1
M
3 P = 1
4) M图与M P图图乘,
CV 1800 EI
小结:超静定结构的位移计算: 1)选某基本体系作出超静定结构的弯矩图,作为MP图 2)任选该超静定结构的一种基本结构,在拟求位移 的位置作用单位力,作出 M 图
超静定结构的位移计算
引言: 超静定结构的位移计算不需要另外推导公式,在力法的计算 过程中,其方法已经存在了。 D 6m
A 6m C 6m
B
1)应用力法求解 150
q X1
30
90 X2
基本体系
弯矩图
X1=-5kN ,
X2=75kN
2)原结构“等价” 于基本体 系
q
- 5 kN
q
C
75 kN
两图的位移相同、受力相同
1 PK=1
7)变形图
P
计算实例
超静定结构的位移计算
-150 +250
3750EI 7 L2
-150
535.17
317.14
218 .75EI 7 L2 静定结构在温度、荷载共 同作用下的位移计算问题
单位:
I
L
弯矩图MP
计算实例
超静定结构的位移计算
535.17 317.14
为求A截面的转角,作P=1
P=1
单位:
1 1 6Pa 1 Pa 1 1 3Pa 7 Pa2 A a 1 a 1 1 a EI 2 44 2 4 44 176EI 2EI 2
力法测验题
1、取半结构
2、用力法计算图示结构作出弯矩图,并求D点水平位移
q
qL
5a 3 6 EI
M 2图
X1 3P 44
22
3a 3 12 21 4 EI
2P
17Pa3 48EI
16 P X2 44
X1
3P 44
EI
p
6Pa/44 3Pa/44
EI
2EI
16 P X2 44
3Pa/44 8Pa/44
M图
1 P=1
3) M图与M P图图乘结果就是所求的 位移。
计算实例 求A截面的转角
EI
p A EI
a
X1
EI
p
EI
2EI
a/2 a/2
a
2EI
X2
1)求出各系数,写力法方程 X1=1 Pa/2 EI P a EI 2EI M P图
3a 3 11 2 EI
1P 3Pa3 8EI
M 1图
X2=1 2a
