模糊逻辑理论及其MATLAB实现
利用Matlab进行模糊逻辑和模糊控制的基本原理
利用Matlab进行模糊逻辑和模糊控制的基本原理Matlab是一种强大的数学计算软件，广泛应用于各个领域的工程和科学研究。
在现实生活中，我们经常会遇到一些模糊不清、不确定的情况，而模糊逻辑和模糊控制正是用来处理这些模糊问题的有效工具。
本文将介绍利用Matlab进行模糊逻辑和模糊控制的基本原理，并通过一些具体案例来说明其在实际应用中的价值。
首先，我们需要了解模糊逻辑和模糊控制的基本概念和原理。
模糊逻辑是Lotfi Zadeh教授于1965年提出的一种处理模糊信息的形式化逻辑系统。
与传统的布尔逻辑只有两个取值（真和假）不同，模糊逻辑引入了模糊概念，可以处理多个取值范围内的逻辑判断。
其基本原理是将模糊的语言描述转化为数学上的模糊集合，然后通过模糊运算进行推理和决策。
在Matlab中，可以使用Fuzzy Logic Toolbox工具箱来进行模糊逻辑的建模和模拟。
该工具箱提供了一系列的函数和工具，可以帮助我们创建模糊逻辑系统、定义模糊集合和模糊规则，并进行输入输出的模糊化和去模糊化运算。
一个典型的模糊逻辑系统包括三个主要组成部分：模糊集合、模糊规则和模糊推理。
模糊集合用于描述模糊化的输入和输出变量，可以是三角形、梯形、高斯等形状。
模糊规则定义了模糊逻辑系统的推理过程，通常由一系列的if-then规则组成，如“如果温度较低，则输出加热”，其中“温度较低”和“加热”为模糊集合的标签。
模糊推理根据输入变量的模糊值和模糊规则，计算出输出变量的模糊值。
为了更好地理解模糊逻辑的原理和应用，我们以一个简单的案例来说明。
假设我们需要设计一个自动化灯光控制系统，使得灯光的亮度能够根据环境光线的强弱自动调节。
首先，我们需要收集一些实际的数据来建立模糊逻辑系统。
通过传感器测量到的环境光强度作为输入变量，设定的亮度值作为输出变量。
在Matlab中，可以使用Fuzzy Logic Designer来创建一个模糊逻辑系统。
首先，我们需要定义输入和输出变量，以及它们的模糊集合。
MATLAB中的模糊逻辑与模糊系统应用
MATLAB中的模糊逻辑与模糊系统应用引言：模糊逻辑是一种处理含糊和不确定性的推理方法，而模糊系统是基于模糊逻辑的一种工程应用。
在实际问题中，很多情况下无法准确界定事物的属性或关系，这就需要使用模糊逻辑和模糊系统进行描述和分析。
MATLAB作为一种强大的数学软件工具，提供了丰富的函数库和模块，可以非常方便地进行模糊逻辑和模糊系统的建模与分析。
本文将探讨MATLAB中的模糊逻辑与模糊系统应用，并介绍一些实际案例。
一、模糊逻辑的基本概念：1.1 模糊集合与隶属度函数在传统的逻辑中，事物的属性通常只有真和假两种取值，而在模糊逻辑中，属性被描述为一个介于[0,1]之间的隶属度。
模糊集合是指由一组对象组成的集合，每个对象在集合中的隶属度不是二进制的，而是介于0和1之间的实数。
隶属度函数是用来描述某个对象对于某个属性的隶属程度，通常使用三角形、梯形等形状的函数来表示。
1.2 模糊逻辑运算模糊逻辑中的运算方式与传统逻辑不同，引入了模糊的概念。
模糊逻辑运算包括交集、并集和补集等操作，用于描述模糊集合之间的关系。
这些运算可以通过模糊控制器、模糊推理等方式进行实现。
MATLAB提供了丰富的函数和工具箱来进行模糊逻辑运算和推理。
二、模糊系统的框架与建模过程：2.1 模糊系统的框架模糊系统通常由模糊化、模糊推理和去模糊化三个主要部分组成。
模糊化是将输入的实际值映射到模糊集合中，模糊推理是根据规则和隶属度函数进行推理，得出输出的模糊结果，去模糊化则是将模糊结果转化为实际值。
2.2 模糊系统的建模过程模糊系统的建模过程包括变量的模糊化、规则的定义、隶属度函数的设定以及模糊推理等步骤。
MATLAB提供了一系列的函数和工具箱用于模糊系统的建模和分析。
利用MATLAB的模糊工具箱，可以方便地进行隶属度函数的设定、规则的定义以及模糊推理的实现。
三、模糊逻辑与模糊系统在实际问题中的应用：3.1 模糊控制器模糊控制器是模糊逻辑和模糊系统的一种应用，它利用模糊推理和模糊系统来实现对控制系统的控制。
Matlab中的模糊逻辑与神经网络
Matlab中的模糊逻辑与神经网络引言近年来，随着计算机科学的快速发展，智能系统的研究也取得了巨大的进展。
其中，模糊逻辑和神经网络作为两种重要的智能系统模型，在现实世界的应用中展现出了巨大的潜力。
而在Matlab这一强大的科学计算软件中，模糊逻辑和神经网络的实现也变得更加便捷和高效。
本文将深入探讨Matlab中模糊逻辑与神经网络的基本原理、实现方法以及它们在应用中的潜力。
一、模糊逻辑1.1 模糊逻辑的基本原理模糊逻辑是建立在模糊集合理论基础上的一种扩展了传统二值逻辑的推理方法。
与传统的二值逻辑只有真和假两种可能性不同，模糊逻辑将事物的陈述表达为程度或概率的形式。
在模糊逻辑中，每个事物都有一个隶属度函数，表示它属于不同模糊集合的程度。
1.2 Matlab中的模糊逻辑工具箱为了便于模糊逻辑的建模和推理，Matlab提供了专门的模糊逻辑工具箱。
该工具箱包含了许多用于模糊集合操作、规则定义和推理等的函数和工具。
用户可以根据具体的需求，使用这些函数和工具快速构建模糊逻辑系统，并进行复杂的推理过程。
二、神经网络2.1 神经网络的基本原理神经网络是模拟人脑神经元间相互作用的一种计算模型。
它由大量的人工神经元（或称为节点）组成，这些神经元通过连接强度（或称为权重）相互连接。
神经网络具有自学习的能力，可以通过训练样本自动调整连接权重以实现任务的学习和推理。
2.2 Matlab中的神经网络工具箱与模糊逻辑类似，Matlab也提供了专门的神经网络工具箱，用于构建和训练神经网络模型。
这个工具箱包括了许多常用的神经网络模型，如前馈神经网络、循环神经网络和自组织神经网络等。
用户可以通过简单的调用这些函数和工具，实现各种复杂的神经网络任务。
三、Matlab中的模糊逻辑与神经网络的结合3.1 模糊神经网络模糊神经网络是将模糊逻辑和神经网络相结合的一种智能系统模型。
它通过在神经网络中引入模糊逻辑的概念，能够更好地处理不确定性和模糊性的问题。
方法二用MATLAB的模糊逻辑工具箱（Fuzzytoolbox）实现.
⽅法⼆⽤MATLAB的模糊逻辑⼯具箱（Fuzzytoolbox）实现.⽅法⼆：⽤MATLAB的模糊逻辑⼯具箱(Fuzzy toolbox)实现（陈⽼师整理）⼀、模糊逻辑推理系统的总体特征模糊控制由于不依赖对象的数学模型⽽受到⼴泛的重视，计算机仿真是研究模糊控制系统的重要⼿段之⼀。
由Math Works公司推出的Matlab软件，为控制系统的计算机仿真提供了强有⼒的⼯具，特别是在Matlab4.2以后的版本中推出的模糊⼯具箱(Fuzzy Toolbox)，为仿真模糊控制系统提供了很⼤的⽅便。
由于这样的模块都是由相关领域的著名学者开发的，所以其可信度都是很⾼的，仿真结果是可靠的。
在Simulink环境下对PID控制系统进⾏建模是⾮常⽅便的，⽽模糊控制系统与PID控制系统的结构基本相同，仅仅是控制器不同。
所以，对模糊控制系统的建模关键是对模糊控制器的建模。
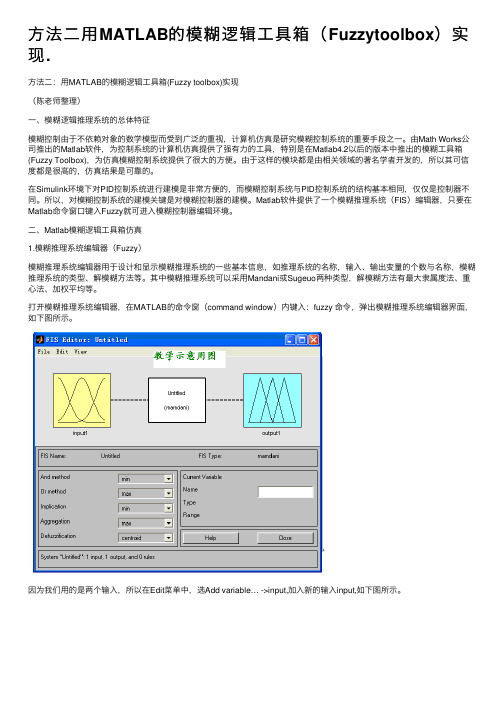
Matlab软件提供了⼀个模糊推理系统（FIS）编辑器，只要在Matlab命令窗⼝键⼊Fuzzy就可进⼊模糊控制器编辑环境。
⼆、Matlab模糊逻辑⼯具箱仿真1.模糊推理系统编辑器（Fuzzy）模糊推理系统编辑器⽤于设计和显⽰模糊推理系统的⼀些基本信息，如推理系统的名称，输⼊、输出变量的个数与名称，模糊推理系统的类型、解模糊⽅法等。
其中模糊推理系统可以采⽤Mandani或Sugeuo两种类型，解模糊⽅法有最⼤⾪属度法、重⼼法、加权平均等。
打开模糊推理系统编辑器，在MATLAB的命令窗（command window）内键⼊：fuzzy 命令，弹出模糊推理系统编辑器界⾯，如下图所⽰。
因为我们⽤的是两个输⼊，所以在Edit菜单中，选Add variable… ->input,加⼊新的输⼊input,如下图所⽰。
选择input(选中为红框),在界⾯右边⽂字输⼊处键⼊相应的输⼊名称，例如,温度输⼊⽤tmp-input, 磁能输⼊⽤ mag-input，等。
如何利用Matlab进行模糊逻辑控制
如何利用Matlab进行模糊逻辑控制Matlab是一种流行的数学软件，广泛应用于科学和工程领域。
其中一个强大的功能是模糊逻辑控制，它可以帮助人们解决模糊问题。
本文将介绍如何利用Matlab进行模糊逻辑控制，以及其在实际应用中的价值和局限性。
1. 什么是模糊逻辑控制？模糊逻辑控制是一种基于模糊推理的控制方法。
与传统的二值逻辑不同，模糊逻辑可以处理模糊的、不确定的信息。
它将模糊集合和模糊规则引入到控制系统中，使得系统能够根据输入数据和模糊规则进行推理，并输出相应的控制信号。
2. Matlab中的模糊逻辑工具箱Matlab提供了强大的模糊逻辑工具箱，可以用于模糊逻辑控制系统的设计和仿真。
该工具箱包含了模糊集合的定义、模糊规则的建立、模糊控制器的设计等功能。
用户可以通过简单的命令和图形界面进行操作，快速构建模糊逻辑控制系统。
3. 模糊集合的定义模糊集合是模糊逻辑的基础，它用来描述对于一个特定的输入值，它属于某个特定集合的程度。
在Matlab中，我们可以使用模糊集合来定义输入和输出的隶属度函数。
例如，对于一个温度控制系统，我们可以定义一个“冷”的模糊集合和一个“热”的模糊集合，它们分别代表了输入量的不同程度。
4. 模糊规则的建立在模糊逻辑控制系统中，模糊规则用于描述输入和输出之间的关系。
在Matlab 中，我们可以使用模糊规则来定义输入值和输出值之间的映射关系。
例如，对于一个简单的车速控制系统，我们可以定义一个模糊规则，如“如果车速较慢，则增加油门”的规则。
通过组合多个模糊规则，可以构建一个复杂的控制策略。
5. 模糊控制器的设计在Matlab中，我们可以使用模糊控制器对象来设计和实现模糊逻辑控制系统。
模糊控制器对象包含了输入集合、输出集合、模糊规则库等属性，以及推理和解糊过程的方法。
用户可以根据系统需求和实际问题，选择合适的模糊集合、模糊规则和解糊方法，设计出一个有效的模糊控制器。
6. 模糊逻辑控制的应用模糊逻辑控制在实际应用中具有广泛的应用价值。
模糊控制介绍及Matlab模糊控制工具箱使用
模糊控制介绍及Matlab模糊控制工具箱使用目录•一、模糊控制的产生•二、模糊逻辑的理论基础•三、模糊控制Matlab工具箱示例•四、模糊控制的基本思想•五、模糊控制器的基本结构•六、模糊控制器的优缺点一、模糊控制的产生在传统控制领域，对于明确系统有强而有力的控制能力，即被控系统的动态信息越详细，越能达到精确控制的目的。
然而，在多变量、非线性的复杂系统中，往往难以完全描述系统的动态信息。
此时，传统的控制理论则显得无能为力，而有经验的专家或工作人员仍能根据长期实践观察和操作经验进行有效控制。
据此引申，是否可将人的操作经验总结为若干条控制规则以避开复杂模型的建立过程？模糊控制最重要的特征是反应人们的经验及推理规则，而这些经验和推理规则是通过自然语言来表达的，如“水温上升过快，则关小燃气阀”。
在控制系统初期，由于对系统缺乏了解，控制效果可能不好，但若干次探索后终能实现预期的控制，这就是经验对模糊控制系统的重要性。
由于模糊控制实质上是用计算机去执行人的控制策略，因而可以避开复杂模型的建立，对人们关于某个控制问题的成功和失败经验加工，总结出知识，从中提炼出控制规则，实现复杂系统的控制。
PS：“模糊”是人类感知万物，获取知识，思维推理，决策实施的重要特征。
“模糊”比“清晰”所拥有的信息量更大，更符合客观世界。
二、模糊逻辑的理论基础模糊逻辑是指模仿人脑不确定性的概念判断和推理思维，对于定性的知识和经验，借助隶属度概念、模糊集合，来处理模糊关系。
模糊逻辑实质上是要对模糊性对象进行精确描述和处理。
模糊逻辑的目的是将一个输入空间映射到一个输出空间，主要要靠一系列的if－then规则。
这些规则包含变量和描述这些变量的形容词，被平行评估，因此它们的顺序不重要。
在进行模糊推理之前，先要定义好输入和输出变量以及描述它们的形容词。
模糊推理的流程如下图所示。
模糊推理流程2.1、模糊集合普通情况下，元素a属于集合A（1）或不属于集合A（0），如下图所示，星期一和星期三都是工作日，而苹果和星星则不是。
Matlab中的模糊逻辑控制方法
Matlab中的模糊逻辑控制方法引言模糊逻辑控制（FLC）是一种常用的控制方法，在很多实际应用中得到了广泛的应用。
Matlab作为一种功能强大的数学计算和工程仿真软件，提供了丰富的工具和函数来支持模糊逻辑控制的设计和实现。
本文将介绍Matlab中的模糊逻辑控制方法及其应用。
一、模糊逻辑控制的基本概念模糊逻辑控制是一种基于模糊逻辑原理的控制方法，它可以处理不确定性信息和模糊概念，适用于那些难以建立精确数学模型的控制系统。
模糊逻辑控制系统由四个基本部分组成：模糊化、推理、解模糊和规则库。
1.1 模糊化模糊化是将输入量从实际值转化为模糊集合的过程。
在Matlab中，可以使用fuzzifier函数将实际输入映射到模糊集合上。
模糊集合可以通过一些参数来描述，如三角形型、梯形型、高斯型等。
1.2 推理推理是根据模糊集合的规则进行推导，得到系统的输出。
在Matlab中，可以使用inference函数进行推理。
推理的方法有三种：基于规则的推理、基于模糊集合的推理和基于模型的推理。
根据应用的需求和系统的复杂程度，可以选择不同的推理方法。
1.3 解模糊解模糊是将模糊输出转化为实际值的过程。
在Matlab中，可以使用defuzzifier 函数进行解模糊。
常用的解模糊方法有：最大值法、平均值法、面积法等。
1.4 规则库规则库是模糊逻辑控制系统的核心，它包含了一系列的模糊规则，用来描述输入和输出之间的关系。
在Matlab中，可以使用fuzzy规则对象来定义规则库。
规则库的设计是模糊逻辑控制系统设计中的关键一步，直接影响系统的性能和稳定性。
二、Matlab中的模糊逻辑控制工具箱Matlab提供了专门的工具箱，用于支持模糊逻辑控制系统的设计和实现。
这个工具箱包含了一些常用的函数和工具，能够帮助用户更加方便快捷地进行模糊逻辑控制系统的设计和仿真。
2.1 模糊逻辑控制系统设计工具Matlab的模糊逻辑控制系统设计工具提供了一种用户友好的可视化界面，用于设计和编辑模糊逻辑控制系统。
模糊推理的MATLAB实现
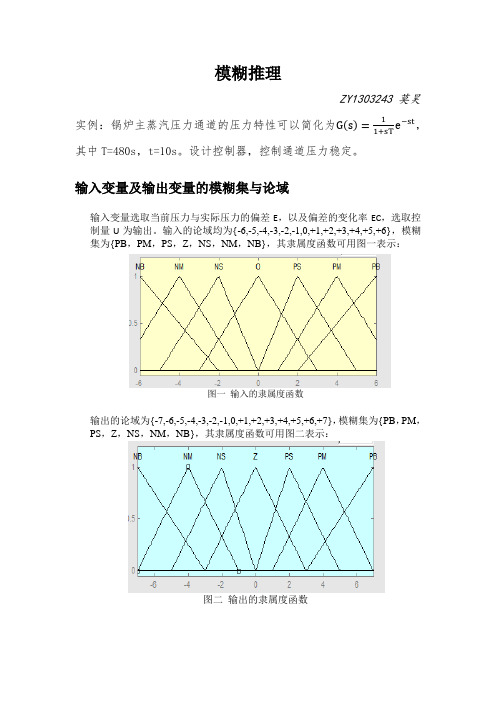
模糊推理ZY1303243 莫昊e−st，实例：锅炉主蒸汽压力通道的压力特性可以简化为G s=11+sT其中T=480s，t=10s。
设计控制器，控制通道压力稳定。
输入变量及输出变量的模糊集与论域输入变量选取当前压力与实际压力的偏差E，以及偏差的变化率EC，选取控制量U为输出。
输入的论域均为{-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6}，模糊集为{PB，PM，PS，Z，NS，NM，NB}，其隶属度函数可用图一表示：图一输入的隶属度函数输出的论域为{-7,-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6,+7}，模糊集为{PB，PM，PS，Z，NS，NM，NB}，其隶属度函数可用图二表示：图二输出的隶属度函数2．模糊推理的规则模糊控制规则的确定不依赖于控制对象的数学模型，而是对熟练操作者理论知识和实践经验的总结一般可将模糊控制规则表达为如下方式：If E is PB and EC is PB then U is NBIf E is NS and EC is NM then U is PM。
可写成表一的形式表示3．模糊化和解糊策略在求得误差和误差变化的模糊集 E 和EC 后,控制量的模糊集U 可由模糊推理综合算法求得：U=E×EC·R式中，R 为模糊关系矩阵。
控制量的模糊集U可变换为精确值，见表二：表二模糊控制表4.模糊控制仿真利用上述模糊推理规则构建模糊控制器，对锅炉主蒸汽压力通道进行控制仿真：图三仿真控制结构图图四仿真结果图5.结论当无法建立条件与结论之间的准确数学关系时，模糊推理是一种方便、有效的方法，但是模糊控制也有其局限性：1、专家控制知识不一定完全正确，这会导致模糊推理的结论不一定准确；2、模糊推理以及模糊控制的精度不高，从例子中可以看出，控制结果中存在一定的稳态误差。
使用Matlab进行模糊逻辑分析的技巧
使用Matlab进行模糊逻辑分析的技巧引言：在现代科学中，逻辑分析在决策、控制系统和模糊推理等领域发挥着重要的作用。
模糊逻辑是一种能够处理复杂和不确定的问题的有效工具。
而Matlab作为一种功能强大的数学软件，也提供了丰富的工具和函数来支持模糊逻辑的建模和分析。
本文将介绍使用Matlab进行模糊逻辑分析的一些技巧和实例。
一、安装模糊逻辑工具箱Matlab提供了自带的模糊逻辑工具箱，可以通过Matlab的插件管理器进行安装。
打开Matlab后，在工具栏中选择"Add-Ons"，然后在搜索框中输入"模糊逻辑工具箱"，点击搜索按钮，选择合适的版本进行安装。
安装完成后，即可在工具箱中找到并使用模糊逻辑相关的函数和工具。
二、建立模糊逻辑系统使用Matlab进行模糊逻辑分析的第一步是建立一个模糊逻辑系统。
可以使用命令"fuzzy"创建一个模糊逻辑系统对象，然后使用该对象进行后续的分析。
例如，创建一个简单的三角形隶属函数的模糊逻辑系统对象：```matlabfis = fuzzyfis = addInput(fis,[0 10],'Name','input1')fis = addOutput(fis,[0 20],'Name','output1')fis = addMF(fis,'input1','trimf',[2 5 7])fis = addMF(fis,'output1','trimf',[4 10 16])```上述代码创建了一个输入变量input1和一个输出变量output1，并添加了三角形隶属函数。
通过这种方式，可以根据实际问题的需求建立模糊逻辑系统。
三、设置模糊规则在模糊逻辑系统中，模糊规则是描述输入和输出之间关系的关键。
Matlab中的模糊逻辑与模糊控制技术
Matlab中的模糊逻辑与模糊控制技术引言:在现代科技快速发展的今天，计算机技术被广泛应用于各个领域。
Matlab作为一种流行的计算机编程环境，为工程师和科学家提供了一个强大的工具，用于解决各种复杂的问题。
本文将重点介绍Matlab中的模糊逻辑与模糊控制技术，并探讨其在实际应用中的重要性和优势。
一、模糊逻辑的概念和基本原理1.1 模糊逻辑的起源和发展模糊逻辑起源于20世纪60年代，由于传统的二值逻辑只能处理确定性的问题，对于一些带有不确定性和模糊性的问题处理能力有限。
模糊逻辑的提出填补了这个空白，使得计算机能够处理更加复杂的问题。
1.2 模糊逻辑的基本原理模糊逻辑是一种基于模糊集合的数学理论，它通过模糊化和解模糊化的过程将模糊的问题转化为可以计算的问题。
模糊逻辑使用隶属度函数来描述事物或条件的模糊性，通过模糊推理的方法来模拟人类的思维方式，以便进行决策、控制和模型建立等任务。
二、Matlab中的模糊逻辑工具箱2.1 Matlab中的模糊逻辑工具箱的介绍Matlab提供了一个专门的工具箱，用于支持模糊逻辑的建模、推理和控制等任务。
这个工具箱提供了一系列的函数和工具，方便用户使用模糊逻辑进行建模和分析。
2.2 Matlab中的模糊逻辑工具箱的功能和特点Matlab的模糊逻辑工具箱具有易用性和灵活性，用户可以根据自己的需求选择不同的模糊逻辑引擎和推理方法。
该工具箱提供了可视化界面，方便用户进行模糊集合和规则的定义，以及结果的可视化和分析。
三、模糊控制技术在Matlab中的应用3.1 模糊控制系统的建立和仿真通过Matlab中的模糊逻辑工具箱，用户可以方便地建立和仿真模糊控制系统。
用户可以定义输入、输出的隶属度函数和规则库，然后进行仿真和分析。
3.2 模糊控制系统的优化和调整Matlab提供了一些优化算法，可以用于模糊控制系统的参数优化和调整。
用户可以使用这些算法，根据实际需求调整模糊控制系统的参数，以满足控制要求。
MATLAB模糊逻辑与控制方法与实践
MATLAB模糊逻辑与控制方法与实践近年来，人工智能和机器学习技术得到了广泛的应用和发展。
其中，模糊逻辑和模糊控制是一种用来处理不确定性和模糊性信息的重要方法。
作为一种数学工具和计算工具，MATLAB在模糊逻辑与控制方法的研究和应用中发挥了重要的作用。
本文将以MATLAB为工具，系统全面地介绍模糊逻辑与控制的原理、方法和实践应用。
一、模糊逻辑的原理与方法模糊逻辑是一种处理模糊信息和模糊关系的数学理论和方法。
传统的逻辑只能处理清晰和确定的关系，而模糊逻辑则可以用来处理不确定和模糊的关系。
模糊集合、模糊关系和模糊推理是模糊逻辑的基本概念和方法。
在MATLAB中，可以利用模糊逻辑工具箱来实现模糊集合和模糊关系的定义和运算。
通过定义模糊集合的隶属函数，可以描述一个对象属于某个模糊集合的程度。
常见的隶属函数包括三角函数、高斯函数等，可以根据实际问题选择合适的隶属函数。
而模糊关系可以通过模糊矩阵来表示，矩阵中的元素表示不同模糊集合之间的关系。
模糊推理是模糊逻辑中的关键技术之一。
在MATLAB中，可以利用模糊规则推理引擎来实现模糊推理。
通过定义一组模糊规则，可以实现从输入到输出的模糊推理过程。
常见的模糊推理方法包括模糊逻辑控制和模糊推理系统。
模糊逻辑控制是一种基于模糊规则的控制方法，可以应用于各种系统的控制问题。
而模糊推理系统则是一种更加通用的模糊推理方法，可以应用于非控制问题的模糊推理和决策。
二、模糊控制的原理与方法模糊控制是一种基于模糊逻辑的控制方法，主要用于处理不确定和模糊的系统。
模糊控制包括模糊建模、模糊推理和模糊控制器设计三个主要步骤。
在MATLAB中，可以利用模糊逻辑工具箱来实现模糊控制的设计和仿真。
通过建立模糊模型，可以将系统的输入和输出用模糊集合表示，从而形成模糊规则。
模糊模型的建立可以基于系统的经验数据或者专家知识，可以采用最小二乘法、最大似然法等方法进行参数估计。
模糊推理是模糊控制的核心，通过模糊规则和模糊推理引擎，将模糊输入转化为模糊输出。
Matlab技术在模糊逻辑中的应用
Matlab技术在模糊逻辑中的应用近年来，模糊逻辑成为了人工智能领域中一项重要的技术和工具。
而Matlab作为一款强大的科学计算软件，已经成为了模糊逻辑研究中广泛使用的工具之一。
本文将探讨Matlab技术在模糊逻辑中的应用，从理论到实践，从基础概念到具体案例，为读者全面介绍Matlab在模糊逻辑领域的强大之处。
第一部分：模糊逻辑基础为了更好地理解Matlab在模糊逻辑中的应用，首先需要了解模糊逻辑的基本概念和原理。
模糊逻辑是一种用来处理不精确或不确定性信息的逻辑系统。
与传统的布尔逻辑只有真和假两种取值不同，模糊逻辑引入了介于0和1之间的模糊概念。
在Matlab中，模糊逻辑的基础是模糊集合和模糊推理。
模糊集合是一种描述不确定性的数学工具，它通过隶属函数来表示元素与模糊集合之间的关系。
而模糊推理则是通过一定的规则和推理机制，基于输入和已知知识来进行推断。
第二部分：Matlab中的模糊逻辑工具箱为了帮助用户更方便地应用模糊逻辑技术，Matlab提供了强大的模糊逻辑工具箱。
该工具箱包含了一系列用于模糊集合表示、模糊推理和模糊控制的函数和算法。
在模糊集合表示方面，Matlab提供了丰富的隶属函数类型，包括三角函数、高斯函数、梯形函数等。
用户可以根据实际应用需求选择合适的函数类型，并利用Matlab提供的函数进行隶属度计算和模糊集合的操作。
在模糊推理和控制方面，Matlab提供了多种推理方法，如模糊关联规则、模糊推理机、模糊神经网络等。
用户可以根据问题的复杂度和实际情况选择合适的方法，并利用Matlab提供的函数进行推理和控制操作。
第三部分：Matlab在模糊逻辑应用领域的案例分析为了更直观地了解Matlab在模糊逻辑应用领域的具体应用，本文将以一个实际案例进行分析。
假设我们要设计一个模糊控制器来控制一辆无人驾驶汽车。
首先，我们需要确定输入、输出和规则库。
然后，通过Matlab工具箱提供的模糊集合表示和模糊推理方法，将输入信号映射到相应的模糊集合，并通过规则库进行推理和控制。
Matlab中的模糊逻辑控制技术介绍
Matlab中的模糊逻辑控制技术介绍引言在科技不断进步的今天，计算机和软件工具已经成为了各个领域中不可或缺的一部分。
对于工程领域而言，控制技术一直是研究的热点之一。
而模糊逻辑控制技术作为一种重要的控制方法，被广泛应用在各个领域，其中包括机器学习、人工智能、自动化等等。
本文将介绍在Matlab中如何使用模糊逻辑控制技术进行控制，同时结合实例来说明其应用的具体步骤和流程。
一、模糊逻辑控制的基本原理模糊逻辑控制是一种模拟人的思维方式，将人类对实际世界的认知抽象为一定的规则，然后通过使用模糊推理来实现控制。
模糊逻辑控制的基本原理是将模糊数学理论应用于控制系统中，通过建立模糊规则数据库和模糊推理机制，实现对系统输入和输出之间的模糊关系的表达和推理。
二、Matlab中的模糊逻辑控制工具箱Matlab是一款非常流行的科学计算软件，其提供了丰富的工具箱，用于实现各种控制算法。
其中，模糊逻辑工具箱（Fuzzy Logic Toolbox）是实现模糊逻辑控制的强大工具之一。
该工具箱提供了用于设计、模拟和分析模糊控制系统的函数和界面，使得使用模糊逻辑控制技术变得更加简单和方便。
三、模糊逻辑控制的设计步骤1. 确定模糊逻辑控制系统的输入和输出在设计模糊逻辑控制系统之前，首先需要明确该系统的输入和输出。
输入通常是一些描述系统状态的变量，如温度、湿度等，输出通常是一些控制变量，如马达转速、电压等。
明确输入和输出有助于建立系统的数学模型，并为后续的划分模糊集合提供参考。
2. 确定模糊集合及其隶属度函数在模糊逻辑控制中，对于每一个输入和输出变量都需要划分出若干个模糊集合，并为每个模糊集合定义一个隶属度函数。
隶属度函数描述了某一个值在某个模糊集合中的隶属程度。
Matlab提供了一些函数，如trimf、trapmf等，用于定义不同形状的隶属度函数。
3. 构建模糊规则库模糊规则库是模糊逻辑控制系统的核心，它由一系列的模糊规则组成。
每条模糊规则由若干个前提条件和一个结论组成，描述了输入和输出之间的关系。
如何在MATLAB中进行模糊控制
如何在MATLAB中进行模糊控制模糊控制是一种基于模糊逻辑理论的控制方法，它通过建立模糊规则、模糊集合和模糊推理等步骤，实现对复杂系统的控制。
在MATLAB中，我们可以利用模糊控制工具箱进行模糊控制设计和仿真。
本文将从模糊控制的基本原理、MATLAB中的模糊控制工具箱的使用以及实例应用等方面进行讨论。
一、模糊控制基本原理模糊控制的基本原理是将人类的经验和模糊逻辑理论应用于系统控制中。
它不需要准确的数学模型，而是通过模糊集合、模糊规则和模糊推理等方法来描述和制定控制策略。
下面我们将简要介绍一下模糊控制中的基本概念。
1. 模糊集合模糊集合是一种可以容纳不确定性的集合。
与传统集合论不同，模糊集合中的元素可以部分地、模糊地属于该集合。
在模糊控制中，我们通常使用隶属度函数来描述元素对模糊集合的隶属程度。
2. 模糊规则模糊规则是一种将输入和输出间的关系表示为一组语义规则的方法。
它基于专家的经验和知识，将输入变量的模糊集合与输出变量的模糊集合之间建立映射关系。
模糊规则通常采用IF-THEN的形式表示，例如：“IF 温度冷 AND 湿度高 THEN 空调制冷”。
3. 模糊推理模糊推理是基于模糊规则进行推理和决策的过程。
它通过对模糊集合的隶属度进行运算，计算出输出变量的模糊集合。
常用的推理方法有模糊关联、模糊交集和模糊合取等。
二、MATLAB中的模糊控制工具箱MATLAB提供了一套完整的模糊控制工具箱，包括模糊集合的创建、模糊规则的定义、模糊推理和模糊控制系统的仿真等功能。
下面我们将逐步介绍这些功能的使用方法。
1. 模糊集合的创建在MATLAB中，我们可以使用fuzzymf函数来创建模糊集合的隶属度函数。
该函数可以根据用户指定的类型和参数生成不同形状的隶属度函数。
常用的隶属度函数有三角型函数、梯形函数和高斯型函数等。
2. 模糊规则的定义在MATLAB中，我们可以使用addrule函数来定义模糊规则。
该函数将用户指定的输入变量、模糊集合和输出变量、模糊集合之间的关系转化为模糊规则，并添加到模糊推理系统中。
如何进行模糊控制的Matlab实现
如何进行模糊控制的Matlab实现模糊控制是一种基于模糊逻辑的控制方法，它能够在复杂的环境下进行精确的控制。
在现实世界中，很多问题存在不确定性和模糊性，传统的控制方法很难解决这些问题。
而模糊控制通过建立模糊规则来模拟人的思维过程，能够灵活地应对这些问题。
Matlab是一种功能强大的科学计算软件，它提供了丰富的工具箱和函数，可以帮助我们快速实现模糊控制算法。
本文将介绍如何使用Matlab进行模糊控制的实现，并结合一个实际案例进行说明。
首先，我们需要了解模糊控制的基本原理。
模糊控制是基于模糊逻辑进行推理和决策的一种方法。
它将输入和输出的模糊集合表示为隶属度函数，并通过模糊规则对模糊输入进行推理，得到模糊输出。
最后，将模糊输出通过去模糊化方法转换为具体的控制量。
在Matlab中，可以使用Fuzzy Logic Toolbox工具箱来实现模糊控制。
首先，需要定义输入和输出的模糊集合。
可以使用trimf函数来定义三角形隶属度函数，也可以使用gaussmf函数来定义高斯隶属度函数。
然后，需要定义模糊规则。
可以使用fuzarith函数来定义规则的操作，如AND、OR、NOT等。
最后，使用evalfis 函数对输入进行推理，得到模糊输出。
接下来，我们以温度控制为例，介绍如何使用Matlab进行模糊控制的实现。
假设我们要设计一个模糊控制器来控制一个房间的温度，使其尽可能接近一个设定的目标温度。
首先，定义输入的模糊集合和隶属度函数。
假设输入是当前的温度，模糊集合包括"冷"、"舒适"和"热"三个隶属度函数。
可以使用trimf函数来定义这些隶属度函数。
然后，定义输出的模糊集合和隶属度函数。
假设输出是空调的功率，模糊集合包括"低"、"中"和"高"三个隶属度函数。
同样，可以使用trimf函数来定义这些隶属度函数。
Matlab中的模糊逻辑应用技术
Matlab中的模糊逻辑应用技术引言:Matlab是一种广泛应用于科学研究与工程技术的数学软件，而模糊逻辑则是一种应用于各个领域的有效工具。
本文将探讨如何在Matlab中应用模糊逻辑技术，以提高问题的解决能力和决策质量。
通过具体的案例分析和实践经验，我们将深入探讨模糊逻辑的原理、模糊集合的建立、模糊推理的实现等方面的内容。
一、模糊逻辑的原理和概念传统的逻辑处理方法是基于精确度的，即通过确定的规则和条件来进行精确的判断和推理。
然而，在现实世界中，很多问题是模糊和不确定的，我们难以用精确的语言来描述和处理。
因此，模糊逻辑就应运而生了。
模糊逻辑是一种扩展了传统逻辑的数学工具，它能够处理模糊和不确定的信息，使得我们能够更好地处理模糊性的问题。
模糊逻辑的核心概念是模糊集合和隶属度。
在传统的逻辑中，一个元素要么属于某个集合，要么不属于某个集合。
而在模糊逻辑中，一个元素可以以一定的隶属度属于一个集合。
通过隶属度函数，我们可以将一个元素与多个集合进行模糊划分，并计算它与每个集合的隶属度。
二、模糊集合的建立与表示在Matlab中，我们可以通过编写代码或使用模糊逻辑工具箱来建立和表示模糊集合。
模糊逻辑工具箱提供了一系列函数，用于创建和操作模糊集合。
我们可以通过指定隶属度函数的形状、参数和范围来定义一个模糊集合。
常见的隶属度函数包括三角函数、梯形函数、高斯函数等。
通过调整参数和形状，我们能够准确地描述元素与模糊集合的隶属度关系。
三、模糊推理的实现与应用模糊推理是模糊逻辑的核心应用之一，它通过推理规则和条件来做出模糊决策。
在Matlab中，我们可以使用模糊推理工具箱来实现模糊推理。
模糊推理工具箱提供了一系列函数和方法，用于定义和运行模糊推理系统。
模糊推理系统由输入、输出和规则三部分组成。
输入是通过模糊化处理将精确的输入转化为模糊集合，输出是通过去模糊化处理将模糊的输出转化为精确的结果。
规则是系统的核心，它由一系列条件和结论组成。
模糊控制的MATLAB实现具体过程(强势吐血推荐)
例：a=newfis(‘tipper’); a=addvar(a,’input’,’service’,[0 10]); a=addmf(a,’input’,1,’poor’,’guassmf’,[1.5 0]); a=addmf(a,’input’,1,’good’,’guassmf’,[1.5 5]); a=addmf(a,’input’,1,’excellent’,’guassmf’,[1.5 10]); plot(a,’input’,1)
如果输入U是M*N矩阵，则系统是N输入的， 返回的Y是M*L矩阵，L是系统的输出的数目。
例：fis=readfis(‘tipper’); out=evalfis([2 1; 4 9],fis)
输出结果：out=7.0169 19.6810
MATLAB模糊控制系统设计实例1
一、设计目的：了解用MATLAB模糊工具箱的图形界面可视化 工具实现模糊控制系统的方法。
例： x=0:0.1:10; y=smf(x, [2 8]); plot(x,y) xlable(‘smf,P=[2 8]’)
2、模糊逻辑系统输入输出变量及隶属度函数的添加 ①函数addvar 功能：向模糊推理系统中添加语言变量。 格式：a=addvar(a, varType, varName, varBounds)
②函数showrule
格式：showrule(fis)
showrule(fis,indexlist)
showrule(fis,indexlist,format)
说明：fis为模糊推理系统矩阵变量的名称；indexlist为 规则编号，可以以向量形式指定显示多条规则； format为显示方式，有三种显示方式，即语句方式 （verbose），符号方式（symbolic）和索引方式 （indexed）。
使用Matlab进行模糊逻辑系统设计与仿真
使用Matlab进行模糊逻辑系统设计与仿真引言：现代科技的发展迅速，计算机和人工智能在我们的生活中发挥着越来越重要的作用。
模糊逻辑是一种可以处理不确定性和模糊信息的推理方法，广泛应用于控制系统、决策支持系统等领域。
而Matlab作为一种功能强大、易于使用的科学计算软件，为我们提供了丰富的功能和工具来进行模糊逻辑系统的设计与仿真。
本文将介绍如何使用Matlab进行模糊逻辑系统的设计与仿真，并探讨其应用前景。
第一部分：模糊逻辑基础在进入Matlab的应用前，我们先简要介绍一下模糊逻辑的基本概念和原理。
模糊逻辑是建立在模糊集合理论基础上的一种推理方法，它不同于传统的二值逻辑，可以处理模糊、不确定性的问题。
模糊逻辑系统由模糊化、表达式建立、推理和去模糊化四个部分组成。
第二部分：Matlab的应用2.1 模糊逻辑工具箱Matlab提供了强大的模糊逻辑工具箱，该工具箱包含了众多的模糊逻辑函数和算法，方便我们进行模糊逻辑系统的设计与仿真。
我们可以通过命令窗口直接调用这些函数，也可以使用GUI界面进行可视化操作。
2.2 模糊集合的定义与模糊化在Matlab中，我们可以使用模糊集合来表示模糊概念。
模糊集合包括两个主要组成部分：隶属函数和隶属度。
隶属函数描述了元素对于该概念的隶属程度，而隶属度表示了元素属于该概念的程度。
Matlab提供了丰富的方法来定义和操作模糊集合，我们可以使用类似“trimf”、“gaussmf”等函数来定义不同形状的隶属函数。
2.3 模糊推理与规则建立在模糊逻辑系统中，推理是非常重要的一部分。
Matlab提供了一些函数和算法来进行模糊推理，如模糊推理引擎FIS对规则库进行匹配和推理操作。
我们可以使用Matlab来建立和优化模糊规则库，提高系统的推理准确性和效率。
2.4 模糊系统的仿真与评估一旦建立了模糊逻辑系统，我们就可以使用Matlab进行仿真和评估。
Matlab提供了强大的绘图函数和工具，可以将模糊逻辑系统的输入输出关系进行可视化展示。
如何使用Matlab进行模糊逻辑控制系统设计
如何使用Matlab进行模糊逻辑控制系统设计使用Matlab进行模糊逻辑控制系统设计摘要：模糊逻辑控制是一种模拟人类认知规则和思维方式的控制方法。
它可以处理不确定性和模糊性，并在不确定的环境中实现智能控制。
本文将介绍如何利用Matlab软件进行模糊逻辑控制系统设计，包括模糊逻辑原理、建立模糊控制器、模糊推理和控制器的优化。
1. 引言2. 模糊逻辑原理2.1 模糊集合和隶属函数2.2 模糊规则2.3 模糊推理3. 建立模糊控制器3.1 输入和输出变量定义3.2 规则库的建立3.3 建立模糊控制器4. 模糊推理4.1 模糊化4.2 模糊推理4.3 去模糊化5. 模糊控制器的优化5.1 控制器参数优化5.2 控制规则优化6. 实例分析7. 结论1. 引言现代工业控制系统中，需要根据不确定性和模糊性的环境来实现自适应和智能的控制。
模糊逻辑控制是一种基于模糊集合和模糊规则的控制方法，能够处理模糊的输入和模糊的输出。
Matlab是一款功能强大的数学软件，提供了丰富的工具箱用于模糊逻辑控制系统的设计和模拟。
在本文中，我们将介绍如何使用Matlab进行模糊逻辑控制系统设计的方法和步骤。
2. 模糊逻辑原理2.1 模糊集合和隶属函数模糊逻辑控制的核心是模糊集合和隶属函数的定义和运算。
模糊集合是一种特殊的集合，其中的元素具有模糊性和不确定性，可以用隶属函数来表示。
隶属函数描述了一个元素对一个模糊集合的隶属程度，通常以曲线、图像或数学方程的形式表示。
2.2 模糊规则模糊规则是模糊逻辑控制的基本规则。
它采用IF-THEN的形式，其中IF部分是输入变量的模糊集合，THEN部分是输出变量的模糊集合。
模糊规则通常是基于专家知识和经验得到的，可以用模糊控制的方式来实现复杂的控制逻辑。
2.3 模糊推理模糊推理是根据输入变量和模糊规则来获得输出变量的过程。
在模糊推理中，通过模糊化、模糊推理和去模糊化三个步骤来实现。
模糊化将输入变量映射为模糊集合，模糊推理使用模糊规则来计算输出变量的模糊集合，去模糊化将模糊集合映射为具体的输出值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
都确定U的一个模糊集合A，A称为模糊集合A的隶 属函数，它反映了模糊集合中的元素属于该集合的 程度。若A中的元素用x表示，则A(x)称为x属于A 的隶属度。A(x)的取值范围为闭区间[0，1]，若 A(x)接近1，表示x属于A的程度高，A(x)接近0， 表示x属于A的程度低。可见，模糊集合完全由隶属 函数所描述。
解 模糊集合A可表示为：
A 0 0 0.3 0.7 1 1 0.7 0.3 0 0 0.3 0.7 1 1 0.7 0.3 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8
A={(1,0),(2,0),(3,0.3),(4,0.7),(5,1),(6,1), (7,0.7),(8,0.3), (9,0),(10,0)}={(3,0.3),(4,0.7),(5,1),(6,1),(7,0.7),(8,0.3),} A=[0 0 0.3 0.7 1 1 0.7 0 0]
2
应用的研究已取得了丰富的 成果。尤其是随着模糊逻辑在自动控制领域的成 功应用，模糊控制理论和方法的研究引起了学术 界和工业界的广泛关注。在模糊理论研究方面， 以Zadeh提出的分解定理和扩张原则为基础的模糊 数学理论已有大量的成果问世。1984年成立了国 际模糊系统协会（IFSA），FUZZY SETS AND SYSTEMS（模糊集与系统）杂志与IEEE（美国 电气与电于工程师协会）“模糊系统”杂志也先 后创刊。
7
模糊集合有很多表示方法，最常用的有以下几种：
1) 当论域U为有限集{x1,x2,…,xn}时，通常有以下三 种方式
(a) Zadeh表示法
将论域中的元素xi与其隶属度A (xi)按下式表示A，
则
A A (x1 ) A (x2 ) A (xn )
x1
x2
xn
其中 A(xi)/xi并不表示“分数”，而是表示论域中 的元素xi与其隶属度A(xi)之间的对应关系。“+” 也不表示“求和”，而是表示模糊集合在论域U上 的整体。在Zadeh表示法中，隶属度为零的项可不写 入。
9
若A为以实数R为论域的模糊集合，其隶属函数 为A(x)，如果对任意实数a<x<b，都有
A(x)min{A(a),A(b)} 则称A为凸模糊集。凸模糊集实质上就是隶属函数 具有单峰值特性。今后所用的模糊集合一般均指凸 模糊集。
10
例 4-1 在 整 数 1,2,…,10 组 成 的 论 域 中 ， 即 论 域 U={1,2,…,10}，用A表示模糊集合“几个”。 并设 各 元 素 的 隶 属 函 数 A 依 次 为 {0,0,0.3,0.7,1,1,0.7,0.3,0,0}。
11
2) 当论域U为有限连续域时，Zadeh表示法为
A A (x)
Ux
其中 A(xi)/xi也不表示“分数”，而是表示论域中 的元素xi与其隶属度A(xi)之间的对应关系。“”也 不表示“积分”，而是表示模糊集合在论域U上的 元素x与其隶属度A(x)对应关系的一个整体。同样 在有限连续域表示法中，隶属度为零的部分可不写 入。
第4章 模糊逻辑控制理论
❖ 4.1模糊逻辑理论的基本概念 ❖ 4.2 模糊逻辑控制系统的基本结构 ❖ 4.3 模糊逻辑控制系统的基本原理 ❖ 4.4 离散论域的模糊控制系统的设计 ❖ 4.5 具有PID功能的模糊控制器
1
控制论的创始人维纳教授在谈到人胜过最完善的 机器时说：“人具有运用模糊概念的能力”。这清楚 地指明了人脑与电脑之间有着本质的区别，人脑具有 善于判断和处理模糊现象的能力。“模糊”是与“精 确”相对的概念。模糊性普遍存在于人类思维和语言 交流中，是一种不确定性的表现。随机性则是客观存 在的另一类不确定性，两者虽然都是不确定性，但存 在本质的区别。模糊性主要是人对概念外延的的主观 理解上的不确定性。随机性则主要反映客观上的自然 的不确定性，即对事件或行为的发生与否的不确定性。
那么“高温”、“中温”、“低温”等也都没有明
确的外延。所以诸如此类的概念都是模糊概念。模
糊概念不能用经典集合加以描述，因为它不能绝对
地用“属于”或“不属于”某集合来表示，也就是
说论域上的元素符合概念的程度不是绝对的0或1，
而是介于0和1之间的一个实数。
6
1．模糊集合的定义及表示方法 Zadeh在1965年对模糊集合的定义为：给定论域
8
(b) 序偶表示法 将论域中的元素xi与其隶属度A(xi)构成序偶来表示A， 则
A={(x1,A(x1)),(x2,A(x2)),…,(xN,A(xN)) | xU} 在序偶表示法中，隶属度为零的项可省略。
(c) 向量表示法 将论域中元素xi的隶属度A(xi)构成向量来表示A，则
A=[A(x1) A(x2) … A(xN)] 在向量表示法中，隶属度为零的项不能省略。
5
在康托创立的经典集合论中，一事物要么属于
某集合，要么不属于某集合，二者必居其一，没有
模棱两可的情况。即经典集合所表达概念的内涵和
外延都必须是明确的。
在人们的思维中，有许多没有明确外延的概念，
即模糊概念。表现在语言上有许多模糊概念的词，
如以人的年龄为论域，那么“年青”、“中年”、
“年老”都没有明确的外延。再如以某炉温为论域，
3
在模糊逻辑的应用方面，自从1974年英国的 Mamdani首次将模糊逻辑用于蒸汽机的控制后， 模糊控制在工业过程控制、机器人、交通运输等 方面得到了广泛而卓有成效的应用。与传统控制 方法如PID控制相比，模糊控制利用人类专家控 制经验，对于非线性、复杂对象的控制显示了鲁 棒性好、控制性能高的优点。模糊逻辑的其他应 用领域包括：聚类分析、故障诊断、专家系统和 图像识别等。
4
4.1 模糊逻辑理论的基本概念
4.1.1 模糊集合及其运算 集合一般指具有某种属性的、确定的、彼此
间可以区别的事物的全体。将组成集合的事物称 为集合的元素或元。通常用大写字母A，B，C， ，X，Y，Z等表示集合，而用小写字母 a,b,c,…,x,y,z表示集合内元素。被考虑对象的所有 元素的全体称为论域，一般用大写字母U表示。