全新苏教版六年级数学上册1-6单元知识点汇总(全册)
苏教版小学六年级数学上册知识点(最新最全)
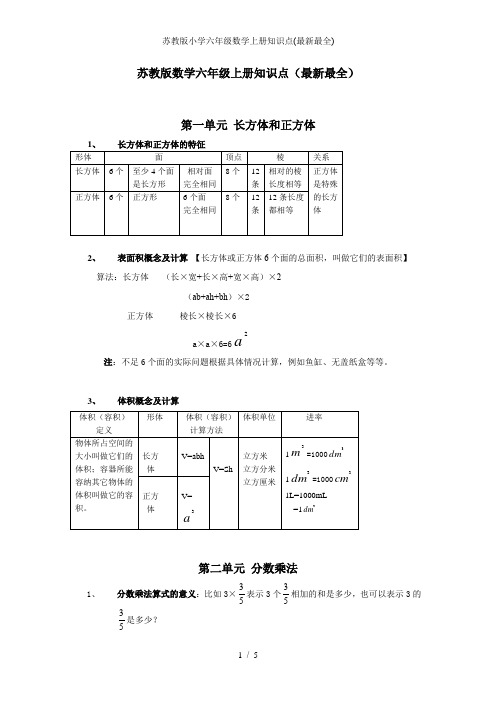
苏教版数学六年级上册知识点(最新最全)第一单元 长方体和正方体2、表面积概念及计算 【长方体或正方体6个面的总面积,叫做它们的表面积】算法:长方体 (长×宽+长×高+宽×高)×2 (ab+ah+bh )×2正方体 棱长×棱长×6a ×a ×6=62a注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
3、体积概念及计算第二单元 分数乘法1、分数乘法算式的意义:比如3×53表示3个53相加的和是多少,也可以表示3的53是多少?注:【求一个数的几分之几用乘法解答】2、分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
或者先将整数与分数的分母进行约分,再应用前面计算法则。
注:【任何整数都可以看作为分母是1的分数】3、分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
4、分数连乘:可用分子连乘的积作为分母,分母连乘的积作分母,计算过程中能约分的先约分,可以使计算简便。
倒数的认识5、乘积是1的两个数互为倒数。
6、求一个数(不为0)的倒数,只要将这个数的分子与分母交换位置。
【整数是分母为1的分数】7、 1的倒数是1 , 0没有倒数。
8、假分数的倒数都小于或等于1(或者说不大于1);真分数的倒数都大于1。
第三单元分数除法1、分数除法计算法则:甲数除以乙数(不为0)等于甲数乘乙数的倒数。
2、分数连除或乘除混合计算:可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算。
【转化成分数的连乘来计算】3、除数大于1,商小于被除数;除数小于1,商大于被除数;除数等于1,商等于被除数。
4、分数除法的意义:已知一个数的几分之几是多少,求这个数?可以用列方程的方法来解,也可以直接用除法。
注:在单位换算中,要弄清需要换算的单位之间的进率是多少。
苏教版六年级数学上册(全册)知识点

苏教版六年级数学上册(全册)知识点(一)长方体和正方体长方体和正方体的特征:长方体和正方体的表面积:概念:长方体或正方体 6 个面的总面积,叫做它们的表面积计算公式:长方体表面积=(长×宽+长×高+宽×高)×2正方体表面积=棱长×棱长×6注:不足 6 个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
体积(容积)单位进率换算:1 立方米=1000 立方分米 1 立方分米=1000 立方厘米1m³=1000dm³1dm³=1000cm³1 升=1000 毫升 1 立方分米=1 升 1 立方厘米=1 毫升1L=1000mL 1dm=1L 1cm³=1mL长方体和正方体的体积(容积):概念:物体所占空间的大小叫做它们的体积(容器所能容纳其它物体的体积叫做它的容积)。
计算公式:长方体体积公式=长×宽×高正方体体积公式=棱长×棱长×棱长长方体和正方体的体积=底面积×高(二)分数乘法分数与整数相乘及实际问题:1.分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
或者先将整数与分数的分母进行约分,再应用前面计算法则。
注:【任何整数都可以看作为分母是 1 的分数】2.求一个数的几分之几是多少,可以用乘法计算。
3.解题时可以根据表示几分之几的条件,确定单位 1 的量,想单位 1 的几分之几是哪个数量,找出数量关系式,再根据数量关系式列式解答。
分数与分数相乘及连乘:1.分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
2.分数连乘:通过几个分数的分子与分母直接约分再进行计算3.一个数与比 1 小的数相乘,积小于原数;一个数与比 1 大的数相乘,积大于原数。
倒数的认识:1.乘积是 1 的两个数互为倒数。
苏教版小学六年级数学上各单元知识点公式、总结、册期末复习用

苏教版小学六年级数学上各单元知识点公式、总结、册期末复习用一、长方体和正方体2、表面积概念及计算【长方体或正方体6个面的总面积,叫做它们的表面积】算法:长方体 =(长×宽+长×高+宽×高)×2= 长×宽×2+长×高×2+宽×高×2正方体 = 棱长×棱长×6 =6a 2注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
4、正方体的棱长扩大或缩小n 倍,表面积会扩大或缩小n 的平方倍,体积会扩大或缩小n 的立方倍。
二、分数乘法(一)分数乘整数1、分数乘整数的意义:表示求几个相同加数的和的简便运算,与整数乘法的意义相同。
2、计算方法:分母不变,分子乘整数。
(二)分数乘分数1、意义:表示求一个分数的几分之几是多少。
2、计算方法:用分子相乘的积作为分子,用分母相乘的积作为分母,能约分的要先约分。
2、一个数乘比1大的数,所得的结果比原来的数大;一个数乘比1小的数,所得的结果比原来的数小。
(三)分数乘加、乘减混合运算及简算1、分数混合运算的运算顺序与整数混合运算的运算顺序相同。
整数乘法的运算定律对于分数乘法也同样适用。
2、合理地应用运算定律,可以使一些分数计算变得简便。
(四)求一个数的几分之几是多少的问题解题规律:一个数×几分之几三、倒数的认识1、乘积是1的两个数互为倒数。
2、求一个数(不为0)的倒数,只要将这个数的分子与分母交换位置。
3、1的倒数是1,0没有倒数。
4、大于1的假分数的倒数都小于1 ,真分数的倒数都大于1。
四、分数除法1、分数除法计算法则:甲数除以乙数(0除外)等于甲数乘乙数的倒数。
2、分数连除或乘除混合计算:可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算。
【转化成分数的连乘来计算】3、一个数除以比1大的数,所得的结果比原来的数小;一个数除以比1小的数,所得的结果比原来的数大。
(完整版)苏教版小学六年级上册数学知识点总结,推荐文档

第一单元长方体和正方体1、两个面相交的线叫做棱。
三条棱相交的点叫做顶点。
2、长方体相交于同一顶点的三条棱的长度,分别叫做它的长、宽、高。
3、长方体的棱长总和=(长+宽+高)×4正方体的棱长总和=棱长×12 4、长方体和正方体的特征:注意:长方体的面是长方形(也有可能有两个相对的面是正方形。
长方体或正方体放在桌面上,最多只能看到 3 个面。
5、正方体的展开图:形 体 面 顶点棱关系长方体6 个 至少4 个面是长方形相对面完全相同8 个 12条相对的棱 长度相等正方体是特殊的长方 体正方体也叫立方体6 个正方形6 个面完全相同8 个 12 条 12 条棱长度都相等注意:找相对面的方法:三连块、Z 字型。
长、正方体的展开图,相对的面不相邻,相对的面安全相同。
6、表面积概念及计算【长方体或正方体6 个面的总面积,叫做它们的表面积】算法:长方体的表面积=(长×宽+长×高+宽×高)×2S=(ab+ah+bh)×2正方体的表面积= 棱长×棱长×62S= a×a×6=6a注:不足6 个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
7、体积概念及计算注意:体积公式的推到:其实就是求单位体积的小正方体的个数(小正方体的个数就是长、正方体的体积。
就是看沿着长一排可以放几个小正方体、沿着宽可以放几排,沿着高可以放几层。
体积(容积)定义 形体体积(容积)计算方法体积单位进率物体所占空间长 方体3 31 m =1000dm 331dm =1000cm31L=1000mL=1dm31 cm =1mL的V=abh大小叫做它们的立方米正方体体积;容器所立方分能V=Sh米 容纳其它物体立方厘 的 3V=a米体积叫做它的容 积。
8、棱长1 厘米的正方体,体积是 1 立方厘米。
(一个手指头的体积、一粒蚕豆大约是 1 立方厘米)棱长1 分米的正方体,体积是 1 立方分米。
2021新苏教版六年级数学上册知识点归纳总结

新苏教版六年级数学上册知识点总结(一)长方体和正方体 (1)长方体和正方体的特征:形体 面顶点 棱 关系 长方体 6个 至多2个面是正方形相对面完全相同 8个 12 条 相对的棱 长度相等 正方体 是特殊 的长方体正方体 6个 正方形 6个面完全相同 8个 12 条 12条棱长度都相等 长方体的一个顶点引出一条长、一条宽和一条高。
长方体的棱长和=(长+宽+高)×4 正方体的棱长和=棱长×12(2)长方体和正方体的表面积:概念:长方体或正方体6个面的总面积,叫做它们的表面积.长方体表面积=(长×宽+长×高+宽×高)×2或=)2S a b a c b c ⨯+⨯+⨯⨯表(正方体表面积=棱长×棱长×6或2=66S a a a ⨯⨯=表注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒、管道等等。
长方体侧面积=底面周长×高 S 侧=C ×h=(a+b )×2×h 正方体展开图有11种:(3)体积(容积)单位进率换算:1立方米=1000立方分米 1立方分米=1000立方厘米3311000m dm = 3311000dm cm =1升=1000毫升 1立方分米=1升 1立方厘米=1毫升 1L=1000m L 31dm =1L 31cm =1m L 计量液体的体积,常用升和毫升作单位。
(4)长方体和正方体的体积(容积):概念:物体所占空间的大小叫做它们的体积(容器所能容纳物体的体积叫容积)。
长方体体积公式=长×宽×高 或 V a b h =⨯⨯正方体体积公式=棱长×棱长×棱长 或 3V a a a a =⨯⨯=长方体和正方体的体积=底面积×高 或 ×V S h =底(5)13=1 23=8 33=27 43=64 53=125 63=216 103=1000 长方体的长、宽、高均扩大n 倍,表面积会扩大n 的平方倍,体积n 的立方 正方体的棱长扩大n 倍,表面积会扩大n 的平方倍,体积会扩大n 的立方(二)分数乘法(1)分数与整数相乘及实际问题:1.分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
苏教版六年级数学上册各单元知识点汇总

苏教版六年级数学上册期末知识点复习要点长方体和正方体的表面积:概念:长方体或正方体6个面的总面积,叫做它们的表面积计算公式:长方体表面积=(长×宽+长×高+宽×高)×2正方体表面积=棱长×棱长×6注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
体积(容积)单位进率换算:1立方米=1000立方分米1立方分米=1000立方厘米1m³=1000dm³1dm³=1000cm³1升=1000毫升1立方分米=1升1立方厘米=1毫升1L=1000mL 1dm³=1L 1cm³=1mL长方体和正方体的体积(容积):概念:物体所占空间的大小叫做它们的体积(容器所能容纳其它物体的体积叫做它的容积)。
计算公式:长方体体积公式=长×宽×高正方体体积公式=棱长×棱长×棱长长方体和正方体的体积=底面积×高第二单元:分数乘法分数与整数相乘及实际问题:1.分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
或者先将整数与分数的分母进行约分,再应用前面计算法则。
注:【任何整数都可以看作为分母是1的分数】2.求一个数的几分之几是多少,可以用乘法计算。
3.解题时可以根据表示几分之几的条件,确定单位1的量,想单位1的几分之几是哪个数量,找出数量关系式,再根据数量关系式列式解答。
分数与分数相乘及连乘:1.分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
2.分数连乘:通过几个分数的分子与分母直接约分再进行计算3.一个数与比1小的数相乘,积小于原数;一个数与比1大的数相乘,积大于原数。
倒数的认识:1.乘积是1的两个数互为倒数。
2.求一个数(不为0)的倒数,只要将这个数的分子与分母交换位置。
苏教版小学六年级数学上册知识点(最全)-小学六年级上册苏教版
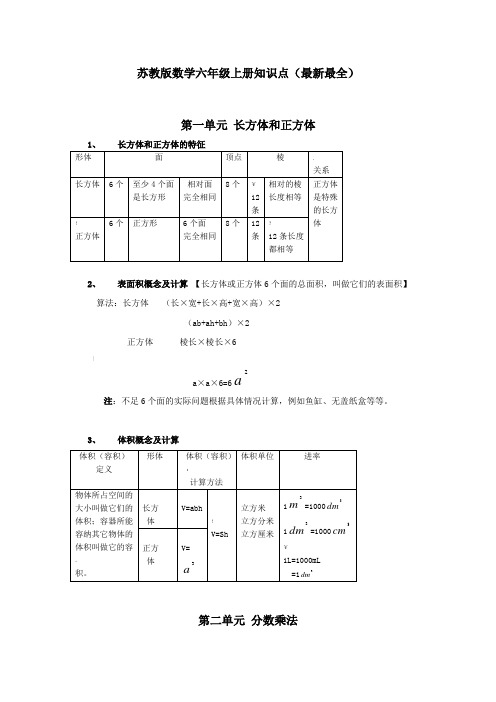
苏教版数学六年级上册知识点(最新最全)第一单元 长方体和正方体2、表面积概念及计算 【长方体或正方体6个面的总面积,叫做它们的表面积】算法:长方体 (长×宽+长×高+宽×高)×2 (ab+ah+bh )×2正方体 棱长×棱长×6|a ×a ×6=62a注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
3、体积概念及计算第二单元 分数乘法1、 分数乘法算式的意义:比如3×53表示3个53相加的和是多少,也可以表示3的53是多少 注:【求一个数的几分之几用乘法解答】 2、(3、分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。
或者先将整数与分数的分母进行约分,再应用前面计算法则。
注:【任何整数都可以看作为分母是1的分数】 4、分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
5、分数连乘:可用分子连乘的积作为分母,分母连乘的积作分母,计算过程中能约分的先约分,可以使计算简便。
倒数的认识 6、乘积是1的两个数互为倒数。
6、 求一个数(不为0)的倒数,只要将这个数的分子与分母交换位置。
【整数是分母为1的分数】7、 1的倒数是1 , 0没有倒数。
@8、 假分数的倒数都小于或等于1(或者说不大于1);真分数的倒数都大于1。
第三单元 分数除法1、 分数除法计算法则:甲数除以乙数(不为0)等于甲数乘乙数的倒数。
2、分数连除或乘除混合计算:可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算。
【转化成分数的连乘来计算】3、除数大于1,商小于被除数;除数小于1,商大于被除数;除数等于1,商等于被除数。
4、;5、分数除法的意义:已知一个数的几分之几是多少,求这个数可以用列方程的方法来解,也可以直接用除法。
苏教版六年级上册数学知识点汇总

苏教版六年级上册数学知识点汇总第一单元:长方体和正方体•长方体和正方体的认识:•理解长方体和正方体的基本特征,包括面、棱、顶点的数量及位置关系。
•掌握长方体和正方体的长、宽、高(或棱长)的概念。
•表面积和体积:•学习计算长方体和正方体的表面积和体积的公式。
•应用公式解决实际问题,如包装纸的大小、容器的容量等。
第二单元:分数乘法•分数乘法的意义:•理解分数乘法的意义,即求一个数的几分之几是多少。
•分数乘法的计算:•掌握分数乘法的计算方法,包括分数乘整数、分数乘分数。
•学习约分和通分的技巧,以简化计算过程。
•分数乘法的应用:•应用分数乘法解决实际问题,如分数的加减混合运算、分数的比较等。
第三单元:分数除法•分数除法的意义:•理解分数除法的意义,即已知一个数的几分之几是多少,求这个数。
•分数除法的计算:•掌握分数除法的计算方法,通常转化为乘法进行计算(除以一个数等于乘以这个数的倒数)。
•分数四则混合运算:•学习分数四则混合运算的顺序和计算方法,注意运算律的应用。
第四单元:分数四则混合运算•运算顺序:•掌握分数四则混合运算的顺序,即先乘除后加减,有括号先算括号里的。
•简便运算:•学习利用运算律进行简便运算,提高计算效率。
•实际问题解决:•应用分数四则混合运算解决实际问题,如分数的应用题、比例问题等。
第五单元:比•比的意义:•理解比的意义,即两个数相除又叫做两个数的比。
•比的基本性质:•掌握比的基本性质,即比的前项和后项同时乘或除以相同的数(0除外),比值不变。
•比的应用:•学习化简比、求比值的方法,并应用比解决实际问题,如按比例分配等。
第六单元:百分数•百分数的意义:•理解百分数的意义,即表示一个数是另一个数的百分之几的数。
•百分数与小数、分数的互化:•掌握百分数与小数、分数之间的互化方法。
•百分数的应用:•学习百分数的计算方法,如求一个数的百分之几是多少、已知一个数的百分之几是多少求这个数等。
•应用百分数解决实际问题,如折扣问题、纳税问题、利息问题等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全新苏教版六年级数学上册1-6单元知识点汇总(全册)以下是格式修正后的文章:全新苏教版六年级数学上册1-6单元知识点汇总(全册)班级:______________ 姓名:______________第一单元长方体和正方体1.两个面相交的线叫做棱,三条棱相交的点叫做顶点。
2.长方体和正方体的相同点和不同点如下:相同点:面的形状:长方形(长方体)或正方形(正方体)。
棱的数量:12 条。
顶点数量:8 个。
相对的面的面积相等。
棱长:平行的四条棱长度相等。
正方体是特殊的长方体。
不同点:面的大小:长方体的相对面的面积不一定相等,正方体的六个面的面积相等。
棱长:长方体的棱长不一定相等,正方体的六条棱长都相等。
长方体相交于同一顶点的三条棱的长度,分别叫做它的长、宽、高。
长方体的 12 条棱有 3 组,每组的四条棱长度相等。
长方体的棱长总和为 (长+宽+高)×4.长方体放在桌面上,最多只能看到 3 个面。
3.正方体的展开方式有以下几种:141型”,中间一行 4 个图,作侧面,上下两个各作为上下底面,共有 6 种基本图形。
231型”,中间 3 个作侧面,共 3 种基本图形。
222”型,两行只能有 1 个正方形相连。
33”型,两行只能有 1 个正方形相连。
4.长方体和正方体的表面积计算方式如下:长方体的表面积为 (长×宽+长×高+宽×高)×2.正方体的表面积为棱长×棱长×6.5.在解决一些问题时,要充分考虑实际情况,想清楚要算几个面。
在解答时,可以把这几个面的面积分别算出来,再相加,也可以先算出六个面的面积总和,再减去不需要的那个(些)面。
例如,一个抽屉有 5 个面,分别是前面、后面、左面、右面、底面。
所以做这样一个抽屉所需要的木板,只要算出这 5 个面的面积就可以了。
通风管顾名思义是通风用的,没有底面。
所以只要算四个侧面就可以了。
(注意:一般是最小的口通风)以下是一些长方体和正方体物品的面数:具有六个面的长方体、正方体物品:油箱、罐头盒、纸箱子等。
具有五个面的长方体、正方体物品:水池、鱼缸等。
具有四个面的长方体、正方体物品:水管、烟囱等。
6.体积和容积的定义如下:体积:物体所占空间的大小。
容积:所能容纳物体的体积。
这篇文章介绍了关于体积的知识,包括体积单位、长方体和正方体的体积公式,以及如何分割长方体和正方体。
下面对每段话进行小幅度的改写。
第7段:体积单位可以用列表的形式来表述,以方便记忆。
体积单位包括立方厘米、立方分米和立方米,它们分别对应着不同大小的正方体。
体积与容积单位之间的关系是1立方厘米等于1毫升,1立方分米等于1升。
第8段:长方体和正方体的体积公式分别为长×宽×高和棱长×棱长×棱长。
它们也可以用底面积和高来表示,即长方体的体积等于底面积×高,正方体的体积等于底面积×高。
第9段:将一个长方体截成两段后,表面积会增加两个底面。
因此,求它的体积需要用到“底面积×高”的公式。
每截一次,增加的面就会增加两个。
第10段:将一个大的形体分成小的形体,可以运用体积单位和长度单位的知识。
将小正方体排成一排,能排多少米就是这些小正方体的棱长加起来的长度。
1立方米等于1000立方分米,因此可以分成1000个小正方体,排成100米。
第11段:正方体的棱长扩大n倍,表面积就扩大n²倍,体积就扩大n³倍。
表面涂色的正方体:将一个涂色的正方体的每条棱分成n等分,然后将其切成同样大小的小正方体。
根据涂色情况,可以得出以下结论:1.三面涂色的正方体有8个,分别位于大正方体的顶点位置。
2.两面涂色的正方体有12(n-2)个,分别位于大正方体的棱位置,因此数量一定是12的倍数。
3.一面涂色的正方体有6(n-2)²个,分别位于大正方体的面位置,因此数量一定是6的倍数。
4.没有涂色的正方体有(n-2)³个,全部位于大正方体的内部。
5.在大正方体的顶点处挖去小正方体,表面积不变。
6.在大正方体的棱上挖去小正方体,表面积会变大,每挖去一个小正方体就会比原来多2个面。
7.在大正方体的面上挖去小正方体,表面积会变大,每挖去一个小正方体就会比原来多4个面。
第二单元分数乘法:1.将分数和整数相乘,可以表示求几个几分之几相加的和。
2.求一个数的几分之几是多少,可以使用乘法计算。
3.分数和整数相乘时,分子和整数相乘的积作为新分数的分子,分母不变。
如果整数能够和分数的分母约分,应该先约分再计算。
4.在解答分数乘法的实际问题时,需要找准单位“1”的量。
数量关系式为:单位“1”×分率=分率对应的量。
5.求一个数的几分之几(几倍)是多少的分数应用题的解题思路和解答方法与求解其他分数应用题相同:用一个数乘以几分之几。
解题思路中将一个数视为单位“1”,提示我们在解答分数应用题时需要先找准单位“1”。
同样,在画线段图时,也应该先画出单位“1”的量。
6.在解答分数应用题时,不仅要找准单位“1”的量,还需要知道分率对应的量是什么。
一般来说,如果分率是多(少)的分率,那么分率对应的量就是多的部分(少)。
7.分数和分数相乘,表示求一个数的几分之几相加的和。
分数和分数相乘时,分子相乘的积作为新分数的分子,分母相乘的积作为新分数的分母。
8.因为整数可以看作分母为1的假分数,所以分数和分数相乘的计算方法适用于分数和整数相乘。
9.三个数相乘时,可以先将前两个数相乘,得到的积再和第三个数相乘。
但为了简便,可以先将所有分数的分子和分母约分,再将约分后的分子和分母相乘。
10.当一个数与真分数相乘时,所得积小于这个数;当一个数与假分数相乘时,所得积大于或等于这个数。
11.解答分数乘法应用题时,可以利用线段图来分析数量关系。
在绘制线段图时,先画出单位“1”的量。
数量关系式为:单位“1”×分数比率=分数比率对应的量。
12.乘积为1的两个数互为倒数。
要求一个数(除0外)的倒数,只需将这个数的分子、分母互换位置。
13.1的倒数是1,没有倒数,真分数的倒数都大于1,自然数的倒数都是分子为1的真分数,假分数的倒数小于或等于1.14.典型例题1:下面的长方形代表1公顷,请在图中表示出公顷的面积,结果是多少公顷?分析与解:这个题目需要逐步展开思考。
(1)1公顷是1公顷的一半;(2)将1公顷平均分成3份,表示出2份。
因此,1公顷的面积是大长方形的2/6(或1/3)。
例2:一袋大米重25千克,先吃去这袋大米的1/5,又吃去1/1千克,两次一共吃去多少千克?分析与解:要求两次共吃去多少千克,需将第一次吃的千克数加上第二次吃的千克数。
第一次吃了这袋大米的1/5,相当于吃去25×1/5=5千克。
第二次吃去1/1千克。
因此,两次一共吃去5+1=6千克。
例3:填空。
()×4/5=7×()=()×1=0.8×()分析与解:这是一道连等式填空题。
从题目中可以看出,四个乘法算式的积都相等,但是都等于多少呢?题目中没有明确要求,说明有多种填法。
但是要快速又正确地解答,可以从倒数的角度入手,即考虑每个算式的积都是1.因此,在相应的括号里只需填上与之相乘的数的倒数即可。
如果给定一个确定的数值作为积,那么解答此题时需要逐一思考解答。
例如,()÷7=()÷1=0.8×(xxxxxxx)÷=10.答案为10.已知a×3=×b=×c,且a、b、c都不相等,将a、b、c按从小到大的顺序排列为a<c<b。
例如,a×3=×b=×c=1,那么a=1/3,b=1,c=3,因此a<c<b,所以排列为1/3<1<3.例4、(1)一根钢管截成两段,第一段占1/3,第二段长米。
哪一根长?可以用画图的方法表示题意,如下图所示:第一段占1/3,第二段占2/3.因此第二段长一些。
2)两根一样长的钢管,第一根截去1/3,第二根截去1/5.哪一根剩下的长?无法比较。
3)两根1米长的钢管,第一根截去1/3,第二根截去1/5.哪一根剩下的长?一样长。
分数除以整数可以通过将分数的分子除以整数得到,但不能总得到整数的商,因此通常将分数除以整数转化为分数乘以这个整数的倒数。
一个数除以分数,等于乘以这个分数的倒数。
甲数除以乙数(除非乙数为0),等于甲数乘以乙数的倒数。
一个数除以真分数所得的商大于这个数;一个数除以假分数,所得的商小于或等于这个数。
例如,55÷2表示已知两个因数的积是110,其中一个因数是2,求另一个因数是多少?答案为55.一台榨油机每小时榨油5吨,平均每小时榨油多少吨?榨1吨油要多少小时?平均每小时榨油5吨,榨1吨油需要1/5小时。
在分数连除或分数乘除混合运算中,遇到除以一个数时,只要乘以这个数的倒数就可以了。
在解答分数除法应用题时要找准单位“1”的量,而简单的分数除法应用题就是要求单位“1”的量。
分数除法应用题的数量关系式是:单位“1”×分率=分率对应的量。
9.解答分数除法应用题时,可以借助线段图来分析数量关系。
在画线段图时,先画单位“1”的量。
分析思路与乘法应用题一致,根据题里叙述的条件,明确哪个数量看作单位“1”。
但单位“1”的数量是未知的,因此先根据一个数和分数相乘的意义列出等量关系式,然后设未知数,列出相应的方程并解答。
解答应用题时最关键的是对应用题的数量关系进行分析,而不能套用解题思路。
可以这样总结:当应用题中单位“1”已知时,用乘法解;当单位“1”未知,要求单位“1”时,用除法解或列方程解。
第四单元:认识比1.两个数相除即为两个数的比,如3÷2为3:2.比的前项除以后项所得的商为比值。
比值通常用分数表示,也可以用小数表示,有时也可以是整数。
3:2的比值为 1.5.(比值没有单位)2.与除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商;与分数比较,比的前项相当于分子,后项相当于分母,比值相当于分数值。
3.比的基本性质相当于除法中的商不变性质和分数中的基本性质。
因此应用比的基本性质可以将比进行化简。
比的前项和后项为互质数时,这个比就是最简整数比。
在化简过程中,如果比的前项和后项都是整数,就同时除以它们的最大公约数;如果前项和后项是小数或分数,先将它们同时乘一个数化成整数,再化简。
最后化简到比的前项和后项是互质数的比为最简整数比。
4.求比值和化简比的核心区别在于结果的表达形式不同,求比值的结果一定是一个数,化简比的结果一定是一个比。
5.把一个数量按照一定的比来进行分配,这种分配的方法叫做按比例分配。
