数学物理方程期末试题B卷参考答案
数学物理方程试卷及答案

参考解答: 一、 填空题1. A 定解 B 初值(或Cauchy 问题) C 存在性、唯一性和稳定性2. D 双曲3. E (1)(2)(4)4. F [x-3t,x+t] ,G 决定区域5. H 222(21)(1,2,)4n n L πλ-== I(21)cos (1,2,)2n x X n Lπ-== 二、解:无界区域上波动方程200,,0|(),|()tt tt t t t u a u x t u x u x ϕψ==⎧=-∞<<+∞>⎪⎨==⎪⎩ 的达朗贝尔公式为:22()()1(,)()22x atx at x at x at u x t d aϕϕψξξ+--++=+⎰ 对于本题所给半无界区域上的自由端点定解问题,只需对初始条件作偶延拓,即令:2(),()||x x x x ϕψ==即可,2a = ,代入达朗贝尔公式得22222222(2)(2)1()||2224,25(4),24x tx tx t x t u x d x xt t x tx t x t ξξ+--++=+⨯⎧++≥⎪=⎨+<⎪⎩⎰ 二、 解:设(,)()()u x t X x T t =,则()''()4''()()X x T t X x T t =,分离变量成为''()''()4()()T t X x T t X x λ==-,则''()()0,'(0)'(1)0''()4()0X x X x X X T t T t λλ+===⎧⎨+=⎩, 解前一方程,得固有值22(0,1,2,)n n n λπ==和固有函数()cos X x n x π=,代入方程''()4()0T t T t λ+=中可得()cos 2sin 2T t A n t B n t ππ=+,1,2,3,)n =(由叠加原理,原方程有解1(,)(cos 2sin 2)cos nnn u x t A n t Bn t n x πππ∞==+∑。
研究生数理方程期末试题-10-11-1-A-答案
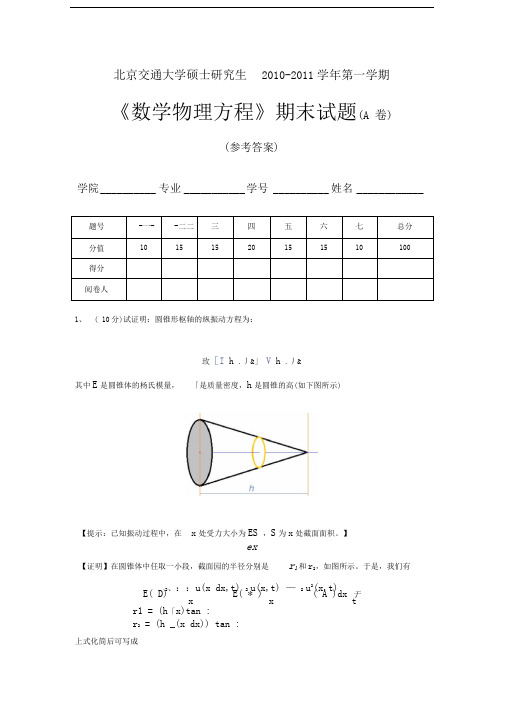
北京交通大学硕士研究生2010-2011学年第一学期《数学物理方程》期末试题(A 卷)(参考答案)学院__________ 专业___________ 学号 __________ 姓名____________1、( 10分)试证明:圆锥形枢轴的纵振动方程为:玫[I h .丿&」V h .丿&其中E是圆锥体的杨氏模量,「是质量密度,h是圆锥的高(如下图所示)【提示:已知振动过程中,在x处受力大小为ES ,S为x处截面面积。
】ex【证明】在圆锥体中任取一小段,截面园的半径分别是r1和r2,如图所示。
于是,我们有2、::u(x dx,t) 2 u(x,t) — 2 u2(x,t)E( D) E( * ) ( A )dx 于x x t r1 = (h「x)tan :r2= (h _(x dx)) tan :上式化简后可写成22::U(X,t)2::u(x,t) 2, ;u (x,t)E[(h -x)卜亠 & -(h -'X) 〔x J - - (h -'X)dx 2从而有E ::[(^x)2;:U(x ,t)H-(^x)2::u2(x,t) .x :X:t 或成2::[(1「)2汽("]“2(1「)小叩).xh ::x h ;:t其中a^E,证明完毕。
2、 (20分)考虑横截面为矩形的散热片, 它的一边y=b 处于较高温度U ,其它三边y=0.x = 0和x = a 则处于冷却介质中,因而保持较低的温度 u o 。
试求该截面上的稳定温度分布u(x,y),即求解以下定解问题:u|y 卫二 %, u|y 生二 U, 0 x a. 【提示:可以令u(x, y)二u 0 v(x, y),然后再用分离变量方法求解。
】【解】令u(x, y) v(x, y),则原定解问题变为Wl x£=0, V=0, 0cy <b;v|y/0, v|y 子U _u °,0 x a.分离变量:f 2\dU;:2U=0, 0 : x : a, 0 : y : b;y=0, 0 : x :: a, 0 : y : b;■ 2y »2 -2v(x,y) =X(x)Y(y)代入方程得到关于X和Y的常微分方程以及关于X的定解条件:X X = 0,X(0) =0,X(a) =0;Y - Y =0可以判定,特征值(n =1,,2,3J||)特征函数n 二X(x) = X n(x) =C n S in—x (n=1,,2,3JI|)利用特征值、可以求得丫(y) =Y n(y) =A n e叨B n^;y(n = 1,,2,3,l|l) 于是求得特征解n r n iy n,1V n(x,y)=(代e= B n e^ )sin x (n =1,,2,3JI|)a形式解为n -y _j-y门二v(x, y)二為V n(x, y)二為(A n e~ B n e^ )sin x吕 3r Q Qv(x,0)=迟(An+B n)sinO0 bv(x,b)八(A n e吗B n en =1pg na )sin——x 二U -u0得到A nB n =0八也如二 4 “,、A e aB e a(U - u。
数学物理方程答案(全)

利用微分中值定理可得
T
(
x)ux
x
utt
将T (x) 的表达式代入可得
utt g(l x)uxx gux
2.长为 L,均匀细杆,x=0 端固定,另一端沿杆的轴线方向拉长 b 静止后(在弹性限 度内)突然放手,细杆做自由振动。试写出振动方程的定解条件。
T(x,t) T(x+dx,t)
界条件之一:
(1)一端(x=0)绝热,另一端(x=L)保持常温 0
解:边界条件 ux x0 0, u xL u0
(2)两端分别有热流密度 q1 和 q2 进入
解:边界条件 ux
x0
g1 k
,ux
xL
g2 k
(3)一端(x=0)温度为 1(t) ,另一端(x=L)与温度为 (t) 的介质有热交换
F ( x,
t)dtdxS
u x
cSdtdx
k
2u x2
F (x,t)
u x
c
ut
k c
uxx
F ( x, t ) c
ut
k c
uxx
(
j)2 c
习题 2.3
1.半径为
r0
的球面,在的 0
2
半球面上电势为
0
,在
2
的半球面上
电势为 0 。求空间各点应满足的泛定方程与定解条件。
解:泛定方程
4.
由静电场
Gauss
定理
s
E
dS
1 0
V
dV
,求证:
E
0
,并由此导出
静电势 u 所满足的 Poisson 方程。
西安邮电大学期末数理方程试题+答案

数学物理方程与特殊函数09级试题选讲一、求解定解问题22200,0,(0,0)x x lt u u a t x u u x l t xx u x ===춶=ﶶﶶï==<<>í¶¶ïï=ïî)()(),(t T x X t x u =)()()()(2t T x X a t T x X ¢¢=¢22)()()()(b -=¢¢=¢x X x X t T a t T 0>b 设,代入原方程得,则)()(22=+¢t T a t T b 0)()(2=+¢¢x X x X b 则,0x x lu u xx==¶¶==¶¶'(0)'()0X X l Þ==又因为得固有值问题2()()0'(0)'()0X x X x X X l b ¢¢ì+=í==î22)(ln pb =()cos 0,1,2,n n n xX x A n lp ==则固有值固有函数,数学物理方程与特殊函数09级试题选讲)()()(2=+¢t T la n t T p 2()()n a tl n T t C ep -Þ=2()01(,)cosn a tln n n x u x t C C elp p ¥-==+å从而0t ux==有因为01cosnn n x x C C lp ¥==+å所以220022[(1)1]cos 12n ln l n x l C x dx l l nl C xdx lp p --====òò2()2212(1)1(,)cos 2n a ntln l l n xu x t enlp p p¥-=--=+å数学物理方程与特殊函数09级试题选讲二、求解定解问题2222,,0(),0(),0(0)(0)t x t x u ut x t t t x ux x u x x =-=춶=-<<>ﶶïï=F £íï=Y ³ïïF =Y î解:特征变换为x t x tx h =-ìí=+î2u x h¶=¶¶原方程化为12()()u f f x h =+则它的通解为00(),()()(),()()2222t xt x ux u x u u h x x h x h x h=-====F =Y +-Þ=F =F =Y =Y 又因为数学物理方程与特殊函数09级试题选讲1212(0)()()2()(0)()2f f f f h h xx +=Y +=F 2112()()(0)2()()(0)2f f f f h h x x ì=Y -ïïÞíï=F -ïî12()()((0)(0))22()()(0)22u f f x t x tx h=F +Y -+-+=F +Y -F 则它的解为三、求解定解问题)0,(,0,3,03202022222>+¥<<-¥ïïïîïïíì=¶¶==¶¶-¶¶¶+¶¶==y x y ux u y uy x u x u y y 解:原方程的特征方程为22()23()0dy dydx dx --=13C x y +=2C x y +-=,则特征线为3x y x yx h =-ìí=+î特征变换20ux h¶=¶¶原方程化为12()()u f f x h =+则它的通解为数学物理方程与特殊函数09级试题选讲12(,)(3)()u x y f x y f x y =-++即203,y y u ux y==¶==¶又因为21212(3)()3(3)()0f x f x xf x f x ì+=í¢¢-+=î则可得C x x f¢-=2149)3(C x x f ¢+=2243)(C x x f¢-=2141)(222234)(34)3(),(yx y x y x y x u +=++-=22()()C Du vv u u v d v u ds n n s ¶¶Ñ-Ñ=-¶¶òòò 四、证明平面上的格林公式其中n 为曲线的外法线向量。
数学物理方程期末试卷

数学物理方程期末试卷第一部分:选择题请在每个题目中选择仅一个正确答案并将字母填入括号内。
1.求解y″+y=0有解的方法是?A. 特征根法 ( )B. 系数法 ( )C. 齐次线性微分方程法 ( )D. 变量分离法 ( )2.求解 $\\frac{\\partial^2u}{\\partialx^2}+\\frac{\\partial^2u}{\\partial y^2}=0$ 有解的条件是?A. u在区域内为调和函数 ( )B. u在区域内为多项式函数 ( )C. 区域的边界条件为第一类边界条件 ( )D. 区域的边界条件为第二类边界条件 ( )3.解 $\\frac{\\partial u}{\\partial t}+2u=0$,u(x,0)=x,在t=1时,u(x,1)=?A. $\\frac{x}{2}$B. xe−2C. $\\frac{x}{e^2}$D. xe2 ( )4.对于一般的偏微分方程,逐步消去导数的方法称为?A. 特征线法 ( )B. 微分方程求解法 ( )C. 变量分离法 ( )D. 特征值法 ( )5.$y=A\\cos(x)-B\\sin(x)$ 是如下微分方程的?A. $y''+y=\\sin(x)$B. $y''-y=\\cos(x)$ ( )C. $y''+y=\\cos(x)$D. $y''-y=\\sin(x)$第二部分:填空题请在每个题目中填入恰当的答案。
1.y″−2y′+2y=0的通解为______。
2.$\\frac{\\partial^2 u}{\\partial t^2}-c^2\\frac{\\partial^2u}{\\partial x^2}=0$ 的波动方程,初始时刻条件为$u(x,0)=\\varphi(x)$,$u_t(x,0)=\\psi(x)$,其解为$u(x,t)=\\frac{1}{2}(f_1(x-ct)+f_2(x+ct))$,其中f1(x),f2(x)分别是u(x,0)和u t(x,0)的__________。
大学数学专业《大学物理(二)》期末考试试卷B卷 含答案

大学数学专业《大学物理(二)》期末考试试卷B卷含答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、一个质点的运动方程为(SI),则在由0至4s的时间间隔内,质点的位移大小为___________,在由0到4s的时间间用内质点走过的路程为___________。
2、真空中有一半径为R均匀带正电的细圆环,其电荷线密度为λ,则电荷在圆心处产生的电场强度的大小为____。
3、沿半径为R的圆周运动,运动学方程为 (SI) ,则t时刻质点的法向加速度大小为________;角加速度=________。
4、一质量为0.2kg的弹簧振子, 周期为2s,此振动系统的劲度系数k为_______ N/m。
5、已知质点的运动方程为,式中r的单位为m,t的单位为s。
则质点的运动轨迹方程,由t=0到t=2s内质点的位移矢量______m。
6、一弹簧振子系统具有1.OJ的振动能量,0.10m的振幅和1.0m/s的最大速率,则弹簧的倔强系数为_______,振子的振动频率为_______。
7、将热量Q传给一定量的理想气体:(1)若气体的体积不变,则热量转化为_____________________________。
(2)若气体的温度不变,则热量转化为_____________________________。
(3)若气体的压强不变,则热量转化为_____________________________。
8、质点p在一直线上运动,其坐标x与时间t有如下关系:(A为常数) (1) 任意时刻t,质点的加速度a =_______; (2) 质点速度为零的时刻t =__________.9、一个半径为、面密度为的均匀带电圆盘,以角速度绕过圆心且垂直盘面的轴线旋转;今将其放入磁感应强度为的均匀外磁场中,的方向垂直于轴线。
2011-2012数学物理方程-B卷-答案

u ( x0 , y 0 ) = −
1 ∂ 1 1 ∂u u ln − ln ds , ∫ 2π Γ ∂n r r ∂n r
其中 ( x0 , y 0 ) 为平面有界区域 Ω 内任一点,Γ 是区域 Ω 的边界曲线, 且光滑,n 为 Γ 的外法向量, ds 是弧微分; (2)证明格林函数的性质:
∂G( M , M 0 ) ds M = −1 。 ∫∫ ∂ n Γ
1 ∂ 1 1 ∂u u ln − ln ds , ∫ 2π Γ ∂n r r ∂n r
证: (1)证明: = −
其中 ( x 0 , y 0 ) 为平面有界区域 Ω 内任一点,Γ 是区域 Ω 的边界曲线, 且光滑,n 为 Γ 的外法向量, ds 是弧微分; 证:记 M 0 ( x 0 , y 0 ) , K ε :以 M 0 为中心半径为 ε 的圆且包含在 Ω 内,
u tt = a 2 u xx , 0 < x < π , t > 0, t ≥ 0, ; u (0, t ) = u x (π , t ) = 0, 3 u ( x,0 ) = x , u t ( x,0 ) = 0, 0 ≤ x ≤ π .
解:分析知,其形式解
u ( x, t ) = ∑ sin
sin
nπ x l
再由初始值得
f ( x) − u 0 = ∑ An sin
n =1
l
∞
nπ x l
5分
故
2 nπ An = ∫ [ f ( x) − u 0 ] sin xdx l 0 l u ( x, t ) = u 0 + v( x, t )e − βt
∞ l
因此
数学物理方法期末试题(5年试题含答案)

………密………封………线………以………内………答………题………无………效……附:拉普拉斯方程02=∇u 在柱坐标系和球坐标系下的表达式 柱坐标系:2222222110u u u uzρρρρϕ∂∂∂∂+++=∂∂∂∂球坐标系:2222222111sin 0sin sin u u ur r r r r r θθθθθϕ∂∂∂∂∂⎛⎫⎛⎫++= ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭一、填空题36分(每空2分)1、 数量场2322u x z y z =+在点(2, 0, -1)处沿2423x xy z =-+l i j k 方向的方向导数是。
2、 矢量场()xyz x y z ==+A r r i +j k 在点(1, 3, 3)处的散度为 。
3、 面单连域内设有矢量场A ,若其散度0∇⋅A =,则称此矢量场为 。
4、 高斯公式Sd ⋅=⎰⎰ A S ;斯托克斯公式ld ⋅=⎰ A l 。
5、 将泛定方程和 结合在一起,就构成了一个定解问题。
只有初始条件,没有边界条件的定解问题称为 ;只有边界条件,没有初始条件的定解问题称为 ;既有边界条件,又有初始条件的定解问题称为 。
………密………封………线………以………内………答………题………无………效……6、 ()l P x 是l 次勒让德多项式,则11()()l l P x P x +-''-= ; m n =时,11()()mn P x P x dx -=⎰。
7、 已知()n J x 和()n N x 分别为n 阶贝塞尔函数和n 阶诺依曼函数(其中n 为整数),那么可知(1)()n H x = 。
(2)()n H x = 。
8、 定解问题2222000(0,0)|0,||0,|0x x ay y bu ux a y b x y u u V u u ====⎧∂∂+=<<<<⎪∂∂⎪⎪==⎨⎪==⎪⎪⎩的本征函数为 ,本征值为 。
