专题训练(六)求锐角三角函数的四种方法
人教版九年级下册数学作业课件 第二十八章锐角三角函数 专题:求锐角三角函数常用的3种方法(一题多变)

∴BD=CD=k,AD=2k. ∴tanA=BADD=12.
方法总结:作垂线构造直角三角形时“不破坏”特殊 角(30°,45°,60°),如下展示部分常见构造方 法:
题型二 不含特殊角的非直角三角形 3.(1)[延长+连接线段构造直角三角形]如图,在正 方形网格中,已知△ABC 的三个顶点均在格点上, 则∠ACB 的正切值为( D )
◆类型一 构造直角三角形求解 题型一 含特殊角的非直角三角形 1.如图,在△ABC 中,∠B=45°,∠A=75°, AC=8,求 BC 和 AB 的长. 解:如图,过点 A 作 AD⊥BC,垂足为点 D. ∵在 Rt△ABD 中,∠B=45°, ∴∠BAD=45°,BD=AD,AB= 2AD. ∵∠BAC=75°,
2
2
∴AE=125x.
∴tan∠CAD=EACE=15.
◆类型三 利用等角转化求解【转化思想】 7.如图,CD 是 Rt△ABC 斜边 AB 上的高,AC=8, BC=6,则 cos∠BCD 的值是( D ) A.3 B.3 C.4 D.4
543 5
8.如图,在△ABC 中,AC=BC,过点 C 作 CD⊥AB,
(3)[利用垂径定理构造直角三角形]如图,⊙O 为△ABC
的外接圆,⊙O 的半径为 5,BC=8,则 cosA 的值为
3 5
.
10.如图,在矩形 ABCD 中,AB=2,BC=2 5,E 是 BC 的中点,将△ABE 沿直线 AE 翻折,点 B 落在点 F 处,连接 CF,求 cos∠ECF 的值.
A.2
B.2 5 5
C.
5 5
D.12
(2)如图,△ABC 的三个顶点都在正方形网格线的交 点处,将△ABC 绕着点 A 逆时针旋转得到△AB′C′. 若 A,C,B′三点共线,则 tan∠B′CB= 2 ;
专题01 锐角三角形函数和特殊角的三角函数值压轴题四种模型全攻略(解析版)

专题01 锐角三角形函数和特殊角的三角函数值压轴题四种模型全攻略考点一 正弦、余弦、正切的概念辨析 考点二 求角的正弦值、余弦值、正切值考点三 已知正弦值、余弦值、正切值求边长考点四 求特殊角的三角函数值考点一 正弦、余弦、正切的概念辨析A .sin BCA AB=B .A.CDACB.BDCB【答案】C【分析】根据已知可得∠B=∠ACD 【详解】A.∵CD⊥AB,【点睛】本题考查了锐角三角函数,熟练掌握锐角三角函数只与角度大小有关与角度位置无关是解题的关键.考点二求角的正弦值、余弦值、正切值【答案】5 5【分析】连接AC,根据格点特点得出答案.【详解】解:连接AC(1)求证:四边形OCEB 是矩形;(2)连接DE ,当5AB =,【答案】(1)见解析Q 四边形ABCD 是菱形,OA OC \=,OB OD =在Rt AOB △中,5AB =考点三 已知正弦值、余弦值、正切值求边长Q ∠C =90°,AB =sin 8BC BC A AB \===解得:6BC =,故选:A .【答案】5【分析】根据5sin13A=,可设【详解】解:∵5sin A=,sin【点睛】本题考查锐角三角函数和勾股定理,熟练掌握锐角三角函数的定义和勾股定理的计算是解答本题的关键.3.(2022·安徽宿州【答案】46【分析】首先根据考点四求特殊角的三角函数值A.1B.2【点睛】本题主要考查了求正切,勾股定理,三角形面积,正确求出5.(2022·山东·济南高新区东城逸家初级中学九年级阶段练习)在那么下列结论正确的是(A.3sin4A=B.A.1 2【答案】C【分析】先证四边形90 BFE CÐ=Ð=°【答案】34##0.75【分析】作AB x ^轴,在Rt 【详解】解:如图,作AB ^在Rt AOB V 中,3tan 4AB OB a ==故答案为:34【点睛】本题考查了锐角三角函数、点的坐标与坐标轴的关系;根据点的坐标构造直角三角形是解题关键.【答案】12【分析】连接CA并延长与圆相交于点O(0,0)得到CD=6,CO=3,由圆周角定理得到【详解】解:连接CA并延长与圆相交于点∵CD为直径,∴∠COD=∠yOx=90°,即x轴交⊙A于点∵直径为6的⊙A经过点C(0,3)和点∴CD=6,CO=3.∵∠OBC=∠CDO,∴∠OBC的正弦值为∠CDO的正弦值,31=【答案】533【分析】当F 与A 点重合时和∵四边形ABCD 为矩形,∴ABC ADC DAB Ð=Ð=Ð∵5AB =,60ACB Ð=°,∴5tan tan 60AB BC ACB ==Ð【答案】30°或90°故答案为:30°或90°.【答案】AC=4,sinA=【分析】根据勾股定理求出【详解】解:∵∠C=90∴22=-=AC AB BC∴10cos 2b A c Ð==∵8c =,cos A Ð(1)求∠ABD的正弦值;(2)求BG的长.【答案】(1)613 65(2)5【分析】(1)过点(2)过点F作FP⊥BD于点∵∠C=90°,又DG平分∠BDC,∴CF=FP,又∠DPF=90°,DF=DF ∴Rt△CDF≌Rt△PDF(∴CD=DP,【点睛】本题考查角平分线的性质,勾股定理求三角形的边长,相似三角形的判定和性质,全等三角形的判定和性质以及锐角三角函数的求解,熟练掌握以上内容并熟练运用是解决问题的关键.20.(2022·湖南·长沙市开福区青竹湖湘一外国语学校三模)我们不妨定义:一组对边平行且一组对角互余的四边形称为“求真四边形步得出结果;(3)根据题意可得DCA CBE Ð=Ð,则△CDF 与△BCF 相似只有DCF CBF V V ∽或FCD CBF V V ∽2种情况,分类讨论即可求解.(1)解:∵四边形ABCD 是求真四边形,∴∠A +∠C =90°,∴∠C =90°-∠A =90°-α,∵AD ∥BC ,∴∠C +∠D =180°,∴∠D =180°-(90°-α)=90°+α;即90D aÐ=°+(2)证明:如图1,延长DE 至G ,连接AE ,∵AB 是⊙O 的直径,∴∠AEB =90°,∴∠DEF +∠AFG =90°,∵四边形ACDE 内接于⊙O ,∴∠AGE +∠DCF =90°,∵ CECE =,∴∠EAC =∠CBE ,∵∠DCA =∠CBE ,∴∠AEG =∠EAC ,∴DE ∥CF ,∴四边形DEFC 是“求真四边形”;(3)解:Q DCA CBE Ð=Ð,∵ CECE =,∴∠EAC =∠CBE ,。
初三锐角三角函数知识点总结、典型例题附带部分答案、练习(精选)
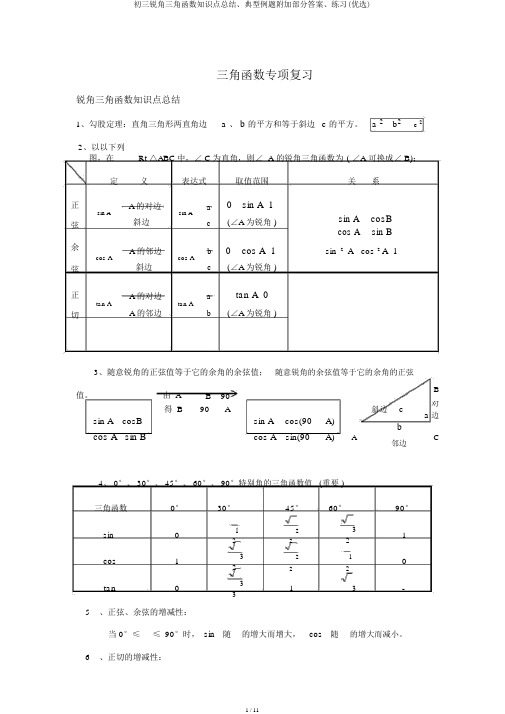
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边 a 、 b 的平方和等于斜边 c 的平方。
a 2 b 2c 22、以以下列图,在Rt △ABC 中,∠ C 为直角,则∠ A 的锐角三角函数为 ( ∠A 可换成∠ B):定 义 表达式取值范围关系正A 的对边 a 0 sin A 1sin A 斜边sin A(∠A 为锐角 )sin A cosB 弦ccos Asin B余A 的邻边 b 0 cos A 1sin 2 A cos 2 A 1cos A 斜边cos A(∠A 为锐角 )弦c正A 的对边atan A 0tan Atan A(∠A 为锐角 )切A 的邻边b3、随意锐角的正弦值等于它的余角的余弦值; 随意锐角的余弦值等于它的余角的正弦值。
由 A B 90 B得 B90A斜边c对a 边sin A cosBsin Acos(90A)bcos A sin Bcos A sin(90A)AC邻边4、 0°、 30°、 45°、 60°、 90°特别角的三角函数值 (重要 )三角函数0° 30°45°60°90°sin0 1 2 3 1 222cos13 2 1 02 22tan0 3 13-35 、正弦、余弦的增减性:当 0°≤≤ 90°时, sin 随 的增大而增大, cos 随的增大而减小。
6 、正切的增减性:当 0° < <90°时, tan随的增大而增大,7、解直角三角形的定义:已知边和角(两个,此中必有一边)→全部未知的边和角。
依照:①边的关系:a2b2c2;②角的关系:A+B=90°;③边角关系:三角函数的定义。
( 注意:尽量防范使用中间数据和除法)8、应用举例:(1)仰角:视野在水平线上方的角;俯角:视野在水平线下方的角。
锐角三角函数的题型及解题技巧

锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础,它应用广泛,解题技巧性强,下面归纳出锐角三角函数的常见题型,并结合例题介绍一些解题技巧。
一、 化简或求值例1 (1)已知tan 2cot 1αα-=,且α的值。
(2)化简()()22sin cos cos sin a b a b αααα++-。
分析 (1)由已知可以求出tan α可用1tan cot αα=⋅;(2)先把平方展开,再利用22sin cos 1αα+=化简。
解 (1)由tan 2cot 1αα-=得2tan 2tan αα-=,解关于tan α的方程得tan 2α=或tan 1α=-。
又α是锐角,∴tan 2α=。
==tan cot αα-。
由tan 2α=,得1cot 2α==tan cot αα-=13222-=。
(2)()()22sin cos cos sin a b a b αααα++-=2222sin 2sin cos cos a ab b αααα+⋅⋅++2222cos 2cos sin sin a ab b αααα-⋅⋅+=()()222222sin cos sin cos a b αααα+++=22a b +。
说明 在化简或求值问题中,经常用到“1”的代换,即22sin cos 1αα+=,tan cot 1αα⋅=等。
二、已知三角函数值,求角例2 在△ABC 中,若223cos sin 022A B ⎛⎫-+-= ⎪ ⎪⎝⎭(),A B ∠∠均为锐角,求C ∠的度数。
分析 几个非负数的和为0,则这几个数均为0。
由此可得cos A 和sin B 的值,进而求出,A B ∠∠的值,然后就可求出C ∠的值。
解 由题意得2cos 0,23sin 0.2A B ⎧-=⎪⎪⎨⎪-=⎪⎩解得2cos ,23sin .3A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角,∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.说明 解这类问题首先要熟记特殊角的三角函数值,还要掌握一些化简的技巧。
九年级数学人教版-8锐角三角函数第5课时求锐角三角函数值的四种常用方法

春季最新PPT课件
1
2
3
4
直接用锐角三角函数的定义求 1 三角函数值 方法 3 1 1.如图,直线y= x+ 与x轴交于点A,与直线y=2x交 2 2 于点B.求:(1)点B的坐标;(2)sin ∠BAO的值.
1 3 y x x 1 解:(1)解方程组 2 2 得 y2 y 2 x ∴点B的坐标为(1,2).
返回
方法
2
利用特殊角求三角函数值
2.由于保管不慎,小明把一道数学题染上了污渍,变成了“ 如图,在△ABC中,∠A=30°,tan B= ,AC= 4 3 ,求AB的长”.这时小明去翻看了标准答案,显示
AB=10.你能帮助小明通过计算说明污渍部分
的内容是什么吗?
解:如图,作CH⊥AB于H.
在Rt△ACH中,CH=AC· sin A=4 3 ×sin 30°=2 3 , AH=AC· cos A=4 3×cos 30°=6, ∴BH=AB-AH=4. CH 3 ∴tan B= . BH 2 3 ∴污渍部分的内容是 . 2
∵BC是直径,∴CD⊥AB.
∵AC=BC,∴D是AB的中点.
又∵O为CB的中点,∴OD∥AC.
∵DF⊥AC,Байду номын сангаасOD⊥EF.
∴直线EF是⊙O的切线.
(2)解:连接BG. ∵BC是直径,∴∠BGC=90°. 在Rt△ACD中,易知AC=10,AD=6, ∴DC= AC 2 AD2 102 62 =8.
(2)过点B作BC⊥x轴于点C,
则OC=1,BC=2. 1 3 由 x+ =0,得x=-3, 2 2 则A(-3,0),∴OA=3.
备考2019年中考数学专题专项突破训练:锐角三角函数的综合(特训篇)(附解析)

中考数学专题训练:锐角三角函数的综合(特训篇)一.选择题1.(2019•郓城县一模)一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α﹣β)=sinα•cosβ﹣cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°==1.类似地,可以求得sin15°的值是()A.B.C.D.2.(2019•东阿县三模)如图,P是∠β的边OA上一点,且点P的坐标为(,1),则tanβ等于()A.B.C.D.3.(2019•西湖区一模)已知△ABC是锐角三角形,若AB>AC,则()A.sin A<sin B B.sin B<sin C C.sin A<sin C D.sin C<sin A 4.(2019•苏州一模)如图,一架无人机航拍过程中在C处测得地面上A,B两个目标点的俯角分别为30°和60°.若A,B两个目标点之间的距离是120米,则此时无人机与目标点A之间的距离(即AC的长)为()A.120米B.米C.60米D.米5.(2019•大渡口区模拟)如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN 和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).则AB的长度约为()(结果精确到0.1米,参考数据:()A.9.4米B.10.6米C.11.4米D.12.6米6.(2019春•宿豫区期中)若2sin A=,则锐角A的度数为()A.30°B.45°C.60°D.75°7.(2019•安丘市一模)已知抛物线y=3x2+1与直线y=4cosα•x只有一个交点,则锐角α等于()A.60°B.45°C.30°D.15°8.(2019•福田区一模)如图,一科珍贵的乌稔树被台风“山竹”吹歪了,处于对它的保护,需要测量它的高度.现采取以下措施:在地面选取一点C,测得∠BCA=45°,AC=20米,∠BAC=60°,则这棵乌稔树的高AB约为()(参考数据: 1.4,≈1.7)A.7米B.14米C.20米D.40米9.(2019•海宁市一模)如图,一块直角三角板和一张光盘竖放在桌面上,其中A是光盘与桌面的切点,∠BAC=60°,光盘的直径是80cm,则斜边AB被光盘截得的线段AD长为()A.20cm B.40cm C.80cm D.80cm 10.(2019•涪城区模拟)如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼钓上的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是()A.3m B. m C. m D.4m 11.(2019•藁城区一模)如图,传送带和地面所成斜坡AB的坡比为1:2,物体沿传送带上升到点B时,距离地面的高度为3米,那么斜坡AB的长度为()A.3米B.5米C.米D.6米12.(2019•河南模拟)如图,斜面AC的坡度(CD与AD的比)为1:2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点之间有一条彩带相连.若AB=13米,则旗杆BC的高度为()A.(+1)米B.5米C.9.5米D.12米二.填空题13.(2019•东阿县二模)如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86nmile 的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处与灯塔P的距离为nmile.(结果保留根号)14.(2019•如皋市一模)如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A,B 的距离,飞机在距海平面垂直高度为100m的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500m,在点D测得端点B的俯角为45°,则岛屿两端A,B 的距离为m(结果保留根号).15.(2019•张家港市模拟)如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏东60°方向行驶12千米至B地,再沿北偏西45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则B,C两地的距离为千米.(结果保留根号)16.(2019•荔湾区一模)如图,在4×4的正方形网格图中有△ABC,则∠ABC的余弦值为.17.(2019•涪城区模拟)如图,△ABC中,∠A=90°,∠ABD=∠ACB,AD=AC,sin∠ABD =.18.(2019•镇海区一模)如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为m(结果保留根号).19.(2019•淮安区模拟)如图,点A(3,m)在第一象限,OA与x轴所夹的锐角为∠1,tan ∠1=,则m的值是.20.(2019•绿园区一模)如图,海面上B、C两岛分别位于A岛的正东和正北方向,A岛与C 岛之间的距离约为36海里,B岛在C岛的南偏东43°,A、B两岛之间的距离约为海里(结果精确到0.1海里)【参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93】三.解答题21.(2019•温岭市一模)某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计, EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)22.(2019•沈北新区一模)在升旗结束后,小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小明从绳子末端C处拿起绳子放在头顶,后退至E点,此时绳子末端D与旗杆的顶端A 成45°仰角,已知小明身高DE=1.5m.求旗杆AB的高度.(结果保留到根号)23.(2019•潮阳区一模)如图,小明站在河岸上的G点,利用测角仪器DG测量小船C到岸边的距离,此时,测得小船C的俯角是∠FDC=30°,若测角仪器DG的高度是2米,BG =1米,BG平行于AC所在的直线,迎水坡AB的坡度i=4:3,坡高BE=8米,求小船C 到岸边的距离CA的长?(结果保留根号)24.(2019•河南模拟)郑东新区是中国河南省郑州市规划建设中的一个城市新区,在2019年春节期间,小明一家人前去观看郑东新区“大玉米”灯光秀.小明想利用刚学过的知识测量大屏幕“新”字的高度:如图,小明先在如意湖湖边A处,测得“新”字底端D 的仰角为58°,再沿着坡面AB向上走到B处,测得“新”字顶端C的仰角为45°,坡面AB的坡度,AB=50m,AE=75m(假设A、B、C、D、E在同一平面内).(1)求点B到水平面的距离BF;(2)求“新”字的高度CD.(结果精确到0.1m,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,,)25.(2019•邛崃市模拟)某市开展一项全民健身跑步运动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向上,C地在A地北偏东75°方向上,且BC=CD=10km,问:沿上述线路从A地到D 地的路程大约是多少?(结果保留1位小数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,,)26.(2019•东阿县三模)一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,准备测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45°,向后退8米到E点,测得条幅底端B 的仰角∠CEB=30°(点C,D,E在同一直线上,EC⊥AC).请你根据以上数据,帮助该兴趣小组计算楼高AC(结果精确到0.01米,参考数据:≈1.732,≈1.414).27.(2019•贵池区二模)如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,)28.(2019•浦东新区二模)如图1,一辆吊车工作时的吊臂AB最长为20米,吊臂与水平线的夹角∠ABC最大为70°,旋转中心点B离地面的距离BD为2米.(1)如图2,求这辆吊车工作时点A离地面的最大距离AH(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75);(2)一天,王师傅接到紧急通知,要求将这辆吊车立即开到40千米远的某工地,因此王师傅以每小时比平时快20千米的速度匀速行驶,结果提前20分钟到达,求这次王师傅所开的吊车速度.29.(2019•海陵区一模)如图,某大楼的顶部竖有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为63°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:3,AB=10米,CD=2米.(1)求点B距地面的高度;(2)求大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据tan63°≈2,≈1.732)30.(2019•洪泽区一模)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行60米到达C处,再测得山顶A的仰角为45°,求山高AD的长度.(测角仪高度忽略不计)参考答案一.选择题1.解:sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=×﹣×=,故选:A.2.解:∵P(,1),∴tanβ==,故选:C.3.解:△ABC是锐角三角形,若AB>AC,则∠C>∠B,则sin B<sin C.故选:B.4.解:设CE=x米,在Rt△ACE中,tan∠CAE=,则AE==x,在Rt△BCE中,tan∠CBE=,则BE==x,由题意得, x﹣x=120,解得,x=60,即CE=60,则AC=2CE=120(米)故选:B.5.解:延长DC交AN于H.∵∠DBH=60°,∠DHB=90°,∴∠BDH=30°,∵∠CBH=30°,∴∠CBD=∠BDC=30°,∴BC=CD=10(米).在Rt△BCH中,CH=BC=5,BH=5≈8.65,∴DH=15,在Rt△ADH中,AH===20,∴AB=AH﹣BH=20﹣8.65≈11.4(米).故选:C.6.解:∵2sin A=∴sin A=∴∠A=45°,故选:B.7.解:根据题意得:3x2+1=4cosα•x,即3x2﹣4cosα•x+1=0,则△=16cos2α﹣4×3×1=0,解得:cosα=,所以α=30°.故选:C.8.解:如图,作BH⊥AC于H.∵∠BCH=45°,∠BHC=90°,∴∠HCB=∠HBC=45°,∴HC=HB,设HC=BH=xm,∵∠A=60°,∴AH=x,∴x+x=20,∴x=10(3﹣),∴AB=2AH=2××10(3﹣)≈14(m)故选:B.9.解:连接DO,AO,过O作OE⊥AD交AD于点E,∵∠BAC=60°,A是光盘与桌面的切点,∴∠OAC=90°,∴∠OAE=30°,∵OA=OD,∴E是AD的中点,在Rt△AEO中,AO=80cm∴AE=40cm,∴AD=80cm;故选:D.10.解:∵sin∠CAB==,∴∠CAB=45°.∵∠C′AC=15°,∴∠C′AB′=60°.∴sin60°==,解得:B′C′=3.故选:B.11.解:作BC⊥地面于点C,设BC=x米,∵传送带和地面所成斜坡AB的坡度为1:2,∴AC=2x米,∵BC=3m,∴AC=6m,∴AB==3(m),故选:A.12.解:设CD=x米,∵斜面AC的坡度为1:2,∴AD=2x,由勾股定理得,x2+(2x)2=()2,解得,x=,∴CD=x=,AD=2x=5,在Rt△ABD中,BD==12,∴BC=BD﹣CD=9.5(米),故选:C.二.填空题(共8小题)13.解:作PC⊥AB于C,在Rt△APC中,cos∠APC=,则PC=PA•cos∠APC=86×=43,在Rt△BCP中,cos∠BPC=,则PB==43(nmile),故答案为:43.14.解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE为矩形.∴AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米.在Rt△AEC中,∠C=60°,AE=100米.∴CE===(米).在Rt△BFD中,∠BDF=45°,BF=100米.∴DF==100(米).∴AB=EF=CD+DF﹣CE=500+100﹣=600﹣(米).答:岛屿两端A、B的距离为(600﹣)米.故答案为:(600﹣).15.解:作BD⊥AC于D,在Rt△ABD中,sin∠DAB=,∴BD=AB•sin∠DAB=6,在Rt△CBD中,cos∠CBD=,∴BC==6(千米),故答案为:6.16.解:设小正方形的边长为1,∵AC==,BC==5,AB==2,∵AB2+AC2=(2)2+()2=25,BC2=52=25,∴AB2+AC2=BC2,∴∠CAB=90°,∴cos∠ABC==;故答案为:.17.解:∵∠A=90°,∠ABD=∠ACB,∴△ABD∽△ACB,∴,∵AD=AC,∴AB=,∴BD=,∴sin∠ABD=,故答案为:.18.解:∵在Rt△ABD中,AD=80,∠BAD=45°,∴BD=AD=80(m),∵在Rt△ACD中,∠CAD=60°,∴CD=AD•tan60°=80×=80(m),∴BC=BD+CD=(80+80)(m)答:该建筑物的高度BC约为=(80+80)米.故答案为:(80+80).19.解:解:作AB⊥x轴于点B.∵A的坐标是(3,m),∴OB=3,AB=m.又∵tan∠1==,即,∴m=5故答案为:520.解:由题意得,AC=36海里,∠ACB=43°.在Rt△ABC中,∵∠A=90°,∴AB=AC•tan∠ACB=36×0.93≈33.5海里.故A、B两岛之间的距离约为33.5海里.故答案为:33.5.三.解答题(共10小题)21.解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠EHG=∠HEF=90°,∵∠AEF=143°,∴∠AEH=∠AEF﹣∠HEF=53°,∠EAH=37°,在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.2米,∴EH=AE•sin∠EAH≈1.2×0.60=0.72(米),∵AB=1.2米,∴AB+EH≈1.2+0.72=1.92>1.9米.∴该地下车库出口的车辆限高标志牌设置如图4合理.22.解:过点D作DFEB交AB于点F,则BF=DE=1.5.设AB=x.在Rt△ABC中,∠ABC=90°,AC===,在Rt△ADF中,∠AFD=90°,AF=x﹣1.5,AD==(x﹣),又AD=AC,∴=(x﹣),解得:x=,即旗杆AB的高为m.23.解:∵坡AB的坡度i=4:3,坡高BE=8,∴AE=6,由题意得,四边形BEHG为矩形,∴GH=BE=8,EH=BG=2,∴DH=DGDG+GH=9,在Rt△DCH中,tan C=,则CH==9,∴AC=CH﹣AE﹣EH=9﹣8,答:小船C到岸边的距离CA的长为(9﹣8)米.24.解:作BH⊥CE于H,∵坡面AB的坡度,∴tan∠BAF=,∴∠BAF=30°,∴BF=AB=25;(2)由勾股定理得,AF==25,在Rt△DAE中,tan∠DAE=,则DE=AE•tan∠DAE≈75,∴BH=FE=25+75,∵∠CBH=45°,∴CH=BH=25+75,∴CD=CH+H E﹣DE=25+75+25﹣120=25﹣20=23.25≈≈23.5(米)25.解:过D作DM⊥AC于M,则∠DAM=45°,∠DCM=60°,∴△BCD为等边三角形,∴BD=BC=CD=10,∵DM⊥AC,∴CM=BM=5,∴AM=DM=CD•cos∠DCM=10×sin60°≈8.5,∴AM+MC+CD=8.5+5+10=23.5答:从A地到D地的路程大约是23.5km.26.解:设AC=x米,则BC=(x﹣10)米,在Rt△ACD中,∠CDA=∠CAD=45°,所以CD=AC=x,在Rt△ECB中,CE=CD+DE=x+8.所以tan∠CEB=,即=tan30°=.解得,x=≈34.59.答:楼高AC约为34.59米.27.解:分别过A、C作AM、CN垂直于EF,垂足为M、N,设EM为xm,则EN为(10+x)m.在Rt△CEN中,tan45°=,∴CN=10+x,∴AM=40+x,在Rt△AEM中,tan37°=,即,解得,x=120,则EF=x+20=140(m)答:电视踏高度EF为140m.28.解:(1)根据题意,得AB =20,∠ABC =70°,CH =BD =2, 在Rt △ACB 中,∵∠ACB =90°,∴AC =AB •sin70°=20×0.94=18.8,∴AH =20.8.答:这辆吊车工作时点A 离地面的最大距离AH 为20.8米;(2)设这次王师傅所开的吊车的速度为每小时x 千米,由题意,得,解得,x 1=60,x 2=﹣40,经检验:x 1=60,x 2=﹣40都是原方程的解,但x 2=﹣40符合题意,舍去, 答:这次王师傅所开的吊车的速度为每小时60千米.29.解:(1)作BG ⊥AE 于点G ,由山坡AB 的坡度i =1:,AB =10,得:BG =5.; (2)可求得AG =,作BF ⊥DE 与点F ,设DE =x 米,在Rt △ADE 中∵tan ∠DAE =, ∴AE =≈x∴EF =BG =5,BF =AG +AE =+x , ∵∠CBF =45°,∴CF =BF ,∴CD +DE ﹣EF =BF ,∴2+x ﹣5=+x , 解得:x =≈23.3(米)答:大楼DE 的高度约为23.3米.30.解:由题意得,∠ABD=30°,∠ACD=45°,BC=60m,设AD=xm,在Rt△ACD中,∵tan∠ACD=,∴CD=AD=x,∴BD=BC+CD=x+60,在Rt△ABD中,∵tan∠ABD=,∴x=(x+60),∴x=30(+1)米,答:山高AD为30(+1)米.。
求锐角三角函数值的常用方法(20200714092427)

第28章锐角三角函数专项训练专训1求锐角三角函数值的常用方法名师点金:锐角三角函数刻画了直角三角形中边和角之间的关系,对于斜三角形,要把它转化为直角三角形求解.在求锐角的三角函数值时,首先要明确是求锐角的正弦值,余弦值还是正切值,其次要弄清是哪两条边的比.直接用锐角三角函数的定义1.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,若CD =5,AC =6,则tan B 的值是() A.45 B.35C.34D.43(第1题)2.如图,在△ABC 中,AD ⊥BC ,垂足是D ,若BC =14,AD =12,tan ∠BAD =34,求sin C 的值.(第2题)3.如图,直线y =12x +32与x 轴交于点A ,与直线y =2x 交于点B.(1)求点B 的坐标;(2)求sin ∠BAO 的值.(第3题)利用同角或互余两角三角函数间的关系4.若∠A 为锐角,且sin A =32,则cos A =() A .1 B.32 C.22 D.125.若α为锐角,且cos α=1213,则sin(90°-α)=() A.513 B.1213 C.512 D.1256.若α为锐角,且sin 2α+cos 230°=1,则α=______.巧设参数7.在Rt △ABC 中,∠C =90°,若sin A =45,则tan B 的值为()A.43B.34C.35D.458.已知,在△ABC 中,∠A ,∠B ,∠C 所对的边长分别为a ,b ,c ,且a ,b ,c 满足b 2=(c +a)(c -a).若5b -4c =0,求sin A +sin B 的值.利用等角来替换9.如图,已知Rt △ABC 中,∠ACB =90°,CD 是斜边AB 的中线,过点A 作AE ⊥CD ,AE 分别与CD ,CB 相交于点H ,E 且AH =2CH ,求sin B 的值.(第9题)专训2同角或互余两角的三角函数关系的应用名师点金:1.同角三角函数关系:sin 2α+cos 2α=1,tan α=sin αcos α. 2.互余两角的三角函数关系:sin α=cos(90°-α),cos α=sin(90°-α),tan α·tan(90°-α)=1.同角间的三角函数的应用1.已知sin Acos A=4,求sin A-3cos A4sin A+cos A的值.2.若α为锐角,sinα-cosα=22,求sinα+cosα的值.余角间的三角函数的应用3.若45°-α和45°+α均为锐角,则下列关系式正确的是() A.sin(45°-α)=sin(45°+α)B.sin2(45°-α)+cos2(45°+α)=1C.sin2(45°-α)+sin2(45°+α)=1D.cos2(45°-α)+sin2(45°+α)=14.计算tan 1°·tan 2°·tan 3°·…·tan 88°·tan 89°的值.同角的三角函数间的关系在一元二次方程中的应用5.已知sinα·cosα=1225(α为锐角),求一个一元二次方程,使其两根分别为sinα和cosα.6.已知α为锐角且sinα是方程2x2-7x+3=0的一个根,求1-2sinαcosα的值.。
初中数学专题:锐角三角函数学习

专题:锐角三角函数一、从梯子的倾斜程度谈起一、知识要点1、解直角三角形的公式:(1)三边关系:a2+b2=c2,(2)角关系:∠A+∠B=_____,(3)边角关系:正弦sinA=ac,余弦 cosA=bc,正切tanA=ab余切 cotA=ba同样:sinB=bc, cosB=ac,tanB=ba,cotB=ab.2.注意:0<sinα=bc<1,0<cosα=_______<1,tanα3.sinα,cosα,tanα,cotα之间的关系:(1)sin2α+cos2α=1,tanα·cotα=1, tanα=sin cosαα(2)sin(90°-α)=cosα,cos(90°-α)=sinα tan(90°-α)=cotα,cot(90°-α)=tanα4、坡度:AB的坡度iAB =ACBC,∠α叫坡角,tanα=i=ACBC二、知识运用典型例题例1.在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA,例2.若三角形三边的比是25:24:7,BAC例3.如图,在△ABC 中,∠C =90°,点D 在BC 上, BD =4,AD =BC ,53cos =∠ADC . 求:(1)DC 的长;(2)B sin 的值.例4.如图2,水库大坝的横断面是梯形,坝顶宽5 m ,坝高20 m ,斜坡AB 的坡度为1∶2.5,斜坡CD 的坡度为1∶2,则坝底宽AD 等于______.AB CDE三、知识运用课堂训练一、填空题:1.在Rt△ABC 中,∠C=90°,AB=3,BC=1,则sinA=______, tanA= _______, cosA=_______.2.在Rt△ABC 中,∠C=90°,tanA=34,则sinB=_______,tanB=______. 3.在△ABC 中,AB=AC=3,BC=4,则tanC=______,cosB=________. 4.在Rt△ABC 中,∠C=90°,AB=41,sinA=941,则AC=______,BC=_______. 5.在△ABC 中,AB=AC=10,sinC=45,则BC=_____. 二、选择题:6.如图,在△ABC 中,∠C=90°,sinA=35, 则BCAC 等于( ) A.34B.43C.35D.457.Rt△ABC 中,∠C=90°,已知cosA=35,那么tanA 等于( ) A.43B.34C.45D.548.已知甲、乙两坡的坡角分别为α、β, 甲坡比乙坡更徒些, 则下列结论正确( )ABC DDB A CE DBACBDACA.tanα<tanβB.sinα<sinβ;C.cosα<cosβD.cosα>cosβ9.如图,在Rt△ABC中,CD是斜边AB上的高,则下列线段的比中不等于sinA的是( )A CDACB.DBCBC.CBABD.CDCB10.某人沿倾斜角为β的斜坡前进100m,则他上升的最大高度是( )mA.100sinβB.100sinβ⋅ C.100cosβD.100cosβ⋅三、解答题:11.在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a、b、c,且a=24,c= 25,求sinA、cosA、tanA、sinB、cosB、tanB的值.12.如图,在菱形ABCD中,AE⊥BC于E,EC=1,sinB=513, 求菱形的边长和四边形AECD的周长.13.如图,已知四边形ABCD中,BC=CD=DB,∠ADB=90°,cos∠ABD=45.求: ABD BCDS S∆∆:.二、30°,45°,60°角的三角函数值一、知识要点:特殊角三角函数值:CB A例1、1、(2007山东济宁)计算45tan 30cos 60sin -的值是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(六) 求锐角三角函数的四种方法► 方法一 运用定义求锐角三角函数值1.如图6-ZT -1,在Rt △ABC 中,∠C =90°,BC =3,AC =4,那么sin A 的值为( ) A .34 B .43 C .35 D .45图6-ZT -1 图6-ZT -22.如图6-ZT -2,在Rt △ABC 中,CD 是斜边AB 上的中线.若CD =5,AC =6,则tan B 的值是( )A .45B .35C .34D .433.a ,b ,c 是△ABC 中∠A ,∠B ,∠C 的对边,且a ∶b ∶c =1∶2∶3,则cos B 的值为( )A .63 B .33 C .22 D .244.如图6-ZT -3,△ABC 的顶点都在小正方形组成的网格的格点上,则cos C 的值为( )图6-ZT -3A .12B .32C .55D .2 555.如图6-ZT -4,在△ABC 中, ∠C =90°,BC =3,AB =5,求sin A ,cos A ,tan A 的值.图6-ZT -46.如图6-ZT -5,在正方形ABCD 中,M 是AD 的中点,BE =3AE ,试求sin ∠ECM 的值.图6-ZT -5► 方法二 利用互余两角三角函数的关系求锐角三角函数值 7.在△ABC 中,cos A =513,则sin (90°-∠A)的值为( )A .513B .1213C .813D .5128.小明在某次作业中得到如下结果: sin 27°+sin 283°≈0.122+0.992=0.9945, sin 222°+sin 268°≈0.372+0.932=1.0018, sin 229°+sin 261°≈0.482+0.872=0.9873,sin 237°+sin 253°≈0.602+0.802=1.0000, sin 245°+sin 245°=(22)2+(22)2=1. 据此,小明猜想:对于任意锐角α,均有sin 2α+sin 2(90°-α)=1. (1)当α=30°时,说明sin 2α+sin 2(90°-α)=1是否成立;(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.► 方法三 利用等角求锐角三角函数值9.如图6-ZT -6,已知l 1∥l 2∥l 3,相邻两条平行直线间的距离相等.若等腰直角三角形ABC 的三个顶点分别在这三条平行直线上,则sin α的值是( )A .13B .617C .55D .1010图6-ZT -6 图6-ZT -710.如图6-ZT -7,在△ABC 中,AB =AC =5,BC =8.∠ABC 和∠ACD 的平分线交于点P ,则tan P =________.11.如图6-ZT-8,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A 作AE⊥CD,AE与CD,CB分别相交于点H,E,且AH=2CH.(1)求sin B的值;(2)如果CD=5,求BE的长.图6-ZT-812.如图6-ZT-9,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D.(1)求AD的长;(2)求cos∠DBC的值.图6-ZT-9 ►方法四利用同角三角函数的关系求锐角三角函数值13.若∠A为锐角,且sin A=32,则cos A的值为()A .1B .32 C .22 D .1214.在△ABC 中,∠C =90°,如果sin A =35,那么tan A 的值为( )A .34B .54C .35D .4315.已知tan α=25,α是锐角,求tan (90°-α),sin α,cos α的值.16.计算:sin 215°+cos 215°-cos 30°tan 60°.教师详解详析1.[解析] C 在Rt △ABC 中,由勾股定理,得AB =32+42=5,所以sin A =BC AB =35.故选C.2.C3.[解析] B 设a =k ,则b =2k ,c =3k ,则a 2+b 2=k 2+(2k )2=3k 2,c 2=(3k )2=3k 2,∴a 2+b 2=c 2,∴△ABC 是直角三角形,且∠C =90°,∴cos B =a c =k 3k =33.故选B.4.[解析] D 设每个小正方形的边长均为1.如图,过点A 作AD ⊥BC ,交CB 的延长线于点D ,则AD =2,CD =4,∴AC =AD 2+CD 2=22+42=2 5,故cos C =CD AC =42 5=2 55.5.解:∵在Rt △ABC 中,∠C =90°,BC =3,AB =5, ∴AC =52-32=4,∴sin A =BC AB =35,cos A =AC AB =45,tan A =BC AC =34.6.解:设AE =x ,则BE =3x ,BC =4x ,AM =DM =2x ,CD =4x , ∴CE =(3x )2+(4x )2=5x ,EM =x 2+(2x )2=5x ,CM =(2x )2+(4x )2=2 5x , ∴EM 2+CM 2=CE 2,∴△CEM 是直角三角形,且∠CME =90°,∴sin ∠ECM =EM CE =55.7.A8.[解析] (1)将α=30°代入,根据三角函数值计算可得; (2)α和90°-α互余,由此可在直角三角形中根据勾股定理验证.解:(1)当α=30°时,sin 2α+sin 2(90°-α)=sin 230°+sin 260°=(12)2+(32)2=1.(2)小明的猜想成立,证明如下:如图,在△ABC 中,∠C =90°,设∠A =α,则∠B =90°-α.∴sin 2α+sin 2(90°-α)=(BC AB )2+(AC AB )2=BC 2+AC 2AB 2=AB 2AB2=1.9.[解析] D 如图所示,过点A 作AD ⊥l 1于点D ,交l 2于点F ,则AF ⊥l 2,过点B 作BE ⊥l 1于点E ,设l 1和l 2之间的距离为1,则l 2和l 3之间的距离也为1.∵∠CAD +∠ACD =90°,∠BCE +∠ACD =90°,∴∠CAD =∠BCE .在等腰直角三角形ABC 中,AC =CB .在△ACD 和△CBE 中,∵⎩⎨⎧∠CAD =∠BCE ,∠ADC =∠CEB =90°,AC =CB ,∴△ACD ≌△CBE , ∴CD =BE =1.在Rt △ACD 中,AC =AD 2+CD 2=5,在等腰直角三角形ABC 中, AB =AC 2+CB 2=10,∴sin α=sin ∠ABF =AF AB =110=1010.10.[答案] 43[解析] ∵∠ACD =∠BAC +∠ABC ,CP 平分∠ACD , BP 平分∠ABC ,∠PCD =∠PBC +∠P , ∴2(∠PBC +∠P )=∠BAC +∠ABC , ∴∠P =12∠BAC .如图,过点A 作AE ⊥BC 于点E .∵AB =AC =5,∴BE =12BC =12×8=4,∠BAE =12∠BAC .∵∠P =12∠BAC ,∴∠P =∠BAE .在Rt △BAE 中,由勾股定理,得AE =AB 2-BE 2=52-42=3, ∴tan P =tan ∠BAE =BE AE =43.11.解:(1)∵在Rt △ABC 中,CD 是斜边AB 上的中线, ∴CD =AD =BD ,∴∠DCB =∠B . ∵AE ⊥CD ,∴∠AHC =90°, ∴∠ACD +∠CAH =90°.∵∠ACD +∠DCB =90°,∴∠DCB =∠CAH ,∴∠B =∠CAH . 在Rt △ACH 中,AH =2CH ,∴AC =5CH .∴sin B =sin ∠CAH =CH AC =CH 5CH =55.(2)由(1)知sin B =55. ∵CD =5,∴AB =2CD =2 5, ∴AC =2,∴BC =AB 2-AC 2=4. ∵∠B =∠CAH ,∴sin ∠CAH =CE AE =55,∴AE =5CE ,由CE 2+AC 2=(5CE )2, 解得CE =1, ∴BE =BC -CE =3.12.解:(1)设AD =x ,则CD =1-x . ∵∠A =36°,AB =AC , ∴∠ABC =∠C =72°. 又∵BD 平分∠ABC ,∴∠ABD =∠CBD =∠A =36°, ∴∠BDC =∠C =72°,BD =AD , ∴BC =BD =AD =x ,△ABC ∽△BCD , ∴AB BC =BCCD,∴BC 2=AB ·CD , 即x 2=1-x ,解得x =5-12(负值已舍去). 即AD =5-12. (2)过点D 作DE ⊥AB 于点E .∵BD =AD ,∴AE =BE =12.在Rt △ADE 中,cos ∠DBC =cos A =AEAD =5+14.13.D14.[解析] A ∵sin A =35,∴cos A =1-sin 2A =1-⎝⎛⎭⎫352=45,∴tan A =sin A cos A =3545=34.故选A.15.解:如图所示,tan B =tan α=25.设AC =2x ,则BC =5x ,则AB =29x , ∴tan(90°-α)=tan A =5x 2x =52,sin α=AC AB =2x 29x =22929,cos α=BC AB =5x 29x =52929.16.解:原式=1-32×3=-12.。
