2015年东北三省三校高考数学二模试卷(理科)
东北三省四市教研联合体2015届高考数学二模试卷理(含解析)(精)

东北三省四市教研联合体2015届高考数学二模试卷(理科)项是符合题目要求的1. (5 分)已知集合 A={x| - K x w 1},2. (5分)设复数z=1+i (i 是虚数单位) A. 1+iB . 1 - i,则上 +z 2=()zC. - 1 - iD. - 1+i2 2 24. (5分)已知△ ABC 中,内角A, B , C 的对边分别为 a , b , c ,若a =b+c - be , bc=4,则厶ABC的面积为()、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选項中,只有 A. [ - 1, 0] B . [ - 1, 2]C. [0 , 1]D.(-8,1] U [2 , +s )3. (5分) 已知|目|=1 , | b |=逅,且◎丄(◎ - b ),贝U 向量扫与向量b 的夹角为()A. B .4B={x|x 2 -2x < 0},贝U AA B=()A.B . 1 2A.:5C.二1, 3, 4} , b € {1 , 2},则函数 fC.2D. 2(x ) = ( a 2 - 2) x+b 为增函数D.106. (5分)阅读如图所示的程序框图,运行相应的程序,若输出的S为J 则判断框中填写B . n v 6 C. n W6 D. n W85. (5 分)已知 a € { - 2, 0,的概率是()的内容可以是()7. ( 5分)如图,网格纸上小正方形的边长为1粗线画出的是某多面体的三视图,则该多面&( 5分)已知直线y=2 -(x - 1 )与抛物线 C :y 2=4x 交于A, B 两点,点(-1, m ),若 打?「=0, 则 m=() A.-9. ( 5分)对定义在[0 , 1]上,并且同时满足以下两个条件的函数f (x )成为M 函数:①对任意的 x € [0 , 1]恒有 f (x ) >0;②当 x i >0, X 2>0, X 1+X 2WI 时,总有 f (X i +X 2)>f ( x i ) +f (X 2)成立,则下列函数不是M 函数的是()2x22A. f ( x ) =x B . f (x ) =2 - 1 C . f (x ) =ln (x +1) D. f ( x ) =x +1K - 4y+4<010 . ( 5分)在平面直角坐标系中,若P (X , y )满足-2x+y- 10<0,则当xy 取得最大值时,- 2y+2^0点P 的坐标为()A. (4, 2) B . (2, 2) C. (2, 6) D. ( ', 5)22 211. ( 5分)已知双曲线一-二==1 (a > 0, b > 0)与函数y=p 1的图象交于点P ,若函数y=:. a 2 IT的图象在点P 处的切线过双曲线左焦点F ( - 1 , 0),则双曲线的离心率是()A. :「B .C.匚「D.;22 2 212. ( 5分)若对? x , y € [0 , +s),不等式 4ax We X+y -2+e 「y -2+2 恒成立,则实数 是()C. 2 二、填空题:本大题共 4小题,每小题5分,满分20分。
2015哈三中二模 黑龙江省哈尔滨市第三中学2015届高三第二次模拟考试数学(理)试卷 扫描版含答案

2015年哈尔滨市第三中学第二次高考模拟考试数学(理工)答案 一、选择题 二、 1-5 BADBC 6-10CCDDA 11-12 AB二、填空题(13) 39 (14)72 (15)332(16)32 17. (Ⅰ)由c B a B a 3cos 3sin =+,得分2sin 3cos sin 3sin sin C B A B A =+ ),sin(3cos sin 3sin sin B A B A B A +=+分4sin cos 3sin sin B A B A = 分63,3tan π==A A (Ⅱ)分87cos 22222 b A bc c b a =-+=分107212cos 222 -=-+=ab c b a C 分1233tan ,7233sin -==C C18.(Ⅰ)由题知,25.0=a ,设该群中某成员抢到钱数不小于3元为事件A ,则 35.01.025.0)(=+=A P . ………………………………4分 (Ⅱ)(2) 由直方图知,抢到钱数在2元以下的共15人,其中1元以下的有3人. 所以X 可能取值为0,1,2,3,455220)0(315312===C C X P ,455198)1(31521213===C C C X P , 45536)2(31511223===C C C X P 4551)3(31533===C C X P ,……………8分 列为 所以X 的分布…………10分 所以X 的期望为534551345536245519814552200)(=⨯+⨯+⨯+⨯=X E …………………12分19.(Ⅰ)连结C B 1,交1BC 于点M ,则M 为1BC 中点,又D 为AC 中点,故MD ∥1AB ,又因为11BDC AB 平面⊄,1BDC MD 平面⊂,所以1AB ∥面1BDC . ------------------------4分(Ⅱ)以1C 为原点,如图建立空间直角坐标系. 设a AA =1,则)2,0,0(),0,,2(1B a A ,)0,0,2(),0,,1(1A a D ,)2,,2(1-=a A B ,)0,0,1(=DA ,)2,,1(1-=a D B ,)2,0,2(11-=B A ,设平面D AB 1的法向量为),,(z y x m =,则⎪⎩⎪⎨⎧=⋅=⋅01DA m A B m ,得),2,0(a m =, ----------5分同理得平面D B A 11的法向量为),1,(a a n =, ------6分cos 45cos =︒2=a . - ------------------8分)0,2,2(1--=AC ,)2,2,0(=m ,设直线1AC 与平面D AB 1所成角为θ,则21cos sin =θ,︒=30θ. ------------12分 20.126)1(22=+y x ----------4分024)3(1262),(),()2(22222211=--+⇒⎪⎩⎪⎨⎧=+-=my y m y xmy x y x N y x M θθcos 364sin =⋅ON OM ,90οθ=当02121=+y y x x ,0434232)1(,04)(2)1(22221212=++-+-+=++-+m mm m m y y m y y m 315±=m ----------7分 当,90οθ≠θθcos 364sin =⋅ON OM ,364sin ||||=θON OM21362sin ||||21y y ON OM S -===θ,384)(21221=-+y y y y 38324)34(222=+++m m m 0,3=±=m m ,综上所述,0,3=±=m m ,315±=m - ---------12分 21.(Ⅰ)当29=a 时,22)1(125)(++-='x x x x x f ,………………………………2分单调区间为⎪⎭⎫ ⎝⎛21,0和()+∞,2为增函数;⎪⎭⎫ ⎝⎛2,21上为减函数…………………4分(Ⅱ)由22)1(1)2()(++-+='x x x a x x f ,要使)(x f 在),0(+∞上为增函数 只需1)2(2+-+x a x 在),0(+∞恒大于等于0,得xx x a 122++≤恒成立,由421122≥++=++xx x x x ,得实数a 的取值范围为]4,(-∞;……………8分先考察当4=a 时方程32)(2+-=x x x f 的解的个数 由14ln )(++=x x x f 在),0(+∞上为增函数,且21141ln )1(=++=f , 而322+-x x 也当1=x 时得2,且函数322+-=x x y 在)1,0(上递减,所以方程14ln ++x x 322+-=x x 在]1,0(上有且只有一个解1=x ……………9分下面证明方程14ln ++x x 322+-=x x 在),1(+∞上无解易证1ln -<x x 在),1(+∞上恒成立 只需证明-+-322x x 114->+x x 在),1(+∞上恒成立即可, 记24()341F x x x x =-+-+,得()21432)(++-='x x x F , 再记()2142)(++=x x x G ,得()0182)(3>+-='x x G 在),1(+∞上恒成立所以)(x G 在),1(+∞上增,而3)1(=G ,所以)(x F '在),1(+∞上恒正,所以)(x F 在),1(+∞上增,而0)1(=F ,所以-+-322x x 114->+x x 在),1(+∞上成立 综上:当4=a 时,方程1ln ++x ax 322+-=x x 只有一个解……………10分 而当4<a 时,14ln 1ln ++<++x x x a x , 且由上知≤++14ln x x 322+-x x ,所以4<a 时方程无解……………12分22. (Ⅰ)由DBC ACD ∠=∠,得DBC ∆∽分3 DCE ∆DCDB DE DC =,分52 DB DE DC ⋅= (Ⅱ)设M AC OD =⋂222r CM OM =+;分8222 CD CM MD =+分103,12)1(122 ==-+-r r r23. (Ⅰ)由已知[]2,2,1:2-∈-=x x y M ;分2: t y x N =+联立方程有一个解,可得11t +<≤+或54t =-分5(Ⅱ)当2-=t 时,直线N: 2-=+y x ,设M 上点为)1,(200-x x,则823243)21(212002≥++=++=x x x d , 当012x =-,所以所求的最小距离为823分10 24. (Ⅰ)2-=a ,原不等式分1122 +≤-⇔x x31221221≤⇔+≤-⇔+≤-≥x x x x x x 时分3311221221≥⇔+≤-⇔+≤-≤x x x x x x 时综上原不等式的解集为分53,31 ⎥⎦⎤⎢⎣⎡(Ⅱ)323)(+≤++⇔+≤x x a x x x f 分723233232ax a a x x x a x -≤≤--⇔≤+⇔+≤++ 15223123-≤≤-⇔≥-≤--a aa 且分10注明:数学勘误文理第6题,改为文理第19题及答题卡中,立体图形中左下角的改为。
2015年东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(理科)

2015年东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合A={x|﹣2<x<1},B={x|x2﹣2x≤0},则A∩B=()A.{x|0<x<1}B.{x|0≤x<1}C.{x|﹣1<x≤1}D.{x|﹣2<x≤1} 2.(5分)复数=()A.2(+i)B.1+i C.i D.﹣i3.(5分)点M(1,1)到抛物线y=ax2准线的距离为2,则a的值为()A.B.﹣C.或﹣D.﹣或4.(5分)设S n是公差不为零的等差数列{a n}的前n项和,且a1>0,若S5=S9,则当S n最大时,n=()A.6B.7C.10D.95.(5分)执行如图所示的程序框图,要使输出的S值小于1,则输入的t值不能是下面的()A.2012B.2016C.2014D.20156.(5分)下列命题中正确命题的个数是()①对于命题p:∃x∈R,使得x2+x﹣1<0,则¬p:∀x∈R,均有x2+x﹣1>0;②p是q的必要不充分条件,则¬p是¬q的充分不必要条件;③命题“若x=y,则sinx=siny”的逆否命题为真命题;④“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件.A.1个B.2个C.3个D.4个7.(5分)如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.8C.10D.128.(5分)设双曲线的一个焦点为F,虚轴的一个端点为B,焦点F到一条渐近线的距离为d,若|FB|≥d,则双曲线离心率的取值范围是()A.(1,]B.[,+∞)C.(1,3]D.[,+∞)9.(5分)不等式组表示的点集记为A,不等式组表示的点集记为B,在A中任取一点P,则P∈B的概率为()A.B.C.D.10.(5分)设二项式(x﹣)n(n∈N*)展开式的二项式系数和与各项系数和分别为a n,b n,则=()A.2n﹣1+3B.2(2n﹣1+1)C.2n+1D.111.(5分)已知数列{a n}满足a n=n3﹣n2+3+m,若数列的最小项为1,则m 的值为()A.B.C.﹣D.﹣12.(5分)已知函数f(x)=,若函数F(x)=f(x)﹣kx 有且只有两个零点,则k的取值范围为()A.(0,1)B.(0,)C.(,1)D.(1,+∞)二、填空题(本大题共4小题,每小题5分,共20分.)13.(5分)向量,满足||=1,||=,(+)⊥(2﹣),则向量与的夹角为.14.(5分)三棱柱ABC﹣A1B1C1各顶点都在一个球面上,侧棱与底面垂直,∠ACB=120°,CA=CB=2,AA1=4,则这个球的表面积为.15.(5分)某校高一开设4门选修课,有4名同学,每人只选一门,恰有2门课程没有同学选修,共有种不同选课方案(用数字作答).16.(5分)已知函数y=sin(πx+φ)﹣2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知△ABC的面积为2,且满足0<•≤4,设和的夹角为θ.(1)求θ的取值范围;(2)求函数f(θ)=2sin2(+θ)﹣cos2θ的取值范围.18.(12分)为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2频率分布表Ⅰ(1)频率分布表中的①②位置应填什么数?并补全频率分布直方图,再根据频率分布直方图统计这500名志愿者得平均年龄;(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.19.(12分)如图,四棱锥P﹣ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.(Ⅰ)求证:EF∥平面PAD;(Ⅱ)若PA=2,试问在线段EF上是否存在点Q,使得二面角Q﹣AP﹣D的余弦值为?若存在,确定点Q的位置;若不存在,请说明理由.20.(12分)已知椭圆+=1(a>b>0)的左、右焦点为F1、F2,点A(2,)在椭圆上,且AF2与x轴垂直.(1)求椭圆的方程;(2)过A作直线与椭圆交于另外一点B,求△AOB面积的最大值.21.(12分)已知a是实常数,函数f(x)=xlnx+ax2.(1)若曲线y=f(x)在x=1处的切线过点A(0,﹣2),求实数a的值;(2)若f(x)有两个极值点x1,x2(x1<x2),①求证:﹣<a<0;②求证:f(x2)>f(x1)>﹣.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.【选修4-1:几何证明选讲】22.(10分)如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边上的中点,连接OD交圆O与点M.(1)求证:DE是圆O的切线;(2)求证:DE•BC=DM•AC+DM•AB.【选修4-4:坐标系与参数方程】23.已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是(t为参数).(1)求曲线C的直角坐标方程和直线L的普通方程;(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA|•|PB|=1,求实数m的值.【选修4-5:不等式选讲】24.设函数f(x)=|2x﹣1|﹣|x+2|.(1)解不等式f(x)>0;(2)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.2015年东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学一模试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合A={x|﹣2<x<1},B={x|x2﹣2x≤0},则A∩B=()A.{x|0<x<1}B.{x|0≤x<1}C.{x|﹣1<x≤1}D.{x|﹣2<x≤1}【解答】解:∵集合A={x|﹣2<x<1},B={x|x2﹣2x≤0}={x|0≤x≤2},∴A∩B={x|0≤x<1},故选:B.2.(5分)复数=()A.2(+i)B.1+i C.i D.﹣i【解答】解:==i,故选:C.3.(5分)点M(1,1)到抛物线y=ax2准线的距离为2,则a的值为()A.B.﹣C.或﹣D.﹣或【解答】解:抛物线y=ax2化为:x2=,它的准线方程为:y=﹣,点M(1,1)到抛物线y=ax2准线的距离为2,可得|1+|=2,解得a=或﹣.故选:C.4.(5分)设S n是公差不为零的等差数列{a n}的前n项和,且a1>0,若S5=S9,则当S n最大时,n=()A.6B.7C.10D.9【解答】解:由题意可得S9﹣S5=a6+a7+a8+a9=0,∴2(a7+a8)=0,∴a7+a8=0,又a1>0,∴该等差数列的前7项为正数,从第8项开始为负数,∴当S n最大时,n=7故选:B.5.(5分)执行如图所示的程序框图,要使输出的S值小于1,则输入的t值不能是下面的()A.2012B.2016C.2014D.2015【解答】解:模拟执行程序框图,可得程序框图的功能是求S=sin+sin+…sin的值,因为sin的取值以6为周期,且sin+sin+…sin=0,由2012=335*6+2,所以输入的t值是2012时,S=sin+sin=>12014=335*6+4,所以输入的t值是2014时,S=sin+sin+sin+sin=<12015=335*6+5,所以输入的t值是2015时,S=sin+sin+sin+sin+sin=0<12016=335*6+6,所以输入的t值是2016时,S=sin+sin+sin+sin+sin+sin2π=0<1故选:A.6.(5分)下列命题中正确命题的个数是()①对于命题p:∃x∈R,使得x2+x﹣1<0,则¬p:∀x∈R,均有x2+x﹣1>0;②p是q的必要不充分条件,则¬p是¬q的充分不必要条件;③命题“若x=y,则sinx=siny”的逆否命题为真命题;④“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的充要条件.A.1个B.2个C.3个D.4个【解答】解:①对于命题p:∃x∈R,使得x2+x﹣1<0,则¬p:∀x∈R,均有x2+x﹣1≥0,因此不正确;②p是q的必要不充分条件,则¬p是¬q的充分不必要条件,正确;③由于命题“若x=y,则si nx=siny”是真命题,因此其逆否命题也为真命题,正确;④当m=0时,直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直;m≠0时,若两条直线垂直,则=﹣1,解得m=﹣1,可知:“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的充分不必要条件,因此不正确.综上可得:正确命题的个数为:2.故选:B.7.(5分)如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.8C.10D.12【解答】解:由三视图可知该几何体的直观图是三棱锥,其中面VAB⊥面ABC,VE⊥AB,CD⊥AB,且AB=5,VE=3,CD=4,则该三棱锥的体积V=×AB•CD•VE==10,故选:C.8.(5分)设双曲线的一个焦点为F,虚轴的一个端点为B,焦点F到一条渐近线的距离为d,若|FB|≥d,则双曲线离心率的取值范围是()A.(1,]B.[,+∞)C.(1,3]D.[,+∞)【解答】解:设F(c,0),B(0,b),一条渐近线的方程为bx+ay=0,则d==b,|FB|=,因为|FB|≥d,所以≥b,所以c2≥2c2﹣2a2,所以2a2≥c2,所以1<e≤.故选:A.9.(5分)不等式组表示的点集记为A,不等式组表示的点集记为B,在A中任取一点P,则P∈B的概率为()A.B.C.D.【解答】解:分别画出点集A,B如图,A对应的区域面积为4×4=16,B对应的区域面积如图阴影部分面积为=()|=,由几何概型公式得,在A中任取一点P,则P∈B的概率为;故选:A.10.(5分)设二项式(x﹣)n(n∈N*)展开式的二项式系数和与各项系数和分别为a n,b n,则=()A.2n﹣1+3B.2(2n﹣1+1)C.2n+1D.1【解答】解:由于二项式(x﹣)n(n∈N*)展开式的二项式系数和与各项系数和分别为a n、b n,则a n =2n,b n =2﹣n,所以===2n+1故选:C.11.(5分)已知数列{a n}满足a n=n3﹣n2+3+m,若数列的最小项为1,则m 的值为()A.B.C.﹣D.﹣【解答】解:数列a n=n3﹣n2+3+m,令f(x)=x3﹣x2+3+m,(x≥1).f′(x)=x2﹣x,由f′(x)>0,解得x>,此时函数f(x)单调递增;由f′(x)<0,解得1≤x<,此时函数f(x)单调递减.∴对于f(n)来说,最小值只能是f(2)或f(3)中的最小值.f(3)﹣f(2)=9﹣﹣(﹣5)>0,∴f(2)最小,∴×8﹣5+3+m=1,解得m=.故选:B.12.(5分)已知函数f(x)=,若函数F(x)=f(x)﹣kx 有且只有两个零点,则k的取值范围为()A.(0,1)B.(0,)C.(,1)D.(1,+∞)【解答】解:由题意,x≥0,f(x)=为双曲线4y2﹣x2=1在第一象限的部分,渐近线方程为y=±x;当k=1时,由y=﹣ln(1﹣x),可得y′==1可得x=0,即y=﹣ln(1﹣x)在x=0处的切线方程为y=x,此时函数F(x)=f(x)﹣kx有且只有1个零点,∴若函数F(x)=f(x)﹣kx有且只有两个零点,则k的取值范围为(,1),故选:C.二、填空题(本大题共4小题,每小题5分,共20分.)13.(5分)向量,满足||=1,||=,(+)⊥(2﹣),则向量与的夹角为90°.【解答】解:因为||=1,||=,(+)⊥(2﹣),所以(+)•(2﹣)=2+﹣=0,则2+﹣2=0,即=0,所以,则向量与的夹角为90°,故答案为:90°.14.(5分)三棱柱ABC﹣A1B1C1各顶点都在一个球面上,侧棱与底面垂直,∠ACB=120°,CA=CB=2,AA1=4,则这个球的表面积为64π.【解答】解:在△ABC中,∠ACB=120°,CA=CB=2,由余弦定理可得AB=6,由正弦定理,可得△ABC外接圆半径r=2,设此圆圆心为O′,球心为O,在RT△OAO′中,得球半径R==4,故此球的表面积为4πR2=64π.故答案为:64π.15.(5分)某校高一开设4门选修课,有4名同学,每人只选一门,恰有2门课程没有同学选修,共有84种不同选课方案(用数字作答).【解答】解:恰有2门选修课没有被这4名学生选择,先从4门课中任选2门,为=6种,四个学生选这两种课共有24=16中,排除四个人全选其中一门课程为16﹣2=14种,故有14=84种.故答案为:84.16.(5分)已知函数y=sin(πx+φ)﹣2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=.【解答】解:y=sin(πx+φ)﹣2cos(πx+φ)=[sin(πx+φ)﹣cos(πx+φ)],令sinα=,cosα=,则y=[sin(πx+φ)cosα﹣cos(πx+φ)sinα]=sin(πx+φ﹣α),∵函数的图象关于直线x=1对称,∴π+φ﹣α=+kπ,即φ=α﹣+kπ,则sin2φ=sin2(α﹣+kπ)=sin(2α﹣π+2kπ)=sin(2α﹣π)=﹣sin2α=﹣2sinαcosα=﹣2××=,故答案为:三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知△ABC的面积为2,且满足0<•≤4,设和的夹角为θ.(1)求θ的取值范围;(2)求函数f(θ)=2sin2(+θ)﹣cos2θ的取值范围.【解答】解:(1)由题意可得•=cbcosθ,∵△ABC的面积为2,∴bcsinθ=2,变形可得cb=,∴•=cbcosθ==,由0<•≤4,可得0<≤4解得tanθ≥1,又∵0<θ<π,∴向量夹角θ的范围为[,);(2)化简可得f(θ)=2sin2(+θ)﹣cos2θ=2×﹣cos2θ=1+sin2θ﹣cos2θ=1+2sin(2θ﹣)∵由(1)知θ∈[,),∴2θ﹣∈[,),∴sin(2θ﹣)∈[,1],∴1+2sin(2θ﹣)∈[2,3],∴f(θ)的取值范围为:[2,3]18.(12分)为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2频率分布表Ⅰ(1)频率分布表中的①②位置应填什么数?并补全频率分布直方图,再根据频率分布直方图统计这500名志愿者得平均年龄;(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.【解答】解:(1)由题意知频率分布表中的①位置应填数字为:100﹣5﹣20﹣30﹣10=35,②位置应填数字为:=0.30.补全频率分布直方图,如右图所示.平均年龄估值为:(45×0.05+55×0.2+65×0.35+75×0.3+85×0.1)=33.5(岁).(2)由表知,抽取的20人中,年龄低于30岁的有5人,故X的可能取值为0,1,2,P(X=0)==,P(X=1)==,P(X=2)==,∴X的分布列为:EX==.19.(12分)如图,四棱锥P﹣ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.(Ⅰ)求证:EF∥平面PAD;(Ⅱ)若PA=2,试问在线段EF上是否存在点Q,使得二面角Q﹣AP﹣D的余弦值为?若存在,确定点Q的位置;若不存在,请说明理由.【解答】证明:(Ⅰ)取PD中点M,连接MF、MA,在△PCD中,F为PC的中点,∴MF,正方形ABCD中E为AB中点,∴AE,∴AE MF,故四边形EFMA为平行四边形,∴EF∥AM,又∵EF⊄平面PAD,AM⊂平面PAD,∴EF∥平面PAD;(Ⅱ)结论:满足条件的Q存在,是EF中点.理由如下:如图:以点A为坐标原点建立空间直角坐标系,则P(0,0,2),B(0,1,0),C(1,1,0),E(0,,0),F(,,1),由题易知平面PAD的法向量为=(0,1,0),假设存在Q满足条件:设=λ,∵=(,0,1),∴Q(,,λ),=(,,λ),λ∈[0,1],设平面PAQ的法向量为=(x,y,z),由,可得=(1,﹣λ,0),∴==,由已知:=,解得:,所以满足条件的Q存在,是EF中点.20.(12分)已知椭圆+=1(a>b>0)的左、右焦点为F1、F2,点A(2,)在椭圆上,且AF2与x轴垂直.(1)求椭圆的方程;(2)过A作直线与椭圆交于另外一点B,求△AOB面积的最大值.【解答】解:(1)有已知:c=2,∴a=,b2=4,故椭圆方程为;(2)当AB斜率不存在时:,当AB斜率存在时:设其方程为:,由得,由已知:△=16﹣8(2k2+1)=8,即:,|AB|=•,O到直线AB的距离:d=,==,∴S△AOB∴2k2+1∈[1,2)∪(2,+∞),∴,∴此时,综上所求:当AB斜率不存在或斜率存在时:△AOB面积取最大值为.21.(12分)已知a是实常数,函数f(x)=xlnx+ax2.(1)若曲线y=f(x)在x=1处的切线过点A(0,﹣2),求实数a的值;(2)若f(x)有两个极值点x1,x2(x1<x2),①求证:﹣<a<0;②求证:f(x2)>f(x1)>﹣.【解答】(1)解:由已知可得,f′(x)=lnx+1+2ax(x>0),切点P(1,a),f(x)在x=1处的切线斜率为k=1+2a,切线方程:y﹣a=(2a+1)(x﹣1),把(0,﹣2)代入得:a=1;(2)证明:①依题意:f′(x)=0 有两个不等实根x1,x2(x1<x2),设g(x)=lnx+2ax+1 则:g′(x)=+2a(x>0)当a≥0时,有g′(x)>0,所以g(x)是增函数,不符合题意;当a<0时:由g′(x)=0得:x=﹣>0,列表如下:依题意:g(﹣)=ln(﹣)>0,解得:﹣<a<0,综上可得,﹣<a<0得证;②由①知:f(x),f′(x)变化如下:由表可知:f(x)在[x1,x2]上为增函数,所以:f(x2)>f(x1)又f′(1)=g(1)=1+2a>0,故x1∈(0,1),由(1)知:ax1=,f(x1)=x1lnx1+ax12=(x1lnx1﹣x1)(0<x1<1)设h(x)=(xlnx﹣x)(0<x<1),则h′(x)=lnx<0成立,所以h(x)单调递减,故:h(x)>h(1)=﹣,也就是f(x1)>﹣综上所证:f(x2)>f(x1)>﹣成立.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.【选修4-1:几何证明选讲】22.(10分)如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边上的中点,连接OD交圆O与点M.(1)求证:DE是圆O的切线;(2)求证:DE•BC=DM•AC+DM•AB.【解答】证明:(1)连接BE,OE,∵AB是直径,∴∠AEB=90°,∵∠ABC=90°=∠AEB,∠A=∠A,∴△AEB∽△ABC,∴∠ABE=∠C,∵BE⊥AC,D为BC的中点,∴DE=BD=DC,∴∠DEC=∠DCE=∠ABE=∠BEO,∠DBE=∠DEB,∴∠BEO+∠DEB=∠DCE+∠CBE=90°,∴∠OED=90°,∴DE是圆O的切线.(2)证明:∵O、D分别为AB、BC的中点,∴DM=OD﹣OM=(AC﹣AB),∴DM•AC+DM•AB=DM•(AC+AB)=(AC﹣AB)•(AC+AB)=(AC2﹣AB2)=BC2=DE•BC.∴DE•BC=DM•AC+DM•AB.【选修4-4:坐标系与参数方程】23.已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是(t为参数).(1)求曲线C的直角坐标方程和直线L的普通方程;(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA|•|PB|=1,求实数m的值.【解答】解:(1)曲线C的极坐标方程是ρ=2cosθ,化为ρ2=2ρcosθ,可得直角坐标方程:x2+y2=2x.直线L的参数方程是(t为参数),消去参数t可得.(2)把(t为参数),代入方程:x2+y2=2x化为:+m2﹣2m=0,由△>0,解得﹣1<m<3.∴t1t2=m2﹣2m.∵|PA|•|PB|=1=|t1t2|,∴m2﹣2m=±1,解得,1.又满足△>0.∴实数m=1,1.【选修4-5:不等式选讲】24.设函数f(x)=|2x﹣1|﹣|x+2|.(1)解不等式f(x)>0;(2)若∃x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.【解答】解:(1)函数f(x)=|2x﹣1|﹣|x+2|=,令f(x)=0,求得x=﹣,或x=3,故不等式f(x)>0的解集为{x|x<﹣,或x>3}.(2)若存在x0∈R,使得f(x0)+2m2<4m,即f(x0)<4m﹣2m2 有解,由(1)可得f(x)的最小值为f()=﹣3•﹣1=﹣,故﹣<4m﹣2m2 ,求得﹣<m<.。
2015东北四市二模 东北三省四市教研联合体2015届高三第二次模拟考试 全科答案

2015东北四市二模东北三省四市教研联合体2015届高三第二次模拟考试试题及答案语文答案(不全) (2)英语学科答案 (3)数学(文科)参考答案与评分标准 (6)数学(理科)参考答案与评分标准 (11)地理参考答案 (18)历史答案 (21)政治参考答案及评分参考 (23)化学答案 (23)物理答案 (25)生物答案 (29)语文答案(不全)2014—2015年一模考试语文试题参考答案一、现代文阅读(9分)1.(3分)C(不符合题干要求,不属于汉字对中华民族文化的影响的表述)2.(3分)D(汉字不是绝无仅有的表意文字)3.(3分)A(不是“形声字”而是“汉字”的字形少变)二、古代诗文阅读(36分)(一)文言文阅读(19分)4.(3分)A(逾:超过,越过。
)5.(3分)C6.(3分)B(“始终赞同皇帝看法”不准确,“认为可以重惩”应为“皇帝最终听从他的意见,重新拟定了处罚办法”。
)7.(10分)(1)(5分)皇帝责问翟銮,翟銮就叩头谢罪说:“陛下圣明,我要顺从还来不及,有什么建议呢。
”(译出大意给2分;“诘”“谢”“不暇”三处,每译对一处给1分。
)(2)(5分)事毕之后,翟銮归来时装了千辆车的财物,用来赠送权贵,得以再次执掌政事,他的声誉立刻就衰落了。
(译出大意给2分;“竣”“遗”“柄政”三处,每译对一处给1分。
)【参考译文】翟銮,字仲鸣,考中弘治十八年进士。
嘉靖年间,他几经迁升,做了礼部右侍郎。
六年春天,朝廷推举阁臣,世宗有意用张孚敬,(群臣)不赞同。
就命令再一次推举,才提及翟銮。
侍从宦官大多称赞翟銮,皇帝于是越级任用他。
杨一清认为翟銮名望低,请求任用吴一鹏、罗钦顺。
世宗不答应,命令翟銮入值文渊阁。
翟銮刚入内阁时,杨一清辅佐政事,不久孚敬与桂萼入阁,翟銮都小心服事。
孚敬、桂萼都用世宗赐给他们的银章密封上书奏事,唯独翟銮无所进言。
皇帝责问翟銮,翟銮就叩头谢罪说:“陛下圣明,我要顺从还来不及,有什么建议呢。
2015年辽宁省大连市高考数学二模试卷(理科)
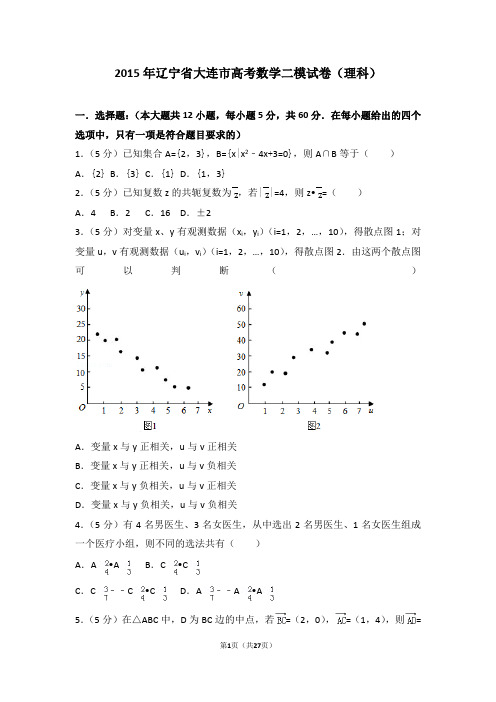
2015年辽宁省大连市高考数学二模试卷(理科)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={2,3},B={x|x2﹣4x+3=0},则A∩B等于()A.{2}B.{3}C.{1}D.{1,3}2.(5分)已知复数z的共轭复数为,若||=4,则z•=()A.4 B.2 C.16 D.±23.(5分)对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关4.(5分)有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.A•A B.C•CC.C﹣﹣C•C D.A﹣﹣A•A5.(5分)在△ABC中,D为BC边的中点,若=(2,0),=(1,4),则=()A.(﹣2,﹣4)B.(0,﹣4)C.(2,4) D.(0,4)6.(5分)如图为一个观览车示意图,该观览车圆半径为4.8m,圆上最低点与地面距离为0.8m,图中OA与地面垂直,以OA为始边,逆时针转动θ(θ>0)角到OB,设B点与地面距离为h,则h与θ的关系式为()A.h=5.6+4.8sinθB.h=5.6+4.8cosθC.h=5.6+4.8cos(θ+)D.h=5.6+4.8sin(θ﹣)7.(5分)如图所示的流程图,最后输出n的值是()A.3 B.4 C.5 D.68.(5分)设F为抛物线C:y2=2px的焦点,过F且倾斜角为60°的直线交曲线C 于A,B两点(B点在第一象限,A点在第四象限),O为坐标原点,过A作C的准线的垂线,垂足为M,则|OB|与|OM|的比为()A.B.2 C.3 D.49.(5分)用一个平面去截正四面体,使它成为形状,大小都相同的两个几何体,则这样的平面的个数有()A.6个 B.7个 C.10个D.无数个10.(5分)已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为()A.B.C.D.11.(5分)定义[X]表示不超过X的最大整数.设n∈N*,且M=(n+1)2+n﹣[]2,则下列不等式恒成立的是()A.M2≥2n+1B.当n≥2时,2M≥4n﹣2C.M2≥2n+1 D.当n≥3时,2M≥2n+212.(5分)对∀x∈(0,),下列四个命题:①sinx+tanx>2x;②sinx•tanx>x2;③sinx+tanx>x;④sinx•tanx>2x2,则正确命题的序号是()A.①、②B.①、③C.③、④D.②、④二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.(5分)如图,设抛物线y=﹣x2+1的顶点为A,与x轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点,则点P落在△AOB内的概率是.14.(5分)若(1﹣3x)2015=a0+a1x+a2x2+…+a2015x2015,则++…+的值为.15.(5分)设点P在曲线y=x2+1(x≥0)上,点Q在曲线y=(x≥1)上,则|PQ|的最小值为.16.(5分)已知双曲线C :﹣=1(a>0,b>0)左右顶点为A1,A2,左右焦点为F1,F2,P为双曲线C上异于顶点的一动点,直线PA1斜率为k1,直线PA2斜率为k2,且k1k2=1,又△PF1F2内切圆与x轴切于点(1,0),则双曲线方程为.三.解答题:(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)已知两个数列{a n},{b n},其中{a n}是等比数列,且a2=,a5=﹣,b n =(1﹣a n).(Ⅰ)求{b n}的通项公式;(Ⅱ)设{b n}的前n项和为S n,求证:S n ≥+.18.(12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如表:甲厂:乙厂:(Ⅰ)由以上统计数据填下面2×2列联表,并问是否有99.9%的把握认为“生产的零件是否为优质品与不同的分厂有关”.附:x2=(Ⅱ)现用分层抽样方法(按优质品和非优质品分二层)从两厂中各抽取五件零件,然后从每个厂的五件产品中各抽取两件,将这四件产品中的优质品数记为X,求X的分布列.19.(12分)在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=.(Ⅰ)求证:BD⊥PC;(Ⅱ)求证:MN∥平面PDC;(Ⅲ)求二面角A﹣PC﹣B的余弦值.20.(12分)如图,已知椭圆C中心在原点,焦点在x轴上,F1,F2分别为左右焦点,椭圆的短轴长为2,过F2的直线与椭圆C交于A,B两点,三角形F1BF2面积的最大值为(a>1).(Ⅰ)求椭圆C的方程(用a表示);(Ⅱ)求三角形F1AB面积的最大值.21.(12分)已知函数f(x)=e x﹣ax2+(a﹣e+1)x﹣1,(e=2.71828…是自然对数的底数,a为常数).(Ⅰ)当a=0时,求f(x)的单调区间;(Ⅱ)若函数g(x)=f(x)﹣x•f′(x)在区间[1,+∞)上单调递减,求a的范围(Ⅲ)当a∈(e﹣2,1)时,函数f(x)=e x﹣ax2+(a﹣e+1)x﹣1在区间(0,1)上是否有零点?并说明理由.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.选修4-1:几何证明选讲22.(10分)如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O 于点H,直线HF交BC的延长线于点G.(1)求证:圆心O在直线AD上.(2)求证:点C是线段GD的中点.选修4-4:坐标系与参数方程23.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线C2的参数方程为(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(1)求C1和C2的极坐标方程;(2)已知射线l1:θ=α(0<α<),将l1逆时针旋转得到l2:θ=α+,且l1与C1交于O,P两点,l2与C2交于O,Q两点,求|OP|•|OQ|取最大值时点P 的极坐标.选修4-5:不等式选讲24.已知a和b是任意非零实数.(1)求的最小值.(2)若不等式|2a+b|+|2a﹣b|≥|a|(|2+x|+|2﹣x|)恒成立,求实数x的取值范围.2015年辽宁省大连市高考数学二模试卷(理科)参考答案与试题解析一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={2,3},B={x|x2﹣4x+3=0},则A∩B等于()A.{2}B.{3}C.{1}D.{1,3}【解答】解:由B中方程变形得:(x﹣1)(x﹣3)=0,解得:x=1或x=3,即B={1,3},∵A={2,3},∴A∩B={3},故选:B.2.(5分)已知复数z的共轭复数为,若||=4,则z•=()A.4 B.2 C.16 D.±2【解答】解:设则=a﹣bi,∵||=,∴z•=(a+bi)•(a﹣bi)=a2+b2=42=16.故选:C.3.(5分)对变量x、y有观测数据(x i,y i)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图2.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关【解答】解:由题图1可知,y随x的增大而减小,各点整体呈下降趋势,x与y 负相关,由题图2可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关.故选C4.(5分)有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有()A.A•A B.C•CC.C﹣﹣C•C D.A﹣﹣A•A【解答】解:根据题意,先从4名男医生中选2人,有C42种选法,再从3名女医生中选出1人,有C31种选法,则不同的选法共有C42C31种;故选:B5.(5分)在△ABC中,D为BC边的中点,若=(2,0),=(1,4),则=()A.(﹣2,﹣4)B.(0,﹣4)C.(2,4) D.(0,4)【解答】解:=﹣=﹣=(1,4)﹣(2,0)=(1,4)﹣(1,0)=(0,4),故选:D.6.(5分)如图为一个观览车示意图,该观览车圆半径为4.8m,圆上最低点与地面距离为0.8m,图中OA与地面垂直,以OA为始边,逆时针转动θ(θ>0)角到OB,设B点与地面距离为h,则h与θ的关系式为()A.h=5.6+4.8sinθB.h=5.6+4.8cosθC.h=5.6+4.8cos(θ+)D.h=5.6+4.8sin(θ﹣)【解答】解:过点O作平行于地面的直线l,再过点B作l的垂线,垂足为P,则∠BOP=θ﹣,根据三角函数的定义得:BP=OBsin(θ﹣)=4.8sin(θ﹣)h=4.8+0.8+BP=5.6+4.8sin(θ﹣)故选:D7.(5分)如图所示的流程图,最后输出n的值是()A.3 B.4 C.5 D.6【解答】解:模拟执行程序框图,可得n=1,n=2不满足条件2n>n2,n=3不满足条件2n>n2,n=4不满足条件2n>n2,n=5满足条件2n=32>n2=25,退出循环,输出n的值为5.故选:C.8.(5分)设F为抛物线C:y2=2px的焦点,过F且倾斜角为60°的直线交曲线C 于A,B两点(B点在第一象限,A点在第四象限),O为坐标原点,过A作C的准线的垂线,垂足为M,则|OB|与|OM|的比为()A.B.2 C.3 D.4【解答】解:抛物线C:y2=2px的焦点F(,0),准线为x=﹣,设直线AB:y=(x﹣),联立抛物线方程,消去x,可得y2﹣2py﹣p2=0,设A(x1,y1),B(x2,y2),则y1=﹣p,y2=p,由M(﹣,y1),则|OM|===p,|OB|====p,即有|OB|=3|OM|.故选C.9.(5分)用一个平面去截正四面体,使它成为形状,大小都相同的两个几何体,则这样的平面的个数有()A.6个 B.7个 C.10个D.无数个【解答】解:∵正四面体是中心对称图形,∴平面过正四面体的中心,则分成为形状,大小都相同的两个几何体,可判断这样的平面有无数个,故选;D10.(5分)已知某几何体的三视图如图所示,三视图是边长为1的等腰直角三角形和边长为1的正方形,则该几何体的体积为()A.B.C.D.【解答】解:根据几何体的三视图,得;该几何体是棱长为1的正方体中一三棱锥P﹣ABC,如图所示;∴该三棱锥的体积为××12×1=.故选:A.11.(5分)定义[X]表示不超过X的最大整数.设n∈N*,且M=(n+1)2+n﹣[]2,则下列不等式恒成立的是()A.M2≥2n+1B.当n≥2时,2M≥4n﹣2C.M2≥2n+1 D.当n≥3时,2M≥2n+2【解答】解:∵则n是正整数,∴[]2=[(n+1)(n+2)]2=(n+1)2等式成立,∴M=(n+1)2+n﹣(n+1)2=n>0,对于选项A:M2=n2≥2n+1当n=1不成立,对于选项B:2M=2n≥4n﹣2,当n=3时,不成立对于选项C:M2=n2≥2n+1当n=1不成立,对于选项D:2M=2n≥2n+2,分别画出y=2x与y=2x+1的图象,如图所示,由图象可知,当n≥3时,2M≥2n+2恒成立,故选:D12.(5分)对∀x∈(0,),下列四个命题:①sinx+tanx>2x;②sinx•tanx>x2;③sinx+tanx>x;④sinx•tanx>2x2,则正确命题的序号是()A.①、②B.①、③C.③、④D.②、④【解答】解:①令f(x)=sinx+tanx﹣2x,求导f′(x)=cosx+sec2x﹣2=,∵x∈(0,),∴0<cosx<1,∴f′(x)>0,即函数单调递增,又f(0)=0,∴f(x)>0,∴sinx+tanx﹣2x>0,即sinx+tanx>2x,故①正确;②令f(x)=sinxtanx﹣x2,f′(x)=cosxtanx+sinxsec2x﹣2x=sinx+﹣2x,g(x)=sinx+﹣2x,g′(x)=cosx+﹣2=cosx+﹣2+,由0<x<,则cosx∈(0,1),cosx+>2,则g′(x)>0,g(x)在(0,)递增,即有g(x)>g(0)=0,即f′(x)>0,f(x)在(0,)递增,即有f(x)>f(0)=0,故②正确;③令x=,则sinx+tanx=sin+tan=,x=,由>,故③错误;④令x=,则sinxtanx=,2x2=,<,故④错误.故选A.二.填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.(5分)如图,设抛物线y=﹣x2+1的顶点为A,与x轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点,则点P落在△AOB内的概率是.【解答】解:由已知区域M的面积为=,△AOB 的面积为=,由几何概型可得点P落在△AOB内的概率是;故答案为:.14.(5分)若(1﹣3x)2015=a0+a1x+a2x2+…+a2015x2015,则++…+的值为﹣1.【解答】由(1﹣3x)2015=a0+a1x+a2x2+…+a2015x2015,取x=0,得a0=1,再取x=,得,∴.故答案为:﹣1.15.(5分)设点P在曲线y=x2+1(x≥0)上,点Q在曲线y=(x≥1)上,则|PQ|的最小值为.【解答】解:由y=x2+1,得:x2=y﹣1,x=.所以,y=x2+1(x≥0)与y=互为反函数.它们的图象关于y=x对称.P在曲线y=x2+1上,点Q在曲线y=上,设P(x,1+x2),Q(x,)要使|PQ|的距离最小,则P应在y=x2+1(x≥0)上,又P,Q的距离为P或Q中一个点到y=x的最短距离的两倍.以Q点为例,Q点到直线y=x的最短距离d===.所以当=,即x=时,d取得最小值,则|PQ|的最小值等于2×=.故答案为:.16.(5分)已知双曲线C:﹣=1(a>0,b>0)左右顶点为A1,A2,左右焦点为F1,F2,P为双曲线C上异于顶点的一动点,直线PA1斜率为k1,直线PA2斜率为k2,且k1k2=1,又△PF1F2内切圆与x轴切于点(1,0),则双曲线方程为x2﹣y2=1.【解答】解:设点P是双曲线右支上一点,∴按双曲线的定义,|PF1|﹣|PF2|=2a,若设三角形PF1F2的内切圆心在横轴上的投影为A(x,0),该点也是内切圆与横轴的切点.设B、C分别为内切圆与PF1、PF2的切点.考虑到同一点向圆引的两条切线相等:则有:PF1﹣PF2=(PB+BF1)﹣(PC+CF2)=BF1﹣CF2=AF1﹣F2A=(c+x)﹣(c﹣x)=2x=2a,即x=a所以内切圆的圆心横坐标为a.由题意可得a=1,顶点A1(﹣1,0),A2(1,0),设P(m,n),则m2﹣=1,即n2=b2(m2﹣1),k1k2=1,可得•=1,即有=b2=1,即有双曲线的方程为x2﹣y2=1.故答案为:x2﹣y2=1.三.解答题:(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)已知两个数列{a n},{b n},其中{a n}是等比数列,且a2=,a5=﹣,b n=(1﹣a n).(Ⅰ)求{b n}的通项公式;(Ⅱ)设{b n}的前n项和为S n,求证:S n≥+.【解答】(Ⅰ)解:∵a3==,∴q=﹣,∴a n=a2•q n﹣2=•=,∴b n =[1﹣];(Ⅱ)证明:S n =b 1+b 2+…+b n=﹣[++…+]=﹣•=+[1﹣],当n 为奇数时,S n =+(1+)>+; 当n 为偶数时,S n =+(1﹣)≥+×=+;综上:S n ≥+.18.(12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm )的值落在(29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,结果如表: 甲厂:乙厂:(Ⅰ)由以上统计数据填下面2×2列联表,并问是否有99.9%的把握认为“生产的零件是否为优质品与不同的分厂有关”.附:x2=(Ⅱ)现用分层抽样方法(按优质品和非优质品分二层)从两厂中各抽取五件零件,然后从每个厂的五件产品中各抽取两件,将这四件产品中的优质品数记为X,求X的分布列.【解答】解:(Ⅰ)列联表如下x2=47.619,∵47.619>10.828,∴有99.9%的把握认为“生产的零件是否为优质品与不同的分厂有关”.(6分)(Ⅱ)甲厂有4件优质品,1件非优质品,乙厂有3件优质品,2件非优质品.从两个厂各抽取2件产品,优质品数X的取值为1,2,3,4.P(X=1)==;P(X=2)==;P(X=4)==,所以P(X=3)=1﹣﹣﹣=(10分)所以X的分布列为(12分)19.(12分)在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=.(Ⅰ)求证:BD⊥PC;(Ⅱ)求证:MN∥平面PDC;(Ⅲ)求二面角A﹣PC﹣B的余弦值.【解答】证明:(I)∵△ABC是正三角形,M是AC中点,∴BM⊥AC,即BD⊥AC.又∵PA⊥平面ABCD,∴PA⊥BD.又PA∩AC=A,∴BD⊥平面PAC.∴BD⊥PC.(Ⅱ)在正△ABC中,BM=.在△ACD中,∵M为AC中点,DM⊥AC,∴AD=CD.∠ADC=120°,∴,∴.在等腰直角△PAB中,PA=AB=4,PB=,∴,∴,∴MN∥PD.又MN⊄平面PDC,PD⊂平面PDC,∴MN∥平面PDC.(Ⅲ)∵∠BAD=∠BAC+∠CAD=90°,∴AB⊥AD,分别以AB,AD,AP为x轴,y轴,z轴建立如图的空间直角坐标系,∴B(4,0,0),C,,P(0,0,4).由(Ⅱ)可知,为平面PAC的法向量.,.设平面PBC的一个法向量为,则,即,令z=3,得x=3,,则平面PBC的一个法向量为,设二面角A﹣PC﹣B的大小为θ,则.所以二面角A﹣PC﹣B余弦值为.20.(12分)如图,已知椭圆C中心在原点,焦点在x轴上,F1,F2分别为左右焦点,椭圆的短轴长为2,过F2的直线与椭圆C交于A,B两点,三角形F1BF2面积的最大值为(a>1).(Ⅰ)求椭圆C的方程(用a表示);(Ⅱ)求三角形F1AB面积的最大值.【解答】解:(Ⅰ)由题意,椭圆的上顶点为(0,1),下顶点为(0,﹣1),当B与上(或下)顶点重合时,三角形F1BF2面积最大S==,∴c=,∴椭圆C的方程为;(Ⅱ)三角形F1AB面积S==c•AB•sinα(α为F2B与x轴正向所成的角)设F2(c,0),A(x1,y1),B(x2,y2),AB:y=k(x﹣c),代入椭圆方程可得(1+a2k2)x2﹣2a2k2cx+a2k2c2﹣a2=0,∴x1+x2=,x1x2=∴AB=|x1﹣x2|=,∴S=c•AB•sinα=,a时,S≤=a;1<a<时,S≤=.21.(12分)已知函数f(x)=e x﹣ax2+(a﹣e+1)x﹣1,(e=2.71828…是自然对数的底数,a为常数).(Ⅰ)当a=0时,求f(x)的单调区间;(Ⅱ)若函数g(x)=f(x)﹣x•f′(x)在区间[1,+∞)上单调递减,求a的范围(Ⅲ)当a∈(e﹣2,1)时,函数f(x)=e x﹣ax2+(a﹣e+1)x﹣1在区间(0,1)上是否有零点?并说明理由.【解答】解:(Ⅰ)当a=0时,f(x)=e x+(1﹣e)x﹣1,f′(x)=e x+(1﹣e);∴f(x)的单调增区间为(ln(e﹣1),+∞),f(x)的单调减区间为(﹣∞,ln(e﹣1));(Ⅱ),;∴,x∈[1,+∞);∴g″(x)<0,∴g′(x)在[1,+∞)上单调递减;又g(x)在[1,+∞)上单调递减;∴;∴a≤e﹣1;∴a的范围为(﹣∞,e﹣1];(Ⅲ)假设函数f(x)在区间(0,1)上有零点;即存在x∈(0,1),使得e x﹣ax2+(a﹣e+1)x﹣1=0;即,记;①若h(x)<1,∴,即:;由于x∈(0,1),有x2﹣x<0;即证e x﹣x2+(2﹣e)x﹣1>0在x∈(0,1)恒成立;令H(x)=e x﹣x2+(2﹣e)x﹣1,x∈(0,1);H′(x)=e x﹣2x+2﹣e,H″=e x﹣2;当x∈(0,ln2),H″(x)<0,当x∈(ln2,1),H″(x)>0;∴当x∈(0,ln2),H′(x)单调递减,x∈(ln2,1),H′(x)单调递增;而H′(0)=1﹣0+2﹣e>0,H′(1)=e﹣2+2﹣e=0,H′(ln2)=e ln2﹣2ln2+2﹣e=4﹣e﹣2ln2<0;故在(0,ln2)上存在唯一的实数x0使得H′(x0)=0;所以,在(0,x0)上H(x)单调递增,在(x0,1)上H(x)单调递减;而H(0)=0,H(1)=0;故H(x)>0在(0,1)成立;即成立;②若h(x)>e﹣2;∴,即;由于x∈(0,1),有x2﹣x<0;即证e x﹣(e﹣2)x2﹣x﹣1<0在x∈(0,1)恒成立;令H(x)=e x﹣(e﹣2)x2﹣x﹣1,H′(x)=e x﹣2(e﹣2)x﹣1,H″(x)=e x﹣2(e﹣2);当x∈(0,ln2(e﹣2)),H″(x)<0,H′(x)单调递减;当x∈(ln2(e﹣2),1),H″(x)>0,H′(x)单调递增;而H′(0)=0,H′(1)=3﹣e>0;∴在(ln2(e﹣2),1)上存在唯一的实数x0使得H′(x0)=0;所以,在(0,x0)上H(x)单调递减,在(x0,1)上H(x)单调递增;又H(0)=0,H(1)=0;故H(x)<0在(0,1)成立,即成立.由①②可得,a∈(e﹣2,1)时,h(x)存在零点.请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.选修4-1:几何证明选讲22.(10分)如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O 于点H,直线HF交BC的延长线于点G.(1)求证:圆心O在直线AD上.(2)求证:点C是线段GD的中点.【解答】证明:(1)∵AB=AC,AF=AE∴CD=BE又∵CF=CD,BD=BE∴CF=BD又∵△ABC是等腰三角形,∴AD是∠CAB的角分线∴圆心O在直线AD上.(5分)(II)连接DF,由(I)知,DH是⊙O的直径,∴∠HFD=90°,∴∠FDH+∠FHD=90°又∵∠G+∠FHD=90°∴∠FDH=∠G∵⊙O与AC相切于点F∴∠AFH=∠GFC=∠FDH∴∠GFC=∠G∴CG=CF=CD∴点C是线段GD的中点.(10分)选修4-4:坐标系与参数方程23.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线C2的参数方程为(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.(1)求C1和C2的极坐标方程;(2)已知射线l1:θ=α(0<α<),将l1逆时针旋转得到l2:θ=α+,且l1与C1交于O,P两点,l2与C2交于O,Q两点,求|OP|•|OQ|取最大值时点P 的极坐标.【解答】解:(1)曲线C1的直角坐标方程为(x﹣2)2+y2=4,所以C1极坐标方程为ρ=4cosθ,曲线C2的直角坐标方程为x2+(y﹣2)2=4,所以C2极坐标方程为ρ=4sinθ (2)设点P极点坐标(ρ1,α),即ρ1=4cosα,点Q极坐标为(ρ2,α+),即ρ2=4sin(α+),则|OP||OQ|=ρ1ρ2=4cosα•4sin(α+)=16cosα(sinα+cosα)=8sin(2α+)+4∵α∈(0,),∴2α+∈(,),当2α+=,即α=时,|OP|•|OQ|取最大值,此时P极点坐标(2,).选修4-5:不等式选讲24.已知a和b是任意非零实数.(1)求的最小值.(2)若不等式|2a+b|+|2a﹣b|≥|a|(|2+x|+|2﹣x|)恒成立,求实数x的取值范围.【解答】解:(1)∵≥==4,故的最小值为4.(2)若不等式|2a+b|+|2a﹣b|≥|a|(|2+x|+|2﹣x|)恒成立,即|2+x|+|2﹣x|≤恒成立,故|2+x|+|2﹣x|不大于的最小值.(4分)由(1)可知,的最小值为4,当且仅当(2a+b)(2a﹣b)≥0时取等号,∴的最小值等于4.(8分)∴x的范围即为不等式|2+x|+|2﹣x|≤4的解集.解不等式得﹣2≤x≤2,故实数x的取值范围为[﹣2,2].(10分)。
2015东北四市二模 东北三省四市教研联合体2015届高三第二次模拟考试理科综合试题及答案

2015年东北三省四市教研联合体高考模拟试卷(二)参考答案化学答案一、选择题7 8 9 10 11 12 13D C B A D C A二、非选择题26. (15分)(1)第四周期第VIII 族(2分)(2)TiO2++2H 2O H2TiO3+2H+或者TiO2++2H2O TiO(OH)2+2H+(2分)①防止Fe2+氧化为Fe3+ (1分)②消耗溶液中H+,促使TiO2+的水解平衡正向移动(1分)(3)蒸发浓缩、冷却结晶(2分)(4)TiCl4+(2+x)H2O(过量)TiO2·xH2O ↓+4HCl(2分);加入大量的水并加热,能促进水解趋于完全。
(1分)(5)2Cl--2e- = Cl2↑(2分);2TiCl42TiCl3+ Cl2↑(1分)TiCl4TiCl2+ Cl2↑(1分)(写TiCl2+TiCl4 = 2TiCl3 1分)27.(14分)(1)0.15mol/(L·min) (2分)(2)①ABC (2分)②υ(C)> υ(B)> υ(A) (2分)③4L (2分)(3)2CH4(g)+O2(g)=2CH3OH(g) ΔH=(a+2b)kJ/mol (2分)(4)①2CH3OH+3O2+4OH-=2CO32-+6H2O (2分)②c (K+)>c(CO32-)>c(HCO3-)>c(OH-)>c(H+) (2分)28. (14分)(1)HCOOH 浓硫酸△CO↑ + H2O(2分)(2)验纯(1分) II(1分)(3)继续通入氢气(或答隔绝空气)(1分)(4)9(2分)(5)12(2分)(6)长时间集中加热使局部温度达到还原生成铁所需要的温度(2分,合理答案参考给分)3Fe2O3 + CO △2Fe3O4 + CO2 (1分)Fe2O3 + CO△2FeO + CO2(1分)Fe2O3 + 3CO △2Fe + 3CO2(1分)36. (15分)(1)合成塔(1分)A(2分)(2)C+H2O CO+H2 (2分)(3)防止催化剂中毒(2分)CO32-+CO2+H2O=2HCO3-(2分)(4)在电磁场的作用下,氮氮三键更容易断裂,减少了合成氨反应所需的能量(1分)降低能耗,使反应更容易进行(其他合理答案均给分)(1分)(5)3(2分)2NH3-6e-=N2+6H+(2分)37. (15分)(1)O (1分)N (1分)(2)极性(1分)分子间可以形成氢键(2分)(3)SP2、SP3(各1分,共2分)(2分)(4)8 (2分)列式:(2分)结果:(2分)38. (15分)(1)消去反应(2分);碳碳双键、羧基(各1分,共2分)(2)(2分)(3)(2分)(4)CH2(OH)CH(OH)CH3CH3COCOOH CH3CH(OH)COOH (3分,合理答案参考给分)(5)11 (2分);(2分,其它合理答案也可)2015年三省四市第二次模拟考试参考答案及评分标准物理答案二、选择题:本题共8小题,每小题6分。
2015年普通高中高三第二次联合考试理科数学附答案

BA BC 2 ,则 ABC 的面积为 (
A. 2
2
) C. 2 2 D. 4 2
B.
3 2
(10)已知抛物线 y =2px(p>0)与双曲线 2- 2=1(a>0,b>0)有相同的焦点 F,点 A 是两曲线的一个交点,且 AF⊥x 轴,则双曲线的离心率为( ( ) A. 2+2 B. 5+1 C. 3+1
2015 年普通高中高三第二次联合考试理科数学
注意事项: 1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的 姓名、准考证号填写在答题卡上。 2. 回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号框 涂黑。如 需改动,用橡皮擦干净后,再选涂其它答案标号框。写在本试卷上无效。 3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。 4. 考试结束后,将本试卷和答题卡一并交回。
D. 1,1
第Ⅱ卷
本卷包括必考题和选考题两部分。 第 13 题~第 21 题为必考题, 每个试题考生都必须做 答。第 22 题~第 24 题为选考题,考生根据要求做答。 二、填空题:本大题共 4 小题,每小题 5 分。
(13)若复数 z
(a 2 4) (a 2)i 为纯虚数,则
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只 有一项是符合题目要求的。
(1)设集合 A
x y lg(3 2x),集合 B y y
B. (﹣∞,1] C.
)
A. [ 0, )
3 2
(2) 若命题 p 为真命题,命题 q 为假命题,则以下为真命题的是(
A. p q
【2015长春二模】吉林省长春市普通高中2015届高三质量监测(二)数学(理)试题 Word版含答案

长春市普通高中2015届高三质量监测(二)数 学(理 科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}0x x P =≥,1Q 02x x x ⎧+⎫=≥⎨⎬-⎩⎭,则()RQ P=ð( )A .(),2-∞B .(],1-∞-C .()1,0-D .[]0,2 2、复数12ii--的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3、已知随机变量ξ服从正态分布()21,σN ,若()20.15ξP >=,则()01ξP ≤≤=( )A .0.85 B .0.70 C .0.35 D .0.15 4、已知:p 函数()f x x a =+在(),1-∞-上是单调函数,:q 函数()()log 1a g x x =+(0a >且1a ≠)在()1,-+∞上是增函数,则p ⌝成立是q 成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5、若x ,y 满足约束条件5315153x y y x x y +≤⎧⎪≤+⎨⎪-≤⎩,则35x y +的取值范围是( )A .[]13,15-B .[]13,17-C .[]11,15-D .[]11,17- 6、一个几何体的三视图如图所示,则该几何体的体积为( ) A .163 B .203 C .152 D .1327、已知平面向量a ,b 满足3a =,2b =,3a b ⋅=-,则2a b +=( ) A .1BC .4+D .8、下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为1A 、2A 、⋅⋅⋅⋅⋅⋅、16A ,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )A .6B .10C .91D .929、已知函数()1cos cos 22f x x x x =+,若将其图象向右平移ϕ(0ϕ>)个单位后所得的图象关于原点对称,则ϕ的最小值为( )A .6π B .56π C .12π D .512π10、设m ,R n ∈,若直线()()1120m x n y +++-=与圆()()22111x y -+-=相切,则m n +的取值范围是( )A .(),2222,⎡-∞-++∞⎣ B .(),22,⎡-∞-+∞⎣C .22⎡-+⎣D .(][),22,-∞-+∞11、若()F ,0c 是双曲线22221x y a b-=(0a b >>)的右焦点,过F 作该双曲线一条渐近线的垂线与两条渐近线交于A ,B 两点,O 为坐标原点,∆OAB 的面积为2127a ,则该双曲线的离心率e =( )A .53B .43C .54D .8512、设数列{}n a 的前n 项和为n S ,且121a a ==,(){}2n n nS n a ++为等差数列,则n a =( )A .12n n - B .1121n n -++ C .2121n n -- D .112n n ++ 二、填空题(本大题共4小题,每小题5分,共20分.)13、62x ⎛- ⎝的展开式中常数项为 .14、已知0a >且曲线y =x a =与0y =所围成的封闭区域的面积为2a ,则a = .15、正四面体CD AB 的外接球半径为2,过棱AB 作该球的截面,则截面面积的最小值为 .16、已知函数()f x 为偶函数且()()4f x f x =-,又()235,01222,12x x x x x f x x -⎧--+≤≤⎪=⎨⎪+<≤⎩,函数()12xg x a ⎛⎫=+ ⎪⎝⎭,若()()()F x f x g x =-恰好有4个零点,则a 的取值范围是 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17、(本小题满分12分)在C ∆AB 中,tan 2A =,tan 3B =. ()1求角C 的值;()2设AB =C A .18、(本小题满分12分)根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如下图显示.()1已知[)30,40、[)40,50、[)50,60三个年龄段的上网购物者人数成等差数列,求a ,b 的值;()2该电子商务平台将年龄在[)30,50之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此三人获得代金券总和X 的分布列与数学期望.19、(本小题满分12分)如图,在四棱锥CD P -AB 中,PA ⊥平面CD AB ,D 2PA =AB =A =,四边形CD AB 满足D AB ⊥A ,C//D B A 且C 4B =,点M 为CP 中点,点E 为C B 边上的动点,且CλBE=E . ()1求证:平面D A M ⊥平面C PB ;()2是否存在实数λ,使得二面角D P -E -B 的余弦值为23?若存在,试求出实数λ的值;若不存在,说明理由.20、(本小题满分12分)在C ∆AB 中,顶点()1,0B -,()C 1,0,G 、I 分别是C ∆AB 的重心和内心,且G//C I B . ()1求顶点A 的轨迹M 的方程;()2过点C 的直线交曲线M 于P 、Q 两点,H 是直线4x =上一点,设直线C H 、PH 、Q H 的斜率分别为1k ,2k ,3k ,试比较12k 与23k k +的大小,并加以证明.21、(本小题满分12分)设函数()()()1ln 1f x ax x bx =-+-,其中a 和b 是实数,曲线()y f x =恒与x 轴相切于坐标原点.()1求常数b 的值;()2当01x ≤≤时,关于x 的不等式()0f x ≥恒成立,求实数a 的取值范围;()3求证:10000.41000.5100011001100001000e ⎛⎫⎛⎫<< ⎪⎪⎝⎭⎝⎭.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分. 22、(本小题满分10分)选修4-1:几何证明选讲如图,过点P 作圆O 的割线PBA 与切线PE ,E 为切点,连接AE ,BE ,∠APE 的平分线与AE ,BE 分别交于点C ,D ,其中30∠AEB =.()1求证:D DD CE PB P ⋅=B PA P ; ()2求C ∠P E 的大小.23、(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系x y O 中,曲线1C的参数方程为21x y ⎧=⎪⎨=-+⎪⎩(t 为参数),以原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为ρ=. ()1求曲线1C 的普通方程与曲线2C 的直角坐标方程;()2试判断曲线1C 与2C 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由. 24、(本小题满分10分)选修4-5:不等式选讲 设函数()212f x x x a a =++-+,R x ∈.()1当3a =时,求不等式()7f x >的解集;()2对任意R x ∈恒有()3f x ≥,求实数a 的取值范围.长春市普通高中2015届高三质量监测(二)数学(理科)参考答案及评分标准一、选择题(本大题包括12小题,每小题5分,共60分)1.D2.A3.C4.C5.D6.D7.B8.B9.C 10.A 11.C 12.A 简答与提示:1. 【命题意图】本题主要考查集合交集与补集的运算,属于基础题.【试题解析】D 由题意可知{|1Q x x =-≤或2}x >,则{|12}Q x x =-<≤R ð,所以{|02}P Q x x =≤≤R ð. 故选D.2. 【命题意图】本题考查复数的除法运算,以及复平面上的点与复数的关系,属于基础题.【试题解析】A131255i i i -=--,所以其共轭复数为3155i +. 故选A. 3. 【命题意图】本题考查正态分布的概念,属于基础题,要求学生对统计学原理有全面的认识.【试题解析】C (01)(12)0.5(2)0.35P P P ξξξ==->=≤≤≤≤. 故选C. 4. 【命题意图】本题借助不等式来考查命题逻辑,属于基础题.【试题解析】C 由p 成立,则1a ≤,由q 成立,则1a >,所以p ⌝成立时1a >是q 的充要条件.故选C.5. 【命题意图】本题主要考查线性规划,是书中的原题改编,要求学生有一定的运算能力.【试题解析】D由题意可知,35x y +在(2,1)--处取得最小值,在35(,)22处取得最大值,即35[11,17]x y +∈-.故选D.6. 【命题意图】本题通过正方体的三视图来考查组合体体积的求法,对学生运算求解能力有一定要求.【试题解析】D 该几何体可视为正方体截去两个三棱锥,所以其体积为41138362--=. 故选D.7. 【命题意图】本题考查向量模的运算.【试题解析】B |2|+==a b 故选B.8. 【命题意图】本题考查学生对茎叶图的认识,通过统计学知识考查程序流程图的认识,是一道综合题.【试题解析】B 由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10. 故选B. 9. 【命题意图】本题主要考查三角函数的图像和性质,属于基础题.【试题解析】C由题意()sin(2)6f x x π=+,将其图像向右平移ϕ(0)ϕ>个单位后解析式为()sin[2()]6f x x πϕ=-+,则26k πϕπ-=,即212k ππϕ=+()k ∈N ,所以ϕ的最小值为12π. 故选C.10. 【命题意图】本题借助基本不等式考查点到直线的距离,属于中档题.【试题解析】A由直线与圆相切可知||m n +=1mn m n =++,由2()2m n mn +≤可知211()4m n m n ++≤+,解得(,2[222,)m n +∈-∞-++∞. 故选A.11. 【命题意图】本题主要考查双曲线的几何性质,结合着较大的运算量,属于难题.【试题解析】C 由题可知,过I 、III 象限的渐近线的倾斜角为θ,则tan b aθ=,222tan 2aba b θ=-,因此△OAB 的面积可以表示为3222112tan 227a b a a a a b θ⋅⋅==-,解得34b a =,则54e =. 故选C. 12. 【命题意图】本题是最近热点的复杂数列问题,属于难题.【试题解析】A 设(2)n n n b nS n a =++,有14b =,28b =,则4n b n =,即(2)4n n n b nS n a n =++=当2n ≥时,1122(1)(1)01n n n n S S a a nn ---++-+=- 所以12(1)11n n n n a a n n -++=-,即121n n a a n n -⋅=-,所以{}n a n 是以12为公比,1为首项的等比数列,所以11()2n n a n -=,12n n na -=. 故选A.二、填空题(本大题包括4小题,每小题5分,共20分) 13.60 14.49 15.83π 16.192,8⎛⎫ ⎪⎝⎭简答与提示:13. 【命题意图】本题主要考查二项式定理的有关知识,属于基础题.【试题解析】由题意可知常数项为2246(2)(60C x =. 14. 【命题意图】本题考查定积分的几何意义及微积分基本定理,属于基础题.【试题解析】由题意322023aa x ==⎰,所以49a =.15. 【命题意图】球的内接几何体问题是高考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.【试题解析】由题意,面积最小的截面是以AB 为直径,可求得AB =,进而截面面积的最小值为283ππ=.16. 【命题意图】本题主要考查数形结合以及函数的零点与交点的相关问题,需要学生对图像进行理解,对学生的能力提出很高要求,属于难题.【试题解析】由题意可知()f x 是周期为4的偶函数,对称轴为直线2x =. 若()F x 恰有4个零点,有(1)(1)(3)(3)g f g f >⎧⎨<⎩,解得19(2,)8a ∈.17. (本小题满分12分)【命题意图】本小题主要考查两角和的正切公式,以及同角三角函数的应用,并借助正弦定理考查边角关系的运算,对考生的化归与转化能力有较高要求.【试题解析】解:(1) +,tan tan()A B C C A B π+=∴=-+ (3分)tan 2,tan 3,tan 1,4A B C C π==∴=∴=(6分)(2)因为tan 3B =sin 3sin 3cos cos BB B B⇒=⇒=,而22sin cos 1B B +=,且B 为锐角,可求得sin B =. (9分)所以在△ABC中,由正弦定理得,sin sin AB AC B C =⨯=.(12分)18. (本小题满分12分)【命题意图】本小题主要考查统计与概率的相关知识、离散型随机变量的分布列以及数学期望的求法. 本题主要考查数据处理能力. 【试题解析】(1)由图可知0.035a =,0.025b =. (4分)(2) 利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人. (6分) 从中取出三人,并计算三人所获得代金券的总和X , 则X 的所有可能取值为:150,200,250,300.363101(150)6C P X C ===, 21643101(200)2C C P X C ===,12643103(250)10C C P X C ===, 343101(300)30C P X C ===, (10分) 且1131150200250300210621030EX =⨯+⨯+⨯+⨯=.(12分)19. (本小题满分12分)【命题意图】本小题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用. 本小题对考生的空间想象能力与运算求解能力有较高要求.【试题解析】解:(1) 取PB 中点N ,连结MN 、AN ,M 是PC 中点,1//,22MN BC MN BC ∴==, 又//BC AD ,//,MN AD MN AD ∴=,∴四边形ADMN 为平行四边形 ,AP AD AB AD ⊥⊥,AD ∴⊥平面PAB ,AD AN ∴⊥,AN MN ∴⊥ AP AB =,AN PB ∴⊥,AN ∴⊥平面PBC , AN ⊂平面ADM ,∴平面ADM ⊥平面PBC . (6分)(2) 存在符合条件的λ.以A 为原点,AB 方向为x 轴,AD 方向为y 轴,AP 方向为z 轴,建立空间直角坐标系A xyz -,设(2,,0)E t ,(0,0,2)P ,(0,2,0)D ,(2,0,0)B 从而(0,2,2)PD =-,(2,2,0)DE t =-,则平面PDE 的法向量为1(2,2,2)n t =-, 又平面DEB 即为xAy 平面,其法向量2(0,0,1)n =,则1212122cos ,3||||(2n n n n n n ⋅<>===⋅,解得3t =或1t =,进而3λ=或13λ=. (12分)20. (本小题满分12分)【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法,椭圆方程的求法、直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.【试题解析】解:(1) 已知11(||||||)||||22ABC A S AB AC BC r BC y ∆=++⋅=⋅,且||2BC =,||3A y r =,其中r 为内切圆半径,化简得:||||4AB AC +=,顶点A 的轨迹是以B C 、为焦点,长轴长为4的椭圆(去掉长轴端点),其中2,1,a c b ===进而其方程为22143x y +=(0)y ≠.(5分)(2) 1232k k k =+,以下进行证明:当直线PQ 斜率存在时,设直线:(1)PQ y k x =-且11(,)P x y ,22(,)Q x y ,(4,)H m联立22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩可得2122834k x x k +=+,212241234k x x k -=+. (8分)由题意:13mk =,1214y m k x -=-,2324y m k x -=-.11212312()(4)()(4)(4)(4)y m x y m x k k x x --+--+=-- 21212121212882(5)()2424224()1636363m k kx x m k x x mk m mk x x x x k ++-+++====-+++ 当直线PQ 斜率不存在时,33(1,),(1,)22P Q -,231332222333m m m k k k -++=+== 综上可得1232k k k =+. (12分)21. (本小题满分12分)【命题意图】本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值以及函数零点的情况. 本小题对考生的逻辑推理能力与运算求解有较高要求.【试题解析】解:(1) 对()f x 求导得:1()ln(1)1axf x a x b x-'=-++-+,根据条件知(0)0f '=,所以101b b -=⇒=. (3分)(2) 由(1)得()(1)ln(1)f x ax x x =-+-,01x ≤≤1()ln(1)11axf x a x x-'=-++-+ 22(1)(1)21()1(1)(1)a a x ax ax a f x x x x -+--++''=-+=-+++. ① 当12a ≤-时,由于01x ≤≤,有221()()0(1)a a x a f x x ++''=-≥+,于是()f x '在[0,1]上单调递增,从而()(0)0f x f ''≥=,因此()f x 在[0,1]上单调递增,即()(0)0f x f ≥=而且仅有(0)0f =;②当0a ≥时,由于01x ≤≤,有221()0(1)ax a f x x ++''=-<+,于是()f x '在[0,1]上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,1]上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =;③当102a -<<时,令21min{1,}a m a+=-,当0x m ≤≤时,221()()0(1)a a x a f x x ++''=-≤+,于是()f x '在[0,]m 上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,]m 上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =.综上可知,所求实数a 的取值范围是1(,]2-∞-. (8分)(3) 对要证明的不等式等价变形如下:2110000100010000.41000.55210001100111()()(1)(1)100001000100001000e e ++<<⇔+<<+ 所以可以考虑证明:对于任意的正整数n ,不等式215211(1)(1)n n e n n+++<<+恒成立. 并且继续作如下等价变形2152112111(1)(1)()ln(1)1()ln(1)52n n e n n n n n n+++<<+⇔++<<++211(1)ln(1)0()5111(1)ln(1)0()2p n n n q n n n ⎧++-<⎪⎪⇔⎨⎪++->⎪⎩对于()p 相当于(2)中21(,0)52a =-∈-,12m =情形,有()f x 在1[0,]2上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =.取1x n =,当2n ≥时,211(1)ln(1)05n n n++-<成立;当1n =时,277(1)ln 21ln 210.710555+-=-<⨯-<.从而对于任意正整数n 都有211(1)ln(1)05n n n++-<成立.对于()q 相当于(2)中12a =-情形,对于任意x ∈[0,1],恒有()0f x ≥而且仅有(0)0f =. 取1x n =,得:对于任意正整数n 都有111(1)ln(1)02n n n ++->成立. 因此对于任意正整数n ,不等式215211(1)(1)n n e n n +++<<+恒成立. 这样依据不等式215211(1)(1)n n e n n +++<<+,再令10000n =利用左边,令1000n = 利用右边,即可得到10000.41000.5100011001()()100001000e <<成立. (12分)22. (本小题满分10分)【命题意图】本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形 相似等内容. 本小题重点考查考生对平面几何推理能力.【试题解析】解:(1) 由题意可知,EPC APC ∠=∠,PEB PAC ∠=∠,则△PED ∽△PAC ,则PE PD PA PC =,又PE ED PB BD =,则ED PB PD BD PA PC⋅=. (5分) (2) 由EPC APC ∠=∠,PEB PAC ∠=∠,可得CDE ECD ∠=∠,在△ECD 中,30CED ∠=,可知75PCE ∠=. (10分) 23. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、利用直线的参数方程的几何意义求解直线与曲线交点的距离等内容. 本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求.【试题解析】解:(1) 对于曲线1C 有1x y +=,对于曲线2C 有2214x y +=.(5分) (2) 显然曲线1C :1x y +=为直线,则其参数方程可写为21x y ⎧=⎪⎪⎨⎪=-+⎪⎩(为参数)与曲线2C :2214x y +=联立,可知0∆>,所以1C 与2C 存在两个交点,由12t t +=,1285t t =,得21||d t t =-==. (10分) 24. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及绝对值不等式及不等式证明等内容. 本小题重点考查考生的化归与转化思想.【试题解析】解:(1)当3a =时,()174,2135,22341,2x x f x x x x ⎧-≤⎪⎪⎪=<<⎨⎪⎪-≥⎪⎩所以()7f x >的解集为{}02x x x <>或 (5分)(2)()2122121f x x a x a x a x a a a =-+-+≥-+-+=-+由()3f x ≥恒成立,有13a a -+≥,解得2a ≥所以a 的取值范围是[)2,+∞ (10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年东北三省三校高考数学二模试卷(理科)一、选择题(本大题共l2小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)设集合M={x|x2﹣2x﹣3<0,x∈Z},则集合M的真子集个数为()A.8B.7C.4D.32.(5分)命题“若x>1,则x>0”的否命题是()A.若x≤1,则x≤0B.若x≤1,则x>0C.若x>1,则x≤0D.若x<1,则x<03.(5分)复数z1,z2在复平面内对应的点关于原点对称,若z1z2=﹣2i,则|z1|=()A.1B.C.2D.44.(5分)已知a,b,m,n是四条不同的直线,其中a,b是异面直线,则下列命题正确的个数为()①若m⊥a,m⊥b,n⊥a,n⊥b,则m∥n;②若m∥a,n∥b,则m,n是异面直线;③若m与a,b都相交,n与a,b都相交,则m,n是异面直线.A.0B.1C.2D.35.(5分)已知向量与向量=(1,﹣2)的夹角为π,||=2,点A的坐标为(3,﹣4).则点B坐标为()A.(1,0)B.(0,1)C.(5,﹣8)D.(﹣8,5)6.(5分)函数f(x)=sinx+sin(﹣x)的图象的一条对称轴为()A.x=B.x=πC.x=D.x=7.(5分)阅读程序框图,若输出结果S=,则整数m的值为()A.7B.8C.9D.108.(5分)设F1、F2分别为椭圆+y2=1的左、右焦点,点P在椭圆上,且|+|=2,则∠F1PF2=()A.B.C.D.9.(5分)一个三棱锥的三视图如图所示,其中俯视图为等腰直角三角形,正视图和侧视图是全等的等腰三角形,则此三棱外接球的表面积为()A.16πB.9πC.4πD.π10.(5分)已知f(x)是定义在R上的奇函数,f(x+1)是偶函数,当x∈(2,4)时,f(x)=|x﹣3|,则f(1)+f(2)+f(3)+f(4)=()A.1B.0C.2D.﹣211.(5分)已知双曲线﹣=1(a>0,b>0的左、右焦点分别为F1、F2,以F1F2为直径的圆被直线+=1截得的弦长为a,则双曲线的离心率为()A.3B.2C.D.12.(5分)若函数y=sin2x+acosx在区间(0,π)上是增函数,则实数a的取值范围是()A.(﹣∞,﹣l]B.[﹣1,+∞)C.(﹣∞,0)D.(0,+∞)二、填空题(本大题共4小题,每小题5分.)13.(5分)(x+1)(x﹣2)4的展开式中含x3项的系数为.14.(5分)设某城市居民私家车平均每辆车每月汽油费用为随机变量ξ(单位为:元),经统计得ξ~N(520,14400),从该城市私家车中随机选取容量为l0000的样本,其中每月汽油费用在(400,640)之间的私家车估计有辆.(附:若ξ~N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6826,P(μ﹣2σ<ξ<μ+2σ)=0.9544,P(μ﹣3σ<ξμ+3σ)=0.9974)15.(5分)△ABC的内角A,B,C所对的边分别为a,b,c,且a,b,c成等比数列,若sinB=,cosB=,则a+c的值为.16.(5分)在平面直角坐标系xOy中,已知圆O:x2+y2=16,点P(2,2),M、N是圆O上相异两点,且PM⊥PN,若=+,则||的取值范围是.三、解答题:(解答应写出文字说明,证明过程或演算步骤)17.(12分)已知数列{a n}前n项和为S n,满足S n=2a n﹣2n(n∈N*).(I)证明:{a n+2}是等比数列,并求{a n}的通项公式;(Ⅱ)数列{b n}满足b n=log2(a n+2),T n为数列{}的前n项和,若T n<a 对正整数a都成立,求a的取值范围.18.(12分)微信是现代生活进行信息交流的重要工具,对某城市年龄在20岁至60岁的微信用户进行有关调查发现,有的用户平均每天使用微信时间不超过1小时,其他人都在1小时以上;若将这些微信用户按年龄分成青年人(20岁至40岁)和中年人(40岁至60岁)两个阶段,那么其中是青年人;若规定:平均每天使用微信时间在1小时以上为经常使用微信,经常使用微信的用户中有是青年人.(I)现对该市微信用户进行“经常使用微信与年龄关系”的调查,采用随机抽样的方法选取容量为l80的一个样本,假设该样本有关数据与调查结果完全相同,列出2×2列联表.青年人中年人合计经常使用微信不经常使用微信合计(Ⅱ)由列表中的数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?(Ⅲ)从该城市微信用户中任取3人,其中经常使用微信的中年人人数为X,求出X的期望.附:K2=P(K2≥k)0.1000.0500.0250.0100.001 k 2.706 3.841 5.024 6.63510.828 19.(12分)如图,在直三棱柱ABC﹣A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,平面A1MC⊥平面ACC1A1.(1)求证:M是棱BB1的中点;(2)求平面A1MC与平面ABC所成锐二面角的余弦值.20.(12分)设F是抛物线C:y2=4x的焦点,P是C上一点,斜率为﹣l的直线l 交C于不同两点A,B(l不过P点),且△PAB重心的纵坐标为﹣.(I)记直线PA,PB的斜率分别为k1,k2.求k1+k2的值;(Ⅱ)求+的最大值.21.(12分)已知函数f(x)=e x﹣1﹣,g(x)=ax2+x﹣(a﹣1).(Ⅰ)曲线f(x)在x=1处的切线与直线x+2y﹣1=0垂直,求实数a的值;(Ⅱ)当a=﹣时,求证:f(x)在(1,+∞)上单调递增;(Ⅲ)当x≥1时,f(x)≥g(x)恒成立,求实数a的取值范围.四、选做题(请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号).【选修4-1:几何证明选讲】22.(10分)如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD 是∠ACB的平分线,交AE于点F,交AB于点D.(Ⅰ)求证:CE•AB=AE•AC(Ⅱ)若AD:DB=1:2,求证:CF=DF.【选修4-4:坐标系与参数方程】23.已知点P的直角坐标是(x,y).以平面直角坐标系的原点为极坐标的极点,x轴的正半轴为极轴,建立极坐标系.设点P的极坐标是(ρ,θ),点Q的极坐标是(ρ,θ+θ0),其中θ0是常数.设点Q的平面直角坐标是(m,n).(I)用x,y,θ0表示m,n;(Ⅱ)若m,n满足mn=1,且θ0=,求点P的直角坐标(x,y)满足的方程.【选修4-5:不等式选讲】24.已知a,b,c>0,a+b+c=1.求证:(Ⅰ)++≤(Ⅱ)++≥.2015年东北三省三校高考数学二模试卷(理科)参考答案与试题解析一、选择题(本大题共l2小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)设集合M={x|x2﹣2x﹣3<0,x∈Z},则集合M的真子集个数为()A.8B.7C.4D.3【解答】解:集合M={x|x|x2﹣2x﹣3<0,x∈Z}={x|﹣1<x<3,x∈Z}={0,1,2},所以集合M的真子集个数为:23﹣1=7个.故选:B.2.(5分)命题“若x>1,则x>0”的否命题是()A.若x≤1,则x≤0B.若x≤1,则x>0C.若x>1,则x≤0D.若x<1,则x<0【解答】解:根据否命题的定义,x>1的否定是:x≤1;x>0的否定是:x≤0,所以命题“若x>1,则x>0”的否命题是:“若x≤1,则x≤0”.故选:A.3.(5分)复数z1,z2在复平面内对应的点关于原点对称,若z1z2=﹣2i,则|z1|=()A.1B.C.2D.4【解答】解:根据复数z1,z2在复平面内对应的点关于原点对称,可得|z1|=|z2|,再根据z1z2=﹣2i,可得|z1|•|z2|=|z1•z2|=|2i|=2,∴|z1|=,故选:B.4.(5分)已知a,b,m,n是四条不同的直线,其中a,b是异面直线,则下列命题正确的个数为()①若m⊥a,m⊥b,n⊥a,n⊥b,则m∥n;②若m∥a,n∥b,则m,n是异面直线;③若m与a,b都相交,n与a,b都相交,则m,n是异面直线.A.0B.1C.2D.3【解答】解:对于①,若m⊥a,m⊥b,n⊥a,n⊥b,在b上一点作a'∥a,则m⊥a',b所在的平面,同理,n垂直a'b所在的平面所以m∥n;故①正确;对于②,若m∥a,n∥b,则m,n是异面直线或者相交;故②错误;对于③,若m与a,b都相交,n与a,b都相交,则m,n是异面直线或者相交;故③错误;所以正确的命题只有①;故选:B.5.(5分)已知向量与向量=(1,﹣2)的夹角为π,||=2,点A的坐标为(3,﹣4).则点B坐标为()A.(1,0)B.(0,1)C.(5,﹣8)D.(﹣8,5)【解答】解:由题意可得||==,∴•=||•||•cosπ=•2•(﹣1)=﹣10.设点B的坐标为(a,b),则=(a﹣3,b+4),由•=1×(a﹣3)+(﹣2)(b+4)=﹣10,求得a﹣2b=1 ①.再根据向量与向量=(1,﹣2)的夹角为π,可得(a﹣3,b+4)=k(1,﹣2),k<0,即b=2﹣2a ②.结合①②求得a=1,b=0,故点B的坐标为(1,0),故选:A.6.(5分)函数f(x)=sinx+sin(﹣x)的图象的一条对称轴为()A.x=B.x=πC.x=D.x=【解答】解:f(x)=sinx+sin(﹣x)=sinx+cosx+sinx=sin(x+),∴x=是函数f(x)=sinx+sin(﹣x)的图象的一条对称轴,故选:D.7.(5分)阅读程序框图,若输出结果S=,则整数m的值为()A.7B.8C.9D.10【解答】解:模拟执行程序框图,可得S=0,n=1满足条件n≤m,S=,n=2满足条件n≤m,S=+,n=3…满足条件n≤m,S=++…++=(1﹣)+()+…+()+()=1﹣=,n=10由题意,此时应该不满足条件,退出循环,输出S的值为,故判断框内的条件应该为:n≤9.故选:C.8.(5分)设F1、F2分别为椭圆+y2=1的左、右焦点,点P在椭圆上,且|+|=2,则∠F1PF2=()A.B.C.D.【解答】解:如图,由椭圆+y2=1,得a=2,b=1,c=,,则,即=12,由|+|=2,得,∴,即,∴∠F1PF2=.故选:D.9.(5分)一个三棱锥的三视图如图所示,其中俯视图为等腰直角三角形,正视图和侧视图是全等的等腰三角形,则此三棱外接球的表面积为()A.16πB.9πC.4πD.π【解答】解:由题意,三棱锥的一个侧面垂直于底面,底面是等腰直角三角形,顶点在底面中的射影是底面斜边的中点,设三棱锥外接球的半径为r,则r2=(2﹣r)2+()2,∴r=,∴三棱锥外接球的表面积为4π×=9π,故选:B.10.(5分)已知f(x)是定义在R上的奇函数,f(x+1)是偶函数,当x∈(2,4)时,f(x)=|x﹣3|,则f(1)+f(2)+f(3)+f(4)=()A.1B.0C.2D.﹣2【解答】解:∵f(x)是定义在R上的奇函数,f(x+1)是偶函数,∴f(0)=0,f(﹣x)=﹣f(x),f(﹣x+1)=f(x+1),∴f(x+4)=f[(x+3)+1]=f[﹣(x+3)+1]=f(﹣x﹣2)=﹣f(x+2)=﹣f[(x+1)+1]=﹣f[﹣(x+1)+1]=﹣f(﹣x)=f(x),∴函数f(x)是周期为4的周期函数,f(4)=f(0)=0,∵当x∈(2,4)时,f(x)=|x﹣3|,∴f(3)=0,f(4)=0,f(1)=﹣f(﹣1)=﹣f(3)=0,f(2)=﹣f(﹣2)=﹣f(2)=0,故f(1)+f(2)+f(3)+f(4)=0,故选:B.11.(5分)已知双曲线﹣=1(a>0,b>0的左、右焦点分别为F1、F2,以F1F2为直径的圆被直线+=1截得的弦长为a,则双曲线的离心率为()A.3B.2C.D.【解答】解:由题意,圆心到直线的距离为d==,∵以F1F2为直径的圆被直线+=1截得的弦长为a,∴2=a,∴2(c4﹣a2b2)=3a2c2,∴2c4﹣2a2(c2﹣a2)=3a2c2,∴2e4﹣5e2+2=0,∵e>1,∴e=.故选:D.12.(5分)若函数y=sin2x+acosx在区间(0,π)上是增函数,则实数a的取值范围是()A.(﹣∞,﹣l]B.[﹣1,+∞)C.(﹣∞,0)D.(0,+∞)【解答】解:解:∵y=sin2x+acosx在区间(0,π)上是增函数,∴y′=cos2x﹣asinx>0,∴1﹣2sinx2﹣asinx>0,即﹣2x2﹣ax+1>0,x∈(0,1],∴a<﹣2x+,令g(x)=﹣2x+,则g′(x)=﹣2﹣<0,∴g(x)在(0,1]递减,∴a<g(1)=﹣1,故答案为:a<﹣1.故选:A.二、填空题(本大题共4小题,每小题5分.)13.(5分)(x+1)(x﹣2)4的展开式中含x3项的系数为16.【解答】解:∵(x﹣2)4=x4﹣8x3+24x2﹣32x+16∴(x+1)(x﹣2)4的展开式中含x3项的系数为24﹣8=16.故答案为:16.14.(5分)设某城市居民私家车平均每辆车每月汽油费用为随机变量ξ(单位为:元),经统计得ξ~N(520,14400),从该城市私家车中随机选取容量为l0000的样本,其中每月汽油费用在(400,640)之间的私家车估计有6826辆.(附:若ξ~N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6826,P(μ﹣2σ<ξ<μ+2σ)=0.9544,P(μ﹣3σ<ξμ+3σ)=0.9974)【解答】解:ξ~N(520,14400),则μ=520,σ=120,所以P(400,640)=P(520﹣120,520+120)=0.6826,所以每月汽油费用在(400,640)之间的私家车估计有l0000×0.6826=6826.故答案为:6826.15.(5分)△ABC的内角A,B,C所对的边分别为a,b,c,且a,b,c成等比数列,若sinB=,cosB=,则a+c的值为3.【解答】解:∵a,b,c成等比数列,∴b2=ac,∵sinB=,cosB=,∴可得=1﹣,解得:ac=13,∵由余弦定理:b2=a2+c2﹣2accosB=ac=a2+c2﹣ac×,解得:a2+c2=37.∴(a+c)2=a2+c2+2ac=37+2×13=63,故解得a+c=3.故答案为:3.16.(5分)在平面直角坐标系xOy中,已知圆O:x2+y2=16,点P(2,2),M、N是圆O上相异两点,且PM⊥PN,若=+,则||的取值范围是[2﹣2,2+2] .【解答】解:如图所示,设MN中点为G(x,y),由PG=GN,得G点轨迹方程为(x﹣1)2+(y﹣1)2=6,又PQ=2PG,所以﹣≤PG≤+,所以2﹣2≤PQ≤2+2故答案为:[2﹣2,2+2].三、解答题:(解答应写出文字说明,证明过程或演算步骤)17.(12分)已知数列{a n}前n项和为S n,满足S n=2a n﹣2n(n∈N*).(I)证明:{a n+2}是等比数列,并求{a n}的通项公式;(Ⅱ)数列{b n}满足b n=log2(a n+2),T n为数列{}的前n项和,若T n<a 对正整数a都成立,求a的取值范围.【解答】(Ⅰ)证明:由题设S n=2a n﹣2n(n∈N*),S n﹣1=2a n﹣1﹣2(n﹣1),n≥2,两式相减得a n=2a n﹣1+2,即a n+2=2(a n﹣1+2),又a1+2=4,所以{a n+2}是以4为首项,2为公比的等比数列,a n+2=4•2n﹣1,即a n=2n+1﹣2(n≥2)又a1=2,所以a n=2n+1﹣2(n∈N*);(Ⅱ)解:因为b n=log2(a n+2)=log22n+1=n+1,即有==﹣,故T n=﹣+﹣+…+﹣=﹣<,依题意得:a≥.18.(12分)微信是现代生活进行信息交流的重要工具,对某城市年龄在20岁至60岁的微信用户进行有关调查发现,有的用户平均每天使用微信时间不超过1小时,其他人都在1小时以上;若将这些微信用户按年龄分成青年人(20岁至40岁)和中年人(40岁至60岁)两个阶段,那么其中是青年人;若规定:平均每天使用微信时间在1小时以上为经常使用微信,经常使用微信的用户中有是青年人.(I)现对该市微信用户进行“经常使用微信与年龄关系”的调查,采用随机抽样的方法选取容量为l80的一个样本,假设该样本有关数据与调查结果完全相同,列出2×2列联表.青年人中年人合计经常使用微信不经常使用微信合计(Ⅱ)由列表中的数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?(Ⅲ)从该城市微信用户中任取3人,其中经常使用微信的中年人人数为X,求出X的期望.附:K2=P(K2≥k)0.1000.0500.0250.0100.001 k 2.706 3.841 5.024 6.63510.828【解答】解:(Ⅰ)由已知可得:下面2×2列联表:青年人中年人合计经常使用微信8040120不经常使用微信55560合计13545180…(4分)(Ⅱ)将列联表中数据代入公式可得:K2=≈13.33>10.828所以有99%的把握认为经常使用微信与年龄有关.…(8分)(III)从该市微信用户中任取一人,取到经常使用微信的中年人的概率为=由题意,X~B(3,),所以:E(X)=3×=.…(12分)19.(12分)如图,在直三棱柱ABC﹣A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,平面A1MC⊥平面ACC1A1.(1)求证:M是棱BB1的中点;(2)求平面A1MC与平面ABC所成锐二面角的余弦值.【解答】证明:(1)取AC中点O,连OB.在平面ACC1A1上过O作AC垂线交A1C1于N.∵平面ACC1A1⊥平面ABC.∴ON⊥平面ABC,如图:以O为坐标原点,建立空间直角坐标系由已知:A(2,0,0),B(0,2,0),C(﹣2,0,0),A1(2,0,5),B1(0,2,5),C1(﹣2,0,5),M(0,2,m),…(3分)设=(x,y,z)为平面A1MC法向量,,取x=5,z=﹣4,y=2m﹣5,即:=(5,2m﹣5,﹣4),又=(0,1,0)为平面ACC1A1法向量依题意:,解得m=∴M为棱BB1的中点…(8分)(2)由(1)知:=(5,2m﹣5,﹣4)为平面A1MC法向量又=(0,0,1)为平面ABC法向量∴cos<>==﹣,∴平面A1MC与平面ABC所成锐二面角余弦值为.…(12分)20.(12分)设F是抛物线C:y2=4x的焦点,P是C上一点,斜率为﹣l的直线l 交C于不同两点A,B(l不过P点),且△PAB重心的纵坐标为﹣.(I)记直线PA,PB的斜率分别为k1,k2.求k1+k2的值;(Ⅱ)求+的最大值.【解答】解:(I)设直线l的方程为:y=﹣x+b,将它代入C:y2=4x得:x2﹣2(b+2)x+b2=0,令A(x1,y1)、B(x2,y2),则x1+x2=2(b+2),x1x2=b2,y1+y2=﹣(x1+x2)+2b=﹣4,…(3分)因为△PAB重心的纵坐标为﹣,所以y1+y2+y P=﹣2,所以,y P=2,x P=1.所以k1+k2=+===0所以:k1+k2=0.…(6分)(Ⅱ)+=+==,…(8分)由△=16(b+1)>0得b>﹣1,又l不过P点,则b≠3.令t=b+3,则t>2且t≠6.则+===≤=当t=,即t=2,b=2﹣3时,+的最大值为.…(12分)21.(12分)已知函数f(x)=e x﹣1﹣,g(x)=ax2+x﹣(a﹣1).(Ⅰ)曲线f(x)在x=1处的切线与直线x+2y﹣1=0垂直,求实数a的值;(Ⅱ)当a=﹣时,求证:f(x)在(1,+∞)上单调递增;(Ⅲ)当x≥1时,f(x)≥g(x)恒成立,求实数a的取值范围.【解答】(Ⅰ)解:,依题意得:,解得:;(Ⅱ)证明:当时,,∴.∴对x∈(1,+∞)成立,即:f′(x)在(1,+∞)上为增函数,又f′(1)=0,故f′(x)>0对x∈(1,+∞)成立,∴f(x)在(1,+∞)上为增函数;(Ⅲ)解:由f(x)≥g(x),得:(x≥1),设(x≥1),∴h′(x)=(x+1)e x﹣1﹣ax2﹣x+a﹣1=(x+1)[e x﹣1﹣a(x﹣1)﹣1](x≥1),设k(x)=e x﹣1﹣a(x﹣1)﹣1(x≥1),∴k′(x)=e x﹣1﹣a.①当a≤1时:k′(x)≥0对x∈[1,+∞)成立,又k(1)=0,故k(x)≥0,即:h′(x)≥0.又h(1)=0,故h(x)≥0;②当a>1时:由k′(x)=0,得x=1+lna>1,当x∈(1,1+lna)时:k′(x)<0,又k(1)=0,故:k(x)<0,即:h′(x)<0,又h(1)=0,故h(x)<0这与已知不符.综上所述:实数a的取值范围为(﹣∞,1].四、选做题(请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号).【选修4-1:几何证明选讲】22.(10分)如图,已知点C在圆O直径BE的延长线上,CA切圆O于点A,CD 是∠ACB的平分线,交AE于点F,交AB于点D.(Ⅰ)求证:CE•AB=AE•AC(Ⅱ)若AD:DB=1:2,求证:CF=DF.【解答】(Ⅰ)证明:由C在圆O直径BE的延长线上,CA切圆O于点A,得△ACE∽△BCA,∴,∴CE•AB=AE•AC;…(5分)(Ⅱ)证明:∵CD是∠ACB的平分线,∴∠ACF=∠BCD,∵AC为圆的切线,∴∠CAE=∠CBD,∴∠ACF+∠CAE=∠BCD+∠CBD,即∠AFD=∠ADF,∴AF=AD∴△ACF∽△BCD,∴=,∴CF=DF.…(10分)【选修4-4:坐标系与参数方程】23.已知点P的直角坐标是(x,y).以平面直角坐标系的原点为极坐标的极点,x轴的正半轴为极轴,建立极坐标系.设点P的极坐标是(ρ,θ),点Q的极坐标是(ρ,θ+θ0),其中θ0是常数.设点Q的平面直角坐标是(m,n).(I)用x,y,θ0表示m,n;(Ⅱ)若m,n满足mn=1,且θ0=,求点P的直角坐标(x,y)满足的方程.【解答】解:(Ⅰ)由题意知:,和,即:,所以:,(Ⅱ)由题意知:,所以:,.整理得:.【选修4-5:不等式选讲】24.已知a,b,c>0,a+b+c=1.求证:(Ⅰ)++≤(Ⅱ)++≥.【解答】证明:(Ⅰ)由柯西不等式得:(++)2≤(12+12+12)[()2+()2+()2]=3,∴++≤.(Ⅱ)由柯西不等式得:[(3a+1)+(3b+1)+(3c+1)](++)≥(•+•+•)2=9∴++≥.。
