抗扭惯性矩计算程序
使用AutoCAD计算复杂截面的抗弯抗扭惯性矩的方法

遇到一些复杂的截面形状,要计算其抗弯和抗扭的刚度,需要知道对主轴的惯性矩,手算通过叠加无疑麻烦而容易出错,实际上AutoCAD已经自带了计算截面特性的工具,大家也不必到网上搜所谓的计算截面特性的小工具和小软件了。
下面来做一个简单的验证和复杂点的例子,通过例子说明使用方法:实例1:矩形截面长x宽=54*88,如下图。
第一:绘制一个矩形。
第二,将矩形定义成面域第三,查询截面的性质信息如图通过工具--查询--面域/质量特性然后选择矩形,点右键结束,得到的结果如下由结果可以看到截面的如下信息面积: 4752.0000周长: 284.0000边界框: X: 1417.1659 -- 1471.1659Y: 1335.2082 -- 1423.2082质心: X: 1444.1659Y: 1379.2082惯性矩: X: 9042393679.3373Y: 9911997397.1524惯性积: XY: 9465059334.6342旋转半径: X: 1379.4421Y: 1444.2500主力矩与质心的X-Y 方向:I: 3066624.0000 沿[1.0000 0.0000](这个是形心平移到原点得到的惯性矩,我们可以直接使用的)J: 1154736.0000 沿[0.0000 1.0000](这个是形心平移到原点得到的惯性矩,我们可以直接使用的)内部带孔的截面,需要分别对外部轮廓包围的面域和内部轮廓包围的面域做一个布尔运算——差集,具体步骤如下建立封闭的外轮廓,定义为面域定义封闭的内轮廓,定义为面域进行布尔运算,大面域减去小面域得到一个带孔的面域接下来按照上面的方法查询惯性矩信息。
下面来求一个简单的带孔的截面先将矩形定义成面域再将圆定义成面域然后布尔运算,求差,如下图下面进行查询截面性质,得到的结果如下由于是对称的,可以手算一下结果,进行对比上面是简单的例子,为了说明步骤以及方便手算对比检验计算结果的正确性,正常需要的是计算复杂截面的惯性矩下面的一个例子如图。
材料抗扭计算公式

材料抗扭计算公式
1.扭转公式:
扭转公式可以表示为:
T=K*τ*A
其中,T为极限扭矩,K为比例系数,τ为材料的切应力,A为截面积。
2.扭转角度公式:
扭转角度公式可以表示为:
θ=(TL*L)/(G*J)
其中,θ为扭转角度,TL为加载扭矩,L为材料的长度,G为剪切模量,J为挠度抵抗矩。
3.最大剪应力公式:
最大剪应力公式可以表示为:
τ_max = T * r / (J * φ)
其中,τ_max为最大剪应力,T为扭矩,r为材料中的半径,J为挠度抵抗矩,φ为截面形状修正系数。
总结:
材料抗扭计算的公式主要包括扭转公式、扭转角度公式和最大剪应力公式。
这些公式根据材料的力学性质和几何形状,可以计算出材料的极限
抗扭力、扭转角度和最大剪应力等参数。
在工程设计和材料选择中,这些
公式可以用于评估材料的强度和稳定性,从而确保设计的可靠性和安全性。
利用桥梁博士软件计算截面抗弯惯矩和抗扭惯矩
利用桥梁博士软件计算截面抗弯惯矩和抗扭惯矩
对桥梁荷载进行横向分布系数的计算时,会用到抗弯惯矩和抗扭惯矩。
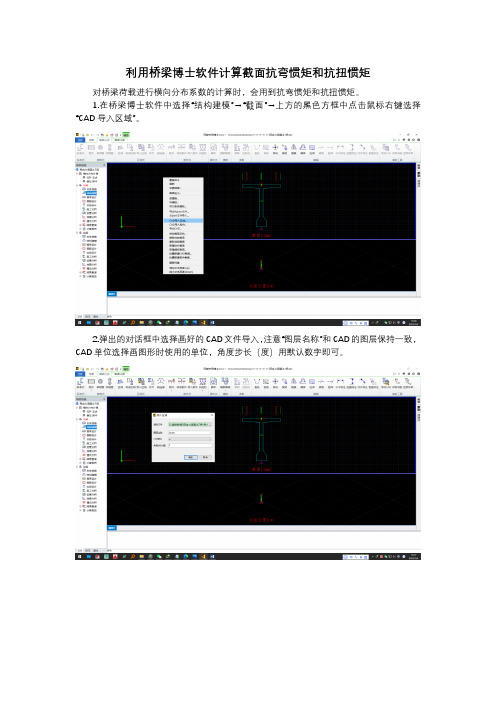
1.在桥梁博士软件中选择“结构建模”→“截面”→上方的黑色方框中点击鼠标右键选择“CAD导入区域”。
2.弹出的对话框中选择画好的CAD文件导入,注意“图层名称”和CAD的图层保持一致,CAD单位选择画图形时使用的单位,角度步长(度)用默认数字即可。
3.在下方的黑色方框区域点击鼠标右键选择“截面检查”。
4.在下方的黑色方框区域点击鼠标右键选择“截面检查点位置”。
5.一般选择跨中的位置,按照需要填入数值。
6.在下方的黑色方框区域点击鼠标右键选择“查看截面特性”。
7.弹出的表格表示当前截面位置的数据信息。
惯性矩IX即抗弯惯矩,扭转惯量J即抗扭惯矩。
惯性矩计算方法范文

惯性矩计算方法范文惯性矩是描述物体对于转动而言的惯性特性的物理量。
它可以用于计算物体在转动时所受到的惯性力矩,进而揭示物体的转动稳定性等信息。
惯性矩的计算方法有几种不同的途径,下面将详细介绍。
1.基本概念在进行惯性矩的计算之前,首先需要了解一些基本概念。
(1) 质量:物体所含有的物质的量度。
常用单位是千克(kg)。
(2) 密度:物体的质量和体积之比。
密度可以用来描述物质的紧密程度。
常用单位是千克每立方米(kg/m³)。
(3)面积:物体表面的二维度量。
常用单位是平方米(㎡)。
(4)半径:物体圆形截面的中心到圆周上一点的距离。
2.离轴旋转体的惯性矩计算对于一个离轴旋转体,惯性矩的计算分为以下两种情况。
(1)绕坐标轴旋转的惯性矩计算:当物体绕其中一固定坐标轴旋转时,该坐标轴称为旋转轴。
惯性矩可由以下公式计算:I = ∫r² dm其中,I为惯性矩,r为距离旋转轴的距离,dm为质量要素。
(2)绕离轴点旋转的惯性矩计算:当物体绕离质心的离轴点旋转时,需使用平行轴定理。
平行轴定理指出,物体绕通过质心的其中一轴旋转的惯性矩等于其绕通过离质心距离为d的平行轴旋转的惯性矩与物体质量的乘积之和。
即:I = Icm + md²其中,I为绕离轴点旋转的惯性矩,Icm为绕质心旋转的惯性矩,m 为物体的质量,d为离质心的距离。
3.均匀物体的惯性矩计算对于均匀物体来说,它的质量和密度分布是均匀的,因此可以使用以下公式计算其惯性矩:(1)绕质心旋转的惯性矩计算:对于一个均匀物体绕质心旋转时,可根据其形状使用相应的公式计算惯性矩。
-球体的惯性矩:I = (2/5)mr²其中,I为球体的惯性矩,m为球体的质量,r为球体的半径。
-圆盘的惯性矩:I = (1/2)mr²其中,I为圆盘的惯性矩,m为圆盘的质量,r为圆盘的半径。
-圆环的惯性矩:I = mr²其中,I为圆环的惯性矩,m为圆环的质量,r为圆环的半径。
抗扭刚度计算公式

抗扭刚度计算公式在我们的工程世界里,抗扭刚度计算公式可是个相当重要的家伙!它就像是一把神奇的钥匙,能帮助我们解开很多结构力学中的谜题。
先来说说抗扭刚度到底是个啥。
想象一下,一根轴在扭转力的作用下,就像是我们拧毛巾一样,如果它不容易被拧动,那就说明它的抗扭刚度大;反之,如果轻轻一拧就变形了,那抗扭刚度就小。
而计算这个抗扭刚度的公式,就是我们用来衡量它到底有多“坚强”的工具。
抗扭刚度的计算公式通常与材料的性质、截面的形状和尺寸等因素密切相关。
比如说,对于实心圆形截面的轴,其抗扭刚度计算公式是GIp ,其中 G 是材料的剪切模量,Ip 是极惯性矩。
那这个极惯性矩又咋算呢?对于实心圆截面,Ip = πd^4/32 ,这里的 d 就是轴的直径。
给您讲个我亲身经历的事儿吧。
有一次,我在一个机械加工厂实习,碰到了一个关于传动轴设计的问题。
这根传动轴要在高速旋转的情况下传递很大的扭矩,如果抗扭刚度不够,那可就麻烦大了。
当时,我们的工程师师傅就带着我们,一步步地运用抗扭刚度计算公式来确定轴的尺寸。
师傅先让我们测量了材料的剪切模量,然后仔细地测量了轴的预计直径。
接着,就开始在纸上一笔一划地计算极惯性矩,再代入抗扭刚度公式中。
我在旁边看着,心里那叫一个紧张,生怕算错了一个数,整个设计就出问题。
师傅倒是淡定得很,嘴里还念叨着:“这可不能马虎,一个数错了,这轴可就转不起来喽!”最后,经过反复的计算和校验,终于确定了合适的轴径。
当看到那根按照我们计算结果加工出来的传动轴稳稳地转动起来,没有出现任何扭曲变形的时候,我心里别提多有成就感了!再来说说其他形状的截面,比如空心圆形截面、矩形截面等等,它们也都有各自相应的抗扭刚度计算公式。
而且在实际应用中,还得考虑到各种复杂的情况,比如温度变化、应力集中等等。
总之,抗扭刚度计算公式虽然看起来有点复杂,但只要我们掌握了其中的原理,再结合实际情况,就能让它为我们的工程设计服务,打造出更坚固、更可靠的结构。
混凝土梁抗扭承载力计算技术规程

混凝土梁抗扭承载力计算技术规程一、前言混凝土梁在各种工程中广泛使用,因其具有高强度、耐久性和耐候性等特点,但在实际应用中,混凝土梁往往会受到扭矩的影响,因此需要进行抗扭设计。
本文旨在介绍混凝土梁抗扭承载力计算的技术规程,以供工程师和技术人员参考。
二、混凝土梁抗扭承载力计算的基本原理混凝土梁抗扭承载力的计算主要基于以下原理:1. 梁在扭矩作用下,会产生剪力和弯矩,剪力会引起梁的横向变形,而弯矩则会引起梁的纵向变形。
2. 在混凝土梁的抗扭计算中,需要考虑剪力和弯矩的相互作用,同时还需要考虑混凝土的弹性模量、截面形状和受力状态等因素。
3. 混凝土的弹性模量会随着应力的增加而降低,因此在计算中需要考虑混凝土的应力状态。
三、混凝土梁抗扭承载力计算的基本公式混凝土梁抗扭承载力的计算主要基于以下公式:1. 混凝土梁的抗扭承载力公式:T = Kt * V * jd * b * d^2其中,T为混凝土梁的抗扭承载力,Kt为抗扭系数,V为混凝土剪切强度,jd为混凝土的等效厚度,b为梁的宽度,d为梁的高度。
2. 混凝土的等效厚度计算公式:jd = 2 * I / b * h其中,I为截面的惯性矩,b为截面的宽度,h为截面的高度。
3. 抗扭系数计算公式:Kt = 0.35 + 0.25 * (d / h)其中,d为梁的高度,h为截面的高度。
四、混凝土梁抗扭承载力计算的具体步骤混凝土梁抗扭承载力的计算步骤如下:1. 确定混凝土梁的截面形状和尺寸,计算截面的惯性矩。
2. 计算混凝土的等效厚度。
3. 计算抗扭系数。
4. 根据公式计算混凝土梁的抗扭承载力。
5. 比较计算结果与设计要求,如果不符合要求,则需要进行进一步的设计或者修改。
五、混凝土梁抗扭承载力计算的注意事项在进行混凝土梁抗扭承载力计算时,需要注意以下几个方面:1. 梁的截面形状和尺寸应该符合设计要求,否则将会影响混凝土梁的抗扭承载力。
2. 混凝土的弹性模量随着应力的增加而降低,因此考虑混凝土的应力状态是非常重要的。
惯性矩的计算方法

惯性矩的计算⽅法第1节静矩和形⼼静矩和形⼼任何受⼒构件的承载能⼒不仅与材料性能和加载⽅式有关,⽽且与构件截⾯的⼏何形状和尺⼨有关.如:计算杆的拉伸与压缩变形时⽤到截⾯⾯积 A ,计算圆轴扭转变形时⽤到横截⾯的极惯性矩 I等. A 、 I等是从不同⾓度反映了截⾯的⼏何特性,因此称它们为截⾯图形的⼏何性质.静矩和形⼼设有⼀任意截⾯图形如图 4 — 1 所⽰,其⾯积为 A .选取直⾓坐标系 yoz ,在坐标为 (y,z) 处取⼀微⼩⾯积 dA ,定义微⾯积dA 乘以到 y 轴的距离 z ,沿整个截⾯的积分,为图形对 y 轴的静矩 S,其数学表达式(4 -1a )同理,图形对 z 轴的静矩为(4-1b)图 4-1截⾯静矩与坐标轴的选取有关,它随坐标轴 y 、 z 的不同⽽不同.所以静矩的数值可能是正,也可能是负或是零.静矩的量纲为长度的三次⽅.确定截⾯图形的形⼼位置 ( 图 4-1 中 C 点 ):(4 -2a )(4-2b)式中 y、 z 为截⾯图形形⼼的坐标值.若把式 (4-2) 改写成(4-3)性质:若截⾯图形的静矩等于零,则此坐标轴必定通过截⾯的形⼼.若坐标轴通过截⾯形⼼,则截⾯对此轴的静矩必为零.由于截⾯图形的对称轴必定通过截⾯形⼼,故图形对其对称轴的静矩恒为零。
4 )⼯程实际中,有些构件的截⾯形状⽐较复杂,将这些复杂的截⾯形状看成是由若⼲简单图形 ( 如矩形、圆形等 ) 组合⽽成的.对于这样的组合截⾯图形,计算静矩 (S) 与形⼼坐标 (y、 z ) 时,可⽤以下公式(4-4)(4-5)式中 A, y , z 分别表⽰第个简单图形的⾯积及其形⼼坐标值, n 为组成组合图形的简单图形个数.即:组合图形对某⼀轴的静矩等于组成它的简单图形对同⼀轴的静矩的代数和.组合图形的形⼼坐标值等于组合图形对相应坐标轴的静矩除以组合图形的⾯积.组合截⾯图形有时还可以认为是由⼀种简单图形减去另⼀种简单图形所组成的.例 4-1 已知 T 形截⾯尺⼨如图 4-2 所⽰,试确定此截⾯的形⼼坐标值.图 4-2解: (1) 选参考轴为 y 轴, z 轴为对称轴,(2) 将图形分成 I 、两个矩形,则(3) 代⼊公式 (4-5)惯性矩、惯性积和惯性半径设任⼀截⾯图形 ( 图 4 — 3) ,其⾯积为 A .选取直⾓坐标系 yoz ,在坐标为 (y 、 z) 处取⼀微⼩⾯积 dA ,定义此微⾯积 dA 乘以到坐标原点o的距离的平⽅,沿整个截⾯积分,为截⾯图形的极惯性矩 I.微⾯积 dA 乘以到坐标轴 y 的距离的平⽅,沿整个截⾯积分为截⾯图形对 y 轴的惯性矩 I.极惯性矩、惯性矩常简称极惯矩、惯矩.数学表达式为极惯性矩 (4-6)对 y 轴惯性矩 (4 -7a )同理,对 z 轴惯性矩 (4-7b)图 4-3由图 4-3 看到所以有即(4-8) 式 (4 — 8) 说明截⾯对任⼀对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
抗扭惯性矩计算

抗扭惯性矩计算
1.圆形截面
圆形截面的抗扭惯性矩I T 就等于它的极惯矩I P
I T =I P
2.矩形截面
对于一般矩形,抗扭惯性矩按下式进行计算:
结果0.00847b t
t/b
a 1.13
0.30.265487
0.277604式中:b--矩形宽度#DIV/0!#DIV/0! t--矩形高度
#DIV/0!#DIV/0!#DIV/0!
#DIV/0!
(二)薄壁闭合截面
1.薄壁箱形截面
0.0008330.015758
0.016591
式中:t--箱的侧壁厚度 s--箱的侧壁斜长 h--箱的高度s s1
s2 s1--顶板宽度0.50.10.1
s2--底板宽度t1--顶板厚度悬出部分看实体矩形截面计算t2--底板厚度
对于由n个箱拼连成的截面,其抗扭惯性矩可近似得按各个单箱截面抗扭矩之和计算
2.薄壁矩形截面空心板可当作薄壁矩形闭合截面
4b^2h^2/(2*h/t+b/t1+b/t2)
结果
b h t 0.94
0.6150.13
式中:t--空心板的侧壁厚度
b--空心板的宽度 h--空心板的高度
中到中长度
中到中长度
输
输入数据0.045615206
I T
抗扭惯性矩计算公式
(一)实体截面孔室高度大于等于截面高度0.6倍的截面,可称为薄壁截面(s1+s2)^2h^2/(2*s/t+s1/t+s2/t)结果
悬壁部分I T2
I T abt^3
输入数据箱部分I T1
t1--顶板厚度 t2--底板厚度
输入数据
h t1t2t
0.50.10.10.1
据
t1t2
0.10.09。
