数据分析SAS报告
SAS统计分析报告教程方法总结材料

SAS统计分析报告教程方法总结材料统计分析是对数据进行理性、全面和深入的分析,以发现其中的规律、趋势和关联性。
SAS(Statistical Analysis System)是一个流行的统计分析软件,广泛应用于数据分析、研究和报告编制领域。
本文将介绍SAS统计分析报告的编制方法,帮助读者了解如何利用SAS软件进行统计分析,并撰写专业的统计分析报告。
一、数据导入与准备在进行统计分析之前,首先需要导入数据并对数据进行清洗和准备。
SAS软件支持多种数据格式的导入,包括CSV、Excel、数据库等。
可以使用PROC IMPORT或DATA STEP语句来将数据导入SAS环境中,并使用DATA STEP或PROC SQL语句对数据进行清洗和准备,包括删除缺失值、解决数据异常值等。
二、描述性统计分析描述性统计分析是对数据集中的变量进行统计概括和描述。
在SAS中,可以使用PROCMEANS、PROCFREQ、PROCUNIVARIATE等过程来计算变量的均值、标准差、中位数、众数、频数分布等描述性统计指标。
通过描述性统计分析可以初步了解数据的分布情况,为后续的统计测试和模型建立奠定基础。
三、统计检验统计检验是用来检验数据之间的关系或差异是否显著的一种方法。
在SAS中,可以使用PROCTTEST、PROCANOVA、PROCCORR等过程进行假设检验,检验两组或多组数据之间的显著性差异或相关性。
在进行统计检验时,需要设置显著性水平和备择假设,以便进行准确的统计分析。
四、图形展示图形展示是将数据通过图表的形式呈现出来,更直观地展示数据的特征和规律。
在SAS中,可以使用PROCGPLOT、PROCSGPLOT、PROCGCHART等过程来绘制各种类型的图表,包括直方图、散点图、折线图、饼图等。
通过图形展示,可以更清晰地了解数据的分布情况和变量之间的关系,为数据分析和报告提供有力支持。
五、报告编制报告编制是统计分析的最后一步,将分析结果整理成报告文档,进行数据解释和结论归纳。
sas数据分析报告

sas数据分析报告摘要:本文介绍了基于SAS软件进行的数据分析报告。
首先,对数据进行了简要的介绍和处理,并对数据进行了可视化处理。
然后我们使用SAS建立了模型,并对模型进行了评估。
最后,我们对结果进行了解释和分析,并提出了相关的建议。
关键词:SAS,数据分析,模型建立,可视化,结果解释1. 简介SAS是一款广泛应用于数据分析领域的统计软件,其丰富的统计函数和数据可视化功能使得它成为了数据分析师不可或缺的工具。
本文使用SAS对某公司的销售数据进行分析,以帮助公司管理者更好地了解企业的经营情况和预测未来的发展趋势。
2. 数据处理与可视化我们先对数据进行了初步的清理和整理,去除了缺失值和异常值,并对数据进行了标准化处理。
然后,我们使用SAS的数据可视化功能对数据进行了可视化处理,包括制作散点图、直方图和箱线图等,以便更好地了解数据的分布情况和相关性。
3. 模型建立与评估我们基于数据建立了模型,并使用SAS对模型进行了评估。
在模型建立过程中,我们采用了多元线性回归模型,考虑了各个变量之间的相互关系和影响。
在模型评估过程中,我们采用了交叉验证和R方值等指标,对模型的预测能力进行了评估。
4. 结果解释与分析根据模型的预测结果,我们对数据进行了解释和分析,并提出了相关的建议。
我们确定了销售额、广告投放、促销活动等因素对销售额的影响,根据模型结果提出了优化销售策略的建议。
同时,我们进一步分析了销售额的趋势,预测了未来的销售情况,为公司的经营决策提供了有力的支持。
结论:本文基于SAS进行了数据分析报告,利用SAS的数据处理、可视化、模型建立和评估等功能,全面分析了某公司的销售数据。
通过对数据的解释和分析,我们提出了相关的建议,为公司的经营决策提供了参考。
这表明SAS在数据分析领域的应用效果显著,对于企业的发展和决策具有重要的意义。
sas数据分析

sas数据分析标题:SAS数据分析与决策支持引言:在当今信息化的时代,数据已经成为企业决策的重要依据。
然而,海量的数据如何进行有效地整理和分析已经成为企业面临的挑战。
SAS作为一个强大的数据分析工具,通过其丰富的功能和灵活的应用,为企业提供了一种有效的决策支持方法。
本文将详细介绍SAS数据分析的概念、应用和优势,以及它如何为企业决策提供支持。
一、SAS数据分析的概念SAS(Statistical Analysis System)是一种常用的统计分析软件,它通过收集、整合、管理和分析数据,帮助用户在决策过程中作出有效的预测和判断。
SAS数据分析可以应用于各个领域,包括市场营销、金融风险评估、医疗保健、生物信息学等。
二、SAS数据分析的应用1. 市场营销决策支持:SAS数据分析可以帮助企业对产品销售进行预测和监测,分析市场竞争对手的策略,并优化企业的市场定位和营销策略。
2. 金融风险评估:SAS数据分析可以对金融数据进行建模和分析,帮助金融机构评估风险、监控市场波动,并制定相应的风险管理策略。
3. 医疗保健决策支持:SAS数据分析可以通过分析大量的医疗数据,辅助医疗机构提供个性化的诊断和治疗方案,提高医疗效率和病人满意度。
4. 生物信息学研究:SAS数据分析可以处理大规模的生物数据,帮助生物学家解决基因组学、蛋白质组学等领域的问题,加速科学研究的进展。
三、SAS数据分析的优势1. 数据整合能力:SAS可以集成多种类型的数据,并通过其强大的数据处理功能进行统一管理和整合,使得数据的利用更加高效和便捷。
2. 统计分析功能:SAS提供了丰富的统计分析方法和模型,可以通过这些方法和模型对数据进行深入分析和挖掘,从而发现数据背后的规律和关联。
3. 可视化分析:SAS提供了强大的可视化分析功能,可以通过图表、图像和地图等形式呈现数据分析结果,帮助用户更加直观地理解和解释数据。
4. 高性能计算:SAS具备较强的计算能力,可以处理大规模的数据和复杂的计算任务,加速数据分析和决策过程。
SAS数据分析实验报告

SAS数据分析实验报告摘要:本文使用SAS软件对一组数据集进行了分析。
通过数据清洗、数据变换、数据建模和数据评估等步骤,得出了相关的结论。
实验结果表明,使用SAS软件进行数据分析可以有效地处理和分析大型数据集,得出可靠的结论。
1.引言数据分析在各个领域中都扮演着重要的角色,可以帮助人们从大量的数据中提取有用信息。
SAS是一种常用的数据分析软件,被广泛应用于统计分析、商业决策、运营管理等领域。
本实验旨在探究如何使用SAS软件进行数据分析。
2.数据集描述本实验使用了一个包含1000个样本的数据集。
数据集包括了各个样本的性别、年龄、身高、体重等多种变量。
3.数据清洗在进行数据分析之前,首先需要对数据进行清洗。
数据清洗包括缺失值处理、异常值处理和重复值处理等步骤。
通过使用SAS软件中的相应函数和命令,我们对数据集进行了清洗,确保数据的质量和准确性。
4.数据变换在进行数据分析之前,还需要对数据进行变换。
数据变换包括数据标准化、数据离散化和数据归一化等操作。
通过使用SAS软件中的变换函数和操作符,我们对数据集进行了变换,使其符合分析的需要。
5.数据建模数据建模是数据分析的核心过程,包括回归分析、聚类分析和分类分析等。
在本实验中,我们使用SAS软件的回归、聚类和分类函数,对数据集进行了建模分析。
首先,我们进行了回归分析,通过拟合回归模型,找到了自变量对因变量的影响。
通过回归模型,我们可以预测因变量的值,并分析自变量的影响因素。
其次,我们进行了聚类分析,根据样本的特征将其分类到不同的群组中。
通过聚类分析,我们可以发现样本之间的相似性和差异性,从而做出针对性的决策。
最后,我们进行了分类分析,根据样本的特征判断其所属的类别。
通过分类分析,我们可以根据样本的特征预测其所属的类别,并进行相关的决策。
6.数据评估在进行数据分析之后,还需要对结果进行评估。
评估包括模型的拟合程度、变量的显著性和模型的稳定性等。
通过使用SAS软件的评估函数和指标,我们对数据分析的结果进行了评估。
SAS数据分析实验报告
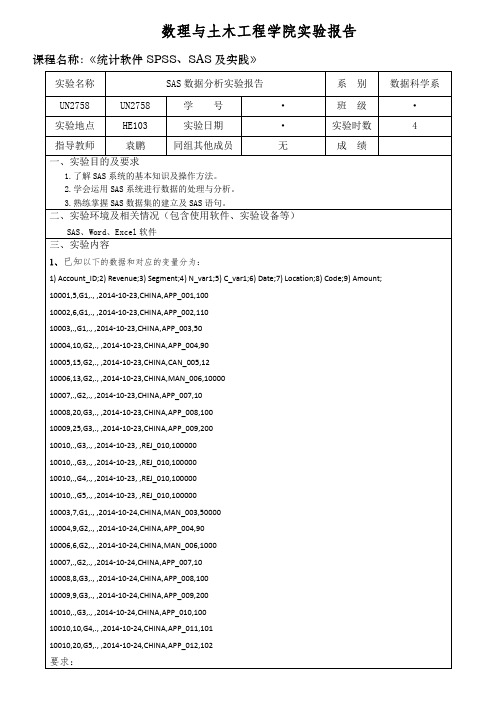
数理与土木工程学院实验报告课程名称:《统计软件SPSS、SAS及实践》实验结果(包括程序代码、程序结果分析)第一题:②基于数据集transaction,将变量“Revenue”中的缺失数据用其均值代替;data a;set a;array s(*) aa1-aa2;n=n(of s(*));mean=mean(of s(*));sum=sum( of s(*));do i=1to dim(s);if s(i)=.then s(i)=mean;end;run;proc print;run;③基于②,将取值全部缺失的变量删除。
data a;set a;array aa aa1-aa2;do over aa;if col=.then delete;end;run;proc transpose data=a out=transaction(drop=_name_);var aa1-aa2;run;proc print;run;第二题:a) 建立一个数据集合读入数据,变量为length,width和 height;data b;input length width height;cards;32 18 1216 15 2448 12 3215 30 4520 30 36;run;proc print data=b;run;b) 使用 set 语句,利用a)的数据集建立一个新数据集,它包括a)的所有数据,并建立三个新变量:每个c) 使用b)建立的数据集建立一个新数据集,只包括其中的volume 和 cost 变量。
data d;set c(keep=volume cost);run;proc print data=d;run;第三题:a)对车的标志(brand)的频数画竖直条形图。
libname mydata 'D:\data';proc print data=edcar;run;data e;set edcar; run;proc gchart;vbar brand;run;b)c)data g;set f;proc means data=g ;run;第四题:试分析:该地区单身人士的收入与住房面积之间是否相关?如果线性相关,确定一元线性回归方程,并做显著性检验。
sas实验报告

sas实验报告SAS实验报告。
一、实验目的。
本实验旨在通过使用SAS软件对实验数据进行分析,掌握SAS软件的基本操作和数据处理技能,进一步提高数据分析能力。
二、实验内容。
1. 数据导入,将实验数据导入SAS软件中,建立数据集。
2. 数据清洗,对数据进行缺失值处理、异常值处理等清洗工作,保证数据的准确性和完整性。
3. 描述统计分析,对数据进行描述性统计分析,包括均值、标准差、频数分布等。
4. 数据可视化,利用SAS软件绘制数据的直方图、箱线图等可视化图表,直观展现数据分布情况。
5. 假设检验,对数据进行假设检验,验证数据之间的关系和差异性。
三、实验步骤。
1. 数据导入,首先打开SAS软件,利用导入数据功能将实验数据导入SAS环境中,创建数据集。
2. 数据清洗,对导入的数据进行缺失值处理和异常值处理,保证数据的完整性和准确性。
3. 描述统计分析,利用SAS软件进行描述统计分析,得出数据的均值、标准差、频数分布等统计指标。
4. 数据可视化,利用SAS软件绘制数据的直方图、箱线图等可视化图表,直观展现数据的分布情况。
5. 假设检验,利用SAS软件进行假设检验,验证数据之间的关系和差异性。
四、实验结果分析。
通过SAS软件的操作,我们成功完成了对实验数据的导入、清洗、描述统计分析、数据可视化和假设检验等工作。
通过分析结果,我们得出了实验数据的基本特征和规律,验证了数据之间的关系和差异性,为进一步的数据分析工作奠定了基础。
五、实验总结与体会。
通过本次实验,我们深刻体会到了SAS软件在数据分析领域的强大功能和广泛应用。
掌握了SAS软件的基本操作和数据处理技能,提高了数据分析能力。
同时,也加深了对数据分析方法和技巧的理解和应用,为今后的科研工作打下了坚实的基础。
六、参考文献。
[1] 《SAS统计分析实战指南》。
[2] 《SAS数据分析与挖掘实战》。
七、附录。
实验数据集,xxx.xlsx。
以上为本次SAS实验报告的全部内容。
sas数据分析报告

SAS数据分析报告1. 引言SAS(统计分析系统)是一款广泛应用于数据分析和统计建模的软件工具。
本报告将介绍如何使用SAS进行数据分析,并提供一系列步骤,以帮助读者快速上手。
2. 数据准备在开始数据分析之前,我们首先需要准备好待分析的数据集。
数据集应包含所需的变量和观测值,并且应该经过清洗和预处理,以确保数据的准确性和一致性。
3. SAS环境设置在使用SAS进行数据分析之前,我们需要设置SAS环境。
这包括设置工作目录、导入数据和加载所需的SAS库。
markdown sas ** 设置工作目录** libname mydata ‘/path/to/data/’;** 导入数据** data mydata.mydataset; infile ‘/path/to/dataset.csv’ delimiter = ‘,’ firstobs = 2; input var1 var2 var3; run;** 加载SAS库 ** proc sql; create table mydata.mytable as select * from mydata.mydataset; quit; ```4. 数据探索一旦准备好数据并设置好SAS环境,我们可以开始进行数据探索。
这包括计算描述性统计量、绘制图表和查找数据间的相关性等操作。
markdown sas ** 计算描述性统计量 ** proc means data = mydata.mytable; var var1 var2 var3; output out = mydata.summary_stats mean = mean std = std min = min max = max; run;** 绘制直方图 ** proc univariate data = mydata.mytable; histogram var1; run;** 计算相关性 ** proc corr data = mydata.mytable; var var1 var2 var3; run; ```5. 数据分析有了对数据的初步了解后,我们可以开始进行更深入的数据分析。
sas实验报告

sas实验报告SAS实验报告一、实验目的:1.了解SAS软件的使用方法和基本操作2.熟悉SAS数据处理和分析的流程3.掌握SAS数据导入和导出的方法二、实验原理:SAS(Statistical Analysis System)是一个用于统计分析的软件系统,包括数据管理、数据挖掘、报告和图形展示等功能。
SAS语言是一种功能强大的编程语言,通过SAS语言,可以对数据进行处理、分析和建模。
三、实验内容和步骤:1.打开SAS软件,创建一个新的SAS工作空间。
2.使用DATA和SET语句导入外部数据文件,并观察数据的结构和变量。
3.使用PROC PRINT和PROC FREQ等语句对数据进行描述性统计和频数分析。
4.使用PROC MEANS和PROC UNIVARIATE等语句对数据进行均值分析和单变量分析。
5.使用PROC CORR和PROC REG等语句进行相关分析和回归分析。
6.使用PROC GRAPH和PROC PLOT等语句绘制图形。
四、实验结果分析:通过使用SAS软件进行数据处理和分析,我们得到了以下结果:1.数据结构和变量分析:数据包含了10个变量,其中包括年龄、性别、教育水平、职业等信息。
2.描述性统计和频数分析:我们对数据进行了描述性统计,包括计算了平均值、中位数、标准差等统计量,并使用频数分析对变量进行了分组统计。
3.均值分析和单变量分析:我们使用PROC MEANS和PROC UNIVARIATE进行了变量的均值分析和单变量分析,得到了各变量的均值、标准差、四分位数等统计量。
4.相关分析和回归分析:我们使用PROC CORR和PROC REG 对变量之间的相关性进行了分析,并使用回归分析模型进行了拟合。
5.图形绘制:我们使用PROC GRAPH和PROC PLOT对数据进行了可视化展示,绘制了直方图、散点图等图形。
通过对实验结果的分析,我们可以对数据进行进一步的理解和解读,得到了对变量之间关系和趋势的更深入的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
90-08年人民消费能力分析一、问题提出改革开放以来中国经济飞速发展,GDP连续超过德国、日本,现以成为世界上第二大经济体,人民生活水平不断提高,但受金融危机的影响,近几年来物价持续上涨,本月CPI创历史新高,人民的消费能力是否随着GDP的增加而增加呢?本文以中国经济年鉴中的“人民消费支出构成”的数据为依据利用统计软件SAS 进行了相关分析。
数据如下食品衣着居住家庭设备用品及服务交通通讯文教娱乐用品及服务医疗保健其他商品及服务1990 58.8000 7.7700 17.3400 5.2900 1.4400 5.3700 3.2500 0.7400 1995 58.6200 6.8500 13.9100 5.2300 2.5800 7.8100 3.2400 1.7600 2000 49.1300 5.7500 15.4700 4.5200 5.5800 11.1800 5.2400 3.1400 2005 45.4800 5.8100 14.4900 4.3600 9.5900 11.5600 6.5800 2.1300 2007 43.0800 6.0000 17.8000 4.6300 10.1900 9.4800 6.5200 2.3000 2008 43.6700 5.7900 18.5400 4.7500 9.8400 8.5900 6.7200 2.0900二、问题分析1、通过对消费种类进行主成分分析判断人民的消费情况。
2、对主成分标准化后在分析各年的消费能力排名。
三、解决问题3.1 SAS程序:data examp4_4;input id x1-x8;cards;1990 58.8000 7.7700 17.3400 5.2900 1.4400 5.3700 3.2500 0.74001995 58.6200 6.8500 13.9100 5.2300 2.5800 7.8100 3.2400 1.76002000 49.1300 5.7500 15.4700 4.5200 5.5800 11.1800 5.2400 3.14002005 45.4800 5.8100 14.4900 4.3600 9.5900 11.5600 6.5800 2.13002007 43.0800 6.0000 17.8000 4.6300 10.1900 9.4800 6.5200 2.30002008 43.6700 5.7900 18.5400 4.7500 9.8400 8.5900 6.7200 2.0900;run;proc corr cov nosimple data=examp4_4;var x1-x8;run;proc princomp data=examp4_4 out=bb;var x1-x8;run;data score1; /*以下程序是对各年按第一主成分得分进行排名并打印结果*/set bb;keep id prin1;proc sort data=score1;by descending prin1;run;proc print data=score1;run;3.2程序结果:SAS 系统 2011年06月14日星期二下午09时09分56秒 1 CORR PROCEDURE8 变量: x1 x2 x3 x4 x5 x6 x7 x8协方差矩阵,自由度 = 5x1 x2 x3 x4 x5 x6 x7 x8x1 52.12778667 5.14183333 -5.43130667 2.34796667 -27.62341333 -11.27958667 -11.80248667 -3.46987333x2 5.14183333 0.67025667 -0.00552333 0.28069333 -2.68378667 -1.67572333 -1.16476333 -0.56306667x3 -5.43130667 -0.00552333 3.60317667 0.02857333 2.46057333 -1.51458333 1.10495667 -0.25200667x4 2.34796667 0.28069333 0.02857333 0.14566667 -1.21211333 -0.81766667 -0.54318667 -0.23039333x5 -27.62341333 -2.68378667 2.46057333 -1.21211333 15.22562667 5.86791333 6.34247333 1.61420667x6 -11.27958667 -1.67572333 -1.51458333 -0.81766667 5.86791333 5.25949667 2.60837667 1.55695333x7 -11.80248667 -1.16476333 1.10495667 -0.54318667 6.34247333 2.60837667 2.71649667 0.73517333x8 -3.46987333 -0.56306667 -0.25200667 -0.23039333 1.61420667 1.55695333 0.73517333 0.61110667Pearson 相关系数, N = 6当 H0: Rho=0 时,Prob > |r|x1 x2 x3 x4 x5 x6 x7 x8x1 1.00000 0.86989 -0.39630 0.85207 -0.98052 -0.68122 -0.99182 -0.614780.0243 0.4367 0.0312 0.0006 0.1362 0.0001 0.1940x2 0.86989 1.00000 -0.00355 0.89832 -0.84012 -0.89250 -0.86320 -0.879790.0243 0.9947 0.0150 0.0363 0.0167 0.0268 0.0208x3 -0.39630 -0.00355 1.00000 0.03944 0.33220 -0.34792 0.35318 -0.169830.4367 0.9947 0.9409 0.5200 0.4992 0.4923 0.7477x4 0.85207 0.89832 0.03944 1.00000 -0.81391 -0.93417 -0.86350 -0.772200.0312 0.0150 0.9409 0.0487 0.0064 0.0267 0.0719x5 -0.98052 -0.84012 0.33220 -0.81391 1.00000 0.65573 0.98620 0.529190.0006 0.0363 0.5200 0.0487 0.1574 0.0003 0.2803x6 -0.68122 -0.89250 -0.34792 -0.93417 0.65573 1.00000 0.69007 0.868450.1362 0.0167 0.4992 0.0064 0.1574 0.1292 0.0248x7 -0.99182 -0.86320 0.35318 -0.86350 0.98620 0.69007 1.00000 0.570590.0001 0.0268 0.4923 0.0267 0.0003 0.1292 0.2370x8 -0.61478 -0.87979 -0.16983 -0.77220 0.52919 0.86845 0.57059 1.000000.1940 0.0208 0.7477 0.0719 0.2803 0.0248 0.2370SAS 系统 2011年06月14日星期二下午09时09分56秒 2 The PRINCOMP ProcedureObservations 6Variables 8Simple Statisticsx1 x2 x3 x4 x5 x6 x7 x8Mean 49.79666667 6.328333333 16.25833333 4.796666667 6.536666667 8.998333333 5.258333333 2.026666667StD 7.21995753 0.818692046 1.89820354 0.381663028 3.902002904 2.293359254 1.648179804 0.781733117Correlation Matrixx1 x2 x3 x4 x5 x6 x7 x8x1 1.0000 0.8699 -.3963 0.8521 -.9805 -.6812 -.9918 -.6148x2 0.8699 1.0000 -.0036 0.8983 -.8401 -.8925 -.8632 -.8798x3 -.3963 -.0036 1.0000 0.0394 0.3322 -.3479 0.3532 -.1698x4 0.8521 0.8983 0.0394 1.0000 -.8139 -.9342 -.8635 -.7722x5 -.9805 -.8401 0.3322 -.8139 1.0000 0.6557 0.9862 0.5292x6 -.6812 -.8925 -.3479 -.9342 0.6557 1.0000 0.6901 0.8685x7 -.9918 -.8632 0.3532 -.8635 0.9862 0.6901 1.0000 0.5706x8 -.6148 -.8798 -.1698 -.7722 0.5292 0.8685 0.5706 1.0000Eigenvalues of the Correlation MatrixEigenvalue Difference Proportion Cumulative1 5.89746633 4.28709253 0.7372 0.73722 1.61037380 1.25296800 0.2013 0.93853 0.35740580 0.23990054 0.0447 0.98324 0.11750526 0.10025645 0.0147 0.99785 0.01724881 0.01724881 0.0022 1.00006 0.00000000 0.00000000 0.0000 1.00007 0.00000000 0.00000000 0.0000 1.00008 0.00000000 0.0000 1.0000EigenvectorsPrin1 Prin2 Prin3 Prin4 Prin5 Prin6 Prin7 Prin8x1 -.388779 -.255521 0.065754 -.053972 -.301799 0.827792 0.000000 0.000000x2 -.399550 0.099491 -.188366 -.430585 0.686086 0.080082 -.009088 0.363823x3 0.044856 0.746089 0.474521 -.307596 -.085587 0.162417 0.260725 -.140969x4 -.392797 0.115755 0.175040 0.698509 0.113186 -.075845 0.471865 0.269326x5 0.376954 0.252020 -.327681 0.389201 0.453421 0.471547 -.050611 -.324084x6 0.362360 -.365307 -.083990 -.262653 0.077957 0.075391 0.804639 0.000000x7 0.387184 0.242582 -.233722 0.041098 -.286309 0.173586 -.063738 0.786613x8 0.331056 -.314568 0.731663 0.083664 0.352742 0.134323 -.234979 0.226790SAS 系统 2011年06月14日星期二下午09时09分56秒 3Obs id Prin11 2005 1.946992 2007 1.571053 2008 1.319374 2000 1.303735 1995 -2.388246 1990 -3.752893.3结果分析利用SAS得到样本的协方差矩阵为S=[52.12779 5.141833 -5.43131 2.347967 -27.6234 -11.2796 -11.8025 -3.46987 5.141833 0.670257 -0.00552 0.280693 -2.68379 -1.67572 -1.16476 -0.56307 -5.43131 -0.00552 3.603177 0.028573 2.460573 -1.51458 1.104957 -0.252012.347967 0.280693 0.028573 0.145667 -1.21211 -0.81767 -0.54319 -0.23039 -27.6234 -2.68379 2.460573 -1.21211 15.22563 5.867913 6.342473 1.614207 -11.2796 -1.67572 -1.51458 -0.81767 5.867913 5.259497 2.608377 1.556953 -11.8025 -1.16476 1.104957 -0.54319 6.342473 2.608377 2.716497 0.735173 -3.46987 -0.56307 -0.25201 -0.23039 1.614207 1.556953 0.735173 0.611107 ]由此看出,各个指标的样本方差差异很大,因此从样本相关系数矩阵出发做主成分分析,得到下面的相关系数矩阵R=[1 0.86989 -0.3963 0.85207 -0.98052 -0.68122 -0.99182 -0.61478 0.86989 1 -0.00355 0.89832 -0.84012 -0.8925 -0.8632 -0.87979 -0.3963 -0.00355 1 0.03944 0.3322 -0.34792 0.35318 -0.16983 0.85207 0.89832 0.03944 1 -0.81391 -0.93417 -0.8635 -0.7722 -0.98052 -0.84012 0.3322 -0.81391 1 0.65573 0.9862 0.52919 -0.68122 -0.8925 -0.34792 -0.93417 0.65573 1 0.69007 0.86845 -0.99182 -0.8632 0.35318 -0.8635 0.9862 0.69007 1 0.57059 -0.61478 -0.87979 -0.16983 -0.7722 0.52919 0.86845 0.57059 1 ]要集中在衣食住行上面,下面我们只取这两个样本做进一步分析,利用SAS得到对应于λ̂1∗和λ̂2∗的正交单位化特征向量ê1∗和ê2∗,如下表*********1123456780.388780.399550.0448560.39280.3769540.362360.3871840.331056y x x x x x x x x =--+-++++*********2123456780.255520.0994910.7460890.1157550.252020.365310.2425820.31457y x x x x x x x x =-++++-+- *1y 和*2y 中关于各项消费水平的指标系数有正有负,说明了消费种类的差异性较大。
