MATLAB实验报告,遗传算法解最短路径以及函数最小值问题讲解
使用Matlab进行遗传算法优化问题求解的方法

使用Matlab进行遗传算法优化问题求解的方法引言在现代科技发展的背景下,优化算法成为解决各种问题的重要工具之一。
遗传算法作为一种生物启发式算法,具有全局寻优能力和适应性强的特点,在许多领域中被广泛应用。
本文将介绍如何使用Matlab进行遗传算法优化问题求解,包括问题建模、遗传算子设计、遗传算法编码、适应度评价和求解过程控制等方面。
一、问题建模在使用遗传算法求解优化问题之前,我们首先需要将问题定义为数学模型。
这包括确定问题的目标函数和约束条件。
例如,假设我们要最小化一个多变量函数f(x),其中x=(x1,x2,...,xn),同时还有一些约束条件g(x)<=0和h(x)=0。
在Matlab中,我们可通过定义一个函数来表示目标函数和约束条件。
具体实现时,我们需要在目标函数和约束函数中设置输入参数,通过调整这些参数进行优化。
二、遗传算子设计遗传算法的核心是遗传算子的设计,包括选择(Selection)、交叉(Crossover)、变异(Mutation)和替代(Replacement)等。
选择操作通过一定的策略从种群中选择出适应度较高的个体,作为进行交叉和变异的父代个体。
交叉操作通过将两个父代个体的基因片段进行交换,产生新的子代个体。
变异操作通过改变个体某些基因的值,引入新的基因信息。
替代操作通过选择适应度较低的个体将其替换为新产生的子代个体。
三、遗传算法编码在遗传算法中,个体的编码方式决定了问题的解空间。
常见的编码方式有二进制编码和实数编码等。
当问题的变量是二进制形式时,采用二进制编码。
当问题的变量是实数形式时,采用实数编码。
在Matlab中,我们可以使用矩阵或向量来表示个体的基因型,通过制定编码方式来实现遗传算法的编码过程。
四、适应度评价适应度评价是遗传算法中判断个体优劣的指标。
在适应度评价过程中,我们将问题的目标函数和约束条件应用于个体的解,计算得到一个适应度值。
适应度值越大表示个体越优。
遗传算法详解(含MATLAB代码)

遗传算法详解(含MATLAB代码)Python遗传算法框架使用实例(一)使用Geatpy实现句子匹配在前面几篇文章中,我们已经介绍了高性能Python遗传和进化算法框架——Geatpy的使用。
本篇就一个案例进行展开讲述:pip install geatpy更新至Geatpy2的方法:pip install --upgrade --user geatpy查看版本号,在Python中执行:import geatpyprint(geatpy.__version__)我们都听过“无限猴子定理”,说的是有无限只猴子用无限的时间会产生特定的文章。
在无限猴子定理中,我们“假定”猴子们是没有像人类那样“智能”的,而且“假定”猴子不会自我学习。
因此,这些猴子需要“无限的时间"。
而在遗传算法中,由于采用的是启发式的进化搜索,因此不需要”无限的时间“就可以完成类似的工作。
当然,需要产生的文章篇幅越长,那么就需要越久的时间才能完成。
下面以产生"T om is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much."的句子为例,讲述如何利用Geatpy实现句子的搜索。
之前的文章中我们已经讲述过如何使用Geatpy的进化算法框架实现遗传算法编程。
这里就直接用框架。
把自定义问题类和执行脚本编写在下面的"main.py”文件中:# -*- coding: utf-8 -*-import numpy as npimport geatpy as eaclass MyProblem(ea.Problem): # 继承Problem父类def __init__(self):name = 'MyProblem' # 初始化name(函数名称,可以随意设置) # 定义需要匹配的句子strs = 'Tom is a little boy, isn't he? Yes he is, he is a good and smart child and he is always ready to help others, all in all we all like him very much.'self.words = []for c in strs:self.words.append(ord(c)) # 把字符串转成ASCII码M = 1 # 初始化M(目标维数)maxormins = [1] # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标)Dim = len(self.words) # 初始化Dim(决策变量维数)varTypes = [1] * Dim # 初始化varTypes(决策变量的类型,元素为0表示对应的变量是连续的;1表示是离散的)lb = [32] * Dim # 决策变量下界ub = [122] * Dim # 决策变量上界lbin = [1] * Dim # 决策变量下边界ubin = [1] * Dim # 决策变量上边界# 调用父类构造方法完成实例化ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)def aimFunc(self, pop): # 目标函数Vars = pop.Phen # 得到决策变量矩阵diff = np.sum((Vars - self.words)**2, 1)pop.ObjV = np.array([diff]).T # 把求得的目标函数值赋值给种群pop的ObjV执行脚本if __name__ == "__main__":"""================================实例化问题对象============================="""problem = MyProblem() # 生成问题对象"""==================================种群设置================================"""Encoding = 'RI' # 编码方式NIND = 50 # 种群规模Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化)"""================================算法参数设置=============================="""myAlgorithm = ea.soea_DE_rand_1_L_templet(problem, population) # 实例化一个算法模板对象myAlgorithm.MAXGEN = 2000 # 最大进化代数"""===========================调用算法模板进行种群进化========================="""[population, obj_trace, var_trace] = myAlgorithm.run() # 执行算法模板population.save() # 把最后一代种群的信息保存到文件中# 输出结果best_gen = np.argmin(obj_trace[:, 1]) # 记录最优种群是在哪一代best_ObjV = obj_trace[best_gen, 1]print('最优的目标函数值为:%s'%(best_ObjV))print('有效进化代数:%s'%(obj_trace.shape[0]))print('最优的一代是第 %s 代'%(best_gen + 1))print('评价次数:%s'%(myAlgorithm.evalsNum))print('时间已过 %s 秒'%(myAlgorithm.passTime))for num in var_trace[best_gen, :]:print(chr(int(num)), end = '')上述代码中首先定义了一个问题类MyProblem,然后调用Geatpy内置的soea_DE_rand_1_L_templet算法模板,它实现的是差分进化算法DE-rand-1-L,详见源码:运行结果如下:种群信息导出完毕。
matlab遗传算法求函数最小值

题目:使用Matlab遗传算法求解函数最小值的步骤及实例分析目录一、概述二、Matlab遗传算法概述1. 遗传算法原理2. Matlab中的遗传算法工具箱介绍三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙2. 适应度函数的定义3. 轮盘赌选择4. 交叉与变异5. 更新种裙6. 终止条件的设置四、实例分析1. 实例背景2. 实例分析步骤五、总结一、概述在实际工程和科学研究中,经常需要求解函数的最小值,这涉及到优化问题。
遗传算法是一种基于自然选择和遗传机制的全局优化算法,在求解函数最小值问题上具有一定的优势。
Matlab作为一款强大的科学计算软件,具备丰富的数值计算工具和优化算法库,其中也包括遗传算法工具箱。
本文将介绍如何使用Matlab中的遗传算法工具箱求解函数最小值的步骤,并通过一个实例进行分析。
二、Matlab遗传算法概述1. 遗传算法原理遗传算法是一种通过模拟自然界生物进化过程进行优化的算法。
其基本思想是将待优化问题映射成遗传个体的表示形式,并通过种裙的进化过程求解最优解。
遗传算法包括选择、交叉和变异等操作,通过这些操作不断迭代种裙,最终得到最优解。
2. Matlab中的遗传算法工具箱介绍Matlab中提供了用于实现遗传算法的专门工具箱,包括遗传算法函数和用于可视化和评估遗传算法的函数。
使用Matlab的遗传算法工具箱,可以方便地实现遗传算法对函数的全局优化。
三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙在使用Matlab遗传算法工具箱时,需要首先对种裙进行初始化。
可以选择随机生成初始种裙,也可以根据问题的特点进行指定初始种裙。
2. 适应度函数的定义适应度函数是遗传算法中用于评价个体优劣的函数,它的设计直接影响遗传算法的求解效果。
在使用Matlab遗传算法工具箱时,需要根据实际的优化问题设计适应度函数。
3. 轮盘赌选择在遗传算法中,选择操作决定了哪些个体会被选择进行繁殖,而轮盘赌选择是一种常用的选择策略。
matlab遗传算法计算函数区间最大值和最小值

matlab遗传算法计算函数区间最大值和最小值下面是用matlab实现遗传算法计算函数区间最大值和最小值的示例代码:首先定义函数(此处以f(x)=x*sin(10*pi*x)+1为例):matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;end然后设置遗传算法参数:matlaboptions = gaoptimset('Generations', 1000, 'PopulationSize', 50,'StallGenLimit', 200, 'TolCon', 1e-10);其中,Generations表示遗传算法的迭代次数,PopulationSize表示种群大小,StallGenLimit表示在连续多少代没有改变时停止迭代,TolCon表示收敛精度。
接着,编写遗传算法主函数:matlab[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);其中,第一个参数为要优化的函数,第二个参数为变量维度,后面的参数为变量的取值范围。
最后,输出结果:matlabfprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);其中,-fval表示函数最大值,fval表示函数最小值。
完整代码如下:matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;endoptions = gaoptimset('Generations', 1000, 'PopulationSize', 50, 'StallGenLimit', 200, 'TolCon', 1e-10);[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);fprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);参考资料:[1][2]。
Matlab中的遗传算法与优化问题求解方法介绍

Matlab中的遗传算法与优化问题求解方法介绍引言随着科技的不断进步,优化问题在各个领域中的应用越来越广泛。
在实际问题中,我们往往需要找到一个最优解或者接近最优解的近似解。
为了解决这类问题,遗传算法作为一种自适应的搜索算法,被广泛应用于各个领域。
而Matlab作为一种功能强大的数学软件,提供了丰富的遗传算法工具箱,为优化问题的求解提供了便利。
本文将介绍Matlab中的遗传算法和一些常用的优化问题求解方法。
一、遗传算法概述遗传算法是源于达尔文的进化论思想的一种优化算法。
它是通过模拟自然选择、交叉、变异等生物遗传的过程来搜索最优解的方法。
遗传算法由编码、适应度评估、选择、交叉和变异等基本操作组成。
1. 编码:遗传算法使用二进制编码或者其他离散编码,将问题的解表示为一串二进制码或离散码。
2. 适应度评估:将编码得到的解转化为问题的实际解,并计算该解的适应度,即问题的目标函数值。
3. 选择:根据适应度对解进行选择,适应度越大的解,被选中的概率越大。
4. 交叉:从父代中选择两个个体,通过某种交叉方式生成子代。
5. 变异:对子代进行变异操作,以增加解的多样性。
二、Matlab中的遗传算法函数在Matlab的遗传算法工具箱中,包含了一系列的遗传算法函数,可以快速实现遗传算法优化问题的求解。
1. ga函数:这是Matlab中最基本的遗传算法函数,用于求解普通的优化问题。
它可以通过改变种群大小、交叉概率、变异概率等参数来调整算法的性能。
2. gamultiobj函数:这个函数是用于解决多目标优化问题的。
它使用了帕累托前沿的概念,可以得到一系列的非支配解,以帮助决策者选择最优解。
3. gaplotbestf函数:这个函数可以绘制遗传算法的收敛曲线,直观地展示算法求解的过程。
三、优化问题求解方法除了遗传算法外,Matlab还提供了其他一些常用的优化问题求解方法。
1. 粒子群算法(PSO):这是一种群体智能算法,通过模拟鸟群或鱼群的行为,寻找最优解。
基于遗传算法的最短路径问题及其MATLAB实现
TRANSPOWORLD 2009 No.12(Jun)104前言在现实生活中,我们经常遇到最短路问题,例如寻找两点之间总长度最短或者费用最低的路径。
在运输、物流、设施选址以及人员调度问题中,最短路径是很常见的问题。
解决最短路问题的方法有很多,例如迪杰斯特拉算法、福特算法。
在这里我们介绍基于遗传算法的最短路径问题的解决方案。
模型遗传算法基本模型遗传算法是模仿生物进化过程,针对复杂问题开发出来的非常有效的方基于遗传算法的最短路径问题及其MATLAB 实现文/张书源 郭 聪法。
根据生物进化过程中的选择机制,在问题的解空间中进行选择,实现“物竞天择,适者生存”。
在遗传算法中,一条染色体代表问题的一个可行解,该染色体的适应值即为对应于该可行解的函数值。
一般来说,遗传算法包括以下几个主要组成部分。
编码即将问题的解表示成一个编码串(染色体),每一染色体对应问题的一个解。
遗传过程对染色体进行操作,以产生新的染色体,通常有不同染色体之间的交叉操作以及一条染色体的变异操作。
评价与选择对每条染色体计算其适应值,用以评价染色体的优劣,从而从父代和子代中选择较优的染色体,进入下一代的繁殖。
初试种群的创建方法其作为问题可行解的集合。
初始种群中染色体个数称为种群规模。
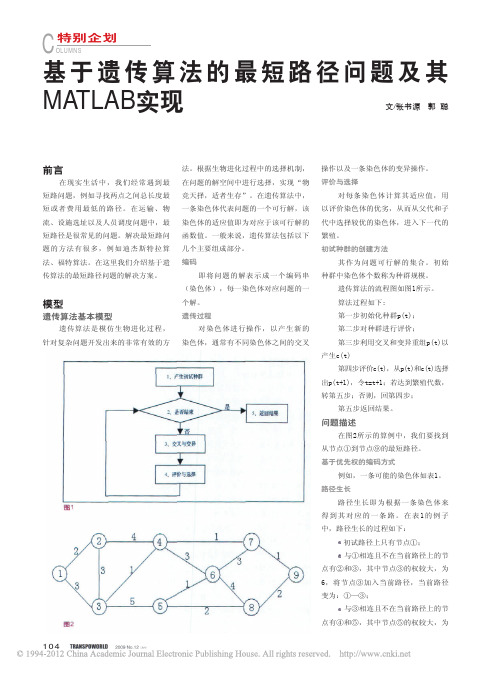
遗传算法的流程图如图1所示。
算法过程如下:第一步初始化种群p(t);第二步对种群进行评价;第三步利用交叉和变异重组p(t)以产生c(t)第四步评价c(t),从p(t)和c(t)选择出p(t+1),令t=t+1;若达到繁殖代数,转第五步;否则,回第四步;第五步返回结果。
问题描述在图2所示的算例中,我们要找到从节点①到节点⑨的最短路径。
基于优先权的编码方式例如,一条可能的染色体如表1。
路径生长路径生长即为根据一条染色体来得到其对应的一条路。
在表1的例子中,路径生长的过程如下:初试路径上只有节点①; 与①相连且不在当前路径上的节点有②和③,其中节点③的权较大,为6,将节点③加入当前路径,当前路径变为:①—③;与③相连且不在当前路径上的节点有④和⑤,其中节点⑤的权较大,为图2COLUMNS特别企划1052009年第12期 《交通世界》(6月下)5,将节点⑤加入到当前路径中,当前路径变为①—③—⑤;与⑤相连且不在当前路径上的节点有⑥和⑧,其中节点⑧的权较大,为9,将节点⑧加入到当前路径中,当前路径变为①—③—⑤—⑧;与⑧相连且不在当前路径上的节点有⑥和⑨,其中节点⑨的权较大,为8,将节点⑨加入到当前路径中,当前路径变为①—③—⑤—⑧—⑨。
基于Matlab的遗传算法解决TSP问题的报告

报告题目:基于Matlab的遗传算法解决TSP问题说明:该文包括了基于Matlab的遗传算法解决TSP问题的基本说明,并在文后附录了实现该算法的所有源代码。
此代码经过本人的运行,没有发现错误,结果比较接近理论最优值,虽然最优路径图有点交叉。
因为本人才疏学浅,本报告及源代码的编译耗费了本人较多的时间与精力,特收取下载积分,还请见谅。
若有什么问题,可以私信,我们共同探讨这一问题。
希望能对需要这方面的知识的人有所帮助!1.问题介绍旅行商问题(Traveling Salesman Problem,简称TSP)是一个经典的组合优化问题。
它可以描述为:一个商品推销员要去若干个城市推销商品,从一个城市出发,需要经过所有城市后,回到出发地,应如何选择行进路线,以使总行程最短。
从图论的角度看,该问题实质是在一个带权完全无向图中。
找一个权值最小的Hemilton回路。
其数学描述为:设有一个城市集合其中每对城市之间的距离(),i j d c c R +∈,求一对经过C中每个城市一次的路线()12,,n c c c ΠΠΠ⋯使()()()1111min ,,n i n i i d c c d c c −ΠΠΠΠ+=+∑其中()12,,12n n ΠΠΠ⋯⋯是,的一个置换。
2.遗传算法2.1遗传算法基本原理遗传算法是由美国J.Holland 教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的,它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
遗传算法模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标从解群中选取较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行组合,产生新一代的候选解群,重复此过程,直到满足某种收敛指标为止。
遗传算法,在本质上是一种不依赖具体问题的直接搜索方法,是一种求解问题的高效并行全局搜索方法。
遗传算法在模式识别、神经网络、图像处理、机器学习、工业优化控制、自适应控制、负载平衡、电磁系统设计、生物科学、社会科学等方面都得到了应用。
matlab最短路径实验报告

matlab最短路径实验报告一、实验目的本实验的目的是通过使用Matlab软件来实现最短路径算法,掌握最短路径算法的基本思路和实现方法,加深对图论知识的理解和应用能力。
二、实验原理最短路径算法是图论中一个重要的问题,它是指在一个加权有向图或无向图中从一个顶点到另一个顶点之间经过的边权值之和最小的路径。
常见的最短路径算法有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
本次实验采用Dijkstra算法来求解最短路径。
Dijkstra算法是一种贪心算法,它通过维护一个集合S来不断扩展已知最短路径集合S中所有节点到未知节点v之间的距离,并选取其中距离最小的节点u加入S中,直到所有节点都被加入S为止。
三、实验步骤1. 构建图首先需要构建一个加权有向图或无向图。
本次实验采用无向图,并使用邻接矩阵表示。
具体步骤如下:(1)定义节点数n和边数m;(2)定义邻接矩阵A(n*n),其中A(i,j)表示从i到j是否有边,如果有则为边的权值,如果没有则为无穷大。
2. 初始化(1)定义两个数组dist和visited,其中dist(i)表示从起点到节点i 的最短距离,visited(i)表示节点i是否已经加入集合S中;(2)将起点加入集合S中,并将visited数组对应位置设为1;(3)初始化dist数组,将所有非起点节点的距离设为无穷大。
3. 迭代更新(1)遍历集合S中所有节点u的邻居节点v,如果v未被加入集合S 中,则更新dist(v)的值。
具体而言,如果dist(u)+A(u,v)<dist(v),则更新dist(v)=dist(u)+A(u,v);(2)在所有未加入集合S中的节点中选取距离最小的节点u,并将其加入集合S中。
4. 输出结果输出起点到各个终点的最短路径长度和路径。
四、实验结果与分析本次实验构建了一个无向图,并使用Dijkstra算法求解了最短路径。
具体实现过程如下:1. 构建图构建了一个6个节点、8条边的无向图,邻接矩阵如下:0 6 4 Inf Inf Inf6 0 1 5 Inf Inf4 1 0 Inf Inf InfInf5InfInf0 Inf 1InfInfInf Inf0 2InfInfInf 1 2 0其中,Inf表示两个节点之间没有边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
硕士生考查课程考试试卷考试科目:MATLAB教程考生姓名:考生学号:学院:专业:考生成绩:任课老师(签名)考试日期:20 年月日午时至时《MATLAB 教程》试题:A 、利用MATLAB 设计遗传算法程序,寻找下图11个端点的最短路径,其中没有连接的端点表示没有路径。
要求设计遗传算法对该问题求解。
ad ehkB 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
C 、利用MATLAB 编程实现:三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行,随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人手中,商人们怎样才能安全渡河?D 、结合自己的研究方向选择合适的问题,利用MATLAB 进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目: A 一、问题分析(10分)141011如图如示,将节点编号,依次为 1.2.3.4.5.6.7.8.9.10.11,由图论知识,则可写出其带权邻接矩阵为:0 2 8 1 500 500 500 500 500 500 500 2 0 6 500 1 500 500 500 500 500 500 8 6 0 7 500 1 500 500 500 500 500 1 500 7 0 500 500 9 500 500 500 500 500 1 500 500 0 3 500 2 500 500 500 500 500 1 500 3 0 4 500 6 500 500 500 500 500 9 500 4 0 500 500 1 500 500 500 500 500 2 500 500 0 7 500 9 500 500 500 500 500 6 500 7 0 1 2 500 500 500 500 500 500 1 500 1 0 4 500 500 500 500 500 500 500 9 2 4 0 注:为避免计算时无穷大数吃掉小数,此处为令inf=500。
问题要求求出任意两点间的最短路径,Floyd 算法采用的是在两点间尝试插入顶点,比较距离长短的方法。
我思考后认为,用遗传算法很难找到一个可以统一表示最短路径的函数,但是可以对每一对点分别计算,然后加入for 循环,可将相互之间的所有情况解出。
观察本题可发现,所有节点都是可双向行走,则可只计算i 到j 的路径与距离,然后将矩阵按主对角线翻折即可得到全部数据。
二、实验原理与数学模型(20分)实现原理为遗传算法原理:按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选,使得适应度高的个体被保留下来,组成新的群体,新的群体既继承了上一代的信息,又优于上一代。
这样周而复始,群体中个体适应度不断提高,直到满足一定的条件。
数学模型如下: 设图G 由非空点集合12{,...}n V V V V = 和边集合12{,...}m E e e e = 组成,其中121221(,)e ,P ,)(P ,P ),i i i i i i i i e P P E P =∈≠且若(则G 为一个有向图; 又设i e 的值为i a ,12{,...},m A a a a = 故G 可表示为一个三元组{,,}G P E A = 则求最短路径的数学模型可以描述为:1min *..ni ii i i A E s t A A E E=⎧⎪⎨⎪∈∈⎩∑ 实验具体:第一:编码与初始化因采用自然编码,且产生的编码不能重复,于是我采用了randperm 函数产生不重复的随机自然数。
因解题方法是使用的是计算每一对点,则我们编码时将第一个节点单独放入,合并成完整编码。
因为节点有11个,可采用一个1行11列的矩阵储存数据,同时,由于编号为数字,可直接使用数字编码表示路径的染色体。
具体如下:采用等长可变染色体的方式,例如由2到9的路径,染色体编码可能为(2,5,1,8,4,6,9,3,10,7,11),超过9之后的编码,用来进行算子的运算,不具备实际意义。
第二:计算适应度,因取最短路径值,即最小值,常用方法为C-F(x)或C/F(x)(C 为一常数),此处采用前一种方式。
于是,可进一步计算相对适应度。
第三:选择与复制采用轮盘赌算法,产生一个随机值,比较它与累计相对适应度的关系,从而选择出优良个体进入下一代。
第四:交叉。
因编码是不重复的数字,所以采用传统的交叉方法,即上一行与下一行对位交叉,会产生无效路径,于是,采用了不同的交叉方法,具体如下:(1)在表示路径的染色体Tx 和Ty 中,随机选取两个基因座(不能为起点基因座)i 和j, 即将i 个基因座和第j 个基因座之间的各个基因座定义为交叉域,并将交叉的内容分别记忆为temp1和temp2。
(2)根据交叉区域中的映射关系,在个体Tx 中找出所有与temp2相同的元素,在个体Ty 中找出所有与temp1相同的元素,全部置为0。
(3)将个体Tx 、Ty 进行循环左移,遇到0就删除,直到编码串中交叉区域的左端不再有0:然后将所有空位集中到交叉区域,而将交叉区域内原有的基因依次向后移动。
因0元素可能较多,在程序实现时,我是将非零元素提出,后面再合成。
(4)将temp2插入到Tx 的交叉区域,temp1插入到Ty 的交叉区域。
形成新的染色体[1]。
第五:变异染色体编码为从1到11的无重复编码,所以不能采用一般的生成一个随机数替代的办法。
此处采用交换变异法。
即随机产生两个数,交换两个节点的顺序。
例:[1,2,3,4,5,6,7,8,9,10,11],13,28p K K === 则新染色体编码为:[1,2,8,4,5,6,7,3,9,10,11]p =三、实验过程记录(含基本步骤、程序代码及异常情况记录等)(60分)首先,写程序,修复Bug 。
然后,调试种群数量,遗传代数,交叉概率,变异概率等,不断运行程序,以达到较理想的状态。
有一次异常情况:算出来的最短距离均为0,最短路径没有终点出现,经过分析发现,因为交叉处的代码较复杂,弄错了一点,导致新基因有部分为非法基因。
最后采用提出非零数值组成向量,再合成新基因的方式解决。
Matlab程序代码如下:clc;clear;%初始化参数%注:popsize=200,MaxGeneration=100,约跑2分钟。
若不要求太精确,可减少循环次数。
pointnumber=11; %节点个数Popsize=200; %种群规模,只能取偶数(因67行的循环)MaxGeneration=100; %最大代数Pc=0.8;Pm=0.3; %交叉概率和变异概率A=[0 2 8 1 50 50 50 50 50 50 502 0 6 50 1 50 50 50 50 50 508 6 0 7 50 1 50 50 50 50 501 50 7 0 50 50 9 50 50 50 5050 1 50 50 0 3 50 2 50 50 5050 50 1 50 3 0 4 50 6 50 5050 50 50 9 50 4 0 50 50 1 5050 50 50 50 2 50 50 0 7 50 950 50 50 50 50 6 50 7 0 1 250 50 50 50 50 50 1 50 1 0 450 50 50 50 50 50 50 9 2 4 0]; %带权邻接矩阵。
A(A==50)=500; %取值50过小而修正为500;Bestindividual=zeros(MaxGeneration,1);outdistance=zeros(11,11);outpath=cell(11,11); %用于存放11个点相互之间的最短路径%****** 生成初始种群******for a=1:pointnumber %起点的编号%a=1;tempvary=[1 2 3 4 5 6 7 8 9 10 11];tempvary(a)=[]; %暂时剔除起点tempmatrix=a*ones(Popsize,1); %将起点单独放一矩阵path=zeros(Popsize,pointnumber-1); %声明矩阵大小,避免减慢速度for i=1:Popsizetemprand=randperm(pointnumber-1);path(i,:)=tempvary(temprand(1:end)); %生成一系列剔除起点的随机路线endpath=[tempmatrix path]; %合成包括起点的完整路线[row,col]=size(path);for b=a:pointnumber %终点的编号%b=10;for k=1:1:MaxGenerationfor i=1:rowposition2=find(path(i,:)==b); %找出终点在路线中的位置pathlong(i)=0;for j=1:position2-1pathlong(i)=pathlong(i)+A(path(i,j),path(i,j+1));endend%计算适应度Fitness=length(A)*max(max(A))-pathlong; %因要求最小值,采且常数减函数值构造适应度Fitness=Fitness./sum(Fitness);%****** Step 1 : 选择最优个体******Bestindividual(k)=min(pathlong);[Orderfi,Indexfi]=sort(Fitness); %按照适应度大小排序Bestfi=Orderfi(Popsize); %Oderfi中最后一个即是最大的适应度BestS=path(Indexfi(Popsize),:); %记录每一代中最优个体的路线%****** Step 2 : 选择与复制操作******temppath=path;roulette=cumsum(Fitness);for i=1:PopsizetempP=rand(1);for j=1:length(roulette)if tempP<roulette(j)break;endendpath(i,:)=temppath(j,:);end%************ Step 3 : 交叉操作************temppath2=path;for i=1:2:rowtempP2=rand(1);if(tempP2<rand(1))temPm2=fix((rand(1)+0.2)*10); %因起点基因不能改变temPm3=fix((rand(1)+0.2)*10); %随机取出两个位置为2到11基因座temPm4=min(temPm2,temPm3);temPm5=max(temPm2,temPm3);temp1=path(i,temPm4:temPm5); %将两点之间的基因储存,方便交叉temp2=path(i+1,temPm4:temPm5);[c d]=find(ismember(path(i,:),temp2));path(i,d)=0; %找出i行在i+1行取出区域中的数,置为0[e f]=find(ismember(path(i+1,:),temp1));path(i+1,f)=0; %找出i+1行在i行取出区域中的数,置为0[g h]=find(path(i,:)~=0);v1=path(i,h); %取出i行的非零元素,成一向量[l m]=find(path(i+1,:)~=0);v2=path(i+1,m); %取出i+1行的非零元素,成一向量path(i,:)=[v1(1:temPm4-1) temp2 v1(temPm4-1+size(temp1):end)];path(i+1,:)=[v2(1:temPm4-1) temp1 v2(temPm4-1+size(temp2):end)]; %基因交叉endendpath(Popsize,:)=BestS;%************ Step 4: 变异操作**************for i=1:PopsizetempPm=rand(1);if(tempPm<Pm)temPm6=fix((rand(1)+0.2)*10);temPm7=fix((rand(1)+0.2)*10); %产生两个用于交换的随机数tempvessel=path(i,temPm6); %交换前用一临时容器存放数据path(i,temPm6)=path(i,temPm7);path(i,temPm7)=tempvessel; %变异交换endendpath(Popsize,:)=BestS;end[aa bb]=find(BestS==b); %找出终点Bestpath=BestS(1:bb); %剔除后面无用的点,留下实际路线outdistance(a,b)=Bestindividual(k); %将最短距离写入矩阵outpath{a,b}=Bestpath; %写入路径,因数据类型为矩阵,所以采用元胞数组储存endendfor i=1:pointnumberfor j=1:ioutdistance(i,j)=outdistance(j,i); %实现距离的对称outpath{i,j}=fliplr(outpath{j,i}); %实现路径的对称与翻转endend%*************** 结果输出*****************outdistancecelldisp(outpath)%xlswrite('tempdata.xls', outpath) %存入excel中进行操作四、实验结果与总结(10分)距离矩阵:a(i,j) i表示起点,j表示终点。
