2001考研数一真题及答案解析

合集下载

2001考研数学一试题及答案解析

2001考研数学一试题及答案解析2001年考研数学一试题及答案解析一、选择题1.设A是n阶实对称矩阵，B是n阶对称矩阵，则下列结论正确的是（）A. AB是对称矩阵B. AB是反对称矩阵C. AB是零矩阵D. AB不一定是对称矩阵答案：D解析：对称矩阵的乘积不一定是对称矩阵，故选D。

2.设A是n阶矩阵，|A|≠0，则下列结论正确的是（）A. A是可逆矩阵B. A的行列式不等于0C. A的秩等于nD. A的特征值不等于0答案：A解析：根据矩阵可逆的定义，可知选项A正确。

3.设函数f(x)在区间[a,b]上连续，且在(a,b)内可导，则下列结论正确的是（）A. 函数f(x)在[a,b]上一定有最大值和最小值B. 函数f(x)在(a,b)内一定有极值点C. 函数f(x)在[a,b]上一定有极值点D. 函数f(x)在(a,b)内一定有最大值和最小值答案：B解析：根据极值定理，可知选项B正确。

4.设函数f(x)在区间[a,b]上连续，且在(a,b)内可导，则函数f(x)在[a,b]上（）A. 一定有最大值和最小值B. 一定有极值点C. 一定有极大值和极小值D. 不一定有极值点答案：D解析：函数在区间[a,b]上连续，且在(a,b)内可导并不意味着一定有极值点，故选D。

5.若f(x)在区间[a,b]上连续，且在(a,b)内可导，且f'(x)>0，则下列结论正确的是（）A. 函数f(x)在[a,b]上单调递减B. 函数f(x)在[a,b]上单调递增C. 函数f(x)在(a,b)内存在极大值D. 函数f(x)在[a,b]上存在极小值答案：B解析：根据导数的定义，可知选项B正确。

二、填空题1.设A是n阶实对称矩阵，且A的主对角线元素都为1，则A的特征值之和为____。

答案：n+1解析：根据实对称矩阵的特征值之和等于主对角线元素之和，故特征值之和为n+1。

2.设z为复数，|z|=1，则z^3的实部为____。

2001年考研数学一试题答案与解析

（C）曲线
⎧⎪⎪⎨⎪⎪⎩z
= y
f (x,
=0
y)
在点
(0,
0,
f
(0,
0))
的切向量为
{1,
0,
3}
。
NBF 考研辅导，全程包过，不4过退款! QQ 客服：296312040
NBF 辅导，真正为考研人着想的辅导!
（
D
）
曲
线
⎧⎪⎪⎨⎪⎪⎩z
= y
f (x,
=0
y)
在
点
(0, 0,
可判定正确选项。详解由 y = f (x) 的图形可知，当 x < 0 时， f (x) 单调增加，
从而 f ' (x)> 0 ，所以选项(A)、(C)可以排除，此外由 y = f (x) 的图形可知，在
x > 0 部分 f ' (x)有两个零点，在较小的零点左侧， y = f (x) 单调增加，因此
令 ε = 2, DX = 2 ，则 P{ X − E ( X ) ≥ 2} ≤ D( X )/ 22 = 1 。
2 由于多年以来一直未靠过切比雪夫不等式或极限定理中有关的内容，可能有不少考生在复习时未予重视，从而对此看来十分简单的填空，一片茫然。束手无策。本题难度值为0.60，区分度为0.44，属于第Ⅴ类试题。
二、选择题(本题共 5 小题，每小题 3 分，满分 15 分)
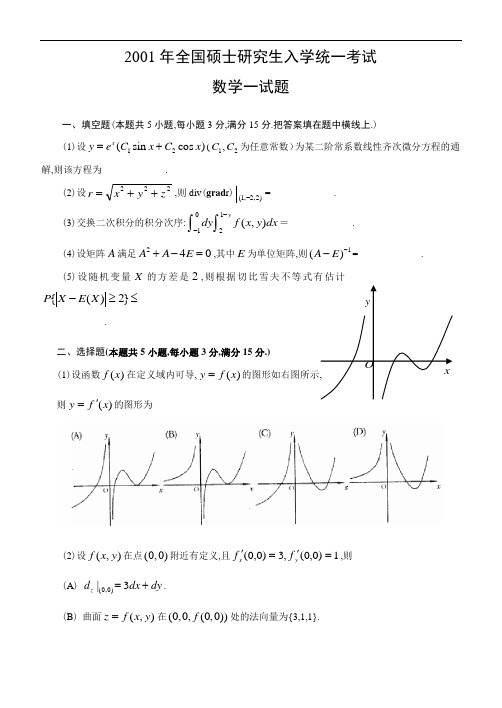
（1）设函数 f (x) 在定义域内可导， y = f (x) 的图形如下图所示，则导函数
y = f ' (x)的图形为
NBF 考研辅导，全程包过，不3过退款! QQ 客服：296312040
NBF 辅导，真正为考研人着想的辅导!

2001年北京大学经济学院考研真题及答案解析

官方网址北大、人大、中财、北外教授创办集训营、一对一保分、视频、小班、少干、强军 2001年北京大学经济学院考研真题及答案解析微观经济学部分一、（8分）简答下列问题（1）规模报酬和规模经济的区别和联系；（2）利用效用论的有关原理，说明一个经济社会中不可能所有的商品都是劣等品。

二、（9分）在产品市场和要素市场均为完全竞争的前提下，单个厂商的要素需求曲线在什么条件下与其边际产品价值曲线（VMP ）完全重合？若厂商只使用一种要素，如何从单个厂商的要素需求曲线推导出要素的市场需求曲线？三、（8分）设某行业的需求曲线为Q ＝250－P ，行业中每家厂商的边际成本均为4。

（1）假定该行业中由两个厂商，写出相应的古诺模型的反应函数并求出古诺解的均衡产量和均衡价格。

（2）假定该寡头行业由n 个厂商（n>2）则相应的古诺解的均衡产量和均衡价格是多少？（3）试证明：当该行业中厂商数目无穷多时，该行业的古诺解趋向于完全竞争解。

宏观经济学部分一、（4分）设总量生产函数Y ＝F （K ，L ），其中Y 代表总产量，K 代表总资本量，L 代表总劳动量。

试说明，如果规模效益不变，则人均产量唯一地取决于人均资本量。

二、（9分）已知：线性生产函数、成本加成的定价原则和菲利普斯曲线，菲利普斯曲线为：，其中gw 为名义工资增长率，为实际失业率，为自然失业率，为名义工资增长率对失业率变动的敏感程度。

试推导凯恩斯主义的短期总供给曲线。

三、（12分）在封闭经济的产品市场收入－支出模型中，运用投资－储蓄法：（1）推导三部门产品市场的储蓄函数。

（2）作四象限图说明，如果政府将税率从提升到，对储蓄、投资、均衡利率水平和IS 曲线的影响。

政治经济学部分一、（6分）社会总资本的再生产和流通与单个资本的再生产和流通相比较，其研究对象和范围的主要区别是什么？二、（19分）在马克思的经济理论中，是如何论述商品生产所有权规律转变为资本主义占有规律的？三、（25分）试述我国国有企业改革的进程及面临的主要任务。

考研数学一(常微分方程)历年真题试卷汇编2(题后含答案及解析)

考研数学一（常微分方程）历年真题试卷汇编2(题后含答案及解析) 题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(1989年)设线性无关的函数y1，y2，y3都是二阶非齐次线性方程y”+p(x)y’+q(x)y=f(x)的解，c1，c2是任意常数，则该非齐次方程的通解是A．c1 y1+c2y2+y3B．c1y1+c2y2一(c1+c2)y3C．c1y1+c2y2一(1一c1—c2)y3D．c1y1+c2y2+(1一c1一c2)y3正确答案：D解析：由于(D)中的y=C1y1+C2y2+(1一C1—C2)y3=C1(y1一y3)+C2(y2一y3)+y3其中y1一y3和y2一y3是对应的齐次方程的两个解，且y1一y3与y2—y3线性无关．事实上，若令A(y1—y3)+B(y2一y3)=0即Ay1+By2一(A+B)y3=0由于y1，y2，y3线性无关，则A=0，B=0，一(A+B)=0因此y1一y3与y2一y3线性无关，故y=C1y1+C2y2+(1一C1—C2)y3是原方程通解．知识模块：常微分方程2．(1991年)若连续函数f(x)满足关系式则f(x)等于A．exln2B．e2xln2C．ex+ln2D．e2x+ln2正确答案：B解析：等式两边求导得f’(x)=2f(x)解此方程得f(x)=Ce2x由原方程可知f(0)=ln2，代入f(x)=Ce2x得C=ln2.故f(x)=e2xln2 知识模块：常微分方程3．(1993年)设曲线积分与路径无关，其中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于A．B．C．D．正确答案：B解析：由得f’(x)+f(x)=ex解此方程得f(x)=e-x(e2x+C)由f(0)=0得，故知识模块：常微分方程填空题4．(1992年)微分方程y’+ytanx=cosx的通解为y=_____________．正确答案：(x+c)cosx．解析：由线性方程通解公式得知识模块：常微分方程5．(1996年)微分方程y”一2y’+2y=ex的通解为___________．正确答案：特征方程为λ2一2λ+2=0，解得λ1，2=1±i，则齐次方程通解为y=ex(C1cosx+C2sinx)易观察出y=ex是非齐次方程的一个特解．则原方程通解为y=ex(C1cosx+C2sinx)+ex 涉及知识点：常微分方程6．(1999年)y”一4y—e2x的通解为y=____________．正确答案：C1e-2x+C2e2x+xe2x．解析：特征方程为λ2一4=0，则λ=一2，λ2=2，从而齐次方程的解为由于λ=2为特征方程单根，则非齐次待定特解可设为y*=Axe2x代入原方程得故所求通解为y=C1e-2x+C2e2x+xe2x 知识模块：常微分方程7．(2000年)微分方程xy”+3y’=0的通解为____________．正确答案：解析：令y’=p，则y”=p’．代入原方程得解得因此知识模块：常微分方程8．(2001年)设y=ex(C1sinx+C2cosx)(C1，C2为任意常数)为某二阶常系数线性齐次微分方程的通解，则该方程为___________．正确答案：y”-2y’+2y=0解析：所求方程的特征根为λ1，2=1,±i则其特征方程为λ2一2λ+2=0故所求方程为y”一2y’+2y=0 知识模块：常微分方程9．(2002年)微分方程yy”+y’2一0满足初始条件的特解是____________．正确答案：y2=x+1或解析：解 1 令y’=P，则代入原方程得解得可知，则所求的特解为y2=x+1 解2 由于原方程左端从而原方程可改写为因此yy’=C1以下求解同解1．知识模块：常微分方程10．(2004年)欧拉方程的通解为___________．正确答案：解析：令z=et 代入原方程所得新方程的特征方程为ρ(ρ一1)+4ρ+2=0 解得ρ1=一1，ρ2=一2则新方程通解为y=C1e-t+C2e-2t，将x=et代入得原方程通解为知识模块：常微分方程解答题解答应写出文字说明、证明过程或演算步骤。

2001年考研数学一试题及完全解析(Word版)

yOx2001年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设12(sin cos )xy e C x C x =+(12,C C 为任意常数）为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)设222z y x r++=,则div (grad r ))2,2,1(-=_____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy ＝_____________.(4)设矩阵A 满足240A A E +-=,其中E 为单位矩阵,则1()A E --=_____________.(5)设随机变量X 的方差是2,则根据切比雪夫不等式有估计≤≥-}2)({X E X P_____________.二、选择题(本题共5小题,每小题3分,满分15分.) (1)设函数)(x f 在定义域内可导,)(x f y =的图形如右图所示,则)(x f y'=的图形为(2)设),(y x f 在点(0,0)附近有定义,且1)0,0(,3)0,0(='='y x f f ,则(A ) (0,0)|3z d dx dy =+. (B ) 曲面),(y x f z=在(0,0,(0,0))f 处的法向量为{3,1,1}.(C ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{1,0,3}.(D ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{3,0,1}.(3)设0)0(=f ,则)(x f 在x =0处可导的充要条件为(A ) 201lim (1cosh)h f h →-存在.(B )01lim(1)h h f e h →-存在. (C ) 201lim (sinh)h f h h→-存在.(D ) 01lim [(2)()]h f h f h h→-存在.(4)设1111400011110000,,1111000011110000A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则A 与B (A ) 合同且相似. (B ) 合同但不相似. (C ) 不合同但相似.(D ) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 的相关系数等于(A )-1.(B ) 0.(C )12. (D ) 1.三、(本题满分6分)求dx e e xx⎰2arctan .四、(本题满分6分) 设函数),(y x f z=在点(1,1)处可微,且(1,1)1f =,(1,1)|2fx∂=∂,(1,1)|3f y ∂=∂,()(,x f x ϕ=(,))f x x .求13)(=x x dxd ϕ.五、(本题满分8分)设)(x f =210,arctan ,0,1,x x x x x +⎧≠⎨=⎩将)(x f 展开成x 的幂级数,并求级数∑∞=--1241)1(n nn 的和.六、(本题满分7分) 计算dz y x dy x z dx z y I L)3()2()(222222-+-+-=⎰,其中L 是平面2=++z y x 与柱面1=+y x 的交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分) 设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内的任一0x ≠,存在惟一的)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立;(2)01lim ()2x x θ→=.八、(本题满分8分)设有一高度为()h t (t 为时间)的雪堆在融化过程,其侧面满足方程)()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)的雪堆全部融化需多少小时?九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =的一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =的一个基础解系.十、(本题满分8分) 已知3阶矩阵A 与三维向量x ,使得向量组2,,x Ax A x 线性无关,且满足x A Ax x A 2323-=.(1)记P =（x A Ax x 2,,）,求3阶矩阵B ,使1-=PBP A ;(2)计算行列式E A +.十一、(本题满分7分)设某班车起点站上客人数X 服从参数为λ(0λ>)的泊松分布,每位乘客在中途下车的概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率; (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分) 设总体X 服从正态分布2(,)N μσ(0σ>),从该总体中抽取简单随机样本12,X X ,,2n X (2n ≥),其样本均值为∑==ni i X n X 2121,求统计量∑=+-+=ni i n i X X X Y 12)2(的数学期望()E Y .2001年考研数学一试题答案与解析一、填空题(1)【分析】由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】先求grad r .grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭. 再求 div grad r=()()()x y zx r y r z r∂∂∂++∂∂∂=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】矩阵A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即 2()2A EA E E +-⋅=. 按定义知11()(2)2A E A E --=+.(5)【分析】根据切比雪夫不等式2(){()}D x P X E X εε-≥≤,于是2()1{()2}22D x P XE X -≥≤=.二、选择题(1)【分析】当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ).(2)【分析】我们逐一分析.关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面(,)z f x y =在 (0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭，，{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点(0,0,(0,0))f 处的切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===. 因此,(C )成立.(3)【分析】当(0)0f =时,'0()(0)limx f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知 201lim (1cos )h f h h→-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃. 关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0lim((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时).注意,易求得20sin lim0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t→(即 '(0)f ∃).因为只要()f t t有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同的特征值,从而二次型T x Ax 与T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦, 它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】解本题的关键是明确X 和Y 的关系:XY n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即YaX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2xx x x e e e e C ---+++.四、【解】先求(1)(1,(1,1))(1,1)1f f f ϕ===.求 32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法 '''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意'1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y ∂==∂. 因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=.五、【分析与求解】关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121n n n x n n ∞=+--+-∑221(1)2114n nn x n ∞=-=+-∑ ,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f n ππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L 的定向,按右手法则S 取上侧,S 的单位法向量(cos ,cos ,cos )3n αβγ==. 于是由斯托克斯公式得222222cos cos cos 23SI dS x y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=[(24(26(22]333Sy z z x x y dS --+--+--⎰⎰=(423)(2)(6)33S Sx y z dS x y z x y dS ++++=-+-利用. 于是'2'211113x y Z Z ++=++=按第一类曲面积分化为二重积分得(6)32(6)3D DI x y dxdy x y dxdy =+-=-+-⎰⎰, 其中D 围S 在xy 平面上的投影区域||||1x y +≤(图）.由D 关于,x y 轴的对称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒21212(2)24DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x xθθθ---⋅=, 解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八、【解】 (1)设t 时刻雪堆的体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤. ⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒()xyxyD D S t dxdy ==⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r t θπ≤≤≤≤.⇒2(003()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==⋅+=⎰用先二后一的积分顺序求三重积分()()()h t D x V t dzdxdy =⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-. ⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件.体积减少的速度是dV dt -,它与侧面积成正比(比例系数0.9),即 0.9dVS dt=- 将()V t 与()S t 的表达式代入得 22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-.①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时.九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于 12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-, 所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】 (1)由于AP PB = ,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知AB ,那么A E B E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,mmn mn P Y m X n C p p m n n -===-≤≤=.(2){,}P Xn Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσ的一个容量为n 的简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑, 样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即2()2(1)E Y n σ=-.。

2001-2011考研(数一)概率论部分历年真题

一、填空题
(6)从数 1,2,3,4 中任取一个数,记为 X , 再从1,2,, X 中任取一个数,记为Y , 则 P{Y 2} =____________.
二、选择题
(13)设二维随机变量 (X ,Y ) 的概率分布为
X
Y
0
1
0
0.4
a
1
b
0.1
已知随机事件{X 0}与{X Y 1} 相互独立,则
EX
(A)0
(B)0.3
(C)0.7
(D)1
(8)设随机变量
X
与Y
相互独立,且
X
服从标准正态分布
N 0,1 ,Y
的概率分布为
PY
0
PY
1
1 2
,记
FZ
z
为随机变量 Z
XY
的分布函数,则函
数 FZ z 的间断点个数为
(A)0
(B)1
(C)2
(D)3
二、填空题
(14) 设 X1, X 2 , , X m 为来自二项分布总体 B n, p 的简单随机样本 , X 和 S 2 分别为样本均值和样本方差 . 若 X kS 2 为 np2 的无偏估计量 , 则
(1)求 P{X 2Y}.
(2)求 Z X Y 的概率密度.
(24)(本题满分 11 分)
设总体 X 的概率密度为
f
(x,
y)
2
x
y,
0 x 1,0 0, 其他
y
1
X1, X 2 , X n 是来自总体 x 的简单随机样本, X 是样本均值 (1)求参数的矩估计量ˆ . (2)判断 4X 2 是否为 2 的无偏估计量,并说明理由.

国防科技大学国防科技大 01 02年操作系统 01 02年离散数学考研真题及答案解析

国防科技大学研究生院2001年硕士生入学考试试题考试科目：操作系统考生注意：1．答案必须写在我校统一配发的专用答题纸上2．统考生做一、二、三、四、五；3．单独考生做一、二、三、六、七；一．（58分）回答如下问题1．（6分）假定有一个支持实时、分时和批处理的操作系统，对该系统应如何设计进程调度策略？2．（5分）什么叫线程？为什么要引进线程？3．（6分）某计算机系统设计成只有一级中断(该级中有多个中断)的中断系统，简述当中断发生时，是如何进入该中断处理程序的？4．（5分）在文件系统中为什么要引进“Open”系统调用？操作系统是如何处理的？5．(5分)假定存储器空闲块有如下结构：请你构造一串内存请求序列，对该请求序列首次满足分配算法能满足，而最佳满足分配法则不能。

6．(6分)为什么要在设备管理中引入缓冲技术？操作系统如何实现缓冲技术？7．(6分)用什么办法可以破坏死锁的循环等待条件？为什么？8．(6分)进程的状态主要有哪些？当发生状态转换时，操作系统完成哪些工作？9．(6分)在文件系统中，为什么要设立“当前目录”？操作系统如何实现改变“当前目录”？10．(7分)举例说明P、V操作为什么要用原语实现？操作系统如何实现这种原语操作？二．(12分)设有四个进程P1，P2，P3，P4，它们到达就绪队列的时刻，运行时间及优先级如下表所示：运行时间(基本时间单位)优先级进程到达就绪队列时间(基本时间单位)P1 0 9 1P2 1 4 2P3 2 8 3P4 3 10 4问：(1)若采用可剥夺的优先级调度算法，给出各进程的调度次序以及每个进程的等待时间。

(2)若采用时间片轮转调度算法，且时间片为2个基本时间单位，试给出各进程的调度次序及平均周围时间。

三．(8分)假设系统由相同类型的m个资源组成，有 n 个进程，每个进程至少请求一个资源。

证明：当n个进程最多需要的资源数之和小于m+n时，该系统无死锁。

四．(12分)在页式虚存系统中，一程序的页面走向(访问串)为 1，2，3，4，1，2，5，1，2，3，4，5 ，设分配给该程序的驻留集为m，试分别计算m=3和m=4时，FIFO和LRU两种算法的页故障次数。

2001数一数三考研数学真题及解析

2001年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设生产函数为Q AL K αβ=,其中Q 是产出量,L 是劳动投入量,K 是资本投入量,而,,A αβ均为大于零的参数,则当1Q=时K 关于L 的弹性为.(2)某公司每年的工资总额在比上一年增加20%的基础上再追加2百万元,若以i W 表示第i 年的工资总额(单位:百万元),则t W 满足的差分方程是.(3)设矩阵111111111111k k A k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,且秩()3r A =,则k = .(4)设随机变量和的数学期望分别为2-和2,方差分别为1和4,而相关系数为0.5-,则根据切比雪夫不等式{6}P XY +≥≤.(5)设总体X 服从正态分布2(0,2)N ,而1215,,,X X X L 是来自总体X 的简单随机样本,则随机变量221102211152()X X Y X X ++=++L L 服从分布,参数为.二、选择题(本题共5小题,每小题3分,满分15分.每题小给出的四个选项中,只有一个选项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设()f x 的导数在x a =处连续,又'()lim1x af x x a→=--,则 (A ) x a =是()f x 的极小值点. (B ) x a =是()f x 的极大值点. (C ) (,())a f a 是曲线()y f x =的拐点(D ) x a =不是()f x 的极值点, (,())a f a 也不是曲线()y f x =的拐点.(2)设0()()xg x f u du =⎰,其中21(1),01,2()1(1),12,3x x f x x x ⎧+≤<⎪⎪=⎨⎪-≤≤⎪⎩则()g x 在区间(0,2)内(A ) 无界(B ) 递减(C ) 不连续(D ) 连续(3)设1112131414131211212223242423222113132333434333231414243444443424100010100,,,00101000a a a a a a a a a a a a a a a a A B P a a a a a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 21000001001000001P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,其中A 可逆,则1B -等于 (A ) 112A P P -.(B ) 112P A P -.(C ) 112P P A -.(D ) 121P A P -.(4)设A 是n 阶矩阵,α是n 维列向量.若秩0TA αα⎛⎫⎪⎝⎭=秩()A ,则线性方程组(A ) AXα=必有无穷多解.(B ) AX α=必有唯一解.(C ) 00TA X y αα⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭仅有零解. (D ) 00TA X y αα⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭必有非零解.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于(A ) 1-.(B ) 0.(C )12.(D ) 1.三、(本题满分5分)设(,,)u f x y z =有连续的一阶偏导数,又函数()y y x =及()z z x =分别由下列两式确定:2xy e xy -=和0sin x txte dt t-=⎰, 求du dx.四、(本题满分6分)已知()f x 在(,)-∞+∞内可导,且lim '(),lim()lim[()(1)],xx x x x c f x e f x f x x c→∞→∞→∞+==---求c 的值.五、(本题满分6分) 求二重积分221()2[1]x y Dy xedxdy ++⎰⎰的值,其中D 是由直线,1y x y ==-及1x =围成的平面区域.六、(本题满分7分)已知抛物线2y px qx =+(其中0,0p q <>)在第一象限内与直线5x y +=相切,且此抛物线与x 轴围成的平面图形的面积为S .(1)问p 和q 为何值时,S 达到最大值?(2)求出此最大值.七、(本题满分6分)设()f x 在[0,1]上连续,在(0,1)内可导,且满足110(1)()(1),x k f k xe f x dx k -=>⎰证明至少存在一点(0,1)ξ∈,使得1'()(1)().f f ξξξ-=-八、(本题满分7分) 已知()n f x 满足'1()()n x n n f x f x x e -=+(n 为正整数),且(1)n ef n =,求函数项级数1()n n f x ∞=∑之和.九、(本题满分9分)设矩阵111111a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,112β⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.已知线性方程组Ax β=有解但不唯一,试求: (1)a 的值;(2)正交矩阵Q ,使TQ AQ 为对角矩阵.十、(本题满分8分)设A 为n 阶实对称矩阵,秩(),ij A n A =是()ij n n A a ⨯=中元素ij a 的代数余子式(,1,2,i j =,)n L ,二次型1211(,,,)n nij n i j i j A f x x x x x A===∑∑L .(1)记12(,,,)Tn X x x x =L ,把12(,,,)n f x x x L 写成矩阵形式,并证明二次型()f X 的矩阵为1A -;(2)二次型()Tg X X AX =与()f X 的规范型是否相同?说明理由.十一、(本题满分8分)一生产线生产的产品成箱包装,每箱的重量是随机的.假设每箱平均重50千克,标准差为5千克.若用最大载重量为5吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少箱,才能保障不超载的概率大于0,977.((2)0,977,φ=其中()x φ是标准正态分布函数.)十二、(本题满分8分)设随机变量X 和Y 的联合分布是正方形{(,)13,13}G x y x y ≤≤≤≤上的均匀分布,试求随机变量U X Y =-的概率密度()p u .2001年考研数学三试题答案与解析一、填空题(1)【分析】当1Q =时,1AL K αβ=,等式两边对L 求导得110.dK dK KAL K AL K dL dL Lαβαβααββ--=+⇒=- 由弹性计算公式知,当1Q =时K 关于L 的弹性为.dK L K L dL K L K ααββ⋅=-⋅=-(2)【分析】由题设知第t 年的工资总额t W (百万元)是两部分之和,其中一部分是固定追加额2(百万元),另一部分比前一年的工资总额1i W -多20%,即是1t W -的1.2倍.于是可得t W 满足的差分方程是11.2 2.t t W W -=+(3)【分析】由于11133331111111111111(3)111111111111111111k k k k k kk kA k kk kkkk++++===+311110100(3)(3)(1),00100001k k k k k k -=+=+--- 那么()30.r A A =⇒=而1k =时,显然()1r A =,故必有3k =-.(4)【分析】 ()0,E X Y EX EY +=+=()2cov()2D X Y DX X Y DY DX DY ρ+=+++=+143,=+=231{6}.612P X Y +≥≤=(5)【分析】根据简单随机样本的性质,1215,,,X X X L 相互独立同分布2(0,2)N ,易见11022X X ++L 与111522X X ++L 也相互独立.并且由于2~(0,2)i X N ,故 1101522222101222221511111~(0,1),()()()~(10),22241()()()~(5).224i X X X N X X X X X X χχ++=++++=++L L L L从而有11011011151115222222221()104~(10,5).12()()54X X X X F X X X X ++++=++++L L L L 即~(10,5)Y F .因此第1空应填:F ,第2空应填:(10,5).二、选择题(1)【分析】排除法.取21()()2f x x a =--,易验证()f x 满足题目条件,但x a =是()f x 的极大值点而不是极小值点,故(A )和(D )不正确,又(,())a f a 也不是曲线()y f x =的拐点,故(C )也不正确.所以应选(B ).(2)【分析】可直接用已有结论“若()f x 在[,]a b 上可积,于是0()()xg x f u du =⎰是[,]a b 上的连续函数”.本题中()f x 在[0,2]上分段连续,且有界,从而在[0,1]上可积,于是0()()xg x f u du =⎰在[0,2]上连续,故应选(D ).(3)【分析】把矩阵A 的14、两列对换,23、两列对换即得到矩阵B ,根据初等矩阵的性质,有 12B APP =或21.B AP P =那么1121()B AP P --==11111212P P A PP A ----=.所以应选(C ).(4)【分析】因为“0Ax =仅有零解”与“0Ax =必有非零解”这两个命题必然是一对一错,不可能两个命题同时正确,也不可能两个命题同时错误.所以本题应当从(C )或(D )入手.由于0TA αα⎡⎤⎢⎥⎣⎦是1n +阶矩阵,A 是n 阶矩阵,故必有 () 1.0T A r r A n n αα⎡⎤=≤<+⎢⎥⎣⎦因此(D )正确.(5)【分析】依题意Y n X =-,因此X 和Y 的相关系数等于1-,应选(A ).事实上,(,)(,),,Cov X Y Cov X n X DX DY DX =-=-=因此1.XY ρ===-三、【解】.du f f dy f dz dx x y dx z dx∂∂∂=++∂∂∂ (*)由2xyexy -=两边对x 求导,得()()0.xy dy dy dy y e y xy x dx dx dx x+-+=⇒=- ①又由0sin x txte dt t-=⎰两边对x 求导,得 sin()()(1)1.sin()x xx z dz dz e x z e x z dx dx x z --=⋅-⇒=---②将①、②两式代入(*)式,得()[1].sin()x du f y f e x z f dx x x y x z z∂∂-∂=-+-∂∂-∂四、【解】若0c =,则lim() 1.xx x c x c→∞+=-若0c ≠则 2222lim()lim[(1)].x c cxx c c xc x x x c c e x c x c--→∞→∞+=+=-- 由拉格朗日中值定理,有()(1)'()1f x f x f ξ--=⋅,其中ξ介于1x -与x 之间.那么当x →∞时也有ξ→∞,故lim[()(1)]lim '().x x f x f x f e ξ→∞→∞--==于是题设条件可改写为2ce e =,故1.2c =五、【解】积分区域D 如图所示.222211()()22[1]x y x y DDDy xedxdy ydxdy xyedxdy +++=+⎰⎰⎰⎰⎰⎰,其中111112(1),3y Dydxdy dy ydx y y dy --==-=-⎰⎰⎰⎰⎰ 22221111()()221x y x y yDxyedxdy ydy xedx ++-=⎰⎰⎰⎰2211(1)21[]0.y y y ee dy +-=-=⎰于是221()22[1].3x y Dy xedxdy ++=-⎰⎰六、【分析】先求出本题中的面积S .此时S 中有两个参数p 和q ,再根据抛物线2y px qx =+与5x y +=相切,求出p 和q 的关系,带入S 中只剩一个参数,最后求S 的最大值.【解】依题意,抛物线如图所示求.得它与x 轴交点的横坐标为10x =,2q x p=-. 面积323202()().326q qppp qq S px qx dx x x p --=+=+=⎰(*)因直线5x y +=与抛物线2y px qx =+相切,故他们有唯一公共点,由方程组25,x y y px qx+=⎧⎨=+⎩得2(1)50px q x ++-=.其判别式必等于零,即221(1)200,(1)20q p p q =++==-+V . 将上式代入(*)式得34200().3(1)q S q q =+ 因250,03,200(3)'()0,3,3(1)0,3,q q q S q q q q ><<⎧-⎪===⎨+⎪<>⎩于是当3q =时,()S q 取最大值,此时45p =-.从而得S 的最大值是22532.七、【证明】分析略令1()()xF x xef x -=,于是(1)(1)F f =,由积分中值定理得,存在满足101c k<<<的c ,使得 1110()()()x e k k xe f x dx ce f c F c --==⎰.由原式110(1)()x k f k xe f x dx -=⎰知,()(1)F c F =.从而()F x 在[,1]c 上满足罗尔定理条件,故存在(,1)(0,1)c ξ∈⊂,使'()0F ξ=,即11['()(1)()]0.e f f ξξξξξ----=而10e ξξ-≠,故1'()(1)()0f f ξξξ---=,即1'()(1)().f f ξξξ-=-八、【解】由已知条件可知()n f x 满足一阶线性微分方程'1()(),n xnn f x f x x e --=⇒其通解为()()nxn x f x e C n=+.由条件(1)n ef n=,得0C =,故()n x n x e f x n =.从而111().n x n xn n n n x e x f x e n n∞∞∞=====∑∑∑记1()nn x S x n ∞==∑,其收敛域为[1,1)-,且(0)0S =,当(1,1)x ∈-时,有111'()1n n s x x x∞-===-∑. 故01()(0)'()ln(1).1xxS x S S t dt dt x t=+==---⎰⎰由()S x 与ln(1)x --在1x =-的连续性知,上述和函数公式在1x =-处也成立.于是,当11x -≤<时,有1()()ln(1).x x n n f x e S x e x ∞===--∑九、【分析】方程组有解且不唯一,即方程组有无穷多解,故可由()()3r A r A =<来求a 的值.而T Q AQ Λ=即1Q AQ Λ-=,为此应当求出A 的特征值与特征向量再构造正交矩阵Q .【解】对方程组Ax β=的增广矩阵作初等行变换,有211111111111101100110112011200(1)(2)2a a a A a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=→--→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----++⎣⎦⎣⎦⎣⎦.因为方程组有无穷多解,所以()()3r A r A =<,故2a =-.112121121211211E A λλλλλλλλλ---=-+-=-+-----11110012113(3)(3)211233λλλλλλλλλ=-+-=-+=+-----,故矩阵A 的特征值为:13λ=,20λ=,33λ=-.当13λ=时,由212151(3)0,151090,212000E A x --⎡⎤⎡⎤⎢⎥⎢⎥-=--→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦得到属于特征值3λ=的特征向量1(1,0,1)T α=-.当20λ=时,由112112(0)0,121033,211000E A x ---⎡⎤⎡⎤⎢⎥⎢⎥-=--→-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦得到属于特征值0λ=的特征向量2(1,1,1)T α=.当33λ=-时,由412111(3)0,111012,214000E A x --⎡⎤⎡⎤⎢⎥⎢⎥--=---→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦得到属于特征值3λ=-的特征向量3(1,2,1)Tα=-.实对称矩阵的特征值不同时,其特征向量已经正交,故只需单位化.1231110,1,2.111βββ⎡⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥===-⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥-⎦⎣⎦⎣⎦那么令123(,,)0,Q βββ⎡⎤⎢⎥⎢⎥⎢==⎢⎢⎢⎥⎢⎥⎣⎦得1.T Q AQ Q AQ Λ=-3⎡⎤⎢⎥==0⎢⎥⎢⎥-3⎣⎦十、【分析】如果()T f X X AX =,其中A 是实对称矩阵,那么T X AX 就是二次型()f X 的矩阵表示,为此应读出双和号的含义.两个二次型如果其正负惯性指数相同,他们的规范形就一样,反之亦然.而根据惯性定理.经坐标变换二次型的正负惯性指数不变,因而规范形相同.【解】由于1211(,,,)n n ij n i j i j A f x x x x x A ===∑∑L11121121222212121(,,,),n n n n n nn n A A A x A A A x x x x A A A A x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦L L L M M M M L因为()r A n =,知A 可逆,又因A 是实对称的,有111()()T T A A A ---==. 得知1A A A*-=是实对称矩阵,于是A *是对称的,故二次型()f X 的矩阵是1A -. (2)经坐标变换1X A Y -=,有1111()()()()()T T T T T g X X AX A Y A A Y Y A Y Y Y A Y f Y ----=====,即()g X 与()f X 有相同的规范形.十一、【解】设(1,2,,)i X i n =L 是装运的第i 箱的重量(单位:千克),n 是所求箱数.由条件可以把12,,,n X X X L 视为独立同分布随机变量,而n 箱的总重量12n n T X X X =+++L 是独立同分布随机变量之和.由条件知5;i EX ==50i ET n ==单位:千克). 根据列维-林德伯格中心极限定理,n T 近似服从正态分布(50,25)N n n .箱数n 决定于条件{5000}0.977(2)n p T P φφ≤=≤≈>=.2>,从而98.0199n <,即最多可以装98箱.十二、【解】由条件知X 和Y 的联合密度为 1,13,13,(,)40,x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩若其他.以(){}()F u P U u u =≤-∞<<∞表示随机变量U 的分布函数.显然,当0u ≤时,()0F u =,当2u ≥时,()1F u =.当02u <<时,如图,则(,)1()(,)4x y u x y ux y G F u f x y dxdy dxdy -≤-≤∈==⎰⎰⎰⎰ 2211[4(2)]1(2)44u u =--=--. 于是,随机变量U 的概率密度为1(2),02,()20,.u u p u ⎧-<<⎪=⎨⎪⎩若其他。

考研数学一解答题专项强化真题试卷22(题后含答案及解析)

考研数学一解答题专项强化真题试卷22(题后含答案及解析)题型有：1.1．(1999年)为清除井底的污泥，用缆绳将抓斗放入井底．抓起污泥后提出井口，已知井深30m，抓斗自重400 N，缆绳每米重50 N，抓斗抓起的污泥重2000N．提升速度为3 m/s，在提升过程中，污泥以20N／s的速率从抓斗缝隙中漏掉．现将抓起污泥的抓斗提升到井口，问克服重力需作多少焦耳的功? (说明：①l N×1 m=1 J；m，N，s，J分别表示米、牛顿、秒、焦耳；②抓斗的高度及位于井口上方的缆绳长度忽略不计)正确答案：解1 作x轴如图2．6．将抓起污泥的抓斗提升到井口需作功ω=ω1+ω2+ω3 其中ω1是克服抓斗自重作的功，ω2是克服缆绳重量所作的功；ω3是提出污泥所作的功．由题设可知ω1=400×30=12 000 dω2=50(30—x)dx从而在时间间隔[t，t+dt]内提升污泥所作的功为dω3=3(2 000—20t)dt将污泥从井底提升到井口共需时间所以则共需作功ω=1 2 000+22 500+57 000=91 500 (J) △解2 以时间t为积分变量，在时间间隔[t，t+dt]内克服重力所作的功为dω=[400+(30—3t)50+(2 000—20t)=3dt 涉及知识点：一元函数积分学2．(2002年试题。

八)设有一小山，取它的底面所在的平面为xOy坐标面，其底部所占的区域为D={(x，y){x2+y2一xy≤75}，小山的高度函数为h(x，y)=75一x2一y2+xy．(1)设M(x0，y0)为区域D上一点，问h(x，y)在该点沿平面上什么方向的方向导数最大?若记此方向导数的最大值为g(x0，y0)，试写出g(x0，y0)的表达式；(2)现欲利用此小山开展攀岩活动，为此需要在山脚寻找一上山坡度最大的点作为攀登的起点．也就是说，要在D的边界线x2+y2一xy=75上找出使(1)中的g(x，y)达到最大值的点．试确定攀登起点的位置．正确答案：(1)由题设，结合方向导数取最大值的方向是梯度方向这一性质，则因此h(x，y)沿方向(y0—2x0)i+(x0一2y0)j方向导数为最大值，且此最大值为(2)令f(x，y)=g2(x，y)=(y一2x)2+(x一2y)2，由题意只需求f(x，y)在约束条件φ(x，y)=75一x2一y2+xy=0下的条件最大值点，由拉格朗日乘数法，记F(x，y，λ)=f(x，y)+Aλφ(x，y)=(y一2x)2+(x一2y)2+λ(75一x2一y2+xy)则由可解得λ=2或x+y=0．当λ=2时，可解出可能条件极值点为当x+y=0时，可解出可能条件极值点为(5，一5)，(一5，5)．由于，而f(x，y)｜(5,-5)=f(x，y)｜(-5,5)=450所以点(5，一5)和点(一5，5)可作为攀登的起点．解析：许多求极值和最值的问题中，需根据实际问题首先建立目标函数或约束条件，然后再求极，最值．本题中因｜gradh｜为方向导数的最大值，故而将代为求｜gradh｜在条件x2+y2一xy=75F的条件极值，用拉格朗日乘数法求该条件极值．知识模块：多元函数微分学3．(07年)求函数f(x，y)=x2+2y2一x2y2在区域D={(x，y)|x2+y2≤4，y≥0}上的最大值和最小值．正确答案：(1)求f(x，y)在D内的驻点，由得f(x，y)在D内的驻点为(2)考察边界y=0(一2≤x≤2)f(x，0)=x2 一2≤x≤2最大值f(±2，0)=4，最小值f(0，0)=0(3)考察边界x2+y2=4，y＞0由x2+y2=4知，y2=4一x2f(x，y)=x2+2y2一x 涉及知识点：高等数学4．(2001年试题，十二)设总体X服从正态分布N(μ，σ2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，X2n(n≥2)，其样本均值为求统计量的数学期望E(Y)．正确答案：由题设所给统计量的结构特点，可视(X1+Xn+1)，(X2+Xn+2)，…，(Xn+X2n)为取自总体N(2μ，2σ2)的简单随机样本，则该样本均值为且有样本方差为由于已知，因此E(Y)=(n—1)(2σ2)=2(n一1)σ2解析二设则，因此解析三设Z=Xi+Xn+i，i=1，2，…，n．因为X1，X2，…，Xn(n≥2)相互独立且同服从正态分布N(μ，σ2)(σ>0)，所以Z1，Z2，…，Zn也相互独立且服从正态分布．E(Zi)=E(Xi+Xn+i)=E(Xi)+E(Xn+i)=2μ，D(Zi)=D(Xi+Xn+i)=D(Xi)+D(Xn+i)=2σ2，即有Zi一N(2μ，2σ2)，i=1，2，…，n．从而Zn，Z2，…，Zn可视为取从总体N(2μ，2σ2)的简单随机样本，进而有：故又则即有E(Y)=2(n一1)σ2[解析四]因为X1，X2，…，Xn(n≥2)相互立且同服从正态分布N(μ，σ2)(σ>0)，所以有：g(Xi)=μ，D(Xi)=σ2，E(Xi2)=D(Xi)+E2(Xi)=σ2+μ2，i=1，2，…，2n；又故而解析：解析中的几种解法包括直接计算的(解析四)、利用样本方差性质的(解析一)、利用随机变量的独立性的(解析二)和利用x2分布的构成与性质的(解析三)．总体来讲，直接计算的计算量最大，也最容易出错，也是最容易想到的而其他几种解法则要求考生熟练掌握相关的知识点，会灵活运用．知识模块：数理统计的基本概念5．求幂级数的收敛域及和函数．正确答案：涉及知识点：高等数学6．(89年)假设λ为n阶可逆矩阵A的一个特征值，证明：(1)为A-1的特征值；(2)为A的伴随矩阵A*的特征值．正确答案：(1)由已知，有非零向量ξ满足Aξ=λξ，两端左乘A-1，得ξ=λA-1ξ．因ξ≠0，故λ≠0，于是有A-1ξ=为A-1的一个特征值(ξ为对应的一个特征向量)．(2)由于为A*的特征值．涉及知识点：线性代数7．设，E为3阶单位矩阵．(Ⅰ)求方程组Ax=0的一个基础解系；(Ⅱ)求满足AB=E的所有矩阵B．正确答案：(Ⅰ)用初等行变换化A为简单阶梯形矩阵：得Ax=0的同解方程组：求得一个非零解a=(-1，2，3，1)T，它构成Ax=0的基础解系．(Ⅱ)所求矩阵B应该是4×3矩阵．一种做法是把B的3个列向量分别作为3个线性方程组AX=(1，0，0)T，AX=(0，1，0)T和AX=(0，0，1)T的解来计算．下面的方法比较简单．思路：满足AB=E的任何两个解的差都是AB=0的解．先求出AB=0的所有解，再求AB=E的一个特解，就可以得到满足AB=E的所有矩阵．①AB=0的解是一个4×3矩阵，他的每一列都是Ax=0的解，因此是a 的倍数，通解为(c1a，c2a，c3a)，c1，c2，c3为任意常数．②求AB=E 的一个特解．用初等行变换化(A｜E)为简单阶梯形矩阵：③AB=E的通解为B0+(c1a，c2a，c3a)，c1，c2，c3为任意常数．8．从学校乘汽车到火车站的途中有3个交通岗，假设在各个交通岗遇到红灯的事件是相互独立的，并且概率都是2／5．设X为途中遇到红灯的次数，求随机变量X的分布函数、数学期望．正确答案：当x＜0时，F(x)==0；当0≤x＜1时，F(x)=P(X=0)=27／125；当1≤x＜2时，F(x)=P(X=0)+P(X=1)=27／125+54／125=81／125；当2≤x＜3时，F(x)=P(X=0)+P(X=1)+P(X=2)=117／125；当X≥3时，F(x)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=1．综上所述，因此，X的数学期望为E(X)=np=3×(2／5)=6／5，或E(X)=0×(2／125)+1×(54／125)+2×(36／125)+3×(8／125)=6／5．涉及知识点：一维随机变量及其分布[2017年] 设随机变量X，Y相互独立，，Y的概率密度为fY(y)=9．求P{Y≤E(Y)}；正确答案：因E(Y)=∫-∞+∞yfY(y)dy=∫01 y·2ydy=，故涉及知识点：二维随机变量及其分布10．求Z=X+Y的概率密度．正确答案：Z的分布函数FZ(Z)=P{X+Y≤z，X=0}+P{X+Y≤z，X=2}=P{X=0，Y≤z}+P{X=2，Y+2≤z}=，故Z的概率密度函数为涉及知识点：二维随机变量及其分布。

2001年考研数学一真题

f ( x, y ) 在(0,0)存在偏导数
f (0,0) f (0,0) ,不保证曲面 z f ( x, y ) 在 , x y
f (0,0) f (0,0) (0, 0, f (0, 0)) 存在切平面.若存在时,法向量 n= ，， 1 {3,1,-1}与{3,1,1}不 y x
f ( x) 单调增 f ' ( x) 0 ,(A),(C)不对;
f ( x) :增——减——增 f ' ( x) :正——负——正,(B)不对,(D)对.
关于(A),涉及可微与可偏导的关系 .由微.因此(A)不一定成立. 关于(B)只能假设
f ( x, y ) 在(0,0)存在两个偏导数 f ( x, y ) 在(0,0)处可
=(
于是
divgradr| (1, 2,2) =
2 2 |(1,2,2) . r 3
y 0时
(3)【分析】这个二次积分不是二重积分的累次积分,因为 1
1 y 2 .由此看出二次积分 dy
1
0
2
1 y
f ( x, y)dx 是二重积分的一个累次
积分,它与原式只差一个符号.先把此累次积分表为
y'' 2 y' 2 y 0 .
(2)【分析】先求 gradr. gradr=
r r r x y z , , , , . x y z r r r
再求
divgradr=
x y z ( ) ( ) ( ) x r y r z r 1 x2 1 y2 1 z2 3 x2 y 2 z 2 2 3 )( 3 )( 3 ) . r r r r r r r r3 r

历年考研数一真题及答案

历年考研数一真题及答案【篇一：历年考研数学一真题及答案(1987-2013)】ss=txt>数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)?=_____________.(2)曲面x2?2y2?3z2?21在点(1,?2,?2)的法线方程为_____________.(3)微分方程xy???3y??0的通解为_____________.?121?(4)已知方程组??23a?2???x1??1?x???3??1a?2???2无解,则a= ???????x3????0??_____________.(5)设两个相互独立的事件a和b都不发生的概率为19,a发生b不发生的概率与b发生a不发生的概率相等,则p(a)=_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设f(x)、g(x)是恒大于零的可导函数,且f?(x)g(x)?f(x)g?(x)?0,则当a?x?b时,有(a)f(x)g(b)?f(b)g(x)(b)f(x)g(a)?f(a)g(x)(c)f(x)g(x)?f(b)g(b)(d)f(x)g(x)?f(a)g(a)(2)设s:x2?y2?z2?a2(z?0),s1为s在第一卦限中的部分,则有(a)??xds?4s??xdss1(b)??yds?4??xdsss1(c)??zds?4??xdsss1(d)??xyzds?4??xyzdsss1(3)设级数??un收敛,则必收敛的级数为n?1(a)??(?1)nun (b)??u2nn?1nn?1(c)??(u2n?1?u2n)n?1(d)??(un?un?1)n?1(a)e(x)?e(y)(b)e(x2)?[e(x)]2?e(y2)?[e(y)]2(c)e(x2)?e(y2) (d)e(x2)?[e(x)]2?e(y2)?[e(y)]2三、(本题满分6分) 1求lim(2?exx??4?sinx).1?exx四、(本题满分5分) 设z?f(xy,xy)?g(xy),其中f具有二阶连续偏导数,g具有二阶连续导数,求?2z?x?y.五、(本题满分6分) 计算曲线积分i??xdy?ydxl4x2?y2,其中l是以点(1,0)为中心,r为半径的圆周(r?1),取逆时针方向.六、(本题满分7分)设对于半空间x?0内任意的光滑有向封闭曲面s,都有??xf(x)dydz?xyf(x)dzdx?e2xzdxdy?0,其中函数f(x)在s(0,??)内具有连续的一阶导数,且xlim?0?f(x)?1,求f(x).七、(本题满分6分)求幂级数??1xnn?13n?(?2)nn的收敛区间,并讨论该区间端点处的收敛性.八、(本题满分7分)设有一半径为r的球体,p0是此球的表面上的一个定点,球体上任一点的密度与该点到p0距离的平方成正比(比例常数k?0),求球体的重心位置.九、(本题满分6分) 设函数f(x)在[0,?]上连续,且???f(x)dx?0,?0f(x)cosxdx?0.试证:在(0,?)内至少存在两个不同的点?1,?2,使f(?1)?f(?2)?0.十、(本题满分6分)??1000?000? 设矩阵a的伴随矩阵a*??1??1010??,且?0?308??aba?1?ba?1?3e,其中e为4阶单位矩阵,求矩阵b.十一、(本题满分8分)某适应性生产线每年1月份进行熟练工与非熟练工的人数统计,然后将16熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有25成为熟练工.设第n年1月份统计的熟练工与非熟练工所占百分比分别为xn和yn,记成向量??xn?y??. ?n(1)求??xn?1?与??xn?的关系式并写成矩阵形?y?n?1??y?n?式:??xn?1??xn?y??a???. n?1??yn??1??是a的两个线性无关的特征向量,并求出相应的特征值.?1?(3)当??x1??2?时,求??y?????xn?1??. 1???1??yn?1??2??十二、(本题满分8分)某流水线上每个产品不合格的概率为p(0?p?1),各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为x,求x的数学期望e(x)和方差d(x).十三、(本题满分6分) 设某种元件的使用寿命x的概率密度为?2e?2(x??)x??f(x;?)??x???0x1,x2,,其中??0为未知参数.又设,xn是x的一组样本观测值,求参数?的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设y?ex(asinx?bcosx)(a,b为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________. (2)r?x2?y2?z2,则div(gradr)(1,?2,2)=_____________.(3)交换二次积分的积分次序:?01?y?1dy?2f(x,y)dx＝_____________. (4)设a2?a?4e?o,则(a?2e)?1= _____________.(5)d(x)?2,则根据车贝晓夫不等式有估计p{x?e(x)?2}? _____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设函数f(x)在定义域内可导,y?f(x)的图形如右图所示,则y?f?(x)的图形为(a)(b)(c)【篇二：2000年-2016年考研数学一历年真题完整版(word版)】ss=txt>数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)?=_____________.(2)曲面x2?2y2?3z2?21在点(1,?2,?2)的法线方程为_____________. (3)微分方程xy???3y??0的通解为_____________.1??x1??1??12??????(4)已知方程组23a?2x2?3无解,则a=_____________. ????????1a?2????x3????0??(5)设两个相互独立的事件a和b都不发生的概率为生的概率相等,则p(a)=_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设f(x)、g(x)是恒大于零的可导函数,且f?(x)g(x)?f(x)g?(x)?0,则当a?x?b时,有 (a)f(x)g(b)?f(b)g(x) (c)f(x)g(x)?f(b)g(b)(b)f(x)g(a)?f(a)g(x) (d)f(x)g(x)?f(a)g(a)1,a发生b不发生的概率与b发生a不发9(2)设s:x2?y2?z2?a2(z?0),s1为s在第一卦限中的部分,则有 (a)(c) ??xds?4??xdsss1(b)(d)??yds?4??xdsss1ss1??zds?4??xdsss1??xyzds?4??xyzds(3)设级数?un?1?n收敛,则必收敛的级数为u(a)?(?1)nnn?1n?(b)?un?1?2n(c)?(un?1?2n?1?u2n)(d)?(un?1?n?un?1)(5)设二维随机变量(x,y)服从二维正态分布,则随机变量??x?y 与 ??x?y不相关的充分必要条件为(a)e(x)?e(y)(c)e(x2)?e(y2)三、(本题满分6分)(d)e(x2)?[e(x)]2?e(y2)?[e(y)]2(b)e(x2)?[e(x)]2?e(y2)?[e(y)]2求lim(x??2?e1?e1x4x?sinx). x四、(本题满分5分)xx?2z设z?f(xy,)?g(),其中f具有二阶连续偏导数,g具有二阶连续导数,求. yy?x?y五、(本题满分6分)计算曲线积分i?xdy?ydx??l4x2?y2,其中l是以点(1,0)为中心,r为半径的圆周(r?1),取逆时针方向.六、(本题满分7分)设对于半空间x?0内任意的光滑有向封闭曲面s,都有???xsx?0?(f)x?dyd(z)x?2xyfex?dzd0x,f(x)在z(0,d??x)内具有连续的一阶导数dy其中函数,且limf(x)?1,求f(x).七、(本题满分6分)八、(本题满分7分)1xn求幂级数?n的收敛区间,并讨论该区间端点处的收敛性. n3?(?2)nn?1?设有一半径为r的球体,p0是此球的表面上的一个定点,球体上任一点的密度与该点到p0距离的平方成正比(比例常数k?0),求球体的重心位置.九、(本题满分6分)设函数f(x)在[0,?]上连续,且??f(x)dx?0,?f(x)cosxdx?0.试证:在(0,?)内至少存在两?个不同的点?1,?2,使f(?1)?f(?2)?0.十、(本题满分6分)?10?01*?设矩阵a的伴随矩阵a??10??0?300100?0??,?1?1且aba?ba?3e,其中e为4阶单位矩阵,求0??8?矩阵b.十一、(本题满分8分)1熟练工支援其他生产部62门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有成为熟练工.设第5某适应性生产线每年1月份进行熟练工与非熟练工的人数统计,然后将n年1月份统计的熟练工与非熟练工所占百分比分别为xn和yn,记成向量??xn?1??xn??xn?1??xn?与的关系式并写成矩阵形式:?a???????.?yn?1??yn??yn?1??yn??xn??. ?yn?(1)求??4???1??1??1??1??x1??2??xn?1?(3)当?????时,求??.y1y?1????n?1????2?十二、(本题满分8分)某流水线上每个产品不合格的概率为p(0?p?1),各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为x,求x的数学期望e(x)和方差d(x).十三、(本题满分6分)?2e?2(x??)x??设某种元件的使用寿命x的概率密度为f(x;?)??,其中??0为未知参数.又设x???0x1,x2,?,xn是x的一组样本观测值,求参数?的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设y?ex(asinx?bcosx)(a,b为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)r?x2?y2?z2,则div(gradr)(1,?2,2)= _____________.(3)交换二次积分的积分次序:?0?1dy?1?y2f(x,y)dx＝_____________.2(4)设a?a?4e?o,则(a?2e)?1= _____________.(5)d(x)?2,则根据车贝晓夫不等式有估计p{x?e(x)?2}?_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设函数f(x)在定义域内可导,y?f(x)的图形如右图所示,则y?f?(x)的图形为(a) (b)(c) (d)(2)设f(x,y)在点(0,0)的附近有定义,且fx?(0,0)?3,fy?(0,0)?1则(a)dz|(0,0)?3dx?dy(b)曲面z?f(x,y)在(0,0,f(0,0))处的法向量为{3,1,1}(c)曲线z?f(x,y)在(0,0,f(0,0))处的切向量为{1,0,3}y?0z?f(x,y)(d)曲线在(0,0,f(0,0))处的切向量为{3,0,1}y?0(3)设f(0)?0则f(x)在x=0处可导?f(1?cosh)(a)lim存在2h?0h(c)limh?0f(1?eh)(b) lim存在h?0h(d)limh?0f(h?sinh)存在h2111111111??4??1?0,b???01???1??00000000f(2h)?f(h)存在h?1?(4)设a??1?1??10??0?,则a与b 0??0?(a)合同且相似 (c)不合同但相似(b)合同但不相似 (d)不合同且不相似(5)将一枚硬币重复掷n次,以x和y分别表示正面向上和反面向上的次数, 则x和y相关系数为(a) -1 (c)(b)0 (d)11 2三、(本题满分6分)arctanex. 求?e2x四、(本题满分6分)【篇三：历年考研数学一真题及答案(1987-2015)】1987-2014 （经典珍藏版）1987年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)当x=_____________时,函数y?x?2x取得极小值.(2)由曲线y?lnx与两直线y?e?1?x及y?0所围成的平面图形的面积是_____________.1?x(3)与两直线y??1?tz?2?t及x?1y?2z?11?1?1都平行且过原点的平面方程为_____________.(4)设l为取正向的圆周x2?y2?9,则曲线积分??l(2xy?2y)dx?(x2?4x)dy= _____________.(5)已知三维向量空间的基底为此基底下的坐标是_____________.二、(本题满分8分) 求正的常数a与b,使等式lim1x2x?0bx?sinx?0?1成立.三、(本题满分7分)1(1)设f、g为连续可微函数,u?f(x,xy),v?g(x?xy),求?u?x,?v?x. (2)设矩阵a和b满足关系式ab=a?2b,其中?301?a???110?,求矩阵 ?4?b.?01??四、(本题满分8分)求微分方程y????6y???(9?a2)y??1的通解,其中常数a?0.五、选择题(本题共4小题,每小题3分,满分12分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设limf(x)?f(a)x?a(x?a)2??1,则在x?a处(a)f(x)的导数存在,且f?(a)?0 (b)f(x)取得极大值(c)f(x)取得极小值 (d)f(x)的导数不存在 (2)设f(x)为已知连续函数s,i?t?t0f(tx)dx,其中t?0,s?0,则i的值(a)依赖于s和t (b)依赖于s、t和x(c)依赖于t、x,不依赖于s (d)依赖于s,不依赖于t (3)设常数?k?0,则级数?(?1)nk?nn2n?1(a)发散(b)绝对收敛2(c)条件收敛(d)散敛性与k的取值有关(4)设a为n阶方阵，且a的行列式|a|?a?0,而a*六、（本题满分10分）求幂级数?a1n?1的收敛域，并求其和函数. xnn?2n?1?是a的伴随矩阵，则|a*|等于(a)a (b)1 (c)an?1七、（本题满分10分）求曲面积分i???x(8y?1)dydz?2(1?y2)dzdx?4yzdxdy,?(d)an??z?1?y?3f(x)?其中?是由曲线绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于?. ?2x?0??八、（本题满分10分）设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f?(x)?1,证明在(0,1)内有且仅有一个x,使得f(x)?x.九、（本题满分8分）3问a,b为何值时,现线性方程组?x2?x3?x4?02?2x3?2x4?1x2?(a?3)x3?2x4?bx1?2x2?x3?ax4?? 1有唯一解,无解,有无穷多解?并求出有无穷多解时的通解.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件a发生的概率为p,现进行n次独立试验,则a至少发生一次的概率为____________;而事件a至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________. (3)已知连续随机变量____________.4x的概率密度函数为f(x)??x2?2x?1,则x的数学期望为____________,x的方差为十一、（本题满分6分）设随机变量x,y相互独立,其概率密度函数分别为fx(x)?10?x?1,fy(y)? y?0,求z?2x?y的概率密度函数.?y其它y?05。

育明考研：2001-2013年北京大学行政管理考研真题及答案解析

2004 年北京大学政府管理学院行政管理专业课真题简答： 1 评述深圳特区“行政三分制”。 2 评述亚当斯”公平理论”。 3 考任、选任、委任的适用条件和局限。 4 全球化和信息化对我国政府管理的影响。论述： 1 评述新公共管理。 2 人力资源开发对我国经济发展的意义和作用。
2 精英决策模型的主要内容
3 风险型决策的主要内容
三论述
1 试析公共政策分析中所涉及到的哲学问题 2 试评析我国当前的财政政策
专业课三：组织管理
一、名词
T 式训练组二、简答
知识经理
工作生活质量
J·马奇
1 榜样的力量是无穷的？为什么？ 2 按照获取服从的手段，可将组织分为几种类型？
3 行为科学时期组织设计的特点？三、论述
2002 年北京大学行政管理专业课真题专业课一：行政管理学一名词解释： 1 绩效评估 2 指数工职制 3 网络结构组织 4 PPBS
育明教育官网
北大、人大、中财、北外、中传教授创办
集训营、一对一保分、视频、小班
二简答题： 1 简述政府失灵论与市场失灵论的主要理论观点。 2 依法行政与行政道德建设的关系。 3 行政发展与发展行政的区别与联系。三论述题： 1 试论西方国家文官制度在实践中的弊端，并说明英美国家文官制度的最新发展趋势。 2 辨析“政府能力的重要性是显而易见的”。专业课二：公共政策分析一名词解释： 1 政策监控 2 系统决策模型 3 成本效益分析 4 政策评价二简答题： 1 简述浴盆模型的基本内容及其研究意义 2 简述公共政策分析的基本要素。 3 简述拟订备选方案中应注意的基本问题。三论述题： 1 试论利益集团对政府决策的影响。 2 试论不确定性决策所具备的基本条件并从公共政策实践中举例说明。专业课三：组织与管理一名词解释： 1 组织政治 2 威廉姆森 3 目标置换 4 组织亚文化二简答题： 1 工作设计的主要方法有哪些。 2 计算机与信息技术的应用对组织结构设计的影响表现在哪些方面。 3 简述成就需要论的主要内容。三论述题： 1 试论政府组织有效性的衡量。 2 结合实际，试述组织变革是不同力量作用的结果，是一种动态平衡。

历年考研数学真题及答案

历年考研数学真题及答案【篇一：历年考研数学一真题及答案(1987-2014)】ss=txt>（经典珍藏版）1987年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)当x=_____________时,函数y?x?2x取得极小值.(2)由曲线y?lnx与两直线y?e?1?x及y?0所围成的平面图形的面积是_____________.1?x(3)与两直线y??1?tz?2?t及x?1y?1?2z?11?1都平行且过原点的平面方程为_____________.(4)设l为取正向的圆周x2?y2?9,则曲线积分??l(2xy?2y)dx?(x2?4x)dy= _____________.(5)已知三维向量空间的基底为坐标是_____________.二、(本题满分8分)求正的常数a与b,使等式lim1x2x?0bx?sinx?0?1成立.三、(本题满分7分)(1)设f、g为连续可微函数,u?f(x,xy),v?g(x?xy),求?u?x,?v?x. (2)设矩阵a和b满足关系式ab=a?2b,其中??301?a??110?,求矩阵b.?4??01??四、(本题满分8分)求微分方程y????6y???(9?a2)y??1的通解,其中常数a?0.五、选择题(本题共4小题,每小题3分,满分12分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设limf(x)?f(a)x?a(x?a)2??1,则在x?a处 (a)f(x)的导数存在,且f?(a)?0 (b)f(x)取得极大值(c)f(x)取得极小值 (d)f(x)的导数不存在 (2)设f(x)为已知连续函数s,i?t?t0f(tx)dx,其中t?0,s?0,则i的值(a)依赖于s和t (b)依赖于s、t和x(c)依赖于t、x,不依赖于s (d)依赖于s,不依赖于t(3)设常数?k?0,则级数?(?1)nk?nn2n?1(a)发散(b)绝对收敛(c)条件收敛(d)散敛性与k的取值有关(4)设a为n阶方阵，且a的行列式|a|?a?0,而a*是a的伴随矩阵，则|a*|等于(a)a (b)1a(c)an?1(d)an六、（本题满分10分）求幂级数??1n?1n?1n?2nx的收敛域，并求其和函数.七、（本题满分10分）求曲面积分i???x(8y?1)dydz?2(1?y2)dzdx?4yzdxdy,?其中?是由曲线f(x)???z?1?y?3?绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于?.2x?0??八、（本题满分10分）设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f?(x)?1,证明在(0,1)内有且仅有一个x,使得f(x)?x.九、（本题满分8分）问a,b为何值时,现线性方程组x1?x2?x3?x4?0x2?2x3?2x4?1?x2?(a?3)x3?2x4?b3x1?2x2?x3? ax4??1有唯一解,无解,有无穷多解?并求出有无穷多解时的通解.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件a发生的概率为p,现进行n次独立试验,则a至少发生一次的概率为____________;而事件a至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________. (3)已知连续随机变量x的概率密度函数为f(x)?十一、（本题满分6分）设随机变量x,y相互独立,其概率密度函数分别为fx(x)??x2?2x?1,则x的数学期望为____________,x的方差为____________.10?x?1其它,?yy?0,求zfy(y)?y?00?2x?y的概率密度函数.【篇二：历年考研数学一真题及答案(1987-2014)】ass=txt>数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)二、(本题满分8分)(1)当x=_____________时,函数y?x?2x取得极小值. (2)由曲线y?lnx与两直线y?e?1?x及y?0所围成的平面图形的面积是_____________.1?xx12求正的常数a与b,使等式lim?1成立. x?0bx?sinx?0(5)已知三维向量空间的基底为坐标是_____________.三、(本题满分7分)(1)设f、g为连续可微函数,u??u?v,. ?x?xf(x,xy),v?g(x?xy),(3)与两直线y??1?tz?2?t及x?1y?2z?1??111都平行且过原点的平面方程为_____________.(4)设l(2)设矩阵?3a???1??011a和b满足关系式ab=a?2b,其中l为取正向的圆周x2?y2?9,则曲线积分21??求矩阵0b. ?,?4???(2xy?2y)dx?(x?4x)dy= _____________.第 1 页共 1 页四、(本题满分8分)求微分方程y????6y???(9?a2)y??1的通解,其中常数a?0.五、选择题(本题共4小题,每小题3分,满分12分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设limx?at和x(c)依赖于t、x,不依赖于s (d)依赖于s,不依赖于t(3)设常数k?0,则级数?(?1)nk?2nn?1n(a)发散(b)绝对收敛(c)条件收敛(d)散敛性f(x)?f(a)??1,则在x?a处 2(x?a)f(x)(a)f(x)的导数存在,且f?(a)?0 (b)得极大值(c)f(x)取得极小值 (d)导数不存在(2)设f(x)为已知连续函数,i?t?ist0取与k的取值有关(4)设a为n阶方阵，且a的行列式|a|?a?0,而a是a的伴*f(x)(a)a (b)1af(tx)dx,其中t?0,s?0,则(c)a (d)an?1n的值(a)依赖于s和t (b)依赖于s、六、（本题满分10分）第 2 页共 2 页求幂级数?七、（本题满分10分）??z?1?y?3其中?是由曲线f(x)??绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于?.2x?0??1n?1的收敛域，并求其和函数. xn2n?1n??求曲面积分i???x(8y?1)dydz?2(1?y2)dzdx?4yzdxdy,八、（本题满分10分）设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f?(x)?1,证明在(0,1)内有且仅有一个x,使得f(x)?x.九、（本题满分8分）问a,b为何值时,现线性方程组x1?x2?x3?x4?0x2?2x3?2x4?1?x2?(a?3)x3?2x4?b3x1?2x2?x3? ax4??1第 3 页共 3 页有唯一解,无解,有无穷多解?并求出有无穷多解时的通解.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件a发生的概率为p,现进行n次独立试验,则a至少发生一次的概率为____________;而事件a至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________. (3)已知连续随机变量x的概率密度函数为f(x)?十一、（本题满分6分）设随机变量x,y相互独立,其概率密度函数分别为fx(x)?1?x2?2x?1,则x的数学期望为____________,x的方差为____________.0?x?1其它,fy(y)? y?0,求z?2x?y的概率密度函数.?yy?0第 4 页共 4 页第 5 页共 5 页【篇三：历年考研数学一真题及答案(1987-2013)】ss=txt>数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)?=_____________.(2)曲面x2?2y2?3z2?21在点(1,?2,?2)的法线方程为_____________.(3)微分方程xy???3y??0的通解为_____________.?121?(4)已知方程组??23a?2???x1??1?x???3??1a?2???2无解,则a= ???????x3????0??_____________.(5)设两个相互独立的事件a和b都不发生的概率为19,a发生b不发生的概率与b发生a不发生的概率相等,则p(a)=_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设f(x)、g(x)是恒大于零的可导函数,且f?(x)g(x)?f(x)g?(x)?0,则当a?x?b时,有(a)f(x)g(b)?f(b)g(x)(b)f(x)g(a)?f(a)g(x)(c)f(x)g(x)?f(b)g(b)(d)f(x)g(x)?f(a)g(a)(2)设s:x2?y2?z2?a2(z?0),s1为s在第一卦限中的部分,则有(a)??xds?4s??xdss1(b)??yds?4??xdsss1(c)??zds?4??xdsss1(d)??xyzds?4??xyzdsss1(3)设级数??un收敛,则必收敛的级数为n?1(a)??(?1)nun (b)??u2nn?1nn?1(c)??(u2n?1?u2n)n?1(d)??(un?un?1)n?1(a)e(x)?e(y)(b)e(x2)?[e(x)]2?e(y2)?[e(y)]2(c)e(x2)?e(y2) (d)e(x2)?[e(x)]2?e(y2)?[e(y)]2三、(本题满分6分) 1求lim(2?exx??4?sinx).1?exx四、(本题满分5分) 设z?f(xy,xy)?g(xy),其中f具有二阶连续偏导数,g具有二阶连续导数,求?2z?x?y.五、(本题满分6分) 计算曲线积分i??xdy?ydxl4x2?y2,其中l是以点(1,0)为中心,r为半径的圆周(r?1),取逆时针方向.六、(本题满分7分)设对于半空间x?0内任意的光滑有向封闭曲面s,都有??xf(x)dydz?xyf(x)dzdx?e2xzdxdy?0,其中函数f(x)在s(0,??)内具有连续的一阶导数,且xlim?0?f(x)?1,求f(x).七、(本题满分6分)求幂级数??1xnn?13n?(?2)nn的收敛区间,并讨论该区间端点处的收敛性.八、(本题满分7分)设有一半径为r的球体,p0是此球的表面上的一个定点,球体上任一点的密度与该点到p0距离的平方成正比(比例常数k?0),求球体的重心位置.九、(本题满分6分) 设函数f(x)在[0,?]上连续,且???f(x)dx?0,?0f(x)cosxdx?0.试证:在(0,?)内至少存在两个不同的点?1,?2,使f(?1)?f(?2)?0.十、(本题满分6分)??1000?000? 设矩阵a的伴随矩阵a*??1??1010??,且?0?308??aba?1?ba?1?3e,其中e为4阶单位矩阵,求矩阵b.十一、(本题满分8分)某适应性生产线每年1月份进行熟练工与非熟练工的人数统计,然后将16熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有25成为熟练工.设第n年1月份统计的熟练工与非熟练工所占百分比分别为xn和yn,记成向量??xn?y??. ?n(1)求??xn?1?与??xn?的关系式并写成矩阵形?y?n?1??y?n?式:??xn?1??xn?y??a???. n?1??yn??1??是a的两个线性无关的特征向量,并求出相应的特征值.?1?(3)当??x1??2?时,求??y?????xn?1??. 1???1??yn?1??2??十二、(本题满分8分)某流水线上每个产品不合格的概率为p(0?p?1),各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为x,求x的数学期望e(x)和方差d(x).十三、(本题满分6分) 设某种元件的使用寿命x的概率密度为?2e?2(x??)x??f(x;?)??x???0x1,x2,,其中??0为未知参数.又设,xn是x的一组样本观测值,求参数?的最大似然估计值.2001年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设y?ex(asinx?bcosx)(a,b为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________. (2)r?x2?y2?z2,则div(gradr)(1,?2,2)=_____________.(3)交换二次积分的积分次序:?01?y?1dy?2f(x,y)dx＝_____________. (4)设a2?a?4e?o,则(a?2e)?1= _____________.(5)d(x)?2,则根据车贝晓夫不等式有估计p{x?e(x)?2}? _____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设函数f(x)在定义域内可导,y?f(x)的图形如右图所示,则y?f?(x)的图形为(a)(b)(c)。

2001考研数一真题答案及详细解析

一、填空题(1)【答案】220y y y '''-+=.【详解】因为二阶常系数线性齐次微分方程0y py qy '''++=的通解为12(sin cos )x y e c x c x αββ=+时，则特征方程20r pr q ++=对应的两个根为一对共轭复根：1,2i λαβ=±，所以根据题设12(sin cos )xy e c x c x =+(12,c c 为任意常数)为某二阶常系数线性齐次微分方程的通解，知：1,1αβ==，特征根为1,2λi αβ=±1,i =±从而对应的特征方程为：()()2(1)(1)220,i i λλλλ-+--=-+=于是所求二阶常系数线性齐次微分方程为220y y y '''-+=.(2)【答案】2.3【分析】若(),,r x y z 具有连续的一阶偏导数，梯度gr adr 在直角坐标中的计算公式为：r r r gradr i j k x y z∂∂∂=++∂∂∂设()()()(),,,,,,,,A x y z P x y z i Q x y z j R x y z k =++，其中,,P Q R 具有一阶连续偏导数，散度d ivA 在直角坐标中的计算公式为：P Q R divA x y z∂∂∂=++∂∂∂若(),,r x y z 具有二阶连续偏导数，则在直角坐标中有计算公式：222222()r r rdiv gradr x y z∂∂∂=++∂∂∂【详解】本题实际上是计算222222r r rx y z∂∂∂++∂∂∂r x ∂∂222x y z x ∂++=∂22222xx y z=++222x x y z =++xr=2001年全国硕士研究生入学统一考试数学一试题解析22r x ∂∂x x r ∂⎛⎫= ⎪∂⎝⎭2rr xx r∂-∂=2x r x r x r x r r -∂ = ∂223r x r -=类似可得r y y r ∂=∂，22r y ∂∂223r y r -=；r z z r ∂=∂，22r z ∂∂223r z r -=根据定义有()div gradr 222222r r r x y z ∂∂∂=++∂∂∂222222333r x r y r z r r r ---=++222233r x y z r ---=2233r r r-=232r r =2r =2222x y z =++于是(1,2,2)()|div gradr -()2221,2,22x y z -=++2222231(2)2==+-+(3)【答案】211(,).xdx f x y dy -⎰⎰【详解】由题设二次积分的限，画出对应的积分区域，如图阴影部分.但在10y -≤≤内，21y ≥-，题设的二次积分并不是(,)f x y 在某区域上的二重积分，因此，应先将题设给的二次积分变形为：1021211(,)(,),yydy f x y dx dy f x y dx ----=-⎰⎰⎰⎰其中{}(,)10,12,D x y y y x =-≤≤-≤≤再由图所示，又可将D 改写为{}(,)12,10,D x y x x y =≤≤-≤≤于是112(,)ydy f x y dx --⎰⎰211(,)ydy f x y dx --=-⎰⎰2011(,)xdx f x y dy-=-⎰⎰211(,).xdx f x y dy -=⎰⎰(4)【答案】1(2).2A E +【详解】要求()A E -的逆，应努力把题中所给条件化成()A EB E -=的形式.由题设240A A E +-=⇒222A A E E +-=⇒()()22A E A E E-+=Oxyx+y=1x=21即()()12,2A E A E E -⋅+=故()()1122A E A E --=+.(5)【答案】12【分析】切比雪夫不等式：{}2()()D X P X E X εε-≥≤【详解】根据切比雪夫不等式有{}22()21()2222D X P XE X -≥≤==二、选择题(1)【答案】(D)【详解】从题设图形可见，在y 轴的左侧，曲线()y f x =是严格单调增加的，因此当0x <时，一定有'()0f x >，对应()y f x '=图形必在x 轴的上方，由此可排除(A)，(C)；又()y f x =的图形在y 轴右侧靠近y 轴部分是单调增，所以在这一段内一定有'()0f x >，对应()y f x '=图形必在x 轴的上方，进一步可排除(B)，故正确答案为(D).(2)【答案】(C)【详解】题目仅设函数(,)f x y 在点(0,0)附近有定义及''(0,0)3,(0,0)1,x y f f ==未设(,)f x y 在点(0,0)可微，也没设(,)z f x y =，所以谈不上dz ，因此可立即排除(A)；令(,,)(,)F x y z z f x y =-，则有''''',,1x x y y z F f F f F =-=-=.因此过点(0,0,(0,0))f 的法向量为{}''',,x y z F F F ±={}'',,1x y f f ±--=±{−3,−1,1}，可排除(B)；曲线(,)z f x y y =⎧⎨=⎩可表示为参数形式：0,(,0)x x y z f x =⎧⎪=⎨⎪=⎩点(0,0,(0,0))f 的切向量为{}{}'1,0,(0,0)1,0,3x f ±=±.故正确选项为(C).(3)【答案】(B)【详解】方法1：因为001()()lim (1)1lim lim ln(1)ln(1)h h h x x f x f x xf e e x h x x x →→→--==⋅--0()ln(1)limx f x x x x x x → -- ⋅- ()()00()0()lim 0limx x f x f f x f x x →→-=- =0 -()0f '=可见，若()f x 在点0x =可导，则极限01lim(1)h h f e h→-一定存在；反过来也成立.方法2：排除法：举反例说明(A)，(C)，(D)说明不成立.比如，()f x x =,在0x =处不可导，但2220001cos 11cos lim (1cos )lim lim h h h h h f h h h h →→→---==22012sin 2lim h h h →⎛⎫ ⎪⎝⎭=2201112sin lim 22h h h h h →⎛⎫ ⎪⎝⎭ 12=，故排除(A)2200sin 1lim (sin )lim h h h h f h h h h→→--=30sin lim h h h h h →-=⋅其中，30sin limh h h h →-30sin lim h h h h →-=201cos lim 3h h h →- 洛22012sin 2lim 3h h h →⎛⎫ ⎪⎝⎭=22012lim 3h hh → 等16=根据有界量与无穷小的乘积为无穷小，所以3sinhlim0h h h h→-⋅=.故排除(C).又如1,0()0,0x f x x ≠⎧=⎨=⎩在0x =处不可导，但[]00111lim (2)()lim0h h f h f h h h →→--==存在，进一步可排除(D).(4)【答案】(A)【详解】方法1：因为A 是实对称矩阵，必相似于对角阵Λ.1111111111111111E A λλλλλ---------=--------44442,3,41111111111111λλλλλλλ----------------行分别加到行111111111(4)111141111λλλλλ--------------行提出公因子()11111000(4)000000λλλλ-行分别加到2,3,4行34λλ=-()=0得A 的特征值为：12344,0,λλλλ====故必存在正交矩阵Q ,使得14000000000000000T Q AQ Q AQ -⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦因此，A B 与相似.由两矩阵合同的充要条件：实对称矩阵A B 与合同的充要条件是A B 与相似.因此，A B 与也合同.即A B 与既合同且相似.应选(A).方法2：因为A 是实对称矩阵，故A 必相似于一对角阵Λ.又由相似矩阵有相同的特征值,相同的秩,知A 与Λ有相同的秩，故()()1,r r A Λ==即Λ对角线上有3个元素为零.因此,1230λλλ===是A 的特征值.求另一个特征值，由特征值的和等于矩阵主对角线元素之和，知444114.iii i i a λλ=====∑∑故，44λ=.即A 有特征值40λλ==和(三重根)，和对角阵B 的特征值完全一致，故A ,B 相似.又由两矩阵合同的充要条件：实对称矩阵A B 与合同的充要条件是A B 与相似.知A ,B 合同.(5)【答案】A【详解】掷硬币结果不是正面向上就是反面向上，所以X Y n +=，从而Y n X =-，故()DY D n X DX=-=由方差的定义：22()DX EX EX =-,所以[]22()()()DY D n X E n X E n X =-=---222(2)()E n nX X n EX =-+--222222()n nEX EX n nEX EX =-+-+-22()EX EX DX =-=)由协方差的性质：c ov(,)0X c =(c 为常数)；c ov(,)cov(,)aX bY ab X Y =1212cov(,)cov(,)cov(,)X X Y X Y X Y +=+)所以c ov(,)cov(,)cov(,)cov(,)0X Y X n X X n X X DX DX=-=-=-=-由相关系数的定义，得c ov(,)(,)1X Y DX X Y DX DYDX DXρ-===-三【详解】2a rctan x x e dx e⎰2a rctan x x e e dx -=⎰()21arctan 22x xe e d x -=--⎰()21arctan 2x x e d e -=-⎰()221arctan arctan 2x x x xe e e d e ----⎰分部2221arctan 2(1)x x xx x de e e e e -⎛⎫=-- ⎪+⎝⎭⎰222111arctan 21x x x x x e e de ee -⎛⎫⎛⎫=---⎪ ⎪+⎝⎭⎝⎭⎰22211arctan 21x x x x x x e e e de de e --⎛⎫=--+ ⎪+⎝⎭⎰⎰()21arctan arctan 2xx x x e e e e C --=-+++四【详解】由题设，()d x dx ϕ[](,(,))df x f x x dx=()12(,(,))(,(,))(,)f x f x x f x f x x f x x '''=+1212(,(,))(,(,))(,)(,)f x f x x f x f x x f x x f x x ⎡⎤''''=++⎣⎦这里1f f x ∂'=∂，2ff y∂'=∂，所以1()x d x dx ϕ={}12121(,(,))(,(,))(,)(,)x f x f x x f x f x x f x x f x x =⎡⎤''''=++⎣⎦1212(1,1)(1,1)(1,1)(1,1)f f f f ⎡⎤''''=++⎣⎦[]2323=+⋅+17=又(1,1)1,f =()(,(,))x f x f x x ϕ=，所以(1)(1,(1,1))f f ϕ=(1,1)1(1,1)f f = 1,=所以3211()()3()x x d d x x x dxdx ϕϕϕ==⎡⎤=⎢⎥⎣⎦21()3(1)x d x dx ϕϕ==1()(1)1,173117x d x dx ϕϕ= == ⋅⋅51=五【详解】首先将a rctan x 展开.因为()a rctan 'x =2211(1),(1,1)1n n n x x x ∞==-∈-+∑故()0arctan arctan 0arctan 'xx x dx =+⎰2000(1)xn n n x dx ∞=⎛⎫=+- ⎪⎝⎭∑⎰22100(1)(1)21n xnnn n n x dx x n ∞∞+==-=-=+∑∑⎰，()1,1x ∈-于是21()arctan x f x x x +=22101(1)21n n n x x x n ∞+=+-=+∑220(1)(1)21n n n x x n ∞=-=++∑22200(1)(1)2121n n n n n n x x n n ∞∞+==--=+++∑∑()()011210210(1)(1)(1)20121211n n n n n n x x x n n +-∞∞+==---=++⋅+++-∑∑12211(1)(1)12121n n n n n n x x n n -∞∞==--=+++-∑∑2211(1)(1)12121n n n nn n x xn n ∞∞==--=+-+-∑∑21111(1)2121nn n x n n ∞=⎛⎫=+-- ⎪+-⎝⎭∑221(1)2114n n n x n ∞=-=+-∑，()1,1,0x x ∈-≠又0lim ()x f x →2201(1)2lim 114n n x n x n ∞→=⎛⎫-=+ ⎪-⎝⎭∑1=，且(0)1f =，所以()f x 在0x =处连续，从而0x =时，()f x 221(1)2114n n n x n ∞=-=+-∑也成立.进而()f x 221(1)2114n nn x n∞=-=+-∑，(1,1)x ∈-，又在1x =±处级数22211(1)2(1)21414n n n n n x n n ∞∞==--=--∑∑收敛，2111lim ()lim arctan x x x f x x x --→→+=2111lim lim arctanx x xx x --→→+=⋅242ππ=⋅=()1f =，2111lim ()lim arctan x x x f x x x ++→-→-+=2111lim lim arctan x x xx x ++→-→-+=⋅()2142f ππ⎛⎫=-⋅-==- ⎪⎝⎭，所以()f x 在1x =处左连续，在1x =-处右连续，所以等式可扩大到1x =±，从而221(1)2()114n n n f x x n ∞=-=+-∑，[]1,1x ∈-，变形得221(1)()1142n n n f x x n∞=--=-∑因此21(1)14n n n ∞=--∑221(1)114n n n n ∞=-=⋅-∑[]1(1)12f =-1122π⎡⎤=⋅-⎢⎥⎣⎦1.42π=-六【详解】方法1：用斯托克斯公式之后化成第一型曲面积分计算.记S 为平面2x y z ++=上由L 所围成的有界部分的上侧，(曲线的正向与曲面的侧的方向符合右手法则)D 为S 在x oy 坐标面上的投影，{(,)| 1 }D x y x y =+={}221cos ,cos ,cos {,,1}1x y x yz z z zαβγ''=--''++在2x y z ++=中，左右两边关于x 求偏导，得10x z '+=，得1x z '=-.在2x y z ++=中，左右两边关于y 求偏导，得10y z '+=，得1y z '=-.代入上式得{}111cos ,cos ,cos ,,333αβγ⎧⎫=⎨⎬⎩⎭为S 指定侧方向的单位法向量，由斯托克斯公式得I 222222()(2)(3)Ly z dx z x dy x y dz=-+-+-⎰Sdy dz dzdx dxdy x y z P Q R∂∂∂=∂∂∂⎰⎰22222223Sdydzdzdx dxdy x y z y z z x x y ∂∂∂=∂∂∂---⎰⎰(24)(26)(22)Sy z dydz z x dzdx x y dxdy=--+--+--⎰⎰将题中的空间曲线积分化为第二类曲面积分，而对于第二类曲面积分，一般的解答方法是将它先化为第一类曲面积分，进而化为二重积分进行计算.把111,,cos cos cos dS dydz dS dzdx dS dxdy αβλ===代入上式，I [](24)cos (26)cos (22)cos Sy z z x x y dSαβγ=--+--+--⎰⎰[]1(24)(26)(22)3Sy z z x x y dS =--+--+--⎰⎰[]18463S x y z dS =---⎰⎰2(423)3Sx y z dS =-++⎰⎰按第一型曲面积分的算法，将S 投影到x oy ，记为σ.d S 与它在x oy 平面上的投影d σ的关系是2211cos x y dS d z z d σσγ''==++故3dS d σ=，将2x y z ++=代入2(423)3S I x y z dS =-++⎰⎰2[423(2)](3)3Sx y x y d σ=-++--⎰⎰2(6)Dx y d σ=--+⎰⎰由于D 关于y 轴对称，利用区域的对称性，因为区域关于y 轴对称，被积函数是关于x 的奇函数，所以0Dxd σ=⎰⎰.D 关于x 轴对称，利用区域的对称性，因为区域关于x 轴对称，被积函数是关于y 的奇函数，故0Dyd σ=⎰⎰，所以2(6)DI x y d σ=--+⎰⎰2212DDDxd yd d σσσ=-+-⎰⎰⎰⎰⎰⎰12Ddxdy=-⎰⎰12D =-⋅的面积(由二重积分的几何意义知，Ddxdy ⎰⎰即D 的面积)其中，D 为1x y +≤，D 的面积141122=⋅⋅⋅=，所以12224.I =-⋅=-方法2：转换投影法.用斯托克斯公式，取平面2x y z ++=被L 所围成的部分为S ，按斯托克斯公式的规定，它的方向向上(曲线的正向与曲面的侧的方向符合右手法则)，S 在x oy 平面上的投影域记为{(,)| 1 }D x y x y =+=.由斯托克斯公式得I 222222()(2)(3)Ly z dx z x dy x y dz=-+-+-⎰ Sdy dz dzdx dxdy x y z P Q R ∂∂∂=∂∂∂⎰⎰22222223Sdydzdzdxdxdy x y z y z z x x y ∂∂∂=∂∂∂---⎰⎰(24)(26)(22)Sy z dydz z x dzdx x y dxdy=--+--+--⎰⎰由111,,cos cos cos dS dydz dS dzdx dS dxdy αβλ===，及{}221cos ,cos ,cos {,,1}1x y x yz z z zαβγ''=--''++知11cos cos dS dydz dxdy αλ==，11cos cos dS dzdx dxdy βλ==，故22221cos 1cos 1xx yx x yz z z dydz dxdy dxdy z dxdy z z αλ'-''++'===-''++22221cos 1cos 1yx yy x yz z z dzdx dxdy dxdy z dxdy z z βλ'-''++'===-''++因为S 为2z x y =--，式子左右两端分别关于,x y 求偏导，1,1,z zx y∂∂=-=-∂∂于是(24)(26)(26)SI y z dydz z x dzdx x y dxdy=--+--+--⎰⎰{}24,26,26,,1S z z y z z x x y dxdyx y ⎧⎫∂∂=------⋅--⎨⎬∂∂⎩⎭⎰⎰2(423)2(6)SDx y z dxdy x y dxdy=-++=--+⎰⎰⎰⎰因为区域D 关于y 轴对称，被积函数是关于x 的奇函数，所以0Dxd σ=⎰⎰.类似的，因为区域D 关于x 轴对称，被积函数是关于y 的奇函数，故0Dyd σ=⎰⎰，所以2(6)DI x y d σ=--+⎰⎰2212DDDxd yd d σσσ=-+-⎰⎰⎰⎰⎰⎰12Ddxdy=-⎰⎰12D =-⋅的面积(由二重积分的几何意义知，Ddxdy ⎰⎰即D 的面积)D 为1x y +≤，D 的面积141122=⋅⋅⋅=，所以12224.I =-⋅=-方法3：降维法.记S 为平面2x y z ++=上由L 所围成的有界部分的上侧(曲线的正向与曲面的侧的方向符合右手法则)，D 为S 在x oy 坐标面上的投影，{(,)| 1 }D x y x y =+=把2x y z ++=代入I 中，1L 为L 在x oy 平面上投影，逆时针.1222222((2))(2(2))(3)()L I y x y dx x y x dy x y dx dy =---+---+---⎰ 12222(42444)(324888)L y x xy x y dx y x xy x y dy =--++-+-+--+⎰ 12222(324888)(42444)[]L y x xy x y y x xy x y dxdy x y ∂-+--+∂--++--∂∂⎰ 格林公式2(6)24Dx y dxdy =--+=-⎰⎰方法4：用斯托克斯公式后用第二型曲面积分逐个投影法.记S 为平面2x y z ++=上由L 所围成的有界部分的上侧，(曲线的正向与曲面的侧的方向符合右手法则){}221cos ,cos ,cos {,,1}1x y x yz z z zαβγ''=--''++在2x y z ++=中，左右两边关于x 求偏导，得10x z '+=，得1x z '=-.在2x y z ++=中，左右两边关于y 求偏导，得10y z '+=，得1y z '=-.代入上式得{}111cos ,cos ,cos ,,333αβγ⎧⎫=⎨⎬⎩⎭为S 指定侧方向的单位法向量，由斯托克斯公式得I 222222()(2)(3)Ly z dx z x dy x y dz=-+-+-⎰ Sdy dz dzdx dxdy x y z P Q R∂∂∂=∂∂∂⎰⎰22222223Sdydzdzdx dxdy x y z y z z x x y ∂∂∂=∂∂∂---⎰⎰(24)(26)(22)Sy z dydz z x dzdx x y dxdy=--+--+--⎰⎰用逐个投影法，先计算1(24),SI y z dydz =--⎰⎰其中{}(,)|21yz D y z y z y =--+≤为S 在y oz 平面上的投影，分别令0,0,20,20y y y z y z ≥≤--≥--≤,可得到y z D 的4条边界线的方程：右：23y z +=；上：3z =；左：21y z +=；下：1z =.于是13(3)2111(1)22(2)16z z I dz y z dy --=-+=-⎰⎰再计算2(26)SI z x dzdx =--⎰⎰，其中{}(,)|21xzD x z x x z =+--≤为S 在xoz 平面上的投影，分别令0,0,20,20x x x z x z ≥≤--≥--≤,可得到x z D 的4条边界线的方程：右：23y z +=；上：3z =；左：21y z +=；下：1z =.于是13(3)321211(1)22(3)(6)8z z I dz z x dx z dz --=-+=-=-⎰⎰⎰再计算3(22)D I x y dxdy =--⎰⎰，其中{}(,)|1xyDx y x y =+≤为S 在xoy 平面上的投影，因为区域关于y 轴和x 轴均对称，被积函数是关于x 和y 都是奇函数，于是32()0SI x y dxdy =-+=⎰⎰故12324.I I I I =++=-方法5：参数式法.L 是平面2x y z ++=与柱面1x y +=的交线，是由4条直线段构成的封闭折线，将题中要求的空间曲线积分分成四部分来求.当0,0x y ≥≥时，1:1,2L y x z x y =-=--,则,dy dx dz dx =-=-，x 从1到0.以x 为参数，于是222222()(2)(3)y z dx z x dy x y dz-+-+-222222[(1)(2)][2(2)]()[3(1)]()x x y dx x y x dx x x dx =----+----+---22[(1)1(2)(1)]x x dx=--+--则1222222()(2)(3)L y z dx z x dy x y dz-+-+-⎰221(1)1(2)(1)x x dx ⎡⎤=--+--⎣⎦⎰7.3=当0,0x y ≤≥,2:1,12L y x z x =+=-,则,2dy dx dz dx ==-，x 从0到1-于是222222()(2)(3)y z dx z x dy x y dz-+-+-222222[(1)(12)][2(12)][3(1)](2)x x dx x x dx x x dx =+--+--+-+-(24)x dx=+所以212222220()(2)(3)(24)3L y z dx z x dy x y dz x dx --+-+-=+=-⎰⎰ 当0,0x y ≤≤,3:1,3L y x z =-=,则,0dy dx dz =-=，x 从1-到0，于是222222()(2)(3)y z dx z x dy x y dz-+-+-222222[(1)3][23]()[3(1)]0x dx x dx x x =--+⋅--+--⋅2(2226)x x dx=+-所以32222222179()(2)(3)(2226)3L y z dx z x dy x y dz x x dx --+-+-=+-=-⎰⎰ 当0,0x y ≥≤,4:1,32L y x z x =-=-，则,2dy dx dz dx ==-，x 从0到1，于是222222()(2)(3)y z dx z x dy x y dz-+-+-222222[(1)(32)][2(32)][3(1)](2)x x dx x x dx x x dx =---+--+---(1812)x dx=-+所以412222220()(2)(3)(1812) 3.L y z dx z x dy x y dz x dx -+-+-=-+=⎰⎰ 所以123424.LL L L L I ==+++=-⎰⎰⎰⎰⎰ 七【分析】拉格朗日中值定理：如果()f x 满足在闭区间[],a b 上连续，在开区间(),a b 内可导，则至少存在一点(),a b ξ∈，使等式()()()()f b f a f b a ξ'-=-成立【详解】(1)因为()y f x =在(1,1)-内具有二阶连续导数，所以一阶导数存在，由拉格朗日中值定理得，任给非零(1,1)x ∈-，存在()x θ∈(0,1)，()(1,1)x x θ⋅∈-，使[]()(0)'()f x f xf x x θ=+⋅，(0()1)x θ<<成立.因为()f x ''在(1,1)-内连续且"()0,f x ≠所以()f x ''在(1,1)-内不变号，不妨设"()0,f x >则()f x '在(1,1)-内严格单调且增加，故()x θ唯一.(2)方法1：由(1)知[]()(0)'()f x f xf x x θ=+⋅，(0()1)x θ<<于是有[]'()()(0)xf x x f x f θ=-，即[]()(0)'()f x f f x x xθ-=所以[]2'()'(0)()(0)'(0)f x x f f x f f xxx θ---=上式两边取极限，再根据导数定义，得左端＝[]0'()'(0)limx f x x f x θ→-[]0'()'(0)lim ()()x f x x f x x x θθθ→-=[]0'()'(0)limlim ()()x x f x x f x x xθθθ→→-=0"(0)lim ()x f x θ→=右端＝20()(0)'(0)limx f x f f x x →--0'()'(0)lim2x f x f x →- 洛01'()'(0)lim 20x f x f x →-=-1"(0)2f 导数定义左边=右边，即01"(0)lim ()"(0)2x f x f θ→=，故01lim ().2x x θ→=方法2：由泰勒公式得()21()(0)'(0)"(),02f x f f x f x x ξξ=++ ∈，再与(1)中的[]()(0)'()(0()1)f x f xf x x x θθ=+<<比较，所以[]21'()()(0)'(0)"(),2xf x x f x f f x f x θξ=-=+约去x ，有[]1'()'(0)"(),2f x x f f x θξ=+凑成[]'()'(0)1()"(),()2f x x f x f x xθθξθ-=由于[]0'()'(0)lim "(0)()x f x x f f x xθθ→-=，00lim "()lim "()"(0)x f x f f ξξ→→==所以01"(0)lim ()"(0)2x f x f θ→=故01lim ().2x x θ→=八【详解】222222()1()0()()2x y z h t x y h t h t +=-≥⇒+≤，所以侧面在x oy 面上的投影为：()2221,:()2D x y x y h t ⎧⎫=+≤⎨⎬⎩⎭记V 为雪堆体积，S 为雪堆的侧面积，则由体积公式V (),Df x y dxdy =⎰⎰Dzdxdy =⎰⎰222()()()D x y h t dxdy h t ⎡⎤+=-⎢⎥⎣⎦⎰⎰化为极坐标，令c os ,sin x r y r θθ= =，()0,022h t r πθ≤≤≤≤V ()22202()()h t r d h t rdr h t πθ⎛⎫=- ⎪⎝⎭⎰⎰()22022()()h tr h t rdr h t π⎛⎫=- ⎪⎝⎭⎰()()22222()()h t h t r h t rdr rdr h t π⎛⎫=--⎪ ⎪⎝⎭⎰⎰()()24222()22()h t h t r r h t h t π⎛⎫ ⎪=-⎪⎪⎝⎭33()()248h t h t π⎛⎫=- ⎪⎝⎭3()4h t π=再由侧面积公式：()()22''1x y DS f f dxdy =++⎰⎰()()221xy Dz z dxdy''=++⎰⎰22441()()Dx y dxdy h t h t ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭⎰⎰22216()1()D x y dxdy h t +=+⎰⎰化为极坐标，令c os ,sin x r y r θθ= =，()0,022h t r πθ≤≤≤≤S =()()22220161h t r d rdr h t πθ+⎰⎰()()22201621h t r rdr h t π=+⎰()()22220161h t r dr h t π=+⎰()()()()22222201616116h t h t r r d h t h t π=+⎰()()()32222202161163h t h t r h t π⎛⎫=⋅⋅+ ⎪ ⎪⎝⎭()()()32232228211163h t h t h t π⎡⎤⎛⎫⎢⎥=⋅⋅+- ⎪ ⎪⎢⎥⎝⎭⎢⎥⎣⎦()()22271163h t π=⋅⋅-213()12h t π=由题意知0.9(),dVS t dt =-将上述()V t 和()S t 代入，得32()13()40.912dh t h t dt ππ=-⋅223()13()()0.9412dh t h t h t dt ππ⇒=-⋅() 1.3dh t dt ⇒=-积分解得13()10h t t C =-+由()0130h =,得130C =.所以13()130.10h t t =-+令()0h t →，即13130010t -+→100t ⇒→因此高度为130厘米的雪堆全部融化所需要时间为100小时.九【详解】由题设知，12,,,s βββ 均为12,,,s ααα 的线性组合，齐次方程组当有非零解时，解向量的任意组合仍是该齐次方程组的解向量，所以12,,,s βββ 均为0Ax =的解.下面证明12,,,s βββ 线性无关.设11220s s k k k βββ+++= ()*把11122,t t βαα=+21223,t t βαα=+121,,s s t t βαα=+ 代入整理得，()()()1121211222110s s s s t k t k t k t k t k t k ααα-++++++= 由12,,,s ααα 为线性方程组0Ax =的一个基础解系，知12,,,s ααα 线性无关，由线性无关的定义，知()*中其系数全为零，即112211221100 0s s s t k t k t k t k t k t k -+=⎧⎪+=⎪⎨⎪⎪+=⎩ 其系数行列式122121210000000000t t t t t t t t122211321211211100000000000(1)ss s t t t t t t t t t t t +--*+-（）1121111(1)ss s s t tt t -+-⎛⎫=+- ⎪⎝⎭112(1)s s s t t +=+-(*（）变换：把原行列式第i 行乘以21t t -加到第1i +行，其中1,, 1.i s =- )由齐次线性方程组只有零解得充要条件，可见，当12(1)0,sst t +-≠，即12(),sst t ≠-即当s 为偶数，12;t t ≠±当s 为奇数，12t t ≠时，上述方程组只有零解120,s k k k ==== 因此向量组12,,,s βββ 线性无关，故当12122,21,s n t t s n t t =≠±⎧⎨=+≠⎩时，12,,,s βββ 也是方程组0A x =的基础解系.十【详解】(1)方法1：求B ，使1A PBP -=成立，等式两边右乘P ，即AP PB =成立.由题设知，AP ()2,,A x Ax A x =()23,,Ax A x A x =，又3232A x Ax A x =-，故有AP ()22,,32Ax A x Ax A x =-()2000,,103012x Ax A x ⎛⎫⎪= ⎪ ⎪-⎝⎭000103012P ⎛⎫⎪= ⎪⎪-⎝⎭即如果取000103012B ⎛⎫⎪= ⎪ ⎪-⎝⎭，此时的B 满足1A PBP -=，即为所求.方法2：由题设条件()2,,P x Ax A x =是可逆矩阵，由可逆的定义，知有1P -使11PP P P --=()()121112,,,,P x Ax A x P x P Ax P A x ----==E =100010001⎛⎫ ⎪= ⎪⎪⎝⎭即有11121000,1,0001P x P Ax P A x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由题设条件，3232A x Ax A x =-，有()131232P A x P Ax A x --=-11232P Ax P A x --=-00312001⎛⎫⎛⎫ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭032⎛⎫⎪= ⎪ ⎪-⎝⎭由1A PBP -=，得1B P AP -=()12,,P A x Ax A x -=()123,,P Ax A x A x -=()11213,,P Ax P A x P A x ---=000103012⎛⎫⎪= ⎪⎪-⎝⎭(2)由(1)及矩阵相似的定义知，A 与B 相似.由矩阵相似的性质：若A B ，则()()f A f B ，则A E +与A E -也相似.又由相似矩阵的行列式相等，得100113011A E B E ⎡⎤⎢⎥+=+=⎢⎥⎢⎥-⎣⎦1001(1)0132011⎡⎤⨯-⎢⎥⎢⎥⎢⎥-⎣⎦行加到行1113(1)11+=--4=-十一【分析】首先需要清楚二项分布的产生背景.它的背景是：做n 次独立重复试验，每次试验的结果只有两个(要么成功，要么失败)，每次试验成功的概率都为p ，随机变量X 表示n 次试验成功的次数，则~(,)X B n p .在此题中，每位乘客在中途下车看成是一次实验，每个人下车是独立的，有n 个人相当于做了n 次独立重复实验，把乘客下车看成实验成功，不下车看成实验失败，而且每次实验成功的概率都为p ，则问题(1)成为n 重伯努利实验中有m 次成功.【详解】(1)求在发车时有n 个乘客的条件下，中途有m 人下车的概率，相当于求条件概率{}|P Y m X n ==，由题设知，此条件概率服从二项分布，因此根据二项分布的分布律有:{}|(1),0,0,1,2m mn m n P Y m X n C P P m n n -===-≤≤=(2)求二维随机变量(,)X Y 的概率分布，其实就是求{},P X n Y m ==，利用乘法公式，有{}{}{},|P X n Y m P Y m X n P X n ======又X 服从参数(0)λλ>的泊松分布，由泊松分布的分布律有{}!nP X n en λλ-==故{}{}{},|(1)!m mn mn neP X n Y m P Y m X n P X n C P P n λλ--=======-⋅，其中0,0,1,2m n n ≤≤=十二【详解】记121111,n n i n i i i X X X X n n +====∑∑，则()1212X X X =+，即122X X X =+且1111nin i i i E Xnu E X E X u n nn ==⎛⎫==== ⎪⎝⎭∑∑，211n n i i E X E X u n +=⎛⎫== ⎪⎝⎭∑因此()()()221211()2nn i n i i n i i i E Y E X X XE X X X X ++==⎡⎤⎧⎫⎡⎤=+-=-+-⎨⎬⎢⎥⎣⎦⎣⎦⎩⎭∑∑()()()()22112212n i i n i n i i E X X X X XX X X ++=⎧⎫⎡⎤=-+--+-⎨⎬⎢⎥⎣⎦⎩⎭∑()()()()2211221112n n ni i n i n i i i i E X X E X X X X E X X ++===⎡⎤⎧⎫⎡⎤⎡⎤=-+--+-⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎣⎦∑∑∑因为样本方差()221111n i i S X X n =⎡⎤=-⎢⎥-⎣⎦∑是总体方差的无偏估计，则22ES σ=，即()2221111ni i ES E X X n σ=⎡⎤=-=⎢⎥-⎣⎦∑所以()2211(1)ni i E X X n σ=⎡⎤-=-⎢⎥⎣⎦∑，同理()2221(1)nn i i E X X n σ+=⎡⎤-=-⎢⎥⎣⎦∑而()()()()12121122n n i n i i n ii i E X X X X E X X XX ++==⎧⎫⎧⎫⎡⎤⎡⎤--=--⎨⎬⎨⎬⎣⎦⎣⎦⎩⎭⎩⎭∑∑()()1212ni n ii E X X XX +=⎡⎤=--⎣⎦∑()21121ni n i i n i i E X X X X X X X X ++==--+∑()21121ni n i i n i i EX X EX X E X X E X X ++==--+∑由于122,,,(2)n X X X n ≥ 相互独立同分布，则2i X X 与，1n i X X +与，12X X 与也独立(1,2i n = ).而由独立随机变量期望的性质(若随机变量,X Y 独立，且,E X EY 都存在，则E XY EXEY =)，所以2i n i i n i EX X EX EX u ++==，222i i EX X EX E X u ==211n i n i E X X E X EX u ++==，21212E X X E X E X u ==故有()()121n i n i i E X X XX +=⎧⎫⎡⎤--⎨⎬⎣⎦⎩⎭∑()21121ni n i i n i i EX X EX X E X X E X X ++==--+∑()22221ni u u u u ==--+=∑即()()()()221122111()2n n n i i n i n i i i i E Y E X X E X X X X E X X ++===⎡⎤⎧⎫⎡⎤⎡⎤=-+--+-⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎣⎦∑∑∑()()()2221121n n n σσσ=-+-=-。

考研数学一高等数学-试卷8_真题(含答案与解析)-交互

考研数学一（高等数学）-试卷8(总分102, 做题时间90分钟)1. 选择题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1.累次积分可以写成SSS_SINGLE_SELABCD该题您未回答:х该问题分值: 2答案:D2.设S是平面x+y+z=4被圆柱面x 2 +y 2 =1截出的有限部分，则曲面积分的值是SSS_SINGLE_SELA 0BCD π该题您未回答:х该问题分值: 2答案:A2. 填空题1.交换积分次序：=___________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：2.=____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：3.交换积分次序：=____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：4.=_____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：5.=_____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：6.设曲线C为，则=_____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：7.设C为椭圆，则=_____________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：πab8.设u=x 2 +y 2 +z 2，则div(gradu)=__________SSS_FILL该题您未回答:х该问题分值: 2答案:正确答案：63. 解答题解答题解答应写出文字说明、证明过程或演算步骤。

1.计算二重积分，其中D是直线y=2，y=x和双曲线xy=1所围成的平面区域．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：2.计算SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：3.计算，其中区域D由y=x 2，y=4x 2，y=1所围成．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：4.计算，其中D由直线x=一2，y=0，y=2以及曲线所围成．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：5.计算，其中D：x 2 +y 2≤4．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：9π6.计算，其中D由不等式x 2 +y 2≤x+y所确定．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：7.计算，D是由(0≤t≤2π)与x轴所围成的区域．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：8.求，其中D是由y=x 3，y=1，x=一1所围成的区域，f(u)是连续函数．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2答案:正确答案：9.设f(x，y)是定义在区域0≤x≤1，x≤y≤1上的二元连续函数，f(0，0)=一1，求极限。

2001考研数学一真题及答案解析

2001年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设12(sin cos )xy e C x C x =+(12,C C 为任意常数）为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)设222z y x r++=,则div (grad r ))2,2,1(-=_____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy ＝_____________.(4)设矩阵A 满足240A A E +-=,其中E 为单位矩阵,则1()A E --=_____________. (5)设随机变量X 的方差是2,则根据切比雪夫不等式有估计≤≥-}2)({X E X P_____________.二、选择题(本题共5小题,3分,满分15分.)(1)设函数)(x f 在定义域内可导,)(x f y =的图形如右图所示,则)(x f y'=的图形为(2)设),(y x f 在点(0,0)附近有定义,且1)0,0(,3)0,0(='='y x f f ,则 (A ) (0,0)|3z d dx dy =+.(B ) 曲面),(y x f z =在(0,0,(0,0))f 处的法向量为{3,1,1}.(C ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{1,0,3}.(D ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{3,0,1}.(3)设0)0(=f ,则)(x f 在x =0处可导的充要条件为(A ) 201lim (1cosh)h f h →-存在.(B )01lim(1)h h f e h →-存在. (C ) 201lim (sinh)h f h h→-存在.(D ) 01lim [(2)()]h f h f h h→-存在.(4)设1111400011110000,,1111000011110000A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则A 与B (A ) 合同且相似. (B ) 合同但不相似. (C ) 不合同但相似.(D ) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 的相关系数等于(A )-1.(B ) 0.(C )12. (D ) 1.三、(本题满分6分)求dx ee xx⎰2arctan .四、(本题满分6分)设函数),(y x f z =在点(1,1)处可微,且(1,1)1f =,(1,1)|2fx∂=∂,(1,1)|3f y ∂=∂,()(,x f x ϕ=(,))f x x .求13)(=x x dxd ϕ.设)(x f =210,arctan ,0,1,x x x x x +⎧≠⎨=⎩将)(x f 展开成x 的幂级数,并求级数∑∞=--1241)1(n nn 的和.六、(本题满分7分) 计算dz y x dy x z dx z y I L)3()2()(222222-+-+-=⎰,其中L 是平面2=++z y x 与柱面1=+y x 的交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分)设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内的任一0x ≠,存在惟一的)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立; (2)01lim ()2x x θ→=.八、(本题满分8分)设有一高度为()h t (t 为时间)的雪堆在融化过程,其侧面满足方程)()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)的雪堆全部融化需多少小时?九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =的一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =的一个基础解系.十、(本题满分8分) 已知3阶矩阵A 与三维向量x ,使得向量组2,,x Ax A x 线性无关,且满足x A Ax x A 2323-=.(1)记P =（x A Ax x 2,,）,求3阶矩阵B ,使1-=PBP A ;(2)计算行列式E A +.设某班车起点站上客人数X 服从参数为λ(0λ>)的泊松分布,每位乘客在中途下车的概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率; (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分) 设总体X 服从正态分布2(,)N μσ(0σ>),从该总体中抽取简单随机样本12,X X ,,2n X (2n ≥),其样本均值为∑==ni i X n X 2121,求统计量∑=+-+=ni i n i X X X Y 12)2(的数学期望()E Y .2001年考研数学一试题答案与解析一、填空题(1)【分析】由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】先求grad r .grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭. 再求 div grad r=()()()x y z x r y r z r∂∂∂++∂∂∂=222222333311132()()()x y z x y z ++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】矩阵A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即 2()2A EA E E +-⋅=. 按定义知11()(2)2A E A E --=+.(5)【分析】根据切比雪夫不等式2(){()}D x P X E X εε-≥≤,于是2()1{()2}22D x P XE X -≥≤=.二、选择题(1)【分析】当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对. 应选(D ).关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面(,)z f x y =在 (0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭，，{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点(0,0,(0,0))f 处的切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===. 因此,(C )成立.(3)【分析】当(0)0f =时,'0()(0)limx f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知 201lim (1cos )h f h h→-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃. 关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0lim((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时).注意,易求得20sin lim0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t→(即 '(0)f ∃).因为只要()f t t有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同的特征值,从而二次型T x Ax 与T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦, 它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】解本题的关键是明确X 和Y 的关系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即YaX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2xx x x e e e e C ---+++.四、【解】先求(1)(1,(1,1))(1,1)1f f f ϕ===.求 32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法 '''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意'1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y ∂==∂. 因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=.五、【分析与求解】关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121n n n x n n ∞=+--+-∑22(1)21n nx ∞-=+∑ ,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f n ππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L 的定向,按右手法则S 取上侧,S 的单位法向量(cos ,cos ,cos )n αβγ==. 于是由斯托克斯公式得222222cos cos cos 23SI dS x y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=[(24(26(22Sy z z x x y dS ------⎰⎰=(423)(2)(6)S Sx y z dS x y z x y dS ++++=+-利用. 于是==按第一类曲面积分化为二重积分得(62(6)D DI x y x y dxdy =+-=-+-⎰⎰, 其中D 围S 在xy 平面上的投影区域||||1x y +≤(图）.由D 关于,x y 轴的对称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒21224DI dxdy =-=-=-⎰⎰.'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x xθθθ---⋅=, 解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八、【解】 (1)设t 时刻雪堆的体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤. ⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒()xyxyD D S t dxdy ==⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r t θπ≤≤≤≤.⇒2(003()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==⋅+=⎰用先二后一的积分顺序求三重积分()()()h t D x V t dzdxdy =⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-. ⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件.体积减少的速度是dV dt -,它与侧面积成正比(比例系数0.9),即 0.9dVS dt=- 将()V t 与()S t 的表达式代入得 22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-.①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时.九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于 12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-, 所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】 (1)由于AP PB = ,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知AB ,那么A E B E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,mmn mn P Y m X n C p p m n n -===-≤≤=.(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσ的一个容量为n 的简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑, 样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即2()2(1)E Y n σ=-.。

【考研数学】2001年一数一真题、标准答案及解析

[作者姓名]1理工数学一试题详解及评析xsincosx )（c ,c 为任意常数）为某二阶常系数线性齐次微分方程的12(1)设2详解】方法一看出所给解对应的特征根为λ =1± i ，从而特征方程为 λ − 1+ i ,( ( )) 1,2 ( ( ))−2− 2λ + 2 = 0,于是所求方程为y ' 2y '方法二将已知解代入y ' + by + cy = 0，得' ( ( ) ) ( ( ) )xxsin x ⋅ b c − c + cc − 2c +e xcos x ⋅ b c + c + cc + 2c . 由于 e sin x 与x1 2 1 2 1 22 1= −2,c = 2cc 1 2c ,b c c 2c ，解得b 2 12 1 xsin x + c 2((c − c )sin x + (c + c )cos x 1212)y y ' = e '= e (−2c sin x + 2c cos x )2 1 从这三个式子消去c 与c ，得 y ' − 2y ' + 2y = 0 1 2r = x 2 + y 2 + z 2 , 则div gradr ( =3∂r ∂r ∂y ∂r ∂z x y zgradr = i + j + k = i +j + k ∂x r r r ⎛ ⎝ ∂x ⎞ r ⎠ x ⎛ y ⎞ ⎝ r ⎠∂y ⎛ z ⎞ ⎝ r ⎠ ∂z ∂ ∂ ⎜ ⎟ ⎜ ⎟ 2 2 2 2 2 2 2 r − x r − y r − z 2 2 ( ) = + + = + + = = div gradr r 3 r 3 r 3 r 3 r2 ==21 2 + (−2) + 220 1−y∫( )f x , y dx =−122 1−x∫( )f x , y dy .1∫−1 2∫−10 1−y2( )D = {(x , y )| −1≤ y ≤ 0,1− y ≤ x ≤ 2},又可将 D 改写为{( ) } D = x , y |1≤ x ≤ 2,1− x ≤ y ≤ 2 ,0 2 2 0( )f x , y dy 12−11−y1dx∫1−x2( )=1( − )−1+ A − 4E = O ,其中 E 为单位矩阵，则 A E(4)设矩阵 A 满足 A212A 2 + A − 4E = O ，A 2 + A − 2E = 2E ，( − )( +) =A E A 2E 2E ,1( − )⋅ ( + ) =A E A 2E E , 2 1( − )−1 ( + A 2E)A E 2 { ( ) } 5）设随机变量 X 的方差为 2，则根据切比雪夫不等式有估计 P X − E X ≥ 2 ≤.12( ) D X 12{ ( ) } P X − E X ≥ 2 ≤= 2 2( ) = ( )= ' ( )1）设函数 f x 在定义域内可导， y f x 的图形如右图所示，则导函数 y f x 的【】( )是严格单调增加的，因此当 x < 0 详解】从题设图形可见，在 y 轴的左侧，曲线 y f x= y = f (x )图形必在 x 轴的上方，由此可排除（A ），（C ）； ' ( )的图形在 y 轴右侧有三个零点，因此由罗尔中值定理知，其导函数 y = f (x )图' = 形在 y 轴一定有两个零点，进一步可排除（B ）. 故正确答案为（D ）.( ) '(0, 0) ='2）设函数 f x , y 在点 0,0 附近有定义，且 fx= 3dx + dy .(0,0)（（ = ( )在点(0, 0, f (0, 0))的法向量为{3, 1, 1}B ）曲面 z f x , y ⎧ z = ( f x , y )( ( )){ }C ）曲线 ⎨在点 0, 0, f 0,0 的切向量为 1, 0,3 y = 0⎩⎧z f x , y )( ( )) { }D ）曲线 ⎨在点 0, 0, f 0,0 的切向量为 3, 0,1 ⎩【】答】应选（C ）详解】题设只知道一点的偏导数存在，但不一定可微，因此可立即排除（A ）；( ) = − ( )令 F x , y , z z f x , y ，则有 F ' ' ' ' ' x xyyz( { }因此过点 0, 0, f 0,0 的法向量为 ± −3,−1,1 ，可排除（B ）； x = x⎧ z f x , y )( ( ))可表示为参数形式： ⎨ y = 0 ，其中点 0, 0, f 0,0 的切向量为 ⎩⎪ ) z = ⎩( 0,0 = ±1, 0, 3} )} { 'x( ) = = 3）设 f 0 0，则 f x 在点 x 0 可导的充要条件为 11 ( − ) hA ） lim→ 0 h 2h →0 h 1h 1( − ) f h ⎦ 存在 ⎡ ( )− ( )⎤C ） lim f h sinh 存在.（D ） lim ⎣ f 2h → 0 h2 h →0 hh 【】f (x ) 1x(lim f 1− e h = x lim⋅ h → 0 hx → 0x1 ( ) = ( − h ) 可见，若 f x 在点 x 0 可导，则极限 lim f 1 e 一定存在；反过来，若 h → 0 h1( )lim f 1− e hh → 0 h( ) ( )f x xf 1 e − h f 1 e h h1− e lim x =1− e hlim⋅ = −lim h hx → 0 h → 0 h h → 0 ( ) = 存在，即 f x 在点 x 0可导，因此正确选项为（B ）.( ) = 至于（A ），（C ）,(D)均为必要而非充分条件，可举反例说明不成立.比如， f x x ,在1 cosh − 1 cosh− 1( − ) = limf 1 cosh lim lim2 h 2h 2h → 0 h h → 0h → 0 1 ( − ) = lim f h sinh lim lim2 h 2 h 3h → 0 h h → 0 h → 0⎧⎨ ⎩ 1, x ≠ 0=0, x = 011−1 ( )− ()⎤ = = 0 limf 2h f h lim h → 0 h h → 0 h1 1 1 1⎤⎡4 0 0 0⎤4）设 A =，则 A 与 B1 1 1 1⎦ ⎣0 0 0 0⎦【】A 是实对称矩阵，且其特征值为： λ = 4,λ = λ = λ = 0, 故存在正交矩阵Q ,使得1 2 3 4 4 0 0 0⎤0 =TAQ可见，则 A 与 B 既合同又相似.(5)将一枚硬币重复掷 n 次，以 X 和Y 分别表示正面向上和反面向上的次数，则 X 和Y 的相1 2【】详解】设 X 和Y 分别表示正面向上和反面向上的次数，则有Y = n − X ，因此 X 和Y 的相关系数为 r = −1arctan ex∫ 三、求 dxe2xarctan e x∫ ∫arctan e x() − dxd e 2x e 2x⎛ ⎞ ⎟ ⎠ 1 de x− ⎜ e −2x arctan e x − ⎜ (1+ e 2x ) ⎟ 2 e ⎝1 ( − e −2x arctan e x + e −x arctan e + x 2()在点(1, 1)处可微，且= f| = |= ϕ ( )= ( ( )) 2, 3, x f x , f x, x . x (1,1)d 3ϕ dxx =1详解】由题设，有1 f 1, f 1,1f 1,1 1,ϕ ( ) = ( ( ))= ( ) =⎡ d ϕ ( )⎤ x (x )|(x ) ϕ 3 = 3ϕ 2 ⎢ ⎥dxx =1dx ⎣ ⎦⎡ (x , f (x , x ))+ f (x , x )+ fy= = 3ϕ 2 (x ) f ' ' '' ⎣ x y x 3 1 2 3 2 3 ⋅ ⋅⎡ + ( + )⎤ =51⎣ ⎦ ⎧ 1+ x 2 (− )n⎪∞ 1 ∑( ) = 五、设 f x ⎨ x1 − 4n 2n =11 + x ∞∑ 【详解】因 = 2 (− ) 1 x , x 1, 1 n2n ∈(− ) 1 n =1(− ) n∞1 ∑∫ x( )'x 2n +1, x1,1∈[− ]= arctan x dx = 2 n +1 0n =1(− )n(− )n∞1 ∞1 ∑ ∑( )= ++ f x 1 2 n +1n =1 (− )n(− )n∞1 ∞1 ∑∑= 1+ x 2n+ x 2n2n +1 2n +1n =1 n =1n∞∑=1 + x∈[− ] 2n , x 1, 12 n +1n =1(− )n 1π 1∞1 ∑ =− . 1 − 4n224 2n =1∫ () () ( )dz ，其中 L 是平面 x y z 2 + =I = y 2 2dx + 2z 2− x 2dy + 3x2− y 2+ 与L柱面 x + y =1的交线，从 z 轴正向看去， L 为逆时针方向.详解 1】记 S 为平面 x + y + z = 2 上 L 所围成部分的上侧， D 为 S 在 xOy 坐标面上的投影.由斯托克斯公式得∫2z 6x dzdx+ (− − ) 2x 6y dxdy + (− − )I =S 2∫ ∫ (4 + ) = −x 2y 3z dS + 3 S∫ ∫= −2 D∫ ∫ = = −12 dxdyD−24.【详解 2】转换投影法.用斯托克斯公式，取平面 x + y + z = 2 被 L 所围成的部分为 S ，按斯托克斯公式的规定，它的方向向上， S 在 xOy 平面上的投影域记为 z ∂z D , D = x , y | x + y ≤1 . S 为z = 2 − x − y , = −1, = −1, 于是 ∂y{( ) } ∂x∫ ( ) ( ) ( I = y 2 − z 2dx+ 2z 2− x 2 dy + 3x2− y+ (− − ) 2L∫ ∫(−2 − ) y 4z dydz 2z 6x dzdx+ (− − )= 2x 6y dxdyS⎧ ∂z ∂z ⎫ ∫ ∫{−2− }⋅ − = = = y 4z , 2z 6x , 2x 2y ⎨ − − − − ∂⎩ ⎭S−2∫∫(4x 2y 3z dxdy = −2 x y 6 dxdy ( − + ) + + ) ∫∫SD∫ ∫ −12 dxdy = −24D∫ ∫( − ) = ∫∫ =−∫∫ x y dxdy xdxdy ydxdy = 0 − 0 = 0 ，用得性质：x 为 x 得奇函数，D 对DDD称于 y 轴； y 为 y 的奇函数， D 对称于 x 轴；积分均应为零.降维法，取 S 如解法 1 中定义，代入 I 中，∫ () ( ( )) ( I = y 2 2dx + 2 (2 − x − y )22dy + 3x2− y2L 1∫ ( )()= y 2222+8xy −8x −8y +8 dy L 1∫ ∫格林公式− 2 D1逐个投影法，由斯托克斯公式∫− ) ∫∫ ( + ) I 1 =2y 4z dydz 2 y 2z dydz , − SD{( ) } 其中 D = y , z | 2 − y − z + y ≤1 , 分别令 y ≥ 0, y ≤ 0,2 − y − z ≥ 0,2 − y − z ≤ 0, 可 yz 得到 D 的 4 条边的方程：yz 右： 2y + z = 3 ；上： z = 3；左： 2y + z =1；下： z =1.13(3−z ) ∫ ∫(y + 2z )dy = −16于是 I 1 = − 2dz 2 112(1−z )∫ ∫( + ) 类似地， I 2−2 2 3x dzdx = −8 = S∫ ∫I 3 = −2 ( + ) x y dxdy = 0 （由奇、偶数及对称性）SI = I + I + I = −24 1 2 31( ) () ( y 2 − z 2 dx + 2z 2− x 2dy + 3x 2 21∫ 0⎡ ( − ) 2)(− ) ⎤= 1 x 21 1 7 3⎣ ⎦= . 当 x ≤ 0, y ≥ 0, L : y =1+ x , z =1− 2x , x 从 0 到-12 −1 ∫ (2 + )= − x 4= 3 0 37 9∫= −13当 x ≥ 0, y ≤ 0, L : y = x −1, z = 3− 2x , x 从 0 到 14 ∫ 1(−1 + ) = 8x 12 dx 3.= 0 ∫ = + + + = −24L= ( )在(−1, 1)内具有二阶连续导数且 f ' (x ) ≠ 0,试证：七、设 y f x(− ) ≠ 0,1 ，使 f x θ ( )∈( ) ( )= ( )+ ' ⎡θ ( ) ⎤f 0 xf ⎣ x x ⎦1）对于 1,1 内的任意 x 0, 存在唯一的 x 2）lim θ ( ) = x .x → 01）任给非零 x1,1∈(− )，由拉格朗日中值定理得( )= ( )+ '⎡θ ( ) ⎤( <θ ( )< )f x ⎣ ⎦ ' (x ) 在1,1 内连续且 f(− ) '( ) ≠'( ) (− )0, 所以 f x 在1,1 内不变号，不妨设因为 f x ' (x ) > 0，则f'(x )在(−1, 1)内严格单调且增加，故唯一.f(− )，由拉格朗日中值定理得1,1( )= ( )+ ' ⎡θ ( )⎤( <θ ( )< )f x f 0 xf x x 0 x 1 ⎣ ⎦ f ' ⎡θ (x )x ⎤ − f ' (0) f (x )− f ( )− f 0 '⎣ ⎦ =x x 2f ' ' ⎡θ (x )x ⎤ − f ' (0) ⎣ ⎦ θ ( )= ' ( ) θ ( )x f 0 lim x x → 0x → 0(x )− f 2x ' (0) 1f lim= x → 0 2 1 lim θ ( ) = x . x → 0 2( )= ( )+ ' ( )+ ' (ξ ) 2 εf x f 0 f 0 x f 1 (0)x + xf f ' ⎡θ (x )x ⎤ = f (x )− f (0)= f ' ⎣ ⎦ 2 ' '⎣⎦'(ξ ),fθ ( ) =x ' ⎡θ (x )x ⎤ − f '(0) f ⎣ ⎦ '''= f ' (0)，lim flim θ ( )x x x → 0 x →0 ξ →0lim θ () = x .x → 0' (x ) ≠ 0,故 ' (x )存在单值连续可导的反函数，记为ϕ (x ), 则有f f⎡ ⎢⎣f x f 0 ( )− ( )⎤, ⎥ x ⎦ ⎡ f x f 0⎥ = 0, lim ϕ ⎢ x → 0 ⎣ x ⎦⎡ f x f 0 ( )− ( )⎤ ϕ ⎢ ⎣ ⎥⎡ f x f 0 ( )− ( )⎤ 'x ⎦ ' lim θ ( ) =x lim = lim ϕ ⋅ 2x → 0 x → 0 x x → 0 xx xf ' (x ) 2xϕ '⎡ f ' (0)⎤ lim ⎣ ⎦ x →0 ϕ ' ⎡ f''⎣ ⎦ϕ ⎡ f ' (x )⎤ = x ，两边对x 求导，有⎣ ⎦ ϕ ' ⎡ f ' (x )⎤ f ' (x )=1，以x = 0 代入，⎣ ⎦ 1 lim θ ( ) = x . x → 0 2' (θ ( ) ) '(θ ( ) )2）由 f x f 0f x x x ,将 fx x 再展开，有 ( ) ( ) ( ) ( ( ) )f ''0 + f ' 0 θ x x + o θ x x 代入上式，得'( ) + ' ( )θ ( )2f x( )− ( )− ' ( ) − (θ ( ) )f x f 0 f 0 x o x x x θ ( ) =x ' (0) xf ( )− ( )+ ' ( )f x f 0 f 0 x = '(0)flim2 x → 0 x ( () ) o θ x x xlim == 0. 2x → 0x) 八、设有一高度为 h t t 为时间得雪堆再融化过程中，其侧面积满足方程2(x + y) 2 2()−z h t = （设长度单位为厘米，时间单位为小时），已知体积减少的速率与侧面积成正比（比例系数 0.9），问高度为 130 厘米）的雪堆全部融化需多少小时？h (t )∫ ∫∫ V =dz =dxdy0 1 x 2 + y 2≤ h (t )2 −h (t )z ⎤ ⎡ ⎢⎣ ⎥⎦ 2 1 h (t ) ∫ ⎡ h t h t z dz ( ) − ( )2⎤ = = π 0⎣ ⎦2 π h 34∫ ∫( ) 2 2S =1+ z ' + z ' x yh 2 (t )x 2 + y 2≤2( ) 1 6 x 2 + y 2 ∫ ∫=1+ dxdy 2(t ) h h 2 (t ) x 2 + y 2≤21h (t )2π( )h t 2∫ ⎡(t ) 16r ⎤ = h 2+ 2rdr 2 ⎣ ⎦ 0 12=12()dVdt dh t = − ( ) 将上述V (t )和 S (t )代入，得 0.9S t ,= − dt13( )= − t + Ch t 1 1 1= 0 得t 100（小时）. 九、设 α ,α ,L ,α 为线性方程组 Ax = 0 的一个基础解系，1 2 sβ = t α + t α ,β = t α + t α ,L ,β = t α + t α , 其中t ,t 为实常数.试问t ,t 满足什 1 1 1 2 2 2 1 2 2 3 s 1 s 2 1 1 21 2 么关系时，β ,β ,L ,β 也为Ax = 0的一个基础解系.1 2 s 由于α ,α ,L ,α 为均为α ,α ,L ,α 的线性组合，所以α ,α ,L ,α 为均为Ax = 0的解. 1 2 s 1 2 s 1 2 s 下面证明β ,β ,L ,β 线性无关.设1 2 s 1 122ss( + )α + ( + )α +L + (+t k t k t k t k 1 1 2 s 1 2 1 1 2 2 s −112s⎧t k + t k = 0 2 1 1 2 M ⎪ ⎪ t k + t k = 0⎩ 2 s −1 1 s t 1 0 0 0 0 t 2 t 1 0 L 0t 2 t 1 0 s 1 s 2 L M = t + (− )t 1 M M M M 0 0 0 t 2 t 1+ (− )t 0 ≠ ，即当s 为偶数，t ≠ ±t ；当s 为奇数，t ≠ t 时，上述方程组2 1 2 1 2 可见，当ts 1 s1只有零解k = k =L = k = 0，因此向量组β ,β ,L ,β 线性无关， 1 2 s 1 2 s 从而β ,β ,L ,β也为Ax = 0的一个基础解系.1 2 s 十、已知3 阶矩阵A 与三维向量x , 使得向量组x , Ax , A2x 线性无关，且满足A32( ) P = x , Ax , A2x ,求2 阶矩阵B , 使A PBP −1= ;（ 2）计算行列式 A + E . 【详解】Ax = Ax ( ) = 2 A Ax A x A A 232( A x , Ax , A2 2x , A 32 20 0 0 ⎤⎥ =x 1 0 3 , )⎢ 0 1⎡ ⎢ 0 0 0 ⎤⎥ AP = P 1 0 3 = PB⎢ ⎥ ⎦ ⎢ ⎣0 1 ⎡ 0 0 0 ⎤ ⎢ ⎥A = PBP −1 ; ⎢ ⎥⎢ 0 1 ⎣ ⎦⎡ ⎢ a 1 a 2 a ⎤ 3 ⎥ 设 b b 2 b , 则由 AP = PB 得⎢ ⎥ 1 3 ⎢ ⎣ ⎥ ⎦c 1 c 2 c 3 a 1 a 2 a ⎤3 ⎥ ( ) Ax , A2x , A 32x b b 2 b , ⎢ ⎥ 1 3 ⎢ ⎣c 1 c 2 c 3 Ax = a x + b Ax + c A 2 x ,(1)(2) (3)1 1 1 A2 x = a x + b Ax + c A2x ,2 2 2A 3x = a x + b Ax + c A2 x ,3 3 3A 3 x = 3Ax − 2AAx − 2A x = a x + b Ax + c A x , Ax , A23 2 2 x（4）3 332x 线性无关，故由于a =b = 0,c =1; 2 2 1 a = 0,b = 0,c = −2;333⎡ ⎢ 0 0 0 ⎤⎥ B = 1 0 3 − ⎥2⎢ ⎥⎢ 0 1 ⎣ ⎦ A32( ) (A A 2 2故 λ = −3 为 A 的特征值， A 2x − Ax 为属于-3 的特征向量；1 λ =1为 A 的特征值， A 2x + 3Ax 为属于 1 的特征向量；2λ = 0 为 A 的特征值， A x + 2Ax −3Ax 为属于-3 的特征向量；2 3 ⎡ ⎢ 0 0 −3⎤ ⎡ 0 0 −3⎤⎥ ⎢ ⎥ ( ) Q = x , Ax , A2 x −13 2 = P −13 2 , ⎢ ⎥ ⎢ ⎥ ⎢ ⎣1 1 1 1 1 1 −1⎡ ⎢ 0 0 −3⎤⎡ 0 0 −3⎤ ⎥ ⎢ ⎥ ⎥Q −1 AQ = − 1 3 P − AP −1 3 1 ⎢ ⎥ ⎢ ⎢ ⎥ ⎦ ⎢ ⎥ ⎦1 1 1 1⎣ ⎣ −1 ⎡ 0 0 −3⎤ ⎡ 0 0 −3⎤ ⎢ ⎢ ⎥ ⎢ ⎥ ⎥ = −1 3 B −1 3 ⎥ ⎢ ⎢ ⎣ ⎥ ⎦ ⎢ ⎥ ⎦1 1 1 1 ⎣ 但另一方面，Q 为特征向量组成的矩阵，所以 Q −1 AQ 为由对应的特征值组成的对角矩阵：⎡ ⎢ ⎢−3 0 0⎤⎥ Q −1 AQ = 0 0 1 0 , ⎥ ⎢ ⎣⎥ 0 0 ⎦1 ⎡ ⎢ 0 0 −3⎤ ⎡−3 0 0⎤ ⎡ 0 0 −3⎤−⎡0 0 0 ⎤ ⎢ B = −1 3 =1 0 ⎢ ⎢ ⎢ ⎥ ⎢ ⎢ 1 1 0 0 1 1 0 1 ⎣ ⎦ ⎣ ⎣ ⎦2）由（1）知，A 与B 相似，故A + E 与B + E 也相似，于是有⎡ ⎢ 1 0 0 ⎤⎥ A + E = B + E = 1 13 = −4 ⎢ ⎥ ⎦ ⎢ ⎣0 1 十一、设某班车起点站上客人数X 服从参数 λ (λ >)的泊松分布，每位乘客在中途下车的0 ( < < ) 概率为P 0 P 1 ，且途中下车与否相互独立，以Y 表示在中途下车的人数，求： 1）在发车时有n 个乘客的条件下，中途有m 人下车的概率； 2）二维随机变量 X ,Y 的概率分布.1）求在发车时有n 个乘客的条件下，中途有m 人下车的概率，相当于求条件概率{ = = }因此有:{ = m m P Y m | XC P 1 Pn 2）利用乘法公式，得{ = = }= { = = } { = }P Y m | X n P x nP X n |Y m e −λ m = C n m P m ⋅ λn n !( )( ) 十二、设总体 X 服从证态分布 N µ,σ 2 σ > 0 ，从该总体中抽取简单随机样本21 2nn∑ ∑( )2X( ≥ )= = + X , X ,L , Xn 2 其样本均值为X X ，求统计量Y i X X 1 2 2n i 2 n i =1 i =1( )的数学期望E Y .1 n 1 n∑ ∑ X , X = X 则有 2X = X + X n +i 121i 2n n i =1 i =1 ⎡ 2⎤ n ⎧ n∑( − ) = ∑ ⎡( − )+ ( − )⎤ 2 + E ⎢ X X 2X ⎥ E ⎨ X X X X ⎣ ⎦ i n +i i 1 n +i 2 ⎢ ⎣ ⎩ i =1 i =1 ⎧ n ∑ ⎡( ) 2 ( )( ) ( 2 X − X + X − X ⎢ n +i n +i ⎣i i 1 2 2 i =1 ⎡ n⎤ ⎡ n⎤∑( ) 2 ∑( 2X − X 1 + 0 + E X ⎢ ⎥ ⎢ ⎥ i n +i⎣ i =1 ⎦⎣ i =1⎦= = ( − )σ n 1 2 + ( − )σn 1 2( − )σ2 2 n 1。