编译原理简明教程(第2版)第5章
编译原理课件Chapter_5

•
结点N的属性值由N的产生式所关联的语义规则来定义 通过N的子结点或N本身的属性值来定义
结点N的属性值由N的父结点所关联的语义规则来定义 依赖于N的父结点、N本身和N的兄弟结点上的属性值 不允许N的继承属性通过N的子结点上的属性来定义, 但允许N的综合属性依赖于N本身的继承属性 终结符号有综合属性 (来自词法分析),但无继承属性
–
每个语义规则都根据产生式体中的属性值来计算头部 非终结符号的属性值
栈中的状态/文法符号可以附加相应的属性值 归约时,按照语义规则计算归约得到的符号的属性值 要求副作用不影响其它属性的求值 没有副作用的SDD称为属性文法
•
S属性的SDD可以和LR语法分析器一起实现
– –
•
语义规则不应该有复杂的副作用
•
•
•
抽象语法树的表示方法
– –
叶子结点中只存放词法值 内部结点中存放了op值和参数 (通常指向其它结点)
30
构造简单表达式的抽象语法树的SDD
属性E.node指向E对应的抽象语法树的根结点
31
表达式抽象语法树的构造过程
•
输入
•
a–4+c
•
步骤
p1 = new Leaf(id, entry_a); p2 = new Leaf(num, 4); p3 = new Node('–', p1, p2); p4 = new Leaf(id, entry_c); p5 = new Node('+', p3, p4);
–
–
9
语法分析树上的SDD求值 (1)
•
•
实践中很少先构造语法分析树再进行SDD求值, 但在分析树上求值有助于翻译方案的可视化,便 于理解 注释语法分析树
编译原理课后答案-第二版
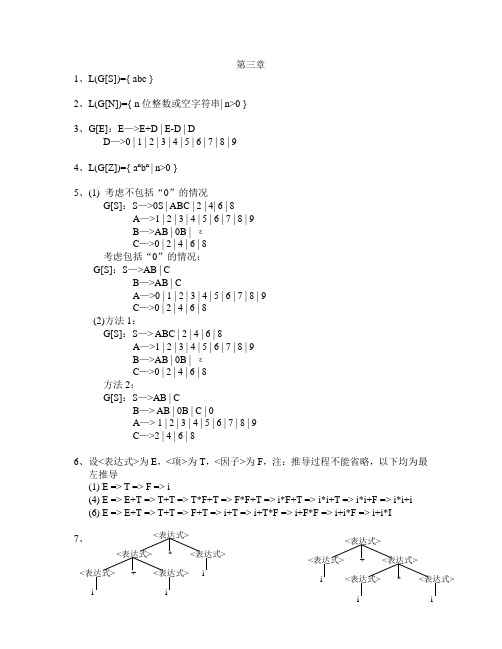
第三章1、L(G[S])={ abc }2、L(G[N])={ n位整数或空字符串| n>0 }3、G[E]:E—>E+D | E-D | DD—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 94、L(G[Z])={ a n b n | n>0 }5、(1) 考虑不包括“0”的情况G[S]:S—>0S | ABC | 2 | 4| 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8考虑包括“0”的情况:G[S]:S—>AB | CB—>AB | CA—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>0 | 2 | 4 | 6 | 8(2)方法1:G[S]:S—> ABC | 2 | 4 | 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8方法2:G[S]:S—>AB | CB—> AB | 0B | C | 0A—> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>2 | 4 | 6 | 86、设<表达式>为E,<项>为T,<因子>为F,注:推导过程不能省略,以下均为最左推导(1) E => T => F => i(4) E => E+T => T+T => T*F+T => F*F+T => i*F+T => i*i+T => i*i+F => i*i+i(6) E => E+T => T+T => F+T => i+T => i+T*F => i+F*F => i+i*F => i+i*I7、<表达式><表达式>*<表达式><表达式>+<表达式>i i i<表达式><表达式>+<表达式>i <表达式>*<表达式>i i8、是有二义性的,因为句子abc 有两棵语法树(或称有两个最左推导或有两个最右推导)最左推导1:S => Ac => abc 最左推导2:S => aB => abc 9、(1)(2) 该文法描述了变量a 和运算符+、*组成的逆波兰表达式10、(1) 该文法描述了各种成对圆括号的语法结构(2) 是有二义性的,因为该文法的句子()()存在两种不同的最左推导: 最左推导1:S => S(S)S => (S)S => ()S => ()S(S)S => ()(S)S => ()()S => ()()最左推导2:S => S(S)S => S(S)S(S)S => (S)S(S)S=> ()S(S)S => ()(S)S => ()()S => ()()11、(1) 因为从文法的开始符E 出发可推导出E+T*F ,推导过程如下:E => E+T =>E+T*F ,所以E+T*F 是句型。
编译原理第二版第五章答案

第五章第5章自顶向下语法分析方法练习(P99)1.文法S->a|^|(T)T->T,S|S(1) 对(a,(a,a)和(((a,a),^,(a)),a)的最左推导。
(3)经改写后的文法是否为LL(1)的?给出它的预测分析表。
(4)给出输入串(a,a)#的分析过程,并说明该串是否为G的句子。
(1) 对(a,(a,a)的最左推导为:S=>(T)=>(T,S) =>(S,S) =>(a,S) =>(a,(T)) =>(a,(T,S)) =>(a,(S,S))=>(a,(a,S)) =>(a,(a,a))对(((a,a),^,(a)),a) 的最左推导为:S=>(T) =>(T,S) =>(S,S) =>((T),S) =>((T,S),S) =>((T,S,S),S)=>((S,S,S),S) =>(((T),S,S),S) =>(((T,S),S,S),S) =>(((S,S),S,S),S)=>(((a,S),S,S),S) =>(((a,a),S,S),S) =>(((a,a),^,S),S) =>(((a,a),^,(T)),S) =>(((a,a),^,(S)),S) =>(((a,a),^,(a)),S) =>(((a,a),^,(a)),a)(3)改写文法为:0) S->a1) S->^2) S->( T )3) T->S N4) N->, S N5) N->ε对左部为N2的产生式可知:FIRST (->, S N2)={,}FIRST (->ε)={ε}FOLLOW (N2)={)}{,}∩ { )}=Ø所以文法是LL(1)的。
也可由预测分析表中无多重入口判定文法是LL(1)的。
清华大学编译原理第二版课后习答案

《编译原理》课后习题答案第一章第 4 题对下列错误信息,请指出可能是编译的哪个阶段(词法分析、语法分析、语义分析、代码生成)报告的。
(1) else 没有匹配的if(2)数组下标越界(3)使用的函数没有定义(4)在数中出现非数字字符答案:(1)语法分析(2)语义分析(3)语法分析(4)词法分析《编译原理》课后习题答案第三章第1 题文法G=({A,B,S},{a,b,c},P,S)其中P 为:S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案:L(G[S])={abc}第2 题文法G[N]为:N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?答案:G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D或者:允许0 开头的非负整数?第3题为只包含数字、加号和减号的表达式,例如9-2+5,3-1,7等构造一个文法。
答案:G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4 题已知文法G[Z]:Z→aZb|ab写出L(G[Z])的全部元素。
答案:Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={anbn|n>=1}第5 题写一文法,使其语言是偶正整数的集合。
要求:(1) 允许0 打头;(2)不允许0 打头。
答案:(1)允许0 开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0 开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6 题已知文法G:<表达式>::=<项>|<表达式>+<项><项>::=<因子>|<项>*<因子><因子>::=(<表达式>)|i试给出下述表达式的推导及语法树。
编译原理CHAPTER 5(Semantic Analysis and Intermediate Code Generation-2)ppt课件

2018/11/15
12
P 1M ε id1
t1 8
D
id1 : T1 ; proc id2 ; id3 : T2 ; S
D2 5 ; 3 N
2
D1 :
;
T1 proc id2
D3 4 ;
id3 : T2
S
ε
5. t := top ( tblptr ) addwidth ( t, top ( offset ) ) pop ( tblptr ) pop ( offset ) enterproc ( top( tblptr), , t )
2018/11/15
11
P 1M ε id1
t2 t1 4 8
D
id1 : T1 ; proc id2 ; id3 : T2 ; S
D2 ; 3 N
2
D1 :
;
T1 proc id2
D3 4 ;
id3 : T2
S
ε
4. enter ( top( tblptr), , T2.type, top(offset) ) top( offset ) := top(offset) + T2.width
2018/11/15 13
P7 1M ε id1 D
6
D2 5 ; 3 N
id1 : T1 ; proc id2 ; id3 : T2 ; S
2
D1 :
;
T1 proc id2
D3 4 ;
id3 : T2
S
ε
6. 7. addwidth ( top ( tblptr ), top ( offset ) ) pop ( tblptr ) pop ( offset )
编译原理 龙书 第二版 第5、6章

2)E->T
E.type=T.type
3)T->num
T.type=integer
4)T->num.num
T.type=float
(2)
产生式
语义规则
1)E->E1+T
If E1.type ==T.type then E.type=E1.type
Else begin
E.type=float
105: goto–
6)按照产生式B->B1 || M B2进行归约
7)按照产生式B->(B1)进行归约
8)按照产生式B->B1 && M B2进行归约
9)各子表达式的truelist和falselist在上图中已标出
3)三元式序列
4)间接三元式序列
答:(1)抽象语法树
(2) 四元式序列
t1=b+c
t2=minus t1
t3=a+t2
op
Arg1
result
0
+
b
c
T1
1
minus
T1
T2
2
+
a
T2
T3
(3)三元式序列
op
Arg1
Arg2
0
+
b
c
1
minus
(0)
2
+
a
(1)
(4)间接三元式序列
10
(0)
E.type=T.type; E.val=T.val
3)T->num
T.type=integer; T.val=num
编译原理 第五章

一个文法符号串的开始符号集合定义如下: 定义5.1 设G=(VT,VN,S,P)是上下文无关文法 FIRST(α)={a|α aβ,a∈VT,α,β∈V*} 若α ε,则规定ε∈FIRST(α).
不难求出在例5.2文法G2中 FIRST(Ap)={a,c} FIRST(Bq)={b,d} 因此有 FIRST(A)∩(FIRST(B)= 这样文法G2中,关于S的两个产生式的右部虽然都以非 终结符开始,但它们右部的符号串可能推导出的首符号集 合不相交,因而可以根据当前的输入符号是属于哪个产生 式右部的首符号集合而决定选择相应产生式进行推导,因 此仍能构造确定的自顶向下分析。
定义5.4 一个上下文无关文法是LL(1)文法的充分 必要条件是:对每个非终结符A的两个不同产生式, A→α, A→β,满足 SELECT(A→α)∩SELECT(A→β)= 其中α,β不同时能 ε。
LL(1)文法也可定义为: 一个文法G是LL(1)的,当且仅当对于G的每 一个非终结符A的任何两个不同产生式 A→α|β, 下面的条件成立: ① FIRST(α)∩FIRST(β)= ,也就是α和 β推导不出以某个相同的终结符a为首的符号串; 它们不应该都能推出空字ε. ② 假若β ε那么, FIRST(α)∩ FOLLOW(A)= 也就是,若β ε 则α所能推出的串的首符号不应在FOLLOW(A) 中(如例5.3)。这种表示与定义5.4相比计算步骤 少,但不如定义5.4清晰。
编译原理-第五章习题答案

上一页
下一页
11
例:5.3 文法:SaAcBe A bAb B d 句子:abbcde
步骤 (1) (2) (3) (4) (5) (6)
栈
# #a #ab #aA #aAb #aA #aAc #aAcd #aAcB #aAcBe #S
输入 abbcde# bbcde# bcde# bcde# cde# cde#
上一页
下一页
20
5)构造算符优先文法G的优先表的算法
思路:对文法中的每一个产生式的候选式检查,判断句型中相邻符号之间 的关系 来构造优先表; 具体算法: FOR 每条产生式P→X1X2…Xn FOR i=1 TO n-1 IF Xi,Xi+1∈VT,THEN Xi=Xi+1; IF i ≤n-2且Xi,Xi+2∈VT,Xi+1∈VN THEN Xi=Xi+2; IF Xi∈VT,Xi+1∈VN THEN FOR FIRSTVT(Xi+1)中的每个a Xi <. a; NEXT IF Xi∈VN,Xi+1∈VT THEN FOR LASTVT(Xi)中的每个a DO a .> Xi+1; NEXT NEXT NEXT
上一页
下一页
8
例:5.1 P85 文法: E→T|E+T T→F|T*F F→i|(E) 句型:i1*i2+i3其中:短语有i1、i2、i3、i1*i2、 i1*i2+i3 直接短语:i1、i2、i3;句柄:i1 例:5.2 P85 文法如上 E 句型:E+T*F+i 短语:E+T*F+i,E+T*F,T*F,i 直接短语:T*F和i E + 句柄:T*F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. Select集(可选集)
定义:文法G[S],有规则Aβ ,则该规则的可选集为: First(β ), 当β ≠ε Select(Aβ )= Follow(A), 当β =ε 例: 对于G[E] select(EE+T)=First(E+T)={(,i} select(ET)=First(T)={(,i} select(TT*F)=First(T*F)={(,i} select(TF)=First(F)={(,i} select(F(E))=First((E))={(} select(Fi)=First(i)={i}
2
LL(1)分析表
x1
(1) LL(1)分析过程 x2 当前句型的右端部分x1x2…xm# (xi∈V) 待分析串的右端部分y1y2…yn# (yi∈VT) … 分几种情况: xm 1)当x1∈VN,由y1选择相应规则替换x1 2)当x1∈VT,若x1=y1≠#,则说明x1与y1匹配,分 别删去x1,y1, 继续分析. 若x1 ≠ y1,则说明不匹配,进行出错处理 3)若x1=y1=#,说明全部匹配,分析成功. LL(1)分析程序见P77--78
5.4.2
a1 a2
LL(1)分析方法的逻辑结构
a3 … ai … am #
输入串
x1
分析表 控制程序 分析器
x2 …. xn
分析栈
#
输入串a1a2a3…am#,以定界符”#”作为结尾
分析表:M[A,a] (A为栈中元素,a为输入字符)
5.4.3
1. LL(1)文法
LL(1)分析方法
对于文法G[S],其每个非终结符的不同规则具 有不相交的select集. 即对于Ux1|x2|…|xn,有 select(Uxi)∩select(Uxj)=Φ, (i≠j)
例:文法G[S]:SAB Aab Bcd|cBd 判断abccdd是否是句子。 (1)自顶向下构造语法树 S A B a b c B d c d
(2)推导 S AB AcBd Accdd abccdd
5.2
不确定的自顶向下分析思想
例: G[S]: SxAy Aab|a S x A y x (1)
First(dB)={d}
First(Bq)={b,d}
例: G[E]:
EE+T|T TT*F|F F(E)|I First(F)={(,i} First((E))={(} First(i)={i}
则: First(E+T)={(,i} First(T)={(,i} First(T*F)={(,i}
注:有些不是LL(1)文法的文法,经过修改 (如左提左因子,消除递归等)可化为 LL(1)文法,但并不是所有的非LL(1)文法 都能改造为LL(1)文法。
例 对于文法G [Z]:
ZAU |BR AaAU|b BaBR|b Uc Rd
First(AU) ∩First(BR)={a,b} ≠Φ 所以,不是一个LL(1)文法
第5章 语法分析 ----自顶向下分析方法
学习目标
自上而下语法分析的基本思想 自上而下语法分析面临的问题及解决方 消除左递归的方法 FIRST(x)的求法、FOLLOW(U)的求法 递归子程序的构造方法 LL(1)文法 LL(1)分析表的构造方法
语法分析是编译过程的核心部分。 -----在词法分析识别出单词符号串的基础上, 分析并判定程序的语法结构是否符合语法规则。
例: G[S]: SaBc|bB BbB|d|ε Select(Bε)=Follow(B)={#,c}
5.2.2
自顶向下分析过程中存在的问题 及解决办法
1. 左递归问题 例:G[S]: SSa|b S
b S
分析baa
S
a S
S
a
S
S a
S
S a
S
S a
b
S a
S a
b
S
a…Biblioteka 分析时可能出现:例 5-6 ① 消除左递归 ② 求select 集 ③ 构造分析表 ④ 分析符号串 例 文法G [S] S abB A SC|BAA|ε B AbA C B|c
VN={S,A,B,C} VT={a,b,c}
判断此文法是不是LL(1)文法: Select (SabB)={a} Select (ASC)={a} ∩≠Φ Select (ABAA)={a,b} Select (Aε)={a,b,#} Select (CB)={a,b} ∩=Φ Select (Cc)={c} Selcet (BAbA)={a,b} ∴不是LL(1)文法。构造出的分析表含有多重定义。
AaBc
a
BbB b BbB b Bd
d c
(2)
LL(1)分析表构造
LL(1)分析表反映分析栈中元素与输入串中元 素的匹配关系.记M[A,a]
几个约定: C:继续读入下一字符 R:重读当前字符
RE(β):用β 的逆串替换栈顶符号.
构造LL(1)分析表的算法如下:
(1)对于ADβ (D∈VN)且 select(ADβ )={b1,b2…bn} 则M[A,bi]=RE(Dβ )/R 表示:用Dβ 的逆替换A,重读当前字符. (2)对于Aaβ (a∈VT) 则M[A,a]= RE(β )/C 表示:用β 的逆替换A,继续读入下一字符. (3)对于Aε 且select(Aε )={b1,b2…bn} 则M[A,bi]=RE(ε )/R=ε /R
构造LL(1)分析表:
a A b B/C ε/C succ c d ε/C e B/C #
cB/C
B
c #
分析abbedc的过程 分析栈 余留输入串 动作
#A
#cB #cB #cB #cB #c #
abbedc#
bbedc# bedc# edc# dc# c# #
cB/C
B/C B/C B/C ε/C ε/C succ
自顶向下
语法分析
如 LL(k), 递归下降分法等 如LR(K), 算符优先分析法等
自底向上
目
录
5.1 自顶向下分析技术 5.2 不确定的自顶向下分析技术 5.3 确定的自顶向下分析技术 5.4 LL(K)分析方法 5.5 递归下降分析方法
5.1
分析思想:
自顶向下分析技术
从文法的开始符号出发,向下推导, 看能否推出 待分析的符号串,如果能推出,说明该符号串是符合 语言语法的句子,否则不是句子。
(1) 回溯
(2) 死循环, 在没有对当前输入符号匹配就进入处 理S的过程,无法确定什么时候才用Sb替换, 造成死循环. 解决方法:
文法的实用限制(算法6)
消除左递归
扩充的BNF表示法
2.
回溯问题 在分析中,假定被代换的最左非终结符A存在n 条规则,Ax1|x2|…|xn,难以确定采用哪个规则,若 从x1到xn逐个来试,则效率太低。
(2) 首符号相同
First(xi)∩First(xj)≠Φ
即对于 Aα x1|α x2 ...|α xn 改为 Aα (x1|x2 ...|xn) 进一步Aα B Bx1|x2 ...|xn
(i≠j)
解决方法:”左提左因子”修改文法
例: Uα x1|α x2 |x3|…|xn
且First(xi)∩First(xj)=Φ , (i,j≥3,i≠j)
(1)首符号不同
First(xi)∩First(xj)=Φ (i≠j) 若a∈First(xk),则选用Axk来推导 例: G[S]: AaB|bA BbaA|c {First(aB)={a}} ∩ {First(bA)={b}} = Φ {First(baA)={b}} ∩ {First(c)={c}} = Φ 分析符号串bbabaac A bA bbA bbaB bbabaA bbabaB bbabaac
First(xi) ≠α , (i=3,4,…n) 采用 U α V|x3|…|xn Vx1|x2
例: G[S]: Sif B then S1 else S2|if B then S1 改为: Sif B then S1 T T else S2 | ε
5.3
确定的自顶向下分析思想
文法是非左递归的
2.
Follow集(向前看集)
定义:文法G[S],非终结符号U的向前看集 Follow(U)={a|S * …Ua…,a∈VTU{#}} 特别,当a=ε时,视U后面的符号为”#” ∵E * E, E * E+T, E * (E) ∴Follow(E)={#,+,)} Follow(T)={#,+,*,)} Follow(F)={#,+,*,)}
推导过程是一个不断试探的过程,出现回溯现象, 所以又称带回溯的自顶向下分析方法(效率低,代价高) 原因:推导过程中有多个侯选式可供选择.
5.2.1
三种终结符集
1.First集 (首符号集) 定义: 文法G[S]:字汇表V,则符号串β 的首符号集 First(β )={a|β * ay,a∈VT,y∈V*} 特别,若β =ε ,则First(β )=Φ 例:G[S]: SAp SBq Aa|cA Bb|dB First(Ap)={a,c}
例:G[A]: AaBc BbB|eB|d 分析abbdc# 设计文法的分析表: a AaBc b c d e
A
B
BbB
Bd
BeB
分析过程:
分析栈 输入符号
产生式
匹配删除
#A #cBa #cB #cBb #cB #cBb #cB #cd #c #
abbdc# abbdc# bbdc# bbdc# bdc# bdc# dc# dc# c# #
分析xay是否句子 S S x A y A y a a b (3) (2)
