小学一年级奥数复习立体几何
一年级奥数——数立体图形之欧阳道创编

数立体图形善智知识点:1.数平面图形:先数小,再数大(不能看到几个就是几个)2.数立体图形注意:一层一层数,每一层都不能遗漏被挡住的个数.认真思考,结果要用算式表达出来.3.数图形歌数图形,按顺序,先数小,再数大.立体的,有隐藏,分层数,再相加.课堂共同练习:1.下图有()个正方形?2.下图有()个长方形?3.下图有()个三角形?4.数图形:()个长方形()个三角形()个正方形5.数一数下面的图形各由几个小正方体组成,并画出从它们的正面看到的形状.6.用正方体摆成下图,数一数一共有几个小正方体,其中几个能看见,几个看不见?一共()个一共()个一共()个看见()个看见()个看见()个看不见()个看不见()个看不见()个7.数一数下面每个立体图形各有几个小正方体.8.数一数,下面的立体图形是由几个小正方体搭成的?9.给下列图形,再添加()个小正方体,就能组成一个大正方体.10.数一数下面物体中各有几个小正方体.()个()个11.数一数下面物体中各有几个小正方体.()个()个12.数一数,下图中一共有()个正方体.A.6个B.7个C.8个课后自我提升:1.数一数下图分别有几个图形?()个正方形()个长方形()个三角形2.数一数,下图有几个三角形?()个()个3.摆一摆,数一数.下面每个图形分别是由几个小正方体组成的.4.数一数,填一填(1)按层数:下面一层有个正方体,中间一层有个正方体,上面一层有个正方体.(2)按前后排数:前排有个正方体,后排有个正方体.(3)一共有个正方体.5.数一数下列物体是由几个小正方体拼成的.()个()个()个6.数一数下面物体中各有几个小正方体.()个()个()个7.数一数下面物体中各有几个小正方体.()个()个参考答案:课堂共同练习:5 6 10 5、4、7 5、8、7 6题略 5、9、813、10、10 3个 8、10 20、30 C课后自我提升5、6、10 5、8 5、5、5、5、6 5、3、1、3、6、9.7、9、9 1、8、27 20、30。
小学奥数-立体几何-题库学生版

第五讲 几何——立体部分教学目标:对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥例题精讲:【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【例 2】 右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】 下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】 一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【巩固】(2008年走美六年级初赛)一个表面积为256cm 的长方体如图切成27个小长方体,这27个小长方体表面积的和是 2cm .【例 5】 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木【例 6】 要把12件同样的长a 、宽b 、高h 的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【例 7】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【例 8】(2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【例 9】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?【例 10】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【例 11】棱长是m厘米(m为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m的最小值是多少?【例 12】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【例 13】三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【例 14】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【例 15】把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【例 16】一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【例 17】有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A的为黑色,图中共有黑色积木多少块?A【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成?【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【例 18】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方【例 19】 (2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的 倍.⑷⑶⑵⑴ ⑾⑽⑼⑻⑺⑹⑸【例 20】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵【例 21】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【例 22】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【例 24】 如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【例 25】 把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【例 26】 一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【例 27】 (2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)(单位:厘米)【巩固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?【巩固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是______.7cm4cm5cm【例 28】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?【例 29】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【例 30】如图,甲、乙两容器相同,甲容器中水的高度是锥高的13,乙容器中水的高度是锥高的23,比较甲、乙两容器,哪一只容器中盛的水多?多的是少的的几倍?甲乙【例 31】(2008年仁华考题)如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是平方米.20cm8cm100cm【巩固】图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?【例 32】如图,ABC是直角三角形,AB、AC的长分别是3和4.将ABC∆绕AC旋转一周,求ABC∆扫出的立体图形的体积.(π 3.14=)CBA43【例 33】 已知直角三角形的三条边长分别为3cm ,4cm ,5cm ,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米?(π取3.14)【巩固】如图,直角三角形如果以BC 边为轴旋转一周,那么所形成的圆锥的体积为16π,以AC 边为轴旋转一周,那么所形成的圆锥的体积为12π,那么如果以AB 为轴旋转一周,那么所形成的几何体的体积是多少?ABC【例 34】 如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .E 、F 分别是AD 与BC的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)ABAB【巩固】(2006年第十一届华杯赛决赛试题)如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD相交O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?B A【例 35】 (人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下底面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积.课后练习练习1.(《小学生数学报》邀请赛)从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?(写出符合要求的全部答案)练习2.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)302515练习3.如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?练习4.(2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大22008cm,则这个圆柱体木棒的侧面积是________2cm.(π取3.14)第2题练习5.如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50厘米.这卷铜版纸的总长是多少米?月测备选【备选1】如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?【备选2】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm11cm【备选3】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?【备选4】一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?4cm【备选5】(2009年”希望杯”一试六年级)如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水升.。
一年级上 数学思维训练 奥数 第6讲 有趣的立体图形
立体几何图形是数学中一个重要的组成部分。
这节课通过看一看、认一认、想一想等活动使大家认识最基础的立体几何图形,从而增加对图形的感性认识,培养初步的图形概念认识,为以后的学习打下良好的基础。
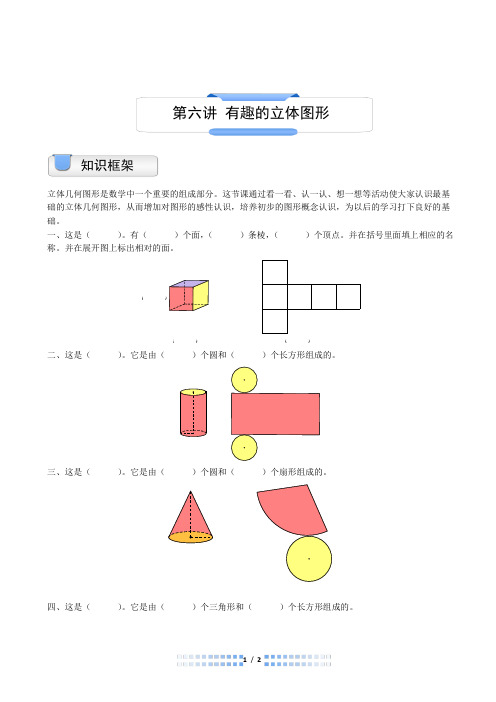
一、这是( )。
有( )个面,( )条棱,( )个顶点。
并在括号里面填上相应的名称。
并在展开图上标出相对的面。
二、这是( )。
它是由( )个圆和( )个长方形组成的。
三、这是( )。
它是由( )个圆和( )个扇形组成的。
四、这是( )。
它是由( )个三角形和( )个长方形组成的。
( )
( )( )知识框架
第六讲 有趣的立体图形
五、将下图中(1)、(2)号棱锥剪开铺平后,哪一个是它对应的展开图,请用线连起来。
六、下图有哪些图形组成?
七、请你将能找到的包装盒如:月饼盒、冷饮盒、鞋盒等等,用剪刀剪开,平铺在桌面上观察并画出展开图。
一年级基本立体几何通用版(奥数拓展+测试)

基本立体几何(一)基本立体图形的概括所有点不在同一平面上的图形叫立体图形。
对现实物体认识上的一种抽象,即把现实的物体在只考虑其形状和大小,而忽略其它因素的基础上在平面上的表示。
(二)基本立体图形的表示例1、在括号中写出下面立体图形的名称【练习1.1】下面立体图形名称是________。
知识本源典型例题【练习1.2】下面立体图形名称是______体。
例2、数一数,图中分别有几个,将数字填入()中。
【练习2.1】下面立体图形名称是______体。
【练习2.2】数一数有_______个正方体。
例3、如图所示的三角形旋转形成什么图形?【练习3.1】绕着正方形的一条边旋转得到体。
【练习3.2】绕着长方形的一条边旋转得到体。
例4、把立体与其展开图用线连接起来【练习4.1】下面的图形可以形成体。
【练习4.2】下面的图形可以折叠成的立体图形的名称是。
例5、如图,正方体展开图中数字1对面上是数字_________。
【练习5.1】正方体展开得到个面。
【练习5.2】圆柱体展开,其中有个圆。
例6、由正方体和四棱锥组成的立体,沿着红色虚线展开,画出展开图。
【练习6.1】对一个球体横着切一刀,切得的截面是形【练习6.2】立体图形展开变成图形。
基本立体几何-测试卷A姓名:分数:时间:分钟1、(单选题)下面立体图形名称是_______。
A、长方体B、正方体C、圆柱D、圆锥2、(单选题)下面立体图形的名称是_______。
A、长方体B、正方体C、圆柱D、圆锥3、(单选题)下面立体图形的名称是_______。
A、长方体B、正方体C、圆柱D、圆锥4、数一数,下图中有_______个正方体。
5、(单选题)绕着正方形的一条边旋转得到_________。
A、长方体B、正方体C、圆柱D、圆锥6、(单选题)绕着长方形的一条边旋转得到_________。
A、长方体B、正方体C、圆柱D、圆锥7、(单选题)下面的图形可以形成_________立体图形。
(完整word)一年级数学几何图形常见考题及答案(奥数)

3、四、数一数,下面共有多少个长方形? ( 9分)——沿虚线对折,折后的图形是三角形。
O1填 一填数 一f t 方册&S 1 方角形 卡---m H、你能数出图形中有几个三角形吗?(9分))个)个9 分)(( 、数一数,下面的图形中有多少个正方形?( ()个(五、数一数,图中共有多少个圆?六、辨一辨。
(对的画“两个三角形一定能拼成一个长方形。
()个1、 2、(个(8 分)((3、是由6个阴影部分的小三角形组成的5、用2个二可以拼成一个三角形,也可以拼成一个长方形,还可以拼成一个平行四边形4、一个能剪成两个相同的三角形或正方形。
七、选一选。
(把正确答案的序号填在括号里)(15分) 把一个正方形的纸折一次,可能折出图( )二1、 2、 用两个 能拼成一个() 3、 4、 正方形 三角形 长方形 用()个相同的| |可以拼成一个大正方形。
4)根同样长的 拼成一个长方形。
至少用( 5、 )个三角形?二八、折一折,填一填。
(9分)正方形的对面是 三角形的对面是 长方形的对面是r~九、数一数,填一填。
(9分)()块 0十、用4个丄可以拼成 分一分,画一画。
(12分) 你知道分别是怎样拼成的吗?请在图中答案一、4, 7, 4, 4, 4二、6, 7, 12三、5, 3, 10四、7, 9, 5五、11, 5六、1(X), 2 (V), 3 (V), 4(X), 5( V)3. 4. 5.七、 1. 2.平形四边形。
一年级数学知识点:立体图形知识点

一年级数学知识点:立体图形知识点小学生想要学好数学,做题是最好的办法,但想要奏效,还得靠自己的积累。
小学一年级数学知识点需要大家熟记,下面是立体图形知识点供大家复习!【立体图形知识点】1、长方体长方体是长长的,有6个平平的面,有些面是一样的,有些面是不一样,长方体对面相等,用它可以画出长方形。
平时见到的火柴盒、文具盒都是长方体。
2、正方体正方体四四方方的,它也有6个平平的面,它的边也是直直的。
而且它的棱都是一样长,每个面都一样大,无论怎么平放在桌子上,它的高矮都都是一样的,用它可以画出正方形。
魔方就是正方体。
3、圆柱体圆柱就像一根柱子。
它有上下两个圆圆的面,而且大小一样,用它可以画出圆形;另一个面是弯曲的,我们把弯曲的面放在桌子上就可以滚动它。
4、球圆圆的,可以滚来滚去的就是球。
平时玩的皮球、篮球、踢的足球都是球。
【课后练习题】1.填空.(1)长方体有( )个面,正方体有( )个面.(2)用手摸一摸,圆柱上下两个面,它们的大小( ).(3)用2块完全一样的正方体可以拼成一个( ).(4)听装可乐的形状是( ).2.填空.(1)以上图形中( )号是球体.( )号是长方体.( )号是正方体.教师范读的是阅读教学中不可缺少的部分,我常采用范读,让幼儿学习、模仿。
如领读,我读一句,让幼儿读一句,边读边记;第二通读,我大声读,我大声读,幼儿小声读,边学边仿;第三赏读,我借用录好配朗读磁带,一边放录音,一边幼儿反复倾听,在反复倾听中体验、品味。
( )号是圆柱体.(2)足球是( )体.课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也很难做到恰如其分。
为什么?还是没有彻底“记死”的缘故。
要解决这个问题,方法很简单,每天花3-5分钟左右的时间记一条成语、一则名言警句即可。
可以写在后黑板的“积累专栏”上每日一换,可以在每天课前的3分钟让学生轮流讲解,也可让学生个人搜集,每天往笔记本上抄写,教师定期检查等等。
小学奥数题目-一年级-几何-基本立体几何测试卷

基本立体几何自测卷1、
(单选题)下面立体图形名称是_______。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
2、
(单选题)下面立体图形的名称是_______。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
3、
(单选题)下面立体图形的名称是_______。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
4、
数一数,下图中有_______个正方体。
5、
(单选题)绕着正方形的一条边旋转得到_________。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
6、
(单选题)绕着长方形的一条边旋转得到_________。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
7、
(单选题)下面的图形可以形成_________立体图形。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
8、
(单选题)下面的图形可以形成_________立体图形。
∙A、长方体
∙B、正方体
∙C、圆柱
∙D、圆锥
9、
圆锥有________个面。
10、
长方体有_______个面。
最新小学奥数之立体几何问题

立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改.又是多少?【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一次增加两个面)练习.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.表面积最小:互相重合的面最多时表面积最小【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1. 如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2. 某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1. 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2. 如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学一年级奥数复习立体
几何
The latest revision on November 22, 2020
小学一年级奥数:立体几何
我们称之为:体。
长方体,立方体,圆柱,圆锥,棱柱,棱锥,球体。
关于立体几何,有很多的公式,要求有丰富的空间想象能力,可以把它和我们的现实生活联系起来。
对于下面研究的图例,它们的面积和体积全部都有
长方体
就是每个面由长方形构成,总共有6个面,就有6
个长方形。
正方体 由
6个正方形构成,每条边长都一样。
有12
条棱。
圆柱体 两个底面是完全相同的圆。
三棱柱 上下底面是三角形
柱体与锥体:两端相同的,成对称的立方体;而锥体是一端是点,另一端是图形(圆或者多边形)。
圆锥三棱锥(四面体)四棱锥
球,可以理解为是圆的立体化。
最中心的地方叫做球心,到球面的距离叫做球的半径。
立体图形,要有立体的想象能力,下面,我们把立体的图形解剖开来,看看它
长方体展开图示:
圆锥展开图形
你能看出来它们是什么吗
你知道他展开后是什么样子的吗
图形的等积变化和等积划分问题:
在奥数中通常会碰到一些比较怪异的图形,我们最常用的方法就是把它进行等积变化,变成可以计算的规则的图形。
等积划分就是把一个不规则的图形如何分为面积相等的两份,观察是最重要的途径。
1,变梯形为三角形:
可以自己动手做一做!
2,经典问题:五个小正方形,变成一个大正方形:
3,如何把正方形再拼成一个等腰直角三角形
部分有相同的形状和结构。
1,分下面图形成面积相等的两部分:
2,分下面的图两个相等的部分:
有3棵树。
