推荐--1整式的乘法(六)——乘法公式二
第二讲 整式的乘法---完美版

第二讲 整式的乘法【知识梳理】:1、整式包括单项式和多项式⑴单项式是数与字母的积,单个数或字母也是单项式。
⑵多项式是几个单项式的和.。
⑶同类项:在多项式中,所含字母相同....,并且相同字母的指数也相同..........的项,叫同类项。
⑷把一个多项式按同一字母的指数从大(小)到小(大)的顺序排列起来,叫做把这个多项式进行降(升)幂排列。
⑸掌握去括号、添括号法则,能熟练地进行同类项的合并。
2、幂的运算(m 、n 都是正整数) ⑴;m n m n a a a +⋅= ⑵();m n m n a a = ⑶();n n n ab a b =⋅ ⑷(0);m n m n a a a a -÷=≠ ⑸1(0);a a =≠⑹1(0).p pa a a-=≠3、乘法公式⑴22()()a b a b a b +-=- ⑵222()2a b a ab b ±=±+ ⑶2233()()a b a ab b a b +-+=+ ⑷2233()()a b a ab b a b -++=- ⑸2()()()x a x b x a b x ab ++=+++⑹2222()222a b c a b c ab ac bc++=+++++⑺33223()33a b a a b ab b +=+++ ⑻33223()33a b a a b ab b -=-+-⑼3332222221()()3()[()()()]32a b c a b c a b c ab bc ca abc a b c a b b c c a abc++=++++---+=++-+-+-+【专题精讲】【例1】若代数式22(26)(2351)x ax y bx x y +-+--+-的值与字母x 的取值无关,求代数式234a -+22212(3)4b a b --的值【例2】化简))()()()()()((12121212121212643216842+++++++【例3】已知a=2005x+2004,b=2005x+2005,c=2005x+2006,则多项式ca bc ab c b a ---++222的值为多少?【例4】(1)已知,比较的大小(2)已知 找出之间的等量关系;(3)试比较与的大小.【例5】求证:无论x 、y 为何值,3530912422+++-y y x x 的值恒为正.【例6】1、已知22114a a+=,求①1a a+;②21()a a-2、已知31=+aa ,求172++a a a 的值【例7】已知210,x x --= 则32231999x x x --+的值为( )A.1997B.1998C. 2001D.2002【例8】已知a 为实数,且使323320a a a +++=,求199619971998(1)(1)(1)a a a +++++的值.【课后作业】1、已知19992000a x =+,19992001b x =+,19992002c x =+,则多项式222a b c ab bc ca++---的值为( )A.0B.1C.2D.32、已知,,a b c 均不为0,且0a b c ++=,那么111111()()()a b c bccaab+++++的值为 .3、若3a =-,25b =,则20072006a b +的个位数字是( ) A.3 B.5 C.8 D.94、当2x =时,代数式31ax bx -+的值等于17-,那么当1x =-时,代数式31235ax bx --的值 .5、设1abc =.试求111a b c ab a bc b ca c ++++++++的值.6、计算:242(1)(1)(1)(1)na a a a ++++7、计算:()()()()12121212242++++n8、计算:2481111(1)(1)(1)(1)2222++++9、己知: (x+1)(x 2+mx+n) 的计算结果不含x 2和x 项,求m ,n.10、已知()()q x x px x +-++3822的展开式中不含32,x x 项,求p 、q 的值.11、已知252510a b c d⨯=⨯=。
乘法口诀表(打印版)
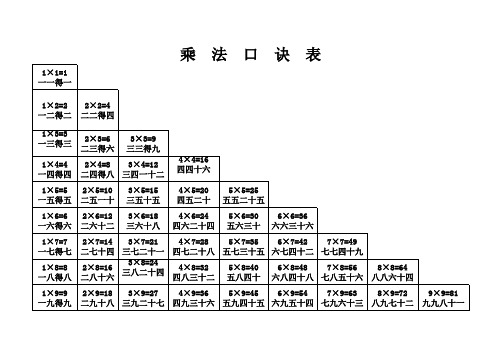
一九得九 二九十八 三九二十七 四九三十六 五九四十五 六九五十四 七九六十三 八九七十二 九九八十一
1×1=1
乘法口诀表
1×2=2 2×2=4
1×3=3 2×3=6 3×3=9
1×4=4 2×4=8 3×4=12 4×4=16
1×5=5 2×5=10 3×5=15 4×5=20 5×5=25
1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36
1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49
1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64
1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 一六得六 二六十二 三六十八 四六二十四 五六三十 六六三十六
1×7=7 一七得七
1×8=8 一八得八
2×7=14 二七十四
2×8=16 二八十六
3×7=21 三七二十一
3×8=24 三八二十四
4×7=28 5×7=35 6×7=42 7×7=49 四七二十八 五七三十五 六七四十二 七七四十九
ห้องสมุดไป่ตู้
一一得一
乘法口诀表
一二得二 二二得四
一三得三 二三得六 三三得九
一四得四 二四得八 三四十二 四四十六
一五得五 二五一十 三五十五 四五二十 五五二十五
一六得六 二六十二 三六十八 四六二十四 五六三十 六六三十六
一七得七 二七十四 三七二十一 四七二十八 五七三十五 六七四十二 七七四十九
乘法公式

生活中的数学
有一个正方形的花园,若它的边长增加3米,则花园面积将增 加39平方米,求原来花园的面积.
x
3
解:设原正方形花园的边长x为米,那么 增加后的边长为(x+3)米由题意得
x
3
x2
3x
3x
32
(x+3)2-x2=39
X2+6x+9-x2=39 6x=30
∵X=5
∴X2=25 答:原来花园的面积为25平方米.
整式的乘法 公式(1)
温
故
多项式与多项式相乘的法则
2
(x+y)(c+d) = xc +xd +yc +yd
3 4
1
1
2
3
4
多项式与多项式相乘,先用其中 一个多项式的每一项去乘另一个多项 式的每一项,再把所得的积相加。
学习目标:
2、会计算形如(x+a)(x+b)
练习&反馈
1、理解形如(x+a)(x+b)的两个一次二项式相乘法则
—
2
长方形的面积=(45+15) ×(45-15) =60×30 =1800
结论: (45+15)(45-15)=452-152
几何意义
a a
b
a
2
b2
剩下的面积=a2-b2
长方形的面积=(a+b)(a-b)
结论: (a+b)(a-b)=a2-b2
典型例题
利用平方差公式计算 (1) (5+6x) (5-6x)
( x 5)
2
2
2 2 4 x 12 mx 9 m (2x 3m)
整式的乘法和乘法公式复习课课件

• 整式的乘法复习 • 乘法公式复习 • 整式的乘法与乘法公式的应用 • 整式的乘法和乘法公式的注意事项 • 练习与巩固
01
整式的乘法复习
单项式乘单项式
总结词
直接相乘,系数相乘,同底数幂 相乘。
详细描述
单项式与单项式相乘时,只需将 它们的系数相乘,并将相同的字 母的幂相加。例如,$2x^3y$与 $3xy^2$相乘得到$6x^4y^3$。
提高练习题
提高练习题1
计算 (x + y)^2(x - y)^2。
提高练习题2
化简 (a^2 - b^2) / (a^2 + ab + b^2)。
提高练习题3
求 (a^2 + 2ab + b^2) / (a^2 - b^2) 的值。
综合练习题
1 2
综合练习题1
计算 ((x + y)(x - y))^2。
VS
公式范围
整式的乘法公式有一定的适用范围,如完 全平方公式适用于任意实数a、b的情况; 平方差公式适用于任意实数a、b(a≠b) 的情况等。
公式推导和证明方法
推导方法
整式的乘法公式可以通过基本的运算法则进 行推导,如通过同底数幂的乘法法则推导出 幂的乘方公式;通过单项式乘以多项式的法 则推导出分配律等。
02
乘法公式复习
平方差公式
总结词
理解平方差公式的结构特点
总结词
掌握平方差公式的应用
详细描述
平方差公式是整式乘法中的重要公式之一,表示 两个平方数的差等于它们的线性组合的平方。这 个公式在代数和几何中都有广泛的应用,是解决 数学问题的关键工具。
详细描述
整式乘除知识点

整式乘除知识点在数学的学习中,整式乘除是一个重要的部分,它不仅是后续学习代数运算的基础,也在解决实际问题中有着广泛的应用。
下面就让我们一起来深入了解整式乘除的相关知识点。
一、整式的乘法(一)单项式乘以单项式法则:把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
例如:3x²y × 5xy³= 15x³y⁴(二)单项式乘以多项式法则:用单项式去乘多项式的每一项,再把所得的积相加。
例如:2x(3x² 5x + 1) = 6x³ 10x²+ 2x(三)多项式乘以多项式法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
例如:(x + 2)(x 3) = x² 3x + 2x 6 = x² x 6二、整式的除法(一)单项式除以单项式法则:把系数、同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式。
例如:18x⁴y³z² ÷ 3x²y²z = 6x²yz(二)多项式除以单项式法则:先把这个多项式的每一项分别除以这个单项式,然后把所得的商相加。
例如:(9x³y 18x²y²+ 3xy³) ÷ 3xy = 3x² 6xy + y²三、乘法公式(一)平方差公式(a + b)(a b) = a² b²例如:(3x + 2)(3x 2) = 9x² 4(二)完全平方公式(a + b)²= a²+ 2ab + b²(a b)²= a² 2ab + b²例如:(x + 5)²= x²+ 10x + 25四、整式乘除的应用(一)几何图形中的应用在求解长方形、正方形等图形的面积和周长时,经常会用到整式的乘除。
整式的乘法第课件ppt

实际生活中的问题
1 2
计算面积和体积
整式乘法在计算矩形、三角形、立方体等面积 和体积的应用中非常重要。
计算路程
在计算两点之间路程的问题中,需要使用整式 乘法来计算两点之间的距离。
3
计算时间
在计算运动过程中时间的问题中,需要使用整 式乘法来计算运动的时间。
在数学中的重要性
基础运算
01
整式乘法是数学运算中的基础运算之一,掌握好整式乘法可以
《整式的乘法第课件ppt》
xx年xx月xx日
目录
• 课程介绍 • 整式乘法基本概念 • 整式乘法基本运算规则 • 整式乘法的应用 • 复习与巩固 • 总结与展望
01
课程介绍
课程背景
整式的乘法是数学中的重要概念,是后续学习多项式、方程 等知识的基础。
对于初中生而言,掌握整式的乘法能够为他们的数学学习打 下坚实的基础。
总结词
用单项式去乘多项式的每一项,再把所得的积相加。
详细描述
例如,单项式3a乘以多项式2x-5y,首先用3a乘以2x得到6ax,再用3a乘以-5y得 到-15ay,最后将6ax和-15ay相加得到6ax-15ay。
多项式乘多项式
总结词
用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。
02
整式乘法基本概念
单项式
总结词
单项式是一种特殊的代数式,它只包含一个字母和一个数字,并且这个数字 必须是整数。
详细描述
单项式是由一个字母和一个数字组成的代数式,例如:3x、4y等。其中,字 母表示未知数,数字表示该未知数的具体数值。单项式是整式乘法中的基本 元素之一。
多项式
总结词
多项式是由多个单项式组成的代数式,每个单项式之间用加号或减号连接。
整式的乘法公式与因式分解方法

整式的乘法公式与因式分解方法整式是由数、字母和运算符号(仅限于加法、减法、乘法和乘方)组成的代数表达式。
在代数学中,整式的乘法公式和因式分解是非常重要的概念和方法。
一、整式的乘法公式在解决整式的乘法运算时,乘法公式起到了关键的作用,它能够帮助我们简化计算过程,提高效率。
1. 二项式的乘法公式二项式的乘法公式是指两个二项式相乘时的简化方法。
设有两个二项式$(a + b)$和$(c + d)$,它们的乘积可以通过使用FOIL法则来计算。
FOIL法则指的是先相乘、外乘再相加、内乘再相加、最后相加的步骤。
举个例子,我们计算$(2x + 3)(4x + 5)$的乘积:首先,先相乘:$2x \cdot 4x = 8x^2$;然后,外乘再相加:$2x \cdot 5 + 3 \cdot 4x = 10x + 12x = 22x$;接着,内乘再相加:$3 \cdot 5 = 15$;最后,相加结果:$8x^2 + 22x + 15$。
因此,$(2x + 3)(4x + 5)$的乘积为$8x^2 + 22x + 15$。
2. 三项式的乘法公式三项式的乘法公式是指两个三项式相乘时的简化方法。
与二项式的乘法公式类似,计算过程同样采用FOIL法则。
举个例子,我们计算$(2x + 3)(4x + 5)(x + 1)$的乘积:首先,先计算$(2x + 3)(4x + 5)$的乘积,结果为$8x^2 + 22x + 15$;然后,再乘以$(x + 1)$,使用FOIL法则,计算过程如下:一次相乘:$(8x^2 + 22x + 15)(x) = 8x^3 + 22x^2 + 15x$;外乘再相加:$(8x^2 + 22x + 15)(1) + (8x^3 + 22x^2 + 15x) = 8x^2 + 22x + 15 + 8x^3 + 22x^2 + 15x = 8x^3 + 30x^2 + 37x + 15$。
因此,$(2x + 3)(4x + 5)(x + 1)$的乘积为$8x^3 + 30x^2 + 37x + 15$。
六年级整式知识点总结

六年级整式知识点总结整式是数学中的一个重要概念,是培养学生逻辑思维和数学推理能力的重要内容。
在六年级的数学学习过程中,我们接触了各种各样的整式知识点,下面就对这些知识点进行一个总结。
1. 整式的定义:整式是由常数、变量和它们的积、商、正、负、指数和幂等有理数次加、减的和。
2. 整式的基本运算:(1) 加法和减法:将同类项合并,并保持同类项的次数不变。
(2) 乘法:运用分配律进行拆分、合并和化简。
(3) 除法:运用乘法的逆运算进行分解和化简。
3. 整式的化简:整式的化简就是将多项式通过合并同类项、拆分因式、运用分配律等方法,简化为最简形式。
4. 整式的因式分解:(1) 提取公因式法:将整式中的公因子提取出来。
(2) 公式法:利用代数公式进行因式分解。
(3) 分组分解法:将整式中的项进行分组,然后利用公因式提取法进行因式分解。
(4) 完全平方公式法:利用完全平方公式将整式分解。
(5) 公式法:利用二次根式公式将整式分解。
5. 整式的乘法公式:(1) 两个一次整式的乘法:$(a + b)(c + d) = ac + ad + bc + bd$(2) 两个二次整式的乘法:$(a + b)(c + d) = ac + (ad + bc) + bd$(3) 一个一次整式和一个二次整式的乘法:$(a + b)(c + dx) = ac + adx + bc + bdx$(4) 平方差公式:$(a + b)(a - b) = a^2 - b^2$6. 整式的除法公式:(1) 整式除以一次整式:按照多项式的长除法进行计算。
(2) 整式除以二次整式:运用因式分解的方法进行计算。
7. 整式的应用:整式在数学中有广泛的应用,特别是在代数方程的解法、几何问题的求解以及物理问题的建模等方面都具有重要作用。
以上就是六年级整式的知识点总结。
通过学习和掌握这些知识,我们能够更好地理解和运用整式,为以后的学习打下坚实的基础。
希望同学们能够认真学习,不断巩固和提高自己的数学能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(八年级数学)整式的乘法(六)——乘法公式(2)
第 周星期 班别 姓名 学号
一、学习目标:
自主探索总结出两数和的平方与两数差的平方规律,并能正确运用完全平方
公式进行多项式的乘法。
二、问题情境
问题1:街心花园有一块边长为a 米的正方形草坪,经统一规划后,南北向
要加长2米,东西向也要加长2米。
问改造后的长方形草坪的面积是多少?
解:
问题2:==
问题3:将2改为b ,结果如何?即
三、结论:
完全平方和公式: ①
两数和的平方,等于它们的 加上它们 的2倍。
猜想: ②
比较①、②两个公式:
2(2)a +)2)(2++a a (2()a b +=______________))((=++b a b a 2()a b +=_______________________)(2=-b a
1、 计算结果只有___________与______________符号不同
2、 计算结果:右边中间项的符号都与左边___________符号相同
四、练习(A 组)
1、判断下列各式是否正确。
如果错误,请改正在横线上。
(1) ( ) (2) ( ) (3) ( )
(4) ( )
2、你准备好了吗?请对照平方差公式完成以下练习:
(1)
(2)
(3)
(4)=
(5) 3.请用公式写出以下多项式乘以多项式的结果:
222()
a b a b +=+2
22()2a b a ab b +=++222()a b a b -=-22(2)4x x -=-222()2a b a a b b += + + 222(21)()2()()()a += + + ==+-=-222)())((2)()2(y x 222(32)()2()()()x y += + + =222)())((2)()21+-=-y (2221(3)()2()()()2
a b += + + =
(1)
(2)
(3)
(4)
(5) (6)
4.能快速求出下列各式的结果?请试一试:
(1)
解:= =
(2) 解:
(B 组)
1、计算:
(1) (2) 2(2)x y +=2(3)m n -=(2)(2)x y x y -+=2(23)x y -=2(2)2
b a +=(23)(23)a b a b --=2982298(100)=-⎽⎽⎽⎽⎽⎽21(30)2
211()23
a b -2(2)m n -+。
