几何体的三视图还原直观图
3.2由三视图还原成实物图1

(2)三视图b.
主视图 左视图
俯视图 俯视图
(a)
(b)
由三视图还原成实物图的基本思路(逆向思维): (1)分别由主视图、左视图、俯视图想象直观图的正面、 侧面和底面及侧棱的形状;
(2)由主视图、左视图、俯视图所对应的高来想象侧面和
底面的位置关系; (3)注意“长对正,高平齐,宽相等”的基本特征及三视图 中的虚线.
练习1.P18/练习1,2.
练习:
主视图
左视
俯视图 答案:两个圆台组合
而成的简单组合体。
二、思考交流 下图是一个奖杯的三视图,请画出它的实物图并与同伴交流.
主视图 左视图
俯视图
三、课堂小结 由三视图还原成实物图是个难点. 解答相关题目时, 大家要多观察、多思考、多想象, 掌握还原的方法和步
骤. 做到三看(看三视图); 三想(想正面、想侧面、想底面
由三视图还原 成实物图
复习回顾
从正面看到的图形,称为主视图或 1.三视图的概念 : 正视图;从左面看到的图形,称为左视图;从 空间几何体 上面看到的图形,称为俯视图; 的三视图 2.柱、锥、台、球的三视图 3.简单组合体的三视图 绘制三视图时, 要注意: (1)俯视图与主视图上下要长对正; (2)主视图与左视图左右要高平齐;
主视图 左视图 俯视图
(3)俯视图与左视图的宽要相等. 其次, 简单组合体是由哪几个基本几何体组成的, 并注意 它们的组成方式, 特别是它们的交线位置.
不可见的轮廓线要用虚线表示.
由三视图还原实物 图时,要根据三视图判 断实物是由什么几何体 组成的。
以下图形的视图,可能是哪种立 体图形的视图?
与侧(面)所对应的平面几何图形的形状); 再一画(实物的 直观图).
2019高中数学 考点08 由三视图还原实物图庖丁解题 新人教A版必修2

考点08 由三视图还原实物图1.由空间几何体的三视图还原直观图时,遵循的原则:长对正 高平齐,宽相等的基本原则,特别注意几何体中与投影面垂直或平行的线及面的关系. 2.根据三视图还原成实物图应注意:(1)由三视图还原成实物图是由实物图画三视图的逆过程,在该过程中注意理解实物图画三视图的原理,并联想柱、锥、台、球体的三视图.(2)由三视图还原成实物图时,一般以俯视图为基础再结合正(主)视图和侧(左)视图. (3)根据三视图还原实物图:需要综合正(主)视图、侧(左)视图、俯视图的特征,确定分界线,找出组成几何体的简单几何体,再将组合还原,其中确定分界线是正确还原的关键.【例】如图是正四棱锥PABCD 的三视图,其中主视图和左视图都是边长为1的正三角形,求这个四棱锥的侧棱长.【解析】由条件知,正四棱锥底面边长AB =1,高PO =23(O 是底面中心),OB =22AB =22,故侧棱长: PB ==42=25.1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是( ) A .正方体 B .长方体 C .三棱锥 D .圆 【答案】C【解析】由三视图的知识,可知答案为C .2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为( )①长方体;②圆锥;③三棱锥;④圆柱. A .④③② B .①③② C .①②③ D .④②③ 【答案】A3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )图1A BC D【答案】D4.在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为( )A BC D【答案】D【解析】本题考查三视图,可用排除法或特例求答.由正视图知A、B不正确,又由俯视图知C不正确,选D.本题的几何体也可看成是一个圆锥的一半与一个三棱锥的组合体.5.如图是一个物体的三视图,则该物体对应的直观图为( )【答案】C【解析】从俯视图看,A,C,D均符合,再结合主视图看,只有C符合.故选C.6.给出下列命题:①如果一个几何体的三个视图是完全相同的,则这个几何体是正方体;②如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③如果一个几何体的三个视图都是矩形,则这个几何体是长方体:④如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.其中正确的是______.(将正确的全都写在横线上)【答案】③1.右图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图②存在四棱柱,其正(主)视图、俯视图如右图③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是( )A.3 B.2C.1 D.0【答案】A【解析】主要考查三视图知识.这一知识点近几年都有考查.①正确,比如一个平放的两底面是等腰直角三角形的直三棱柱.②显然正确,③中可以是一个平放的圆柱.2.正视图为一个三角形的几何体可以是________(写出三种).【答案】三棱锥、三棱柱、圆锥3.如图所示为一个简单组合体的主视图和左视图,则该几何体可能是________(填序号).【答案】①【解析】由主视图中左下角至右上角有一实对角线,可知所给的几何体中只有①符合,又根据左视图知①符合,所以选①.4.根据图中的三视图想象物体原形,并画出物体的实物草图.如何画人物素描中的轮廓画人物素描的基础就是画人物的轮廓.画轮廓要抓住头部基本形状、五官位置、明暗交界线的位置、头与肩的关系.要画准轮廓,就必须整体观察,整体比较,多运用辅助线帮助确定位置.在抓外形时要狠抓特征,要画得像.外形初见端倪,形象呼之欲出.就如公园门口的艺人用剪子剪影,轻而易举地将人物形象显现出来,尽管看不清过细的内部结构,我们照样能够认出他来.有些人不注意这一步,形还非常含糊,便匆匆忙忙去画五官了.这样画出来的画怎么能逼近形象呢!画人物素描就是要先画出人体的直观图.。
几何体的三视图还原

正四棱台
主
左
俯
主视图
左视图
俯视图
主 左 俯 主视图 左视图 俯视图
正六棱柱
主
左
俯
主视图
左视图
俯视图
圆台
主
左
俯
主视图
左视图
俯视图
由三视图想象实物模型
笔筒
下面是组合图形的三视图,请描述物体形状.
由三视图想象实物模型
热水瓶
由三视图还原成实物图
螺丝钉
2 下面所给的三视图表示什么几何体?
左视图
正四棱锥 例:下面的三视图表示的几何ቤተ መጻሕፍቲ ባይዱ是什么?
练习:还原实物图:
三棱柱
三棱柱
练习:还原实物图:
俯视图
左视图
六棱柱
主视图
答案:一个四棱柱和一个球组成的简单组合体。 主视图 左视图 俯视图 例1:
主视图
俯视图
左视图
例2:
答案:一个四棱柱和一个圆柱体组成的简单组合体。
长方体
主
左
俯
主视图
左视图
俯视图
空间几何体的三视图还原
基本几何体的三视图
从上面看
从左面看
从正面看
主视图
左视图
俯视图
正视图——光线从几何体的前面向后面正投影,得到的投影图(从正面看到的图)
左视图——
俯视图——
三视图之间的投影规律
长对正
高平齐
宽相等
三视图能反映物体真实的形状和长、宽、高.
正视图
俯视图
把每个视图分解为基本图形(如三角形、圆等)
结合对应部分的三视图,想象对应的基本几何体
结合虚实线,概括组合体. 如何把组合体的三视图还原成几何体的实形?
由三视图还原立体图形

思考:狗蛋回家,只找到了主视图和俯视图, 仍然可以恢复狗蛋的积木原来的形状吗?如果 不能,那么按照这2个图,对应的立体图形最 少有几个正方体?最多有几个正方体?
主视图
俯视图
最少
最多
方法:从一张视图开始, 从另一张视图研究最少 或最多的情况
由三视图描述几何体(或实物原型), 一般先根据各视图想像从各个方向看到 的几何体形状, 然后综合起来确定几何 体(或实物原型)的形状, 再根据三视图 “长对正、高平齐、宽相等”的关系, 确定轮廓线的位置,以及各个方向的尺 寸.
挑战:
一个直棱柱的主视图和俯视图如图所示.描述这个 直棱柱的形状,并补画它的左视图.
直五棱柱,底面是五边形
(第6题)
探究活动
用6个相同的小方块搭成一 个几何体,它的俯视图如图所示.则 一共有几种不同形状的搭法(你可 以用实物模型动手试一试)?你能 用三视图表示你探究的结果吗?
探究活动
用6个相同的小方块搭成一 个几何体,它的俯视图如图所示.则 一共有几种不同形状的搭法(你可 以用实物模型动手试一试)?你能 用三视图表示你探究的结果吗?
• ⒉由三视图描述几何体(或实物原型),一
般步骤为几何体形状; • ② 定形:综合确定几何体(或实物原型)
的形状; • ③ 定大小位置:根据三个视图“长对正,
高平齐,宽相等”的关系,确定轮廓线的位 置,以及各个方向的尺寸.
狗蛋按照三视图堆好了积木,很有成就感,高高兴 兴地玩去了,等他回来,积木被淘气的小狗弄散了, 你能帮他重新堆起来吗?
主视图 左视图 俯视图
引 言
前面我们讨论了由立体图形(实物) 画出三视图,下面我们讨论由三视图 想象出立体图形(实物).
例1 根据三视图说出立体图形的名称.
由三视图还原直观图第1节

由三视图还原直观图3-1四川省华蓥中学 叶超由于三视图问题是高考数学的重要题型,于是网络上就出现了各种各样的所谓的“神级结论”,这些“神级结论”真有那么神吗?本专题将让你明白,利用那些所谓的“神级结论”是多么的危险!如果让我来命题的话!事实上,三视图问题的顺利求解一般需要将三视图还原成直观图,当然,如果几何体比较简单,可以靠想象来还原,但是,对于稍复杂的几何体,仅靠想象来还原将非常困难,咋办?读罢本文,我们不仅能轻松求解三视图问题,而且还能任意命制此类题目,甚至命制出让所谓的“神级结论”失效的题目,从而成为三视图问题的真正高手!本专题共分三个部分:第1部分:可以解决所有高考题中的三视图问题,但对其中的较难部分不能轻松应对;第2部分:轻松解决所有高考题中的三视图问题,并展示所谓的“神级结论”的失败案例;第3部分:难度高于高考,仅供了解。
关于高考数学的更多问题,请参见我写的一本高考数学书(本文是其中的一篇)。
1、三点说明: ①几何体必在各视图边框所限定的柱体内,几何体的顶点一定在视图中线段的交点处(也即:转角及分叉处),且每一处至少有1个顶点。
示例:如果某几何体的主视图如图甲所示,则:一方面:该几何体必在图乙所示的柱体内。
另一方面:线段AA1上至少有1个顶点,BB1、CC1、DD1同理;平行四边形ABB1A1中,除AA1上与BB1上外,一定没有顶点。
②变换视角:用斜二侧画法画几何体的直观图时,画的是在右侧看到的直观图(如图乙),而三视图中的左视图却是在左侧看到的视图,这是在故意为难我们的学生。
但是,我们没有办法,为便于观察左视图,本文还原 在左侧看到的直观图(如图丙)。
当然,若有必要,你可以在最后改成图乙那样的直观图,或者,如果你的空间想象能力够强,也可以直接画图乙那样的。
丙甲:主视图 乙A B C A1 B1 C1 D1③“长对正,高平齐,宽相等”这句话对还原直观图基本无用(但计算线条长度时可能要用到它)。
由三视图复原几何体小技巧
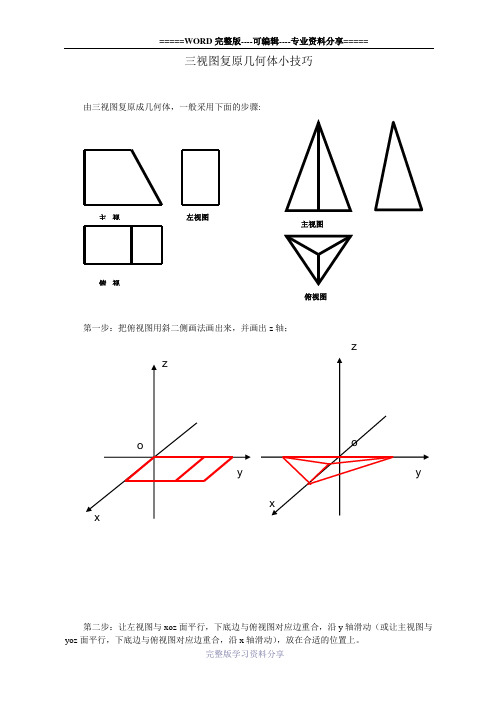
三视图复原几何体小技巧
由三视图复原成几何体,一般采用下面的步骤:
第一步:把俯视图用斜二侧画法画出来,并画出z 轴;
第二步:让左视图与xoz 面平行,下底边与俯视图对应边重合,沿y 轴滑动(或让主视图与yoz 面平行,下底边与俯视图对应边重合,沿x 轴滑动),放在合适的位置上。
俯视图
主视图
主视
左视图
俯
视
z
第三步:让主视图与yoz 面平行,下底边与俯视图对应边重合,沿x 轴滑动,(或让左视图与xoz 面平行,下底边与俯视图对应边重合),沿y 轴滑动放在合适的位置上。
通过上面三个步骤,就可以画出或判断出是什么几何体了。
z
z。
三视图还原成直观图

首先在正方体框架中描出主视图,并将轮廓的边界点平 行延长,如图.
类似地,将俯视图和侧视图也如法炮制.这样就可以找到三个方向 的交叉点.由这些交叉点,不难得到直观图.
例2练习1: 把下图的三视图还原在直观图
例2的练习2
例3:以长方体为模型 (2009辽宁高考理科第15题)某几何体的 三视图如图示,尺寸单位为m,则该几何体的 体积为_______
实例动画
三视图的本质
基本数量关系是长对正,高平齐,宽相等。 图形对应关系如表:
两种对应
三视图 几何体
点
点或线
线
线或面
面
面
两种对应
几何体 三视图
点
点
线
点或线
面
线或面
动画
三视图的本质
1、由直观图作出三视图,可以把多面体放入 长方体,或正方体中,从而可以以长方体,正 方体作为模型来作三视图;这说明由三视图还 原为直观图,也可以把正方体,长方体作为模 型进行还原。
第三步,俯视图有三个顶点,画出它们的原象所在的线段,用绿线表 示,如图(4)
垂
最后一步,三种颜色线的公共点(只有两种颜色线的交 点不行)即为原几何体的顶点,连接各顶点即为原几何 体,如图(5).至此,易知哪条棱是最长棱,求出即 可
此方法更适用于解决三棱锥的问题,画直观 图后需要验证一下是否符合
Y
就是绘制各表面的棱线的投影;
可见棱线画粗实线;
不可见棱线画虚线;
粗实线与虚线重合时,只画粗实线。
2 三视图中虚线产生原因
有实线
有实线
有虚线
无线
两体表面共面时,中间无分界线。
例2:有虚线的情况 三视图如图所示,请原还其直观图
根据三视图还原几何体及相关计算课件(共23张PPT)

29.2.2 根据三视图还原几何体及相关计算
探究
例3 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你 按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
分析:对于某些立体图形,沿着其中一些线 (如棱柱的棱)剪开,可以把立体图形的表面 展开成一个平面图形——展开图. 在实际生产 过程中,三视图和展开图往往结合在一起使用, 解决本题的思路是,先由三视图想象出密封罐 的形状,再进一步画出展开图,然后计算面积.
主视图
左视图
俯视图
29.2.2 根据三视图还原几何体及相关计算
随堂练习
1.如图,是一个几何体的三视图,则这个几何体是( B )
上方是圆锥体
A
B
C
D
下方是长方体
29.2.2 根据三视图还原几何体及相关计算 2. 由若干个相同的小正方体组合而成的一个几何体的三视图如图所示, 则组成这个几何体的小正方体的个数是 ( C )
新课引入
上节课我们学习了如何画一个立体图的三视图,小试一下身手吧~ 下图是两块橡皮组合起来的三视图,请根据三视图描述一下它的形状.
和你想象的一样吗?
29.2.2 根据三视图还原几何体及相关计算
新知学习
思考
我们知道,由几何体可以画出三视图,而上面我们尝试由三视图来还原 几何体,那么具体是怎么做的呢?
29.2.2 根据三视图还原几何体及相关计算
针对训练 1.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面 积为( B )
A. 6
B. 8
C. 12
D. 24
29.2.2 根据三视图还原几何体及相关计算
2. 如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧 面积为______2_π_____cm2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
左视图
俯视图
三棱柱 三棱柱
练习:还原实物图:
主视图
左视图
俯视图
六棱柱
例 1:
主视图
左视图
俯视图
答案:一个四棱柱和 一个球组成的简单组 合体。
例:
主视图
左视图
俯视图
答案:一个四棱柱和 一个圆柱体组成的简 单组合体。
主视图
左视图
俯
左
俯视图
长方体
俯
主视图
左视图
左
俯视图
正四棱台
主视图
左视图
俯
左
俯视图
F
y M 0 B N C E y1
F1
A D x A1 B1
M1 E1
N1 C 1
01
x D1 1
四个步骤:取轴、画轴、平行性、长度.
三、怎样画立体图形的直观图?
例2:用斜二测法画长、宽、高分别是4, 3,2的长方体的直观图. / z D D
/ /
C
/
A
/
B
/
y
/
C
/
A/
B
/
D
A
o
C
B
x
/
D
C
B
A
主视图
左视图
俯视图
圆锥Leabharlann 例:下面的三视图表示的几何体是什么,并画出 直观图?
主视图
左视图
俯视图
长方体
例:下面的三视图表示的几何体是什么?
主视图
左视图
俯视图
球体
例:下面的三视图表示的几何体是什么,并 画出直观图?
主视图
左视图
圆柱 俯视图
练习:还原实物图,并画出直观图:
主视图 主视图 左视图 俯视图
1.把每个视图分解为基本图形(如三角形、圆 等) 2.结合对应部分的三视图,想象对应的基本几 何体 3.结合虚实线,概括组合体.
下列两图分别是两个简单组合体的三视 图,想象它们表示的组合体的结构特征, 并画出其示意图.
主视图
左视图
俯视图
下面所给的三视图表示什么几何体?
下面所给的三视图表示什么几何体?
主
主视图
左视图
俯
左
俯视图
正六棱柱
主视图
左视图
俯
左
俯视图
圆台
由三视图想象实物模型
下面是组合图形的三视图,请描述物体形状.
笔筒
由三视图想象实物模型
热水瓶
由三视图还原成实物图
螺丝钉
2 下面所给的三视图表示什么几何体?
正视图
侧视图
俯视图
由三视图还原成实物图
如何把组合体的三视图还原成几 何体的实形?
四个步骤:画轴、画底面、画侧棱、成图.
例、下面是某一个几何体图形的三视图, 请根据视图说出立体图形的名称,并画出直观 图:
zxxkw
正视图
侧视图
俯视图
四棱柱
例2、下面是某一个几何体图形的三视图, 请根据视图说出立体图形的名称,并画出直观 图:
四棱锥
例:下面的三视图表示的几何体是什么, 并画出直观图?
x
. .
. . o.
②建立∠x’o’y’=45°的坐标系 ③平行于x、y轴的线段在斜二测坐标系中 仍平行于x’、y’轴,但横向长度不变,纵向 长度减半
y
. . . . .
y’ . . . . . o’ x’
. .
. . o.
x
常用的一些空间图形的平面画法
二、平面图形的直观图的画法:
例1:画水平放置的正六边形的直观图.
1.2.3 空间几何体的直观图
一、几何体的直观图:
D1
A1 B1
C1
A1
C1
A1 B1 B1
E1 C1 E
D1
D A
C
C
B
A
B
A
D
B
C
直观图: 表示空间图形的平面图形, 叫做空间图形的直观图.
斜二测画法
思考:如何画一个正方形的直观图?
y . . . . .
①在正方形中建 立适当的平面直 角坐标系;
正视图
侧视图
俯视图
