高等代数多项式月测试题(2010年10月)
数学与应用数学高等代数试卷

数学与应用数学高等代数试卷一、选择题(每题3分,共30分)1. 在多项式f(x)=x^3 - 3x^2 + 2x - 1与g(x)=x^2 - x + 1的带余除法中,f(x)除以g(x)的商式q(x)和余式r(x)分别为()A. q(x)=x - 2,r(x)= - 3x + 1B. q(x)=x - 1,r(x)= - 2xC. q(x)=x,r(x)= - 3x - 1D. q(x)=x + 1,r(x)= - 2x + 12. 设A=(12 34),则| A|=()A. - 2.B. 2.C. - 1.D. 1.3. 向量空间V = { (x,y,z)mid x + y + z = 0,x,y,z∈ R}的维数是()A. 1.B. 2.C. 3.D. 0.4. 设α=(1,2,3),β=(4,5,6),则α·β=()A. 32.B. 30.C. 28.D. 26.5. 若n阶方阵A可逆,则r(A)=()A. n - 1B. nC. 1D. 06. 设A=(100 020 003),则A的特征值为()A. 1,2,3B. - 1,- 2,- 3C. 0,1,2D. 0, - 1, - 27. 二次型f(x,y,z)=x^2 + 2y^2+3z^2 - 2xy + 4yz的矩阵为()A. (1- 10 - 122 023)B. (110 12 - 2 0 - 23)C. (1- 10 - 12 - 2 0 - 23)D. (110 122 023)8. 设W_1={(x,0)mid x∈ R},W_2={(0,y)mid y∈ R},则W_1+W_2=()A. {(x,y)mid x,y∈ R}B. {(x,0)mid x∈ R}C. {(0,y)mid y∈ R}D. {(x,x)mid x∈ R}9. 若线性方程组Ax = b(A为系数矩阵)有解,则()A. r(A)=r(A,b)B. r(A)>r(A,b)C. r(A)D. r(A)与r(A,b)无关系。
多项式练习题带答案

多项式练习题带答案一、选择题1. 下列哪个表达式不是多项式?A. \( x^2 + 3x + 2 \)B. \( 5x - 3 \)C. \( \frac{x}{2} \)D. \( 2x^3 - 4x^2 + 7 \)答案:C2. 多项式 \( P(x) = ax^3 + bx^2 + cx + d \) 中,如果 \( a = 1 \),\( b = -1 \),\( c = 0 \),\( d = 2 \),则 \( P(x) \) 可以表示为:A. \( x^3 - x^2 + 2 \)B. \( x^3 - x^2 - 2 \)C. \( x^3 + x^2 + 2 \)D. \( x^3 - x^2 + 2x \)答案:A3. 如果 \( f(x) = x^3 - 6x^2 + 11x - 6 \),那么 \( f(1) \) 的值是:A. 0B. 1C. 2D. 3答案:B二、填空题1. 多项式 \( 2x^3 - 5x^2 + 3x - 4 \) 的次数是 ______ 。
答案:32. 如果 \( g(x) = x^4 - 3x^3 + 5x^2 - 2x + 1 \),那么 \( g(0) \) 的值是 ______ 。
答案:13. 多项式 \( h(x) = 4x^2 - 7x + 2 \) 与 \( x - 3 \) 的乘积是\( 4x^3 - \) ______ 。
答案:7x^2 + 10x - 6三、解答题1. 给定多项式 \( f(x) = 3x^3 - 2x^2 + 5x - 1 \),求 \( f(-1) \) 的值。
解:将 \( x = -1 \) 代入 \( f(x) \) 中,得到\( f(-1) = 3(-1)^3 - 2(-1)^2 + 5(-1) - 1 = -3 - 2 - 5 - 1 = -11 \)。
2. 已知 \( p(x) = 2x^3 + ax^2 + bx + c \),其中 \( p(1) = 5 \),\( p(-1) = -1 \),求 \( a \),\( b \),\( c \) 的值。
高等代数多项式课外习题

.1 .-1 .±2 .0
6、设 是整系数多项式,当t=()时,f(x)在有理数域上可约。
.1 .0 .-1 .3或-5
7、设 是 的一个因式,则 ( )。
.1 .2 .3 .4
8、令有理数域上的多项式 ,下面只有哪个数可能是它设用x-1除f(x)余数为5,用x+1除f(x)余数为7,则用x2-1除f(x)余数是.
10、已知 为 的一个根,那么 的其余根是.
11、设 是两个不相等的常数,则多项式 除以 所得的余式为____
12、设 。 ,若 ,则 , 。
13、求方程 的所有有理根.
14、求多项式 的最大公因式 .
15、设f(x)=3x5-12x3-104x2-587x-13,求f(5)和f(-5).
16、求g(x)用去除所得的商q(x)及余式r(x):f(x)=3x5+10x4-15x3-9x2-8x-7,g(x)=x+1/3.
19、设f1(x)=af(x)+bg(x),g1(x)=cf(x)+dg(x),且ad-bc≠0,证明:(f(x),g(x))=(f1(x),g1(x)).
20、证明 是两个不相等的常数,则多项式 除以 所得的余式为
4、关于多项式的重因式,以下结论正确的是( )
.若p(x)是f’(x)的k重因式,则p(x)是f(x)的k+1重因式
.若p(x)是f(x)的k重因式,则p(x)是f(x),f’(x)的公因式
.若p(x)是f’(x)的因式,则p(x)是f(x)的重因式
.若p(x)是f(x)的重因式,则p(x)是 的单因式
1、在 里能整除任意多项式的多项式是()。
.零多项式 .零次多项式 .本原多项式 .不可约多项式
(完整版)高等代数多项式习题解答
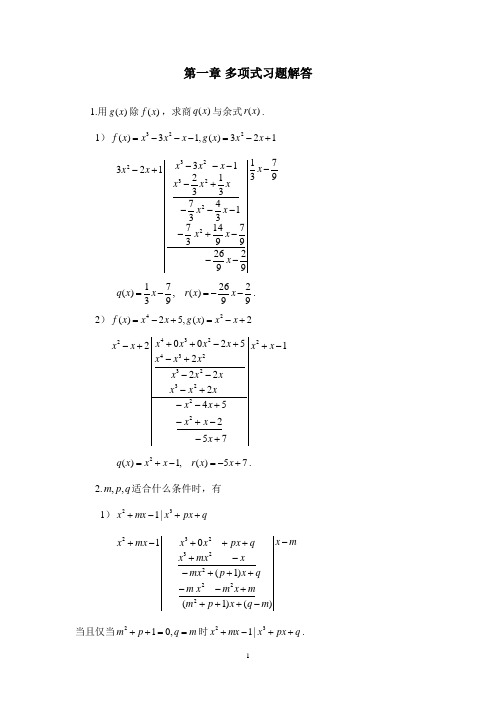
第一章 多项式习题解答1.用)(x g 除)(x f ,求商)(x q 与余式)(x r .1)123)(,13)(223+-=---=x x x g x x x x f9731929269791437134373132131232223232----+----+----+-x x x x x x x x x x x x x x 92926)(,9731)(--=-=x x r x x q . 2)2)(,52)(24+-=+-=x x x g x x x f17525422225200222223232342342-++--+-+--+---+-+-+++-x x x x x x x xx x x x x x x x x x x x x x75)(,1)(2+-=-+=x x r x x x q .2.q p m ,,适合什么条件时,有1)q px x mx x ++-+32|1m x m q x p m mx m x m qx p mx x mx x q px x x mx x --++++--+++--++++-+)()1()1(01222223232 当且仅当m q p m ==++,012时q px x mx x ++-+32|1.本题也可用待定系数法求解.当q px x mx x ++-+32|1时,用12-+mx x 去除q px x ++3,余式为零,比较首项系数及常数项可得其商为q x -.于是有q x mq x q m x mx x q x q px x ++--+=-+-=++)1()()1)((2323.因此有m q p m ==++,012.2)q px x mx x ++++242|1由带余除法可得)1()2()1)(1(2222224m p q x m p m m p mx x mx x q px x --++--++-+-++=++ 当且仅当0)1()2()(22=--++--=m p q x m p m x r 时q px x mx x ++++242|1.即⎩⎨⎧=--+=--010)2(22m p q m p m ,即⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 本题也可用待定系数法求解.当q px x mx x ++++242|1时,用12++mx x 去除q px x ++24,余式为零,比较首项系数及常数项可得其商可设为q ax x ++2.于是有)1)((2224++++=++mx x q ax x q px x.)()1()(234q x mq a x q ma x a m x ++++++++=比较系数可得.0,1,0=+=++=+mq a p q ma a m 消去a 可得⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 3.求)(x g 除)(x f 的商)(x q 与余式)(x r .1);3)(,852)(35+=--=x x g x x x x f解:运用综合除法可得327109391362327117083918605023---------商为109391362)(234+-+-=x x x x x q ,余式为.327)(-=x r2)i x x g x x x x f 21)(,)(23+-=--=.解:运用综合除法得:ii ii i i i 892521892421011121+----+-------商为)25(22i ix x +--,余式为i 89+-. 4.把)(x f 表成0x x -的方幂和,即表示成 +-+-+202010)()(x x c x x c c 的形式.1)1,)(05==x x x f ;2);2,32)(024-=+-=x x x x f3).1,73)1(2)(0234-=++-+-+=x i x x i ix x x f分析:假设)(x f 为n 次多项式,令])()()[()()()()(10021000202010--++-+-+=-++-+-+=n n nn x x c x x c c x x c x x c x x c x x c c x f0c 即为0x x -除)(x f 所得的余式,商为10021)()()(--++-+=n n x x c x x c c x q .类似可得1c 为0x x -除商)(x q 所得的余式,依次继续即可求得展开式的各项系数.解:1)解法一:应用综合除法得.5110141110416311563143211143211111111111100000115)(x x f =1)1(5)1(10)1(10)1(5)1(2345+-+-+-+-+-=x x x x x .解法二:把x 表示成1)1(+-x ,然后用二项式展开1)1(5)1(10)1(10)1(5)1(]1)1[(234555+-+-+-+-+-=+-=x x x x x x x2)仿上可得812226122412210412112082422128442302012-----------------432)2()2(8)2(22)2(2411)(+++-+++-=x x x x x f . 3)因为i iii i i i i i i i i i ii ii i i 2111510157104141173121-----------+-------+---- .)()(2))(1()(5)57(73)1(2)(432234i x i x i i x i i x i ix x i ix x x f +++-++-+-+=++-+-+=5.求)(x f 与)(x g 的最大公因式1)1)(,143)(23234--+=---+=x x x x g x x x x x f解法一:利用因式分解),13)(1(143)(3234--+=---+=x x x x x x x x f).1()1(1)(223-+=--+=x x x x x x g因此最大公因式为1+x .解法二:运用辗转相除法得)(3438)(01122132)(1434343)(41432112321212314121)(3122123423422223232x q x x q x x x x x x x x r x x x x x x x x x x r x x x x x x x x x x x x q =+=---------=--+---+--=------++--++-= 因此最大公因式为1+x .2)13)(,14)(2334+-=+-=x x x g x x x f .解:运用辗转相除法得(注意缺项系数补零)2564411627)(125627)(2565391649216491633323)(10310031004911916)(920910310132310323110391031)(13221232323423422223232--=--=+-+-+-+--=-++-+-+-++-+++--=+--++--+++-+-=x x q x x r x x x x x x x r x x x x x x x x x x x x x x x x r x x x x x x x x x x x x q .1))(),((=x g x f3).124624)(,110)(23424+++-=+-=x x x x x g x x x f)()()22(24)()(123x r x f x x x x f x g +=---=,),()22)((241)122()22)(22()(21223x r x x r x x x x x x x f ++-=---+--= ,)()122(22)(24122231x x r x x x x x x x r -=--=--=- 因此.122))(),((2--=x x x g x f6.求)(),(x v x u 使:))(),(()()()()(x g x f x g x v x f x u =+1);22)(,242)(234234---+=---+=x x x x x g x x x x x f解:运用辗转相除法得:)()(1022)(222422)(222221)(3133123423422323242342x q x x q x x xx x r x x x x x x x x x x r xx x x x x x x x x x x x q ==--=---+---+-=--+----++= 因此2)())(),((22-==x x r x g x f .且有 )()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..2)()(1)(,1)()(212+=+=--=-=x x q x q x v x x q x u2);452)(,951624)(23234+--=++--=x x x x g x x x x x f解:运用辗转相除法得:)(96)(20999966936)(810249516241)(32422324523131)(3122123423422223232x q x x q x x x xx x x x r xx x x x x x x x x r x x x x x x x x x x x x q =+=+-+-+-+--=+--++--+-=+--+---++--+-= 因此1)())(),((2-=-=x x r x g x f .且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..13232)3131(21)()(1)(,3131)()(2212--=+---=--=+-==x x x x x q x q x v x x q x u 3).1)(,144)(2234--=++--=x x x g x x x x x f解:运用辗转相除法得:)(32)(3331431441)(21211)(121222342342222x q x x x r x x x x x x x x x x x x r x x xx x x x x q =--=++-++---++--=-----+= 因此.1)())(),((2==x r x g x f 且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..23)1)(3(1)()(1)(,1)()(232212--+=+-+=+=--=-=x x x x x x q x q x v x x q x u7.设u tx x x g u x x t x x f ++=++++=323)(,22)1()(的最大公因式是一个二次多项式,求u t ,的值.解:运用带余除法有),()()2()1(1)(22)1()(12323x r x g u x t x t u tx x u x x t x x f +=+--++⋅++=++++= 由题意可得,)(1x r 即为)(),(x g x f 的最大公因式.因此有01≠+t .进一步),(])1(211)[()(221x r t t x t x r x g ++-++= ])1(21[)1()2()1()1()(22222t t u x t t t u t t x r +--++-++-+=. 要使)(1x r 为)(),(x g x f 的最大公因式的充要条件是.0)(2=x r 即⎩⎨⎧=--+=-++-+,0)]2()1[(,0)2()1()1(222t t u t t u t t 解得⎪⎩⎪⎨⎧--=+-=⎪⎩⎪⎨⎧+-=--=⎪⎩⎪⎨⎧±==⎩⎨⎧-==.2111,117;2111,117;231,0;4,0i t i u i t i u i t u t u 8.证明:如果),(|)(),(|)(x g x d x f x d 且)(x d 为)(x f 与)(x g 的一个组合,那么)(x d 是)(x f 与)(x g 的一个最大公因式.证明:由)(|)(),(|)(x g x d x f x d 可知)(x d 是)(x f 与)(x g 的一个公因式.下证)(x f 与)(x g 的任意一个公因式是)(x d 的因式.由)(x d 为)(x f 与)(x g 的一个组合可知,存在多项式)(),(x v x u ,使得)()()()()(x g x v x f x u x d +=.设)(x ϕ是)(x f 与)(x g 的任意一个公因式,则)(|)(),(|)(x g x x f x ϕϕ.故)()()()(|)(x g x v x f x u x +ϕ即).(|)(x d x ϕ因此)(x d 是)(x f 与)(x g 的一个最大公因式.9.证明:)()(())(),(())()(),()((x h x h x g x f x h x g x h x f =的首项系数为1). 证明:存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.所以有)()()()()()()())(),((x h x g x v x h x f x u x h x g x f +=.即)())(),((x h x g x f 是 )()(x h x f 与)()(x h x g 的一个组合.显然有)(|))(),((),(|))(),((x g x g x f x f x g x f .从而)()(|)())(),((),()(|)())(),((x h x g x h x g x f x h x f x h x g x f .由第8题结果)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个最大公因式.又)(x h 是首项系数为1的,因此).())(),(())()(),()((x h x g x f x h x g x h x f =10.如果)(x f ,)(x g 不全为零,证明1))(),(()(,)(),(()((=x g x f x g x g x f x f . 证明:由)(x f ,)(x g 不全为零可得其最大公因式不为零多项式,即.0))(),((≠x g x f 又存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.于是))(),(()()())(),(()()(1x g x f x g x v x g x f x f x u +=. 因此1))(),(()(,)(),(()((=x g x f x g x g x f x f . 11.如果)(x f ,)(x g 不全为零,且))(),(()()()()(x g x f x g x v x f x u =+,那么1))(),((=x v x u .证明:由)(x f ,)(x g 不全为零可得.0))(),((≠x g x f 由))(),(()()()()(x g x f x g x v x f x u =+有.1))(),(()()())(),(()()(=+x g x f x g x v x g x f x f x u 于是1))(),((=x v x u .12.证明:如果,1))(),((,1))(),((==x h x f x g x f 那么.1))()(),((=x h x g x f 证法一、由条件1))(),((,1))(),((==x h x f x g x f 可得存在多项式)(),(11x v x u ; )(),(22x v x u 使得1)()()()(11=+x g x v x f x u ,1)()()()(22=+x h x v x f x u .两式相乘得1)()()()()()]()()()()()()()()([21211221=+++x h x g x v x v x f x h x v x u x g x v x u x f x u x u . 因此有.1))()(),((=x h x g x f证法二、反证法证明.显然.0))()(),((≠x h x g x f 若,1))()(),((≠x h x g x f 则存在不可约多项式)(x p ,使得)(x p 为)(x f 与)()(x h x g 的公因式.因此有)(|)(x f x p 且)()(|)(x h x g x p .由)(x p 的不可约性有)(|)(x g x p 或)(|)(x h x p .若)(|)(x g x p ,则)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.若)(|)(x h x p ,则)(x p 为)(x f 与)(x h 的一个公因式,与1))(),((=x h x f 相矛盾.因此1))()(),((≠x h x g x f 不成立,即有.1))()(),((=x h x g x f13.设)(),(),(),(,),(),(2121x g x g x g x f x f x f n m 都是多项式,而且).,,2,1;,,2,1(,1))(),((n j m i x g x f j i ===求证:1))()()(),()()((2121=x g x g x g x f x f x f n m .证明:由),,2,1(1))(),((1n j x g x f j ==,反复利用第12题结果可得1))()()(),((211=x g x g x g x f n .类似可得.,,2,1))()()(),((21m i x g x g x g x f n i ==再反复利用12题结果可得1))()()(),()()((2121=x g x g x g x f x f x f n m .14.证明:如果,1))(),((=x g x f 那么.1))()(),()((=+x g x f x g x f 证明:方法一.由,1))(),((=x g x f 存在多项式)(),(x v x u 使得1)()()()(=+x g x v x f x u .从而有,1)())()(())()()((,1))()()(()())()((111111=+-++=++-x g x v x u x g x f x u x g x f x v x f x v x u 因此有.1))()(),((,1))()(),((=+=+x g x f x g x g x f x f 由12题结果结论成立.方法二:用反证法.若.1))()(),()((≠+x g x f x g x f 则存在不可约多项式)(x p ,使得)(x p 为)()(x g x f 与)()(x g x f +的公因式.即)()(|)(x g x f x p 且)()(|)(x g x f x p +.由)(x p 的不可约性及)()(|)(x g x f x p ,有)(|)(x f x p 或)(|)(x g x p .若)(|)(x f x p ,又)()(|)(x g x f x p +,因此有)]())()([(|)(x f x g x f x p -+,即)(|)(x g x p ,也即)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.类似可得当)(|)(x g x p 时也与已知1))(),((=x g x f 矛盾.所以.1))()(),()((=+x g x f x g x f15.求下列多项式的公共根:.12)(;122)(23423++++=+++=x x x x x g x x x x f解法一:利用因式分解可得);1)(1(122)(223+++=+++=x x x x x x x f ).1)(1(12)(22234+++=++++=x x x x x x x x g因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 解法二:运用辗转相除法求出)(x f 与)(x g 的最大公因式,最大公因式的根即为所求的公共根.),1(2)1)(()(2++--=x x x x f x g ).1)(1()(2+++=x x x x f因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 16.判别下列多项式有无重因式: 1);84275)(2345-+-+-=x x x x x x f 解:,4421205)('234+-+-=x x x x x f运用辗转相除法可得.)2(44))('),((22-=+-=x x x x f x f 因此2-x 为)(x f 的三重因式.解法二:试根可得2为)(x f 的根)1()2()2()2()43)(2()(23232234++-=----=++--=x x x x x x x x x x x x f .因此2-x 为)(x f 的三重因式. 2).344)(24--+=x x x x f解:).12(4484)('33-+=-+=x x x x x f 1))('),((=x f x f .故)(x f 无重因式. 17.求t 值使13)(23-+-=tx x x x f 有重根.解法一:要使)(x f 有重根,则1))('),((≠x f x f ..63)('2t x x x f +-=),12(33)(')3131(13)(23+-+-=-+-=x t x f x tx x x x f .415)41523)(12(63)('2++-+=+-=t x x t x x x f当,033=-t 即3=t 时),(|)(',)1(3363)('22x f x f x x x x f -=+-=2)1())('),((-=x x f x f ,因此1为)(x f 的三重根. 当0415=+t ,即415-=t 时,21))('),((+=x x f x f ,21-为)(x f 的二重根.解法二:设b a x ab a x b a x b x a x x f 22232)2()2()()()(-+++-=--=. 因此有⎪⎩⎪⎨⎧==+=+.1,2,3222b a t ab a b a 由第一个方程有a b 26-=,代人第三个方程有,0132,1)23(232=+-=-a a a a 即0)12()1(2=+-a a .因此有⎪⎩⎪⎨⎧===,3,1,1t b a 或⎪⎪⎩⎪⎪⎨⎧-==-=.415,4,21t b a即当3=t 时1为)(x f 的三重根;当415-=t 时,21-为)(x f 的二重根.18.求多项式q px x ++3有重根的条件.解:令q px x x f ++=3)(.显然当0==q p 时,0为)(x f 的三重根.当0≠p 时, p x x f +=23)(',q x px xf q px x x f ++=++=32)('31)(3,)427()42729)(32()('222p q p p q x p q x p x f ++-+=. 要使)(x f 有重根,则1))('),((≠x f x f .即,042722=+pq p 即.027423=+q p 显然 0==q p 也满足.027423=+q p 因此)(x f 有重根的条件是.027423=+q p19.如果,1|)1(242++-Bx Ax x 求.,B A解法一:利用整除判定方法,1|)1(242++-Bx Ax x 的充要条件是用2)1(-x 除124++Bx Ax ,余式为零.)31()42()32()1(12224B A x A B A B Ax Ax x Bx Ax --++++++-=++.因此有0)31()42(=--++B A x A B ,即⎩⎨⎧-==⎩⎨⎧=--=+.2,1.031,042B A B A A B 解法二:要使1|)1(242++-Bx Ax x 成立,则1至少是124++Bx Ax 的二重根.因此1既是124++Bx Ax 的根,也是其导数的根.而Bx Ax Bx Ax 24)'1(324+=++.故有⎩⎨⎧-==⎩⎨⎧=+=++.2,1.024,01B A B A B A 解法三:利用待定系数法.令Dx D C x D C A x A C Ax D Cx Ax x Bx Ax +-++-+-+=++-=++)2()2()2()()1(12342224因此有⎪⎪⎩⎪⎪⎨⎧==-=+-=-.1,02,2,02D D C B D C A A C 解得⎪⎪⎩⎪⎪⎨⎧==-==.1,2,2,1D C B A 20.证明:!!212n x x x n++++ 不能有重根.证明:令,!!21)(2n x x x x f n++++= 则,)!1(!21)('12-++++=-n x x x x f n因此有,!)(')(n x x f x f n +=从而有)!),('())('),((n x x f x f x f n =.!n x n因式只有)0(≠c c 及)1,0(n k c cx k ≤≤≠.而)1,0(n k c cx k ≤≤≠显然不是)('x f 的因式.因此有1)!),('())('),((==n x x f x f x f n.所以)(x f 没有重根.21.如果a 是)('''x f 的一个k 重根,证明a 是)()()](')('[2)(a f x f a f x f ax x g +-+-=的一个3+k 重根. 证明:)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=).('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=显然有0)(")(')(===a g a g a g .由a 是)('''x f 的一个k 重根可得a 是)(''x g 的一个1+k 重根,设a 是)(x g 的s 重根,则3,12+=+=-k s k s .本题常见错误证法.错误证法一:由a 是)('''x f 的一个k 重根就得出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根,于是)(2)()()()](')('[2)(3x h a x a f x f a f x f a x x g k +-=+-+-=从而a 是)(x g 的3+k 重根.事实上,由a 是)('''x f 的一个k 重根推不出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根. 如3)()()()(23+-+-+-=+a x a x a x x f k ,则1)(2))(3()('2+-+-+=+a x a x k x f k ,2))(2)(3()(''1+-++=+k a x k k x f .a 既不是)(x f 的根,也不是)('x f 与)(''x f 的根.错误证法二:由)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=)('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=得出a 是)(''x g 的1+k 重根,直接得出a 是)(x g 的3+k 重根,缺了a 是)(x g 与)('x g 的根验证.22.证明:0x 是)(x f 的k 重根的充分必要条件是,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k证明:必要性.设0x 是)(x f 的k 重根,从而0x x -是)(x f 的k 重因式,从而是)('x f 的1-k 重因式,是)(''x f 的2-k 重因式,...,是)()1(x f k -的单因式,而不是)()(x f k 的因式.因此0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.故有,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k充分性.由,0)()(')(0)1(00====-x f x f x f k 而0)(0)(≠x f k 可知0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.因此0x 是)()1(x f k -的单根,是)()2(x f k -二重根,依此类推,是)(x f 的k 重根.23.举例说明断语“如果α是)('x f 的m 重根,那么α是)(x f 的1+m 重根”是不对的.解:例如2)()(1+-=+m x x f α,m x m x f ))(1()('α-+=.α是)('x f 的m 重根,但α不是)(x f 的根.24.证明:如果),(|)1(n x f x -那么)(|)1(n n x f x -.证明:由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 因此有),()1()(x h x x f -=从而有).()1()(n n n x h x x f -=即)(|)1(n n x f x -.证法二:要证)(|)1(n n x f x -,只要证1-n x 在复数域上的各个根都是)(n x f 的根.1-n x 的根为.1,,2,1,0,2sin 2cos-=+=n k nk i n k x k ππ由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 从而0)1()(==f x f nk .即,2sin 2cos nk i n k x k ππ+=1,,2,1,0-=n k 都是)(n x f 的根.因此有)(|)1(n n x f x -.25.证明:如果)()(|)1(32312x xf x f x x +++,那么).(|)1(),(|)1(21x f x x f x --证明:要证)(|)1(),(|)1(21x f x x f x --成立,只要证1是)(1x f 和)(2x f 的根.12++x x 的两个根为231,23121ii --=+-=εε.由)()(|)1(32312x xf x f x x +++可得)()1()()(23231x g x x x xf x f ++=+.于是,0)()1()()(,0)()1()()(2223222321112312131121=++=+=++=+εεεεεεεεεεεεg f f g f f即0)1(231)1(,0)1(231)1(2121=+-=--f if f i f .故有.0)1()1(21==f f 所以 )(|)1(),(|)1(21x f x x f x --.26.求多项式1-n x 在复数范围内和在实数范围内的因式分解. 解:1-n x 的根为.1,,2,1,0,2sin 2cos -=+=n k nk i n k k ππε故在复数范围内的分解式为)())()(1(112-----=-n n x x x x x εεε .在实数范围内,因k n k -=εε,)0(n k <<.当n 为奇数时,1-n x 的根中一个为实根,其余为虚根,其分解式为]1)([]1)(][1)()[1(12121222212++-++-++--=-+---x x x x x x x x n n n n nεεεεεε .当n 为偶数时,1-n x 的根中二个为实根,即,1±其余为虚根,其分解式为].1)([]1)(][1)()[1)(1(11212222212++-++-++-+-=-+---x x x x x x x x x n n n n nεεεεεε27.求下列多项式的有理根. 1);1415623-+-x x x解:多项式可能的有理根为.14,7,2,1±±±±由系数取值可知,x 取负数时,多项式的值均为负的,故该多项式没有负根.检验得2为其根,进一步运用综合除法可得074114821415612-----即)74)(2(14156223+--=-+-x x x x x x ,显然742+-x x 没有有理根.因此1415623-+-x x x 仅有一个有理根2,且为单根.2);157424---x x x解:多项式可能的有理根为.41,21,1±±±444222026242113121570421------------因此有)1()12()444()21(1574222224--+=--+=---x x x x x x x x x ,显然12--x x 没有有理根.因此21-为157424---x x x 的二重根.3).3111462345----+x x x x x解:多项式可能的有理根为.3,1±±检验得1-为其根,进一步运用综合除法可得1213630351133511038601138601311146111--------------故)3()1()12)(3()1(3111464222345-+=++-+=----+x x x x x x x x x x x .即1-为其四重跟,3为单根.28.下列多项式在有理数域上是否可约? 1);12+x解:显然12+x 无有理根,又为二次的,故在有理数域上不可约. 2);2128234++-x x x解:取素数2=p ,满足艾森斯坦判别法的条件,因此在有理数域上不可约. 3);136++x x 解:令,1+=y x).(3918211561)1()1(1)(234563636y g y y y y y y y y x x x f =++++++=++++=++=取素数,3=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.4)p px x p ,1++为奇素数;解:令1-=y x ,由p 为奇数可得1)1()1(1)(+-+-=++=y p y px x x f p p).()(1222211y g p y p C y C y C yC y p p p p p p p p p =-++--+-=---- 由组合数定义)11(-≤≤p k C kp 均为整数,且12)1()1()1(⋅-+--= k k k p p p C k p,分子中有因子p ,分母个各数均小于p ,又p 为素数,因此约分时p 不会被约去,因此有kpC p |,取素数为p ,)(y g 满足艾森斯坦判别式条件,因此)(y g 在有理数域上不可约,从而)(x f 在有理数域上不可约. 5)k kx x ,144++为整数. 解:令,1+=y x 则有).(2)1(4641)1(4)1(1423444y g y k y y y y k y kx x =+++++=++++=++取素数,2=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.。
(完整word版)高等代数复习题精选.doc

(完整word版)高等代数复习题精选.doc第一章多项式自测题一、填空题1. 设 g (x) f (x) ,则 f (x)与g( x)的一个最大公因式为.2. f ( x) a n x n a n 1x n 1 a1x a0 P[ x] ,若 x | f (x) ,则 a0 ; 若x 1是 f ( x) 的根,则a0 a1 a2 a n .3.若( f (x), f ( x)) x 1 ,则是 f (x) 的重根 .4. x4 4 在有理数域,实数域,复数域上的标准分解式为, , .二、选择题 (以下所涉及的多项式 ,都是数域 P 上的多项式 )1.设( x) | f ( x), ( x) | g( x),且 ( x) 0, g( x)与 f ( x) 不全为0,则下列命题为假的是 ( ).A. ( x) | (u(x) f ( x) v(x)g( x))B. deg( ( x)) min{deg f ( x),deg( g( x))}( deg 意思为次数)C.若存在u(x), v( x) ,使u(x) f ( x) v( x)g ( x) ( x), 则 ( f ( x), g(x)) ( x)D.若x a | (x), 则 f ( a) g (a) 02.若( f (x), g( x)) 1 ,则以下命题为假的是( ).A. ( f2( x), g3(x)) 1B. ( f (x), f ( x) g( x)) 1C. g( x) | f ( x)h( x)必有g( x) | h( x)D. 以上都不对3.下列命题为假的是 ( ).A.在有理数域上存在任意次不可约多项式B.在实数域上 3 次多项式一定可约C.在复数域上次数大于 0 的多项式都可约D.在实数域上不可约的多项式在复数域上没有重根4.下列命题为真的是 ( ).A.若p2( x) f (x) ,则p( x)是f (x)二重因式B.若p(x)是f ( x), f ( x), f (x) 的公因式,则 p( x) 的根是 f ( x) 的三重根C. f ( x)有重根 f (x), f ( x) 有一次因式D.若f (x)有重根 ,则f ( x)有重因式 ,反之亦然三、判断题1. 设 f ( x), g ( x), h( x) P[ x] , 若 g( x) 不能整除 h(x) ,则 g( x) 不整除( f ( x ) h (x )( ) 2.零多项式能被任意多项式所整除 ,也能整除任意多项式 . () 3. 若 f ( x) g (x)q( x)r ( x), 则 ( f ( x), g( x))(g (x), r ( x)).()4.如果 p( x) 是数域 P 上的不可约多项式 ,那么对于任意的 c P, 且c 0, cp (x)也是 P 上的不可约多项式 .( )5.若一个整系数多项式在有理数域上可约 , 则它一定能分解两个次数较低的整系数多项式之积 .第二章行列式自测题一、填空题1.六级行列式 a ij 6中的项a13a 32a 46a 51a25的符号为.2.设aij nd ,则 ka ij n.a 2 0 x3.已知行列式 0y 2中元素 a 与 b 的代数余子式分别为 -6 和 8 则0 0 2 1b0 0 3x y.x 1 x 2 ax 3 1如果方程组x 1 ax 2 x 3 a 有唯一的解 ,那么 a 满足的条件是.4.ax 1x 2 x 3 a 2a 11a 12 a 13a21a 31 a 11 5.设 a 2123 d ,则 a 22a 32 a12 .a31a 32a33a23a33a13二、选择题a 1 a 2 a 3a 1 2a 1b 1c 11.设 b 1 b 2 b 3 3,则 a 22a 1 b 2 c 2 ( ).c 1 c 2 c 3a 32a 3 b 3 c 3A.3B.-3C.6a b c行列式de f 中,元素 f 的代数余子式为 ( ).2.g h kA.d e B.d e a b a b g hg hC. -hD.hg g3a 1 6b 1 3c 1 a 1 b 1 c 1 3. a 22b 2 c 22, 则 a 2 b 2 c 2 ( ).a 33b 3 c 3a 3b 3c 3A.2B.2C. 113324.下列等式成立的是 ().A.a1c 1 a 2 c 2 a 1 a 2 c 1 c 2b 1 d 1 b 2 d 2 b 1 b 2 d 1 d 2 B.aijn naij nnC. a ij b ijn na ij n nb ij n na 11 a 12 a 13 a 21a22a23D.a 21a 23a 312a11a322a 12 a 332a13a 31 a 32 a 33a 11a 12a 135.下列命题为真的是 ( ).A.将行列式对换两列后,再将其中一列的倍数加到另一行上,行列式的值不变B. 若aij n 中 a ij 的代数余子式为 A ij (i , j 1,2,3, , n) 则na ij n n a i 1A k1 a i 2 A k 2a in A kn (1 k n)C.行列式为 0 的充分必要条件是其两列对应成比例D.系数行列式不为 0 的线性方程组的有且仅有一解三、判断题1、奇数次对换改变排列的奇偶性。
华师大2010高等代数答案pdf版

0 Er ... A2 0
0 1 Q An r
,
记
P
1
0 Er C1 , A1 0
0 1 Er Q C nr , An r 0
0 C i (2≤i≤n-r-1) Ai
0
. 0 0 . . . . 0 0 . . . . . . i 位为 0,其余为 1。. . 0 0 .,对角线上 . . 0 1 . . . . . . . . 0 0 0
∴
Er 0
A P
1
Er 0
0 Er A1 0
所以原结论成立。
0 5.解:①c≠0 时, J n ( c ) cE N ,其中 N 1 0 1 ... 1 0
利用 ( cE N )[( cE ) n 1 ( cE ) n 2 N ... N n 1 ] c n E ,可以证得:
2
1 1 X AX
1 ... 1
n 1
(注: 对于-1 的特征矩阵, 秩为 1, 所以利用第一个方程写出特征向量; 对于 n-1, 容易证明特征矩阵秩为 n-1, 因为其左下角有 n-1 级子式不为 0, 对于特征向量,
只要让最后一个未知元为 1,然后行变换后解方程组即可) 9.解: (注释:此类题可能答案只能是无数个或 0 个) 只要找到一个矩阵, 行列式=1 即可说明。 关键看给出的数字, 9 和 7 是互素的。
f Y '( E )Y 2 B P Y c
2k
4
2 n , n 为有理数 n k 且 2 n 4 为有理数
2010年武汉大学高等代数解答

B2
)− 1
= −1 =0 =1 =3
证明: 对方程组的增广矩阵进行初等行变换: 1 1 1 1 −1 1 1 1 1 −1 1 −1 4 −3 ¯ = 3 2 4 −1 0 → 0 A 5 3 7 −3 1 0 1 − a 5 − a b − a 3 + a . a 1 5 b 3 0 0 0 0 0 (1)设(I)的三个线性无关的解为α1 , α2 , α3 ,令 β1 = α3 − α1 , β2 = α3 − α2 , 则易知β1 , β2 线性无关,且是(I)的导出组Ax = 0的解,从而其基础解系中向量的个数大于大 于2,即 4 − rank (A) ≥ 2, 又由上面的初等变换的结果可知 rank (A) ≥ 2. 从而rank (A) = 2. (2)由rank (A) = 2知 −1 4 1 = = 1−a 5−a b−a
二.(16分)设A, B 是n(n ≥ 2)阶矩阵,A∗ , B ∗ 分别是A, B 的伴随矩阵,已知B 是交换A的 第一行与第二行得到的矩阵.对于下述四个选项,若正确则给予证明,若不正确,请给出反 例. (A)交换A∗ 的第一列与第二列得到B ∗ . (B)交换A∗ 的第一行与第二行得到B ∗ . ◇※☆■◇◇※☆■◇
武汉大学2010年硕士学位研究生(学术型)入学考试 线性代数试题参考解答
2
试题
1 1 1 1 2 3 一.(15分)已知矩阵A = 0 2 0 , B = 2 3 1 ,试求矩阵X,使得AT X − 3X = B. 1 0 3 3 1 2
二.(16分)设A, B 是n(n ≥ 2)阶矩阵,A∗ , B ∗ 分别是A, B 的伴随矩阵,已知B 是交换A的 第一行与第二行得到的矩阵.对于下述四个选项,若正确则给予证明,若不正确,请给出反 例. (A)交换A∗ 的第一列与第二列得到B ∗ . (B)交换A∗ 的第一行与第二行得到B ∗ . (C)交换A∗ 的第一列与第二列得到−B ∗ . (D)交换A∗ 的第一行与第二行得到−B ∗ . 三.(15分)设A是n阶反对称矩阵,b为n维列向量,rank (A) = rank (A, b).求证: ( ) A b rank T = rank (A). b 0 1
《高等代数》习题与参考答案

《高等代数》习题与参考答案数学系第一章 多项式1. 用)(x g 除)(x f ,求商)(x q 与余式)(x r : 1)123)(,13)(223+-=---=x x x g x x x x f ; 2)2)(,52)(24+-=+-=x x x g x x x f 。
解 1)由带余除法,可得92926)(,9731)(--=-=x x r x x q ; 2)同理可得75)(,1)(2+-=-+=x x r x x x q 。
2.q p m ,,适合什么条件时,有 1)q px x mx x ++-+32|1, 2)q px x mx x ++++242|1。
解 1)由假设,所得余式为0,即0)()1(2=-+++m q x m p ,所以当⎩⎨⎧=-=++0012m q m p 时有q px x mx x ++-+32|1。
2)类似可得⎩⎨⎧=--+=--010)2(22m p q m p m ,于是当0=m 时,代入(2)可得1+=q p ;而当022=--m p 时,代入(2)可得1=q 。
综上所诉,当⎩⎨⎧+==10q p m 或⎩⎨⎧=+=212m p q 时,皆有q px x mx x ++++242|1。
3.求()g x 除()f x 的商()q x 与余式:1)53()258,()3f x x x x g x x =--=+; 2)32(),()12f x x x x g x x i =--=-+。
解 1)432()261339109()327q x x x x x r x =-+-+=-;2)2()2(52)()98q x x ix i r x i=--+=-+。
4.把()f x 表示成0x x -的方幂和,即表成2010200()()...()n n c c x x c x x c x x +-+-++-+的形式:1)50(),1f x x x ==;2)420()23,2f x x x x =-+=-;3)4320()2(1)37,f x x ix i x x i x i =+-+-++=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等代数》多项式月测试题
(2010年10月21日
胡付高命题)
一、填空题(每小题5分,共20分)
1.用g (x )=x 2−x +2除f (x )=x 4+2x +5,商式为
;余式为.2.多项式f (x )=[4(5x −4)2000x 2−2x −1]2010(8x 3−11x 2+2)2011的所有系数之和=
,常数项=.3.能被任一多项式整除的多项式是;能整除任意多项式的多项式一定是.4.已知(x −1)2|Ax 4+Bx 2+1,则A =,B =.二、判断题(对的打√,简述原因或证明;错的打×,并举反例.每小题4分,共20分)
1.若p (x )|f (x )g (x ),则p (x )|f (x )或p (x )|g (x ).
2.若整系数多项式在有理数域上可约,则它一定有有理根.
3.若整系数多项式有有理根,则它在有理数域上一定可约.
4.若p (x )在数域P 上不可约,且p (x )|f (x )g (x )以及p (x )|[f (x )+g (x )]成立,则p (x )|f (x )且p (x )|g (x ).
5.若两个多项式在复数域上不互素,则它们一定有公共的复根.
三、设f (x )=x 4+x 3−3x 2−4x −1,g (x )=x 3+x 2−x −1,求(f (x ),g (x )).(共10分)
四、设f (x )=x 5−x 3+4x 2−3x +2.
(1)判断f (x )在R 上有无重因式?如果有,求出所有的重因式及重数;
(2)求f (x )在R 上的标准分解式.(共15分)
五、设f (x )是一个整系数多项式.证明:若对某个整数m ,使得f (m )与f (m +1)都是奇数,则f (x )没有整数根.(共10分)
六、设f (x )与g (x )互素,证明:
(1)f (x )与f (x )−g (x )互素;
(2)f (x )g (x )与f (x )−g (x )互素.(共15分)
七、设p 是素数,a 是整数,f (x )=ax p +px +1,且p 2|a +1.证明:f (x )在有理数域上不可约.(共10分)
选做题:
1、设f (x ),g (x ),h (x )为实系数多项式,它们适合下列关系: (x 2+1)h (x )+(x −1)f (x )+(x −2)g (x )=0
(x 2+1)h (x )+(x +1)f (x )+(x +2)g (x )=0
证明:f (x ),g (x )都能被x 2+1整除.
2、已知f (x )是一个n 次多项式,对于k =0,1,2,···,n 时有f (k )=k k +1,试求f (n +1).提示:作ϕ(x )=(x +1)f (x )−x .。
