20162017学年广东省广州十六中七年级下期中数学试卷
(完整版)广州市2016七年级数学下册期中考试卷(解析版)

广州市2016七年级数学下册期中考试卷(解析版)一、选择题(每小题3分,满分24分)1.方程6+3x=0的解是()A.x=﹣2 B.x=﹣6 C.x=2 D.x=62.不等式的解集在数轴上表示正确的是()A.B.C.D.3.下列长度的各组线段首尾相接能构成的三角形的是()A.2cm、3cm、5cm B.3cm、5cm、6cm C.2cm、2cm、4cm D.3cm、5cm、10cm4.下面图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.5.已知关于x的方程2x+4=m﹣x的解为负数,则m的取值范围是()A.m>4 B.m<4 C.m>D.m<6.小李在解方程5a﹣x=13(x为未知数)时,误将﹣x看作+x,得方程的解为x=﹣2,那么原方程的解为()A.x=﹣3 B.x=0 C.x=2 D.x=17.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于()A.122°B.151°C.116° D.97°8.已知关于x、y的方程组满足x<0且y<0,则m的取值范围是()A.m>B.m<C.<m<D.m<二、填空题(每小题3分,共21分)9.请写出一个以为解的二元一次方程:.10.如图,已知△AOC≌△BOC,∠AOB=70°,则∠1=度.11.如图,将周长为10的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为.12.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD 沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是.13.一个多边形的内角和等于它外角和的7倍,则这个多边形的边数为.14.如图所示,观察下列图形它们是按一定规律构造的,依照此规律,第n个图形中共有个三角形.15.若关于x、y的二元一次方程组的解是,那么关于x、y 的二元一次方程组的解是.三、解答题(本题共10个小题,共75分)16.解方程﹣2=.17.解不等式组把它的解集在数轴上表示出来,并判断﹣1这个数是否为该不等式组的解.18.已知y=kx+b,当x=2时,y=1;当x=﹣1时,y=4.(1)求k、b的值;(2)当x取何值时,y的值是非负数.19.如图,10×10的方格纸的两条对称轴a、b相交于点O,△ABC的顶点均在格点上.(1)对△ABC分别作下列变换:①画出△ABC关于直线a对称的△A1B1C1;②将△ABC向右平移6个单位长度,画出平移后的△A2B2C2;③将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;(2)在△A1B1C1,△A2B2C2,△A3B3C3中,①△与△成轴对称,对称轴是直线;②△与△成中心对称,并在图中标出对称中心D.20.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E,∠BED=65°,∠C=60°,求∠ABC和∠BAC的度数.21.某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.(1)求甲、乙两个班组平均每天各掘进多少米?(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务?22.某养鸡厂计划购买甲、乙两种小鸡苗共2000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.相关资料表示,甲、乙两种小鸡苗的成活率分别是94%和99%,要使这两种小鸡苗成活率不低于95.5%且小鸡苗的总费用最少,应购买甲、乙两种小鸡各多少只?总费用最少是多少元?23.某电脑经销商计划购进一批电脑机箱和液晶显示器,已知:购进电脑机箱2台和液晶显示器5台,共需要资金4120元;购进电脑机箱10台和液晶显示器8台,共需要资金7000元.(1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商购进这两种商品50台,其中电脑机箱不少于24台.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有几种进货方案?24.某物流公司现有31吨货物运往某地,计划同时租用A型车a辆,B型车b 辆,使每辆车都装满货物恰好一次运完.已知每种型号车的载重量和租金如表:车型A B载重量(吨/辆)34租金(元/辆)10001200(1)请你帮该物流公司设计租车方案;(2)请选出最省钱的租车方案,并求出最少租车费.25.如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.(1)指出旋转的中心和旋转角度;(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;(3)△ABF向右平移后与△DCH位置,平移的距离是多少?(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.2015-2016学年河南省新乡市七年级(下)期末数学试卷参考答案与试题解析一、选择题(每小题3分,满分24分)1.方程6+3x=0的解是()A.x=﹣2 B.x=﹣6 C.x=2 D.x=6【考点】一元一次方程的解.【分析】首先移项,然后系数化1,即可求得答案.【解答】解:移项得:3x=﹣6,系数化1得:x=﹣2.故选A.2.不等式的解集在数轴上表示正确的是()A.B.C.D.【考点】在数轴上表示不等式的解集;解一元一次不等式组.【分析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.【解答】解:,由①得,x>﹣2,由②得,x≤3,故此不等式组的解集为:﹣2<x≤3.在数轴上表示为:故选B.3.下列长度的各组线段首尾相接能构成的三角形的是()A.2cm、3cm、5cm B.3cm、5cm、6cm C.2cm、2cm、4cm D.3cm、5cm、10cm【考点】三角形三边关系.【分析】三角形三边关系:三角形任意两边之和大于第三边,据此判断即可.【解答】解:(A)∵2+3=5,∴2cm、3cm、5cm首尾相接不能构成的三角形;(B)∵3+5>6,∴3cm、5cm、6cm首尾相接能构成的三角形;(C)∵2+2=4,∴2cm、2cm、4cm首尾相接不能构成的三角形;(D)∵3+5<10,∴3cm、5cm、10cm首尾相接不能构成的三角形.故选(B)4.下面图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【考点】中心对称图形;轴对称图形.【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【解答】解:A、是轴对称图形,不是中心对称图形,故本选项错误;B、不是轴对称图形,是中心对称图形,故本选项错误;C、是轴对称图形,不是中心对称图形,故本选项错误;D、既是轴对称图形,又是中心对称图形,故本选项正确.故选D.5.已知关于x的方程2x+4=m﹣x的解为负数,则m的取值范围是()A.m>4 B.m<4 C.m>D.m<【考点】解一元一次不等式;一元一次方程的解.【分析】先把m当作已知条件求出x的值,再根据方程的解为负数求出m的取值范围即可.【解答】解:解方程2x+4=m﹣x得,x=,∵方程的解为负数,∴<0,即m<4.故选B.6.小李在解方程5a﹣x=13(x为未知数)时,误将﹣x看作+x,得方程的解为x=﹣2,那么原方程的解为()A.x=﹣3 B.x=0 C.x=2 D.x=1【考点】一元一次方程的解.【分析】本题主要考查方程的解的定义,一个数是方程的解,那么把这个数代入方程左右两边,所得到的式子一定成立.本题中,在解方程5a﹣x=13(x为未知数)时,误将﹣x看作+x,得方程的解为x=﹣2,实际就是说明x=﹣2是方程5a+x=13的解.就可求出a的值,从而原方程就可求出,然后解方程可得原方程的解.【解答】解:如果误将﹣x看作+x,得方程的解为x=﹣2,那么原方程是5a﹣2=13,则a=3,将a=3代入原方程得到:15﹣x=13,解得x=2;故选:C.7.如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于()A.122°B.151°C.116° D.97°【考点】平行线的性质.【分析】根据两直线平行,同位角相等求出∠EFD,再根据角平分线的定义求出∠GFD,然后根据两直线平行,同旁内角互补解答.【解答】解:∵AB∥CD,∠1=58°,∴∠EFD=∠1=58°,∵FG平分∠EFD,∴∠GFD=∠EFD=×58°=29°,∵AB∥CD,∴∠FGB=180°﹣∠GFD=151°.故选B.8.已知关于x、y的方程组满足x<0且y<0,则m的取值范围是()A.m>B.m<C.<m<D.m<【考点】解一元一次不等式组;二元一次方程组的解.【分析】先把m当作已知条件求出x、y的值,再由x<0且y<0得出m的取值范围即可.【解答】解:,①×2﹣②得,x=m﹣,①﹣②×2得,y=m﹣,∵x<0且y<0,∴,解得m<.故选D.二、填空题(每小题3分,共21分)9.请写出一个以为解的二元一次方程:x+y=1.【考点】二元一次方程的解.【分析】根据二元一次方程的解的定义,比如把x与y的值相加得1,即x+y=1是一个符合条件的方程.【解答】解:本题答案不唯一,只要写出的二元一次方程的解为即可,如x+y=1.故答案是:x+y=1.10.如图,已知△AOC≌△BOC,∠AOB=70°,则∠1=35度.【考点】全等三角形的性质.【分析】根据全等的性质可得∠1=∠2,结合题意即可得出答案.【解答】解:∵△AOC≌△BOC,∴∠1=∠2,又∵∠AOB=70°,∴∠1=∠2=35°.故答案为:35°.11.如图,将周长为10的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为14.【考点】平移的性质.【分析】根据平移的性质,对应点的连线AD、CF都等于平移距离,再根据四边形ABFD的周长=△ABC的周长+AD+CF代入数据计算即可得解.【解答】解:∵△ABC沿BC方向平移2个单位得到△DEF,∴AD=CF=2,∴四边形ABFD的周长,=AB+BC+DF+CF+AD,=△ABC的周长+AD+CF,=10+2+2,=14.故答案为:14.12.如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD 沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.【考点】翻折变换(折叠问题).【分析】先根据折叠性质得:∠BAD=∠EAD=30°,∠E=∠B=50°,再根据外角定理求∠AFC=110°,由三角形内角和可以得出∠EDF为20°.【解答】解:由折叠得:∠BAD=∠EAD=30°,∠E=∠B=50°,∵∠B=50°,∴∠AFC=∠B+∠BAE=50°+60°=110°,∴∠DFE=∠AFC=110°,∴∠EDF=180°﹣∠E﹣∠DFE=180°﹣50°﹣110°=20°,故答案为:20°.13.一个多边形的内角和等于它外角和的7倍,则这个多边形的边数为16.【考点】多边形内角与外角.【分析】n边形的内角和可以表示成(n﹣2)•180°,外角和为360°,根据题意列方程求解.【解答】解:设多边形的边数为n,依题意,得:(n﹣2)•180°=7×360°,解得n=16,故答案为:16.14.如图所示,观察下列图形它们是按一定规律构造的,依照此规律,第n个图形中共有4n﹣1个三角形.【考点】规律型:图形的变化类.【分析】易得第1个图形中三角形的个数,进而得到其余图形中三角形的个数在第1个图形中三角形的个数的基础上增加了几个4即可.【解答】解:第1个图形中有3个三角形;第2个图形中有3+4=7个三角形;第3个图形中有3+2×4=11个三角形;…第n个图形中有3+(n﹣1)×4=4n﹣1,故答案为4n﹣1.15.若关于x、y的二元一次方程组的解是,那么关于x、y 的二元一次方程组的解是.【考点】解二元一次方程组.【分析】根据题中方程组的解,把2x+y与x﹣y看做整体,求出解即可.【解答】解:根据题意得:,解得:,故答案为:三、解答题(本题共10个小题,共75分)16.解方程﹣2=.【考点】解一元一次方程.【分析】方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:去分母得:2(2x﹣1)﹣12=3(3x+2),去括号得:4x﹣2﹣12=9x+6,移项合并得:5x=﹣20,解得:x=﹣4.17.解不等式组把它的解集在数轴上表示出来,并判断﹣1这个数是否为该不等式组的解.【考点】解一元一次不等式组;在数轴上表示不等式的解集.【分析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.【解答】解:,由①得,x>﹣2,由②得,x≤1,故不等式组的解集为:﹣2<x≤1.在数轴上表示为:,由图可知,﹣1是该不等式组的解.18.已知y=kx+b,当x=2时,y=1;当x=﹣1时,y=4.(1)求k、b的值;(2)当x取何值时,y的值是非负数.【考点】解二元一次方程组;解一元一次不等式.【分析】(1)将x与y的两对值代入y=kx+b中计算,即可求出k与b的值;(2)y与x的关系式,以及y为非负数,求出x的范围即可.【解答】解:(1)由题意得:,解得:k=﹣1,b=3;(2)由(1)得:y=﹣x+3,根据y为非负数,得到﹣x+3≥0,解得:x≤3,则x≤3时,y的值为非负数.19.如图,10×10的方格纸的两条对称轴a、b相交于点O,△ABC的顶点均在格点上.(1)对△ABC分别作下列变换:①画出△ABC关于直线a对称的△A1B1C1;②将△ABC向右平移6个单位长度,画出平移后的△A2B2C2;③将△ABC绕点O旋转180°,画出旋转后的△A3B3C3;(2)在△A1B1C1,△A2B2C2,△A3B3C3中,①△△A1B1C1与△△A3B3C3成轴对称,对称轴是直线b;②△△A3B3C3与△△A2B2C2成中心对称,并在图中标出对称中心D.【考点】作图-旋转变换;作图-轴对称变换;作图-平移变换.【分析】(1)先根据轴对称、平移和旋转变换的性质,找出对应点,然后顺次连接得出图形;(2)根据图形可得,△A1B1C1和△A3B3C3成轴对称图形,对称轴为直线b,△A3B3C3和△A2B2C2成中心对称图形.【解答】解:(1)所作图形如图所示:;(2)由(1)得:△A1B1C1和△A3B3C3成轴对称图形,对称轴为直线b,△A3B3C3和△A2B2C2成中心对称图形,点D如图所示.20.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E,∠BED=65°,∠C=60°,求∠ABC和∠BAC的度数.【考点】三角形内角和定理.【分析】由直角三角形的性质求出∠DBE=25°,再由角平分线定义得出∠ABC=2∠DBE=50°,然后由三角形内角和定理求出∠BAC的度数即可.【解答】解:∵AD是BC边上的高,∴∠ADB=90°,∴∠DBE+∠BED=90°,∵∠BED=65°,∴∠DBE=25°,∵BE平分∠ABC,∴∠ABC=2∠DBE=50°,∵∠BAC+∠ABC+∠C=180°,∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣50°﹣60°=70°.21.某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.(1)求甲、乙两个班组平均每天各掘进多少米?(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务?【考点】二元一次方程组的应用.【分析】(1)设甲、乙班组平均每天掘进x米,y米,根据已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米两个关系列方程组求解.(2)由(1)和在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米分别求出按原来进度和现在进度的天数,即求出少用天数.【解答】解:(1)设甲、乙班组平均每天掘进x米,y米,得,解得.∴甲班组平均每天掘进4.8米,乙班组平均每天掘进4.2米.(2)设按原来的施工进度和改进施工技术后的进度分别还需a天,b天完成任务,则a=÷(4.8+4.2)=190(天)b=÷(4.8+0.2+4.2+0.3)=180(天)∴a﹣b=10(天)∴少用10天完成任务.22.某养鸡厂计划购买甲、乙两种小鸡苗共2000只进行饲养,已知甲种小鸡苗每只2元,乙种小鸡苗每只3元.相关资料表示,甲、乙两种小鸡苗的成活率分别是94%和99%,要使这两种小鸡苗成活率不低于95.5%且小鸡苗的总费用最少,应购买甲、乙两种小鸡各多少只?总费用最少是多少元?【考点】一元一次不等式的应用.【分析】设购买甲种小鸡x只,购买乙种小鸡只,列出不等式求出x的范围即可.【解答】解:设购买甲种小鸡x只,购买乙种小鸡只,由题意94%x+99%≥2000×95.5%,解得x≤1400,因为甲种小鸡便宜,所以购买甲种小鸡越多费用越少,所以x=1400时,总费用最小,费用为2×1400+3×600=4600(元),答:购买甲种小鸡1400只,乙种小鸡600只时,费用最小,最小费用为4600元.23.某电脑经销商计划购进一批电脑机箱和液晶显示器,已知:购进电脑机箱2台和液晶显示器5台,共需要资金4120元;购进电脑机箱10台和液晶显示器8台,共需要资金7000元.(1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商购进这两种商品50台,其中电脑机箱不少于24台.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有几种进货方案?【考点】一元一次不等式组的应用;二元一次方程组的应用.【分析】(1)设每台电脑机箱的进价是x元,液晶显示器的进价是y元,根据“购进电脑机箱2台和液晶显示器5台,共需要资金4120元;购进电脑机箱10台和液晶显示器8台,共需要资金7000元”,即可得出关于x、y的二元一次方程组,解方程组即可得出结论;(2)设购进电脑机箱a台,则购进液晶显示器(50﹣a)台,根据“电脑机箱不少于24台,该经销商希望销售完这两种商品,所获利润不少于4100元”,即可得出关于a的一元一次不等式组,解不等式组再根据a取整数即可得出结论.【解答】解:(1)设每台电脑机箱的进价是x元,液晶显示器的进价是y元,根据题意得:,解得:.答:每台电脑机箱的进价是60元,液晶显示器的进价是800元.(2)设购进电脑机箱a台,则购进液晶显示器(50﹣a)台,根据题意得:,解得:24≤a≤26.又a为整数,∴a=24,25,26.故该经销商有3种进货方案.24.某物流公司现有31吨货物运往某地,计划同时租用A型车a辆,B型车b 辆,使每辆车都装满货物恰好一次运完.已知每种型号车的载重量和租金如表:车型A B载重量(吨/辆)34租金(元/辆)10001200(1)请你帮该物流公司设计租车方案;(2)请选出最省钱的租车方案,并求出最少租车费.【考点】二元一次方程的应用.【分析】(1)先根据题意得出关于a、b的方程,再根据a、b为正整数即可得出结论;(2)分别求出各方案的租金,再比较大小即可.【解答】解:(1)∵根据题意得,3a+4b=31,∴a=.∵a、b为正整数,∴或或,∴有3种方案:①A型车9辆,B型车1辆;②A型车5辆,B型车4辆;③A 型车1辆,B型车7辆.(2)方案①需租金:9×1000+1200=10200(元);方案②需租金:5×1000+4×1200=9800(元);方案③需租金:1×1000+7×1200=9400(元);∵10200>9800>9400,∴最省钱的方案是A型车1辆,B型车7辆,最少租车费为9400元.25.如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.(1)指出旋转的中心和旋转角度;(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;(3)△ABF向右平移后与△DCH位置,平移的距离是多少?(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.【考点】四边形综合题.【分析】(1)根据旋转的定义,直接得出旋转的中心和旋转的角度;(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;(3)利用旋转中心为正方形对角线的交点,逆时针旋转90°(或逆时针旋转270°),即可得出平移距离等于正方形边长;(4)根据平移的性质得AF∥DH,由(2)得AF⊥AE,所以AE⊥DH,进而得出AE=DH.【解答】解:(1)旋转的中心是点A,旋转的角度是90°;(2)△AEF是等腰直角三角形.理由如下:∵△ADE绕点A顺时针旋转90°后与△ABF重合,∴∠FAE=∠BAD=90°,AF=AE,∴△AEF是等腰直角三角形.(3)∵正方形ABCD的边长是5,∴△ABF向右平移后与△DCH位置,平移的距离是5;(4)AE=DH,AE⊥DH,理由:∵△ABF向右平移后与△DCH重合,∴DH∥AF,DH=AF,又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,∴∠FAE=∠BAD=90°,AF=AE,∴AE⊥AF,∴AE=DH,AE⊥DH.2017年2月23日第21页(共21页)。
16—17学年下学期七年级期中考试数学试题(附答案)(6)

2016-2017学年七年级(下)期中数学试卷一、选择题(每题3分,共24分,答案填在上方的表格里)1.下列图形中,∠1与∠2是内错角的是()A.B.C.D.2.在下面四根木棒中,选一根能与长为4cm,9cm的两根木棒首尾依次相接钉成一个三角形的是()A.4cm B.5cm C.9cm D.13cm3.计算x3•x3的结果是()A.2x3B.2x6C.x6D.x94.下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是()A.①②B.①③ C.②③ D.③④5.计算﹣2a(a2﹣1)的结果是()A.﹣2a3﹣2a B.﹣2a3+a C.﹣2a3+2a D.﹣a3+2a6.下列各式中,计算结果为81﹣x2的是()A.(x+9)(x﹣9)B.(x+9)(﹣x﹣9)C.(﹣x+9)(﹣x﹣9)D.(﹣x﹣9)(x﹣9)7.下列方程中是二元一次方程的是()A.3x+y=0 B.2x﹣1=4 C.2x2﹣y=2 D.2x+y=3z8.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°二、填空题(每题3分,共30分)9.一种细菌的半径是0.00003厘米,这个数用科学记数法表示为厘米.10.已知a+b=3,ab=2,计算:a2b+ab2等于.11.如果一个正多边形的一个外角是36°,那么该正多边形的边数为.12.计算:(2x)2•3x=.13.(y﹣1)2=.14.因式分解:a2﹣4=.15.请你写一个关于x,y的二元一次方程组,使得它的解为.16.如图,已知AB∥CD,则∠1与∠2,∠3的关系是.17.计算0.1252015×(﹣8)2016=.18.小丽在计算一个二项式的平方时,得到正确结果m2﹣10mn+■,但最后一项不慎被墨水污染,这一项应是.三、解答题(本大题共有9小题,满分66分)19.计算(每题4分,共8分):(1)()﹣1+()2×(﹣2)3﹣(π﹣3)0.(2)4xy2•(﹣x2yz3).20.因式分解(每题4分,共8分);(1)2a2﹣2;(2)m2﹣12mn+36n2.21.解下列方程组(每题5分,共10分)(1)(2)22.(8分)已知,如图,在正方形网格中,每个小正方形的边长均为1,将△ABC先向上平移3格,再向左平移2格.(1)画出平移后的图形△A′B′C′;(2)直接写出△A′B′C′的面积.23.(6分)已知:A=4x+y,B=4x﹣y,计算A2﹣B2.24.(6分)已知a x=5,a x+y=30,求a x+a y的值.25.(6分)如图,BD是△ABD与△CBD的公共边,AB∥CD,∠A=∠C,试判断AD与BC的位置关系,并说明理由.26.(6分)七年级一班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:李小波:阿姨,您好!售货员:同学,你好,想买点什么?李小波:我只有100元,请帮我安排买10支钢笔和15本笔记本.售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?27.(8分)如图1,是一个长为2m、宽为2n的长方形,沿图中虚线剪成四个完全一样的小长方形,然后按图2的形状拼成一个正方形.(1)图2中阴影部分的面积为;(2)用两种不同的方法计算图2中阴影部分的面积,可以得到的等式是(只填序号);①(m+n)2=m2+2mn+n2 ②(m﹣n)2=m2﹣2mn+n2③(m﹣n)2=(m+n)2﹣4mn(3)若x﹣y=﹣4,xy=,则x+y=.2016-2017学年七年级(下)期中数学试卷参考答案与试题解析一、选择题(每题3分,共24分)二、填空题(每题3分,共30分)9.3×10﹣510.6.11.10.12. 12x3.13.y2+1﹣2y.14.(a+2)(a﹣2).15..16.∠1=∠2+∠3.178.18.25n2.三、解答题(本大题共有9小题,满分66分)19.计算:(1)()﹣1+()2×(﹣2)3﹣(π﹣3)0.(2)4xy2•(﹣x2yz3).解:(1)原式=﹣2﹣1=3﹣2﹣1=0;(2)4xy2•(﹣x2yz3)=4×(﹣)(x•x2)(y2•y)z3=﹣x3y3z3.20.因式分解;(1)2a2﹣2;(2)m2﹣12mn+36n2.解:(1)原式=2(a2﹣1)=2(a+1)(a﹣1);(2)原式=(m﹣6n)2.21.解:(1),把?代入?得:6y+y+7=0,即y=﹣1,把y=﹣1代入?得:x=﹣3,则方程组的解为;(2),?﹣?×2得:7y=35,即y=5,把y=5代入?得:x=2,则方程组的解为.22.解:(1)如图所示:△A'B'C'即为所求;(2)△A'B'C'的面积为:×4×4=8.故答案为:8.23.已知:A=4x+y,B=4x﹣y,计算A2﹣B2.解:∵A=4x+y,B=4x﹣y,∴A2﹣B2=(A+B)(A﹣B)=(4x+y+4x﹣y)(4x+y﹣4x+y)=8x×2y=16xy.24.已知a x=5,a x+y=30,求a x+a y的值.解:∵a x=5,a x+y=30,∴a y=a x+y﹣x=30÷5=6,∴a x+a y=5+6=11,即a x+a y的值是11.25.解:AD∥BC.理由:∵AB∥CD,∴∠A+∠ADC=180°.∵∠A=∠C,∴∠C+∠ADC=180°,∴AD∥BC.26.解:设钢笔每支为x元,笔记本每本y元,据题意得答:钢笔每支5元,笔记本每本3元。
2016-2017学年七年级下数学期中试卷及答案

2016-2017学年度第二学期期中考试七年级数学试卷一、选择题(本题有10小题,每题4分,共40分) 1、下面四个图形中∠1与∠2是对顶角的是( )A. B. C. D.2、方程组的解为( ) A.B.C.D.3、在①+y=1;②3x ﹣2y=1;③5xy=1;④+y=1四个式子中,不是二元一次方程的有( ) A .1个B .2个C .3个D .4个4、如图所示,图中∠1与∠2是同位角的是( ) A 、1个B 、2个C 、3个D 、4个5.下列运动属于平移的是( )A .冷水加热过程中小气泡上升成为大气泡B .急刹车时汽车在地面上的滑动C .投篮时的篮球运动D .随风飘动的树叶在空中的运动 6、如图1,下列能判定AB ∥CD 的条件有( )个. (1) ︒=∠+∠180BCD B ; (2)21∠=∠; (3) 43∠=∠; (4) 5∠=∠B . A .1 B .2 C .3 D.47、下列语句是真命题的有( )①点到直线的垂线段叫做点到直线的距离; ②内错角相等;③两点之间线段最短; ④过一点有且只有一条直线与已知直线平行; ⑤在同一平面内,若两条直线都与第三条直线垂直,那么这两条直线互相平行. A .2个 B .3个 C .4个 D .5个54D3E21CBA图18、如图2,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′的位置,若∠EFB=65°,则∠AED′=( ) A 、50° B 、55° C 、60° D 、65° 9、如图3,直线21//l l ,∠A=125°,∠B=85°,则∠1+∠2=( )A .30°B .35°C .36°D .40°10、如图4,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到△DEF 的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )A.42B.96C.84D.48 二、填空题(本题有6小题,11题10分,其余每题4分,共30分) 11、﹣125的立方根是,的平方根是 ,如果=3,那么a=,的绝对值是 ,2的小数部分是_______12、命题“对顶角相等”的题设 ,结论13、(1)点P 在第二象限内,P 到x 轴的距离是4,到y 轴的距离是3,那么点P 的坐标为_______; (2)若,则.14、如图5,一艘船在A 处遇险后向相距50 海里位于B 处的救生船 报警.用方向和距离描述遇险船相对于救生船的位置15、∠A 的两边与∠B 的两边互相平行,且∠A 比∠B 的2倍少15°,则∠A 的度数为_______16、在平面直角坐标系xOy 中,对于点P (x ,y ),我们把点P′(-y+1,x+1)叫做点P 的伴随点.已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4,…,这样依次得到点A 1,A 2,A 3,…,A n ,….若点A 1的坐标为(3,1),则点A 3的坐标为 , 点A 2014的坐标为_________三、解答题(本题有10小题,共80分) 17、(本题有6小题,每小题3分,共18分)(一)计算:(1)322769----)( (2))13(28323-++-(3)2(2-2)+3(3+13). 图4图5FEDCB A 音乐台湖心亭牡丹园望春亭游乐园(2,-2)孔桥(二)解方程:(1)9x 2=16. (2)(x ﹣4)2=4 (3)18、(本小题5分)把下列各数分别填入相应的集合里:38,3,-3.14159,3π,722,32-,87-,0,-0.∙∙02,1.414,7-,1.2112111211112…(每两个相邻的2中间依次多1个1).(1)正有理数集合:{ …}; (2)负无理数集合:{ …}; 19、(本小题6分)王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x 轴. y 轴. 只知道游乐园D 的坐标为(2,-2), 请你帮她画出坐标系,并写出其他各景点的坐标.20、(本小题5分)已知2是x 的立方根,且(y-2z+5)2+=0,求的值.21、(本小题8分)如图,直线AB 、CD 、EF 相交于点O . (1)写出∠COE 的邻补角;(2)分别写出∠COE 和∠BOE 的对顶角;(3)如果∠BOD=60°,EF AB ⊥,求∠DOF 和∠FOC 的度数.22、(本小题4分)某公路规定行驶汽车速度不得超过80千米/时,当发生交通事故时,交通警察通常根据刹车后车轮滑过的距离估计车辆的行驶速度,所用的经验公式是,其中v 表示车速(单位:千米/时),d 表示刹车后车轮滑过的距离(单位:米),f 表示摩擦系数.在一次交通事故中,经测量d=32米,f=2.请你判断一下,肇事汽车当时是否超出了规定的速度? 23、(本小题11分)完成下列推理说明:(1)如图,已知∠1=∠2,∠B=∠C ,可推出AB ∥CD .理由如下: 因为∠1=∠2(已知),且∠1=∠4( )所以∠2=∠4(等量代换) 所以CE ∥BF ( ) 所以∠ =∠3( )又因为∠B=∠C(已知)所以∠3=∠B(等量代换)所以AB∥CD()(2)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知),∴AB∥CD ()∴∠B= ()又∵∠B=∠D(已知),∴∠= ∠(等量代换)∴AD∥BE()∴∠E=∠DFE()24、(本小题6分)如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限.(1)写出点B的坐标;(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2:3的两部分,求点D的坐标;(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积.25、(本小题6分)如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.26(本小题11分)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC(1)直接写出点C,D的坐标;(2)若在y轴上存在点M,连接MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标.(3)若点P在直线BD上运动,连接PC,PO.请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.2016-2017学年度第二学期期中联考数学科 评分标准一、选择题(本大题共10小题,每小题4分,共40分) 二、填空题(本大题共6小题,11题10分,其余每小题4分,共30分)11. -5 、 ±3 、 9 、﹣2 、 2 -112.题设 两个角是对顶角 . 结论 这两个角相等 13.(1) (-3,4) .(2) 7.160 14. 南偏西15°,50海里15. 15°或115° . (答出一种情况2分) 16. (-3,1) 、 (0,4) 三、解答题(本大题共11小题,共80分)17(18分)(一)(1)322769----)( (2))13(28323-++-解:原式=3-6-(-3) …2 解:原式=232223-++-……2 =0 ……………………3 =…233-……… 3 (3)2(2-2)+3(3+13).解:原式=13222++- (2)=222+ (3)(二)(1)9x 2=16. (2)(x ﹣4)2=4解:x 2=,......1 x ﹣4=2或x ﹣4=﹣2 (1)x=±,……3 x ═6或x=2……3 (求出一根给2分)(3),(x+3)3=27,......1 x+3=3, (2)题号1 2 3 4 5 6 7 8 9 10答案CDBCBCAAADx=0. (3)18(本小题5分)解:(1)正有理数集合:{38,722,1.414,…} ……3分 (2)负无理数集合:{32-,7-,…}.……5分19(本小题6分)解:(1)正确画出直角坐标系;……1分(2)各点的坐标为A(0,4),B (-3,2),C (﹣2,-1),E (3,3),F (0,0);……6分 20(本小题5分)解:∵2是x 的立方根, ∴x=8,……1 ∵(y ﹣2z+5)2+=0,∴,解得:, (3)∴==3. (5)21(本小题8分)解:(1)∠COF 和∠EOD (2)(2)∠COE 和∠BOE 的对顶角分别为∠DOF 和∠AOF .……4 (3)∵AB ⊥EF ∴∠AOF=∠BOF=90°∴∠DOF=∠BOF-∠BOD=90°-60°=30° (6)又∵∠AOC=∠BOD=60°∴∠FOC=∠AOF+∠AOC=90°+60°=150°. (8)22(本小题4分)解:把d=32,f=2代入v=16,v=16=128(km/h ) (2)∵128>80, (3)∴肇事汽车当时的速度超出了规定的速度. (4)23.(11分)(1)如图,已知∠1=∠2,∠B=∠C ,可推出AB ∥CD .理由如下: 因为∠1=∠2(已知),且∠1=∠4( 对顶角相等 ) (1)所以∠2=∠4(等量代换)所以CE ∥BF ( 同位角相等,两直线平行 )......2 所以∠ C =∠3( 两直线平行,同位角相等 ) (4)又因为∠B=∠C(已知)所以∠3=∠B(等量代换)所以AB∥CD(内错角相等,两直线平行) (5)(2)在括号内填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知),∴AB∥CD (同旁内角互补,两直线平行) (1)∴∠B=∠DCE(两直线平行,同位角相等) (3)又∵∠B=∠D(已知),∴∠DCE=∠D (等量代换) (4)∴AD∥BE(内错角相等,两直线平行) (5)∴∠E=∠DFE(两直线平行,内错角相等) (6)24.(6分)解:(1)点B的坐标(3,2); (1)(2)长方形OABC周长=2×(2+3)=10,∵长方形OABC的周长分成2:3的两部分,∴两个部分的周长分别为4,6,∵OC+OA=5<6∴OC+OD=4∵OC=2,∴OD=2,∴点D的坐标为(2,0); (4)(3)如图所示,△CD′C′即为所求作的三角形, (5)CC′=3,点D′到CC′的距离为2,所以,△CD′C′的面积=×3×2=3. (6)25(6分)解:∠C与∠AED相等, (1)理由为:证明:∵∠1+∠2=180°,∠1+∠DFE=180°,∴∠2=∠DFE (2)∴AB∥EF∴∠3=∠ADE (3)又∠B=∠3∴∠B=∠ADE∴DE∥BC (5)∴∠C=∠AED (6)26、(本小题11分)解:(1)C(0,2),D(4,2); (2)(2)∵AB=4,CO=2,∴S平行四边形ABOC=AB•CO=4×2=8,设M坐标为(0,m),∴×4×|m|=8,解得m=±4∴M点的坐标为(0,4)或(0,﹣4);……5(求出一点给2分)(3)当点P在BD上,如图1,∠DCP+∠BOP=∠CPO; (7)当点P在线段BD的延长线上时,如图2,,∠BOP﹣∠DCP=∠CPO; (9)同理可得当点P在线段DB的延长线上时,∠DCP﹣∠BOP=∠CPO. (11)(每种情况正确画出图形给1分)。
初级中学16—17学年下学期七年级期中考试数学试题(附答案)

54D 3E21C B A2016-2017学年第二学期期中考试七年级数学试卷(问卷)(卷面分值:100分;考试时间:100分钟)同学们,半个学期的勤奋,今天将展现在试卷上,老师相信你一定会把诚信答满试卷,......................................也一定会让努力书写成功,答题时记住细心和耐心。
.......................注意事项:本卷由问卷和答卷两部分组成,其中问卷共4页,答卷共2页,在问卷上答题无效。
一.选择题(本大题共8小题,每小题3分,共24分)1. 4的平方根是( )A . ±2B .2C .±D .2.点P (-1,5)所在的象限是( )A .第一象限B .第二象限C.第三象限 D.第四象限3.下列各组图形,可由一个图形平移得到另一个图形的是( )A B C D4.如图,直线AB 、CD 相交于点O,若∠1+∠2=100°,则∠BOC 等于 ( )A.130°B.140°C.150°D.160 (第4题图)5.已知是二元一次方程4x+ay=7的一组解,则a 的值为( )A .﹣5B .5C .D .﹣6.如右图,下列能判定AB ∥CD 的条件有( )个. (第6题图) (1) ︒=∠+∠180BCD B (2)21∠=∠(3) 43∠=∠ (4) 5∠=∠B A . 1 B .2 C .3D.4 7.下列各组数中,互为相反数的组是( )A .﹣2与B .﹣2和C .﹣与2D .|﹣2|和28.下列命题:①两直线平行,内错角相等;②如果m 是无理数,那么m 是无限小数;③64的立方根是8;④同旁内角相等,两直线平行;⑤如果a 是实数,那么a 是无理数.其中正确的有( )A .1个B .2个C .3个D .4个二.填空(本大题共6小题,每小题3分,共18分)9.若32123=---n m y x 是二元一次方程,则m=____,n=____.10.计算:|3﹣π|+的结果是 .11.已知点P(0,a)在y 轴的负半轴上,则点Q(-2a -1,-a+1)在第 象限.12.已知a 、b 满足方程组2226a b a b -=⎧⎨+=⎩,则3a b +的值为 . (第13题图) 13.如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为 .14.在平面直角坐标系中,点A 的坐标为(﹣1,3),线段AB ∥x 轴,且AB =4,则点B 的坐标为 .三、计算解答题 (每小题5分,共20分)15.计算:364+2)3(--31- 16.1+2)451(- .17.解二元一次方程组:18.已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.四、解答题:(19题6分,20题8分,21题6分,22题8分,23题10分共38分)19. 某工程队承包了修建隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了50米.求甲、乙两个班组平均每天各掘进多少米?20.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.证明:∵∠1=∠2 (已知)∴∥()∴∠E=∠()又∵∠E=∠3 (已知)∴∠3=∠()∴AD∥BE.()21.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.22.如图,已知△ABC平移后得到△A1B1C1,点A(﹣1,3)平移后得到A1(﹣4,2),(1)写出B,C的坐标:B(,),C(,).(2)画出△ABC,并指出平移规律;(3)求△ABC的面积.A PB 1l 2l 3l 1 2 323如图,已知直线 1l ∥2l ,且 3l 和1l 、2l 分别交于A 、B 两点,点P 在直线AB 上.(1)试找出∠1、∠2、∠3之间的关系并说明理由;(2)当点P 在A 、B 两点间运动时,问∠1、∠2、∠3之间的关系是否发生变化?(只写结论)(3)如果点P 在A 、B 两点外侧运动时,试探究∠1、∠2、∠3 之间的关系。
2016-2017学年度第二学期期中数学考试试卷
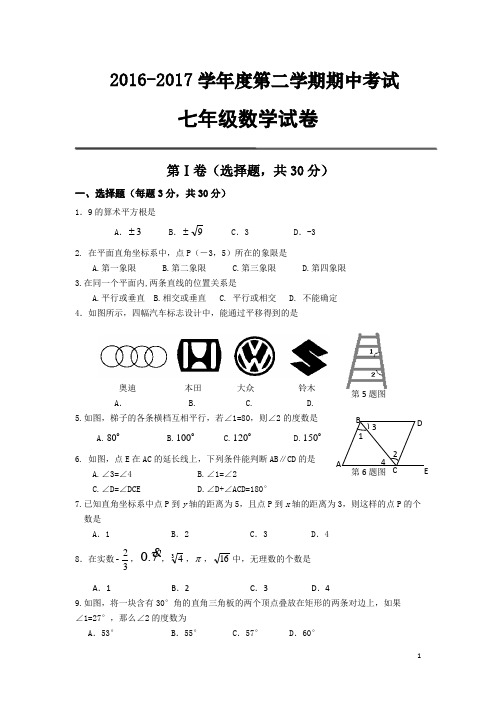
2016-2017学年度第二学期期中考试七年级数学试卷第Ⅰ卷(选择题,共30分)一、选择题(每题3分,共30分)1.9的算术平方根是A .3±B .9±C .3D .-32. 在平面直角坐标系中,点P (-3,5)所在的象限是A.第一象限B.第二象限C.第三象限D.第四象限3.在同一个平面内,两条直线的位置关系是A.平行或垂直B.相交或垂直C. 平行或相交D. 不能确定 4.如图所示,四幅汽车标志设计中,能通过平移得到的是奥迪 本田 大众 铃木A . B. C. D. 5.如图,梯子的各条横档互相平行,若∠1=80,则∠2的度数是A.80B.100C.120D.1506. 如图,点E 在AC 的延长线上,下列条件能判断AB ∥CD 的是A.∠3=∠4B.∠1=∠2C.∠D=∠DCED.∠D+∠ACD=180°7.已知直角坐标系中点P 到y 轴的距离为5,且点P 到x 轴的距离为3,则这样的点P 的个数是 A .1 B .2 C .3D .48.在实数23-,0.7 ,34,π,16中,无理数的个数是 A .1B .2C .3D .49.如图,将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上,如果∠1=27°,那么∠2的度数为A .53°B .55°C .57°D .60°第6题图 第5题图10.如图,直线l 1∥l 2,∠A=125°,∠B=85°,则∠1+∠2= A .30° B .35° C .36° D .40°第Ⅱ卷(非选择题 共90分)二、填空题:(每题3分,共18分)11.在直角坐标系中,写出一个在纵轴的负半轴上点的坐标 . 12.若一个数的平方根等于它本身,则这个数是13.若a 是介于3与7之间的整数,b 是2的小数部分,则ab-22的值为 14. 如图,将△ABC 沿BC 方向平移2cm 得到△DEF,若△ABC 的周长为16cm ,则四边形ABFD 的周长为 cm15.如果两个角的两边分别平行,其中一个角比另一个角的2倍少36°,那么这两个角 是16. 如图,将正整数按如图所示规律排列下去,若用有序数对(m ,n )表示m 排从左到右第n 个数。
【广州】2016-2017广东广州越秀十六中初一下期中

16中2016学年第二学期期中检测初一数学试题一、选择题(共10小题,每题3分)1.下列图形中,不能通过其中一个四边形平移得到的是().A .B .C .D .2.下列命题中真命题的是().A .同位角相等B .两点之间,线段最短C .相等的角是对顶角D .互补的角是邻补角3.实数2(3)-的平方根是().A .3B .3-C .3± D.4π3,107,1.010010001 ,3.14,其中无理数有().A .1个B .2个C .3个D .4个5.点1,12⎛⎫- ⎪⎝⎭在().A .第一象限B .第二象限C .第三象限D .第四象限6.小华将平面直角坐标系中的(4,3)A -沿着x 轴方向向左平移了3个单位得到了B 点,则B 点的坐标是 ().A .(7,3)-B .(1,3)-C .(4,0)-D .(4,6)-7.如图,AB CD ∥,DA AC ⊥,垂足为A ,若35ADC ∠=︒,则1∠的度数是().A .65︒B .55︒C .45︒D .35︒8.小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“你把珠子的一半给我,我就有10颗珠子”,小刚却说:“只要把你的13给我,我就有10颗.”如果设小刚的弹珠数为x 颗,小龙的弹珠数为y 颗,则列出的方程组是().A .220330x y x y +=⎧⎨+=⎩B .210310x y x y +=⎧⎨+=⎩C .220310x y x y +=⎧⎨+=⎩D .210330x y x y +=⎧⎨+=⎩1DC B A9.如果x a y b =⎧⎨=⎩是方程33x y -=-的一组解,那么代数式53a b -+的值是(). A .8 B .5 C .2 D .010.如图,AB CD ∥,ABK ∠的角平分线BE 的反向延长线和DCK ∠的角平分线CF 的反向延长线交于点H ,27K H ∠-∠=︒,则K ∠=().A .76︒B .78︒C .80︒D .82︒二、填空题(共6小题,每题3分)11.如图,已知AC BD ∥,若135∠=︒,则2∠=__________︒.12.点(2,3)P -到x 轴的距离是__________.13.若327x =-,则x =__________.14.已知x 、y 是二元一次方程组2343x y x y -=-⎧⎨+=⎩的解,则x y +=__________.15.如图,已知三角形ABC 的周长为20cm ,现将三角形ABC 沿AB 方向平移2cm 知三角形A B C '''的位置,连接CC ',则四边形AB C C ''的周长是__________cm .16.如图,AB CD ∥,OE 平分BOC ∠,OF OE ⊥,OP CD ⊥,ABO α∠=︒.则下列结论:①1(180)2BOE α∠=-︒;②OF 平分BOD ∠;③POE BOF ∠=∠;④2POB DOF ∠=∠.其中正确结论是__________(填序号). D C E B A H21D CB A C'B'A'C B A三、解答题(共72分)17.(8分)化简求值(1(2)23+18.(10分)解二元一次方程组 (1)23738x y x y +=⎧⎨-=⎩ (2)2541x y x y +=⎧⎨+=-⎩19.(10分)如图,在平面直角坐标系中有三个点(3,2)A -,(5,1)B -,(2,0)C -,(,)P a b 是三角形的边AC 上一点,三角形ABC 经平移后得到三角形A B C ''',点P 的对应点为(4,3)P a b '++.(1)画出平移后的三角形A B C ''',写出点A '、B '、C '三个点的坐标. (2)求四边形ACC A ''的面积.20.(8分)如图,已知AC AB ⊥,ED AB ⊥,垂足分别为A 、D ,65CAF ∠=︒.求DGE ∠的度数.21.(12分)如图,AP 、CP 分别平分BAC ∠、ACD ∠,90P ∠=︒,设BAP x ∠=︒.OD F B PE CA FB GEA C(1)用x 表示ACP ∠.(2)求证:AB CD ∥. (3)若AP CF ∥,求证:FC 平分DCE ∠.22.(12分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?(3)若装修完后,商店每天可赢利200元,根据前面的结论,你认为如何安排施工更有利于商店?请你帮助商店决策.23.(12分)如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点(0,)A a ,(,0)C b20b -=.D 为线段AC 的中点.(1)则A 点的坐标为__________;点C 的坐标为__________.(2)在平面直角坐标系中,以任意两点11(,)P x y 、22(,)Q x y 为端点的线段中点坐标为1212,22x x y y ++⎛⎫ ⎪⎝⎭.则D 点的坐标为__________. (3)已知坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.设运动时间为(0)t t >秒.问:是否存在这样的t ,使ODP ODQ S S =△△,若存在,请求出t 的值;若不存在,请说明理由.(4)点F 是线段AC 上一点,满足FOC FCO ∠=∠,点G 是第二象限中一点,连OG ,使得AOG AOF ∠=∠.点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC ∠+∠∠的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由. ECF DPBA。
(完整版)广州市2016七年级数学下册期中考试卷(解析版)

广州市2016七年级数学下册期中考试卷(解析版)、选择题(每小题3分,满分24分)1 .方程6+3x=0的解是()A. x= - 2B. x=— 6C. x=2D. x=6的解集在数轴上表示正确的是3.下列长度的各组线段首尾相接能构成的三角形的是(A. 2cm、3cm、5cmB. 3cm、5cm、6cmC. 2cm、2cm、4cmD. 3cm、5cm、10cm5.A.6.小李在解方程5a-x=13 (x为未知数)时,误将-x看作+x,得方程的解为x=- 2,那么原方程的解为()A. x=- 3B. x=0C. x=2D. x=17.如图,AB// CD, Z1=58°, FG平分Z EFD 则Z FGB的度数等丁(A. 122°B. 151 °C. 116°D. 97-8 .已知关丁x、y的方程组]_口f满足x< 0且V< 0,则m的取值范围是二、填空题(每小题3分,共21分)r K =29. 请写出一个以 L ■(为解的二元一次方程: 10. 如图,已知△ AOC^A BOC ZAOB=70,则Z 1=度.11 .如图,将周长为10的^ ABC 沿BC 方向平■移2个单位得到△ DEF 12. 如图,在z\ABC 中,点D 是BC 边上的一点,/ B=50°, / BAD=30, 沿AD 折叠得到z\AED, AE 与BC 交丁点F.则Z EDF 的度数是.13. 一个多边形的内角和等丁它外角和的 7倍,则这个多边形的边数为 14. 如图所示,观察下列图形它们是按一定规律构造的,依照此规律,第 形中共有 个三角形.A. m >1_ 4 B. m<—C .<m<XX第2个图形 第3个图形第2页(共21页)则四边形 将 ZXABDn 个图15. 石美于X、y的二元一次"组(wg5的解是K 1 '那么夭于X、yr a(Zx+yJ - mG -y)=ie的二元一次方程组的解是bC2x4y)tn;(x - y)二IS三、解答题(本题共10个小题,共75分)“、e 矗卜1 3M+216. 解方程2^^.J 己17. 解不等式组1 、尸9 把它的解集在数轴上表示出来,并判断-1这个II 5数是否为该不等式组的解.4 -3 :2 -1 0 1 2 V 4Z18. 已知y=kx+b,当x=2 时,y=1 ;当x=- 1 时,y=4.(1) 求k、b的值;(2) 当x取何值时,y的值是非负数.19 .如图,10X 10的方格纸的两条对称轴a、b相交丁点O, A ABC的顶点均在格点上.(1) 对^ABC分别作下列变换:①画出△ ABC关丁直线a对称的△ A1B1C1;②将3B C向右平■移6个单位长度,画出平■移后的^ A2B2C2;③将AABC绕点。
学16—17届七年级下学期期中考试数学试题(附答案)

2016—2017学年度第二学期初一年级数学期中试卷一、选择题(每小题3分,共30分) 1.下列运算中,正确的是 ( )A.326a a a ⋅= B. 448b b b += C.824a a a ÷=D.2363(3)27p q p q -=-2.下列多项式相乘,能用平方差公式计算的是( )A .(2)(2)a b b a +-B .(23)(32)a b b a -+C .(3)(3)m n m n --+D 3. 如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( ) A .30° B .45° C . 60° D .75°第3题图 第5题图4.要使2(2)()x x b x a -+-中不含x 的一次项和二次项,则,a b 的值分别为( ) A .2,4a b =-=- B .2,4a b == C .2,4a b ==- D .2,4a b =-= 5.如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B ;④AD ∥BE ,且∠D=∠B ;⑤∠1+∠3+∠B=180°.其中能说明AB ∥DC 的条件有 ( ) A .5个 B .4个 C . 3个 D .2个6. 海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.如下图所示,是某港口从0时到12时的水深情况,下列说法不正确的是 ( ) A .时间是自变量,水深是因变量;B .3时时水最深,9时时水最浅;C .0时到3时港口水深在增加,3时到12时港口水深在减少;D .图象上共有3个时刻水深恰好为5米.第6题图7. 已知3,2x y xy -=-=,则(2)(2)x y +-的值是( ) A .4 B .-8 C .12 D .08. 下列说法中,正确的个数是( ) (1)在同一平面内,不相交的两条线段一定平行; (2)相等的角是对顶角;(3)两条直线被第三条直线所截,同位角相等;(4)两条平行线被第三条直线所截,一对内错角的角平分线互相平行; (5)从直线外一点到这条直线的垂线段,叫做这个点到直线的距离; (6)两个角互补,则一个角一定是钝角,另一个角一定是锐角. A . 1个 B.2个 C .3个 D .4个9. 如图,直线AB 、CD 相交于点O ,OE 平分∠BOC ,OF ⊥OE 于O ,若∠AOD=70°,则∠AOF=( ).A .35°B .45°C .55°D .65°10. 已知2510a a --= ,则221a a +的值为( ) A .5 B .25 C . 23 D .27第9题图 二、填空题(每小题3分,共18分)11.(1)(1)p p -+= ,62()a a ÷-= ,201620170.25(4)⨯-= ;12. 在电子显微镜下测得一个球体细胞的直径是5510cm -⨯,3102⨯个这样的细胞排成的细AB CDEF1 胞链的长度是 ;13.一个角的余角与它的补角之比为1:4,则这个角的度数是 ; 14. 已知2249x mxy y -+是关于,x y 的完全平方式,则m = ;15. 如图,把矩形ABCD 沿EF 对折,若∠1 = 500,则∠AEF 等于 ;16. 已知 925,310,a b ==则23a b -= .第15题图三、解答题(共52分) 17.(共12分)计算题:(1)22313()2a b ab ⋅-(2)(23)()(2)(2)a b a b a b a b -+--+(3)43()()()x y y x y x -÷-⋅-(4)(23)(23)m n m n -++-18.(5,其中2,1x y =-=.19.(5分)尺规作图(保留作图痕迹,不写作法):已知αβ∠∠、,求作一个角,使它等于αβ∠-∠.20.(5分)如图所示,梯形上底的长是x,下底的长是15,高是8,梯形面积是y .(1)梯形面积y与上底长x之间的关系式是什么?(2)用表格表示当x从10变到15时(每次增加1),y的相应值;(3)当x每增加1时,y如何变化?(4)当x=0时,y等于什么?此时图形是什么?21.(4分)如图所示,一个窗户被装饰布挡住了一部分,其中窗户的长a与宽b之比是3:2,部分的面积.(结果用只含字母b的代数式表示,保留 .)22.(6分)如图,已知∠1=∠2,∠B=∠C,试证明AB∥CD.23.(7分)图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)你认为图②中的阴影部分的正方形的边长等于_____________; (2)请用两种不同的方法求图②中阴影部分的面积:方法1:___________________; 方法2:___________________. (3)根据(2)请写出代数式22(),(),m n m n mn +-之间的等量关系__________________________;(4)根据(3)题中的等量关系,解决如下问题:若7,5,a b ab +==求2()a b -的值.24.(8分)探究:如图①,已知直线12//l l ,直线3l 和12l l 、分别交于点C 和D ,直线3l 上有一点P.(1)若点P 在C 、D 之间运动时,问∠PAC ,∠APB ,∠PBD 之间有怎样的关系?并说明理由.(2)若点P 在C 、D 两点的外侧运动时(点P 与点C 、D 不重合),请尝试自己画图,写出∠PAC ,∠APB ,∠PBD 之间的关系,并说明理由.(3)如图②,AB ∥EF ,∠C=90°,我们可以用类似的方法求出αβγ∠∠∠、、之间的关系,请直接写出αβγ∠∠∠、、之间的关系.图①图②西北大学附中初一年级数学期中试卷答案一、选择题 1. D 2. B 3. C 4. D 5. C 6. C 7. A 8. A 9. C 10. D 一、填空题11. 21p - 4a - -4 12. 1110-⨯cm 或0.1cm 13. 60° 14. 12± 15. 115° 16.120三、解答题17. (1)5738a b -(2)22a ab b -+ (3)222x xy y -+(4)224129m n n -+-18. 3126x x y --- 13319. 图略,注意写结论20.(1)1(15)84602y x x =+⨯=+ (2)(3)增加4(4)y=60 三角形 21.223216S b b π=- 22.141224//33//CE BF C B C B AB CD∠=∠∠=∠∴∠=∠∴∴∠=∠∠=∠∴∠=∠∴23. (1)m-n(2) 22(),()4m n m n mn -+- (3) 22()()4m n m n mn -=+- (4) 2924. (1)APB PAC PBD ∠=∠+∠ (2)上方:APB PBD PAC ∠=∠-∠ 下方:APB PAC PBD ∠=∠-∠(3)90αβγ∠+∠=∠+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年广东省广州十六中七年级(下)期中数学试卷一、选择题(共10小题,每题3分)1.(3分)下列图形中,不能通过其中一个四边形平移得到的是()A. B.C.D.2.(3分)下列命题中真命题是()A.同位角相等B.两点之间,线段最短C.相等的角是对顶角D.互补的角是邻补角3.(3分)实数(﹣3)2的平方根是()A.3 B.﹣3 C.±3 D.±4.(3分)下列实数:,,,,,1.010010001…,3.14,其中无理数有()A.1个 B.2个 C.3个 D.4个5.(3分)点P(﹣,1)在()A.第一象限B.第二象限C.第三象限D.第四象限6.(3分)小华将平面直角坐标系中的A(﹣4,3)沿着x轴方向向左平移了3个单位得到了B点,则B点的坐标是()A.(﹣7,3)B.(﹣1,3)C.(﹣4,0)D.(﹣4,6)7.(3分)如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为()A.65°B.55°C.45°D.35°8.(3分)小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你的给我,我就有10颗”.如果设小刚的弹珠数为x颗,小龙的弹珠数为y颗,则列出的方程组是()A.B.C.D.9.(3分)如果是方程x﹣3y=﹣3的一组解,那么代数式5﹣a+3b的值是()A.8 B.5 C.2 D.010.(3分)如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=()A.76°B.78°C.80°D.82°二、填空题(共6小题,每题3分)11.(3分)如图,已知AC∥BD,若∠1=35°,则∠2=°.12.(3分)点M(﹣2,3)到x轴的距离是.13.(3分)若x3=27,则x=.14.(3分)已知x、y是二元一次方程组的解,则x+y=.15.(3分)如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm 至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是cm.16.(3分)如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号).三、解答题(共72分)17.(8分)化简求值(1)﹣﹣(2)|2﹣|+|3﹣|.18.(10分)解二元一次方程组(1)(2).19.(10分)如图,在平面直角坐标系中有三个点A(﹣3,2),B(﹣5,1),C (﹣2,0),P(a,b)是三角形的边AC上一点,三角形ABC经平移后得到三角形A′B′C′,点P的对应点为P′(a+4,b+3).(1)画出平移后的三角形A′B′C′,写出点A′、B′、C′三个点的坐标.(2)求四边形ACC′A′的面积.20.(8分)如图,已知AC⊥AB,ED⊥AB,垂足为A、D,∠CAF=80°.求∠DGF的度数.21.(12分)如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.(1)用α表示∠ACP;(2)求证:AB∥CD;(3)若AP∥CF,求证:FC平分∠DCE.22.(12分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)23.(12分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足+|b ﹣2|=0.D为线段AC的中点.(1)则A点的坐标为;点C的坐标为.(2)在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(,).则D点的坐标为.(3)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP =S△ODQ,若存在,请求出t的值;若不存在,请说明理由.(4)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E 在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.2016-2017学年广东省广州十六中七年级(下)期中数学试卷参考答案与试题解析一、选择题(共10小题,每题3分)1.(3分)下列图形中,不能通过其中一个四边形平移得到的是()A. B.C.D.【考点】Q1:生活中的平移现象.【分析】根据平移与旋转的性质得出.【解答】解:A、能通过其中一个四边形平移得到,错误;B、能通过其中一个四边形平移得到,错误;C、能通过其中一个四边形平移得到,错误;D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,正确.故选:D.【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,导致误选.2.(3分)下列命题中真命题是()A.同位角相等B.两点之间,线段最短C.相等的角是对顶角D.互补的角是邻补角【考点】O1:命题与定理.【分析】根据平行线的性质对A进行判断;根据线段最短的公理对B进行判断;根据对顶角的定义对C进行判断;根据邻补角的定义对D进行判断.【解答】解:A、两直线平行,同位角相等,所以A选项错误;B、两点之间,线段最短,所以B选项正确;C、相等的角不一定是对顶角,所以C选项错误;D、有一条边共线且互补的两个角是邻补角,所以D选项错误.故选:B.【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.3.(3分)实数(﹣3)2的平方根是()A.3 B.﹣3 C.±3 D.±【考点】21:平方根.【分析】根据平方根的定义解答可得.【解答】解:∵(﹣3)2=9,∴实数(﹣3)2的平方根是±3,故选:C.【点评】本题主要考查平方根,熟练掌握平方根的定义是解题的关键.4.(3分)下列实数:,,,,,1.010010001…,3.14,其中无理数有()A.1个 B.2个 C.3个 D.4个【考点】26:无理数.【分析】根据无理数的定义(无理数是指无限不循环小数)逐个判断即可.【解答】解:无理数有,,1.010010001…,共3个,故选:C.【点评】本题考查了无理数,能熟记无理数的定义是解此题的关键,注意:无理数含有①含π的,②开方开不尽的根式,③一些有规律的数.5.(3分)点P(﹣,1)在()A.第一象限B.第二象限C.第三象限D.第四象限【考点】D1:点的坐标.【分析】根据平面直角坐标系中各象限内坐标符号的特点解答即可.【解答】解:∵点P(﹣,1)的横坐标是负数,纵坐标是正数,∴点P在第二象限.故选:B.【点评】解答此题的关键是熟知平面直角坐标系中四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.6.(3分)小华将平面直角坐标系中的A(﹣4,3)沿着x轴方向向左平移了3个单位得到了B点,则B点的坐标是()A.(﹣7,3)B.(﹣1,3)C.(﹣4,0)D.(﹣4,6)【考点】Q3:坐标与图形变化﹣平移.【分析】将点A的横坐标减去3,纵坐标不变即可得到B点的坐标.【解答】解:将平面直角坐标系中的A(﹣4,3)沿着x轴方向向左平移了3个单位得到了B点,则B点的坐标是(﹣4﹣3,3),即(﹣7,3).故选:A.【点评】此题主要考查坐标与图形变化﹣平移.掌握平移中的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.7.(3分)如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为()A.65°B.55°C.45°D.35°【考点】JA:平行线的性质.【分析】利用已知条件易求∠ACD的度数,再根据两线平行同位角相等即可求出∠1的度数.【解答】解:∵DA⊥AC,垂足为A,∴∠CAD=90°,∵∠ADC=35°,∴∠ACD=55°,∵AB∥CD,∴∠1=∠ACD=55°,故选:B.【点评】本题主要考查了平行线的性质,垂直的定义等知识点,熟记平行线的性质定理是解题关键.8.(3分)小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你的给我,我就有10颗”.如果设小刚的弹珠数为x颗,小龙的弹珠数为y颗,则列出的方程组是()A.B.C.D.【考点】99:由实际问题抽象出二元一次方程组.【分析】设小刚的弹珠数为x颗,小龙的弹珠数为y颗,根据题意,列方程组即可.【解答】解:设小刚的弹珠数为x颗,小龙的弹珠数为y颗,由题意得,x+y=10,x+y=10化简得,.故选:A.【点评】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.9.(3分)如果是方程x﹣3y=﹣3的一组解,那么代数式5﹣a+3b的值是()A.8 B.5 C.2 D.0【考点】92:二元一次方程的解.【分析】把x=a,y=b代入方程,再根据5﹣a+3b=5﹣(a﹣3b),然后代入求值即可.【解答】解:把x=a,y=b代入方程,可得:a﹣3b=﹣3,所以5﹣a+3b=5﹣(a﹣3b)=5+3=8,故选:A.【点评】本题考查了代数式的求值,正确对代数式变形,利用添括号法则是关键.10.(3分)如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=()A.76°B.78°C.80°D.82°【考点】JA:平行线的性质.【分析】分别过K、H作AB的平行线MN和RS,根据平行线的性质和角平分线的性质可用∠ABK和∠DCK分别表示出∠H和∠K,从而可找到∠H和∠K的关系,结合条件可求得∠K.【解答】解:如图,分别过K、H作AB的平行线MN和RS,∵AB∥CD,∴AB∥CD∥RS∥MN,∴∠RHB=∠ABE=∠ABK,∠SHC=∠DCF=∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣(∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC,又∠BKC﹣∠BHC=27°,∴∠BHC=∠BKC﹣27°,∴∠BKC=180°﹣2(∠BKC﹣27°),∴∠BKC=78°,故选:B.【点评】本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a∥b,b∥c⇒a∥c.二、填空题(共6小题,每题3分)11.(3分)如图,已知AC∥BD,若∠1=35°,则∠2=145°.【考点】JA:平行线的性质.【分析】首先根据两直线平行同位角相等可得∠1=∠3=35°,再根据邻补角互补计算出∠2的度数.【解答】解:如图,∵AC∥BD,∴∠1=∠3,∵∠1=35°,∴∠3=35°,∵∠1+∠2=180°,∴∠2=180°﹣∠3=180°﹣35°=145°,故答案为:145.【点评】此题主要考查了平行线的性质,关键是掌握平行线的性质:两直线平行,同位角相等.12.(3分)点M(﹣2,3)到x轴的距离是3.【考点】D1:点的坐标.【分析】根据点的坐标与其到x轴的距离的关系进行解答.【解答】解:M(﹣2,3)到x轴的距离是其纵坐标的绝对值,即为3.故填3.【点评】解答本题的关键是明确点的坐标与其到x轴的距离的关系.13.(3分)若x3=27,则x=3.【考点】24:立方根.【分析】根据立方根的定义解简单的高次方程.【解答】解:∵x3=27,∴x==3,故答案为:3【点评】此题是立方根,主要是用立方根的定义解简单的方程,解本题的关键是理解立方根的定义.14.(3分)已知x、y是二元一次方程组的解,则x+y=0.【考点】97:二元一次方程组的解.【分析】解方程组求得x、y的值,再把x与y的值代入x+y进行计算即可.【解答】解:,由①得,y=2x+3③,把③代入②得,x+8x+12=3,解得x=﹣1把x=﹣1代入③得y=1,∴方程组的解为,∴x+y=﹣1+1=0.故答案为0,【点评】本题考查了二元一次方程组的解和解二元一次方程组:同时满足二元一次方程组中各方程的未知数的值叫二元一次方程组的解;利用加减消元或代入消元解二元一次方程组.15.(3分)如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm 至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是24cm.【考点】Q2:平移的性质.【分析】根据平移的性质,经过平移,对应点所连的线段相等,对应线段相等,找出对应线段和对应点所连的线段,结合四边形的周长公式求解即可.【解答】解:根据题意,得A的对应点为A′,B的对应点为B′,C的对应点为C′,所以BC=B′C′,BB′=CC′,∴四边形AB′C′C的周长=CA+AB+BB′+B′C′+C′C=△ABC的周长+2BB′=20+4=24cm.故答案为:24.【点评】本题主要运用的知识点是:经过平移,对应点所连的线段平行且相等,对应线段平行且相等.16.(3分)如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论①②③(填编号).【考点】JA:平行线的性质.【分析】由于AB∥CD,则∠ABO=∠BOD=40°,利用平角等于得到∠BOC=(180﹣a)°,再根据角平分线定义得到∠BOE=(180﹣a)°;利用OF⊥OE,可计算出∠BOF=a°,则∠BOF=∠BOD,即OF平分∠BOD;利用OP⊥CD,可计算出∠POE=a°,则∠POE=∠BOF;根据∠POB=90°﹣a°,∠DOF=a°,可知④不正确.【解答】解:①∵AB∥CD,∴∠BOD=∠ABO=a°,∴∠COB=180°﹣a°=(180﹣a)°,又∵OE平分∠BOC,∴∠BOE=∠COB=(180﹣a)°.故①正确;②∵OF⊥OE,∴∠EOF=90°,∴∠BOF=90°﹣(180﹣a)°=a°,∴∠BOF=∠BOD,∴OF平分∠BOD所以②正确;③∵OP⊥CD,∴∠COP=90°,∴∠POE=90°﹣∠EOC=a°,∴∠POE=∠BOF;所以③正确;∴∠POB=90°﹣a°,而∠DOF=a°,所以④错误.【点评】本题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补;两直线平行,同位角相等.三、解答题(共72分)17.(8分)化简求值(1)﹣﹣(2)|2﹣|+|3﹣|.【考点】2C:实数的运算.【分析】(1)直接利用算术平方根以及立方根的性质分别化简得出答案;(2)直接利用绝对值的性质化简得出答案.【解答】解:(1)﹣﹣=3﹣+2=2.5;(2)|2﹣|+|3﹣|=﹣2+3﹣=1.【点评】此题主要考查了实数运算,正确化简各数是解题关键.18.(10分)解二元一次方程组(1)(2).【考点】98:解二元一次方程组.【分析】(1)(2)用加减消元法解方程组即可.【解答】解:(1)①+②得到,3x=15,x=5,把x=5代入①得到,y=﹣1,∴.(2)①﹣②×2得到,﹣7x=7,x=﹣1把x=﹣1代入②得到y=3,∴【点评】本题考查二元一次方程组的解法,解题的关键是熟练掌握加减消元法、代入消元法解方程组,属于中考常考题型.19.(10分)如图,在平面直角坐标系中有三个点A(﹣3,2),B(﹣5,1),C (﹣2,0),P(a,b)是三角形的边AC上一点,三角形ABC经平移后得到三角形A′B′C′,点P的对应点为P′(a+4,b+3).(1)画出平移后的三角形A′B′C′,写出点A′、B′、C′三个点的坐标.(2)求四边形ACC′A′的面积.【考点】Q4:作图﹣平移变换.【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;(2)利用四边形ACC′A′所在矩形面积减去周围三角形面积进而得出答案.【解答】解:(1)如图所示:△A′B′C′,即为所求,A′(1,5)、B′(﹣1,4)、C′(2,3);(2)四边形ACC′A′的面积为:5×5﹣×3×4﹣×1×2﹣×3×4﹣×1×2=11.【点评】此题主要考查了平移变换以及四边形面积求法,正确得出对应点位置是解题关键.20.(8分)如图,已知AC⊥AB,ED⊥AB,垂足为A、D,∠CAF=80°.求∠DGF的度数.【考点】J3:垂线.【分析】先根据平行线的性质求出∠EGF,再根据邻补角的性质即可解决问题.【解答】解:∵AC⊥AB,ED⊥AB,∴AC∥DE,∴∠GAC=∠EGF=80°,∴∠DGF=180°﹣∠EGF=180°﹣80°=100°.【点评】本题考查垂线的性质、平行线的性质、邻补角的性质,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.21.(12分)如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.(1)用α表示∠ACP;(2)求证:AB∥CD;(3)若AP∥CF,求证:FC平分∠DCE.【考点】JB:平行线的判定与性质.【分析】(1)由角平分线的定义可得∠PAC=α,在Rt△PAC中根据直角三角形的性质可求得∠ACP;(2)结合(1)可求得∠ACD,可证明∠ACD+∠BAC=180°,可证明AB∥CD;(3)由平行线的性质可得∠ECF=∠CAP,∠ECD=∠CAB,结合条件可证得∠ECF=∠FCD,可证得结论.【解答】(1)解:∵AP平分∠BAC,∴∠CAP=∠BAP=α,∵∠P=90°,∴∠ACP=90°﹣∠CAP=90°﹣α;(2)证明:由(1)可知∠ACP=90°﹣α,∵CP平分∠ACD,∴∠ACD=2∠ACP=180°﹣2α,又∠BAC=2∠BAP=2α,∴∠ACD+∠BAC=180°,∴AB∥CD;(3)证明:∵AP∥CF,∴∠ECF=∠CAP=α,由(2)可知AB∥CD,∴∠ECD=∠CAB=2α,∴∠DCF=∠ECD﹣∠ECF=α,∴∠ECF=∠DCF,∴CF平分∠DCE.【点评】本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a∥b,b∥c⇒a∥c.22.(12分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)【考点】9A:二元一次方程组的应用.【分析】(1)本题的等量关系是:甲做8天需要的费用+乙作8天需要的费用=3520元.甲组6天需付的费用+乙做12天需付的费用=3480元,由此可得出方程组求出解.(2)根据(1)得出的甲乙每工作一天,商店需付的费用,然后分别计算出甲单独做12天需要的费用,乙单独做24天需要的费用,让两者进行比较即可.(3)本题可将每种施工方法的施工费加上施工期间商店损失的费用,然后将不同方案计算出的结果进行比较,损失最少的方案就是最有利商店的方案.【解答】解:(1)设:甲组工作一天商店应付x元,乙组工作一天商店付y元.由题意得解得答:甲、乙两组工作一天,商店各应付300元和140元.(2)单独请甲组需要的费用:300×12=3600元.单独请乙组需要的费用:24×140=3360元.答:单独请乙组需要的费用少.(3)请两组同时装修,理由:甲单独做,需费用3600元,少赢利200×12=2400元,相当于损失6000元;乙单独做,需费用3360元,少赢利200×24=4800元,相当于损失8160元;甲乙合作,需费用3520元,少赢利200×8=1600元,相当于损失5120元;因为5120<6000<8160,所以甲乙合作损失费用最少.答:甲乙合作施工更有利于商店.【点评】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系:甲做8天需要的费用+乙作8天需要的费用=3520元.列出方程组,再求解.23.(12分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足+|b ﹣2|=0.D为线段AC的中点.(1)则A点的坐标为(0,4);点C的坐标为(2,0).(2)在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(,).则D点的坐标为(1,2).(3)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP =S△ODQ,若存在,请求出t的值;若不存在,请说明理由.(4)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E 在线段OA上运动的过程中,的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.【考点】KY:三角形综合题.【分析】(1)根据绝对值和算术平方根的非负性,求得a,b的值即可;(2)根据中点坐标公式进行解答即可;(3)先得出CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,再根据S△ODP =S△ODQ,列出关于t的方程,求得t的值即可;(4)过H点作AC的平行线,交x轴于P,先判定OG∥AC,再根据角的和差关系以及平行线的性质,得出∠PHO=∠GOF=∠1+∠2,∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,最后代入进行计算即可.【解答】解:(1)∵(a﹣2b)2+|b﹣2|=0,∴a﹣2b=0,b﹣2=0,解得a=4,b=2,∴A(0,4),C(2,0);故答案为(0,4),(2,0).(2)∵A(0,4),C(2,0),D为线段AC的中点,∴D(,),即D(1,2).故答案是:(1,2).(3)如图1中,由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,∴0<t≤2时,点Q在线段AO上,即CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,∴S△DOP=OP•y D=(2﹣t)×2=2﹣t,S△DOQ=OQ•x D=×2t×1=t,∵S△ODP =S△ODQ,∴2﹣t=t,∴t=1;(4)的值不变,其值为2.理由如下:如图2中,∵∠2+∠3=90°,又∵∠1=∠2,∠3=∠FCO,∴∠GOC+∠ACO=180°,∴OG∥AC,∴∠1=∠CAO,∴∠OEC=∠CAO+∠4=∠1+∠4,如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,∴∠PHO=∠GOF=∠1+∠2,∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,∴===2.【点评】本题考查三角形综合题、非负数的性质、三角形的面积、平行线的性质等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题,属于中考压轴题.。
