九年级数学一轮复习练习:反比例函数
九年级数学:反比例函数练习题(含解析)

九年级数学:反比例函数练习题(含解析)一、精心选一选1﹒下列函数中,y 是x 的反比例函数的为( )A.y =2x +1B.y =22xC.y =-15xD.y =x 2-2x 2﹒函数y =k 23kx 是反比例函数,则k 的值是( )A.-1B.2C.±2D.±2 3﹒若y 与x 成反比例,x 与z 成反比例,则y 是z 的( )A.正比例函数B.反比例函数C.一次函数D.二次函数4﹒一次函数y =-x +a -3(a 为常数)与反比例函数y =-4x的图象交于A 、B 两点,当A 、B 两点关于原点对称时,a 的值是( )A.0B.-3C.3D.45﹒反比例函数y =-2x的图象上有两点P 1(x 1,y 1),P 2(x 2,y 2),若x 1<0<x 2,则下列结论正确的是( )A.y 1<y 2<0B.y 1<0<y 2C.y 1>y 2>0D. y 1>0>y 26﹒如图,直线y =-x +3与y 轴交于点A ,与反比例函数y =k x(k ≠0)的图象交于点C ,过点C 作CB ⊥x 轴于点B ,AO =3BO ,则反比例函数的解析式为( )A.y =4xB.y =-4xC.y =2xD.y =-2x7﹒已知反比例函数y =kx的图象经过点P (-1,2),则这个函数的图象位于( )A.第二、三象限B.第一、三象限C.第三、四象限D.第二、四象限8﹒如果等腰三角形的底边长为x ,底边上的高为y ,它的面积为10时,则y 与x 的函数关系式为( ) A.y =10x B.y =5xC.y =20xD.y =20x9﹒已知变量y 与x 成反比例函数关系,当x =3时,y =-6,那么当y =3时,x 的值是( )A.6B.-6C.9D.-910. 某次实验中,测得两个变量v 与m 的对应数据如下表,则v 与m 之间的关系最接近下列函数中的是( )m 1 2 3 4 5 6 7v -6.10 -2.90 -2.01 -1.51 -1.19 -1.05 -0.86A.v =m 2-2B.v =-6mC.v =-3m -1D.v =-m二、细心填一填11.若函数y =(m +3)28m x -是反比例函数,则m =_______________. 12.若函数y =1m x-是反比例函数,则m 的取值范围是_______;当m =______时,y 是x 的反比例函数,且比例系数为3.13.若函数y =-kx +2k +2与y =k x(k ≠0)的图象有两个不同的交点,则k 的取值范围是_____. 14.如图,直线y =-x +b 与双曲线y =-1x(x <0)交于点A ,与x 轴交于点B ,则OA 2-OB 2=__________.(第14题图)15.一批零件300个,一个工人每小时做15个,用关系表示人数x 与完成任务所需时间y 之间的函数关系为_______________________.16.把一个长、宽、高分别为3cm ,2cm ,1cm 的长方形铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S (cm 2)与高h (cm )之间的函数关系式为________________________. 三、解答题17.某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t 天完成.(1)写出每天生产夏凉小衫w (件)与生产时间t (天)(t >4)之间的函数关系式; (2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?18.某开发公司计划生产一批产品,需要加工后才能投放市场,已知甲厂每天可加工60件,8天便可完成任务.(1)这批产品的数量是________件;(2)若这批产品由乙厂加工,请写出乙厂每天加工件数M(件)与所需天数t(天)之间的函数表达式;(3)如果要求乙厂在5天内将所有产品加工完,那么乙厂每天至少加工多少件?19.已知y=y1+y2,y1与x2成正比例关系,y2与x成反比例关系,且当x=1时,y=3;当x=-1时,y=1.(1)求y与x之间的函数表达式;(2)当x=-12时,求y的值.20.反比例函数y=k(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)x作AB⊥x轴于点B,交反比例函数图于点D,且AB=3BD.(1)求k的值;(2)求点C的坐标;(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.21.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系;(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?22.某商场出售一批进价为2元的贺卡,在营运过程中发现此商品的日销价为x(元)与销售量y(张)之间有如下关系:x/元 3 4 5 6y/张20 15 12 10(1)猜测并确定y与x的函数关系式;(2)当日销售单价为10元时,贺卡的日销售量是多少张?(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大,并求出最大利润.23.在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(-2,-4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有无数多个.(1)若点M(2,a)是反比例函数y=kx(k为常数,k≠0)图象上的“理想点”,求这个反比例函数的表达式;(2)函数y=3mx-1(m为常数,m≠0)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.21.5 反比例函数课时练习题(1)参考答案一、精心选一选1﹒下列函数中,y 是x 的反比例函数的为()A.y =2x +1B.y =22x C.y =-15xD.y =x 2-2x 解答:A.y =2x+1,y 是x 的一次函数,故A 不合题意;B.y =22x ,y 是x 2的反比例函数,故B 不合题意; C.y =-15x,y 是x 的反比例函数,故C 符合题意;D.y =x 2-2x ,y 是x 的二次函数,故D 不合题意, 故选:C. 2﹒函数y =k 23kx -是反比例函数,则k 的值是( )A.-1B.2C.±2D. 解答:∵y =k 23kx -是反比例函数,∴k 2-3=-1,且k ≠0, 解得:k , 故选:D.3﹒若y 与x 成反比例,x 与z 成反比例,则y 是z 的( )A.正比例函数B.反比例函数C.一次函数D.二次函数 解答:∵y 与x 成反比例,x 与z 成反比例, ∴设y =1k x①,x =k 2z ②, 把②代入①得:y =12k k z, 故y 与z 成反比例函数关系, 故选:B.4﹒一次函数y=-x+a-3(a 为常数)与反比例函数y=-4x的图象交于A、B两点,当A、B 两点关于原点对称时,a的值是()A.0B.-3C.3D.4【解答】设A(t,-4t),∵A、B两点关于原点对称,∴B(-t,4t),把A(t,-4t ),B(-t,4t),分别代入y=-x+a-3得:4343t att at⎧-=-+-⎪⎪⎨⎪=+-⎪⎩①②,①+②得:2a-6=0,则a=3,故选:C.5﹒反比例函数y=-2x的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是()A.y1<y2<0B.y1<0<y2C.y1>y2>0D. y1>0>y2【解答】∵反比例函数y=﹣2x中k=﹣2<0,∴此函数图象在二、四象限,∵x1<0<x2,∴A(x1,y1)在第二象限;点B(x2,y2)在第四象限,∴y1>0>y2,故选:D.6﹒如图,直线y=-x+3与y轴交于点A,与反比例函数y=kx(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为()A.y=4x B.y=-4xC.y=2x D.y=-2x【解答】∵直线y=﹣x+3与y轴交于点A,∴A(0,3),即OA=3,∵AO=3BO,∴OB=1,∴点C的横坐标为﹣1,∵点C在直线y=﹣x+3上,∴点C(﹣1,4),把C(﹣1,4)代入y=kx得:k=-4,∴反比例函数的解析式为:y=-4x.故选:B.7﹒已知反比例函数y=kx的图象经过点P(-1,2),则这个函数的图象位于()A.第二、三象限B.第一、三象限C.第三、四象限D.第二、四象限【解答】∵反比例函数y=kx的图象经过点P(-1,2),∴k=-1×2=-2<0,∴反比例函数的图象分布在二、四象限,故选:D.8﹒如果等腰三角形的底边长为x,底边上的高为y,它的面积为10时,则y与x的函数关系式为()A.y=10xB.y=5xC.y=20xD.y=20x解答:根据题意,得:12xy=10,∴y=20x,故选:C.9﹒已知变量y与x成反比例函数关系,当x=3时,y=-6,那么当y=3时,x的值是()A.-6B. 6C.-9D.9解答:设y=kx,把x=3,y=-6代入得:k=-18,∴y=18x,∴当x=3时,y=-6,故选:A.10. 某次实验中,测得两个变量v 与m 的对应数据如下表,则v 与m 之间的关系最接近下列函数中的是( )A.v =m 2-2B.v =-6mC.v =-3m -1D.v =-m解答:将m 的值代入各选项的函数关系式中,看v 的值是否与表中数据相近,若相近,则为正确的解析式,如把m =1代入各式:A.v =-1;B.v =-6;C.v =-4;D.v =-6.再把m =2代入各式:A.v =2;B.v =-12;C.v =-7;D.v =-3.由此可发现D 选项的值与表中数据相近,故D 选项符合题意, 故选:D. 二、细心填一填11. 3; 12. m ≠1,4; 13. y =6x; 14. 2; 15. y =20x ; 16. S =6h. 11.若函数y =(m +3)28m x -是反比例函数,则m =_______________. 解答:∵函数y =(m +3)28m x-是反比例函数,∴8-m 2=-1,且m +3≠0, ∴m =3, 故答案为:3. 12.若函数y =1m x-是反比例函数,则m 的取值范围是_______;当m =______时,y 是x 的反比例函数,且比例系数为3. 解答:∵函数y =1m x-是反比例函数, ∴m -1≠0,则m ≠1, 由m -1=3得:m =4, 故答案为:m ≠1,4.13.若函数y =-kx +2k +2与y =kx(k ≠0)的图象有两个不同的交点,则k 的取值范围是_____.【解答】把方程组22y kx kkyx=-++⎧⎪⎨=⎪⎩消去y得:-kx+2k+2=kx,整理得:kx2-(2k+2)x+k=0,由题意得:△=(2k+2)2-4k2>0,解得:k>-12,∴当k>-12时,函数y=-kx+2k+2与y=kx(k≠0)的图象有两个不同的交点,故答案为:k>-12且k≠0.14.如图,直线y=-x+b与双曲线y=-1x(x<0)交于点A,与x轴交于点B,则OA2-OB2=__________.【解答】∵直线y=﹣x+b与双曲线y=﹣1x(x<0)交于点A,设A的坐标(x,y),∴x+y=b,xy=﹣1,而直线y=﹣x+b与x轴交于B点,∴OB=b,∴又OA2=x2+y2,OB2=b2,∴OA2﹣OB2=x2+y2﹣b2=(x+y)2﹣2xy﹣b2=b2+2﹣b2=2.故答案为:2.15.一批零件300个,一个工人每小时做15个,用关系表示人数x与完成任务所需时间y之间的函数关系为_______________________.解答:由题意得:人数x与完成任务所需时间y之间的函数关系为y=30015x=20x,故答案为:y=20x.16.把一个长、宽、高分别为3cm,2cm,1cm的长方形铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为________________________.解答:由题意得:Sh=3×2×1,则S=6h,故答案为:S=6h.三、解答题17.某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t 天完成.(1)写出每天生产夏凉小衫w (件)与生产时间t (天)(t >4)之间的函数关系式; (2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?解答:(1)每天生产夏凉小衫w (件)与生产时间t (天)(t >4)之间的函数关系式为:w =1600t(t >4), (2)由题意,得:16004t --1600t=16001600(4)(4)t t t t ---=264004t t -,答:每天要多做264004t t-(t >4)件夏凉小衫才能完成任务. 18.某开发公司计划生产一批产品,需要加工后才能投放市场,已知甲厂每天可加工60件,8天便可完成任务.(1)这批产品的数量是________件;(2)若这批产品由乙厂加工,请写出乙厂每天加工件数M (件)与所需天数t (天)之间的函数表达式;(3)如果要求乙厂在5天内将所有产品加工完,那么乙厂每天至少加工多少件? 解答:(1)60×8=480(件), 故答案为:480;(2)乙厂每天加工件数M (件)与所需天数t (天)之间的函数表达式为y =480t(t >0), (3)把t =5代入上式得M =96,故如果要求乙厂在5天内将所有产品加工完,那么乙厂每天至少加工96件.19.已知y =y 1+y 2,y 1与x 2成正比例关系,y 2与x 成反比例关系,且当x =1时,y =3;当x =-1时,y =1.(1)求y 与x 之间的函数表达式; (2)当x =-12时,求y 的值. 解答:∵y =y 1+y 2,y 1与x 2成正比例关系,y 2与x 成反比例关系, ∴可设y 1=k 1x 2,y 2=2k x,把x =1时,y =3和x =-1时,y =1代入得:121231k k k k +=⎧⎨-=⎩,解得:1221k k =⎧⎨=⎩,∴y 与x 之间的函数表达式为y =2x 2+1x, (2)当x =-12时, y =2×(-12)2+(-2)=-32.20.反比例函数y =k x(k ≠0,x >0)的图象与直线y =3x 相交于点C ,过直线上点A (1,3)作AB ⊥x 轴于点B ,交反比例函数图于点D ,且AB =3BD . (1)求k 的值; (2)求点C 的坐标;(3)在y 轴上确定一点M ,使点M 到C 、D 两点距离之和d =MC +MD 最小,求点M 的坐标. 【解答】(1)∵A (1,3), ∴AB =3,OB =1, ∵AB =3BD , ∴BD =1, ∴D (1,1),将D (1,1)代入反比例函数解析式得:k =1; (2)由(1)知,k =1, ∴反比例函数的解析式为:y =1x,由31y x y x =⎧⎪⎨=⎪⎩得:33x y ⎧=⎪⎨⎪=⎩或33x y ⎧=-⎪⎨⎪=-⎩, ∵x >0,∴C (3,3), (3)如图,作C 关于y 轴的对称点C ′,连接C ′D 交y 轴于M ,则d =MC +MD 最小, ∴C ′(-3,3), 设直线C ′D 的解析式为y =kx +b ,∴331k b k b ⎧=-+⎪⎨⎪=+⎩,解得:323232k b ⎧=-⎪⎨=-⎪⎩, ∴y =(3-23)x +23-2, 当x =0时,y =23-2, ∴M (0,23-2).21.某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y (微克/毫升)与服药时间x (小时)之间的函数关系如图所示(当4≤x ≤10时,y 与x 成反比例).(1)根据图象分别求出血液中药物浓度上升和下降阶段y 与x 之间的函数关系; (2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?【解答】(1)当0≤x <4时,设直线解析式为:y =kx , 将(4,8)代入得:8=4k , 解得:k =2,故直线解析式为:y =2x ,当4≤x ≤10时,设直反比例函数解析式为:y =k x, 将(4,8)代入得:8=4k , 解得:k =32,故反比例函数解析式为:y =32x ; 因此血液中药物浓度上升阶段的函数关系式为y =2x (0≤x <4),下降阶段的函数关系式为y =32x(4≤x ≤10). (2)当y =4,则4=2x ,解得:x =2, 当y =4,则4=32x,解得:x =8, ∵8﹣2=6(小时),∴血液中药物浓度不低于4微克/毫升的持续时间6小时.22.某商场出售一批进价为2元的贺卡,在营运过程中发现此商品的日销价为x (元)与销售量y(张)之间有如下关系:(1)猜测并确定y与x的函数关系式;(2)当日销售单价为10元时,贺卡的日销售量是多少张?(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大,并求出最大利润.解答:(1)由表中数据可以发现x与y的乘积是一个定值,所以可知y与x成反比例,设y=kx,把(3,20)代入得:k=60,∴y与x的函数关系式为y=60x;(2)当x=10时,y=6,所以日销售单价为10元时,贺卡的日销售量是6张;(3)∵W=(x-2)y=60-120x,又∵x≤10,∴当x=10时,W最大=60-12010=48,故日销售单价为10元时,每天获得的利润最大,最大利润为48元.23.在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(-2,-4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有无数多个.(1)若点M(2,a)是反比例函数y=kx(k为常数,k≠0)图象上的“理想点”,求这个反比例函数的表达式;(2)函数y=3mx-1(m为常数,m≠0)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.解答:∵点M(2,a)是反比例函数y=kx(k为常数,k≠0)图象上的“理想点”,∴a=4,∵点M(2,4)在反比例函数y=kx(k为常数,k≠0)图象上∴k=2×4=8,∴反比例函数的解析式为y=8x;(2)假设函数y=3mx-1(m为常数,m≠0)的图象上存在“理想点”(x,2x), 则有3mx-1=2x,整理得:(3m-2)x=1,当3m-2≠0,即m≠23时,函数图象上存在“理想点”,为(132m-,232m-),当3m-2=0,即m=23时,x无解,综合上述,当m≠23时,函数图象上存在“理想点”,为(132m-,232m-),当m=23时,函数图象上不存在“理想点”.。
2024年中考数学一轮复习-反比例函数K值与几何面积综合(解析版)
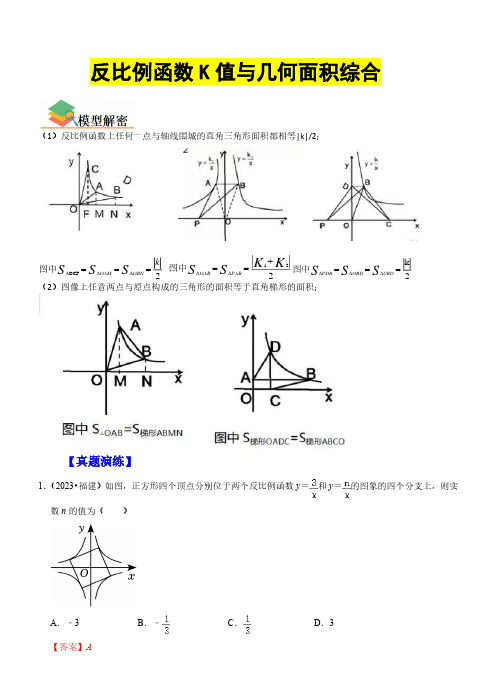
反比例函数K 值与几何面积综合(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;【真题演练】 1.(2023•福建)如图,正方形四个顶点分别位于两个反比例函数y =和y =的图象的四个分支上,则实数n 的值为( )A .﹣3B .﹣C .D .3【答案】A【解答】解:连接正方形的对角线,由正方形的性质知对角线交于原点O,过点A,B分别作x轴的垂线.垂足分别为C、D,点B在函数y=上,如图:∵四边形是正方形,∴AO=BO,∠AOB=∠BDO=∠ACO=90°,∴∠CAO=90°﹣∠AOC=∠BOD,∴△AOC≌△BOD(AAS),∴S△AOC=S△OBD==,∵点A在第二象限,∴n=﹣3,故选:A.2.(2023•张家界)如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,点D在AB上,且AD=AB,反比例函数y=(k>0)的图象经过点D及矩形OABC的对称中心M,连接OD,OM,DM.若△ODM的面积为3,则k的值为()A.2B.3C.4D.5【答案】C【解答】解:解法一:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵矩形OABC的对称中心M,∴延长OM恰好经过点B,M(,),∵点D在AB上,且AD=AB,∴D(,b),∴BD=a,∴S△BDM=BD•h=×a×(b﹣)=ab,∵D在反比例函数的图象上,∴ab=k,∵S△ODM=S△AOB﹣S△AOD﹣S△BDM=ab﹣k﹣ab=3,∴ab=16,∴k=ab=4,解法二:连接BM,因为点M是矩形的对称中心,∴三角形DMO的面积=三角形DMB的面积,则三角形DBO的面积为6,∵AD=1/4AB,∴AD:DB=1:3,∴三角形ADO的面积:三角形DBO的面积为1:3,即三角形ADO的面积为2,∴K=4.故选:C.3.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是()A.﹣6B.﹣12C.﹣D.﹣9【答案】C【解答】解:设BC与y轴的交点为F,B(b,),则A(﹣b,﹣),b>0,由题意知,AO=BO,即O是线段AB的中点,过A作AE⊥BC于点E,∵AC=AB,AE⊥BC,∴BE=CE,AE∥y轴,∴CF=3BF=3b,∴C(﹣3b,),∴D(﹣3b,),∴CD=,BC=4b,∴S△BCD=,∴k=﹣.故选:C.4.(2023•宜宾)如图,在平面直角坐标系xOy中,点A、B分别在y、x轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为()A.B.C.D.【答案】B【解答】解:如图,过点N作NQ⊥x轴于点Q,过C作CT⊥y轴交y轴于T,交NQ于K,设OA=a,OP=b,BM=c,N(m,n),∵OP:BP=1:4,BM=CM,∴A(0,a),B(5b,0),M(5b,c),C(5b,2c),∵∠NCK=∠ACT,∠NKC=90°=∠ATC,∴△NKC∽△ATC,∴==,∵NC=2AN,∴CK=2TK,NK=AT,∴,解得,∴,∴,,∴,∵△APN的面积为3,∴S梯形OANQ﹣S△AOP﹣S△NPQ=3,∴,∴2ab+bc=9,将点M(5b,c),代入得:,整理得:2a=7c,将2a=7c代入2ab+bc=9得:7bc+bc=9,∴,∴,故选:B.5.(2022•日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=()A.3B.﹣3C.D.【答案】B【解答】解:∵y1、y2的图象均在第一象限,∴k1>0,k2>0,∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,∴S△OAM=S△OCN=k1,∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,∴S矩形OABC=k2,∴S四边形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,∴k2﹣k1=3,∴k1﹣k2=﹣3,故选:B.6.(2022•郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x <0)的图象于点B,连接OA,OB,则△AOB的面积是()A.3B.5C.6D.10【答案】B【解答】解:∵点A在函数y=(x>0)的图象上,∴S△AOC=×2=1,又∵点B在反比例函数y=﹣(x<0)的图象上,∴S△BOC=×8=4,∴S△AOB=S△AOC+S△BOC=1+4=5,故选:B.7.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9【答案】B【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图象上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B.8.(2022•黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是()A.2B.1C.﹣1D.﹣2【答案】D【解答】解:设B(a,),∵四边形OBAD是平行四边形,∴AB∥DO,∴A(,),∴AB=a﹣,∵平行四边形OBAD的面积是5,∴(a﹣)=5,解得k=﹣2,故选:D.9.(2023•连云港)如图,矩形OABC的顶点A在反比例函数y=(x<0)的图象上,顶点B、C在第一象限,对角线AC∥x轴,交y轴于点D.若矩形OABC的面积是6,cos∠OAC=,则k=﹣.【答案】﹣.【解答】解:作AE⊥x轴于E,∵矩形OABC的面积是6,∴△AOC的面积是3,∵∠AOC=90°,cos∠OAC=,∴,∵对角线AC∥x轴,∴∠AOE=∠OAC,∵∠OEA=∠AOC=90°,∴△OEA∽△AOC,∴,∴,∴S△OEA=,∵S△OEA=|k|,k<0,∴k=﹣.故答案为:﹣.10.(2023•枣庄)如图,在反比例函数(x>0)的图象上有P1,P2,P3,…P2024等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2023,则S1+S2+S3+…+S2023=.【答案】.【解答】解:∵P1,P2,P3,...P2024的横坐标依次为1,2,3, (2024)∴阴影矩形的一边长都为1,将除第一个矩形外的所有矩形向左平移至y轴,∴S 1+S2+S3+…+S2023=,把x=2024代入关系式得,y=,即OA=,∴S矩形OABC=OA•OC=,由几何意义得,=8,∴=8﹣=.故答案为:.11.(2023•朝阳)如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接P A,PB.若△ABP的面积等于3,则k的值为.【答案】6.【解答】解:设反比例函数的解析式为y=,∵△AOB的面积=△ABP的面积=3,△AOB的面积=|k|,∴|k|=3,∴k=±6;又∵反比例函数的图象的一支位于第一象限,∴k>0.∴k=6.故答案为:6.12.(2023•衢州)如图,点A,B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF,反比例函数y=(k>0)的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为.【答案】见试题解答内容【解答】解:设OA=4a,∵AO=2AB,∴AB=2a,∴OB=AB+OA=6a,则B(6a,0),由于在正方形ABEF中,AB=BE=2a,∵Q为BE中点,∴BQ=AB=a,∴Q(6a,a),∵Q在反比例函数y=(k>0))上,∴k=6a×a=6a2,∵四边形OACD是正方形,∴C(4a,4a),∵P在CD上,∴P点纵坐标为4a,∵P在反比例函数y=(k>0)上,∴P点横坐标为:x=,∴P(,4a),∵作PM⊥x轴于点M,QN⊥y轴于点N,∴四边形OMNH是矩形,∴NH=,MH=a,∴S矩形OMHN=NH×MH=×a=6,则k=24,故答案为:24.13.(2023•锦州)如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC 的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为.【答案】4.【解答】解:过点C作CD⊥y轴于点D,如图:设点C的坐标为(a,b),点A的坐标为(0,c),∴CD=a,OA=c,∵△AOC的面积是6,∴,∴ac=12,∵点C(a,b)在反比例函数(x>0)的图象上,∴k=ab,∵点B为AC的中点,∴点,∵点B在反比例函数(x>0)的图象上,∴,即:4k=a(b+c),∴4k=ab+ac,将ab=k,ac=12代入上式得:k=4.故答案为:4.14.(2023•黄石)如图,点A(a,)和B(b,)在反比例函数y=(k>0)的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为;若△AOB的面积为,则=.【答案】,2.【解答】解:因为点A(a,)在反比例函数y=的图象上,则,又a>0,解得k=5.根据k的几何意义可知,.过点B作x轴的垂线,垂足为D,则S△OBD+S梯形ACDB=S△AOC+S△AOB,又根据k的几何意义可知,S△OBD=S△AOC,则S梯形ACDB=S△AOB.又△AOB的面积为,且A(a,),B(b,),所以,即.解得.又a>b>0,所以.故答案为:,2.15.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为6.【答案】6.【解答】解:如图,延长CD交y轴于E,连接OD,∵矩形ABCD的面积是8,∴S△ADC=4,∵AC=2AO,∴S△ADO=2,∵AD∥OE,∴△ACD∽△OCE,∴AD:OE=AC:OC=2:3,∴S△ODE=3,由几何意义得,=3,∵k>0,∴k=6,故答案为:6.16.(2023•绍兴)如图,在平面直角坐标系xOy中,函数(k为大于0的常数,x>0)图象上的两点A (x1,y1),B(x2,y2),满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是.【答案】2.【解答】解:如图,延长CA交y轴于E,延长CB交x轴于点F,∴CE⊥y轴,CF⊥x轴,∴四边形OECF为矩形,∵x2=2x1,∴点A为CE的中点,由几何意义得,S△OAE=S△OBF,∴点B为CF的中点,∴S△OAB=S矩形OECF=6,∴S矩形OECF=16,∴S△ABC=×16=2.故答案为:2.217.(2022•烟台)如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为.【答案】见试题解答内容【解答】解:因为D为AC的中点,△AOD的面积为3,所以△AOC的面积为6,所以k=12=2m.解得:m=6.故答案为:6.18.(2022•黄石)如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k=.【答案】8.【解答】解:如图,过点E作EH⊥BC于H,设点A(a,),C(c,0),∵点E是矩形ABCD的对角线的交点,∴E(,),∵点E在反比例函数y=的图象上,∴=k,∴c=3a,∵△OCE的面积为6,∴OC•EH=c•=×3a•=6,∴k=8,故答案为:8.19.(2022•衢州)如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC=6,则k=.【答案】.【解答】解:如图,作CM⊥AB于点M,DN⊥AB于点N,设C(m,),则OM=m,CM=,∵OE∥CM,AE=CE,∴==1,∴AO=m,∵DN∥CM,CD=2BD,∴===,∴DN=,∴D的纵坐标为,∴=,∴x=3m,即ON=3m,∴MN=2m,∴BN=m,∴AB=5m,∵S△ABC=6,∴5m•=6,∴k=.故答案为:.20.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为.【答案】9.【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图,∵△OMN是边长为10的等边三角形,∴OM=ON=MN=10,∠MON=∠M=∠MNO=60°设OC=b,则BC=,OB=2b,∴BM=OM﹣OB=10﹣2b,B(b,b),∵∠M=60°,AB⊥OM,∴AM=2BM=20﹣4b,∴AN=MN﹣AM=10﹣(20﹣4b)=4b﹣10,∵∠AND=60°,∴DN==2b﹣5,AD=AN=2b﹣5,∴OD=ON﹣DN=15﹣2b,∴A(15﹣2b,2b﹣5),∵A、B两点都在反比例函数y=(x>0)的图象上,∴k=(15﹣2b)(2b﹣5)=b•b,解得b=3或5,当b=5时,OB=2b=10,此时B与M重合,不符题意,舍去,∴b=3,∴k=b•b=9,故答案为:9.21.(2022•鄂尔多斯)如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2=.【答案】见试题解答内容【解答】解:作EH⊥y轴于点H,则四边形BCHE、AEHO都为矩形,∵∠ECF=45°,∴∠OCD+∠OCF=45°,∵∠DOC+∠OCF=45°,∴∠BCE=∠OCD,∵BC=OC,∠B=∠COD,∴△BCE≌△OCD(ASA),∴S△BCE=S△COD=5,∴S△CEH=5,S矩形BCHE=10,∴根据反比例函数系数k的几何意义得:k1﹣k2=S矩形BCHE=10,故答案为:10.22.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为.【答案】y=﹣.【解答】解:如图,作AD⊥x轴于D,BC⊥x轴于C,∴∠ADO=∠BCO=90°,∵∠AOB=90°,∴∠AOD+∠BOC=90°,∴∠AOD+∠DAO=90°,∴∠BOC=∠DAO,∵OB=OA,∴△BOC≌△OAD(AAS),∵点B在反比例函数y=(x>0)的图象上,∴S△OBC=,∴S△OAD=,∴k=﹣1,∴经过点A的反比例函数解析式为y=﹣.故答案为:y=﹣.23.(2022•绍兴)如图,在平面直角坐标系xOy中,点A(0,4),B(3,4),将△ABO向右平移到△CDE 位置,A的对应点是C,O的对应点是E,函数y=(k≠0)的图象经过点C和DE的中点F,则k的值是.【答案】6.【解答】解:过点F作FG⊥x轴于点G,FH⊥y轴于点H,过点D作DQ⊥x轴于点Q,如图所示,根据题意可知,AC=OE=BD,设AC=OE=BD=a,∴四边形ACEO的面积为4a,∵F为DE的中点,FG⊥x轴,DQ⊥x轴,∴FG为△EDQ的中位线,∴FG=DQ=2,EG=EQ=,∴四边形HFGO的面积为2(a+),∴k=4a=2(a+),解得:a=,∴k=6.故答案为:6.24.(2022•内蒙古)如图,在平面直角坐标系中,Rt△OAB的直角顶点B在x轴的正半轴上,点O与原点重合,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C,交AB于点D,连接CD.若△ACD的面积是1,则k的值是.【答案】.【解答】解:连接OD,过C作CE∥AB,交x轴于E,∵∠ABO=90°,反比例函数y=(x>0)的图象经过OA的中点C,∴S△COE=S△BOD=k,S△ACD=S△OCD=1,∵CE∥AB,∴△OCE∽△OAB,∴△OCE与△OAB得到面积比为1:4,∴4S△OCE=S△OAB,∴4×k=1+1+k,∴k=.故答案为:.。
2023年中考苏科版数学一轮复习专题练习-反比例函数

2023年中考数学一轮复习专题练习反比例函数一、选择题1. 已知反比例函数y =1x,下列结论不正确...的是( ) A .图象经过点(1,1) B .图象在第一. 三象限C. 当x >1时,0<y <1 D .当x <0时,y 随着x 的增大而增大2. 反比例函数)0(1>-=x xy 的图象如图所示,随着x 值的增大,y 值( ) A .增大 B .减小 C .不变 D .先增大后减小3. 在同一平面直角坐标系中,函数y =mx +m 与y =xm (m ≠0)的图象可能是( )A B C D4. 如图,A . B 两点在双曲线3yx上,分别经过A . B 两点向轴作垂线段,已知S 阴影=1,则S 1+S 2=( )A .3B .4C .5D .65. 如图,O 是坐标原点,菱形OABC 的顶点A 的坐标为(﹣3,4),顶点C 在x 轴的负半轴上,函数y=(x <0)的图象经过顶点B ,则k 的值为( )A .﹣12B .﹣27C .﹣32D .﹣36 6. 若点A (﹣5,y 1),B (﹣3,y 2),C (2,y 3)在反比例函数y=的图象上,则y 1,y 2,y 3的大小关系是( )A .y 1<y 2<y 3B .y 1<y 3<y 2C .y 2<y 1<y 3D .y 3<y 2<y 1二、填空题 第2题 第4题 第5题 第13题7. 已知函数y=(k+2)x是反比例函数,则k=.8. 如果反比例函数y=(k为常数)的图象在二. 四象限,那么k的取值范围是.9. 我们知道,一次函数y=x+1的图象可以由正比例函数y=x的图象向上平移1个长度单位得到.将函数y=的图象向平移个长度单位得到函数y=的图象.10. 三个完全相同的小球上分别标有数字﹣1. 2. 3,从这三个球中任意取出一个球,不放回,再取出一个,两次数据依次记为a. b,那么函数过二. 四象限的概率是.11. 已知正比例函数y=-4x与反比例函数的图象交于A. B两点,若点A的坐标为(x,4),则点B的坐标为______12. 直线y=kx(k>0)与双曲线y=交于A(x1,y1)和B(x2,y2)两点,则3x1y2﹣9x2y1的值为_____________.13. 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=______________.三、解答题14. 将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m,若反比例函数y=的图象与直线y=3x+m相交于点A,且点A的纵坐标是3.(1)求m和k的值;(2)结合图象求不等式3x+m>的解集.15. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(3,1)在反比例函数y=的图象上.(1)求反比例函数y=的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP=S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.16. 如图,在平面直角坐标系中A 点的坐标为(8,y ) ,AB ⊥x 轴于点B , sin ∠OAB =54,反比例函数xk y 的图象的一支经过AO 的中点C ,且与AB 交于点D. (1)求反比例函数解析式;(2)若函数y = 3x 与y = k x的图象的另一支交于点M ,求三角形OMB 与四边形OCDB 的面积的比.17. 如图,在直角坐标系中,Rt △ABC 的直角边AC 在x 轴上,∠ACB=90°,AC=1,反比例函数y=(k >0)的图象经过BC 边的中点D (3,1).(1)求这个反比例函数的表达式;(2)若△ABC 与△EFG 成中心对称,且△EFG 的边FG 在y 轴的正半轴上,点E 在这个函数的图象上.①求OF 的长;②连接AF ,BE ,证明四边形ABEF 是正方形.18. 如图,在平面直角坐标系中,▱ABCO的顶点A在x轴正半轴上,两条对角线相交于点D,双曲线y=(x>0)经过C,D两点.(1)求▱ABCO的面积.(2)若▱ABCO是菱形,请直接写出:①tan∠AOC=.②将菱形ABCO沿x轴向左平移,当点A与O点重合时停止,则平移距离t与y轴所扫过菱形的面积S之间的函数关系式:.。
2023年中考九年级数学一轮复习提升练习 综合题 :反比例函数

2023年中考九年级数学一轮复习提升练习(综合题):反比例函数一、综合题1.已知:如图1,函数y1=k x和y2=xk(k>1)的图象相交于点A和点B.(1)求点A和点B的坐标(用含k的式子表示);(2)如图2,点C的坐标为(1,k),点D是第一象限内函数y1的图象上的动点,且在点A的右侧,直线AC、BC、AD、BD分别与x轴相交于点E、F、G、H.①判定△CEF的形状,并说明理由;②点D在运动的过程中,∠CAD和∠CBD的度数和是否变化?如果变化,说明理由;如果不变,求出∠CAD和∠CBD的度数和.2.在平面直角坐标系中,我们把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),(√2,√2),…都是“梦之点”,显然“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=nx(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s-1(k,s为常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由.3.如图,点A是坐标原点,点D是反比例函数y=6x(x>0)图象上一点,点B在x轴上,AD=BD,四边形ABCD是平行四边形,BC交反比例函数y=6x(x>0)图象于点E.(1)平行四边形BCD 的面积等于 ;(2)设D 点横坐标为m ,试用m 表示点E 的坐标;(要有推理和计算过程) (3)求 CE:EB 的值; (4)求 EB 的最小值.4.如图,一次函数y=kx+b 的图象与反比例函数y= mx 的图象交于点A (﹣3,m+8),B (n ,﹣6)两点.(1)求一次函数与反比例函数的解析式; (2)求△AOB 的面积.5.已知双曲线y=1x(x >0),直线l 1:y ﹣√2=k (x ﹣√2)(k <0)过定点F 且与双曲线交于A ,B 两点,设A (x 1,y 1),B (x 2,y 2)(x 1<x 2),直线l 2:y=﹣x+√2. (1)若k=﹣1,求△OAB 的面积S ; (2)若AB=52√2,求k 的值;(3)设N (0,2√2),P 在双曲线上,M 在直线l 2上且PM△x 轴,求PM+PN 最小值,并求PM+PN 取得最小值时P 的坐标.(参考公式:在平面直角坐标系中,若A (x 1,y 1),B (x 2,y 2)则A ,B 两点间的距离为AB=√(x 1−x 2)2+(y 1−y 2)2)6.已知反比例函数y=1−2mx( m为常数)的图象在一、三象限.(1)求m的取值范围.(2)如图,若该反比例函数的图象经过▱ABCD的顶点D,点A,B的坐标分别为(0,3),(-2,0).①求出反比例函数表达式;②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为▲ .若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P的个数为▲ .7.绘制函数y=x+1x的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0;列表﹣﹣描点﹣﹣连线,得到该函数的图象如图所示.x…-4-3-2-1−12−13−141413121234…y…−414−313−212−2−212−313−4144143132122212313414…观察函数图象,回答下列问题:(1)函数图象在第象限;(2)函数图象的对称性是A.既是轴对称图形,又是中心对称图形B.只是轴对称图形,不是中心对称图形C.不是轴对称图形,而是中心对称图形D.既不是轴对称图形,也不是中心对称图形(3)在x>0时,当x=时,函数y有最(大,小)值,且这个最值等于;在x<0时,当x=时,函数y有最(大,小)值,且这个最值等于;(4)方程x+1x=−2x+1是否有实数解?说明理由.8.菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:(1)求点D的坐标;(2)若反比例函数y= kx(k≠0)的图象经过点H,则k=;(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.9.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数解析式,并画出这个函数的图象;(2)若反比例函数y2=k x的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.10.受新冠肺炎疫情的影响,运城市某化工厂从2020年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2020年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:(1)分别写出该化工厂对生产线进行升级改造前后,y与x的函数表达式.(2)到第几个月时,该化工厂月利润才能再次达到100万元?(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?11.(如图,四边形ABCD在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数y1=n x与y2=4n x的图象上,对角线AC△BD于点P,AC△x轴于点N(2,0)(1)若CN=12,试求n的值;(2)当n=2,点P是线段AC的中点时,试判断四边形ABCD的形状,并说明理由;(3)直线AB与y轴相交于E点.当四边形ABCD为正方形时,请求出OE的长度.12.如图点A、B分别在x,y轴上,点D在第一象限内,DC△x轴于点C,AO=CD=2,AB=DA= √5,反比例函数y= k x(k>0)的图象过CD的中点E.(1)求证:△AOB△△DCA;(2)求k的值;(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.13.如图所示,一次函数y=kx+b的图象与x轴、y轴分别交于点A、B,且与反比例函数y=m x的图象在第二象限交于点C,CD⊥x轴,垂足为点D.若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;(2)若两函数图象的另一个交点为E,连结DE,求△CDE的面积;(3)直接写出不等式kx+b≤ mx的解集.14.某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数y1=k1x与y2=k2x(k2>k1>0)在第一象限图象的性质,经历了如下探究过程:操作猜想:(1)如图①,当k1=2,k2=6时,在y轴的正方向上取一点A作x轴的平行线交y1于点B,交y2于点C.当OA=1时,AB=,BC=,BCAB=;当OA=3时,AB=,BC=,BCAB=;当OA=a时,猜想BCAB=(2)在y轴的正方向上任意取点A作x轴的平行线,交y1于点B、交y2于点C,请用含k1、k2的式子表示BCAB的值,并利用图②加以证明.(3)如图③,若k2=12,BCAB=12,在y轴的正方向上分别取点A、D(OD>OA)作x轴的平行线,交y1于点B、E,交y2于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.15.如图,直线y=2x+2与y轴交于A点,与反比例函数y=k x(x>0)的图象交于点M,过M 作MH△x轴于点H,且tan△AHO=2.(1)求H点的坐标及k的值;(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;(3)点N(a,1)是反比例函数y=kx(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.16.如图,双曲线y1=k1x与直线y2=xk2的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=k1x上的任意一点,且0<a<4.(1)分别求出y1、y2的函数表达式;(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;(3)当点P在双曲线y1=k1x上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.答案解析部分1.【答案】(1)解:由题意,联立 {y =k x y =x k,解得 {x =k y =1 或 {x =−ky =−1 , ∵ 点 A 在第一象限,点 B 在第二象限,且 k >1 ,∴A(k ,1),B(−k ,−1)(2)解:①△CEF 是等腰直角三角形,理由如下: 设直线 BC 的解析式为 y =k 0x +b 0 ,将点 B(−k ,−1),C(1,k) 代入得: {−kk 0+b 0=−1k 0+b 0=k ,解得 {k 0=1b 0=k −1 , 则直线 BC 的解析式为 y =x +k −1 ,当 y =0 时, x +k −1=0 ,解得 x =1−k ,即 F(1−k ,0) , 同理可得:点 E 的坐标为 E(1+k ,0) , ∴CF =√(1−k −1)2+(0−k)2=√2k , CE =√(1+k −1)2+(0−k)2=√2k , EF =1+k −(1−k)=2k ,∴CE =CF ,CE 2+CF 2=4k 2=EF 2 , ∴△CEF 是等腰直角三角形;②由题意,设点 D 的坐标为 D(m ,k m ) ,则 m >k >1 , ∵△CEF 是等腰直角三角形, ∴∠CFE =∠CEF =45° , ∴∠BFH =∠AEG =135° ,设直线 BD 的解析式为 y =k 1x +b 1 ,将点 B(−k ,−1),D(m ,k m ) 代入得: {−kk 1+b 1=−1mk 1+b 1=k m ,解得 {k 1=1m b 1=k−m m, 则直线 BD 的解析式为 y =1m x +k−m m,当 y =0 时, 1m x +k−m m =0 ,解得 x =m −k ,即 H(m −k ,0) ,同理可得:点 G 的坐标为 G(k +m ,0) ,∴DH=√(m−k−m)2+(0−k m)2=k m√1+m2,DG=√(k+m−m)2+(0−k m)2=k m√1+m2,∴DH=DG,∴∠DHG=∠DGH,∵∠DHG=∠BHF,∴∠DGH=∠BHF,∴∠CAD+∠CBD=∠AEG+∠DGH+∠CBD,=∠BFH+∠BHF+∠CBD,=180°,即∠CAD与∠CBD的度数和不变,度数和为180°2.【答案】(1)解:根据题意,“梦之点”就是有关函数图象与直线y=x的交点,其坐标就是对应的方程组的解.由题意可得:m=2由点P(2, 2)在反比例函数y=nx图象上,可得n=2×2=4故所求的反比例函数的解析式为y=4 x(2)解:由题意可得:(△)当k=0时,y=s−1,此时“梦之点”的坐标为(s−1, s−1 ).(△)当k≠0 时, (3k−1)x=1−s显然,此方程的解的情况决定函数y=3kx+s−1的图象上“梦之点”的存在情况,当k=13, s≠1时,方程无解,不存在“梦之点”;当k=13, s=1时,方程有无数个解,此时存在无数个“梦之点”,“梦之点”的坐标可表示为(ℎ,ℎ)(ℎ为任意实数);当k≠13时,得{x=1−s3k−1y=1−s3k−1,即“梦之点”的坐标为(1−s3k−1, 1−s 3k−1)3.【答案】(1)12(2)解:由题意D(m,6 m),由(1)可知AB=2m,∵四边形ABCD是平行四边形,∴CD=AB=2m,∴C(3m,6 m).∵B(2m,0),C(3m,6 m),∴直线BC的解析式为y=6m2x−12m,由{y=6xy=6m2x−12m,解得{x=(√2+1)my=6√2−6m或{x=(1−√2)my=6(1+√2)m(舍弃),∴E((√2+1)m,6√2−6m);(3)解:作EF⊥x轴于F,CG⊥x轴于G. ∵EF//CG,∴CEBE=FGBF=√2+1)m(√2+1)m−2m=√2√2−1=√2;(4)解:∵CEBE=√2∴BE=√2+1,要使得BE最小,只要AD最小,∵AD=√m2+36m2=√(m−6m)2+12,∴AD的最小值为2√3,∴BE的最小值为2√3√2+1=2√6−2√3.4.【答案】(1)解:将A(﹣3,m+8)代入反比例函数y= mx得,m−3=m+8,解得m=﹣6,m+8=﹣6+8=2,所以,点A的坐标为(﹣3,2),反比例函数解析式为y=﹣6 x,将点B(n,﹣6)代入y=﹣6x得,﹣6n=﹣6,解得n=1,所以,点B 的坐标为(1,﹣6),将点A (﹣3,2),B (1,﹣6)代入y=kx+b 得, {−3k +b =2k +b =−6 , 解得 {k =−2b =−4,所以,一次函数解析式为y=﹣2x ﹣4; (2)解:设AB 与x 轴相交于点C , 令﹣2x ﹣4=0解得x=﹣2, 所以,点C 的坐标为(﹣2,0), 所以,OC=2, S △AOB =S △AOC +S △BOC , = 12 ×2×3+ 12 ×2×1, =3+1, =4.5.【答案】(1)解:当k=-1时,l 1:y=﹣x+2√2,联立得,{y =−x +2√2y =1x ,化简得x 2﹣2√2x+1=0, 解得:x 1=√2﹣1,x 2=√2+1,设直线l 1与y 轴交于点C ,则C (0,2√2). S △OAB =S △AOC ﹣S △BOC =12•2√2•(x 2﹣x 1)=2√2;(2)解:根据题意得:{y −√2=k(x −√2)y =1x 整理得:kx 2+√2(1﹣k )x ﹣1=0(k <0), ∵△=[√2(1﹣k )]2﹣4×k×(﹣1)=2(1+k 2)>0,∴x 1、x 2 是方程的两根,∴{x 1+x 2=√2(k−1)k x 1·x 2=−1k①, ∴AB=√(x 1−x 2)2+(y 1−y 2)2=√(x 1−x 2)2+(1x 1−1x 2)2=√(x 1−x 2)2(1+1x 12·x 22)=√[(x 1+x 2)2−4x 1x 2](1+1x 12·x 22),将①代入得,AB=√2(k 2+1)2k 2=√2(k 2+1)−k (k <0),∴√2(k 2+1)−k=5√22,整理得:2k 2+5k+2=0, 解得:k=﹣2,或 k=12;(3)解:∵直线l 1:y ﹣√2=k (x ﹣√2)(k <0)过定点F, ∴ F (√2,√2). 如图:设P (x ,1x ),则M (﹣1x +√2,1x),则PM=x+1x ﹣√2=√(x +1x −√2)2=√x 2+1x 2−2√2(x +1x )+4, ∵PF=√(x −√2)2+(1x −√2)2=√x 2+1x2−2√2(x +1x )+4, ∴PM=PF .∴PM+PN=PF+PN≥NF=2,当点P 在NF 上时等号成立,此时NF 的方程为y=﹣x+2√2,由(1)知P(√2﹣1,√2+1),∴当P(√2﹣1,√2+1)时,PM+PN最小值是2.6.【答案】(1)解:根据题意,得1−2m>0,解得m<12,∴m的取值范围是m<12.(2)解:①∵四边形ABCD是平行四边形,A(0,3),B(−2,0),∴D(2,3).把D(2,3)代入y=1−2mx,得3=1−2m2,∴1−2m=6 .∴反比例函数表达式为y=6x;②(3,2)或(-2,-3)或(-3,-2);4 7.【答案】(1)一、三(2)C(3)1;小;2;−1;大;−2(4)解:方程x+1x=﹣2x+1没有实数解,理由为:y=x+1x与y=﹣2x+1在同一直角坐标系中无交点.8.【答案】(1)解:x2﹣9x+18=0,(x﹣3)(x﹣6)=0,x=3或6,∵CD>DE,∴CD=6,DE=3,∵四边形ABCD是菱形,∴AC△BD,AE=EC= √62−32=3 √3,∴△DCA=30°,△EDC=60°,Rt△DEM中,△DEM=30°,∴DM= 12DE= 32,∵OM△AB,∴S菱形ABCD= 12AC•BD=CD•OM,∴12×6√3×6=6OM,OM=3 √3,∴D(﹣32,3 √3)(2)解:(3)解:如图1,①∵DC=BC,△DCB=60°,∴△DCB是等边三角形,∵H是BC的中点,∴DH△BC,∴当Q与B重合时,如图1,四边形CFQP是平行四边形,∵FC=FB,∴△FCB=△FBC=30°,∴△ABF=△ABC﹣△CBF=120°﹣30°=90°,∴AB△BF,CP△AB,Rt△ABF中,△FAB=30°,AB=6,∴FB=2 √3=CP,∴P(92,√3);②如图2,∵四边形QPFC是平行四边形,∴CQ△PH,由①知:PH△BC,∴CQ△BC,Rt△QBC中,BC=6,△QBC=60°,∴△BQC=30°,∴CQ=6 √3,连接QA,∵AE=EC,QE△AC,∴QA=QC=6 √3,∴△QAC=△QCA=60°,△CAB=30°,∴△QAB=90°,∴Q(﹣92,6 √3),由①知:F(32,2 √3),由F到C的平移规律可得P到Q的平移规律,则P(﹣92﹣3,6 √3﹣√3),即P(﹣152,5√3);③如图3,四边形CQFP是平行四边形,同理知:Q(﹣92,6 √3),F(32,2 √3),C(92,3 √3),∴P(212,﹣√3);综上所述,点P的坐标为:(92,√3)或(﹣152,5 √3)或(212,﹣√3).9.【答案】(1)解:由题意y1=|x|.函数图象如图所示:(2)解:①当点A在第一象限时,由题意A(2,2),∴2=k2,∴k=4.同法当点A在第二象限时,k=−4,②观察图象可知:当k>0时,x>2时,y1>y2或x<0时,y1>y2.当k<0时,x<−2时,y1>y2或x>0时,y1>y2.10.【答案】(1)解:由题意得,设前5个月中y= k x,把x=1,y=100代入得,k=100,∴y与x之间的函数关系式为y= 100x(0<x<5,且x为整数),把x=5代入,得y=20,由题意设5月份以后y与x的函数关系式为y=10x+b,把x=5,y=20代入得,20=10×5+b,解得:b=-30,∴y与x之间的函数关系式为y=10x-30(x>5且x为整数);(2)解:在函数y=10x−30中,令y=100,得10x−30=100解得:x=13答:到第13个月时,该化工厂月利润再次达到100万元.(3)解:在函数y=100x中,当y=50时,x=2,∵100>0,y随x的增大而减小,∴当y<50时,x>2在函数y=10x−30中,当y<50时,得10x−30<50解得:x<8∴2<x<8且x为整数;∴x可取3,4,5,6,7;共5个月.答:该化工厂资金紧张期共有5个月.11.【答案】(1)解:∵点N的坐标为(2,0),CN△x轴,且CN=12,∴点C的坐标为(2,1 2).∵点C在反比例函数y1=nx的图象上,∴n=2× 12=1.(2)解:四边形ABCD为菱形,理由如下:当n=2时,y1=nx=2x,y2=4nx=8x.当x=2时,y1=2x=1,y2=8x=4,∴点C的坐标为(2,1),点A的坐标为(2,4).∵点P是线段AC的中点,∴点P的坐标为(2,5 2).当y=52时,2x=52,8x=52,解得:x=45,x=165,∴点B的坐标为(45,52),点D的坐标为(165,52),∴BP=2﹣45=65,DP=165﹣2=65,∴BP=DP.又∵AP=CP,AC△BD,∴四边形ABCD为菱形.(3)解:∵四边形ABCD为正方形,∴AC=BD,且点P为线段AC及BD的中点.当x=2时,y1=12n,y2=2n,∴点A的坐标为(2,2n),点C的坐标为(2,12n),AC=32n,∴点P的坐标为(2,54 n).同理,点B的坐标为(45,54n),点D的坐标为(165,54n),BD=125.∵AC=BD,∴32n=125,∴n=8 5,∴点A的坐标为(2,165),点B的坐标为(45,2).设直线AB的解析式为y=kx+b(k≠0),将A(2,165),B(45,2)代入y=kx+b,得:{2k+b=16545k+b=2,解得:{b=65k=1,∴直线AB的解析式为y=x+ 6 5.当x=0时,y=x+ 65=65,∴点E的坐标为(0,6 5),∴当四边形ABCD为正方形时,OE的长度为6 5.12.【答案】(1)证明:∵点A、B分别在x,y轴上,点D在第一象限内,DC△x轴,∴△AOB=△DCA=90°,在Rt△AOB和Rt△DCA中,AO=CD,AB=DA∴Rt△AOB△Rt△DCA(HL)(2)解:在Rt△ACD中,CD=2,AD= √5,∴AC= =1,∴OC=OA+AC=2+1=3,∴D点坐标为(3,2),∵点E为CD的中点,∴点E的坐标为(3,1),k=3×1=3(3)解:点G在反比例函数的图象上.理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG△△DCA,∴FG=CA=1,BF=DC=2,△BFG=△DCA=90°,而OB=AC=1,∴OF=OB+BF=1+2=3,∴G点坐标为(1,3),∵1×3=3,∴G(1,3)在反比例函数y= 的图象上13.【答案】(1)解:∵OB=2OA=3OD=12∴OA=6,OD=4∴A(6,0),B(0,12)把A(6,0),B(0,12)分别代入y=kx+b得:{6k+b=0b=12,解之得:m=−4×20=−80∴一次函数的解析式为y=−2x+12令x=−4,则y=20∴C(−4,20)把C(−4,20)代入y=mx得:m=−4×20=−80∴反比例函数的解析式为y=−80 x;(2)解:解方程组{y=−2x+12y=−80x得:{x1=−4y1=20,{x2=10y2=−8∴E(10,−8)∴SΔCDE=SΔADC+SΔADE=12AD⋅(CD+|y E|)=12×(4+6)×(20+8)=140(3)解:如图:当x<-4时,y=mx的图象在y=kx+b的下方,即kx+b>mx;当−4≤ x<0时,y=mx的图象在y=kx+b的上方,即kx+b≤mx;当0<x<10时,y=mx的图象在y=kx+b的下方,即kx+b>mx;当x≥10时,y=mx的图象在y=kx+b的上方,即kx+b≤mx;综上可得,不等式kx+b≤ mx的解集为−4≤ x<0或x≥10.14.【答案】(1)2;4;2;23;43;2;2 数学思考:(2)BCAB=k2−k1 k1证明:∵AB·OA=k1,AC·OA=k2,∴AC·OA−AB·OA=BC·OA=k2−k1,∴BCAB=BC·OAAB·OA=k2−k1k1.推广应用:(3)解:若四边形ADFB是正方形,设点B的坐标为(a,b)(a>0,b>0),则有DF=DA=AB=a,OA=b,OD=a+b,∴点F的坐标为(a,a+b).∵k2=12,BCAB=k2−k1k1=12,∴12−k1k1=12,解得:k1=8.∵点B在y=8x图象上,点F在y=12x图象上,∴ab=8,a (a+b)=12,∴a2=12−8=4,∴a=2,∴b=4,∴OA=4,点B的坐标为(2,4).15.【答案】(1)解:由y=2x+2可知A(0,2),即OA=2,∵tan△AHO=2,∴OH=1,∴H (1,0),∵MH△x轴,∴点M的横坐标为1,∵点M在直线y=2x+2上,∴点M的纵坐标为4,即M(1,4),∵点M在y=kx上,∴k=1×4=4;(2)解:①当AM=AP时,∵A(0,2),M(1,4),∴AM=√5,则AP=AM=√5,∴此时点P的坐标为(0,2﹣√5)或(0,2+ √5);②若AM=PM时,设P(0,y),则PM=√(1−0)2+(4−y)2,∴√(1−0)2+(4−y)2=√5,解得y=2(舍)或y=6,此时点P的坐标为(0,6),综上所述,点P的坐标为(0,6)或(0,2+ √5),或(0,2﹣√5);(3)解:∵点N(a,1)在反比例函数y=4x(x>0)图象上,∴a=4,∴点N(4,1),延长MN交x轴于点C,设直线MN的解析式为y=mx+n,则有{m+n=44m+n=1,,解得{m=−1n=5,∴直线MN的解析式为y=﹣x+5.∵点C是直线y=﹣x+5与x轴的交点,∴点C的坐标为(5,0),OC=5,∵S△MNQ=3,∴S△MNQ=S△MQC﹣S△NQC=12×QC×4﹣12×QC×1=32QC=3,∴QC=2,∵C(5,0),Q(m,0),∴|m﹣5|=2,∴m=7或3,故答案为7或3.16.【答案】(1)解:把点A(4,1)代入双曲线y1=k1x得k1=4,∴双曲线的解析式为y1=4x;把点A(4,1)代入直线y2=xk2得k2=4,∴直线的解析式为y2=14x(2)解:∵点P(a,b)在y1=4x的图象上,∴ab=4,∵4a=b,∴4a2=4,则a=±1,∵0<a<4,∴a=1,∴点P的坐标为(1,4),又∵双曲线y1=4x与直线y2=14x的图象交于A、B两点,且点A的坐标为(4,1),∴点B的坐标为(−4,−1),过点P作PG△y轴交AB于点G,如图所示,把x=1代入y2=14x,得到y=14,∴点G的坐标为(1,1 4),∴PG =4−14=154,∴S△ABP=12PG(x A−x B)=12×154×8=15(3)解:PE=PF.理由如下:∵点P(a,b)在y1=4x的图象上,∴b=4 a,∵点B的坐标为(−4,−1),设直线PB的表达式为y=mx+n,∴{am+n=4a−4m+n=−1,∴{m=1an=4a−1,∴直线PB的表达式为y=1a x+4a−1,当y=0时,x=a−4,∴E点的坐标为(a−4,0),同理:直线PA的表达式为y=−1a x+4a+1,当y=0时,x=a+4,∴F点的坐标为(a+4,0),过点P作PH△x轴于H,如图所示,∵P点坐标为(,∴H点的坐标为(a,0),∴EH =x H−x E=a−(a−4)=4,FH =x F−x H=a+4−a=4,∴EH=FH,∴PE=PF.。
中考一轮复习 数学专题09 反比例函数(学生版)

专题09 反比例函数一、单选题1.(2022·天津)若点()()()123,2,,1,,4A x B x C x -都在反比例函数8y x=的图像上,则123,,x x x 的大小关系是( ) A .123x x x <<B .231x x x <<C .132x x x <<D .213x x x <<2.(2022·云南)反比例函数y =6x的图象分别位于( )A .第一、第三象限B .第一、第四象限C .第二、第三象限D .第二、第四象限3.(2022·贵州贵阳)如图,在平面直角坐标系中有P ,Q ,M ,N 四个点,其中恰有三点在反比例函数()0ky k x =>的图象上.根据图中四点的位置,判断这四个点中不在函数k y x=的图象上的点是( )A .点PB .点QC .点MD .点N4.(2021·辽宁阜新)已知点()11,A x y ,()22,B x y 都在反比例函数1y x=-的图象上,且120x x <<,则1y ,2y 的关系是( ) A .12y y >B .12y y <C .120y y +=D .120y y -=5.(2021·广西梧州)如图,在同一平面直角坐标系中,直线y =t (t 为常数)与反比例函数y 14x=,y 21x =-的图象分别交于点A ,B ,连接OA ,OB ,则△OAB 的面积为( )A .5tB .52t C .52D .56.(2020·辽宁营口)反比例函数y =1x(x <0)的图象位于( )A .第一象限B .第二象限C .第三象限D .第四象限7.(2020·广西贺州)在反比例函数2y x=中,当1x =-时,y 的值为( ) A .2B .2-C .12D .12-8.(2020·四川巴中)如图,一次函数y 1=ax +b (a ≠0)与反比例函数2ky x=(k ≠0,x >0)的交点A 坐标为(2,1),当y 1≤y 2时,x 的取值范围是( )A .0<x ≤2B .0<x <2C .x >2D .x ≥29.(2020·辽宁阜新)若()2,4A 与()2,B a -都是反比例函数(0)ky k x=≠图象上的点,则a 的值是( ) A .4B .4-C .2D .2-10.(2020·山东烟台)如图,正比例函数y 1=mx ,一次函数y 2=ax+b 和反比例函数y 3=kx的图象在同一直角坐标系中,若y 3>y 1>y 2,则自变量x 的取值范围是( )A .x <﹣1B .﹣0.5<x <0或x >1C .0<x <1D .x <﹣1或0<x <1 11.(2020·黑龙江大庆)已知正比例函数1y k x =和反比例函数2k y x=,在同一直角坐标系下的图象如图所示,其中符合120k k ⋅>的是( )A .△△B .△△C .△△D .△△12.(2020·山东淄博)如图,在直角坐标系中,以坐标原点O (0,0),A (0,4),B (3,0)为顶点的Rt△AOB ,其两个锐角对应的外角角平分线相交于点P ,且点P 恰好在反比例函数y =kx的图象上,则k 的值为( )A .36B .48C .49D .6413.(2020·山东威海)一次函数y ax a =-与反比例函数(0)ay a x=≠在同一坐标系中的图象可能是( ) A . B .C .D .14.(2020·黑龙江鹤岗)如图,正方形ABCD 的两个顶点B ,D 在反比例函数ky x=的图象上,对角线AC ,BD 的交点恰好是坐标原点O ,已知(1,1)B -,则k 的值是( )A .-5B .-4C .-3D .-115.(2020·湖南娄底)如图,平行于y 轴的直线分别交1k y x=与2ky x =的图象(部分)于点A 、B ,点C 是y轴上的动点,则ABC 的面积为( )A .12k k -B .()1212k k - C .21k k - D .()2112k k - 16.(2021·贵州黔西)对于反比例函数y =﹣5x,下列说法错误的是( )A .图象经过点(1,﹣5)B .图象位于第二、第四象限C .当x <0时,y 随x 的增大而减小D .当x >0时,y 随x 的增大而增大17.(2021·辽宁朝阳)如图,O 是坐标原点,点B 在x 轴上,在OAB 中,AO =AB =5,OB =6,点A 在反比例函数y =kx(k ≠0)图象上,则k 的值( )A .﹣12B .﹣15C .﹣20D .﹣3018.(2021·湖南湘西)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为21yx 的函数图象.根据这个函数的图象,下列说法正确的是( )A .图象与x 轴没有交点B .当0x >时0y >C .图象与y 轴的交点是1(0,)2-D .y 随x 的增大而减小19.(2021·辽宁大连)下列说法正确的是( ) △反比例函数2y x=中自变量x 的取值范围是0x ≠; △点()3,2P -在反比例函数6y x=-的图象上;△反比例函数3y x=的图象,在每一个象限内,y 随x 的增大而增大. A .△△B .△△C .△△D .△△△20.(2022·广西贺州)已知一次函数y kx b =+的图象如图所示,则y kx b =-+与by x=的图象为( )A.B.C.D.21.(2022·吉林长春)如图,在平面直角坐标系中,点P在反比例函数kyx=(0k>,0x>)的图象上,其纵坐标为2,过点P作PQ//y轴,交x轴于点Q,将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图象上,则k的值为()AB C.D.422.(2022·黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数3yx=的图象上,顶点A在反比例函数kyx=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是()A.2B.1C.1-D.2-23.(2022·山东潍坊)地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同,观察图中数据,你发现,正确的是()A .海拔越高,大气压越大B .图中曲线是反比例函数的图象C .海拔为4千米时,大气压约为70千帕D .图中曲线表达了大气压和海拔两个量之间的变化关系24.(2022·四川内江)如图,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l △y 轴,且直线l 分别与反比例函数8y x =和ky x=的图象交于P 、Q 两点.若S △POQ =15,则k 的值为( )A .38B .22C .﹣7D .﹣2225.(2022·湖南怀化)如图,直线AB 交x 轴于点C ,交反比例函数y =1a x-(a >1)的图像于A 、B 两点,过点B 作BD △y 轴,垂足为点D ,若S △BCD =5,则a 的值为( )A .8B .9C .10D .1126.(2022·湖南邵阳)如图是反比例函数y =1x的图象,点A (x ,y )是反比例函数图象上任意一点,过点A 作AB △x 轴于点B ,连接OA ,则△AOB 的面积是( )A .1B .12C .2D .3227.(2022·内蒙古通辽)如图,点D 是OABC 内一点,AD 与x 轴平行,BD 与y 轴平行,BD =120BDC ∠=︒,BCD S =△()0ky x x =<的图像经过C ,D 两点,则k 的值是( )A .-B .6-C .-D .12-28.(2022·湖南郴州)如图,在函数()20=>y x x的图像上任取一点A ,过点A 作y 轴的垂线交函数()80y x x=-<的图像于点B ,连接OA ,OB ,则AOB 的面积是( )A .3B .5C .6D .1029.(2022·湖北荆州)如图是同一直角坐标系中函数12y x =和22y x=的图象.观察图象可得不等式22x x >的解集为( )A .11x -<<B .1x <-或1x >C .1x <-或01x <<D .10x -<<或1x >30.(2022·湖北十堰)如图,正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220ky k x =>的图象上.若BD y ∥轴,点D 的横坐标为3,则12k k +=( )A .36B .18C .12D .931.(2022·湖南娄底)在平面直角坐标系中,O 为坐标原点,已知点(),1P m 、()1,Q m (0m >且1m ≠),过点P 、Q 的直线与两坐标轴相交于A 、B 两点,连接OP 、OQ ,则下列结论中成立的是( ) △点P 、Q 在反比例函数my x=的图象上;△AOB 成等腰直角三角形;△090POQ ︒<∠<︒;△POQ ∠的值随m 的增大而增大. A .△△△B .△△△C .△△△D .△△△32.(2021·山东青岛)已知反比例函数by x=的图象如图所示,则一次函数y cx a =+和二次函数2y ax bx c =++在同一直角坐标系中的图象可能是( )A .B .C .D .33.(2021·山东滨州)如图,在OAB 中,45BOA ∠=︒,点C 为边AB 上一点,且2BC AC =.如果函数()90y x x=>的图象经过点B 和点C ,那么用下列坐标表示的点,在直线BC 上的是( )A .(-2019,674)B .(-2020,675)C .(2021,-669)D .(2022,-670)34.(2021·西藏)如图.在平面直角坐标系中,△AOB 的面积为278,BA 垂直x 轴于点A ,OB 与双曲线y =kx相交于点C ,且BC △OC =1△2,则k 的值为( )A .﹣3B .﹣94C .3D .9235.(2021·山东淄博)如图,在平面直角坐标系中,四边形AOBD 的边OB 与x 轴的正半轴重合,//AD OB ,DB x ⊥轴,对角线,AB OD 交于点M .已知:2:3,AD OB AMD =的面积为4.若反比例函数ky x=的图象恰好经过点M ,则k 的值为( )A .275B .545C .585D .1236.(2020·西藏)如图,在平面直角坐标系中,直线y =x 与反比例函数y =4x(x >0)的图象交于点A ,将直线y =x 沿y 轴向上平移b 个单位长度,交y 轴于点B ,交反比例函数图象于点C .若OA =2BC ,则b 的值为( )A .1B .2C .3D .437.(2020·辽宁辽宁)如图,矩形ABCD 的顶点D 在反比例函数(0)k y x x=>的图象上,点(1,0)E 和点(0,1)F 在AB 边上,AE EF =,连接,//DF DF x 轴,则k 的值为( )A .B .3C .4D .38.(2020·辽宁朝阳)如图,在平面直角坐标系中,一次函数443y x =+的图象与x 轴、y 轴分别相交于点B ,点A ,以线段AB 为边作正方形ABCD ,且点C 在反比例函数(0)ky x x=<的图象上,则k 的值为( )A .12-B .42-C .42D .21-39.(2020·内蒙古赤峰)如图,点B 在反比例函数6y x=(0x >)的图象上,点C 在反比例函数2y x =-(0x >)的图象上,且//BC y 轴,AC BC ⊥,垂足为点C ,交y 轴于点A ,则ABC 的面积为 ( )A .3B .4C .5D .640.(2020·吉林长春)如图,在平面直角坐标系中,点A 的坐标为()3,2,AB x ⊥轴于点B ,点C 是线段OB 上的点,连结AC .点P 在线段AC 上,且2=AP PC .函数()0ky x x=>的图象经过点P .当点C 在线段OB 上运动时,k 的取值范围是( )A .02k <≤B .233k ≤≤ C .232k ≤≤D .834k ≤≤41.(2020·山东威海)如图,点(,1)P m ,点(-2,)Q n 都在反比例函数4y x=的图象上,过点P 分别向x 轴、y 轴作垂线,垂足分别为点M ,N .连接OP ,OQ ,PQ .若四边形OMPN 的面积记作1S ,POQ △的面积记作2S ,则( )A .12:2:3S S =B .12:1:1S S =C .12:4:3S S =D .12:5:3S S =42.(2020·辽宁营口)如图,在平面直角坐标系中,△OAB 的边OA 在x 轴正半轴上,其中△OAB =90°,AO =AB ,点C 为斜边OB 的中点,反比例函数y =kx (k >0,x >0)的图象过点C 且交线段AB 于点D ,连接CD ,OD ,若S △OCD =32,则k 的值为( )A .3B .52C .2D .1二、填空题43.(2022·青海)如图,一块砖的A ,B ,C 三个面的面积之比是5:3:1,如果A ,B ,C 三个面分别向下在地上,地面所受压强分别为1P ,2P ,3P ,压强的计算公式为FP S=,其中P 是压强,F 是压力,S 是受力面积,则1P ,2P ,3P 的大小关系为______(用小于号连接).44.(2022·广西河池)如图,点P (x ,y )在双曲线ky x=的图象上,P A △x 轴,垂足为A ,若S △AOP =2,则该反比例函数的解析式为 _____.45.(2022·辽宁)如图,在平面直角坐标系中,△AOB 的边OB 在y 轴上,边AB 与x 轴交于点D ,且BD =AD ,反比例函数y =kx(x >0)的图像经过点A ,若S △OAB =1,则k 的值为___________.46.(2022·湖北武汉)在反比例1k y x-=的图象的每一支上,y 都随x 的增大而减小,且整式24x kx -+是一个完全平方式,则该反比例函数的解析式为___________. 47.(2022·黑龙江齐齐哈尔)如图,点A 是反比例函数(0)ky x x=<图象上一点,过点A 作AB △y 轴于点D ,且点D 为线段AB 的中点.若点C 为x 轴上任意一点,且△ABC 的面积为4,则k =______________.48.(2022·贵州毕节)如图,在平面直角坐标系中,正方形ABCD 的顶点A ,B 分别在x 轴、y 轴上,对角线交于点E ,反比例函数(0,0)ky x k x=>>的图像经过点C ,E .若点(3,0)A ,则k 的值是_________.49.(2022·湖北鄂州)如图,已知直线y =2x 与双曲线ky x=(k 为大于零的常数,且x >0)交于点A ,若OA k 的值为 _____.50.(2021·江苏徐州)如图,点,A D 分别在函数36,y y x x-==的图像上,点,B C 在x 轴上.若四边形ABCD 为正方形,点D 在第一象限,则D 的坐标是_____________.51.(2021·湖北鄂州)如图,点A 是反比例函数()120y x x=>的图象上一点,过点A 作AC x ⊥轴于点C ,AC交反比例函数()0k y x x=>的图象于点B ,点P 是y 轴正半轴上一点.若PAB ∆的面积为2,则k 的值为_____________.52.(2020·辽宁锦州)如图,平行四边形ABCD 的顶点A 在反比例函数(0)ky x x=>的图象上,点B 在y 轴上,点C ,点D 在x 轴上,AD 与y 轴交于点E ,若3BCES=,则k 的值为_______.53.(2020·辽宁沈阳)如图,在平面直角坐标系中,O 是坐标原点,在OAB 中,,AO AB AC OB =⊥于点C ,点A 在反比例函数(0)ky k x=≠的图象上,若OB =4,AC =3,则k 的值为__________.54.(2020·湖南永州)如图,正比例函数y x =-与反比例函数6y x=-的图象交于A ,C 两点,过点A 作AB x⊥轴于点B ,过点C 作CD x ⊥轴于点D ,则ABD △的面积为_________.55.(2020·湖南株洲)如图所示,在平面直角坐标系Oxy 中,四边形OABC 为矩形,点A 、C 分别在x 轴、y 轴上,点B 在函数1k y x=(0x >,k 为常数且2k >)的图象上,边AB 与函数22(0)y x x =>的图象交于点D ,则阴影部分ODBC 的面积为________(结果用含k 的式子表示)56.(2020·山东日照)如图,在平面直角坐标系中,▱ABCD 的顶点B 位于y 轴的正半轴上,顶点C ,D 位于x 轴的负半轴上,双曲线y =kx(k <0,x <0)与▱ABCD 的边AB ,AD 交于点E 、F ,点A 的纵坐标为10,F (﹣12,5),把△BOC 沿着BC 所在直线翻折,使原点O 落在点G 处,连接EG ,若EG △y 轴,则△BOC 的面积是_____.57.(2020·湖北荆门)如图,矩形OABC 的顶点A 、C 分别在x 轴、y 轴上,()2,1B -,将OAB 绕点O 顺时针旋转,点B 落在y 轴上的点D 处,得到OED ,OE 交BC 于点G ,若反比例函数(0)ky x x=<的图象经过点G ,则k 的值为______.58.(2020·广西)反比例函数y =kx(x <0)的图象如图所示,下列关于该函数图象的四个结论:△k >0;△当x <0时,y 随x 的增大而增大;△该函数图象关于直线y =﹣x 对称;△若点(﹣2,3)在该反比例函数图象上,则点(﹣1,6)也在该函数的图象上.其中正确结论的个数有_____个.59.(2020·贵州黔南)如图,正方形ABCD 的边长为10,点A 的坐标为()8,0-,点B 在y 轴上,若反比例函数(0)ky k x==的图象过点C ,则该反比例函数的解析式为_________.60.(2020·内蒙古呼伦贝尔)如图,在平面直角坐标系中,正方形OABC 的顶点O 与坐标原点重合,点C 的坐标为(0,3),点A 在x 轴的正半轴上.直线1y x =-分别与边,AB OA 相交于,D M 两点,反比例函数(0)ky x x=>的图象经过点D 并与边BC 相交于点N ,连接MN .点P 是直线DM 上的动点,当CP MN =时,点P 的坐标是________________.61.(2020·内蒙古鄂尔多斯)如图,平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与x 轴平行,A ,B 两点的纵坐标分别为6,4,反比例函数y =kx(x >0)的图象经过A ,B 两点,若菱形ABCD 的面积为k 的值为_____.62.(2021·山东日照)如图,在平面直角坐标系xOy 中,正方形OABC 的边OC 、OA 分别在x 轴和y 轴上,10OA =,点D 是边AB 上靠近点A 的三等分点,将OAD △沿直线OD 折叠后得到'OA D △,若反比例函数()0ky k x=≠的图象经过'A 点,则k 的值为_______.63.(2021·辽宁鞍山)如图,ABC 的顶点B 在反比例函数(0)ky x x=>的图象上,顶点C 在x 轴负半轴上,//AB x 轴,AB ,BC 分别交y 轴于点D ,E .若32BE CO CE AD ==,13ABCS =,则k =_____.64.(2021·贵州毕节)如图,直线AB 与反比例函数()0,0ky k x x=>>的图象交于A ,B 两点,与x 轴交于点C ,且AB BC =,连接OA .已知OAC 的面积为12,则k 的值为_____________.65.(2021·黑龙江齐齐哈尔)如图,点A 是反比例函数1(0)k y x x=<图象上一点,AC x ⊥轴于点C 且与反比例函数2(0)k y x x=<的图象交于点B ,3AB BC = ,连接OA ,OB ,若OAB 的面积为6,则12k k +=_________.66.(2022·辽宁辽宁)如图,矩形OABC 的顶点B 在反比例函数y =kx(x >0)的图像上,点A 在x 轴的正半轴上,AB =3BC ,点D 在x 轴的负半轴上,AD =AB ,连接BD ,过点A 作AE △BD 交y 交于点E ,点F 在AE 上,连接FD ,FB .若△BDF 的面积为9,则k 的值是_______.67.(2022·广东深圳)如图,已知直角三角形ABO 中,1AO =,将ABO 绕点O 点旋转至A B O ''△的位置,且A '在OB 的中点,B '在反比例函数ky x=上,则k 的值为________________.68.(2022·山东烟台)如图,A ,B 是双曲线y =kx(x >0)上的两点,连接OA ,O B .过点A 作AC △x 轴于点C ,交OB 于点D .若D 为AC 的中点,△AOD 的面积为3,点B 的坐标为(m ,2),则m 的值为 _____.69.(2022·贵州铜仁)如图,点A 、B 在反比例函数ky x=的图象上,AC y ⊥轴,垂足为D ,BC AC ⊥.若四边形AOBC 间面积为6,12AD AC =,则k 的值为_______.70.(2022·内蒙古包头)如图,反比例函数(0)ky k x=>在第一象限的图象上有(1,6)A ,(3,)B b 两点,直线AB 与x 轴相交于点C ,D 是线段OA 上一点.若AD BC AB DO ⋅=⋅,连接CD ,记,ADC DOC 的面积分别为12,S S ,则12S S -的值为___________.71.(2022·广西梧州)如图,在平面直角坐标系中,一次函数1y kx b =+的图象与反比例函数2my x=的图象交于点()()2,2,,1A B n --.当12y y <时,x 的取值范围是_________.72.(2022·广西玉林)如图,点A 在双曲线(0,0)k y k x x=>>上,点B 在直线2(0,0)y mx b m b =->>上,A 与B 关于x 轴对称,直线l 与y 轴交于点C ,当四边形AOCB 是菱形时,有以下结论:△()A b △当2b =时,k =△m =△22AOCB S b =四边形 则所有正确结论的序号是_____________.73.(2022·四川宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=kx(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB△OM于点B,则k的值为______.74.(2022·四川乐山)如图,平行四边形ABCD的顶点A在x轴上,点D在y=kx(k>0)上,且AD△x轴,CA的延长线交y轴于点E.若S△ABE=32,则k=______.75.(2022·安徽)如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数1yx=的图象经过点C,()0ky kx=≠的图象经过点B.若OC AC=,则k=________.三、解答题76.(2022·辽宁大连)密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:3m)变化时,气体的密度ρ(单位:kg/m)随之变化.已知密度ρ与体积V是反比例函数关系,它的图象如图所示,当35mV=时,31.98kg /m ρ=.(1)求密度ρ关于体积V 的函数解析式; (2)若39V ≤≤,求二氧化碳密度ρ的变化范围.77.(2022·广东广州)某燃气公司计划在地下修建一个容积为V (V 为定值,单位:m 3)的圆柱形天然气储存室,储存室的底面积S (单位:m 2) 与其深度d (单位:m )是反比例函数关系,它的图象如图所示.(1)求储存室的容积V 的值;(2)受地形条件限制,储存室的深度d 需要满足16≤d ≤25,求储存室的底面积S 的取值范围.78.(2022·四川乐山)如图,已知直线1:y =x +4与反比例函数y =kx(x <0)的图象交于点A (−1,n ),直线l ′经过点A ,且与l 关于直线x =−1对称.(1)求反比例函数的解析式; (2)求图中阴影部分的面积.79.(2022·河南)如图,反比例函数()0ky x x=>的图像经过点()2,4A 和点B ,点B 在点A 的下方,AC 平分OAB ∠,交x 轴于点C .(1)求反比例函数的表达式.(2)请用无刻度的直尺和圆规作出线段AC 的垂直平分线.(要求:不写作法,保留作图痕迹,使用2B 铅笔作图)(3)线段OA 与(2)中所作的垂直平分线相交于点D ,连接CD .求证:CD AB ∥.80.(2021·山东德州)已知点A 为函数4(0)y x x=>图象上任意一点,连接OA 并延长至点B ,使AB OA =,过点B 作//BC x 轴交函数图象于点C ,连接OC .(1)如图1,若点A 的坐标为(4,)n ,求点C 的坐标;(2)如图2,过点A 作AD BC ⊥,垂足为D ,求四边形OCDA 的面积.81.(2021·山东淄博)如图,在平面直角坐标系中,直线11y k x b =+与双曲线22k y x=相交于()()2,3,,2A B m --两点.(1)求12,y y 对应的函数表达式;(2)过点B 作//BP x 轴交y 轴于点P ,求ABP △的面积; (3)根据函数图象,直接写出关于x 的不等式21k k x b x+<的解集.82.(2021·湖南岳阳)如图,已知反比例函数()0ky k x=≠与正比例函数2y x =的图象交于()1,A m ,B 两点.(1)求该反比例函数的表达式;(2)若点C 在x 轴上,且BOC 的面积为3,求点C 的坐标.83.(2020·四川广安)如图,直线11y x =+与双曲线2ky x=(k 为常数,k≠0)交于A ,D 两点,与x 轴、y 轴分别交于B ,C 两点,点A 的坐标为(m ,2). (1)求反比例函数的解析式.(2)结合图象直接写出当12y y <时,x 的取值范围.84.(2020·吉林)如图,在平面直角坐标系中,O 为坐标原点,点A ,B 在函数ky x=()0x >的图象上(点B 的横坐标大于点A 的横坐标),点A 的坐示为()2,4,过点A 作AD x ⊥轴于点D ,过点B 作BC x ⊥轴于点C ,连接OA ,AB .(1)求k 的值.(2)若D 为OC 中点,求四边形OABC 的面积.85.(2020·广西贵港)如图,双曲线1k y x =(k 为常数,且0k ≠)与直线22y x b =+交于()1,A m 和1,22B n n ⎛+⎫ ⎪⎝⎭两点.(1)求k ,m 的值;(2)当0x >时,试比较函数值1y 与2y 的大小.86.(2020·广西柳州)如图,平行于y轴的直尺(部分)与反比例函数myx=(x>0)的图象交于A、C两点,与x轴交于B、D两点,连接AC,点A、B对应直尺上的刻度分别为5、2,直尺的宽度BD=2,OB=2.设直线AC的解析式为y=kx+b.(1)请结合图象,直接写出:△点A的坐标是;△不等式mkx bx+>的解集是;(2)求直线AC的解析式.87.(2020·山东济南)如图,矩形OABC的顶点A,C分别落在x轴,y轴的正半轴上,顶点B(2,,反比例函数kyx=(x>0)的图象与BC,AB分别交于D,E,BD=12.(1)求反比例函数关系式和点E的坐标;(2)写出DE与AC的位置关系并说明理由;(3)点F在直线AC上,点G是坐标系内点,当四边形BCFG为菱形时,求出点G的坐标并判断点G是否在反比例函数图象上.88.(2020·四川)如图,一次函数y 1=ax +b 与反比例函数y 2=4x 的图象交于A 、B 两点.点A 的横坐标为2,点B 的纵坐标为1. (1)求a ,b 的值.(2)在反比例y 2=4x第三象限的图象上找一点P ,使点P 到直线AB 的距离最短,求点P 的坐标.89.(2020·辽宁盘锦)如图,A B 、两点的坐标分别为()()2,0,0,3-,将线段AB 绕点B 逆时针旋转90°得到线段BC ,过点C 作CD OB ⊥,垂足为D ,反比例函数ky x=的图象经过点C .(1)直接写出点C 的坐标,并求反比例函数的解析式; (2)点P 在反比例函数ky x=的图象上,当PCD 的面积为3时,求点P 的坐标.90.(2020·四川绵阳)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y=kx(k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.(1)当m=1时,求一次函数的解析式;(2)若点E在x轴上,满足△AEB=90°,且AE=2﹣m,求反比例函数的解析式.91.(2020·云南昆明)为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19min;完成2间办公室和1间教室的药物喷洒要11min.(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.92.(2021·辽宁鞍山)如图,在平面直角坐标系中,一次函数1y k x b =+的图象分别与x 轴、y 轴交于A ,B 两点,与反比例函数2k y x =的图象在第二象限交于C ,(6,2)D -两点,//DE OC 交x 轴于点E ,若13AD AC =. 本号资@料皆来源于微信:数学(1)求一次函数和反比例函数的表达式. (2)求四边形OCDE 的面积.93.(2021·江苏镇江)如图,点A 和点(2,1)E 是反比例函数(0)ky x x=>图象上的两点,点B 在反比例函数6(0)y x x=<的图象上,分别过点A ,B 作y 轴的垂线,垂足分别为点C ,D ,AC BD =,连接AB 交y 轴于点F . (1)k = ;(2)设点A 的横坐标为a ,点F 的纵坐标为m ,求证:2am =-; (3)连接CE ,DE ,当△CED =90°时,直接写出点A 的坐标: .94.(2021·四川巴中)如图,双曲线ymx=与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已知点E(1,0),连接AE、BE.(1)求m,k,b的值;(2)求ABE的面积;(3)作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线ymx=有唯一交点,求n的值.本号资@料皆来源@于微信:数学95.(2022·湖北黄冈)如图,已知一次函数y1=kx+b的图像与函数y2=mx(x>0)的图像交于A(6,-12),B(12,n)两点,与y轴交于点C,将直线AB沿y轴向上平移t个单位长度得到直线DE,DE与y轴交于点F.(1)求y1与y2的解析式;(2)观察图像,直接写出y 1<y 2时x 的取值范围;(3)连接AD ,CD ,若△ACD 的面积为6,则t 的值为 .96.(2022·山东潍坊)某市在盐碱地种植海水稻获得突破性进展,小亮和小莹到海水稻种植基地调研.小莹根据水稻年产量数据,分别在直角坐标系中描出表示2017-2021年△号田和△号田年产量情况的点(记2017年为第1年度,横轴表示年度,纵轴表示年产量),如下图.小亮认为,可以从y =kx +b (k >0) ,y =mx(m >0) ,y =−0.1x 2+ax +c 中选择适当的函数模型,模拟△号田和△号田的年产量变化趋势. (1)小莹认为不能选(0)my m x=>.你认同吗?请说明理由; (2)请从小亮提供的函数模型中,选择适当的模型分别模拟△号田和△号田的年产量变化趋势,并求出函数表达式;(3)根据(2)中你选择的函数模型,请预测△号田和△号田总年产量....在哪一年最大?最大是多少?97.(2022·青海西宁)如图,正比例函数4y x =与反比例函数()0ky x x=>的图象交于点(),4A a ,点B 在反比例函数图象上,连接AB ,过点B 作BC x ⊥轴于点()2,0C .(1)求反比例函数解析式;(2)点D 在第一象限,且以A ,B ,C ,D 为顶点的四边形是平行四边形,请直接写出....点D 的坐标.98.(2022·辽宁锦州)如图,平面直角坐标系xOy 中,四边形OABC 是菱形,点A 在y 轴正半轴上,点B 的坐标是(4,8)-,反比例函数(0)ky x x=<的图像经过点C .(1)求反比例函数的解析式; (2)点D 在边CO 上,且34CD DO =,过点D 作DE x 轴,交反比例函数的图像于点E ,求点E 的坐标.99.(2022·湖北荆州)小华同学学习函数知识后,对函数()()2410410x x y x x x ⎧-<≤⎪=⎨-≤->⎪⎩或通过列表、描点、连线,画出了如图1所示的图象.请根据图象解答:(1)【观察发现】△写出函数的两条性质:______;______;△若函数图象上的两点()11,x y ,()22,x y 满足120x x +=,则120y y +=一定成立吗?______.(填“一定”或“不一定”)(2)【延伸探究】如图2,将过()1,4A -,()4,1B -两点的直线向下平移n 个单位长度后,得到直线l 与函数()41y x x=-≤-的图象交于点P ,连接P A ,PB . △求当n =3时,直线l 的解析式和△P AB 的面积; △直接用含....n 的代数式表示......△P AB 的面积.100.(2022·山东临沂)杠杆原理在生活中被广泛应用(杠杆原理:阻力×阻力臂=动力×动力臂),小明利用这一原理制作了一个称量物体质量的简易“秤”(如图1).制作方法如下:第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm ),确定支点O ,并用细麻绳固定,在支点O 左侧2cm 的A 处固定一个金属吊钩,作为秤钩; 第二步:取一个质量为0.5kg 的金属物体作为秤砣.(1)图1中,把重物挂在秤钩上,秤砣挂在支点О右侧的B 处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB 的长度随之变化.设重物的质量为kg x ,OB 的长为cm y .写出y 关于x 的函数解析式;若048y <<,求x 的取值范围.(2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点О右侧的B 处,使秤杆平衡,如图2.设重物的质量为kg x ,OB 的长为cm y ,写出y 关于x 的函数解析式,完成下表,画出该函数的图象.。
初中数学中考复习 备战2020年中考数学一轮专项复习——反比例函数综合问题(含详细解答)

备战2020年中考数学一轮专项复习——反比例函数综合问题一、反比例函数的概念:知识要点:1、一般地,形如 y = x k ( k 是常数, k = 0 ) 的函数叫做反比例函数。
注意:(1)常数 k 称为比例系数,k 是非零常数;(2)解析式有三种常见的表达形式:(A )y = xk (k ≠ 0) ; (B )xy = k (k ≠ 0); (C )y=kx -1(k ≠0) 二、反比例函数的图象和性质:知识要点:1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第一、三象限内;(2)当k<0时, 双曲线分别位于第二、四象限内。
3、增减性:(1)当k>0时,y = xk (k ≠ 0)为减函数,y 随x 的增大而减小; (2)当k<0时,y = xk (k ≠ 0)为增函数,y 随x 的增大而增大。
4、变化趋势:双曲线无限接近于x 、y 轴,但永远不会与坐标轴相交5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点成中心对称;(2)对于k 取互为相反数的两个反比例函数(如:y =x 6 和y = x 6 )来说,它们是关于x 轴,y 轴成轴对称。
一、选择题:1.下列函数,①y =2x ,②y =x ,③y =x ﹣1,④y =是反比例函数的个数有( ) A .0个 B .1个 C .2个 D .3个【分析】根据反比例函数的定义,反比例函数的一般式是(k ≠0)判定则可. 【解析】①y =2x 是正比例函数;②y =x 是正比例函数;③y =x ﹣1是反比例函数;④y=不是反比例函数,是反比例关系;所以共有1个.故选:B.2.(2019•济南)函数y=﹣ax+a与y=(a≠0)在同一坐标系中的图象可能是()A.B.C.D.【解析】a>0时,﹣a<0,y=﹣ax+a在一、二、四象限,y=在一、三象限,无选项符合.a<0时,﹣a>0,y=﹣ax+a在一、三、四象限,y=(a≠0)在二、四象限,只有D符合;故选:D.3.如图,过原点的直线l与反比例函数y=﹣的图象交于M,N两点,根据图象猜想线段MN的长的最小值是()A.B.2C.2 D.1【分析】设N的横坐标是a,则纵坐标是﹣,利用a即可表示出ON的长度,然后根据不等式的性质即可求解.【解析】设N的横坐标是a,则纵坐标是﹣.则OM=ON=≥.则MN的最小值是2.故选:B.4.(2019•阜新)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y 轴上,则△ABC的面积为()A.3 B.2 C.D.1【解析】连结OA,如图,∵AB⊥x轴,∴OC∥AB,∴S△OAB=S△CAB,而S△OAB=|k|=,∴S△CAB=,故选:C.5.(2019•遵义)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为()A.2 B.3 C.4 D.6【解析】过点A作x轴的垂线,交CB的延长线于点E,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为4,2,∴A(,4),B(,2),∴AE=2,BE=k﹣k=k,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE==1∴k=1,∴k=4.故选:C.6.如图,在菱形ABOC中,∠ABO=120°,它的一个顶点C在反比例函数y=的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则该反比函数的表达式为()A.y=﹣B.y=﹣C.y=﹣D.y=﹣【分析】点C作CD⊥x轴于D,设菱形的边长为a,根据菱形的性质和三角函数分别表示出C,以及点A向下平移2个单位的点,再根据反比例函数图象上点的坐标特征得到方程组求解即可.【解析】过点C作CD⊥x轴于D,设菱形的边长为a,在Rt△CDO中,OD=a•cos60°=a,CD=a•sin60°=a,则C(﹣a,a),点A向下平移2个单位的点为(﹣a﹣a,a﹣2),即(﹣a,a﹣2),则,解得.故反比例函数解析式为y=﹣.故选:B.7.(2019•淄博)如图,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x 轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数y =(x>0)的图象上.则y1+y2+…+y10的值为()A.2B.6 C.4D.2【解析】过C1、C2、C3…分别作x轴的垂线,垂足分别为D1、D2、D3…其斜边的中点C1在反比例函数y=,∴C(2,2)即y1=2,∴OD1=D1A1=2,设A1D2=a,则C2D2=a此时C2(4+a,a),代入y=得:a(4+a)=4,解得:a=,即:y2=,同理:y3=,y 4=,……∴y1+y2+…+y10=2+++……=,故选:A.8.如图,已知点A,B在双曲线y=(x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P 是AC的中点.若△ABP的面积为4,则k的值为().A.16 B.8 C.4 D.24【分析】由△ABP的面积为4,知BP•AP=8.根据反比例函数y=中k的几何意义,知本题k=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.【解答】解:∵△ABP 的面积为•BP •AP =4,∴BP •AP =8,∵P 是AC 的中点,∴A 点的纵坐标是B 点纵坐标的2倍,又∵点A 、B 都在双曲线y =(x >0)上,∴B 点的横坐标是A 点横坐标的2倍,∴OC =DP =BP ,∴k =OC •AC =BP •2AP =16.故选A.二、填空题:9.(2019山西)如图,在平面直角坐标系中,点O 为坐标原点,菱形ABCD 的顶点B 在x 轴的正半轴上,点A 坐标为(-4,0),点D 的坐标为(-1,4),反比例函数)0(>=x xk y 的图象恰好经过点C ,则k 的值为 .【解析】过点D 作DE ⊥AB 于点E ,则AD=5,∵四边形ABCD 为菱形,∴CD=5∴C (4,4),将C 代入x k y =得:44k =,∴16=k10.(2019遂宁中考 第15题 4分)如图,在平面直角坐标系中,矩形OABC 的顶点O 落在坐标原点,点A 、点C 分别位于x 轴,y 轴的正半轴,G 为线段OA 上一点,将△OCG 沿CG 翻折,O 点恰好落在对角线AC 上的点P 处,反比例函数y =经过点B .二次函数y =ax 2+bx +c (a ≠0)的图象经过C (0,3)、G 、A 三点,则该二次函数的解析式为 .(填一般式)【解析】点C (0,3),反比例函数y =经过点B ,则点B (4,3),则OC =3,OA =4,∴AC =5,设OG =PG =x ,则GA =4﹣x ,PA =AC ﹣CP =AC ﹣OC =5﹣3=2, 由勾股定理得:(4﹣x )2=4+x 2,解得:x =,故点G (,0),将点C 、G 、A 坐标代入二次函数表达式得:,解得:,故答案为:y =x 2﹣x +3. 11.如图,已知点(1,3)在函数y =kx (x >0)的图象上,正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数y =kx(x >0)的图象又经过A ,E 两点,则点E 的横坐标为____.【解析】 把(1,3)代入到y =kx,得k =3, 所以函数解析式为y =3x. 设A (a ,b ),根据图象和题意可知,点E ⎝ ⎛⎭⎪⎫a +b 2,b 2.因为y =3x 的图象经过A ,E ,所以分别把点A 和E 代入到函数解析式中得 ab =3,①b 2⎝ ⎛⎭⎪⎫a +b 2=3,② 由②得ab 2+b 24=3,把①代入得32+b 24=3, 即b 2=6,解得b =±6,因为A 在第一象限,所以b >0,所以b = 6.把b =6代入①求得a =62, 所以点E 的横坐标为a +b 2= 6.故答案为 6. 12.如图,Rt △AOB 中,∠OAB =90°,∠OBA =30°,顶点A 在反比例函数y =图象上,若Rt △AOB 的面积恰好被y 轴平分,则进过点B 的反比例函数的解析式为 .【分析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ),则ab =﹣4.根据两角对应相等的两三角形相似,得出△OAE ∽△ABF ,由相似三角形的对应边成比例,则BD 、OD 都可用含a 、b 的代数式表示,从而求出B 的坐标,进而得出结果.【解析】分别过A 、B 作AE ⊥x 轴于E ,BD ⊥y 轴交AE 于F .设A (a ,b ).∵顶点A 在反比例函数y =图象上,∴ab=﹣4.∵∠OAB=90°,∠OAE=90°﹣∠BAF=∠ABF,∠OEA=∠BFA=90°,∴△OAE∽△ABF,∴OA:AB=OE:AF=AE:BF,在Rt△AOB中,∠AOAB=90°,∠OBA=30°,∴OA:AB=1:,∴﹣a:AF=b:BF=1:,∴AF=﹣,BF=b,∵Rt△AOB的面积恰好被y轴平分,∴AC=BC,∴BD=DF=BF=﹣a,OD=AE+AF=b﹣a,∴b=﹣a,∴A(﹣b,b),B(b,b﹣)∴﹣b•b=﹣4,∴b2=,∴k=b(b﹣)=b2﹣ab=10,故答案为:10.13.如图, △OAP ,△ABQ 是等腰直角三角形,点P ,Q 在反比例函数y =4x (x >0)上,直角顶点A ,B 均在x 轴上,则点Q 的坐标为 .【解析】 ∵△OAP 是等腰直角三角形,∴PA =OA .∴设P 点的坐标是(a ,a ),把(a ,a )代入解析式y =4x,解得a =2(a =-2舍去), ∴P 的坐标是(2,2),∴OA =2,∵△ABQ 是等腰直角三角形,∴BQ =AB ,∴可以设Q 的纵坐标是b ,∴横坐标是b +2,把Q 的坐标代入解析式y =4x, 得b =4b +2,∴b =5-1(b =-5-1舍去),∴点Q 的坐标为(5+1,5-1).14.(2019•毕节市)如图,在平面直角坐标中,一次函数y =﹣4x +4的图象与x 轴、y 轴分别交于A 、B 两点.正方形ABCD 的顶点C 、D 在第一象限,顶点D 在反比例函数y =(k ≠0)的图象上.若正方形ABCD 向左平移n 个单位后,顶点C 恰好落在反比例函数的图象上,则n 的值是 .【解析】过点D 作DE ⊥x 轴,过点C 作CF ⊥y 轴,∵AB ⊥AD ,∴∠BAO =∠DAE ,∵AB =AD ,∠BOA =∠DEA ,∴△ABO ≌△DAE (AAS ),∴AE =BO ,DE =OA ,易求A (1,0),B (0,4),∴D (5,1),∵顶点D 在反比例函数y =上,∴k =5,∴y =,易证△CBF ≌△BAO (AAS ),∴CF =4,BF =1,∴C (4,5),∵C 向左移动n 个单位后为(4﹣n ,5),∴5(4﹣n )=5,∴n =3,故答案为3;三、解答题15.如图,一次函数y =kx +2的图象与反比例函数y =m x的图象在第一象限的交点为P .PA 垂直x 轴于点A .PB 垂直y 轴于点B .函数y =kx +2的图象分别交x 轴,y 轴于点C ,D .已知DB =2OD ,△PBD 的面积S △PBD =4.(1)求点D 的坐标;(2)求k ,m 的值;(3)写出当x >0时,使一次函数y =kx +2的值大于反比例函数y =m x的值的x 的取值范围.【解析】(1)在y =kx +2中,令x =0,得y =2,所以点D (0,2).(2)因为OD =2,DB =2OD =4,由S △PBD =4,可得BP =2,而OB =OD +DB =6,所以点P (2,6).将P (2,6)分别代入y =kx +2与y =mx,可得 k =2,m =12.(3) 由图象可知,当x >0时,使一次函数y =kx +2的值大于反比例函数y =mx的值的x 的取值范围是x >2.16.(2019遂宁中考 第23题 10分)如图,一次函数y =x ﹣3的图象与反比例函数y ═(k ≠0)的图象交于点A 与点B (a ,﹣4).(1)求反比例函数的表达式;(2)若动点P 是第一象限内双曲线上的点(不与点A 重合),连接OP ,且过点P 作y 轴的平行线交直线AB于点C,连接OC,若△POC的面积为3,求出点P的坐标.【解析】(1)将B(a,﹣4)代入一次函数y=x﹣3中得:a=﹣1∴B(﹣1,﹣4)将B(﹣1,﹣4)代入反比例函数y═(k≠0)中得:k=4∴反比例函数的表达式为y=;(2)如图:设点P的坐标为(m,)(m>0),则C(m,m﹣3)∴PC=|﹣(m﹣3)|,点O到直线PC的距离为m∴△POC的面积=m×|﹣(m﹣3)|=3解得:m=5或﹣2或1或2∵点P不与点A重合,且A(4,1)∴m≠4又∵m>0∴m=5或1或2∴点P的坐标为(5,)或(1,4)或(2,2).17.(2019•河池)在平面直角坐标系中,矩形ABCD的顶点坐标为A(0,0),B(6,0),C(6,8),D(0,8),AC,BD交于点E.(1)如图(1),双曲线y=过点E,直接写出点E的坐标和双曲线的解析式;(2)如图(2),双曲线y=与BC,CD分别交于点M,N,点C关于MN的对称点C′在y轴上.求证△CMN~△CBD,并求点C′的坐标;(3)如图(3),将矩形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线y=与AD交于点P.当△AEP为等腰三角形时,求m的值.【解析】(1)如图1中,∵四边形ABCD是矩形,∴DE=EB,∵B(6,0),D(0,8),∴E(3,4),∵双曲线y=过点E,∴k1=12.∴反比例函数的解析式为y=.(2)如图2中,∵点M,N在反比例函数的图象上,∴DN•AD=BM•AB,∵BC=AD,AB=CD,∴DN•BC=BM•CD,∴=,∴=,∴=,∵∠MCN=∠BCD,∴△MCN∽△BCD,∴∠CNM=∠CDB,∴MN∥BD,∴△CMN∽△CBD.∵B(6,0),D(0,8),∴直线BD的解析式为y=﹣x+8,∵C,C′关于MN对称,∴CC′⊥MN,∴CC′⊥BD,∵C(6,8),∴直线CC′的解析式为y=x+,∴C′(0,).(3)如图3中,①当AP=AE=5时,∵P(m,5),E(m+3,4),P,E在反比例函数图象上,∴5m=4(m+3),∴m=12.②当EP=AE时,点P与点D重合,∵P(m,8),E(m+3,4),P,E在反比例函数图象上,∴8m=4(m+3),∴m=3.③显然PA≠PE,若相等,则PE∥x轴,显然不可能.综上所述,满足条件的m的值为3或12.18.“六一”儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度)如图,它与两面互相垂直的围墙OP,OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任意一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等.比如:A,B,C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI 的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1,S2,S3,并测得S2=6(单位:平方米),OG=GH=HI.(1)求S1和S3的值;(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数解析式;(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?【解析】(1)∵矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等,∴弯道为反比例函数图象的一部分.设反比例函数的解析式为y =k x (k ≠0),OG =GH =HI =a ,则AG =k a ,BH =k 2a ,CI =k 3a .所以S 2=k 2a •a -k 3a•a =6,解得k =36.所以S 1=k a •a -k 2a •a =12k =12×36=18,S 3=k 3a •a =13k =13×36=12;(2)由(1)得,弯道的函数解析式为y =36x .∵T(x ,y)是弯道MN 上的任一点,∴y =36x ;(3)∵MP =2,NQ =3,∴GM =362=18,OQ =363=12.∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),∴当x =2时,y =18,可以种8棵;当x =4时,y =9,可以种4棵;当x =6时,y =6,可以种2棵;当x =8时,y =4.5,可以种2棵;当x =10时,y =3.6,可以种1棵.故一共可以种8+4+2+2+1=17(棵)花木.19、如图,已知反比例函数k y x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+. (1)试确定这两个函数的表达式;(2)求出这两个函数图象的另一个交点B 的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.【解析】(1)∵已知反比例函数k y x =经过点(1,4)A k -+,∴41k k-+=,即4k k -+= ∴2k =∴A(1,2) ∵一次函数y x b =+的图象经过点A(1,2),∴21b =+∴1b =∴反比例函数的表达式为2y x=, 一次函数的表达式为1y x =+。
备战九年级中考数学一轮复习第12课 反比例函数(全国通用)

y y
3x 2 12
3
,
解得
x1 y1
4 3
,
x2 2
y2
6
x
∴B点坐标为(-4,-3),
对于一次函数y= 3 x+3, 2
当x=0时,y=3,即OC=3,
∴S△AOB=S△ACO+S△BCO
= 1 ×3×2+ 1 ×3×4
2
2
=9.
(3)两个函数的图象交于点A(2,6),B(-4,-3),
x 5 2m
,
令y=0,则x=5m,故点F(5m,0),
故FG=8m-5m=3m,而BD=4m-m=3m=FG,
又FG∥BD,故四边形BDFG为平行四边形.
19.(202X·怀化)如图,△OB1A1,△A1B2A2,△A2B3A3,…,
△An-1BnAn,都是一边在x轴上的等边三角形,点B1,B2, B3,…,Bn都在反比例函数y= 3 (x>0)的图象上,点A1,
A2,A3,…,An都在x轴上,则An的x 坐标为____2__n_,__0___.
20.(202X·温州)点P,Q,R在反比例函数y= k (常数k>0, x
x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的 平行线.图中所构成的阴影部分面积从左到右依次27为S1,S2, S3.若OE=ED=DC,S1+S3=27,则S2的值为____5____.
B.y2>y3>y1
C.y1>y3>y2
D.y3>
8.【例2】(202X·内江)如图,等边△OAB的边OA在x 轴上,反比例函数y= 6 的图象经过点B,则
x △OAB的面积为____6____.
9.(202X·抚顺)如图,在△ABC中,AB=AC,点A在反比例
2023年九年级中考数学一轮复习:反比例函数(含答案)

第三部分 一次函数与反比例函数模块二 反比例函数基础知识梳理考点1 反比例函数的图象 考点4 设参数来帮忙 考点2 比大小(增减性) 考点5 反比例与几何综合考点3面积不变性原理1.如果点A (-2,y 1),B (-1,y 2),C (2,y 3)都在反比例函数y =xk(k >0)的图象上,那么y 1,y 2,y 3的大小关系是( )A. y 1<y 3<y 2B. y 2< y 1 <y 3C. y 1<y 2<y 3D. y 3 <y 2 <y 12如图,已知一次函数y =kx - 4的图象与x 轴,y 轴分别交于A ,B 两点,与反比例函数y =x8在第一象限内的图象交于点C ,且A 为BC 的中点,则k =____________。
3.已知双曲线y =x 3和y =xk的部分图象如图所示,点C 是y 轴正半轴上一点,过点C 作AB ∥x 轴分别交两个图象于点A ,B ,若CB =2CA ,则k =____________。
4.如图,一次函数y = k x - 1的图象与x 轴交于点A ,与反比例函数y =x3(x >0)的图象交于B ,BC 垂直x 轴于点C ,若△ABC 的面积为1,则k 的值是___________。
5.如图,点B (3,3)在双曲线y =x k (x >0)上点D 在双曲线y =x4(x <0)上,点A 和点C 分别在x 轴,y 轴的正半轴上,且点A ,B ,C ,D 构成的四边形为正方形。
(1)求k 的值; (2)求点A 的坐标。
6.在同一平面直角坐标系中,函数y =x - 1与函数y =x1的图象可能是( )7.函数y 1=x 和y 2=x1的图象如图所示,则y 1>y 2的x 的取值范围是( ) A. x < - 1或 x >1 B. x < - 1或0 < x < 1 C. - 1 < x < 0 或 x > 1 D. - 1 < x < 0 或 0 < x < 18.如图,四边形ABCD 为菱形,已知A (0,4),B ( - 3,0) (1)求点D 的坐标;(2)求经过点C 的反比例函数解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一轮复习练习-------反比例函数A组2015年全国中考题组一、选择题1.(2015·重庆,12,3分)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=3x的图象经过A,B两点,则菱形ABCD的面积为() A.2 B.4 C.2 2 D.4 22.(2015·山东青岛,8,3分)如图,正比例函数y1=k1x的图象与反比例函数y2=k2x的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是() A.x<-2或x>2 B.x<-2或0<x<2C.-2<x<0或0<x<2 D.-2<x<0或x>23.(2015·浙江湖州,10,3分)如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=k2x在第一象限内的图象交于点B,连结BO.若S△OBC =1,tan∠BOC=13,则k2的值是()A.-3 B.1 C.2 D.34.(2015·四川凉山州,10,3分)以正方形ABCD 两条对角线的交点O 为坐标原点,建立如图所示的平面直角坐标系,双曲线y =3x 经过点D ,则正方形ABCD 的面积是 ( )A .10B .11C .12D .13二、填空题5.(2015·浙江绍兴,15,5分)在平面直角坐标系的第一象限内,边长为1的正方形ABCD 的边均平行于坐标轴,A 点的坐标为(a ,a ),如图,若曲线y =3x (x >0)与此正方形的边有交点,则a 的取值范围是________.6.(2015·浙江杭州,15,4分)在平面直角坐标系中,O 为坐标原点,设点P (1,t )在反比例函数y =2x 的图象上,过点P 作直线l 与x 轴平行,点Q 在直线l 上,满足QP=OP .若反比例函数y =kx 的图象经过点Q ,则k =________. 7.(2015·浙江宁波,18,4分)如图,已知点A ,C 在反比例函数y =a x (a >0)的图象上,点B ,D 在反比例函数y =bx (b <0)的图象上,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB =3,CD =2,AB 与CD 的距离为5,则a -b 的值是____________.8.(2015·浙江金华,15,4分)如图,在平面直角坐标系中,菱形OBCD 的边OB 在x轴正半轴上,反比例函数y =kx (x >0)的图象经过该菱形对角线的交点A ,且与边BC 交于点F .若点D 的坐标为(6,8),则点F 的坐标是________.9.(2015·浙江丽水,16,4分)如图,反比例函数y =kx 的图象经过点(-1,-22),点A 是该图象第一象限分支上的动点,连结AO 并延长交另一支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC 与x 轴交于点P ,连结BP .(1)k 的值为________;(2)在点A 运动过程中,当BP 平分∠ABC 时,点C 的坐标是________. 三、解答题10.(2015·浙江衢州,19,6分)如图,已知点A (a ,3)是一次函数y 1=x +b 图象与反比例函数y 2=6x 图象的一个交点. (1)求一次函数的解析式;(2)在y 轴的右侧,当y 1>y 2时,直接写出x 的取值范围.11.(2015·四川泸州,23,8分)如图,一次函数y =kx +b (k <0)的图象经过点C (3,0),且与两坐标轴围成的三角形的面积为3. (1)求该一次函数的解析式;(2)若反比例函数y =mx 的图象与该一次函数的图象交于二、四象限内的A ,B 两点,且AC =2BC ,求m 的值.B 组 2014~2011年全国中考题组一、选择题1.(2013·浙江温州,6,4分)已知点P (1,-3)在反比例函数y =kx (k ≠0)的图象上,则k 的值是( )A .3B .-3C.13D .-132.(2013·甘肃兰州,5,4分)当x >0时,函数y =-5x 的图象在( )A .第四象限B .第三象限C .第二象限D .第一象限3.(2013·浙江台州,5,4分)在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m 3)与体积V (单位:m 3)满足函数关系式ρ=k V (k 为常数,k ≠0),其图象如图所示,则k 的值为( )A .9B .-9C .4D .-44.(2014·山东潍坊,11,3分)已知一次函数y 1=kx +b (k <0)与反比例函数y 2=m x (m ≠0)的图象相交于A ,B 两点,其横坐标分别是-1和3,当y 1>y 2时,实数x 的取值范围是( )A .x <-1或0<x <3B .-1<x <0或0<x <3C .-1<x <0或x >3D .0<x <35.(2014·四川自贡,9,4分)关于x 的函数y =k (x +1)和y =k x (k ≠0)在同一坐标系中的图象大致是( )二、填空题6.(2013·浙江绍兴,14,5分)在平面直角坐标系中,O 是原点,A 是x 轴上一点,将射线OA 绕点O 旋转,使点A 与双曲线y =3x 上的点B 重合.若点B 的纵坐标是1,则点A 的横坐标是________.7.(2013·湖南娄底,13,4分)如图,已知A 点是反比例函数y =kx (k ≠0)的图象上一点,AB ⊥y 轴于B ,且△ABO 的面积为3,则k 的值为________.8.(2013·湖北黄冈,12,3分)已知反比例函数y =6x 在第一象限的图象如图所示,点A 在其图象上,点B 为x 轴正半轴上一点,连结AO ,AB ,且AO=AB ,则S △AOB =________. 三、解答题9.(2014·浙江湖州,20,8分)如图,已知在平面直角坐标系xOy 中,O 是坐标原点,点A (2,5)在反比例函数y =kx 的图象上,过点A 的直线y =x +b 交x 轴于点B . (1)求k 和b 的值;(2)求△OAB 的面积.C 组 2016创新导向一、选择题1.(改编题)已知反比例函数y =kx 经过点(1,-2),则k 的值为 ( )A .2B .-12C .1D .-22.(原创题)若反比例函数y =k x 的图象经过点⎝ ⎛⎭⎪⎫-23,3,则这个函数的图象一定经过点( )A.⎝ ⎛⎭⎪⎫12,2 B.⎝ ⎛⎭⎪⎫-12,2 C .(-2,-1) D .(2,-1) 3.(改编题)一次函数y =x +m (m ≠0)与反比例函数y =mx 的图象在同一平面直角坐标系中是( )4.(原创题)在反比例函数y =k x (k <0)的图象上有两点(-1,y 1),⎝ ⎛⎭⎪⎫-14,y 2,则y 1-y 2的值是( )A .负数B .非正数C .正数D .不能确定5.(原创)平面直角坐标系中,反比例函数y =a 2-a +2x 图象的两个分支分别在( )A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限6. (原创题)直线y =-12x -1与反比例函数y =kx 的图象(x <0)交于点A ,与x 轴相交于点B ,过点B 作x 轴垂线交双曲线于点C ,若AB =AC ,则k 的值为 ( )A .-2B .-4C .-6D .-8二、填空题7.(原创题)如图,点P 在双曲线y =kx (k ≠0)上,点P ′(1,2)与点P 关于y 轴对称,则此双曲线的解析式为________.8.(改编题)在直角坐标系中,O 是坐标原点,点P (m ,n )在反比例函数y =kx 的图象上.若m =k ,n =k -2,则k =________;若m +n =2k ,OP =2,且此反比例函数y =k x 满足:当x >0时,y 随x 的增大而减小,则k =________.9.(原创题)在平面直角坐标系xOy 中,点P (2,a )在反比例函数y =2x 的图象上,把点P 向上平移2个单位,再向右平移3个单位得到点Q ,则经过点Q 的反比例函数的解析式为________.10.(原创题)如图,矩形OABC 的顶点A ,C 分别在x 轴和y 轴上,若OA =4,OC =6,写出一个函数y =kx (k ≠0),使它的图象与矩形OABC 的两边AB ,BC 分别交于点D ,E ,这个函数的表达式为________. 三、解答题11.(改编题)如图,已知双曲线y =kx 和直线y =mx +n 交于点A 和B ,B 点的坐标是(2,-3),AC 垂直y 轴于点C ,AC =32.(1)求双曲线和直线的解析式; (2)求△AOB 的面积.12.(原创题)如图,直线y =2x -6与反比例函数y =kx (k >0)的图象交于点A (4,2),与x 轴交于点B .(1)求k 的值及点B 的坐标;(2)当x ________时,2x -6>kx (k >0);(3)在x 轴上是否存在点C ,使得△ABC 为等腰三角形,且AC =AB ?若存在,求出点C 的坐标;若不存在,请说明理由.。
