重庆大学考研材料力学习题集全面分析
更新:重庆大学材料力学考研重点知识点详解

极惯性矩
I p 2dA
抗扭刚度
GI P
max
MT max Wp
MTl GIP
纯弯曲
惯性矩
I z y 2dA
抗弯刚度
EI Z
max
M max WZ
d 2 y M(x)
dx 2
EI Z
( 1 M(x)
挠度y 转角 dy
dx
EI Z
2. 四种基本变形的刚度,都可以写成:
刚度 = 材料的物理常数×截面的几何性质
7) 欧拉临界力,稳定性,压杆稳定性。
8)动荷载,交变应力,疲劳破坏。
二. 杆件四种基本变形的公式及应用
1. 四种基本变形:
基本变形
截面几何
刚度
应力公式
变形公式
备注
性质
拉伸与压缩
面积:A
抗拉(压) 刚度 EA
N A
l Nl EA
注意变截面及 变轴力的情况
剪切
面积:A
——
Q
——
实用计算法
A
圆轴扭转
内力 应力= 截面几何性质
对扭转的最大应力:截面几何性质取抗扭截面模量W p
I max
对弯曲的最大应力:截面几何性质取抗弯截面模量 W Z
IZ ymax
4. 四种基本变形的变形公式,都可写成:
内力 长度 变形= 刚度
因剪切变形为实用计算方法,不考虑计算变形。
弯曲变形的曲率
(1x)
d2y dx 2
,一段长为
1)物理常数:
某种变形引起的正应力:抗拉(压)弹性模量E;
某种变形引起的剪应力:抗剪(扭)弹性模量G。
2)截面几何性质:
拉压和剪切:变形是截面的平移: 取截面面积 A;
重庆大学材料力学答案解析

重庆大学材料力学答案2.9 题图2.9所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图2.9解:(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积 21mm 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)2.10 横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力kN 10==P N (2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ (3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)2.17 题图2.17所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
材料力学 重大版 课后习题答案

F 3
A
D
B
F
1m
1m
FDC
FDC ADC
4 10F
3 d 2
40F 103
3 202 106
FAx
[ ] 160
A
¦ΘD
B
[
F
]
160
3 202
40 103
106
15.1kN
FAy
1m
F
1m
FDC ADC
4 10F
3 d 2
40F 103
A a
B
FN 2
1 2
Fa
2m
M B 0 : F 2 a 2FN1 0,
2 a
FN1 2 F
L1
L2
FN1l1 E1 A1
FN2l2 E2 A2
F 2 - al1 Fal2
2E1 A1
2E2 A2
•d1=20mm,E1=200GPa; •d2=25mm,E2=100GPa。
• q =10kN/m,l =2m,求各杆的最大正应力,并用图形表示
• 正应力沿轴线的变化情况。
• 答 (1)63.55MPa,(2)127.32MPa,(3)63.55MPa,
• (4)-95.5MPa,(5)127.32MPa
10kN
15kN 15kN
20kN
15.82MPa
+
31.85MPa -
FAD
FBD
D
F
2 FAC 2 F
FAD
2F 2
Fx 0 : FAC FAD cos 45o FAB 0; FAB F
重庆大学材料力学习题解答

C 0.75m 1m
A
D 1.5m
B F
1、受力分析
C 0.75m A 1m F D 1.5m B F
FCD
Fx Fy
d=2cm,E=200GPa, []=160MPa
M
A
0
F AB FCD sin AD 0
57.6 kN
3、根据AB杆的强度条件,求许可载荷
查表得水平杆AB的面积为A2=2×12.74cm2
FN 2 A2
3F 2 3F
1 1 6 4 120 10 2 12 . 74 10 A2 1.732 F 3
176.7 kN
4、许可载荷
F min57.6 kN 176.7kN
F 57.6 kN
题8
图示吊环, 载荷F=1000kN,两边 的斜杆均由两个横截面为矩形的钢杆构 成,杆的厚度和宽度分别为b=25mm, h=90mm,斜杆的轴线与吊环对称,轴 线间的夹角为α=200 。钢的许用应力为 〔σ〕=120MPa。试校核斜杆的强度。 解:1、计算各杆件的轴力。研究 节点A为的平衡
第二章
题1:试作此杆的轴力图。 F l 解: FR 1 F F 2 1
q
F l
F
F
F
2l 2 q
l 3 F 3
FR
FR = F
F'=2ql F
F
1
FR = F
F
F
FN1 = F
2
q
3
F x
1
FR = F
2
FN 3 = F
3 F
F
FR = F
重庆大学考研材料力学习题集全面分析

绪论一、是非题1.1材料力学主要研究杆件受力后变形与破坏的规律。
()1.2内力只能是力。
()1.3若物体各点均无位移,则该物体必定无变形。
()1.4截面法是分析应力的基本方法。
()二、选择题1.5构件的强度是指(),刚度是指(),稳定性是指()A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持其原有的平衡状态的能力C.在外力作用下构件抵抗破坏的能力1.6根据均匀性假设,可认为构件的()在各点处相同。
A.应力B.应变C.材料的弹性常数D.位移1.7下列结论中正确的是()A.内力是应力的代数和B.应力是内力的平均值C.应力是内力的集度D.内力必大于应力参考答案:1.1 V 1.2 X 1.3 V 1.4 X 1.5 C,A,B 1.6 C 1.7 C轴向拉压、选择题1.等截面直杆CD位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q,杆CD的横截面面积为A,质量密度为,试问下列结论中哪一个是正确的?(A)q = -gA;(B)杆内最大轴力F zmax =ql ;(C)杆内各横截面上的轴力F N = P ~~;——2(D)杆内各横截面上的轴力F N =0。
2.低碳钢试样拉伸时,横截面上的应力公式c -F N A适用于以下哪一种情况(A)只适用于二<c p; (B)只适用于二w :二e;(C)只适用于二w二s ;(D)在试样拉断前都适用。
3.在A和B两点连接绳索ACB,绳索上悬挂物重P,如图示。
点A和点B的距离保持不变,绳索的许用拉应力为[二]。
试问:当:-角取何值时,绳索的用料最省?(A) 0’ ;(B) 30’ ;(C) 45」; (D) 60」。
4.桁架如图示,载荷F可在横梁(刚性杆)DE上自由移动。
杆1和杆2的横截面面积均为A,许用应力均为[二](拉和压相同)。
求载荷F的许用值。
以下四种答案中哪一种是正确的?(A)(C)[匚]A ;5. 设受力在弹性范围内,问空心圆杆受轴向拉伸时,夕卜径与壁厚的下列四种变形关系中哪一种是正确的?(A)外径和壁厚都增大; (B)外径和壁厚都减小;(C)外径减小,壁厚增大;(D)外径增大,壁厚减小。
重庆大学846材料力学考研复习题及答案,重庆大学土木工程考研专业课资料

重庆大学
土木工程考研笔记
材
料
力
学
复
习
题
及
答
案
赠言:
朋友,如果你不满于现状,希望突破自己,在考研中考的高分,增加入学时拿的奖学金的机率,未来在本专业取得较高的成就;如果你希望打开认知视野,在更高的山间俯瞰这个世界,本资料必将助你一臂之力。
关于付费,原因很简单,免费是找不出对得起你时间的好资料,毕竟在这个时代,个人时间比钱值钱的多;于是乎,我大胆倡议,在你寻求考研资料时,请不要用逛市场、花费买菜的心态,因为你用个人时间需找资料时,你的竞争对手正在学习这本资料;相关,如果你觉得我的考研复习资料对得起你宝贵的时间,对得起你“投资考研”这四个字,就即刻下载吧,那便是对认知二字以及对我分享本考研干货的最大认可与褒奖。
重庆大学材料力学试题二
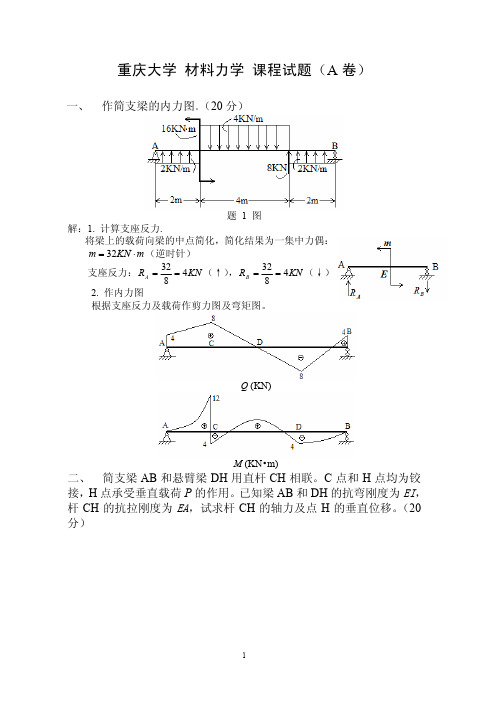
重庆大学 材料力学 课程试题(A 卷)一、 作简支梁的内力图。
(20分)题 1 图解:1. 计算支座反力.将梁上的载荷向梁的中点简化,简化结果为一集中力偶:m KN m ⋅=32(逆时针) 支座反力:KN R A 4832==(↑),KN R B 4832==(↓) 2. 作内力图根据支座反力及载荷作剪力图及弯矩图。
Q (KN)M (KN •m) 二、 简支梁AB 和悬臂梁DH 用直杆CH 相联。
C 点和H 点均为铰接,H 点承受垂直载荷P 的作用。
已知梁AB 和DH 的抗弯刚度为EI ,杆CH 的抗拉刚度为EA ,试求杆CH 的轴力及点H 的垂直位移。
(20分)题 2 图解:1. 静不定次数确定 6,2,3===r n m结构的自由度 16223323−=−×−×=−−=r n m D 1次静不定结构2. 分析计算去掉二力杆CH ,即可得到基本结构,设CH 杆轴向拉力为N ,梁的挠度C δ、H δ以向下为正,则变形集合条件为:CH C H l Δ=−δδ (1)EI a N P H 3)(3−=δ,EI a N C 48)2(3=δ,EANa l CH =Δ 代入式(1),得:EANa EI a N EI a N P =−−48)2(3)(33 由此式解出: )2(3222A a I A Pa N += 代入H δ,即得H 点的垂直位移为:)26(9223Aa I A a I EI Pa H++=δ 三、 直径为20mm 的圆截面平面折杆ADBC 在C 点受竖向力P 的作用,∠ABC =90度,杆的弹性模量E=200Gpa ,泊松比μ=0.3,现由实验测得D点截面处的顶部表面的主应变ε1=508×10-6, ε3=-288×10-6,试确定外力P 及BC 段的长度a 的大小。
已知l =314mm 。
(20分)题 3 图解: 1.应力状态分析AB 杆为弯曲和扭转组合变形,D 点所在截面上的弯矩Pa M =,D 点为二向应力状态 W M =σ,323d W π=,tW T =τ,163d W t π= 2. 分析计算D 点的主应力 ⎪⎪⎭⎪⎪⎬⎫+−=++=τσσστσσσ2121)2(2)2(2 (1) 由广义虎克定律:()3111μσσε−=E ,()1331μσσε−=E可以求得: (2) E E ⎪⎪⎭⎪⎪⎬⎫+−=+−=)(1)(113233121μεεμσμεεμσ联立求解方程(1),(2)可得: μεεσ−+=1)(31E (3) 231231)1()1(2μεεμεετ−+−+−=E (4) GPa E 200=,3.0=μ,,6110508−×=ε6310288−×−=ε代入式(3),(4),得:MPa 86.62=σ,MPa 55.52=τ32/3d Pl W M πσ== ∴ N d l P 2.157322031486.623233=××=⋅=ππσ 16/3d Pa W T t πτ== ∴ mm d P a 1.52516202.15755.521633=××=⋅=ππτ四、 水平梁ABCD 视为刚性杆,杆BE 和CF 采用相同材料制成,其比例极限σp =200Mpa ,许用应力[σ]=140Mpa ,稳定安全系数n st =2,弹性模量E =200Gpa ,①杆CF 直径d 1=10mm ,长度l 1 =1000mm ;②杆BE 直径d 2=20mm ,长度l 2=1000mm ,试求结构容许承受的最大载荷P 。
材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绪论一、是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
()1.2 内力只能是力。
()1.3 若物体各点均无位移,则该物体必定无变形。
()1.4 截面法是分析应力的基本方法。
()二、选择题1.5 构件的强度是指(),刚度是指(),稳定性是指()。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的()在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是()A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力参考答案:1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆(A) q gA ρ=(B) (C) (D) 2. (A) 只适用于(C) 只适用于3. 在A 和B 料最省?(A) 0; (C) 45; 。
4. 均为[]σ(A)[]2A σ; (C) []A σ; 5. (A) (C)6. 三杆结构如图所示。
今欲使杆3(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 伸长和杆2的缩短,种答案中的哪一种?(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1以下四种情况,问哪一种正确? (A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2(D) 杆1轴力增大,杆29. 结构由于温度变化,则:(A) (B) (C) (D) 静定结构中将引起应力和变形,超静定结构中将引起应力。
10. 内力N F (A) pD ; (B) 2pD; (C) 4pD ; (D) 8pD 。
二、填空题11. 图示受力结构中,若杆1和杆A y Δ= ,水平位移A x Δ12. 一轴向拉杆,横截面为a b ⨯(a ﹥b )的矩形,受轴向载荷作用变形后截面长边和短边的比值为 。
另一轴向拉杆,横截面是长半轴和短半轴分别为a 和b 的椭圆形,受轴向载荷作用变形后横截面的形状为 。
13. 一长为l ,横截面面积为A 的等截面直杆,质量密度为ρ,弹性模量为E ,该杆铅垂悬挂时由自重引起的最大应力max σ= ,杆的总伸长l ∆= 。
14. 图示杆1和杆2的材料和长度都相同,但横截面面积12A A >。
若两杆温度都下降T ∆,则两杆轴力之间的关系是N1F N2F ,正应力之间的关系是1σ 2σ。
(填入符号<,=,>) 题1-14答案:1. D2. D3. C4. B5. B6. B7. C8. C9. B 10. B11. Fl EA ; 12. a b ;椭圆形 13. 22gl gl Eρρ, 14. >,= 一、 是非题2.1 使杆件产生轴向拉压变形的外力必须是一对沿杆件轴线的集中力。
( ) 2.2 轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
( ) 2.3 内力是指物体受力后其内部产生的相互作用力。
( ) 2.4 同一截面上, σ 必定大小相等,方向相同。
( )2.5 杆件某个横截面上,若轴力不为零,则各点的正应力均不为零。
( ) 2.6 δ、 y 值越大,说明材料的塑性越大。
( )2.7 研究杆件的应力与变形时,力可按力线平移定理进行移动。
( ) 2.8 杆件伸长后,横向会缩短,这是因为杆有横向应力存在。
( ) 2.9 线应变 e 的单位是长度。
( )2.10 轴向拉伸时,横截面上正应力与纵向线应变成正比。
( ) 2.11 只有静不定结构才可能有温度应力和装配应力。
( )2.12 在工程中,通常取截面上的平均剪应力作为联接件的名义剪应力。
( ) 2.13 剪切工程计算中,剪切强度极限是真实应力。
( )二、选择题2.14变形与位移关系描述正确的是()A. 变形是绝对的,位移是相对的B. 变形是相对的,位移是绝对的C. 两者都是绝对的D. 两者都是相对的2.15轴向拉压中的平面假设适用于()A. 整根杆件长度的各处B. 除杆件两端外的各处C. 距杆件加力端稍远的各处2.16长度和横截面面积均相同的两杆,一为钢杆,一为铝杆,在相同的拉力作用下()A. 铝杆的应力和钢杆相同,而变形大于钢杆B. 铝杆的应力和钢杆相同,而变形小于钢杆C. 铝杆的应力和变形都大于钢杆D. 铝杆的应力和变形都小于钢杆2.17一般情况下,剪切面与外力的关系是()。
A.相互垂直 B.相互平行C.相互成 45 度 D.无规律2.18如图所示,在平板和受拉螺栓之间垫上一个垫圈,可以提高()强度。
A.螺栓的拉伸 B.螺栓的剪切C.螺栓的挤压 D.平板的挤压参考答案2.1 × 2.2 × 2.3 √ 2.4 × 2.5 × 2.6 √ 2.7 × 2.8 × 2.9 ×2.10 × 2.11 √2.12 √ 2.13 × 2.14 A 2.15 C 2.16 A 2.17 B 2.18 D材料的力学性能1. 工程上通常以伸长率区分材料,对于脆性材料有四种结论,哪一个是正确? (A) 5%d < ; (B) 0.5%d < ; (C) 2%d < ; (D) 0.2%d < 。
2. 对于没有明显屈服阶段的塑性材料,通常以0.2s 表示屈服极限。
其定义有以下四个结论,正确的是哪一个?(A) 产生2%的塑性应变所对应的应力值作为屈服极限; (B) 产生0.02%的塑性应变所对应的应力值作为屈服极限; (C) 产生0.2%的塑性应变所对应的应力值作为屈服极限; (D) 产生0.2%的应变所对应的应力值作为屈服极限。
3. 关于材料的冷作硬化现象有以下四种结论,正确的是哪一个? (A) 由于温度降低,其比例极限提高,塑性降低; (B) 由于温度降低,其弹性模量提高,泊松比减小; (C) 经过塑性变形,其比例极限提高,塑性降低; (D) 经过塑性变形,其弹性模量提高,泊松比减小。
4. 关于材料的塑性指标有以下结论,哪个是正确的? (A)s s 和d ; (B) s s 和ψ; (C) d 和ψ; (D) s s 、d 和ψ。
5. 用标距50 mm 和100 mm 的两种拉伸试样,测得低碳钢的屈服极限分别为s1s 、s2s ,伸长率分别为5d 和10d 。
比较两试样的结果,则有以下结论,其中正确的是哪一个?(A )s1s2s s <,510d d >; (B )s1s2s s <,510d d =;(C )s1s2s s =,510d d >; (D )s1s2s s =,510d d =。
6. 圆柱形拉伸试样直径为d ,常用的比例试样其标距长度l 是 或 。
7. 低碳钢拉伸试验进入屈服阶段以后,发生 性变形。
(填“弹”、“塑”、“弹塑”)8. 低碳钢拉伸应力-应变曲线的上、下屈服极限分别为s1s 和s2s ,则其屈服极限s s 为 。
9. 灰口铸铁在拉伸时,从很低的应力开始就不是直线,且没有屈服阶段、强化阶段和局部变形阶段,因此,在工程计算中,通常取总应变为_______%时应力-应变曲线的割线斜率来确定其弹性模量,称为割线弹性模量。
10. 混凝土的标号是根据其_________强度标定的。
11. 混凝土的弹性模量规定以压缩时的se -曲线中 s= 时的割线来确定。
12. 铸铁材料(根据拉伸、压缩、扭转)性能排序:抗拉_______抗剪_______抗压。
参考答案:1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑 8. s2s 9. 0.1 10. 压缩 11. b 0.4σ 12. <;<剪切与挤压的实用计算1. 图示木接头,水平杆与斜杆成α角,其挤压面积为bs A 为 (A )bh ; (B )tan bh α ; (C )cos bh α ; (D )cos sin bhαα⋅ 。
答:C2. 图示铆钉连接,铆钉的挤压应力bs σ有如下四个答案 (A )22π Fd; (B )2F d δ; (C )2F b δ ; (D )24πFd 。
答:B3. 切应力互等定理是由单元体(A )静力平衡关系导出的; (B )几何关系导出的; (C )物理关系导出的; (D )强度条件导出的。
答:A4. 销钉接头如图所示。
销钉的剪切面面积为 ,挤压面面积 。
答:2bh ;bd5. 木榫接头的剪切面面积为和 ,挤压面面积为 。
答:ab ;bd ;bc6. 图示厚度为δ础的剪切面面积为 ,挤压面面积为答: 4a δ; 2a7. 图示直径为d 的圆柱放在直径为3D d =,厚度为δ地基对基座的支反力为均匀分布,圆柱承受轴向压力F 面的剪力S F = 。
答:()22S 2π 48π 49D d F F F D -=⨯=扭 转1. 一直径为1D 的实心轴,另一内径为d ,外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案: (A) 21α-; (B); (C) ; (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案: (A)τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:(A) 必最大; (B)7. 图示圆轴AB ,截面C 的扭转角ϕ(A) 43π128d G a ϕ; (C) 43π32d G a ϕ;8. 一直径为1D 9. 10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲一、是非题3.1 在单元体两个相互垂直的截面上,剪应力的大小可以相等,也可以不等。
