控制工程基础第二版课后复习题答案
机械控制工程基础第二版课后答案

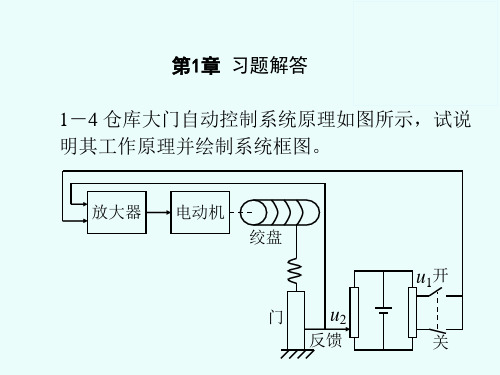
机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c?(idt2?i1)dt得到:cr2du2?(1?r2r1)u2?cr2du1dt?r2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1c?idt消去i得到:(r1?r2)一阶微分方程du2dt?u2c?r2du1dt?u1c第二章2-2解:1)确定输入、输出变量f(t)、x2f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f?f?m2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44?(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33?(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22?(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?1?1s?22e?t?e?2t (4)199s?4e?4t?19119s?1?t?1123(s?1)?t?e?13te1(s?1)2(5)?2(s?2)?2(s?1)??2e?2t?2e?t?te?t (6)?0.25?2ss?42?0.5?2?2s?42?2s?1?2.5s?t?0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,?1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程??mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图??mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x??2x?2x (2) ???2x??2tx?2x xxxoooioooi??2x?2x(4) ???2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》第二版 (董景新 著)课后习题答案 清华出版社

Xi
G1 G2
1+G1 H1+ G2 H2 +G1G2 H3 +G1G2H1H2 )
X0
G (s) =
G 1G 2 1 + G 1 H 1 + G 2 H 2 + G 1G 2 H 3 + G 1G 2 H 1 H 2
第二章习题解
2-7: 求X0(s) 和Xi2(s) (s)之间的闭环传递函数; 求X0(s) 和Xi1(s (s)之间的闭环传递函数;
G (s) =
G1G 2G 3G 4G 5 H 1 1 + G 4 + G1G 2 + G1G 2G 4 − G1G 4G 5 H 1H 2
第二章习题解
4):求出
X 02 ( s ) X i1 ( s )
-
解:第一步,方框图整理
-
G2 G1
Xi1 +
+
+
①
H2 H1
+
② G4 ③
X02 G5 G6
( g )解:设中间变量 : xa (t ) Q k ′ = (Ds + k1 )
x 0(t) k1 k2 m x a(t) (t)
(t) fi(t)
k ′x0 (t ) = k 2 [xa (t ) − x0 (t )] k ′ + k2 D x0 (t ) ∴ xa (t ) = k2 x 又:f i (t ) = m&&a (t ) + k 2 [xa (t ) − x0 (t )] k2 ∴ G (s ) = mDs 3 + m(k1 + k 2 )s 2 + k 2 Ds + k1k 2
控制工程基础第二版(徐立)课后习题答案整理版

二到四章答案2-1试建立题2-1图所示各系统的微分方程[其中外力的),位移x(f)和电压为输入量;位移y⑺和电压顽)为输出量;k(弹性系数),"(阻尼系数),R(电阻),C(电容)和m(质量)均为常数]。
////////m/(O M(a)题2-1图系统原理图解:2-l(a)取质量m为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m上的力有外力f(t),重力mg,这两个力向下,为正。
有弹簧恢复力4X0+Jo]和阻尼力〃也也,这两个力向上,为负。
其中,光为at扣)=0、物体处于静平衡位置时弹簧的预伸长量。
A A dtmv v7(0哗根据牛顿第二定理£F=ma,有f(t)+mg一灯yQ)+为]—#«')=/花』,?)其中:mg=ky0代入上式得f(t)-ky(f)-r顿')=m"半)at dt整理成标准式:d2y(t)dyit)...…..m-—以—ky(t)=/(0dt dt或也可写成:H顷)~dT m at m m它是一个二阶线性定常微分方程。
2-l(b)如图,取A点为辅助质点,设该点位移为x A(t),方向如图。
再取B点也为辅助质点,则该点位移即为输出量X0,方向如图A 点力平衡方程:4M 。
一%“)] = //[竺史一¥]at atB 点力平衡方程:k 2y(t}= 〃[也也—也£1]dt dt由①和②:^[%(z)-x A (O] = k 2y(t}得:xA (t) = x(t)-^y(t)二边微分,办a ") _办⑺ *2 ©(,)dt将③代入②:①dt 、 dt整理成标准式:k 、+ k 2 dy(t) * k 2 y(Q _ dx(t)k 、 dt 〃 dt或也可写成:dy(t)工 k x k 2+ ,,仰)=灯如)dt /u(k\ + 幻) k x +k 2 dt它是一个一阶线性定常微分方程。
控制工程基础课后习题解答
(R1
R2
)C
d dt
uo
(t
)
uo
(t
)
R2C
d dt
ui
(t
)
ui
(t)
xi
xo
K1 K2 B f)
K1(
xi
xo
)
K2
(
xo
x)
B
dx dt
(K1
K2)B
d dt
xo
(t)
K1K 2 xo
(t)
K1B
d dt
xi
(t)
K1K 2 xi
(t)
易见:a)与b)、c)与d)、e)与f)为相似系统。
第2章 习题解答
dx2 dt
B2
dx2 dt
K 2 x2
m2
d 2x2 dt 2
第2章 习题解答
m1m2
d 4x2 dt 4
(m1B2
m1B3
m2 B1
m2 B3 )
d 3x2 dt3
(m1K2
m2 K1
B1B2
B1B3
B2 B3 )
d 2x2 dt 2
( K1B2
K1B3
K 2 B1
K 2 B3 )
dx2 dt
故:G2 (s)
X o (s) Xi (s)
(B1s K1)(B2s K2 ) (B2s K2 )(B1s K1) K1B1s
B1 K1 s 1 B2 K2 s 1
B1 K1 s 1 B2 K2 s 1 B1 K2 s
显然:两系统具有相同形式的传递函数。
第2章 习题解答
2-8 按信息传递和转换过程,绘出图示两机械系 统的方框图。
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u 上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c(idt2i1)dt得到:cr2du2(1?r2r1)u2?cr2du1dtr2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1cidt消去i得到:(r1?r2)一阶微分方程du2dtu2cr2du1dtu1c第二章2-2解:1)确定输入、输出变量f(t)、x2 f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f fm2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?11s?22e?t?e?2t (4)199s?4e4t19119s?1t1123(s?1)te?13te1(s?1)2(5)?2(s?2)2(s?1)2e?2t?2e?t?te?t (6)0.25?2ss?420.5?2?2s?422s?12.5st0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x2x?2x (2) 2x??2tx?2x xxxoooioooi2x?2x(4) 2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》参考复习题及答案

】 】
7.闭环系统前向传递函数是【 】 A.输出信号的拉氏变换与输入信号的拉氏变换之比 B.输入信号的拉氏变换与输出信号的拉氏变换之比 C.输出信号的拉氏变换与误差信号的拉氏变换之比 D.误差信号的拉氏变换与输出信号的拉氏变换之比 8.一阶系统的时间常数为 T,其脉冲响应为【 】 A. 1 e
t T
B. t T Te
t
T
C.
1 tT e T
】
D. T Te
t
T
8-1.一阶系统的时间常数为 T,其单位阶跃响应为【 A. 1 e
t T
B. t T Te
t
T
C.
1 tT e T
】
D. T Te
t
T
8-2.一阶系统的时间常数为 T,其单位斜坡响应为【 A. 1 e
D.线性控制系统
A.2 B.1 C.0 D. 不确定 28.一阶系统的单位阶跃响应在 t=0 处的斜率越大,系统的【 】 A.响应速度越快 B.响应速度越慢 C.响应速度不变 D.响应速度趋于零 29.临界阻尼二阶系统的单位阶跃稳态响应为【 】 A.零 B.常数 C.单调上升曲线 D.等幅衰减曲线 30.欠阻尼二阶系统的输出信号振幅的衰减速度取决于【 】 A. n B. C. g 】 D. D. c
t T
B. t T Te
t
T
C.
1 tT e T
t T
D. T Te
t
T
8-3.一阶系统的时间常数为 T,其单位阶跃响应的稳态误差为【 A.0 B. T C.
】
1 T 1 T
D. T Te
8-4.一阶系统的时间常数为 T,其单位斜坡响应的稳态误差为【 A.0 B. T C. D. T Te
《控制工程基础》第二版课后习题答案
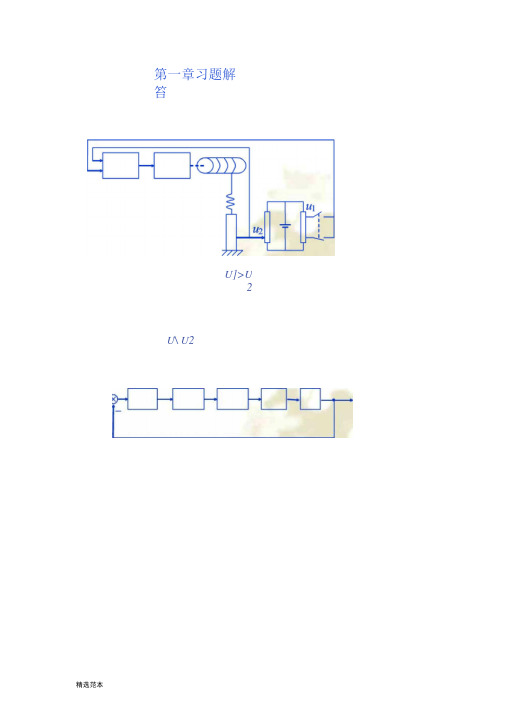
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
控制工程基础(第二版)答案_董景新_赵长德等pdf

Ms 2 X o (s) = k1 X o ( s) + D1sX o ( s) + k 2 ( X o ( s) − X i (s)) + D2 (sX o ( s) − sX i (s))
(b).根据力平衡方程,直接列写系统的方程 k1 Ds ( X i ( s) − X o (s)) = k2 X o ( s) k1 + Ds
(0) = 1, x(0) = 0 带入得: 将已知条件 x
对上式进行拉氏反变换的微分方程的解:
x(t ) =
1 7 −2t 7 −4 t + e − e 8 4 8
2-9 试求机械系统的传递函数 参考答案: (a). 根据牛顿定律,列写系统微分方程为:
进行拉氏变换得:
ms 2Yo ( s ) = f i − k1Yo ( s ) o − k 2 Yo ( s ) − DsYo ( s )
X (s) =
1 s
s 2 + 6s + 1 s ( s 2 + 6 s + 8) 1 7 = − 2 s s ( s + 6s + 8) = 1 ⎛1 1 1 1 1 1 ⎞ − 7⎜ ⋅ − ⋅ + ⋅ ⎟ s ⎝8 s 4 s + 2 8 s + 4⎠ 1 1 7 1 7 1 = ⋅ + ⋅ − ⋅ 8 s 4 s+2 8 s+4
整理得: X o (s) D1s D1 = = 2 X i ( s ) ms + ( D1 + D2 ) s ms + ( D1 + D2 )
(f). 根据牛顿定律,列写系统微分方程为:
o = k1 xo + D1 x o + k 2 ( xo − xi ) + D2 ( x o − x i ) M x
