最新结构力学作业答案
结构力学作业答案
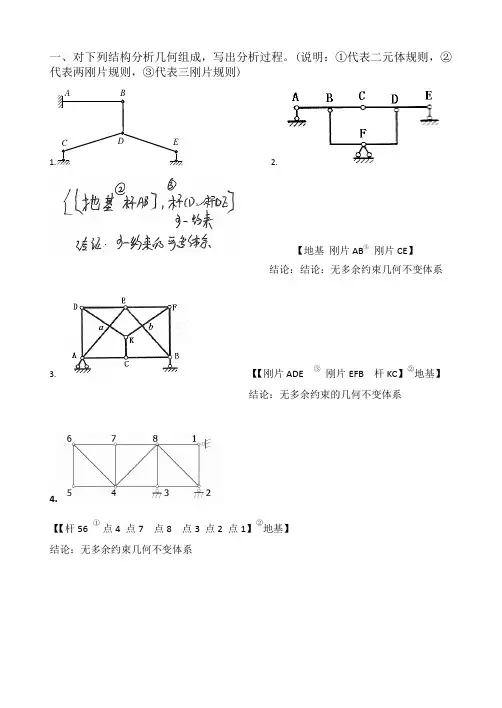
一、对下列结构分析几何组成，写出分析过程。
(说明：①代表二元体规则，②代表两刚片规则，③代表三刚片规则)1.AC DBE2.【地基刚片AB③刚片CE】结论：结论：无多余约束几何不变体系3.【【刚片ADE ③刚片EFB 杆KC】②地基】结论：无多余约束的几何不变体系4.【【杆56①点4 点7 点8 点3 点2 点1】②地基】结论：无多余约束几何不变体系5.【【地基，刚片ABC , ③刚片CDE】点F，点G，①点H，点I】结论：无多余约束几何不变体系6.【【杆AB ②地基】杆CD③杆DE】少一约束结论：可变体系二、判定图示桁架中的零杆。
图中画线的是0杆三、图示桁架，哪些杆件是零杆(不包括支座链杆)。
图中画线的是0杆四、作图示结构的弯矩图qh五、计算图示多跨静定梁，画弯矩图、剪力图.q解：qq0.5q 0.5q 0.5q q / 8M六、计算图示多跨静定梁，画弯矩图、剪力图.七、计算图示静定刚架的内力，并作内力图。
八、 作图示结构的弯矩图解：支座反力： )(42↑=KN Y B )(22↓=KN Y A )(48←=KN X A九、作图示结构的弯矩图北京交通大学现代远程教育昌平学习中心 作业二答案课程名称：结构力学 专业：土木工程本科年级：2011级 学期：2012-2013学年第一学期 学号： 姓名：一、 计算图示桁架a 、b 、c 三杆的轴力。
1）计算此结构的支座反力。
)(40↑=KN Y B )(40↑=KN Y A0=A X 2)计算指定杆内力。
0=Nb FKN F Na 60-=KN F Nc 60=二、求 图 示 桁 架 中 a 和b 杆 的 轴 力。
kn Na 210= kn N b 10-=三、求图示桁架中 a 和b 杆的轴力。
1)计算此结构的支座反力。
)(43↑=P Y A 0=A X2) 计算指定杆内力。
p F a 543= 0=b F四、解：1）设单位力2）画两个状态的弯矩图3）计算位移五、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
结构力学计算题及结构力学练习题含答案
结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学，以下是一篇结构力学计算题及练习题，包括答案的示例。
结构力学计算题题目：一简支梁AB，跨度为4米，受到均布荷载q=2 kN/m，梁的截面惯性矩I=1.2×10^6 mm^4，弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤：1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式：\[ M_{max} = \frac{ql^2}{8} \]代入已知数据：\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式：\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据：\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案：梁的最大弯矩Mmax为4 kN·m，最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD，长度为3米，受到集中力F=5 kN作用在自由端，梁的截面惯性矩I=1.5×10^6 mm^4，弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案：最大弯矩Mmax为5 kN·m，最大挠度y_max为0.013 mm。
2. 一连续梁EF，跨度为6米，分为两段，每段长度为3米，中间有一支点G。
梁上受到均布荷载q=1.5kN/m，梁的截面惯性矩I=2×10^6 mm^4，弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案：支点G的反力为4.5 kN，中间梁段的最大弯矩为2.25 kN·m。
结构力学(一)平时作业参考答案
1.叙述结构力学在实际工程领域中的作用。
答：该题涉及甚广，无标准答案，答题要求能联系教学内容列举一二，且叙述过程做到有理有据即可。
2.简单列举平面体系机动分析的基本方法，并举例说明其中一种方法的使用方法。
答：大体分为两刚片法和三刚片法，其中无多余约束的几何不变体系具有下述特征：1.一个刚片与两根链杆通过3个铰相连，且3个铰不在一直线上。
2.两个刚片用一个铰和一根链杆相联结，且3个铰不在同一直线上。
3.三个刚片用3个铰相连，且3个铰不在同一直线上。
4.两个刚片用3根链杆相连，且链杆不交于同一点。
此外，对于桁架也可尝试从计算自由度，零载法等进行分析，举例只需与其中一种方法相适应，且无原则性错误即可。
3.举例说明截面法和结点法计算静定桁架内力的基本方法。
答：结点法：以桁架结点为分析对象，利用平面汇交力系的基本平衡条件，首先计算支座力，再依次计算各杆内力。
截面法：用截面切断拟求内力的杆件，从桁架中截出一部分为隔离体，利用平面任意力系的基本平衡条件，计算各杆中的未知轴力。
如未知轴力只有三个，既不相交也不平行，则截面法可直接求出未知轴力。
举例要求能正确辨别分析对象，并建立相应的平衡方程。
4.举例说明对称性对简化结构力学分析的作用。
答：对称性通常对于结构形式和加载形式而言。
通常对于对称荷载下的对称结构、反对称荷载下的对称结构、任意荷载下的对称结构的几种典型的情况，均可在很大程度上简化问题，可降低结构的复杂性、减少计算的维数、使问题更加便于求解。
举例无标准答案，要求说明上述1种情况，并指出对称性的效用即可。
5.叙述何为三铰拱的合理轴线。
答：当三铰拱的轴线与压力线重合，各截面的弯矩和剪力都为零，此时轴线即为三铰拱的合理轴线。
6.简述梁、刚架结构在受力与变形方面的区别。
答：在外力作用下，梁承受弯矩和剪力的作用，其变形受制于弯矩和剪力，但通常以弯曲变形为主；刚架结构除了承受弯矩和剪力，可能还抵抗轴力的作用，其变形受制于弯矩、剪力以及轴力，同样地，通常也以弯曲变形为主，但还需要考虑刚架结构的几何形式，因此刚架结构的变形较梁复杂得多。
结构力学试题及参考答案
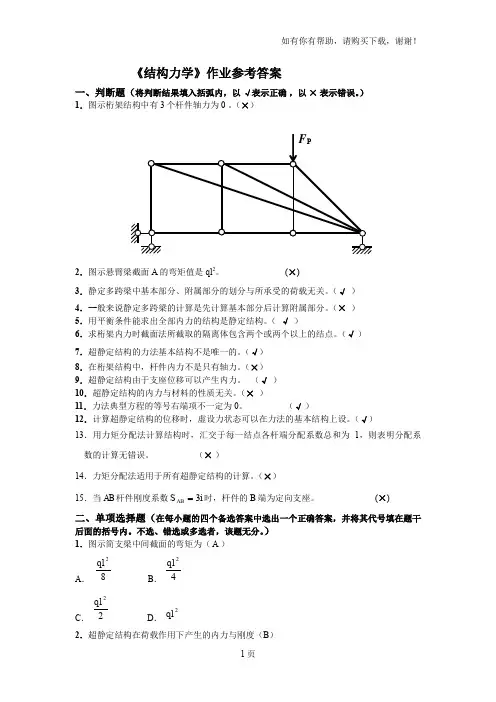
《结构力学》作业参考答案一、判断题（将判断结果填入括弧内，以 √表示正确 ，以 × 表示错误。
）1．图示桁架结构中有3个杆件轴力为0 。
（×）2．图示悬臂梁截面A 的弯矩值是ql 2。
(×)3．静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
（√ ）4．一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。
（× ）5．用平衡条件能求出全部内力的结构是静定结构。
（ √ ）6．求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
（√ ）7．超静定结构的力法基本结构不是唯一的。
（√）8．在桁架结构中，杆件内力不是只有轴力。
（×）9．超静定结构由于支座位移可以产生内力。
（√ ）10．超静定结构的内力与材料的性质无关。
（× ）11．力法典型方程的等号右端项不一定为0。
（√ ）12．计算超静定结构的位移时，虚设力状态可以在力法的基本结构上设。
（√）13．用力矩分配法计算结构时，汇交于每一结点各杆端分配系数总和为1，则表明分配系数的计算无错误。
（× ）14．力矩分配法适用于所有超静定结构的计算。
（×）15．当AB 杆件刚度系数i S AB 3 时，杆件的B 端为定向支座。
(×)二、单项选择题（在每小题的四个备选答案中选出一个正确答案，并将其代号填在题干后面的括号内。
不选、错选或多选者，该题无分。
）1．图示简支梁中间截面的弯矩为（ A ）A ． 82qlB ． 42qlC ． 22ql D ． 2ql2．超静定结构在荷载作用下产生的内力与刚度（B ）A．无关 B．相对值有关C．绝对值有关 D．相对值绝对值都有关3．超静定结构的超静定次数等于结构中（B ）A．约束的数目 B．多余约束的数目C．结点数 D．杆件数4．力法典型方程是根据以下哪个条件得到的（C）。
A．结构的平衡条件B．结构的物理条件C．多余约束处的位移协调条件D．同时满足A、B两个条件5．图示对称结构作用反对称荷载，杆件EI为常量，利用对称性简化后的一半结构为（A ）。
结构力学试题答案
结构力学试题答案结构力学是一门研究结构受力和变形规律的学科，对于工程领域的学生来说，掌握这门学科的知识至关重要。
以下是一套结构力学试题的答案及详细解析。
一、选择题1、关于静定结构的内力，下列说法正确的是（）A 内力与杆件的材料性质无关B 内力与杆件的截面形状无关C 内力与结构所受的荷载有关D 以上都对答案：D解析：静定结构的内力只与结构的几何形状、约束条件和所受荷载有关，而与杆件的材料性质和截面形状无关。
2、图示刚架，支座 A 发生竖向位移 a，支座 B 发生水平位移 b，不计杆件的轴向变形，利用单位荷载法求 C 点的竖向位移时，应在 C 点施加的单位力是（）A 竖向单位集中力B 水平单位集中力C 顺时针单位集中力偶D 逆时针单位集中力偶答案：A解析：要求 C 点的竖向位移，应在 C 点施加竖向单位集中力。
3、力法的基本未知量是（）A 多余约束力B 广义位移C 结点位移D 杆件内力答案：A解析：力法是以多余约束力为基本未知量，将超静定结构转化为静定结构进行分析。
二、填空题1、平面桁架在计算杆件内力时，通常采用__________法。
答案：节点法、截面法解析：节点法是依次取桁架的节点为研究对象，利用平衡条件求出杆件内力；截面法是用一截面截取桁架的一部分作为研究对象，利用平衡条件求出杆件内力。
2、梁在集中力作用处，剪力图发生__________，弯矩图发生__________。
答案：突变、转折解析：集中力会使剪力发生突变，弯矩发生转折。
3、结构的稳定性是指结构在__________作用下，保持其原有平衡状态的能力。
答案：微小干扰解析：稳定性指结构在微小干扰作用下不发生显著的变形或失去平衡。
三、计算题1、图示简支梁，受均布荷载 q 作用，跨度为 l ，求支座 A、B 的反力。
解：对整体进行受力分析，由平衡方程∑Fy ＝ 0 可得：RA ＋ RB ql ＝ 0 （1）对 A 点取矩，由∑MA ＝ 0 可得：RB × l ql × l/2 ＝ 0 （2）联立（1）（2）解得：RA ＝ ql/2 ，RB ＝ ql/22、用力法计算图示超静定梁，EI 为常数。
结构力学的考试题型及答案
结构力学的考试题型及答案一、选择题1. 以下哪个选项是结构力学中的基本假设？A. 结构是连续的B. 结构是刚性的C. 结构是弹性的D. 结构是塑性的答案：C2. 梁在受到弯矩作用时，其截面上的应力分布规律是什么？A. 线性分布B. 抛物线分布C. 正弦分布D. 均匀分布答案：B二、填空题3. 在结构力学中，_______是指结构在受到外力作用时，其内部各点的位移和内力满足平衡条件和变形条件。
答案：结构分析4. 悬臂梁自由端受到集中荷载作用时，其最大弯矩为_______。
答案：P*L/2三、简答题5. 简述结构力学中虚功原理的基本思想。
答案：虚功原理的基本思想是，当一个结构处于平衡状态时，任何虚位移所做的虚功都等于零。
这意味着结构在受到任何虚位移时，外力所做的虚功等于内力所做的虚功。
6. 描述梁的剪力和弯矩之间的关系。
答案：梁的剪力是弯矩随梁长度变化的导数，即剪力等于弯矩对梁长度的一阶导数。
具体来说，弯矩是剪力的积分，而剪力是弯矩的微分。
四、计算题7. 已知一简支梁，跨中集中荷载为P，求梁的跨中挠度。
答案：跨中挠度可以通过弯矩方程和挠度方程计算得出，对于简支梁跨中集中荷载的情况，跨中挠度公式为δ_max = (PL^3) / (48EI)，其中L为梁长，E为材料的弹性模量，I为截面惯性矩。
8. 计算一端固定一端简支梁在固定端集中荷载作用下的固定端弯矩。
答案：固定端弯矩可以通过弯矩分配法或弯矩方程计算得出。
对于一端固定一端简支梁在固定端集中荷载作用的情况，固定端弯矩公式为M_fixed = (P*L) / 2，其中P为集中荷载，L为梁长。
结构力学作业及答案土木工程管理本科课程
(C)第j个结点位移等于单位位移时，产生的第i个附加约束中的反力（矩）
(D)第j个结点位移产生的第j个附加约束中的反力（矩）
正确答案：C
解答参考：
7.
考虑各杆件轴向变形，图示结构若用边界条件先处理法，结构刚度矩阵的容量为：
(A)15×15
(C)可求得支座结点位移
(D)无法求得结点位移
正确答案：D
解答参考：
14.单元刚度矩阵中元素 的物理意义是：（ ）
(A)当且仅当 时引起的与 相应的杆端力
(B)当且仅当 时引起的与 相应的杆端力
(C)当 时引起的与 相应的杆端力
(D)当 时引起的与 相应的杆端力
正确答案：C
解答参考：
15.
图示桁架的动力自由度数为（ ）
正确答案：说法错误
解答参考：
46.频率、主振型是体系本身的固有特性，与外荷载无关。（ ）
正确答案：说法正确
解答参考：
47.在动力荷载作用下，结构的内力和变形不仅与动力荷载的幅值有关，而且与动力荷载的变化规律以及结构本身的动力特性（自振频率、振型和阻尼等因素）有关。( )
正确答案：说法正确
解答参考：
48.结构的自振频率与质量、刚度及荷载有关。 （ ）
正确答案：说法正确
解答参考：
33.一般情况下，矩阵位移法的基本未知量的数目比传统位移法的基本未知量的数目要多。（ )
正确答案：说法正确
解答参考：
34.单元刚度矩阵均具有对称性和奇异性。（ ）
正确答案：说法错误
解答参考：
35.
图示四单元的l、EA、EI相同，所以它们整体坐标系下的单元刚度矩阵也相同。（ ）
结构力学练习册答案
第一章机动分析一、判断题1．( X ) 2．( X ) 3．( X ) 4．( O )二、选择题5．(B) 6．(D) 7．(C) 8．(A) 9．(A) 10．(A) 11．(C) 12．(B) 13．(A)三、填空题14．几何瞬变15． 或不定值16．两刚片用不完全相交及平行的三根链杆连接而的体系。
17．几何不变且无多余约束。
四、分析与计算题18．分析：1、2、3符合三刚片法则，几何不变；它与4、5又符合三刚片法则，几何不变；内部整体与地基符合二刚片三链杆法则。
结论：几何不变且无多余约束。
19．用两刚片法则，三链杆交于一点，几何瞬变。
20．用两刚片三链杆法则，几何不变无多余约束。
21．用两刚片三链杆法则，几何不变无多余约束。
22．用两刚片三链杆法则，几何瞬变。
23．用两刚片三链杆法则(或增加二元件)，几何不变无多余约束。
24．W = 1，几何可变。
125．用两刚片三链杆法则，几何不变无多余约束。
26．用三刚片、六链杆法则，几何不变无多余约束。
27．几何不变，有两个多余约束。
28．几何不变无多余约束。
29．用三刚片、六链杆法则，几何不变无多余约束。
30．用三刚片、六链杆法则，几何不变无多余约束。
2第二章静定梁与静定刚架一、判断题1．（O）2．（O）3．（X）4．（X）5．（X）6．( X ) 7．( O ) 8．( O ) 9．( X ) 10．( O ) 11．( O )二、选择题12．（C）13．（D）14．（A）15．( C )16．( D )17．( C ) 18．( C )19．（C）20．（B）21．（C ）三、填空题22．不变，零23．无关24．位移，变形，内力25．在任意荷载作用下，所有反力和内力都可由静力平衡条件求得确定的、有限的、唯一的解答。
26．0 ，027．20kN·m ，下28．75kN·m ，右29．2Pa，右30．0.5pa ，上31．Pa, 左四、分析与计算题32．33．20.5q lq l28M图PaM图3434． 35．m 16R A ql H 0M B B ql 0.5( )图M Bql 0.522______A36． 37．1050203050().图 M kN m DC BE Aql 20.5ql 2ql20.5图M DC B A38． 39．图M m CAB().图 M kN m 2020AB 5DC40． 41．BC D40120图 M ()kN .m A 408040图M PlPl2Pl ABC D542． 43．().图 M kN m 4441535图M ql 28ql 223ABDC44． 45．()图 M kN .m AB 151515151515C DE F 1515Pa 2/3图Pa 2/3Pa 2/3Pa 2/3M AB46． 47．Pa 2/3Pa /34AB图MPaPa0.5P a0.5P a 图M48． 49．PaPaPaPa图M图M650． 51．ql20.5ql20.5ql20.5ql20.5图M图M mm52． 53．P aPa0.5P a0.5P a0.5M 图m0.5m54． 55．q56． 57．1k N 1k N3k N1k N Q 图 (3.5)N 图 (3.5)758．PPPQ 图N 图59．qaqa qa /2qaqa qa/2qa /232Q 图 N 图60．61．图M图M qa 22qa 2262．ABC ED F Pa Pa 1328第三章 静 定 拱一、判断题1．（X ） 2．（O ）3． ( O )二、选择题4．（C ）5．（B ） 6．（D ） 7．（B ） 8．( B ) 9．( D )三、填空题10． 0 , 011． 7.5kN ·m , 下四、分析与计算题12． M K =0Q K =0N qr K =-13． M =-⋅2013()kN m Q =-531()kNN =-+531()kN14． M M Hy k K=-=-⋅010kN m Q Q H K K=-=00c o s s i n ϕϕN Q H K K=--=-010sin cos ϕϕkNs i n ,c o s ϕϕ= = N Q H KK 00201020=⋅==kN m kN kN ,,9第四章 静定桁架一、判断题1．（O ） 2．（O ） 3．（X ） 4．（X ） 5．（X ） 6．（X ）二、选择题7． ( D ) 8．( D ) 9．( D ) 10．（D ） 11．（D ）三、填空题12． 0 , 013． BC , FG , ED ， DB , DF 14． 1.414P , －2P 15． 0.5P ( 拉 ) 16． P四、分析与计算题17． 18．图M 2Pa2Pa 2Pa Pa6Pa 6ABC D E FG图M 2qa 22qa 22qa 22qa 2qa219．ABDC806020M ()kN .m 图1020．N P ED =2取 隔 离 体 如 下 图 ，N N P P P C ∑==-⋅=0243431 ,()//21．取 截 面 I - I ,得 N 10= 由 结 点 A 平 衡 得 N P 22=22．由 I-I 截 面 ，M A =∑0， 得 N 1=P 由 II-II 截 面 ，M B ∑=0， 得N P 22=-23．由 截 面 I-I ，得 N 310kN = 由NA=∑0，得 N 2=44kN11由 截 面 II-II ，N A =∑0 ，得N 125kN =-24．N 10= N P 2233=/25．由 结 点 A 平 衡 求 1 杆 内 力 ，N 10= 由 结 点 B 平 衡 求 2 杆 内 力 ，N P 2= 由 结 点 C 平 衡 求 3 杆 内 力 ，N P 322=/26．N P 12=，N P 22=-。
结构力学作业参考
结构力学课程作业答案第一章绪论1、按照不同的构造特征和受力特点，平面杆件结构可分为哪几类？2、何为静定结构和超静定结构？从几何构造分析的角度看，结构必须是几何不变体系。
根据多余约束 n ，几何不变体系又分为：有多余约束( n > 0)的几何不变体系——超静定结构；无多余约束( n = 0)的几何不变体系——静定结构。
从求解内力和反力的方法也可以认为：静定结构：凡只需要利用静力平衡条件就能计算出结构的全部支座反力和杆件内力的结构。
超静定结构：若结构的全部支座反力和杆件内力，不能只有静力平衡条件来确定的结构。
3、土建、水利等工程中的荷载，根据其不同的特征，主要有哪些分类？第二章平面结构的几何组成分析作业题：1、何为平面体系的几何组成分析？按照机械运动及几何学的观点，对平面结构或体系的组成情况进行分析，称为平面体系的几何组成分析。
2、何为几何不变体系？何为几何可变体系？几何不变体系—若不考虑材料的应变，体系的位置和形状不会改变。
几何可变体系—若不考虑材料的应变，体系的位置和形状是可以改变的。
3、几何组成分析的目的是什么？1）保证结构的几何不变性,以确保结构能承受荷载和维持体系平衡.2）判别某一体系是否为几何不变,从而决定它能否作为结构.3）研究几何不变体系的组成规则,以保证所设计的结构是几何不变体系,从而能承受荷载而维持平衡.4）根据体系的几何组成分析,正确区分静定结构和超静定结构,从而选择适当的计算方法进行结构的反力和内力计算.5）通过几何组成分析,明确结构的构成特点,从而选择结构受力分析的顺序以简化计算.4、何为一个体系的自由度？知悉体系计算自由度的公式。
5、试对下图所示体系进行几何组成分析。
图1图2图3图46、试求图示各体系的计算自由度数W。
7、例2-1 例2-28、习题 2.1～2.12 试对图示体系作几何组成分析。
第三章静定梁、静定平面刚架和三角拱的计算作业题：1、单跨静定梁有简支梁、外伸梁、悬臂梁等形式。
结构力学试题及答案
结构力学试题及答案一、选择题（每题2分，共20分）1. 下列选项中，哪一个是结构力学中常用的分析方法？A. 能量法B. 静力平衡法C. 动力学分析法D. 热力学分析法答案：A、B2. 梁的弯矩图通常表示的是：A. 剪力B. 弯矩C. 轴力D. 扭矩答案：B3. 悬臂梁在自由端受到垂直向下的集中力作用时，其弯矩图的形状是：A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案：B4. 简支梁在跨中受到垂直向下的集中力作用时，其弯矩图的形状是：A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案：B5. 梁的剪力图通常表示的是：A. 弯矩B. 剪力C. 轴力D. 扭矩答案：B6. 连续梁的内力分布特点是：A. 线性变化B. 非线性变化C. 恒定不变D. 周期性变化答案：B7. 在结构力学中，二阶效应通常指的是：A. 材料的非线性效应B. 几何非线性效应C. 动力效应D. 热效应答案：B8. 桁架结构中，节点的平衡条件是：A. 节点处的力矩平衡B. 节点处的力平衡C. 节点处的力和力矩都平衡D. 节点处的力不平衡答案：C9. 根据结构力学的基本原理，下列说法错误的是：A. 结构的内力与外力有关B. 结构的变形与内力有关C. 结构的稳定性与材料性质有关D. 结构的刚度与外力无关答案：D10. 梁的剪力和弯矩之间的关系是：A. 线性关系B. 非线性关系C. 没有关系D. 互为导数关系答案：D二、填空题（每题2分，共20分）1. 结构力学中，______是结构在荷载作用下产生的位移。
答案：变形2. 梁的剪力和弯矩之间存在______关系。
答案：互为导数3. 在结构力学中，______是结构在荷载作用下产生的内力。
答案：内力4. 悬臂梁在自由端受到垂直向下的集中力作用时，其弯矩图的形状是______。
答案：抛物线5. 简支梁在跨中受到垂直向下的集中力作用时，其弯矩图的形状是______。
答案：抛物线6. 连续梁的内力分布特点是______。
西南大学结构力学作业答案
结构力学1：[论述题]简答题1、简述刚架内力计算步骤。
参考答案：答：（1）求支座反力。
简单刚架可由三个整体平衡方程求出支座反力，三铰刚架及主从刚架等，一般要利用整体平衡和局部平衡求支座反力。
（2）求控制截面的内力。
控制截面一般选在支承点、结点、集中荷载作用点、分布荷载不连续点。
控制截面把刚架划分成受力简单的区段。
运用截面法或直接由截面一边的外力求出控制截面的内力值。
（3）根据每区段内的荷载情况，利用"零平斜弯”及叠加法作出弯矩图。
作刚架Q、N图有两种方法，一是通过求控制截面的内力作出；另一种方法是首先作出M 图；然后取杆件为分离体，建立矩平衡方程，由杆端弯矩求杆端剪力；最后取结点为分离体，利用投影平衡由杆端剪力求杆端轴力。
当刚架构造较复杂（如有斜杆），计算内力较麻烦事，采用第二种方法。
（4）结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。
（5）注意结点的平衡条件。
2：[论述题]简答题2、简述力法的基本思路。
参考答案：答：力法的基本思路：将超静定结构的计算转化为静定结构的计算，首先选择基本结构和基本体系，然后利用基本体系与原结构之间在多余约束方向的位移一致性和变形叠加列出力法典型方程，最后求出多余未知力和原结构的内力。
第一步：去掉原结构的多余约束，代之以多余未知力，得到静定的基本体系。
第二步：基本体系和原结构的变形相同，特别是基本体系上与多余未知力相应的位移与原超静定结构上多余约束处的位移条件一致，这是确定多余未知力大小的依据。
一般情况下，当原结构上在多余约束处没有支座位移时，则基本体系应满足的变形条件是：与多余未知力相应的位移为零。
3：[论述题]简答题3、简述结构力学研究方法。
参考答案：答：结构力学问题的研究手段包含理论分析、实验研究和数值计算，本课程只进行理论分析和计算。
结构力学的计算方法很多，但都要考虑以下三方面的条件：（1）力系的平衡条件或运动条件。
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】「习题11】【习题12】【习题13】【习题14】【参考答衆】习题22-1〜2-14试对图示体系进行儿何组成分析，如果是只有多余联系的儿何不变体系，则应指出多余联系的数目。
d5∑° X 厂^τ"βH题2-2图ΓΛ题2-3图题2-5图题2-6图题2-1图H 2-9 图题2-10图题2-11图题2-12图题2-13图习题3试作图示多跨挣定梁的M及Q图。
(a) (b)题3-1图3-2试不计算反力而绘出梁的M图。
题3-2图习题44-1作图示刚架的M、Q、N图。
40fcN 40kN20kNm4-2作图示刚架的M图。
2OkN m SkN mSkXm 40fcN题4-1图4-3作图示三狡刚架的M图。
4-4作图示刚架的M图。
AEmJnIAr lD1题4-2图4-5己知结构的M图•试绘出荷载。
题4-4图3IOkNnlJ^1.5mC(a)题4-3日6erIB9 9题5-1图5-2带拉杆拱，拱轴线方程y= il(l-χ)χ,求截面K 的弯矩。
题5-2图5-3试求图示带拉杆的半圆三狡拱截面K 的内力・4-6检査F 列刚架的M 图，并予以改正。
题4-5图ω∙I ∣ULL∏ ∏ ⅛)题4-6图习题5图示抛物纟戈三铁拱轴线方程y = ff(l-x)x ，试求D 截面的内力。
IkNm15m [ 5m [ ICm 1=3OmC题5-3图习题6 6-1判定图示桁架中的零杆。
题6-1图6-2用结点法计算图示桁架中各杆内力。
(a) FGH月Λ4x4m=16m题6-2图6-3用截面法计算图示桁架中指定各杆的内力。
40kN题6-3图6-4试求图示组介结构中齐链杆的轴力并作受弯杆件的Q图。
2m ] 2m ]lm]lπ⅝] 2m [题6-4图6-5用适宜方法求桁架中指定杆内力。
题6-6图习题88-1试作图示悬臂梁的反力V B 、MB 及内力Q C 、MC 的影响线。
结构力学考试题及答案
结构力学考试题及答案一、单项选择题（每题2分，共20分）1. 结构力学中，以下哪一项不是结构分析的基本任务？A. 确定结构的内力B. 确定结构的位移C. 确定结构的稳定性D. 确定结构的美观性答案：D2. 在结构力学中，以下哪一项是静定结构的特点？A. 有多余约束B. 无多余约束C. 有多余支座D. 无多余支座答案：B3. 梁在弯曲时，以下哪一项是正确的弯矩图形状？A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案：B4. 以下哪一项不是影响结构稳定性的因素？A. 材料性质B. 几何尺寸C. 载荷大小D. 环境温度答案：D5. 在结构力学中，以下哪一项是超静定结构的特点？A. 内力可以通过平衡方程确定B. 内力不能通过平衡方程确定C. 位移可以通过平衡方程确定D. 位移不能通过平衡方程确定答案：B6. 以下哪一项是结构力学中的动力分析？A. 确定结构在静载荷作用下的内力和位移B. 确定结构在动载荷作用下的内力和位移C. 确定结构在热载荷作用下的内力和位移D. 确定结构在风载荷作用下的内力和位移答案：B7. 以下哪一项是结构力学中的塑性分析？A. 确定结构在弹性范围内的内力和位移B. 确定结构在塑性变形范围内的内力和位移C. 确定结构在断裂时的内力和位移D. 确定结构在疲劳破坏时的内力和位移答案：B8. 在结构力学中，以下哪一项是结构的几何不变性？A. 结构在任何外力作用下形状不变B. 结构在任何外力作用下形状可以改变C. 结构在任何外力作用下形状保持不变D. 结构在任何外力作用下形状可以保持不变答案：C9. 以下哪一项是结构力学中的虚功原理？A. 通过平衡方程确定结构的内力B. 通过虚设位移确定结构的内力C. 通过虚设载荷确定结构的内力D. 通过虚设速度确定结构的内力答案：B10. 在结构力学中，以下哪一项是结构的自由度？A. 结构在空间中的运动方向数B. 结构在平面中的运动方向数C. 结构在空间中的约束数D. 结构在平面中的约束数答案：B二、多项选择题（每题3分，共15分）11. 结构力学中，以下哪些因素会影响结构的内力分布？A. 材料性质B. 几何尺寸C. 载荷分布D. 支撑条件答案：ABCD12. 在结构力学中，以下哪些是静定结构？A. 单跨梁B. 双跨连续梁C. 三铰拱D. 悬索桥答案：AC13. 以下哪些是结构力学中常用的分析方法？A. 弯矩分配法B. 力矩分配法C. 虚功原理D. 能量法答案：ABCD14. 以下哪些是结构力学中的动力分析类型？A. 自由振动B. 强迫振动C. 随机振动D. 瞬态振动答案：ABCD15. 在结构力学中，以下哪些是结构的稳定性问题？A. 屈曲B. 失稳C. 振动D. 疲劳答案：AB三、填空题（每题2分，共20分）16. 结构力学中，结构的内力包括______、______和______。
结构力学第三版课后习题答案精选全文
20kN/m
M图
4.5kN
8.98
4
4.5
6 11
4.5 FQ图
M图 (kN.m)
FQ图(kN)
37
3.3 静定平面刚架
必作题： P.109 3-3 (b) (d) (f) (j) P.110 3-4 (a — i) P.111 3-7 (a) P.112 3-8 (a) (d)
选作题： P.109 3-3 (a) (e) (g) (l) P.112 3-8 (c) P.112 3-9 (a) P.113 3-11
2
P.37 2-1(b)
1
2
3
三链杆交于一点，瞬变
3
P.37 2-2(b)
4几何不变，无多余约束5P.37 2-3(c)
有一个多余 约束
1
2 3
几何不变，有一个多余约束
6
P.37 2-4(d)
O(I、III) O(II、III) I
II
1
2
O(I、II)
III
铰O(I、II)、 O(II、III)的连线与1、2两链 杆不平行，体系几何不变，无多余约束
2.5m 5m 5m 2.5m
FN图
60
3.4 静定平面桁架
必作题：
P.113 P.114 P.115
选作题：
P.116 P.117
3-13 (b) (d) (f) 3-14 (a) (b) (c) 3-17 (a) (d)
3-18 (a) 3-20
P.116 3-18 (b)
61
P.113 3-13 (b) 分析桁架类型，指出零杆
FP
联合桁架，10根零杆。
62
P.113 3-13 (d) 分析桁架类型，指出零杆
结构力学课后习题答案
结构力学课后习题答案(总23页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图，试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。
题5-1图5-2 带拉杆拱，拱轴线方程x x l lf y )(42-=，求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精品文档[0729]《结构力学》1、桁架计算的结点法所选分离体包含几个结点A. 单个2、固定铰支座有几个约束反力分量B. 2个3、从一个无多余约束的几何不变体系上去除二元体后得到的新体系是A. 无多余约束的几何不变体系4、两刚片用三根延长线交于一点的链杆相连组成A. 瞬变体系5、定向滑动支座有几个约束反力分量B. 2个6、结构的刚度是指C. 结构抵抗变形的能力7、桁架计算的截面法所选分离体包含几个结点B. 最少两个8、对结构进行强度计算的目的，是为了保证结构A. 既经济又安全9、可动铰支座有几个约束反力分量A. 1个10、固定支座(固定端)有几个约束反力分量C. 3个11、改变荷载值的大小，三铰拱的合理拱轴线不变。
A.√12、多余约束是体系中不需要的约束。
B.×13、复铰是连接三个或三个以上刚片的铰A.√14、结构发生了变形必然会引起位移，结构有位移必然有变形发生。
B.×精品文档．精品文档15、如果梁的截面刚度是截面位置的函数，则它的位移不能用图乘法计算。
A.√16、一根连杆相当于一个约束。
A.√17、单铰是联接两个刚片的铰。
A.√18、连接四个刚片的复铰相当于四个约束。
B.×19、虚功原理中的力状态和位移状态都是虚设的。
B.×20、带拉杆三铰拱中拉杆的拉力等于无拉杆三铰拱的水平推力。
A.√21、瞬变体系在很小的荷载作用下会产生很大的内力，所以不能作为结构使用。
A.√22、一个无铰封闭框有三个多余约束。
A.√23、三铰拱的水平推力不仅与三铰的位置有关，还与拱轴线的形状有关。
B.×24、三铰拱的主要受力特点是：在竖向荷载作用下产生水平反力。
A.√25、两根链杆的约束作用相当于一个单铰。
B.×26、不能用图乘法求三铰拱的位移。
A.√27、零杆不受力，所以它是桁架中不需要的杆，可以撤除。
B.×28、用图乘法可以求等刚度直杆体系的位移。
A.√29、连接四个刚片的复铰相当于四个约束。
精品文档．精品文档B.×30.:答31.几何组成分析答：依次去掉二元体剩下如图所示的并排简支梁，故原体系为无多余约束的几何不变体系。
精品文档．精品文档32.几何组成分析依次去掉基础、二元体，剩下图示部分为两刚片用两个铰相联，有一个多余约束，故原答：体系为有一个多余约束的几何不变系。
、简述刚架内力计算步骤。
33简单刚架可由三个整体平衡方程求出支座反力，三铰刚架及主从刚架求支座反力。
（1）答：控制截面一般选求控制截面的内力。
（2）等，一般要利用整体平衡和局部平衡求支座反力。
控制截面把刚架划分成受力简单的分布荷载不连续点。
在支承点、结点、集中荷载作用点、根据每区段内的荷（3）区段。
运用截面法或直接由截面一边的外力求出控制截面的内力值。
图有两种方法，一是通过求Q、N载情况，利用“零平斜弯”及叠加法作出弯矩图。
作刚架图；然后取杆件为分离体，建立矩平衡方控制截面的内力作出；另一种方法是首先作出M程，由杆端弯矩求杆端剪力；最后取结点为分离体，利用投影平衡由杆端剪力求杆端轴力。
）结点处有不同（4当刚架构造较复杂（如有斜杆），计算内力较麻烦事，采用第二种方法。
）（5的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。
注意结点的平衡条件。
、结构力学的主要研究内容。
、341 、几何组成分析目的。
2 、如何确定独立角位移数目。
3 、简述刚架内力计算步骤。
4 、简述计算结构位移的目的。
5 6、在位移法中须解决哪些问题。
答：1、结构力学的主要研究内容。
结答：结构由荷载、支座移动、温度变化、制造误差引起的内力计算——称为强度计算；结构由荷载、支座移动、温度变化、制造误差引起的变形及位移计算——称为刚度计算；就是研究结构在荷载作用结构的组成规律及计算简图的选择。
“结构力学”构的稳定计算；下的内力和变形的计算问题。
、几何组成分析目的。
2）区别静定结构、超）判别某一体系是否为几何不变，从而决定它能否作为结构。
（2答：（1）搞清结构各部分间的相互关系，以决定合理的计算3从而选定相应计算方法。
静定结构，（顺序。
3、如何确定独立角位移数目。
因此每一个刚结点只有一个独立的角位由于在同一结点处，答：各杆端的转角都是相等的，精品文档．精品文档移未知量。
在固定支座处，其转角等于零为已知量。
至于铰结点或铰支座处各杆端的转角，它们不是独立的，可不作为基本未知量。
这样，结构独立角位移数目就等于结构刚结点的数目。
4、简述刚架内力计算步骤。
答：（1）求支座反力。
简单刚架可由三个整体平衡方程求出支座反力，三铰刚架及主从刚架等，（2）求控制截面的内力。
控制截面一般选在支承点、一般要利用整体平衡和局部平衡求支座反力。
结点、集中荷载作用点、分布荷载不连续点。
控制截面把刚架划分成受力简单的区段。
运用截面法或直接由截面一边的外力求出控制截面的内力值。
（3）根据每区段内的荷载情况，利用“零平斜弯”及叠加法作出弯矩图。
作刚架Q、N图有两种方法，一是通过求控制截面的内力作出；另一种方法是首先作出M图；然后取杆件为分离体，建立矩平衡方程，由杆端弯矩求杆端剪力；最后取结点为分离体，利用投影平衡由杆端剪力求杆端轴力。
当刚架构造较复杂（如有斜杆），计算内力较麻烦事，采用第二种方法。
（4）结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示，并把该端字母列在前面。
（5）注意结点的平衡条件。
5、简述计算结构位移的目的。
答：(1) 验算结构的刚度。
校核结构的位移是否超过允许限值，以防止构件和结构产生过大的变形而影响结构的正常使用。
(2) 为超静定结构的内力分析打基础。
超静定结构的计算要同时满足平衡条件和变形连续条件。
(3) 结构制作、施工过程中也常需先知道结构的位移。
6、在位移法中须解决哪些问题。
答：（1）单跨超静定梁在杆端发生各种位移、荷载、温度等因素作用下的内力。
（2）哪些结点位移作为基本未知量。
(3)如何确定基本未知量(求出位移)。
35、结构力学的主要研究内容。
答：结构由荷载、支座移动、温度变化、制造误差引起的内力计算——称为强度计算；结构由荷载、支座移动、温度变化、制造误差引起的变形及位移计算——称为刚度计算；结构的稳定计算；结构的组成规律及计算简图的选择。
“结构力学”就是研究结构在荷载作用下的内力和变形的计算问题。
36、1、简述弯矩图叠加的注意事项。
2、简述变形体的虚功原理。
3、简述力法的基本思路。
答：1、简述弯矩图叠加的注意事项。
答：（1）弯矩图叠加是竖标相加，不是图形的拼合；（2）要熟练地掌握简支梁在跨中荷载作用下的弯矩图；（3）利用叠加法可以少求或不求反力，就可绘制弯矩图；（4）利用叠加法可以少求控制截面的弯矩；（5）对于任意直杆段，不论其内力是静定的还是超静定的；不论是等截面杆或是变截面杆；不论该杆段内各相邻截面间是连续的还是定向联结还是铰联结弯矩叠加法均适用2、简述变形体的虚功原理。
答：变形体的虚功原理是力学中的一个基本原理，结构力学中计算位移的方法是以虚功原理为基础的。
刚体体系的虚功原理是变形体虚功原理的特殊形式。
变形体的虚功原理可表述为：设变形体在力系作用下处于平衡状态，又设变形体由于其它原因产生符合约束条件的微小连续变形，则外力在位移上所作外虚功恒等于各个微段的应力合力在变形上所作的内虚功。
精品文档．精品文档3、简述力法的基本思路。
答：力法的基本思路：将超静定结构的计算转化为静定结构的计算，首先选择基本结构和基本体系，然后利用基本体系与原结构之间在多余约束方向的位移一致性和变形叠加列出力法典型方程，最后求出多余未知力和原结构的内力。
第一步：去掉原结构的多余约束，代之以多余未知力，得到静定的基本体系。
第二步：基本体系和原结构的变形相同，特别是基本体系上与多余未知力相应的位移与原超静定结构上多余约束处的位移条件一致，这是确定多余未知力大小的依据。
一般情况下，当原结构上在多余约束处没有支座位移时，则基本体系应满足的变形条件是：与多余未知力相应的位移为零。
37、简述计算结构位移的目的。
答：(1) 验算结构的刚度。
校核结构的位移是否超过允许限值，以防止构件和结构产生过大的变形而影响结构的正常使用。
(2) 为超静定结构的内力分析打基础。
超静定结构的计算要同时满足平衡条件和变形连续条件。
(3) 结构制作、施工过程中也常需先知道结构的位移。
38、在位移法中须解决哪些问题。
答：（1）单跨超静定梁在杆端发生各种位移、荷载、温度等因素作用下的内力。
（2）哪些结点位移作为基本未知量。
(3)如何确定基本未知量(求出位移)。
39、几何组成分析目的。
答：（1）判别某一体系是否为几何不变，从而决定它能否作为结构。
（2）区别静定结构、超静定结构，从而选定相应计算方法。
（3）搞清结构各部分间的相互关系，以决定合理的计算顺序。
40、如何确定独立角位移数目。
答：由于在同一结点处，各杆端的转角都是相等的，因此每一个刚结点只有一个独立的角位移未知量。
在固定支座处，其转角等于零为已知量。
至于铰结点或铰支座处各杆端的转角，它们不是独立的，可不作为基本未知量。
这样，结构独立角位移数目就等于结构刚结点的数目。
41.答：精品文档．精品文档42、用力法计算图示刚架，取图示基本结构，建立力法基本方程，求出方程中的系数和自由项，不必解方程和作弯矩图。
各杆EI=常数答：为常数B、求图示刚架A，两截面的相对转角。
各杆EI43答：精品文档．精品文档44、求图5所示刚架A，B两截面的相对转角。
各杆EI为常数。
答：EI=、试用力法计算图示刚架，并作出弯矩M图。
常数。
45答：精品文档．精品文档46.答：精品文档．精品文档47.答：48.精品文档．精品文档答：，所示梁的弯矩图。
各杆相同，。
、用位移法作图497 答：无i图。
各杆线刚度均为。
M50、试用位移法计算图所示刚架，并作出弯矩答：精品文档．精品文档51.答：精品文档．精品文档l 。
图，各杆线刚度均为4所示结构Mi，各杆长为、用位移法作图52答：精品文档．精品文档53、试用位移法计算图示刚架，并作出弯矩M图。
各杆线刚度均为i。
答：图。
MEI=常数。
、试用力法计算图所示刚架，并作出弯矩54答：精品文档．精品文档EI为常数。
55、试计算如图所示简支梁中点的竖向位移。
答：点的竖向位移。
梁的所示外伸梁、试求如图564CEI为常数。
精品文档．精品文档答：、试计算如图所示简支梁中点的竖向位移。
EI为常数。
57答：精品文档．精品文档58.答：求出方程中的系数和自59、用力法计算图所示刚架，取图示基本结构，建立力法基本方程，常数。
由项，不必解方程和作弯矩图。
各杆EI=精品文档．精品文档答：作图示结构的弯矩图、、1 60答：、3作图示结构的弯矩图61答：精品文档．精品文档作图示结构的弯矩图2、、62答：7、作图示结构的弯矩图、63答：精品文档．精品文档、6、作图示结构的弯矩图64答：65、4、作图示结构的弯矩图答：精品文档．精品文档、作图示结构的弯矩图、665答：精品文档．。