最新高中数学必修二三视图练习题
人教版数学高一-必修二(人教A)练习 1.2空间几何体的三视图
1.2空间几何体的三视图和直观图1．2.1中心投影与平行投影1．2.2空间几何体的三视图1．2.3空间几何体的直观图一、选择题(本大题共7小题，每小题5分，共35分)1．关于几何体的三视图，下列说法正确的是()A．正视图反映物体的长和宽B．俯视图反映物体的长和高C．侧视图反映物体的高和宽D．正视图反映物体的高和宽2．在原来的图形中，两条线段平行且相等，则在直观图中对应的两条线段()A．平行且相等B．平行不相等C．相等不平行D．既不平行也不相等图L1213．一个几何体的三视图如图L121所示，这个几何体可能是一个()A．三棱锥B．底面不规则的四棱锥C．三棱柱D．底面为正方形的四棱锥4．图L122是水平放置的三角形的直观图，D′是△A′B′C′中B′C′边的中点，A′B′，A′D′，A′C′三条线段对应原图形中的线段AB，AD，AC，那么()图L122A．最短的是ACB．最短的是ABC ．最短的是AD D ．无法确定谁最短5．如图L123所示，已知四边形ABCD 的直观图是一个边长为1的正方形，则原图形的周长为( )A ．2 2B ．6C ．8D ．4 2＋2图L123图L1246．图L124为水平放置的正方形ABCO ，在直角坐标系中点B 的坐标为(2，2)，则用斜二测画法画出的正方形的直观图中，点B ′到O ′x ′轴的距离为( )A.12B.22C. 1D. 2 7．用斜二测画法画出的某平面图形的直观图如图L125所示，AB 平行于y ′轴，BC ，AD 平行于x ′轴．已知四边形ABCD 的面积为2 2 cm 2，则原平面图形的面积为( )图L125A ．4 cm 2B ．4 2 cm 2C ．8 cm 2D ．8 2 cm 2二、填空题(本大题共4小题，每小题5分，共20分)8．用斜二测画法画出某三角形的直观图如图L126所示，则原三角形的面积为________．图L1269．利用斜二测画法得到的以下结论中正确的是________．(填序号)①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④圆的直观图是椭圆；⑤菱形的直观图是菱形．10．一张桌子上摆放着若干碟子，其三视图如图L127所示，则这张桌子上共放有________个碟子．图L12711．如图L128所示，在斜二测画法下，四边形ABCD的直观图是底角为45°的等腰梯形，其下底长为5，一腰长为2，则原四边形的面积是________．图L128三、解答题(本大题共2小题，共25分)12．如图L129所示，画出水平放置的四边形OBCD的直观图．图L12913．(13分)图L1210，L1211，L1212分别是三个几何体的三视图，你能画出它们对应的几何体的直观图吗？(1)(2)图L1210图L1211(3)图L121214．(5分)已知点E，F，G分别是正方ABCD-A1B1C1D1的棱AA1，CC1，DD1的中点，点M，N，Q，P分别在线段DF，AG，BE，C1B1上．则三棱锥P-MNQ的俯视图不可能是()图L1213图L121415．(15分)已知正三棱锥V-ABC的正视图、侧视图和俯视图如图L1215所示．(1)画出该三棱锥的直观图；(2)求出侧视图的面积．图L12151．2 空间几何体的三视图和直观图1．2.1 中心投影与平行投影 1．2.2 空间几何体的三视图 1．2.3 空间几何体的直观图1．C [解析] 由三视图的特点可知选项C 正确．2．A [解析] 由斜二测画法规则知平行性是不变的，长度的变化在平行时相同，故仍平行且相等．3．C [解析] 根据三视图，几何体为一个倒放的三棱柱．4．C [解析] 由直观图易知A ′D ′∥y ′轴．根据斜二测画法规则，可知在原图形中应有AD ⊥BC .又AD 为BC 边上的中线，所以△ABC 为等腰三角形，且AD 为BC 边上的高，所以AB ，AC 相等且最长，AD 最短．5．C [解析] 原图形如下图所示．则AD ＝（2 2）2＋12＝3，所以原图形的周长为8. 6．B [解析] 因为BC 垂直于x 轴，所以在直观图中B ′C ′的长度是1，且与O ′x ′轴的夹角是45°，所以B ′到O ′x ′轴的距离是22.7．C [解析] 依题意可知∠BAD ＝45°，则原平面图形为直角梯形，且上下底边的长分别与BC ，AD 相等，高为梯形ABCD 的高的2 2倍，所以原平面图形的面积为8 cm 2.8．4 [解析] 由斜二测画法知，原三角形为直角三角形，且AO ＝4，BO ＝2，故S ＝12×2×4＝4.9．①②④ [解析] ①正确；由原图形中平行的线段在直观图中仍平行可知②正确；原图形中垂直的线段在直观图中一般不垂直，故③错误；④正确；原图形中相等的线段在直观图中不一定相等，故⑤错误．10．12 [解析] 4个，3个，所以碟子共有12个．11．8 2 [解析] 作D ′E ⊥A ′B ′于点E ，C ′F ⊥A ′B ′于点F ， 则A ′E ＝B ′F ＝A ′D ′cos 45°＝1，∴C ′D ′＝EF ＝3.画出原平面图(如图所示)，则原四边形应为直角梯形，∠A ＝90°，AB ＝5，CD ＝3，AD ＝2 2，∴S 四边形ABCD ＝12×(5＋3)×2 2＝8 2.12．解：(1)过点C 作CE ⊥x 轴，垂足为E ，如图(1)所示．画出对应的x ′轴，y ′轴，使∠x ′O ′y ′＝45°，如图(2)所示．(2)如图(2)所示，在x ′轴正半轴上取点B ′，E ′，使得O ′B ′＝OB ，O ′E ′＝OE ；在y ′正半轴上取一点D ′，使得O ′D ′＝12OD ；过E ′作E ′C ′∥y ′轴，使E ′C ′＝12EC .(3)连接B ′C ′，C ′D ′，并擦去x ′轴与y ′轴及其他一些辅助线，如图(3)所示，四边形O ′B ′C ′D ′就是所求作的直观图．13．解：(1)圆柱；(2)四棱锥；(3)三棱锥，且有一条侧棱与底面垂直．画图略．14．C [解析] 当M 与F 重合、N 与G 重合、Q 与E 重合、P 与B 1重合时，三棱锥P -MNQ 的俯视图为A ；当M 、N 、Q 、P 是所在线段的中点时，其俯视图为B ；当M 、N 、P 是所在线段的非端点位置，而Q 与B 重合时，三棱锥P -MNQ 的俯视图可能为选项D.故选C.15．解：(1)三棱锥的直观图如图所示． (2)根据三视图间的关系可得BC ＝2 3. 由俯视图可知三棱锥底面三角形的高为2 3×32＝3. ∵三棱锥的高在底面上的投影是底面的中心，且其到点A 的距离为底面△ABC 高的23，∴底面中心到点A 的距离为23×3＝2，∴侧视图中VA ＝42－22＝2 3，∴S △VBC ＝12×2 3×2 3＝6.。
高中数学1.2.1空间几何体的三视图练习新人教版A版必修2【含答案】
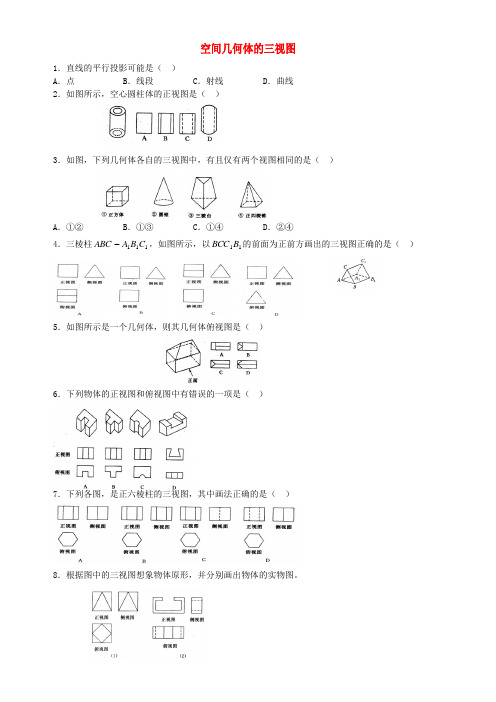
空间几何体的三视图1．直线的平行投影可能是（ ）A ．点B ．线段C ．射线D ．曲线2．如图所示，空心圆柱体的正视图是（ ）3．如图，下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）A ．①②B ．①③C ．①④D ．②④4．三棱柱111C B A ABC ，如图所示，以11B BCC 的前面为正前方画出的三视图正确的是（）5．如图所示是一个几何体，则其几何体俯视图是（ ）6．下列物体的正视图和俯视图中有错误的一项是（ ）7．下列各图，是正六棱柱的三视图，其中画法正确的是（ ）8．根据图中的三视图想象物体原形，并分别画出物体的实物图。
10．如图，E 、F 分别是正方体1AC 的面11A ADD 和面11B BCC 的中心，则四边形E BFD 1在该正方体的面上的正投影（投射线垂直于投影面的投影）可能是图中 （把所有可能图形的序号都填上）。
空间几何体的直观图1．利用斜二测画法叙述正确的是（ ）A ．正三角形的直观图是正三角形B ．平行四边形的直观图是平行四边形C ．矩形的直观图是矩形D ．圆的直观图一定是圆2．下列结论正确的是（ ）A ．相等的线段在直观图中仍然相等B ．若两条线段平行，则在直观图中对应的两条线段仍然平行C ．两个全等三角形的直观图一定也全等D ．两个图形的直观图是全等的三角形，则这两个图形是全等三角形3．直角坐标系中一个平面图形上的一条线段AB 的实际长度为4cm ，若AB//x 轴，则画出直观图后对应的线段=''B A ，若y AB //轴，则画出直观图后对应的线段B A ''= 。
4．水平放置的ABC ∆的斜二测直观图如图所示，已知2,3=''=''C B C A ，则AB 边上的中线的实际长度为 。
四、典例剖析1．已知一个正方形的直观图是一个平行四边形，其中有一边长为4，则此正方形的面积是（ ）A ．16B ．64C ．16或64D ．都不对分析：根据直观图的画法，平行于x 轴的线段长度不变，平行于y 轴的线段变为原来的一半，于是长为4的边如果平行于x 轴，则正方形边长为4，面积为16，边长为4的边如果平行于y 轴，则正方形边长为8，面积是64。
高中数学必修二1.2空间几何体的三视图和直观图习题
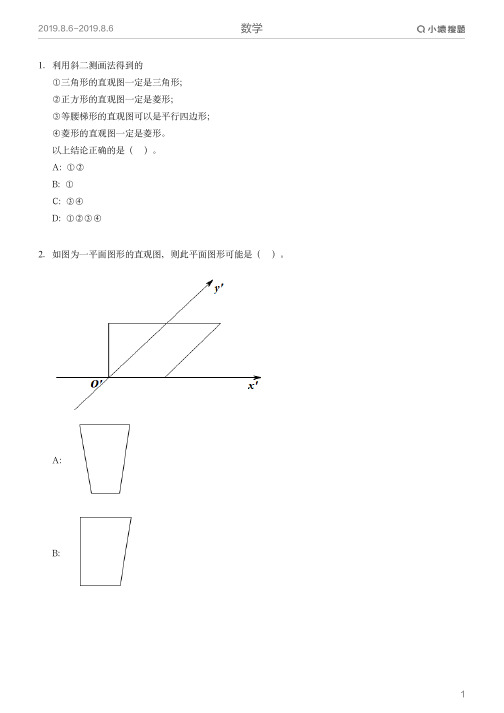
N、 的两个截面截去正方体的两个角后得到的几何体如图1,则该几何体的正视图、
侧视图(左视图)、俯视图依次为图2中的( )
3
2019.8.6-2019.8.6
数学
A. ①、②、③ B. ②、③、④ C. ①、③、④ D. ②、④、③
4
2019.8.6-2019.8.6
数学
答案解析
1. 答案 （本题提供智能家庭教师服务）
2019.8.6-2019.8.6
数学
1. 利用斜二测画法得到的 ①三角形的直观图一定是三角形； ②正方形的直观图一定是菱形； ③等腰梯形的直观图可以是平行四边形； ④菱形的直观图一定是菱形。 以上结论正确的是（ ）。 A: ①② B: ① C: ③④ D: ①②③④
2. 如图为一平面图形的直观图，则此平面图形可能是（ ）。
综上所述，①正确。 故本题正确答案为B。
2. 答案 （本题提供智能家庭教师服务）
C 正确率: 58%, 易错项: B
解析
本题主要考查空间几何体的直观图。 题目中的直观图中有两边分别与 轴和 轴平行，所以原图中这两边必垂直，符合条件的只有 。 故本题正确答案为C。
3. 答案 （本题提供智能家庭教师服务）
8
5
2019.8.6-2019.8.6
数学
③取BB′的中点H，同理可得四边形BFD′E在平面ABB′A′内的投影是四边形A′HBE，四边形 A′HBE是平行四边形且与平行四边形AGD′E边长分别相等，从而③正确. 故①③正确.
解析
【考点提示】 这是一道关于中心投影与平行投影的题目，回忆一下正方体的性质以及空间线、面的位置关系，找到各 点在平面上的投影点是解题的关键. 【解题方法提示】 根据所给图形，易得B、F、D′、E四个顶点在底面ABCD内的投影分别是B、C、D、A，由此可对①作 出判断； 由正方体的性质易得BF∥D′E，BE∥D′F，结合菱形以及平行四边形的判定可对②③进行判断，试试 吧！
必修二-三视图-直观图新课练习加答案
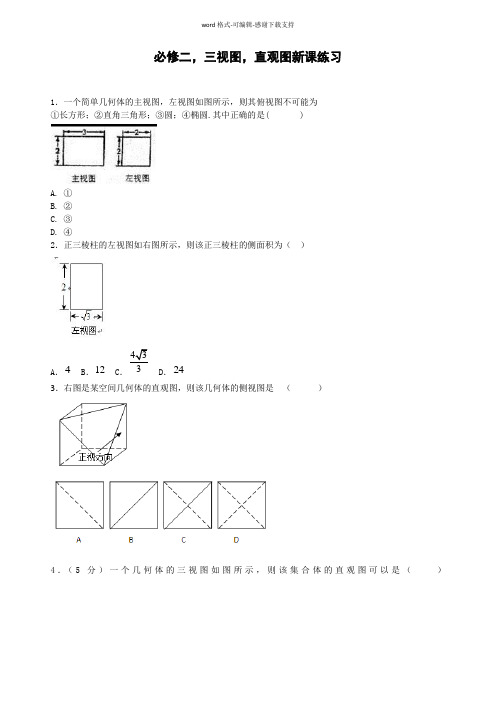
∠ABC＝45°，AB=AD＝1，DC⊥BC，这个平面图形的面积为_____
27．已知△ABC的平面直观图△A′B′C′是边长为a的正三角形，那么原△ABC的面积为____________.
28．水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为.
19．D
【解析】
20．A
【解析】
21．B
【解析】B错误.因为平行于y轴的线段,其对应的线段平行于y′轴,长度变为原来的一半.
22．B
【解析】根据斜二测画法的要求知,正方形的直观图为平行四边形.
23．C.
【解析】由几何体知，该物体是由一个长方体和一个截角三棱柱组成的，结合它们的轮廓线和交线，它的俯视图应为C.
C.梯形的直观图不是梯形
D.正三角形的直观图一定为等腰三角形
23．如图(1)所示的一个几何体，在图(2)中是该几何体俯视图的是( )
(1)
(2)
24．如右图，平行四边形OPQR是四边形OPQR的直观图，若OP＝3, OR＝1，则原四边形OPQR的周长为.
25．如图为一个棱长为2cm的正方体被过其中三个顶点的平面削去一个角后余下的几何体，试画出它的正视图．
B.原图中平行于y轴的线段,其对应线段平行于y′轴,长度不变
C.画与坐标系xOy对应的坐标系x′O′y′时,∠x′O′y′可等于135°
D.作直观图时,由于选轴不同,所画直观图可能不同
22．斜二测画法所得直观图,以下说法正确的是( )
A.等腰三角形的直观图仍是等腰三角形
B.正方形的直观图为平行四边形
9．C
【解析】由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的左侧，
高中数学 必修二 空间几何体及三视图课后练习一(含解析)新人教A版必修2
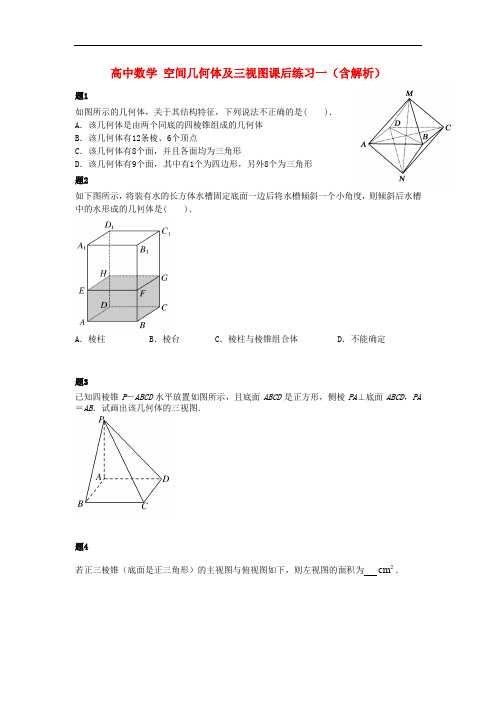
高中数学空间几何体及三视图课后练习一（含解析）题1如图所示的几何体，关于其结构特征，下列说法不正确的是( )．A．该几何体是由两个同底的四棱锥组成的几何体B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中有1个为四边形，另外8个为三角形题2如下图所示，将装有水的长方体水槽固定底面一边后将水槽倾斜一个小角度，则倾斜后水槽中的水形成的几何体是( )．A．棱柱 B．棱台 C．棱柱与棱锥组合体D．不能确定题3已知四棱锥P－ABCD水平放置如图所示，且底面ABCD是正方形，侧棱PA⊥底面ABCD，PA ＝AB．试画出该几何体的三视图．题4cm．若正三棱锥（底面是正三角形）的主视图与俯视图如下，则左视图的面积为2题5一个三棱柱的底面是正三角形，三视图如图所示，求这个三棱柱的表面积和体积．题6如图所示为长方体木块堆成的几何体的三视图，此几何体共由几块木块堆成．题7长方体的主视图、俯视图如图所示，则其左视图面积为（）A．3 B．4 C．12 D．16题8某几何体的三视图如图所示，那么这个几何体是（）．A．三棱锥B．四棱锥C．四棱台D．三棱台题9某个几何体的三视图如图所示，其中正视图与侧视图是完全相同的图形，则这个几何体的体积为多少？题10某四面体的三视图如图所示，该四面体四个面的面积中，最大的是（）(A) 8 (B) (C)10 (D)题11一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱题12如图是一个倒置的四棱柱的两种摆放，试分别画出其三视图，并比较它们的异同．课后练习详解题1答案：D ．详解：四个选项中C 、D 矛盾，所以答案从这两个里选一个，又根据图形几何体有8个面． 题2答案：A ．详解：当固定AB 或CD 中的一边时，可形成以左右侧面为底面的棱柱；当固定AD 或BC 中的一边时，可形成以前后侧面为底面的棱柱．题3答案：见详解．详解：该几何体的三视图如下：注意侧视图的直角顶点位置．题4 答案：342cm ． 详解:三棱锥的左视图肯定还是三角形，需求三角形的底边长和高．根据俯视图知左视图的是边长为的三角形，又由主视图知，，1324S ∴==2cm ． 题5答案：这个三棱柱的表面积为（48+83）cm 2,体积为163cm 3.详解：由三视图易知，该三棱柱的形状如图所示：由左视图可得三棱柱的高为4cm,正三角形ABC和正三角形A′B′C′的高为23cm.∴正三角形ABC的边长为|AB|=sin601×42sin60°2).∴该三棱柱的表面积为S=3×4×4+2×21×42sin60°×3).体积为V=S底·|AA′|=2故这个三棱柱的表面积为2,体积为cm3.题6答案：4．详解:画出三视图复原的几何体，即可判断长方体的木块个数．由直视图知，由4块木块组成．故答案为：4．题7答案：A．详解：根据物体的主视图与俯视图可以得出，物体的长与高以及长与宽，进而得出左视图面积=宽×高．由主视图易得高为1，由俯视图易得宽为3．则左视图面积=1×3=3．题8答案：B．详解：由所给三视图可以判定对应的几何体是四棱锥．题9cm3详解：几何体是正四棱锥，底面是对角线长为2cm，则112232V=⨯⨯⨯= 3题10答案：C．详解：由三视图还原几何体如下图，该四面体四个面的面积中最大的是∆PAC，面积为10，选C．题11答案：①②③⑤．题12详解：如图：。
新高中人教B版数学必修二同步练习：1.1.5_三视图(含答案)
1.1.5 三视图【课时目标】1．了解正投影的概念；2．理解三视图的原理和视图间的相互关系，能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简单组合)的三视图．1．正投影在物体的平行投影中，如果投射线与投射面垂直，则称这样的平行投影为__________．2．三视图(1)一个投射面水平放置，叫做______________，投射到水平投射面的图形叫__________．一个投射面放置在正前方叫做____________，投射到直立投射面内的图形叫__________，和直立、水平两个投射面都垂直的投射面叫做______________，投射到侧立投射面内的图形叫做__________．(2)将空间图形向水平投射面、直立投射面、侧立投射面作正投影，然后把这三个投影按一定的布局(俯视图放在________的下面，长度与__________一样，左视图放在__________的右面，高度与__________一样，宽度与__________的宽度一样即“长对正、高平齐、宽相等”)放在一个平面内，这样构成的图形叫做空间图形的__________．一、选择题1．下列说法正确的是()A．任何几何体的三视图都与其摆放的位置有关B．任何几何体的三视图都与其摆放的位置无关C．有的几何体的三视图与其摆放的位置无关D．正方体的三视图一定是三个全等的正方形2．如图所示的一个几何体，哪一个是该几何体的俯视图()3．如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④4．一个长方体去掉一个小长方体，所得几何体的主视图与左视图分别如图所示，则该几何体的俯视图为()5．如图所示的正方体中，M、N分别是AA1、CC1的中点，作四边形D1MBN，则四边形D1MBN在正方体各个面上的正投影图形中，不可能出现的是()6．一个长方体去掉一角的直观图如图所示，关于它的三视图，下列画法正确的是()二、填空题7．根据如图所示俯视图，找出对应的物体．(1)对应________；(2)对应________；(3)对应________；(4)对应________；(5)对应________．8．若一个三棱柱的三视图如图所示，则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________．9．用小正方体搭成一个几何体，如图是它的主视图和左视图，搭成这个几何体的小正方体的个数最多为________个．三、解答题10．在下面图形中，图(b)是图(a)中实物画出的主视图和俯视图，你认为正确吗？如果不正确，请找出错误并改正，然后画出左视图(尺寸不作严格要求)．11．(1)如图是截去一角的长方体，画出它的三视图．(2)如图，螺栓是棱柱和圆柱的组合体，画出它的三视图．能力提升12．对如图所示的几何体正确的说法是()A．如果把(1)作为主视图，则(2)、(3)分别是俯视图和左视图B．如果把(2)作为主视图，则(1)、(4)分别是俯视图和左视图C．如果把(3)作为主视图，则(2)、(1)分别是俯视图和左视图D．如果把(4)作为主视图，则(2)、(1)分别是俯视图和左视图13．用小立方体搭成一个几何体，使它的主视图和俯视图如图所示，搭建这样的几何体，最多要几个小立方体？最少要几个小立方体？在绘制三视图时，要注意以下三点：1．若两相邻物体的表面相交，表面的交线是它们的原分界线，在三视图中，分界线和可见轮廓都用实线画出，不可见轮廓用虚线画出．2．一个物体的三视图的排列规则是：俯视图放在主视图的下面，长度和主视图一样．左视图放在主视图的右面，高度和主视图一样，宽度和俯视图一样，简记为“长对正，高平齐，宽相等”．3．在画物体的三视图时应注意观察角度，角度不同，往往画出的三视图不同．1．1．5 三视图答案知识梳理1．正投影2．(1)水平投射面俯视图直立投射面主视图侧立投射面左视图(2)主视图主视图主视图主视图俯视图三视图作业设计1．C[球的三视图与其摆放位置无关．]2．C3．D[在各自的三视图中①正方体的三个视图都相同；②圆锥有两个视图相同；③三棱台的三个视图都不同；④正四棱锥有两个视图相同．]4．C[由三视图中的主、左视图得到几何体的直观图如图所示，所以该几何体的俯视图为C．]5．D6．A7．(1)D(2)A(3)E(4)C(5)B8．2 4解析三棱柱的高同左视图的高，左视图的宽度恰为底面正三角形的高，故底边长为4．9．710．解图(a)是由两个长方体组合而成的，主视图正确，俯视图错误，俯视图应该画出不可见轮廓线(用虚线表示)，左视图轮廓是一个矩形，有一条可视的交线(用实线表示)，正确画法如图所示．11．(1)解该图形的三视图如图所示．(2)解该物体是由一个正六棱柱和一个圆柱组合而成的，正视图反映正六棱柱的三个侧面和圆柱侧面，左视图反映正六棱柱的两个侧面和圆柱侧面，俯视图反映该物体投影后是一个正六边形和一个圆(中心重合)．它的三视图如图所示．12．D[物体有不同的放法得到不同的视图，所以把不同的图作为主视图就是考查各种不同的放法时物体的三视图．若(2)为主视图，说明物体已经竖起来放，显然此时(1)(3)(4)里面没有适合的视图作为左视图和俯视图；若(3)为主视图，则俯视图(2)中的正方体小块的位置不正确；若(1)为主视图，则俯视图(2)中的正方体小块的位置不正确．所以D正确，故选D．]13．解由于主视图中每列的层数即是俯视图中该列的最大数字，因此，用的立方块数最多的情况是每个方框都用该列的最大数字，即如图①所示，此种情况共用小立方块17块．数字可减少到最少的1，即如图②所示，这样的摆法只需小立方块11块．。
北师大版高中数学必修2单元练习卷三视图
单元提分卷（3）三视图1、某几何体的三视图如图所示,则该几何体的最长棱的长度为( )A.34B.10C.41D.522、如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的体积为（）A.254210++ B.43C.83D.1633、某几何体的三视图如图所示，则该几何体的体积为( )A.1433B.1333C.43D.334、某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )A. 32B. 23C. 22D. 25、下图是某个三棱锥的三视图，其中主视图是等边三角形，左视图是直角三角形，俯视图是等腰直角三角形，则该三棱锥的体积是（）A．612B．33C．64 D．366、如图为一个几何体的三视图，则该几何体中任意两个顶点间的距离的最大值为（）A.32B.4C.33D.57、某几何体的三视图如下图所示，它的体积为( )A. 72πB. 48πC. 30πD. 24π8、某四棱锥的三视图如图所示，则其体积为（）A. 83B.43C.8D.49、某三棱锥的三视图如图所示，则该三棱锥的各个面中，最大的面积是（）A 6B．1 C2D610、某几何体的三视图如图所示，该几何体表面上的点P与点Q在三视图上的对应点分别为A B,，则在该几何体表面上，从点P到点Q的路径中，最短路径的长度为（）A.14B.23C.10D.2211、某几何体的三视图如图所示, 则该几何体的表面积为____________.12、某几何体的三视图如图所示，则该几何体的体积是，表面积是．13、某几何体的三视图如图所示（单位：cm）,则俯视图的面积为___ 2cm，该几何体的体积为___ 3cm．14、某几何体的三视图如图所示，则该几何体的体积是________．15、“无字证明”就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用甲、乙、丙的面积关系,写出该图所验证的一个三角恒等变换公式:____________.16、若某几何体的三视图(单位:cm)如图所示，则此几何体的体积是3cm，表面积是2cm.17、若某几何体的三视图(单位:cm)如图所示，则此几何体的体积是3cm，表面积是2cm.18、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是__________3cm．答案以及解析1答案及解析： 答案：D解析：由三视图可得该几何体是一个三棱锥，如图中1A BCD -（放在长方体中），其中13,5,4,BC CD AA ===则11141,5,52,A B A D A C ===34,BD =所以最长的棱长是5 2.2答案及解析： 答案：C解析：由三视图知，该几何体为三棱锥A BCD -，如图所示，底面是两条直角边长分别为2，4的直角三角形，高为2，所以此三棱锥的体积1 3A BCD BCD V S h -=⋅△11842323=⨯⨯⨯=.故选C.3答案及解析： 答案：C解析：由三视图知，该几何体是由一个大正四棱锥挖去一个小正四棱锥而得到的，其直观图如图所示，其中两个正四棱锥的底面边长分别为3，1,223333()2-=，所以该几何体的体积为22133(31)433⨯-=故选C.4答案及解析： 答案：B解析：题考査空间几何体的三视图,考查空间想象能力.根据三视图可得该四棱锥的直观图(四棱锥P ABCD -)如图所示,将该四棱锥放入棱长为2的正方体中.由图可知该四棱锥的最长棱为,23PD PD =故选B.5答案及解析： 答案：B 解析：6答案及解析： 答案：C解析：由三视图可得该几何体的直观图如图所示，其中AD AB AG ,,两两垂直，平面AEFG ⊥平面ABCD ，//BC AE ，3AB AD AG BC FG CD DF =======，1DE =，4AE =.根据几何体的性质得32AC BG CF AF GD BD ======，22345BE EG =+=，10EF CE ==因为AD AG ⊥，AD AB ⊥，AB AG A ⋂=，所以AD ⊥平面ABG ，所以BC ⊥平面ABG ，所以BC BG ⊥.同理可得GF BG ⊥.所以()223322733BF CG ==+==故该几何体中任意两个顶点间的距离的最大值为33 C7答案及解析： 答案：C 解析：8答案及解析： 答案：A解析：根据几何体的三视图可得该几何体的直观图，将该几何体放入棱长为2的正方体中，则该几何体为如图所示的四棱锥A BCDE -，所以几何体的体积18222233V =⨯⨯⨯=.9答案及解析： 答案：A 解析：10答案及解析： 答案：D解析：由三视图可知该几何体为正四棱柱，底面边长为1，高为2，点P Q ,位置如图.沿EF 展开，得()2212110PQ =++=FM 展开，得()2221122PQ ++=P 到点Q 的路径中，最短路径的长度为22 D.11答案及解析： 答案：24＋π 解析：12答案及解析： 答案：3π2;5π+2解析：13答案及解析： 答案：6,8 解析：14答案及解析： 答案：16ππ- 解析：15答案及解析：答案：cos()cos cos sin sin αβαβαβ-=+解析：由三角形的面积公式,得图甲的面积为1π1sin cos()222ab ab αβαβ⎛⎫-+=- ⎪⎝⎭,图乙的面积为11cos cos cos cos 22a b ab αβαβ⋅=,图丙的面积为11sin sin sin sin 22a b ab αβαβ⋅=,故111cos()cos cos sin sin 222ab ab ab αβαβαβ-=+,即cos()cos cos sin sin αβαβαβ-=+.16答案及解析： 答案：40 (321613+解析：由该几何体的三视图，知该几何体是三棱柱与两个相同的四棱锥的组合体，如图所示，该几何体的体积为11DEGCFH CBFHB V V V V =++四棱锥DAEGA 三棱柱四棱锥()()()3111243434243824840cm 323⎛⎫=⨯⨯⨯⨯⨯⨯⨯+⨯⨯⨯=++= ⎪⎝⎭;它的表面积为11122ADA ABB A ABCD S S S S =++△矩形梯形()()222221184248232423321613cm 42=⨯+⨯⨯+⨯++⨯⨯⨯+=+.17答案及解析：答案：40 ()321613+解析：由该几何体的三视图，知该几何体是三棱柱与两个相同的四棱锥的组合体，如图所示，该几何体的体积为11DEGCFH CBFHB V V V V =++四棱锥DAEGA 三棱柱四棱锥()()()3111243434243824840cm 323⎛⎫=⨯⨯⨯⨯⨯⨯⨯+⨯⨯⨯=++= ⎪⎝⎭; 它的表面积为11122ADA ABB A ABCD S S S S =++△矩形梯形()()222221184248232423321613cm 42=⨯+⨯⨯+⨯++⨯⨯⨯+=+18答案及解析：答案：212π3解析：知该几何体是一个半球与一个圆台组合成，此几何体的体积是322141212π4π(2244)3π2333⨯⨯++⨯+⨯=．。
高中数学必修二之三视图练习题
三视图练习题一、选择题1．对几何体的三视图，下列说确的是()A．正视图反映物体的长和宽B．俯视图反映物体的长和高C．侧视图反映物体的高和宽D．正视图反映物体的高和宽2．一个空间几何体的正视图与侧视图均为全等的等腰三角形，俯视图为一个圆及其圆心，那么这个几何体为()A．棱锥B．棱柱C．圆锥D．圆柱3．(2011－2012·高三模拟)下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④4.一个几何体的三视图如图，则组成该几何体的简单几何体为()A．圆柱和圆锥B．正方体和圆锥C．四棱柱和圆锥D．正方体和球5．一个几何体的三视图如图，则组成该组合体的简单几何体为()A．圆柱与圆台B．四棱柱与四棱台C．圆柱与四棱台D．四棱柱与圆台6．(2010·理，3)一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如下图所示，则该几何体的俯视图为()7．如图所示几何体的正视图和侧视图都正确的是()8．(2011·新课标全国高考)在一个几何体的三视图中，主视图和俯视图如下图所示，则相应的侧视图可以为()9．如图所示，在正方体ABCD－A1B1C1D1中，M、N分别是BB1、BC的中点，则图中阴影部分在平面ADD1A1上的正投影是()10．某几何体的三视图如图所示，那么这个几何体是()A．三棱锥B．四棱锥C．四棱台D．三棱台二、填空题11．下列图形：①三角形；②直线；③平行四边形；④四面体；⑤球．其中投影不可能是线段的是________．12．(2011·高一检测)已知某一几何体的正视图与侧视图如图所示，则下列图形中，可以是该几何体的俯视图的图形有________．13．(2011－2012·高三“十二校联考”)一个几何体的三视图如图所示，其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形，则用________个这样的几何体可以拼成一个棱长为4的正方体．三、解答题14．如图所示是一个四棱柱铁块，画出它的三视图．15．依所给实物图的形状，画出所给组合体的三视图．16．说出下列三视图表示的几何体：17．根据下列图中所给出的一个物体的三视图，试画出它的形状．详解答案1[答案] C2[答案] C3[答案] D[解析]①正方体，三视图均相同；②圆锥，正视图和侧视图相同；③三棱台，三视图各不相同；④圆台，正视图和侧视图相同．[点评]熟悉常见几何体的三视图特征，对于画几何体的直观图是基本的要求．下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体长方体圆柱圆锥圆台球[解析]由正视图和侧视图可知，该几何体的上部可能为棱锥或圆锥，下部可能为棱柱和圆柱，结合俯视图为圆和圆心及正方形知，上部是圆锥，下部是四棱柱．5[答案] B[解析]该几何体形状如图．上部是一个四棱柱，下部是一个四棱台．6[答案] C[解析]由正视图和侧视图知，该长方体上面去掉的小长方体，从正前方看在观察者左侧，从左向右看时在观察者右侧，故俯视图为C.7[答案] B8[答案] D[解析]此几何体为一个半圆锥和一个半三棱锥的组合体，只有D项符合题意．9[答案] A[解析]N点投影为AD中点，M点投影为AA1中点，故选A.10[答案] B[解析]由正视图与侧视图知，该几何体为棱锥，由俯视图知，该几何体是四棱锥．11[答案]②④⑤[解析]三角形的投影是线段成三角形；直线的投影是点或直线；平行四边形的投影是线段或平行四边形；四面体的投影是三角形或四边形；球的投影是圆．12[答案]①②③④13[答案] 3[解析]该几何体是四棱锥，其底面是边长为4的正方形，高等于4，如图(1)所示的四棱锥A－A1B1C1D1，如图(2)所示，三个相同的四棱锥A－A1B1C1D1，A－BB1C1C，A－DD1C1C 可以拼成一个棱长为4的正方体．14[答案]正视图、俯视图、侧视图分别如图所示．15[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体，在中心以中心轴为轴线挖去一个小圆柱，故其三视图如下：16[解析]17[答案]所对应的空间几何体的图形为：。
高中数学必修2考点知识专题训练3---空间几何体的三视图(含答案解析)
ൌ
ை ை
ൌ
.
答案:
9.画出如图所示的几何体的三视图.
解:该几何体的三视图如图所示.
3/8
10.如图是一个几何体的三视图,想象该几何体的结构特征,画出该几何体的形状.
解:由于俯视图中有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合 体;结合侧视图和正视图,可知该几何体的上面是一个圆柱,下面是一个长方体.该几何体 的形状如图所示.
高中数学必修 2 考点知识专题训练
空间几何体的三视图
课时过关·能力提升
一、基础巩固
1.下列视图不属于三视图的是( )
A.正视图
B.侧视图
C.后视图
D.俯视图
答案:C
2.如果一个空间几何体的正视图与侧视图均为全等的等腰三角形,俯视图为一个圆及其
圆心,那么这个棱柱
C.圆锥
D.圆柱
8.若线段
AB
平行于投影面,O
是线段
AB
上一点,且
ை ை
ൌ
,
点ܣᇱ,
ܱᇱ,
ܤᇱ分别是
'ܱ'ܣ ܣ, ܱ, ܤ在投影面上的投影点, 则 ܱ' 'ܤൌ __________________.
解析:由题意知 AB∥A'B',OO'∥AA',OO'∥BB',
则有
'ை' ை''
答案:D 4.在下列几何体各自的三视图中,有且仅有两个视图相同的是( )
1/8
A.①②
B.①③
C.①④
D.②④
解析:①正方体,三个视图均相同;②圆锥,正视图和侧视图相同;③三棱台,三个视图各不 相同;④四棱锥,正视图和侧视图相同.
北师大版高中数学必修二第一章《三视图》单元测试题.docx
高中数学学习材料鼎尚图文*整理制作北师大版必修2第一章《三视图》单元测试题班级：姓名：一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）．1．给出下列命题，正确命题有( )①如果一个几何体的三视图是完全相同的，则这个几何体是正方体；②如果一个几何体的主视图和俯视图都是矩形，则这个几何体是长方体；③如果一个几何体的三视图都是矩形，则这个几何体是长方体；④如果一个几何体的主视图和左视图都是等腰梯形，则这个几何体是圆台．A．0个B．1个C．2个D．3个2．对几何体的三视图，下列说法正确的是( )A．主视图反映物体的长和宽 B．俯视图反映物体的长和高C．左视图反映物体的高和宽 D．主视图反映物体的高和宽4．如图是底面为正方形、一条侧棱垂直于底面的四棱锥的三视图，那么该四棱锥的直观图是下列各图中的( )5．如图所示，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的主视图是()6．如图所示，甲、乙、丙是三个立体图形的三视图，甲、乙、丙对应的标号正确的是( )．①长方体 ②圆锥 ③三棱锥 ④圆柱A ．④③②B ．②①③C ．①②③D ．③②④7．如图，在下列四个几何体中，其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是()A ．②③④B ．①②③C ．①③④D ．①②④ 8．已知某物体的三视图如图所示，那么这个物体的形状是( ) A ．正六棱柱 B ．正四棱柱 C ．圆柱 D ．正五棱柱 9．一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如右图所示，则该几何体的俯视图为()10．如图，直三棱柱ABC －A 1B 1C 1的侧棱长为2，底面是边长为2的正三角形，正视图是边长为2的正方形，则其左视图的面积为( ) A ．4 B ．2 3 C ．2 2 D. 3二、填空题：请把答案填在题中横线上（每小题5分，共25分）．11．以下说法正确的是________．①任何物体的三视图都与物体摆放位置无关；②任何物体的三视图都与物体摆放位置有关③有的物体的三视图与物体的摆放位置无关；④正方体的三视图一定是三个全等的正方形12．在圆柱、圆锥、圆台、球几种几何体中，其视图中可以为一个圆的有_________．13．正四棱锥的底面边长为2，侧棱长均为3，其正视图(主视图)和侧视图(左视图)是全等的等腰三角形，则正视图的周长为________． 14．如图，△ABC 与△ACD 都是等腰直角三角形，且AD ＝DC ＝2，AC ＝BC.平面ACD ⊥平面ABC ，如果以平面ABC 为水平平面，正视图的观察方向与AB 垂直，则三棱锥D －ABC 的三视图的面积和为________．15．如图所示的几何体中，四边形ABCD 是矩形，平面ABCD ⊥平面ABE ，已知AB ＝2，AE ＝BE ＝3，且当规定正视方向垂直平面ABCD 时，该几何体的侧视图的面积为22.若M ，N 分别是线段DE ，CE 上的动点，则AM ＋MN ＋NB 的最小值为________． 三、解答题：解答应写出文字说明、证明过程或演算步骤(共75分)．16．（12分）画出如图所示的几何体的三视图．17．（12分）根据如图所示的三视图，想象物体原形，并画出所示物体的直观图．18．（12分）补全下图所示物体的三视图．19．（12分）如图(一)是用玻璃制成的正方体，其中的粗线表示一根镶嵌在正方体内的钢丝，图(二)是这个正方体的主视图、左视图、俯视图中的两个，请指出它们是什么视图．20．（13分）已知：图1是截去一个角的长方体，试按图示的方向画出其三视图；图2是某几何体的三视图，试说明该几何体的构成．21．（14分）已知正三棱柱ABC－A′B′C′的正视图和侧视图如图所示，设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度(x可以取到任意一个实数)，对应的俯视图的面积为S(x)，求函数S(x)的最大值及最小正周期．(说明：“三棱柱绕直线OO′旋转”包括逆时针方向和顺时针方向，逆时针方向旋转时，OA旋转所成的角为正角，顺时针方向旋转时，OA旋转所成的角为负角．)北师大版必修2第一章《三视图》单元测试题答案一、选择题：1．[答案]B[解析] 只有③正确．2．[答案]C3．[答案]D4．[答案]D解析：由俯视图排除B、C；由正视图、侧视图可排除A. 5．[答案]B [解析] 结合三视图的画法规则可知B正确．6．答案：A解析：由于甲的俯视图是圆，则该几何体是旋转体，又因主视图和左视图均是矩形，则甲是圆柱；由于乙的俯视图是三角形，则该几何体是多面体，又因主视图和左视图均是三角形，则该多面体的各个面都是三角形，则乙是三棱锥；由于丙的俯视图是圆，则该几何体是旋转体，又因主视图和左视图均是三角形，则丙是圆锥．7．[答案]A解析：①的三个视图都是边长为1的正方形；②的俯视图是圆，正视图、侧视图都是边长为1的正方形；③的俯视图是一个圆及其圆心，正视图、侧视图是相同的等腰三角形；④的俯视图是边长为1的正方形，正视图、侧视图是相同的矩形．8．[答案]A9．[答案]C[解析] 由正视图和侧视图知，该长方体上面去掉的小长方体，从正前方看在观察者左侧，从左向右看时在观察者右侧，故俯视图为C.10．[答案]B[解析] ∵左视图的高与正视图的高相等，故高为2，左视图的宽与俯视图的宽相等，即为直三棱柱底面△ABC的高，故左视图的宽为3，∴左视图的面积为2×3＝2 3.二、填空题：11．[答案]③12．[答案]圆柱、球13．答案：2＋2 2 解析：由题意知，正视图就是如图所示的截面PEF，其中E、F分别是AD、BC的中点，连接AO，易得AO＝2，而PA＝3，于是解得PO＝1，所以PE＝2，故其正视图的周长为2＋2 2. 14．答案：4＋32解析：由题意得AC＝BC＝22，AB＝4，△ACD边AC上的高为2，正视图的面积是12×4×2＝22，侧视图的面积是12×2×2＝2，俯视图的面积是12×22×22＝4，所以三视图的面积和为4＋3 2.15．答案：3 解析：依题意得，点E到直线AB的距离等于32－⎝⎛⎭⎪⎫222＝2，因为该几何体的左侧视图的面积为12·BC×2＝22，所以BC ＝1，DE＝EC＝DC＝2.所以△DEC是正三角形，∠DEC＝60°，tan ∠DEA＝ADAE＝33，∠DEA＝∠CEB＝30°.把△DAE，△DEC与△CEB展在同一平面上，此时连接AB，AE＝BE＝3，∠AEB＝∠DEA＋∠DEC＋∠CEB＝120°，AB2＝AE2＋BE2－2AE·BEcos 120°＝9，即AB＝3，即AM＋MN＋NB的最小值为3.三、解答题：16．[解析]三视图如下图所示．17．[解析]由几何体的三视图可知，此几何体是一个简单组合体，下部是个圆柱，上部是个圆台，且圆台下底与圆柱上底面重合．直观图如图．18．[解析]物体的三视图如下图所示．19．[分析] 根据正方体中钢丝的位置与正方体各面和棱之间的相对位置关系，并从三个视图角度考虑三视图特点． [解析](1)为左视图．(2)为主视图或俯视图． 20．解：图1几何体的三视图为：图2所示的几何体是上面为正六棱柱，下面为倒立的正六棱锥的组合体．21．解析：由题意可知，当三棱柱的一个侧面在水平面内时，该三棱柱的俯视图的面积最大．此时俯视图为一个矩形，其宽为3×tan 30°×2＝2，长为4，故S(x)的最大值为8.当三棱柱绕OO′旋转时，当A 点旋转到B 点，B 点旋转到C 点，C 点旋转到A 点时，所得三角形与原三角形重合，故S(x)的最小正周期为2π3.。
高中数学必修二同步练习题库：空间几何体的三视图和直观图(选择题：较易)
空间几何体的三视图和直观图（选择题：较易）1、如图1-1-14所示的直观图中，O′A′=O′B′=2，则其平面图形的面积是( )图1-1-14A．4 B． C． D．82、已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图可能为（）3、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A．6 B．C． D．44、下图是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体的个数是（）A．8个 B．7个 C．6个 D．5个5、如图所示是由一些同样的正方体块搭成的几何体的三视图，那么构成这个几何体的小正方体个数是（）A．11 B．10 C．9 D．86、某空间几何体的三视图如图所示，则该几何体的体积为（）A． B． C． D．7、如图，在正方体中，分别为的中点，则图中五棱锥的俯视图为（）A．B．C．D．8、某几何体的三视图如图所示，则该几何体的表面积是（）A．90 B．92 C．98 D．1049、由斜二测画法得到：①相等的线段和角在直观图中仍然相等；②正方形在直观图中是矩形；③等腰三角形在直观图中仍然是等腰三角形；④平行四边形的直观图仍然是平行四边形．上述结论正确的个数是（）A．0 B．1 C．2 D．310、某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为A．3 B．2 C．2 D．211、某空间几何体的三视图如图所示，该空间几何体的体积是（）A． B．10 C． D．12、某空间几何体的三视图中，有一个是正方形，则该空间几何体不可能是（）A．圆柱 B．圆锥C．棱锥 D．棱柱13、已知某棱锥的三视图如图所示，则该棱锥的表面积为（）A． B． C． D．14、在下列选项中，利用斜二测画法，边长为1的正三角形ABC的直观图不是全等三角形的一组是( )15、下列关于用斜二测画法画直观图的说法中，正确的是( )A．水平放置的正方形的直观图不可能是平行四边形B．平行四边形的直观图仍是平行四边形C．两条相交直线的直观图可能是平行直线D．两条垂直的直线的直观图仍互相垂直16、如图，用斜二测画法画一个水平放置的平面图形的直观图为一个正方形，则原来图形的形状是( )17、的斜二测直观图如图所示，则的面积为（）A．1 B．2C． D．18、如图所示，已知四边形的直观图是一个边长为的正方形，则原图形的周长为（）A． B．C． D．19、一梯形的直观图是一个如图所示的等腰梯形，且梯形的面积为，则原梯形的面积为（)A． B． C． D．20、将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（）A．B．C．D．21、下列几何体各自的三视图中，有且仅有两个视图相同的是（）A．①② B．①③ C．①④ D．②④22、已知某几何体的正视图和俯视图如图所示，则该几何体的侧视图是（）A． B． C． D．23、已知的平面直观图是边长为的正三角形，那么原的面积为（）A． B．C． D．24、关于“斜二测”直观图的画法，如下说法不正确的是（）A．原图形中平行于轴的线段，其对应线段平行于轴，长度不变B．原图形中平行于轴的线段，其对应线段平行于轴，长度变为原来的C．画与直角坐标系对应的时，必须是45°D．在画直观图时，由于选轴的不同，所得的直观图可能不同25、如图所示，水平放置的圆柱形物体的三视图是（）26、在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为（）27、如图所示，三视图的几何体是（）A．六棱台 B．六棱柱 C．六棱锥 D．六边形28、等腰三角形的直观图是（）A．①② B．②③ C．②④ D．③④29、在底面为正方形的长方体上任意选择个顶点，则以这个顶点为顶点构成的几何形体可能是：①矩形；②不是矩形的平行四边形；③有三个面为直角三角形，一个面为等腰三角形的四面体；④每个面都是等腰三角形的四面体；⑤毎个面都是直角三角形的四面体.则其中正确结论的序号是（）A．①③④⑤ B．①②④⑤C．①②③⑤ D．①②③④30、如图，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是（）A． B． C．6 D．831、若一个几何体的正视图和侧视图是两个全等的正方形，则这个几何体的俯视图不可能是（）32、某几何体的三视图如下图所示，它的体积为( )A． B． C． D．33、如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6 cm，O′C′＝2 cm，则原图形是()A．正方形 B．矩形C．菱形 D．一般的平行四边形34、4.关于斜二侧画法，下列说法正确的是（）A．三角形的直观图可能是一条线段B．平行四边形的直观图一定是平行四边形C．正方形的直观图是正方形D．菱形的直观图是菱形35、一个几何体的三视图如图所示,则该几何体是A．圆柱 B．四棱柱 C．圆台 D．棱台36、如图，在一个正方体内放入两个半径不相等的球、，这两个球相外切，且球与正方体共顶点的三个面相切，球与正方体共顶点的三个面相切，则两球在正方体的面上的正投影是（）37、图1-1-10是一个实物图形，则它的左视图大致为( )图1-1-10 图1-1-1138、如图,A′B′∥O′y′,B′C′∥O′x′,那么,直观图所示的平面图形是( )A．任意三角形 B．锐角三角形 C．直角三角形 D．钝角三角形39、已知某几何体的三视图如图所示，则该几何体的表面积为（）A． B． C． D．40、若一个正三棱柱的三视图如下图所示，则这个正三棱柱的高和底面边长分别为（）．A．， B．， C．， D．，41、如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面中直角三角形的个数是（）A．2 B．3 C．4 D．542、如图，在直角梯形中，，，，，由斜二测画法得到它的直观图为梯形，则（）A． B．梯形的面积为6C． D．梯形为直角梯形43、已知某三棱锥的三视图（单位：）如图所示，那么该三棱锥的体积等于（）A． B． C． D．44、多面体的三视图如图所示，则该多面体体积为（）A．12 B．72 C．48 D．2445、下列几何体各自的三视图中，有且仅有两个视图相同的是（）A．（）（） B．（）（） C．（）（） D．（）（）46、的斜二侧直观图如下图所示，则的面积为（）.A． B． C． D．以上都不对47、已知某几何体的三视图如图所示，则该几何体的表面积为（）A． B．C． D．48、如图，一个水平放置的平面图形的直观图（斜二测画法）是一个底角为、腰和上底长均为2的等腰梯形，则这个平面图形的面积是（）A． B． C． D．49、已知的平面直观图是边长为的等边三角形，则的面积为( )A． B． C． D．50、如图所示，在正方体中，分别是的中点，是正方形的中心，则四边形在该正方体的各面上的投影不可能是()A．三角形 B．正方形 C．四边形 D．等腰三角形51、一个几何体的三视图如图所示，其中正(主)视图和侧(左)视图是腰长为l的两个全等的等腰直角三角形，则该多面体的各条棱中最长棱的长度为（）A． B． C． D．52、某几何体的三视图如图所示，则其表面积为（）A．2π B．3π C．4π D．5π53、一水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为的正方形，则原平面图形的面积为()A． B． C． D．54、榫卯是在两个木构件上所采用的一种凹凸结合的连接方式，凸出部分叫榫，凹进部分叫卯，榫和卯咬合，起到连接作用，代表建筑有：北京的紫禁城、天坛祈年殿、山西悬空寺等，如图所示是一种榫卯的三视图，其表面积为( )A． B． C． D．55、一个几何体由一些完全相同的小正方体搭建而成，它的正视图与侧视图如图所示，那么搭成这个几何体所用的小正方体的个数最少为（）A． B． C． D．56、一个晴朗的上午，小明拿着一块长方形的木板在阳光下做投影实验，长方形的木板在地面上形成的投影不可能是（）A． B． C． D．57、如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A． B．C． D．58、某几何体的三视图如图所示（单位：）则该几何体的体积（单位：）是（）A． B． C． D．59、如图是一个空间几何体的正视图和俯视图，则它的侧视图为（）A． B． C． D．60、若某几何体的三视图如图所示，则此几何体的外接球表面积等于（）A． B．C． D．61、下图是某几何体的三视图，则该几何体的体积为( )A．1 B． C． D．62、某几何体的三视图如图所示，则该几何体的体积为A．＋2π B． C． D．63、如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中俯视图的右边为一个半圆，则此几何体的体积为（）A． B． C． D．64、某几何体的三视图如图所示，则其表面积为A． B． C． D．65、在下列水平放置的几何体中，正视图是如图的是（）A． B． C． D．66、某几何体的三视图如图，则几何体的体积为A．8π﹣16 B．8π+16 C．16π﹣8 D．8π+867、一个空间几何体的正视图、侧视图为两个边长是1的正方形，俯视图是直角边长为1的等腰直角三角形，则这个几何体的表面积等于（）A． B． C． D．668、一几何体的直观图如右图，下列给出的四个俯视图中正确的是（）69、如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体的体积为A． B．C． D．70、某几何体的三视图如图，则几何体的体积为A．8π﹣16 B．8π+16 C．16π﹣8 D．8π+8参考答案1、A2、C3、A4、D5、D6、C7、C8、B9、B10、B11、C12、B13、D14、C15、B16、A17、B18、C19、D20、A21、D22、B23、C24、C25、A26、D27、C28、D29、D30、D31、C32、C33、C34、B35、C36、B37、A38、C39、B40、B41、C42、D43、A44、D45、D46、B47、C48、D49、A50、B51、B52、B53、D54、B55、C56、A57、A58、B59、A60、C61、B62、D63、B64、C65、C66、A67、B68、B69、B70、C【解析】1、作出原来的平面图形(如图)，则OA=4，OB=2，故其面积=×2×4=4.2、试题分析：由俯视图可知三棱锥的底面是个边长为的正三角形，由侧视图可知三棱锥的一条侧棱垂直于底面，且其长度为，故其主视图为直角边长为的等腰直角三角形，且中间有一虚线，故选C．考点：三视图.3、试题分析：由三视图,可判断几何体为四面体,且四面体的长,宽,高均为,故可考虑于棱长为的正方体中研究,如图所示,该四面体为,，故最长的棱长为,选A.考点:三视图.【易错点睛】本题考查了三视图视角下多面体棱长的最值问题,考查了考生的识图能力以及由三视图还原物体的空间想象能力.解答醒的关键是得到该几何体的形状.放在正方体中构造几何体的形状是本题的难点,由正方体还原几何体的形状后就很容易求同各个棱的长度.本题难度中等,对学生的识图能力有一定的要求.4、由三视图可知此几何体是由两层小正方体组成的.其个数有4+1=5主视图、左视图、俯视图是分别从物体正面、左面和上面看，仔细观察图象即可得到图象．解：根据题中图象可知：该几何体的下层分两排，前面一排有三个小正方体，后面一排有一个小正方体，上面一层有一个小正方体．故一共有五个小正方体，故选B．5、略6、由三视图可得，该几何体是一个正方体的前方的左下角割去一个直三棱锥，将其移至正方体的上方且正方体的边长为1，故其体积为V=13=1.故选C7、根据题意，点在底面的射影是，在底面的射影是在底面的射影是，在底面的射影是，而是被挡住的棱，应画出虚线；故选C8、又三视图知几何体为一四棱柱，且四棱柱的高为底面为直角梯形，直角梯形的直角腰为，两边底边长分别为，另一腰长为几何体的表面积故答案选9、逐一考查所给的说法：①相等的线段平行时在直观图中仍然相等，原说法错误；②正方形在直观图中是平行四边形，不是矩形，原说法错误；③等腰三角形在直观图中不是等腰三角形，原说法错误；④平行四边形的直观图仍然是平行四边形，原说法正确．综上可得上述结论正确的个数是1个.本题选择B选项.10、试题分析：几何体是四棱锥，如图.最长的棱长为补成的正方体的体对角线，即该四棱锥的最长棱的长度，故选B. 【考点】三视图【名师点睛】本题考查了空间想象能力，由三视图还原几何体的方法:或者也可根据三视图的形状，将几何体的顶点放在正方体或长方体里面，便于分析问题.11、试题分析：此几何体是三棱锥，底面是直角三角形面积为，三棱锥的高是4，所以几何体的体积,故选C.考点：三视图12、试题分析：当棱锥和棱柱分别为正四棱锥和正四棱柱时，会出现正方形；圆柱的横截面为长方形，当其底面直径和高相等时，就是正方形；对于圆锥，三视图可能出现的有：圆、三角形．所以选A．考点：三视图．13、试题分析：根据三视图可知，几何体是一条侧棱垂直于底面的四棱锥，底面是边长为的正方形，如下图所示，该几何体的四个侧面均为直角三角形，侧面积，底面积，所以该几何体的表面积为，故选D.考点：三视图与表面积.【易错点睛】本题考查三视图与表面积，首先应根据三视图还原几何体，需要一定的空间想象能力，另外解本题时，也可以将几何体置于正方体中，这样便于理解、观察和计算.根据三视图求表面积一定要弄清点、线、面的平行和垂直关系，能根据三视图中的数据找出直观图中的数据，从而进行求解，考查学生空间想象能力和计算能力.14、选项C中前者画成斜二测直观图时，底AB不变，原来高h变为，后者画成斜二测直观图时，高不变，边AB变为原来的.考点：斜二测画法.15、斜二测画法保持平行性不变，正方形的直观图是平行四边形，故选项A错误；平行四边形的对边平行，则在直观图中仍然平行，故选项B正确；斜二测画法保持相交性不变，故两条相交直线的直观图仍是相交直线，故选项C错误；两条垂直直线的直观图应是夹角为45°的两条相交直线，故选项D错误.考点：斜二测画法的基本原理.16、由斜二测画法可知，与y′轴平行的线段在原图中为在直观图中的2倍．故可判断A正确．考点：斜二测画法.17、试题分析：斜二测图象的面积与原图面积的关系是，所以的面积为.考点：斜二测法.18、试题分析：因为四边形的直观图是一个边长为的正方形，所以原图形为平行四边形，一组对边为，另一组对边长为，所以圆图形的周长为，故选C.考点：平面图形的直观图.19、试题分析：由斜二测画法原理知，平面中的图形与直观图中的图形上下底边的长度是一样的，不一样的是两个梯形的高，其高的关系是这样的：平面图中的高是直观图中长度的倍，如直观图，的长度是直观图中梯形的高的倍，由此平面图中梯形的高的长度是直观图中梯形高的倍，故其面积是梯形的面积倍，梯形的面积为，所以原梯形的面积是．故应选D．考点：平面图形的直观图.【方法点晴】常用结论：（1) 斜二侧画法:保平行，长不变，纵减半；（2)斜二侧画法的面积是原来图形面积的倍.原因是原来的高变成了的线段,且长度是原高的一半,因此新图形的高是这个一半线段的倍,故新高是原来高的,而横向长度不变,所以面积变为原面积的.本题中梯形的面积为，故原面积为.20、试题分析：由主视图和俯视图可知切去的棱锥为，棱在左侧面的投影为．考点：1、棱锥，棱柱的结构特征；2、三视图．21、试题分析：①中正，侧，俯三视图均相同，不符合题意；②中正，侧视图均相同，符合题意；③中正，侧，俯三视图均不相同，不符合题意；④中正，侧视图均相同，符合题意；故选D.考点：三视图．22、试题分析：由正视图、俯视图可得该几何体扣除两个三棱锥的正方体，故其侧视图为B.考点：三视图.23、试题分析:如图,过，作，垂足为，作使得，则。
高中数学人教版必修2作业1-2-12空间几何体的三视图2
1.2.1、2 空间几何体的三视图基础巩固一、选择题1．下列投影是平行投影的是()A．俯视图B．路灯底下一个变长的身影C．将书法家的真迹用电灯光投影到墙壁上D．以一只白炽灯为光源的皮影[答案] A[解析]三视图是由平行投影形成的，而B、C、D中由电灯发出的光得到的投影是中心投影．2．对几何体的三视图，下列说法正确的是()A．正视图反映物体的长和宽B．俯视图反映物体的长和高C．侧视图反映物体的高和宽D．正视图反映物体的高和宽[答案] C3．某空间几何体的正视图是三角形，则该几何体不可能是()A．圆柱B．圆锥C．四面体D．三棱柱[答案] A4．小周过生日，公司为她预订的生日蛋糕(示意图)如下图所示，则它的正视图应该是() [答案] B[解析]A为俯视图，注意到封闭的线段情形，正视图应该是B．5．一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台[答案] D[分析]利用三视图逐个排除错误选项即可．[解析]由俯视图可排除A，B，由正视图可排除C，故选D．6．若一个几何体的三视图如下图所示，则这个几何体是()A．三棱锥B．四棱锥C．三棱柱D．四棱柱[答案] B[解析]由俯视图可知底面为四边形，由正视图和侧视图知侧面为三角形，故几何体为四棱锥．二、填空题7．一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号)．①三棱锥；②四棱锥；③三棱柱；④四棱柱；⑤圆锥；⑥圆柱．[答案]①②③⑤[解析]三棱锥、四棱锥和圆锥的正视图都是三角形，当三棱柱的一个侧面平行于水平面，底面对着观测者时其正视图是三角形，四棱柱、圆柱无论怎样放置，其正视图都不可能是三角形．8．下图中三视图表示的几何体是________.[答案]四棱柱三、解答题9．如图，四棱锥的底面是正方形，顶点在底面上的射影是底面正方形的中心，试画出其三视图．[解析]所给四棱锥的三视图如下图．[点评](1)画三视图时，务必做到正视图与侧视图的高度一致(即所谓的高平齐)、正视图与俯视图的长度一致(即所谓的“长对正”)、侧视图与俯视图的宽度一致(即所谓的“宽相等”)．(2)习惯上将侧视图放在正视图的右侧，将俯视图放在正视图的下方．[拓展提高](1)三视图中各种数据的对应关系：①正视图中AB的长对应原四棱锥底面多边形的左右方向的长度，AC、BC的长则不对应侧棱的长，它们对应四棱锥的顶点到底面左、右两边的距离．②侧视图中，EF的长度对应原四棱锥底面的前后长度，GE、GF的长度则是四棱锥顶点与底面前后两边的距离．③俯视图中HIJK的大小与四棱锥底面的大小形状完全一致，而OK，OI，OJ，OH 的大小，则为四棱锥的顶点在底面上的投影到底面各顶点的距离．(2)误区警示：正视图、侧视图中三角形的腰长有的学生会误认为是棱锥的侧棱长，实则不然．弄清一些数据的对应关系，是后面进行相关计算的前提．10．依所给实物图的形状，画出所给组合体的三视图．[解析]图中所给几何体是一个圆柱和一个正六棱柱的组合体，在中心以中心轴为轴线挖去一个小圆柱，故其三视图如下：能力提升一、选择题1．下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④[答案] D[解析]①正方体，三视图均相同；②圆锥，正视图和侧视图相同；③三棱台，三视图各不相同；④圆台，正视图和侧视图相同．[点评]熟悉常见几何体的三视图特征，对于画几何体的直观图是基本的要求．下图是最基本的常见几何体的三视图.几何体直观图形正视图侧视图俯视图正方体长方体圆柱圆锥圆台球[答案] C[分析]本题是组合体的三视图问题，由几何体的正视图和侧视图均如左图所示知，几何体下面为圆柱或直四棱柱，上面是圆柱或直四棱柱或底面是直角三角形的直三棱柱．[解析]A，B，D都可能是该几何体的俯视图，C不可能是该几何体的俯视图，因为它的正视图上面应为如右图所示的矩形．3．如图所示，画出四面体AB1CD1三视图中的正视图，以面AA1D1D为投影面，则得到的正视图可以为()[答案] A[分析]依次确定四面体AB1CD1的每一条棱在面AA1D1D上的投影即可．[解析]显然AB1，AC，B1D1，CD1分别投影得到正视图的外轮廓，B1C为可见实线，AD1为不可见虚线．故A正确．4．若某几何体的三视图如图所示，那么这个几何体是()A．三棱锥B．四棱锥C．四棱台D．三棱台[答案] B[解析]根据三视图的特征可以断定是四棱锥，由正视图和侧视图可知，该四棱锥底面中，必定有一组对边平行，另一组对边不平行．二、填空题5．下列图形：①三角形；②直线；③平行四边形；④四面体；⑤球．其中投影不可能是线段的是________.[答案]②④⑤[解析]三角形的投影是线段或三角形；直线的投影是点或直线；平行四边形的投影是线段或平行四边形；四面体的投影是三角形或四边形；球的投影是圆．6．已知某一几何体的正视图与侧视图如图所示，则下列图形中，可以是该几何体的俯视图的图形有________.[答案]①②③④三、解答题7．说出下列三视图表示的几何体：[解析]8．根据下列图中所给出的一个物体的三视图，试画出它的形状．[答案]所对应的空间几何体的图形为：。
北师大版数学高一必修二练习三视图
§3三视图一、基础过关1. 如右图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为()A. 3 B．23C．4 D．2 22．如图所示的一个几何体，哪一个是该几何体的俯视图()3．如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是()A．①②B．①③C．①④D．②④4．一个长方体去掉一个小长方体，所得几何体的主视图与左视图分别如图所示，则该几何体的俯视图为()5．根据如图所示俯视图，找出对应的物体．(1)对应________；(2)对应________；(3)对应________；(4)对应________；(5)对应________．6．若一个三棱柱的三视图如图所示，则这个三棱柱的高(两底面之间的距离)和底面边长分别是______和________．7．在下面图形中，图(b)是图(a)中实物画出的主视图和俯视图，你认为正确吗？如果不正确，请找出错误并改正，然后画出左视图(尺寸不作严格要求)．8．画出如图所示的四棱锥和三棱柱的三视图．二、能力提升9．一个长方体去掉一角的直观图如图所示，关于它的三视图，下列画法正确的是()10．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是() A．球B．三棱锥C．正方体D．圆柱11．用若干块相同的小正方体搭成一个几何体，该几何体的三视图如图所示，则搭成该几何体需要的小正方体的块数是________．12．下图是一个物体的三视图，试说出物体的形状．三、探究与拓展13．用小立方体搭成一个几何体，使它的主视图和俯视图如图所示，搭建这样的几何体，最多要几个小立方体？最少要几个小立方体？答案1．B2．C 3．D4．C5．(1)D(2)A(3)E(4)C(5)B6．2 47．解图(a)是由两个长方体组合而成的，主视图正确，俯视图错误，俯视图应该画出不可见轮廓线(用虚线表示)，左视图轮廓是一个矩形，有一条可视的交线(用实线表示)，正确画法如图所示．8．解三视图如图所示：9．A10．D11．612．解物体的形状如下图所示．13．解由于主视图中每列的层数即是俯视图中该列的最大数字，因此，用的立方块数最多的情况是每个方框都用该列的最大数字，即如图①所示，此种情况共用小立方块17块．而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字，其他方框内的数字可减少到最少的1，即如图②所示，这样的摆法只需小立方块11块．。
2023年高一下数学必修二《空间几何体的三视图》测试试卷及答案解析
2023年高一下数学必修二《空间几何体的三视图》测试试卷一．选择题（共13小题）1．如图水平放置的正三棱柱的俯视图是（）A．B．C．D．2．如图，长方体ABCD﹣A1B1C1D1，AA1＝AB＝2，BC＝3，点P在线段B1D1上，的方向为正（主）视方向，当AP最短时，棱锥P﹣AA1B1B的左（侧）视图为（）A．B．C．D．3．如图是一个几何体的三视图，它对应的几何体的名称是（）A．棱台B．圆台C．圆柱D．圆锥4．如图是一个正四棱锥，它的俯视图是（）A．B．C．D．5．《九章算术•商功》中记载，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马，将四个面都为直角三角形的四面体称为鳖臑．已知某几何体的正视图与侧视图如图所示，则下列各选项给出的俯视图中，使得该几何体既不是阳马也不是鳖臑的是（）A．B．C．D．6．一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．7．在棱长为1的正方体ABCD﹣A1B1C1D1中，E，F分别为线段CD和A1B1上的动点，且满足CE＝A1F，则四边形D1FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A．有最小值B．有最大值C．为定值3D．为定值2 8．某三棱锥是由一个正方体被四个平面截去四部分得到的，其三视图都是边长为2的正方形，如图，则该三棱锥的表面积为（）A．8B．8C．16D．169．如图，某几何体的三视图都是边长为1的正方形，则该几何体的体积为（）A．B．C．D．10．正方体被切去一个角后得到的几何体如图所示，其侧视图（由左往右看）是（）A．B．C．D．11．如图，水平放置的正三棱柱的俯视图是（）A．B．C．D．12．已知棱长都为2的正三棱柱ABC﹣A1B1C1的直观图如图，若正三棱柱ABC﹣A1B1C1绕着它的一条侧棱AA1所在直线旋转，则它的侧视图可以为（）A．B．C．D．13．如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD1＝1，若此几何体的俯视图如图2所示，则可以作为其正视图的是（）A．B．C．D．2023年高一下数学必修二《空间几何体的三视图》测试试卷参考答案与试题解析一．选择题（共13小题）1．如图水平放置的正三棱柱的俯视图是（）A．B．C．D．【分析】直接利用几何体和三视图之间的转换求出结果．【解答】解：由于正三棱柱的两个下底面为等边三角形，所以上面的棱在下底面的射影在两底边的中线位置．如图所示：故选：B．【点评】本题考查的知识要点：三视图和几何体之间的转换，主要考查学生的空间想象能力，属于基础题型．2．如图，长方体ABCD﹣A1B1C1D1，AA1＝AB＝2，BC＝3，点P在线段B1D1上，的方向为正（主）视方向，当AP最短时，棱锥P﹣AA1B1B的左（侧）视图为（）A．B．C．D．【分析】依题意，棱锥P﹣AA1B1B的左（侧）视图外部轮廓为正方形，且侧棱AP，BP 被底面AA1B1B遮挡，显示为虚线，当AP最短时，AP⊥B1D1，因为A1B1＝2，A1D1＝3，所以B1P＜D1P，所以两虚线的交点离点B1更近，即离右下角更近．【解答】解：依题意，棱锥P﹣AA1B1B的左（侧）视图外部轮廓为正方形，且侧棱AP，BP被底面AA1B1B遮挡，显示为虚线，当AP最短时，AP⊥B1D1，因为A1B1＝2，A1D1＝3，所以B1P＜D1P，所以两虚线的交点离点B1更近，即离右下角更近．故选：B．【点评】本题考查了空间几何体的三视图，注意在三视图中看不到的线画成虚线．本题属于基础题．3．如图是一个几何体的三视图，它对应的几何体的名称是（）A．棱台B．圆台C．圆柱D．圆锥【分析】直接由三视图还原原几何体得答案．【解答】解：由三视图还原原几何体如图，该几何体为圆台．故选：B．【点评】本题考查三视图，关键是由三视图还原原几何体，是基础题．4．如图是一个正四棱锥，它的俯视图是（）A．B．C．D．【分析】该几何体直观图为一个正四棱锥，所以其俯视图轮廓为正方形，并且能够看到其四个侧棱，构成正方形的对角线，只有D选项符合．【解答】解：该几何体直观图为一个正四棱锥，所以其俯视图轮廓为正方形，并且能够看到其四个侧棱，构成正方形的对角线，故选：D．【点评】本题考查了由正四棱锥的直观图得到其俯视图，属于基础题．5．《九章算术•商功》中记载，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马，将四个面都为直角三角形的四面体称为鳖臑．已知某几何体的正视图与侧视图如图所示，则下列各选项给出的俯视图中，使得该几何体既不是阳马也不是鳖臑的是（）A．B．C．D．【分析】画出几何体的直观图即可判断选项．【解答】解：选项A的直观图如图：是阳马；选项B的直观图：既不是阳马也不是鳖臑；选项C的直观图：是鳖臑；选项D的直观图：是鳖臑．故选：B．【点评】本题考查三视图的直观图的判断与应用，是基本知识的考查．6．一个几何体的三视图如图所示，则该几何体的直观图可以是（）A．B．C．D．【分析】直接利用三视图和几何体的转换求出结果．【解答】解：根据几何体得三视图：俯视图的外边是一个圆，故排除A、C．由于俯视图的下面还有一个圆和四边形，故排除D．故选：B．【点评】本题考查的知识要点：三视图和几何体之间的转换，主要考察学生的运算能力和转换能力，属于基础题型．7．在棱长为1的正方体ABCD﹣A1B1C1D1中，E，F分别为线段CD和A1B1上的动点，且满足CE＝A1F，则四边形D1FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和（）A．有最小值B．有最大值C．为定值3D．为定值2【分析】分别在后，上，左三个平面得到该四边形的投影，求其面积和即可．【解答】解：依题意，设四边形D1FBE的四个顶点在后面，上面，左面的投影点分别为D'，F'，B'，E'，则四边形D1FBE在上面，后面，左面的投影分别如上图．＝1×1＝1，所以在后面的投影的面积为S后＝D'E'×1＝DE×1＝DE，在上面的投影面积S上在左面的投影面积S＝B'E'×1＝CE×1＝CE，左所以四边形D1FBE所围成的图形（如图所示阴影部分）分别在该正方体有公共顶点的三个面上的正投影的面积之和S＝S后+S上+S左＝1+DE+CE＝1+CD＝2．故选：D．【点评】本题考查了正方体中四边形的投影问题，考查空间想象能力．属于中档题．8．某三棱锥是由一个正方体被四个平面截去四部分得到的，其三视图都是边长为2的正方形，如图，则该三棱锥的表面积为（）A．8B．8C．16D．16【分析】如图所示，该几何体是正方体的内接正四棱锥，棱长为：2，然后求解表面积即可．【解答】解：如图所示，该几何体是正方体的内接正四棱锥．因此此几何体的棱长为：2，表面积S＝4××（2）2＝8．故选：B．【点评】本题考查了正方体的内接正四棱锥表面积计算公式，考查了推理能力与计算能力，属于基础题．9．如图，某几何体的三视图都是边长为1的正方形，则该几何体的体积为（）A．B．C．D．【分析】画出几何体的直观图，利用三视图的数据求解几何体的体积即可．【解答】解：由题意可知几何体的直观图如图：是正方体去掉2个三棱锥的几何体，几何体的体积为：1﹣2×＝．故选：D．【点评】本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．10．正方体被切去一个角后得到的几何体如图所示，其侧视图（由左往右看）是（）A．B．C．D．【分析】直接利用几何体的三视图的转换求出结果．【解答】解：根据几何体，转换为三视图，所以平面图形的侧视图为：故选：A．【点评】本题考查的知识要点：三视图的转换和几何体的应用，主要考察学生的运算能力和转换能力，属于基础题型．11．如图，水平放置的正三棱柱的俯视图是（）A．B．C．D．【分析】从原图的构特征分析，即可得出该几何体的俯视图．【解答】解：该几何体为水平放置的三棱柱，故俯视图的外部轮廓应为矩形，根据正视的方向，有一条可以看到的水平棱（实线），故选：B．【点评】本题考查了空间几何体的三视图，属于基础题．12．已知棱长都为2的正三棱柱ABC﹣A1B1C1的直观图如图，若正三棱柱ABC﹣A1B1C1绕着它的一条侧棱AA1所在直线旋转，则它的侧视图可以为（）A．B．C．D．【分析】根据所给视图，用排除法可得【解答】解：四个选项高都是2，若侧视图为A，中间应该有一条竖直的实线或虚线．若为C，则其中有两条侧棱重合，不应有中间竖线．若为D，则长应为，而不是1．故选：B．【点评】本题考查三视图，主要是考查空间想象能力，为基础题．13．如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD1＝1，若此几何体的俯视图如图2所示，则可以作为其正视图的是（）A．B．C．D．【分析】根据直观图，结合选项可以推测DD1为正前方，故其正视图的长应为底面正方形的对角线长，宽应为正方体的棱长，故排除B，D．而在三视图中看不见的棱用虚线表示，故排除A，选C．【解答】解：根据直观图，结合选项可以推测DD1为正前方，故其正视图的长应为底面正方形的对角线长，宽应为正方体的棱长，故排除B，D．而在三视图中看不见的棱用虚线表示，故排除A，故选：C．【点评】本题考查空间想象能力及三视图的作法，属于基础题．。
高中数学必修二同步练习题库：空间几何体的三视图和直观图(填空题：一般)
空间几何体的三视图和直观图（填空题：一般）1、某三棱锥的三视图如图所示，则该三棱锥的最长棱的棱长为2、由一个长方体和两个圆柱构成的几何体的三视图如图，则该几何体的体积为___________3、有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形，如图，4、如图所示，四边形OABC 是上底为2，下底为6，底角为45 °的等腰梯形，用斜二测画法画出这个梯形则这块菜地的面积为5、如图是 △AOB 用斜二测画法画出的直观图 △A ′ O ′，B 则′ △AOB 的面积是 _6、下图是一个四棱锥的三视图，则该四棱锥的体积为 ___________7、某几何体的三视图如图所示，它的体积为 __________7、某四棱锥的三视图如图所示，该四棱锥的体积为 _______；表面积为9、如图，三棱柱的侧棱长和底面边长均为，且侧棱底面，其正（主）视图是边长为的正方形，则此三棱柱侧（左）视图的面积为 ____________ ．11、若某空间几何体的三视图如图所示，则该几何体的体积是 ___________ ，表面积是12、某三棱锥的三视图如图所示，则其体积为13、已知某三棱锥的三视图如图所示，则该三棱锥的最长棱的长是14、如图三角形为某平面图形用斜二测画法画出直观图，则其原来平面图形的面积是15、一四面体的三视图如图所示，则该四面体四个面中，面积最大的那个面的面积是17、已知正三棱锥V －ABC 的正视图、侧视图和俯视图如图所示．则侧视图的面积是16、如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，则该几何体的表面积为19、某三棱锥的三视图如右图所示，则该三棱锥最长的棱为20、某组合体的三视图如图所示，其中正视图和侧视图都由正方形和等腰直角三角形组成，正方形的边长18、某几何体的三视图如图所示，且该几何体的体积是，则正视图中的值是为1，则该多面体的体积是 ________ .21、某空间几何体的三视图（单位：cm）, 如图所示，则此几何体侧视图的面积为 _____ ，此几何体的体积为22、已知正四面体 （所有棱长都相等的三棱锥 ）的俯视图如图所示，其中四边形ABCD 是边长为 2 cm 的正方23、一个棱长为 2 的正方体被一个平面截去一部分后，剩下部分的三视图如下图所示，则该几何体的表面24、已知某几何体的三视图如图所示，则该几何体的体积为25、已知空间几何体的三视图如图所示 ,则该几何体的表面积是 __________ ；几何体的体积是形，则这个正四面体的正视图的面积为 积为 ，体积为_______c m26、如图所示的正方体中，E 、F 分别是 AA 1,D 1C 1的中点， G 是正方形 BDB 1D 1的中心，则空间四边形AGEF 在该正方体面上的投影可能是 ________ ．27、某组合体的三视图如图所示，其中正视图和侧视图都由正方形和等腰直角三角形组成，正方形的边长 为 1，则该多面体的体积是是边长为 2 的正方形，则该几何体的外接球的体积是 __________28、一个空间几何体的三视图如图所示，则这个几何体的体积为 29、下图是一个几何体的三视图，其中正视图和侧视图均是高为 2，底边长为 的等腰三角形，俯视图30、一个几何体的三视图如图所示，其中正视图和侧视图均为腰长为_________ 个这样的几何体可以拼成一个棱长为 2 的正方体31、一个几何体的三视图如图所示，其中正视图和侧视图均为腰长为 2 的等腰直角三角形，则用_________ 个这样的几何体可以拼成一个棱长为 2 的正方体32、一个几何体的三视图及其尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三33、一个几何体的三视图如图所示，则该几何体的体积为 ___________ ，表面积为2的等腰直角三角形，则用角形，则这个几何体的表面积是34、由一个长方体和两个圆柱体构成的几何体的三视图如图，则该几何体的体积为35、由一个长方体和两个圆柱构成的几何体的三视图如图，则该几何体的体积为36、某三棱锥的三视图如图所示，则该三棱锥的最长棱的棱长为37、已知一个几何体的三视图如图所示（单位：），其中俯视图为正三角形，则该几何体的体积为39、已知一空间几何体的三视图如图所示，则该几何体的体积为38、一个多面体的三视图如图所示，则该多面体的体积是40、某多面体的三视图如图所示，则该多面体外接球的体积为41、如图是一个正方体被切掉部分后所得几何体的三视图，则该几何体的体积为42、棱长均为的正四面体在平面的一侧，是在平面内的正投影，设的面积为，则的最大值为 _________________ ，最小值为.43、给出下列说法：①正方形的直观图是一个平行四边形，其相邻两边长的比为1∶2，有一内角为45°；②水平放置的正三角形的直观图是一个底边长不变，高为原三角形高的一半的三角形；③不等边三角形水平放置的直观图是不等边三角形；④水平放置的平面图形的直观图是平面图形．其中，正确的说法是．（填序号）44、一个几何体的正视图为一个四边形，则这个几何体可能是下列几何体中的 _____________ .（填入所有可能的几何体的编号）①三棱锥；②四棱锥；③圆锥；④三棱柱；⑤圆柱.出该四面体的正视图时，以平面为投影面，则得到的正视图的面积是 ____________出该四面体的正视图时，以平面为投影面，则得到的正视图的面积是47、某几何体的三视图如图所示，设正方形的边长为，则该三棱锥的表面积为（）48、如图，正方形OABC 的边长为1cm，它是水平放置的一个平面图形的直观图，则原图形的面积是49、如图所示，直观图四边形A′B′C′D′是一个底角为45°，腰和上底均为 1 的等腰梯形，那么原平面图形的50、如图是一个几何体的三视图，则这个几何体的表面积为45、一个四面体的顶点在空间直角坐标系的坐标分别是，，，，画46、一个四面体的顶点在空间直角坐标系的坐标分别是，，，，画A．B．51、一个几何体的三视图如图所示，则该几何体的体积为52、《九章算术》中有这样一个问题：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”大意为：有个圆柱形木头，埋在墙壁中（如图所示），不知道其大小，用锯沿着面锯掉裸露在外面的木头，锯口深寸，锯道长度为尺，问这块圆柱形木料的直径是53、一个正四棱锥的三视图如图所示，则此正四棱锥的侧面积为54、中国古代数学名著《九章算术》中记载了公元前344 年商鞅监制的一种标准量器商鞅铜方升，其三视图如图所示（单位：寸），若取3，其体积为12.6 （立方寸），则图中的为_________ ．（注：55、一个几何体的三视图及其尺寸如下图所示，其中正（主）视图是直角三角形，侧（左）视图是半圆，56、如图，已知正方体的棱长为2，点为线段的中点，点分别是线段与上的动点，当三棱锥的俯视图的面积最大时，该三棱锥的正视图的面积是俯视图是等腰三角形，则这个几何体的体积是57、已知一个几何体的三视图如图所示，则该几何体的表面积是 ___________ ,体积是59、已知某四棱锥的三视图如图所示，俯视图是边长为 4 的正方形，正视图和侧视图是边长为4的等边三角形，则该四棱锥的全面积为58、如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是cm2.60、三条侧棱两两垂直的正三棱锥，其俯视图如图所示，主视图的边界是底边长为 2 的等腰三角形，则主视图的面积等于61、某几何体的三视图如图所示，设该几何体中最长棱所在的直线为，与直线不相交的其中一条棱所在直线为，则直线与所成的角为62、如图，网格纸上小正方形的边长为1，粗实线与粗虚线画出的是某多面体的三视图，则该多面体外接63、一个几何体的三视图如图所示，则这个几何体的体积与其外接球体积之比为球的表面积为64、一个多面体的三视图如图所示，则该多面体的体积是65、如图，网格纸的小正方形的边长是1，粗线画出的是一个几何体的三视图，其中正视图为等边三角形，则该几何体的体积为 _________67、如图，在棱长为 1 的正方体中，点是线段上的动点.当在平面上的正投影都为三角形时，将它们的面积分别记为.(i) 当时，_____________ (填“ >或”“ =或”“ <)”；(ii) 的最大值为________________ .68、已知一个几何体的三视图如图所示(单位：)，其中俯视图为正三角形，则该几何体的体积为66、如图，网格纸上的小正方形边长为，粗线画出的是某几何体的三视图，则该几何体外接球的体积为70、下图是两个腰长均为 的等腰直角三角形拼成的一个四边形 ，现将四边形 沿69、某几何体的三视图（单位： ）如图所示，则此几何体的所有棱长之和为，体积为参考答案1、2、3、4、5、6、7、8、9、10、11、212、13、14、15、16、17、 18、 19、20、21、22、1）（ 2）（ 3）323、24、25、 26、27、28、29、30、31、 32、33、2（1＋）π＋434、35、36、37、38、39、40、41、42、43、①②④⑤44、2＋2 120 60 1.645、46、47、48、49、 50、 51、 52、 53、 54、 55、56、57、58、59、60、61、62、63、64、65、66、67、68、69、2070、解析】1、由三视图可知，三棱锥直观图如图，图中为棱的中点，正四棱柱底面边长为，高为，由直观图知，最长棱长为，故答案为.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.【名师点睛】(1)由实物图画三视图或判断、选择三视图,此时需要注意“长对正、高平齐、宽相等”的原则.2、由三视图可知,长方体的长、宽、高分别为.2,1,1,圆柱的高为1,底面圆半径为1,所以(2) 由三视图还原实物图 ,解题时首先对柱、锥、台、球的三视图要熟悉 ,复杂的几何体也是由这些简单的几 何体组合而成的；其次 ,要遵循以下三步：①看视图 ,明关系；②分部分 ,想整体；③综合起来 ,定整体． 3、在直角梯形中，由 ，可得 ，因此该梯形的面积为 ，原图与对应直观图的面积之比为 ，因此这块菜地的面积为 .考点：平面图形的直观图 .4、因为 OA ＝6，CB ＝2，所以 OD ＝2.又因为∠ COD ＝ 45°，所以 CD ＝ 2.梯形的直观图如图，则 C ′ D ＝′1.考点：平面图形的直观图5、试题分析：由题意得，由图象中可知， ，则对应三角形 中， ，又与 平行的线段的长度为 ，则对应三角形 的高为 ，所以三角形 的面积为 ． 考点：斜二测画的应用．6、由三视图知几何体的底面是底边，高均为 的平行四边形，四棱锥的高为 ．∴几何体的体积 ，故答案： ．点睛：三视图问题的常见类型及解题策略(1) 由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示， 不能看到的部分用虚线表示．(2) 由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形 式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分 三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．7、由题意可知：该几何体为四棱锥，其体积为，其表面积为点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.8、由三视图可知该几何体由圆柱和圆锥组成，，故答案为，∴左视图面积为，故答案为10、几何体由一个半球和一个圆锥组合而成，球半径为，圆锥底面半径为，高为，则，故答案为.11、由已知中的三视图可得该几何体为：以俯视图为底面的半圆锥且底面半径，∴底面面积半圆锥高，点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体9、过于，易知∵，，∵，，母线长，的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.12、由三视图可想象出这个图像是三棱锥，该三棱锥底面积积公式得到，其体积．故得体积为13、由三视图可以知道：该几何体是一个三棱锥．其中则该三棱锥的最长棱的长是，，故答案为．14、原来平面图形是直角边分别为、的直角三角形，15、将该几何体放入边长为的正方体中，由三视图可知该四面体为，由直观图可知，最大的16、由三视图可几何体是三个半正方体构成，其表面积有15 个边长为2的正方形， 1 个边长为2、的矩形构成，∴几何体的表面积底面，，高为，由三棱锥的体面为，在正三角形中，，所以面积，故答案为点睛: 空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量．(2) 多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．(3) 旋转体的表面积问题注意其侧面展开图的应用．17、如图所示，根据三视图之间的关系可得,所以俯视图中,所以三棱锥侧视图面积. 点睛：本题主要考查了简单几何体的三视图，空间几何体的直观图，解答中着重考查了学生的空间想象能力和三视图中数量关系的转化，其中熟记空间几何体的三视图的规则是解答此类问题的关键.19、由三视图得到该几何体如图，CD=1，BC= ，BE= ，CE=2 ，DE=3 ；所以最大值为3，故最长边为DE=3 ；故答案为：3．18、该几何体是四棱锥，底面是直角梯形，，解得．∴剩余部分体积21、此几何体的侧视图为直角三角形，高为 ，底为 ，面积为恢复原几何体是以正视图为底面的四棱锥，其底面为直角梯形，面积是 ，体积为22、这个正四面体的正视图为等腰三角形 （底边边长为 ,底边上高为 2）,面积为∴三棱锥的体积 ，点睛：由三视图画出直观图的步骤和思考方法： 1、首先看俯视图，根据俯视图画出几何体地面的直观 图； 2、观察正视图和侧视图找到几何体前、后、左、右的高度； 3、画出整体，然后再根据三视图进行调 整.20、几何体为如图，两个三棱锥和一个正方体的组合体，所以，高为个三棱锥，∵正方体的棱长是 2，截面为边长为的正三角形，其面积为则该几何体的表面积为24、由题设中提供的三视图的数据信息与图形信息可知：该几何体是底面为直角边长分别的等腰直角三角形高是的直三棱柱与底面是边长为，高是的矩形的四棱锥的组合体。
人教A版高中必修二试题高一三视图专练.docx
高中数学学习材料唐玲出品高一数学三视图专练1．（全国新课标Ⅰ 理 12）如图，网格柢上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）A ．62B ．42C ．6D ．42．（全国新课标Ⅰ 文 8）如图，网格纸的各小纸都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是（ ）A ．三棱锥B ．三棱柱C ．四棱锥D ．四棱柱3．（全国新课标Ⅱ 理 6）如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）A ．1727B ．59C ．1027D ．134．（山东 文 13）一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为_________________。
5．（江苏 8）设甲、乙两个圆柱的底面积相等，且1294S S =，则12V V 的值是_________。
6．（安徽 文 8）一个多面体的三视图如图所示，则该多面体的体积为（ ）A ．233B ．476 C ．6D ．77．（浙江 文 3）某几何体的三视图（单位：cm ）如下图所示，则该几何体的体积是（ ）A ．372cmB ．90cm 3C ．3108cmD ．3138cm7题图 8题图9题图8．（北京 文 11）某三棱锥的三视图如上图所示，则该三棱锥最长棱的棱长为_________。
9．（天津 文史类 10）一个几何体的三视图如上图所示（单位：m ），则该几何体的体积为_________3m 。
10．（辽宁 文 7）某几何体三视图如右图所示，则该几何体的体积为（ ）A ．84π-B ．82π- C ．8π- D ．82π-11．（陕西 文 5）将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（ ）A ．4πB ．3πC ．2πD ．π12．（湖南 文史类 8）一块石材表示的几何体的三视图如右图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（ ）A ．1B ．2C ．3D ．413．（四川 文史类 4）某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（ ）（锥体体积公式：1,3V Sh =其中S 为底面面积，h 为高） A ．3 B ．2C ．3D ．1 14．（重庆 文史类 7）某几何体的三视图如图所示，则该几何体的体积为（ ）A ．12B ．18C ．24D ．30。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三视图练习
1
2
1．下面是一些立体图形的三视图（如图），•请在括号内填上立体图形的名称．
3
4
2．如图4-3-26，下列图形都是几何体的平面展开图，你能说出这些几何体的名称吗？
5
6
3．如图，从不同方向看下面左图中的物体，右图中三个平面图形分别是从哪个方向看7
到的？
8
9
4．一天，小明的爸爸送给小明一个礼物，小明打开包装后画出它的主视图和俯视图如图所10
示．根据小明画的视图，你猜小明的爸爸送给小明的礼物是（）
11
12
A．钢笔 B．生日蛋糕 C．光盘 D．一套衣服
13
5．一个几何体的主视图和左视图如图所示，它是什么几何体？请你补画出这个几何体14
的俯视图．
15
16
17
6．一个物体的三视图如图所示，试举例说明物体的形状．
18
19
7．已知一个几何体的三视图如图所示，则该几何体的体积为多少？
20
21
8．已知几何体的主视图和俯视图如图所示．
22
（1）画出该几何体的左视图；
23
（2）该几何体是几面体？它有多少条棱？多少个顶点？
24
（3）该几何体的表面有哪些你熟悉的平面图形？
25
26
27
9．小刚的桌上放着两个物品，它的三视图如图所示，你知道这两个物品是什么吗？
28
29
30
31
10．一个由几个相同的小立方体搭成的几何体的俯视图如图所示，方格里的数字表示该32
位置的小立方体的个数，请你画出这个几何体的主视图和左视图．
33
34
35
11．如图所示，下列三视图所表示的几何体存在吗？如果存在，请你说出相应的几何体36
的名称．
37
12．由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图38 的方格中的字母和数字表示该位置上小立方体的个数，求x ，y 的值．
39
40
41 13．马小虎准备制作一个封闭的正方体盒子，他先用5•个大小一样的正方形制成如图42 所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在下图中的每个图形上再43 接一个正方形，•使新拼接成的图形经过折叠能成为一个封闭的正方体盒子．（注：添加44 的正方形用阴影表示）
45
46 14．由几个小立方体叠成的几何体的主视图和左视图如图，求组成几何体的小立方体47 个数的最大值与最小值．
48
49 1．如图，在长方体1111ABCD A B C D -中，3cm AB AD ==，12cm AA =， 50 则四棱锥11A BB D D -的体积为 cm 3．
51 2.某三棱锥的三视图如图所示，该三梭锥的表面积是（ ）
52
53 A. 28+65 B. 30+65 C. 56+ 125 D. 60+125
54 55
56
57 58
59 60 61 62
63 64 65 66 67 68
69
D
A
B
C 1C 1
D 1A
1B
7. 一个多面体的三视图分别为正方形、等腰三角形和矩形，如图所示，则该多面体的体积70
为( )
71
A．24 cm3 B．48 cm3 C．32 cm3D．28 cm3
72
73
第7题第8题
74
8.若正四棱锥的正(主)视图和俯视图如图所示，则该几何体的表面积是( )．
75
A．4 B．4＋410 C．8 D．4＋411
76
77
9.如下图是某几何体的三视图，其中正(主)视图是腰长为2的等腰三角形，侧(左)视图是78
半径为1的半圆，则该几何体的体积是( )．
79
A．π B．.π
3
C．3π D．
3π
3
80
81
82
第9题第10题83
84 10.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm ），可得这个几何体的85 体积是（ ）
86 Ａ．
34000cm 3 Ｂ．3
8000cm 3
Ｃ．32000cm
Ｄ．34000cm 87 11.如图，一个空间几何体的正视图、侧视图都是面积为3
，且一个内角为60的菱形，俯88 视图为正方形，那么这个几何体的表面积为（ ） 89 A .23 B .43 C . 4
D . 8
90
91 第11题 第12题 第13题 92 12.一空间几何体的三视图如图所示,则该几何体的体积为( ).
93 A.223π+ B. 423π+ C. 232π+
23
4π+
94 13.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( ) 95 A. 2(202)cm + B.21 cm C. 2(242)cm + D. 24 cm 96 14.若一个螺栓的底面是正六边形，它的正(主)视图和俯视图如图所示，则它的体积是97 ( )．
98
99
A．273＋12π B．93＋12π C．273＋3π D．543＋3π
100
101
第14题第15题
102
15.一个五面体的三视图如下，正视图与侧视图是等腰直角三角形，俯视图为直角梯形，部103
分边长如图所示，则此五面体的体积为___________．
104
105
第16题第17题
106
16. 如图是一个几何体的三视图，若它的体积是33a __________
107
17.设某几何体的三视图如下（尺寸的长度单位为m）。
则该几何体的体积为108
___________ 3
m
109。