中值定理和导数的应用
四章节中值定理与导数应用

9/26/2024
第四章 中值定理与导数应用
第20页
小结
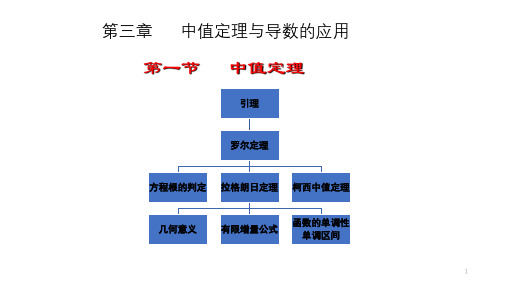
罗尔定理、拉格朗日中值定理及柯西中值定理 之间旳关系;
Rolle f (a) f (b) Lagrange F ( x) x Cauchy
定理
中值定理
中值定理
注意定理成立旳条件; 注意利用中值定理证明等式与不等式旳环节.
嘉兴学院
9/26/2024
欲证: ( x1 , x2 ), 使 f ( ) f ( ) 0 只要证 e f ( ) e f ( ) 0
亦即 [ ex f (x ) ] x 0
作辅助函数F (x) ex f (x ) , 验证 F (x )在 [ x1 , x2 ]上满足
罗尔定理条件.
嘉兴学院
9/26/2024
设
F (x ) f (x )sin x
验证 F (x ) 在 [ 0, π ] 上满足罗尔定理条件.
嘉兴学院
9/26/2024
第四章 中值定理与导数应用
第22页
3. 若 f (x )可导, 试证在其两个零点间一定有
f (x ) f (x ) 旳零点.
提醒: 设 f (x1) f (x2 ) 0, x1 x2 ,
x+
嘉兴学院
9/26/2024
第四章 中值定理与导数应用
三、柯西(Cauchy)中值定理
第15页
柯西(Cauchy)中值定理 如果函数 f ( x)及F ( x) 满
足(1)在闭区间[a, b]上连续,
(2)在开区间(a, b)内可导,
(3) 对(a, b)内每一点均有F ' ( x) 不为零,那么在
f (x1 x2 ) f (x2 ) f (x1)
3.3第三章:中值定理及导数的应用

上连续;
2.按左、右导数的定义不难求出
f
/ 1
f
/ 1 1, 从而
f x 在 0,2 内
可导,且
f
/ x
x,0 x 1,
1 x2 ,1 x
2.
因此, f x 在 0,2上满足拉氏定理的条件.
(二)由拉氏定理的结论: 0,2 ,使
f
/
f
2
2
f 0
0
1 2
.不难算得:
1 或 2
2 0,2.
x 2x
lim x
x 1 21
2 x x
.
对于不直接表现为 0 型或 型的不定型,要首先合理转化,使其成为 0
四.洛必达法则 我们在第一章曾注意到,考试时考察得最多的求极限问题要么是 0 型,要么是 0
。对付这种问题,我们根据具体情形曾给出了因式分解约零因子、根式有理 化约零因子、等价无穷小替换、凑重要极限等方法。现在有一个著名的法则—
—洛必达法则,可用一招统一解决大部分的 0 或 的极限问题。 0
例 6.设 f x x 1x 2x 3x 4 ,证明方程 f x 0 有三个实根,并
且它们分别位于区间 1, 2, 2,3, 3, 4. (见书第 105 页)
例 7.证明方程 x5 x 1 0 只有一个正根.(反证).
拉氏定理有两个重要的的推论,也要会记会用.
推论 1:若对任意 x I , f / x 0 ,则 f x C,x I.
x
x.
.
( .
1,1
x
)
例 3.证明:对 x 0,ex 1 x. .
例 4.证明:对 x 0, ln 1 x x. .
大家自己证明,这两个结论要记住. 三.利用中值定理证明等式成立(或方程有无根)
中值定理与导数的应用

第三章 中值定理与导数的应用§3. 1 中值定理 一、罗尔定理 费马引理设函数f (x )在点x 0的某邻域U (x 0)内有定义, 并且在x 0处可导, 如果对任意x ∈U (x 0), 有 f (x )≤f (x 0) (或f (x )≥f (x 0)), 那么f '(x 0)=0.罗尔定理 如果函数)(x f 满足:(1)在闭区间],[b a 上连续, (2)在开区间),(b a 内可导, (3)在区间端点处的函数值相等,即)()(b f a f =, 那么在),(b a 内至少在一点)(b a <<ξξ , 使得函数)(x f 在该点的导数等于零,即0)('=ξf .例:设函数)(x f 在[0,1]上连续,在(0,1)上可导,0)1(=f ,证明:在(0,1)内存在ξ,使得ξξξ)()(f f -='.【分析】本题的难点是构造辅助函数,可如下分析:()0)(0)()(0)()()()(='→='+→='+→-='x xf x f x x f f f f f ξξξξξξ【证明】令)()(x xf x G =,则)(x G 在[0,1]上连续,在(0,1)上可导,且0)1(1G (1)0,0)(0)0(====f f G ,)()()(x f x x f x G '+=' 由罗尔中值定理知,存在)1,0(∈ξ,使得)()()(ξξξξf f G '+='.即ξξξ)()(f f -='例:设函数f (x ), g (x )在[a , b ]上连续,在(a , b )内具有二阶导数且存在相等的最大值,f (a )=g (a ), f (b )=g (b ), 证明:存在(,)a b ξ∈,使得()().f g ξξ''''=【分析】需要证明的结论与导数有关,自然联想到用微分中值定理,事实上,若令()()()F x f x g x =-,则问题转化为证明()0F ξ''=, 只需对()F x '用罗尔定理,关键是找到()F x '的端点函数值相等的区间(特别是两个一阶导数同时为零的点),而利用F (a )=F (b )=0, 若能再找一点(,)c a b ∈,使得()0F c =,则在区间[,],[,]a c c b 上两次利用罗尔定理有一阶导函数相等的两点,再对()F x '用罗尔定理即可。
中值定理与导数的应用

中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础。
在实际应用中,中值定理与导数的应用非常广泛。
以下是一些具体的应用:
1.判断函数的单调性:通过导数可以判断函数的单调性,如果函数在某个区间内的导数大于0,则
该函数在这个区间内单调递增;如果函数在某个区间内的导数小于0,则该函数在这个区间内单调递减。
2.求函数的极值:导数可以用来求函数的极值。
如果函数在某一点的导数为0,则该点可能是函数
的极值点。
在判断出极值点后,可以通过求导数在该点的左右两侧的符号变化来确定该点是极大值点还是极小值点。
3.判断函数的凹凸性:通过二阶导数可以判断函数的凹凸性。
如果函数在某一点的二阶导数大于0,
则该函数在该点附近是凹函数;如果二阶导数小于0,则该函数在该点附近是凸函数。
4.求函数的拐点:在判断出函数的极值点和凹凸性后,可以进一步求出函数的拐点。
拐点的定义是
函数图像在该点处的切线发生弯曲的地方。
通过求一阶导数在该点的左右两侧的符号变化,可以判断出拐点的位置。
5.判断函数的不等式:通过导数还可以判断函数的不等式。
如果两个函数在某个区间内的导数符号
相反,则这两个函数在该区间内的函数值一定不相等。
6.最优化问题:在工程和经济学中,经常需要解决最优化问题。
使用微积分中的中值定理和导数可
以找到最优解。
例如,在经济学中,可以使用微积分来找到最大化收益或最小化成本的最佳策略。
总的来说,中值定理与导数的应用非常广泛,它们是微积分学的重要基石,可以用于解决各种实际问题。
微分中值定理与导数的应用

微分中值定理与导数的应用微分中值定理是微积分中的一个重要定理,它是导数与函数之间的关系的重要推论。
本文将介绍微分中值定理的概念以及其在实际问题中的应用。
一、微分中值定理的概念微分中值定理是数学分析中的一个重要定理,它是由罗尔定理和拉格朗日中值定理推导出的。
该定理表明,如果函数f(x)在闭区间[a, b]上连续,在开区间(a, b)内可导,并且在区间端点a和b的函数值相等(f(a) = f(b)),那么在(a, b)内至少存在一点c,使得f'(c) = 0。
这一定理的直观解释是:如果一个连续函数在两个点的函数值相等,并且在两点之间的某个地方斜率为零,那么在该点一定存在切线与横轴平行。
二、导数的应用导数是微积分中的重要概念,它描述了函数在某一点的变化率。
通过导数的概念和性质,我们可以在实际问题中进行一些有用的应用。
1. 最值问题导数可以用来求解函数的最值问题。
在闭区间上的连续函数中,如果在某一点的导数为零或不存在,那么这一点可能是函数的极值点。
通过求解导数为零的方程,可以找到函数的极值。
2. 凹凸性和拐点问题导数可以用来研究函数的凹凸性和拐点问题。
通过分析函数的二阶导数(导数的导数),可以确定函数的凹凸性以及拐点的位置。
3. 曲线的切线和法线问题导数可以用来求解曲线的切线和法线问题。
切线的斜率等于函数在该点的导数,而法线的斜率是切线斜率的负倒数。
三、微分中值定理的应用微分中值定理是导数与函数之间的重要关系推论,它在实际问题中有着广泛的应用。
1. 速度与加速度微分中值定理可以用来解决速度与加速度的问题。
对于一个运动的实体,在某一时间段内,他的速度可能为零,这意味着他的加速度为零。
这可以通过微分中值定理得到证明。
2. 经济学中的应用微分中值定理在经济学中也有广泛的应用。
例如,在某个时间段内,一个消费品的价格可能保持不变,这意味着该消费品的边际效用或边际收益为零。
这可以用微分中值定理来解释。
3. 物理学中的应用微分中值定理在物理学中也有重要的应用。
高等数学 第3章 第一节 中值定理
(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
中值定理与导数的应用

中值定理与导数的应用导数是微积分中的重要概念,它描述了函数在某一点的变化率。
而中值定理则是导数的重要应用之一,它揭示了函数在某一区间内必然存在某一点,使得该点的斜率等于该区间的平均斜率。
在实际问题中,中值定理具有广泛的应用,可以帮助我们解决各种与变化率相关的问题。
让我们来了解一下中值定理的基本原理。
根据中值定理,如果一个函数在闭区间[a, b]上连续,并且在开区间(a, b)内可导,那么在(a, b)内至少存在一点c,使得函数在c处的导数等于函数在[a, b]上的平均斜率。
换句话说,函数在区间内的某一点的瞬时变化率与整个区间的平均变化率相等。
中值定理的一个重要推论是拉格朗日中值定理。
根据拉格朗日中值定理,如果一个函数在闭区间[a, b]上连续,并且在开区间(a, b)内可导,那么在(a, b)内至少存在一点c,使得函数在c处的导数等于函数在[a, b]上的斜率。
换句话说,拉格朗日中值定理给出了函数在某一区间内某一点的瞬时变化率与该区间的斜率之间的对应关系。
中值定理的应用非常广泛。
一个常见的应用是求函数在某一区间内的最大值和最小值。
根据极值存在定理,如果一个函数在闭区间[a, b]上连续,那么它在该区间内必然存在最大值和最小值。
根据中值定理,我们可以通过求函数在该区间内的导数为0的点,来确定函数的极值点。
另一个常见的应用是求函数的单调性。
根据中值定理,如果一个函数在某一区间内的导数恒大于0(或恒小于0),那么该函数在该区间内必然是递增的(或递减的)。
因此,我们可以通过求函数的导数来确定函数在某一区间内的单调性。
中值定理还可以用来解决一些与速度和加速度相关的问题。
例如,在物理学中,我们经常需要计算物体在某一时间段内的平均速度和瞬时速度。
根据中值定理,我们可以通过求物体在该时间段内的位移与时间的比值,来确定物体在某一时刻的瞬时速度。
中值定理是导数的重要应用之一,它可以帮助我们解决各种与变化率相关的问题。
微分中值定理与导数的应用总结

微分中值定理与导数的应用总结一、微分中值定理1.拉格朗日中值定理拉格朗日中值定理是微分中值定理的最基本形式,它表述为:如果函数f(x)在区间[a,b]上连续,在开区间(a,b)内可导,则在(a,b)内至少存在一个数c,使得f(b)-f(a)=f'(c)(b-a),其中c属于(a,b)。
拉格朗日中值定理的几何意义是:如果一条曲线在两个点a和b上的斜率相等,则在这两个点之间必然存在一点c,使得曲线在c点和a、b两点之间的切线斜率相等。
2.柯西中值定理柯西中值定理是微分中值定理的推广形式,它给出了两个函数的导数的关系。
设f(x)和g(x)在[a,b]上连续,在开区间(a,b)内可导且g'(x)≠0,则存在一个数c,使得[f(b)-f(a)]/[g(b)-g(a)]=[f'(c)]/[g'(c)]。
柯西中值定理的几何意义是:如果曲线f(x)和g(x)在两个点a和b上的切线斜率之比等于f'(c)和g'(c)的比,则在这两个点之间必然存在一点c,使得曲线f(x)和g(x)在c点的切线斜率之比等于f'(c)和g'(c)的比。
3.罗尔中值定理罗尔中值定理是微分中值定理的特殊形式,它给出了导数为零的充分条件。
设函数f(x)在[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则在(a,b)内至少存在一个数c,使得f'(c)=0。
罗尔中值定理的几何意义是:如果一条曲线在两个端点上的函数值相等,则在这两个端点之间必然存在一个点c,使得曲线在c点的切线斜率为零。
微分中值定理的应用非常广泛,例如在证明极限存在或连续性、研究函数增减性和函数极值、解方程和不等式等问题中都有重要的作用。
在实际生活中,微分中值定理可以应用于求解速度、加速度、距离等问题,帮助我们更好地理解和解决实际问题。
二、导数的应用导数作为微积分的重要概念,具有很多实际应用。
