离散系统的时域分析实验报告
matlab离散信号时域分析实验报告

Matlab离散信号时域分析实验报告1. 引言信号是信息的载体,可以通过对信号进行离散化来进行数字信号的处理和分析。
离散信号时域分析是对离散信号在时域上进行观察和分析的方法。
本实验旨在通过使用Matlab软件对离散信号进行时域分析,掌握离散信号的时域特性和基本分析方法。
2. 实验目的•了解离散信号的概念和特性;•掌握离散信号的时域分析方法;•学会通过Matlab对离散信号进行时域分析。
3. 实验原理离散信号是在时间上呈现离散的特征,可以用离散序列表示。
离散序列可以通过采样连续信号得到,也可以通过数学模型生成。
在时域分析中,通常使用的分析方法包括: - 时域图像绘制:绘制离散信号的时域图像,了解信号的振幅和波形特征; - 时域序列计算:计算离散信号的均值、方差等统计量,了解信号的基本特性;- 时域滤波:对离散信号进行滤波,去除噪声或者突发干扰。
4. 实验步骤4.1 生成离散信号首先需要生成一个离散信号序列,可以使用Matlab的随机数函数生成一个大小为N的随机序列作为离散信号。
N = 100; % 信号长度为100x = rand(1,N); % 生成随机序列4.2 时域图像绘制通过plot函数可以将离散信号在时域上绘制出来,观察信号的振幅和波形特征。
t = 1:N; % 时间序列plot(t, x);title('离散信号时域图像');xlabel('时间');ylabel('幅度');4.3 时域序列计算可以通过内置函数计算离散信号的均值、方差等统计量。
avg = mean(x); % 均值variance = var(x); % 方差4.4 时域滤波可以使用滤波器对离散信号进行滤波,去除噪声或者突发干扰。
这里以均值滤波为例,对信号进行平滑处理。
windowSize = 5; % 滑动窗口大小b = (1/windowSize)*ones(1,windowSize);a = 1;smoothed_x = filter(b, a, x);5. 实验结果与分析通过对生成的离散信号进行时域分析,得到如下结果: - 时域图像:时域图像时域图像•信号均值:0.5231•信号方差:0.0842•平滑后的信号时域图像:平滑后的时域图像平滑后的时域图像从时域图像可以观察到信号的振幅和波形特征。
实验五 离散时间系统的时域分析
实验五 离散时间系统的时域分析一、实验目的:(1)理解离散时间信号的系统及其特性。
(2)对简朴的离散时间系统进行分析,研究其时域特性。
(3)运用MATL AB对离散时间系统进行仿真,观测成果,理解其时域特性。
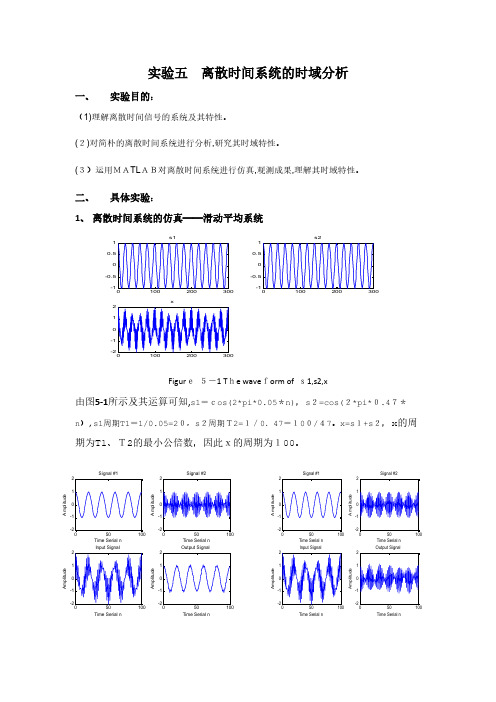
二、具体实验:1、离散时间系统的仿真——滑动平均系统s1s2xFigur e 5-1 T he wave form of s1,s2,x由图5-1所示及其运算可知,s1=cos(2*pi*0.05*n),s 2=cos(2*pi*0.47*n ),s1周期T1=1/0.05=20,s 2周期T2=1/0.47=100/47。
x=s 1+s 2,x 的周期为T1、T2的最小公倍数,因此x的周期为100。
Time Serial n A m p l i t u d eSignal #1Time Serial n A m p l i t u d eSignal #2Time Serial nA m p l i t u d eInput SignalTime Serial nA m p l i t u d eOutput SignalTime Serial n A m p l i t u d eSignal #1Time Serial n A m p l i t u d eSignal #2Time Serial nA m p l i t u d eInput SignalTime Serial nA m p l i t u d eOutput SignalF ig ure 5-2 Fi gure 5-3(1)如图5-2,当M=2时,第一种图显示的是一种低频信号,第二个是高频信号,第三个图是信号一和信号二的合成的输入,第四个是通过函数Y 的得出的输出。
成果是低频信号,前后对比得出是高频信号被克制了。
本系统是滑动平均滤波器,为低通滤波系统,功能就是从信号中滤除高频分量,因此输入的高频分量s2[n]被该系统克制了。
实验2离散时间LTI系统的时域分析

实验二 离散时间LTI 系统的时域分析一 实验目的(1) 学会运用MATLAB 求解离散时间系统的零状态响应;(2) 学会运用MATLAB 求解离散时间系统的单位取样响应;(3) 学会运用MATLAB 求解离散时间系统的卷积和。
二 实验原理及实例分析1、离散时间系统的响应离散时间LTI 系统可用线性常系数差分方程来描述,即∑∑==-=-Mj jN i i j n x b i n y a 00)()( (1) 其中,i a (0=i ,1,…,N )和j b (0=j ,1,…,M )为实常数。
MATLAB 中函数filter 可对式(1)的差分方程在指定时间范围内的输入序列所产生的响应进行求解。
函数filter 的语句格式为y = filter (b , a , x )其中,x 为输入的离散序列;y 为输出的离散序列;y 的长度与x 的长度一样;b 与a 分别为差分方程右端与左端的系数向量。
【实例1】 已知某LTI 系统的差分方程为)1(2)()2(2)1(4)(3-+=-+--n x n x n y n y n y试用MATLAB 命令绘出当激励信号为)()2/1()(n u n x n=时,该系统的零状态响应。
解:MATLAB 源程序为>>a=[3 -4 0 2];>>b=[1 2]; >>n=0:30;>>x=(1/2).^n;>>y=filter(b,a,x);>>stem(n,y,'fill'),grid on>>xlabel('n'),title('系统响应y(n)')程序运行结果如图1所示。
2、离散时间系统的单位取样响应系统的单位取样响应定义为系统在)(n δ激励下系统的零状态响应,用)(n h 表示。
MATLAB 求解单位取样响应可利用函数filter ,并将激励设为前面所定义的impDT 函数。
离散时间信号的时域分析实验报告

离散时间信号的时域分析实验报告实验报告:离散时间信号的时域分析一、实验目的本实验旨在通过MATLAB软件,对离散时间信号进行时域分析,包括信号的显示、基本运算(如加法、减法、乘法、反转等)、以及频域变换(如傅里叶变换)等,以加深对离散时间信号处理的基本概念和原理的理解。
二、实验原理离散时间信号是在时间轴上离散分布的信号,其数学表示为离散时间函数。
与连续时间信号不同,离散时间信号只能在特定的时间点取值。
离散时间信号的时域分析是研究信号的基本属性,包括幅度、时间、频率等。
通过时域分析,我们可以对信号进行各种基本运算和变换,以提取有用的信息。
三、实验步骤1.信号生成:首先,我们使用MATLAB生成两组简单的离散时间信号,一组为正弦波,另一组为方波。
我们将这些信号存储在数组中,以便后续分析和显示。
2.信号显示:利用MATLAB的绘图功能,将生成的信号在时域中显示出来。
这样,我们可以直观地观察信号的基本属性,包括幅度和时间关系。
3.基本运算:对生成的信号进行基本运算,包括加法、减法、乘法、反转等。
将这些运算的结果存储在新的数组中,并绘制出运算后的信号波形。
4.傅里叶变换:使用MATLAB的FFT(快速傅里叶变换)函数,将信号从时域变换到频域。
我们可以得到信号的频谱,进而分析信号的频率属性。
5.结果分析:对上述步骤得到的结果进行分析,包括比较基本运算前后的信号波形变化,以及傅里叶变换前后的频谱差异等。
四、实验结果1.信号显示:通过绘制图形,我们观察到正弦波和方波在时域中的波形特点。
正弦波呈现周期性的波形,方波则呈现明显的阶跃特性。
2.基本运算:通过对比基本运算前后的信号波形图,我们可以观察到信号经过加法、减法、乘法、反转等运算后,其波形发生相应的变化。
例如,两个信号相加后,其幅度和时间与原信号不同。
反转信号则使得波形在时间轴上反向。
3.傅里叶变换:通过FFT变换,我们将时域中的正弦波和方波转换到频域。
正弦波的频谱显示其频率为单一的直流分量,方波的频谱则显示其主要频率分量是直流分量和若干奇数倍的谐波分量。
实验一 离散时间信号的时域分析
实验一 离散时间信号的时域分析实验1 序列的产生1. 目的:熟悉C 语言产生和绘制,熟悉MATLAB 中产生信号和绘制信号的基本命令。
2. 具体实验:2.1 单位样本和单位阶跃序列。
Q1.1 运行程序P1.1 ,以产生单位样本序列u[n]并显示它。
答:如图1-1所示。
Q1.2 命令clf , axis , title , xlabel 和ylabel 的作用是什么? 答:clf :擦除当前图形窗口中的图形。
Axis :调整坐标轴X 轴Y 轴的范围。
Title:给绘制的图形加上标题。
Xlabel:给X 轴加上标注。
Ylabel: 给Y 轴加上标注。
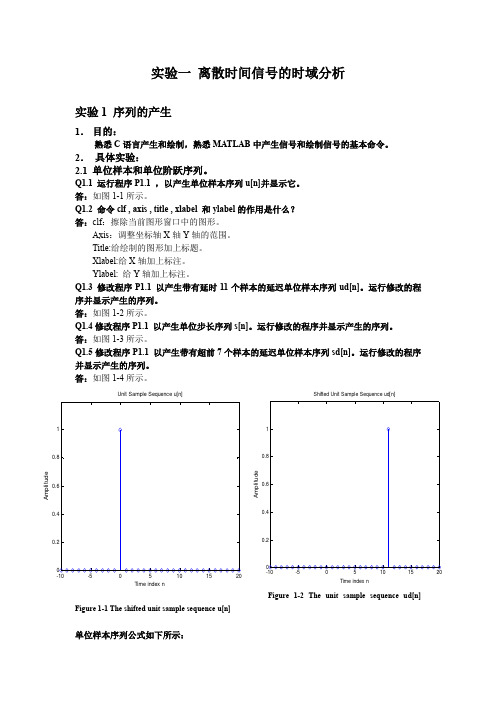
Q1.3 修改程序P1.1 以产生带有延时11个样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
答:如图1-2所示。
Q1.4修改程序P1.1 以产生单位步长序列s[n]。
运行修改的程序并显示产生的序列。
答:如图1-3所示。
Q1.5修改程序P1.1 以产生带有超前7个样本的延迟单位样本序列sd[n]。
运行修改的程序并显示产生的序列。
答:如图1-4所示。
Figure 1-2 The unit sample sequence ud[n]Figure 1-1 The shifted unit sample sequence u[n]单位样本序列公式如下所示:Time index nA m p l i t u d eUnit Sample Sequence u[n]Time index nA m p l i t u d eShifted Unit Sample Sequence ud[n]1 , n=0 1 , n=k δ[n]= δ[n-k]=0 , 0≠0 0 , 0≠kFigure 1-3 The unit step sequence s[n] Figure 1-4 The shifted unit step sequence sd[n]单位阶跃序列公式如下所示:1 , n ≥0 1 , n ≥k μ[n]= μ[n-k]=0 , n <0 0 , n <k2.2 指数信号Q1.6 运行程序P1.2 ,以产生复数值的指数序列。
数字信号处理 实验作业:离散LSI系统的时域分析

实验2 离散LSI 系统的时域分析一、.实验目的:1、加深对离散系统的差分方程、单位脉冲响应、单位阶跃响应和卷积分析方法的理解。
2、初步了解用MA TLAB 语言进行离散时间系统时域分析的基本方法。
3、掌握求解离散时间系统的单位脉冲响应、单位阶跃响应、线性卷积以及差分方程的程序的编写方法,了解常用子函数的调用格式。
二、实验原理:1、离散LSI 系统的响应与激励由离散时间系统的时域分析方法可知,一个离散LSI 系统的响应与激励可以用如下框图表示:其输入、输出关系可用以下差分方程描述:[][]NMkk k k ay n k b x n m ==-=-∑∑2、用函数impz 和dstep 求解离散系统的单位脉冲响应和单位阶跃响应。
例2-1 已知描述某因果系统的差分方程为6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3) 满足初始条件y(-1)=0,x(-1)=0,求系统的单位脉冲响应和单位阶跃响应。
解: 将y(n)项的系数a 0进行归一化,得到y(n)+1/3y(n-2)=1/6x(n)+1/2x(n-1)+1/2x(n-2)+1/6x(n-3)分析上式可知,这是一个3阶系统,列出其b k 和a k 系数: a 0=1, a ,1=0, a ,2=1/3, a ,3=0 b 0=1/6,b ,1=1/2, b ,2=1/2, b ,3=1/6程序清单如下: a=[1,0,1/3,0]; b=[1/6,1/2,1/2,1/6]; N=32; n=0:N-1; hn=impz(b,a,n); gn=dstep(b,a,n);subplot(1,2,1);stem(n,hn,'k');课程名称 数字信号处理 实验成绩 指导教师 ***实 验 报 告院系 班级学号 姓名 日期title('系统的单位序列响应'); ylabel('h(n)');xlabel('n');axis([0,N,1.1*min(hn),1.1*max(hn)]); subplot(1,2,2);stem(n,gn,'k'); title('系统的单位阶跃响应'); ylabel('g(n)');xlabel('n');axis([0,N,1.1*min(gn),1.1*max(gn)]); 程序运行结果如图2-1所示:102030系统的单位序列响应h (n )n1020300.20.30.40.50.60.70.80.911.11.2系统的单位阶跃响应g (n )n图2-13、用函数filtic 和filter 求解离散系统的单位序列响应和单位阶跃响应。
实验一离散时间信号的时域分析
实验一离散时间信号的时域分析离散时间信号是一种离散的信号形式,其具有离散的时间间隔。
这种信号在数字信号处理中得到了广泛的应用。
时域分析是分析信号的一种方法,它通常包括分析信号的幅度、相位、频率等参数,并从中获得信号的特征。
在本实验中,我们将探讨离散时间信号的时域分析方法。
1.实验目的• 了解离散时间信号的基本概念和性质。
• 熟悉MATLAB软件的使用,理解信号处理工具箱的使用方法。
2.实验原理离散时间信号是一种在离散时间点上定义的数列。
它通常用序列来表示,序列的元素是按照一定的时间间隔离散采样得到的。
离散时间信号的采样频率通常表示为Fs,单位是赫兹。
离散时间信号可以写成如下的形式:x(n) = [x(0),x(1),x(2),...,x(N-1)]其中,n表示离散时间点的下标,N表示离散时间信号的长度。
• 幅度分析:指分析离散时间信号的振幅大小。
离散时间信号的幅度、相位、频率的分析通常使用傅里叶变换、离散傅里叶变换等变换方法来实现。
3.实验步骤3.1 生成离散时间信号使用MATLAB编写程序,生成一个离散时间信号。
例如,我们可以生成一个正弦信号:t = 0:0.01:1;x = sin(2*pi*100*t);其中,t表示时间向量,x表示正弦信号。
将信号进行离散化,得到离散时间信号:其中,fs表示采样频率,n表示采样时间点,xn表示采样后的信号。
使用MATLAB的plot函数,绘制离散时间信号的时域图像。
figure(1);plot(n, xn);xlabel('Time');ylabel('Amplitude');其中,figure(1)表示创建一个新的窗口,用于显示图像。
xlabel和ylabel用于设置图像的横轴和纵轴标签。
3.3 使用FFT进行幅度分析X = fft(xn);n = length(X);f = (0:n-1)*(fs/n);power = abs(X).^2/n;其中,X表示离散时间信号的傅里叶变换结果,n表示离散时间信号的长度,f表示频率向量,power表示幅度谱。
离散时间系统的时域分析实验报告
3. clf; h=[-6 5 2 3 -2 0 1 0 5 -3 4 2 -1 -3 2]; %冲激 x=[2 4 -1 3 -5 2 0 -1 2 -1]; %输入序列 y=conv(h,x); n=0:23; subplot(2,1,1); stem(n,y);
4. clf; n=0:301; x=cos((0.5*pi/600)*n.*n+0*n); %计算输出序列 num1=[0.5 0.27 0.77]; y1=filter(num1,1,x);%系统#1 的输出 den2=[1 -0.35 0.46]; num2=[0.45 0.5 0.45]; y2=filter(num2,den2,x);%系统#2 的输出 %画出输入序列 subplot(3,1,1); plot(n,x); axis([0 300 -2 2]); ylabel('振幅'); title('系统的输入'); grid;
四、实验结果与分析
图一 图二
2
图三
图四
五、实验小结
通过这次实验,我熟悉 MATLAB 中产生信号和绘制信号的基本命令,学会 通过 MATLAB 仿真一些简单的离散时间系统,并研究了它们的时域特性。
经过了两次实验课,对于 MATLAB 的一些命令语句的格式熟悉多了。在完 成实验时比第一次更顺利了些。
subplot(3,1,3) d=d(2:42); stem(n,d);
2. clf; n=0:40; D=10; a=3.0; b=-2; x=a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n); xd=[zeros(1,D) x]; nd=0:length(xd)-1; y=(n.*x)+[0 x(1:40)]; yd=(nd.*xd)+[0 xd(1:length(xd)-1)]; d=y-yd(1+D:41+D);
时域离散信号实验报告(3篇)
第1篇一、实验目的1. 理解时域离散信号的基本概念和特性。
2. 掌握时域离散信号的表示方法。
3. 熟悉常用时域离散信号的产生方法。
4. 掌握时域离散信号的基本运算方法。
5. 通过MATLAB软件进行时域离散信号的仿真分析。
二、实验原理时域离散信号是指在时间轴上取离散值的一类信号。
这类信号在时间上不连续,但在数值上可以取到任意值。
时域离散信号在数字信号处理领域有着广泛的应用,如通信、图像处理、语音处理等。
时域离散信号的基本表示方法有:1. 序列表示法:用数学符号表示离散信号,如 \( x[n] \) 表示离散时间信号。
2. 图形表示法:用图形表示离散信号,如用折线图表示序列。
3. 时域波形图表示法:用波形图表示离散信号,如用MATLAB软件生成的波形图。
常用时域离散信号的产生方法包括:1. 单位阶跃信号:表示信号在某个时刻发生突变。
2. 单位冲激信号:表示信号在某个时刻发生瞬时脉冲。
3. 正弦信号:表示信号在时间上呈现正弦波形。
4. 矩形脉冲信号:表示信号在时间上呈现矩形波形。
时域离散信号的基本运算方法包括:1. 加法:将两个离散信号相加。
2. 乘法:将两个离散信号相乘。
3. 卷积:将一个离散信号与另一个离散信号的移位序列进行乘法运算。
4. 反褶:将离散信号沿时间轴翻转。
三、实验内容1. 实验一:时域离散信号的表示方法(1)使用序列表示法表示以下信号:- 单位阶跃信号:\( u[n] \)- 单位冲激信号:\( \delta[n] \)- 正弦信号:\( \sin(2\pi f_0 n) \)- 矩形脉冲信号:\( \text{rect}(n) \)(2)使用图形表示法绘制以上信号。
2. 实验二:时域离散信号的产生方法(1)使用MATLAB软件生成以下信号:- 单位阶跃信号- 单位冲激信号- 正弦信号(频率为1Hz)- 矩形脉冲信号(宽度为2)(2)观察并分析信号的波形。
3. 实验三:时域离散信号的基本运算(1)使用MATLAB软件对以下信号进行加法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(2)使用MATLAB软件对以下信号进行乘法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(3)使用MATLAB软件对以下信号进行卷积运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(4)使用MATLAB软件对以下信号进行反褶运算:- \( u[n] \)4. 实验四:时域离散信号的仿真分析(1)使用MATLAB软件对以下系统进行时域分析:- 系统函数:\( H(z) = \frac{1}{1 - 0.5z^{-1}} \)(2)观察并分析系统的单位冲激响应。
离散时间信号与系统的时域分析实验报告
离散时间信号与系统的时域分析实验报告报告⼆:⼀、设计题⽬1.绘制信号)()(1k k f δ=和)2()(2-=k k f δ的波形2.绘制直流信号)()(1k k f ε=和)2(2-=k f ε的波形3绘制信号)()(6k G k f =的波形⼆实验⽬的1.掌握⽤MATLAB 绘制离散时间信号(序列)波形图的基本原理。
2.掌握⽤MATLAB 绘制典型的离散时间信号(序列)。
3.通过对离散信号波形的绘制与观察,加深理解离散信号的基本特性。
三、设计原理离散时间信号(也称为离放序列)是指在时间上的取值是离散的,只在⼀些离放的瞬间才有定义的,⽽在其他时间没有定义,简称离放信号(也称为离散序列) 序列的离散时间间隔是等间隔(均匀)的,取时间间隔为T.以f(kT)表⽰该离散序列,k 为整数(k=0,±1.±2,...)。
为了简便,取T=1.则f(kT)简记为f(k), k 表⽰各函数值在序列中出现的序号。
序列f(k)的数学表达式可以写成闭合形式,也可逐⼀列出f(k)的值。
通常,把对应某序号K0的序列值称为序列的第K0个样点的“样点值”。
四、设计的过程及仿真1clear all; close all; clc;k1=-4;k2=4;k=k1:k2;n1=0;n2=2;f1=[(k-n1)==0];f2=[(k-n2)==0];subplot(1,2,1)stem(k,f1,'fill','-k','linewidth',2);xlabel('k');ylabel('f_1(k)');title('δ(k)')axis([k1,k2,-0.1,1.1]);subplot(1,2,2)stem(k,f2,'filled','-k','linewidth',2);ylabel('f_2(k)');title('δ(k-2)')axis([k1,k2,-0.1,1.1]);程序运⾏后,仿真绘制的结果如图所⽰:2c lear all; close all; clc;k1=-2;k2=8;k=k1:k2;n1=0;n2=2; %阶跃序列开始出现的位置f1=[(k-n1)>=0]; f2=[(k-n2)>=0];subplot(1,2,1)stem(k,f1,'fill','-k','linewidth',2);xlabel('k');ylabel('f_1(k)');title('ε(k)')axis([k1,k2+0.2,-0.1,1.1])subplot(1,2,2)stem(k,f2,'filled','-k','linewidth',2);xlabel('k');ylabel('f_2(k)');title('ε(k-2)')axis([k1,k2+0.2,-0.1,1.1]);程序运⾏后,仿真绘制的结果如图所⽰:3clear all; close all; clc;k1=-2;k2=7;k=k1:k2; %建⽴时间序列n1=0;n2=6; f1=[(k-n1)>=0];f2=[(k-n2)>=0];f=f1-f2;stem(k,f,'fill','-k','linewidth',2);xlabel('k');ylabel('f(k)');title('G_6(k)')axis([k1,k2,-0.1,1.1]);程序运⾏后,仿真绘制的结果如图所⽰:五、设计的结论及收获实现了⽤matlab绘制离散时间信号, 通过对离散信号波形的绘制与观察,加深理解离散信号的基本特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验2 离散系统的时域分析
一、实验目的
1、熟悉并掌握离散系统的差分方程表示法;
2、加深对冲激响应和卷积分析方法的理解。
二、实验原理
在时域中,离散时间系统对输入信号或者延迟信号进行运算处理,生成具有所需特性的输出信号,具体框图如下:
其输入、输出关系可用以下差分方程描述:
输入信号分解为冲激信号,
记系统单位冲激响应,则系统响应为如下的卷积计算式:
当时,h[n]是有限长度的(),称系统为FIR系统;反之,称系统为IIR系统。
三、实验内容
1、用MATLAB 求系统响应
1) 卷积的实现
线性移不变系统可由它的单位脉冲响应来表征。
若已知了单位脉冲响应和系统激励就
可通过卷积运算来求取系统响应,即)(*)()(n h n x n y
程序:
x=input(‘Type in the input sequence=’); %输入x
h=input(‘Type in the impulse response sequence=’); %输入h
y=conv(x,h); % 对x ,h 进行卷积
N=length(y)-1; %求出N 的值
n=0:1:N; %n 从0开始,间隔为1的取值取到N 为止
disp(‘output sequence=’); disp(y); %输出y
stem(n,y); %画出n 为横轴,y 为纵轴的离散图
xlabel(‘Time index n ’); ylable(‘Amplitude ’); % 规定x 轴y 轴的标签
输入为:
x=[-2 0 1 -1 3]
h=[1 2 0 -1]
图形:
2) 单位脉冲响应的求取
线性时不变因果系统可用MA TLAB 的函数filter 来仿真
y=filter(b,a,x);
其中,x 和y 是长度相等的两个矢量。
矢量x 表示激励,矢量a ,b 表示系统函数形式
滤波器的分子和分母系数,得到的响应为矢量y 。
例如计算以下系统的单位脉冲响应
y(n)+0.7y(n-1)-0.45y(y-2)-0.6y(y-3)=0.8x(n)-0.44x(n-1)+0.36x(n-2)+0.02x(n-3)
程序:
N=input(‘Desired impuse response length=’);
b=input(‘Type in the vector b=’);
a=input(‘Type in the vector a=’);
x=[1 zeros(1,N-1)];
y=filter(b,a,x);
k=0:1:N-1;
stem(k,y);
xlabel(’Time index n’); ylable(‘Amplitude’);
输入:
N=41
b=[0.8 -0.44 0.36 0.02]
a=[1 0.7 -0.45 -0.6]
图形:
2、以下程序中分别使用conv和filter函数计算h和x的卷积y和y1,运行程序,并分析y和y1是否有差别,为什么要使用x[n]补零后的x1来产生y1;具体分析当h[n]有i个值,x[n]有j个值,使用filter完成卷积功能,需要如何补零?
程序:
clf;
h = [3 2 1 -2 1 0 -4 0 3]; %impulse response
x = [1 -2 3 -4 3 2 1]; %input sequence
y = conv(h,x);
n = 0:14;
subplot(2,1,1);
stem(n,y);
xlabel('Time index n'); ylabel('Amplitude');
title('Output Obtained by Convolution'); grid;
x1 = [x zeros(1,8)];
y1 = filter(h,1,x1);
subplot(2,1,2);
stem(n,y1);
xlabel('Time index n'); ylabel('Amplitude');
title('Output Generated by Filtering'); grid;
图形:
因为在y=filter(b,a,x)中,利用给定矢量a和b对x中的数据进行滤波,结果放入y
矢量中,y与x长度要相等,所以要使用x[n]补零后的x1来产生y1。
若h[n]有i个值,x[n]有j个值,则x1 = [x zeros(1,i-1)
3、编制程序求解下列两个系统的单位冲激响应,分别用filter 和 impz实现,并绘出其图形。
给出理论计算结果和程序计算结果并讨论。
第一题:
filter实现:
程序:
N=input('Desired impuse response length=');
b=input('Type in the vector b=');
a=input('Type in the vector a=');
x=[1 zeros(1,N-1)];
y=filter(b,a,x);
k=0:1:N-1;
stem(k,y);
xlabel('Time index n');
ylabel('Amplitude');
图形:
——
impz实现:
程序:
b=input('Type in the vector b=');
a=input('Type in the vector a=');
N=25
y=impz(b,a,N);
k=0:1:N-1;
stem(k,y);
xlabel('Time index n'); ylabel('Amplitude');
图形:
第二题:
filter实现:
程序:
N=input('Desired impuse response length=');
b=input('Type in the vector b=');
a=input('Type in the vector a=');
x=[1 zeros(1,N-1)];
y=filter(b,a,x);
k=0:1:N-1;
stem(k,y);
xlabel('Time index n');
ylabel('Amplitude');
输入:
Type in the vector b=[0.25 0.25 0.25 0.25]
Type in the vector a=1
N =25
——图形:
impz实现:
程序:
b=input('Type in the vector b=');
a=input('Type in the vector a=');
N=30
y=impz(b,a,N);
k=0:1:N-1;
stem(k,y);
xlabel('Time index n'); ylabel('Amplitude');
图形:
四、小结
通过此次实验,了解了卷积在Matlab中计算方法,学会了计算单位脉冲响应的方法。
求系统的脉冲响应由两步组成:
①由y(n)=x(n)*h(n) 求出y(n) 在MA TLAB中用conv(x,h)实现
②用filter(b,a,x)求出单位脉冲响应。
