最新《数据结构》算术表达式求值

二课程设计2——算术表达式求值一、需求分析二、程序的主要功能三、程序运行平台四、数据结构五、算法及时间复杂度六、测试用例七、程序源代码三感想体会与总结算术表达式求值一、需求分析一个算术表达式是由操作数(operand)、运算符(operator)和界限符(delimiter)组成的。

假设操作数是正整数，运算符只含加减乘除等四种运算符，界限符有左右括号和表达式起始、结束符“#”，如：#（7+15）*（23-28/4）#。

引入表达式起始、结束符是为了方便。

编程利用“算符优先法”求算术表达式的值。

二、程序的主要功能（1）从键盘读入一个合法的算术表达式，输出正确的结果。

（2）显示输入序列和栈的变化过程。

三、程序运行平台Visual C++ 6.0版本四、数据结构本程序的数据结构为栈。

（1）运算符栈部分：struct SqStack //定义栈{char *base; //栈底指针char *top; //栈顶指针int stacksize; //栈的长度};int InitStack (SqStack &s) //建立一个空栈S{if (!(s.base = (char *)malloc(50 * sizeof(char))))exit(0);s.top=s.base;s.stacksize=50;return OK;}char GetTop(SqStack s,char &e) //运算符取栈顶元素{if (s.top==s.base) //栈为空的时候返回ERROR{printf("运算符栈为空!\n");return ERROR;}elsee=*(s.top-1); //栈不为空的时候用e做返回值，返回S的栈顶元素，并返回OKreturn OK;}int Push(SqStack &s,char e) //运算符入栈{if (s.top-s.base >= s.stacksize){printf("运算符栈满!\n");s.base=(char*)realloc (s.base,(s.stacksize+5)*sizeof(char) ); //栈满的时候，追加5个存储空间if(!s.base) exit (OVERFLOW);s.top=s.base+s.stacksize;s.stacksize+=5;}*(s.top)++=e; //把e入栈return OK;}int Pop(SqStack &s,char &e) //运算符出栈{if (s.top==s.base) //栈为空栈的时候，返回ERROR{printf("运算符栈为空!\n");return ERROR;}else{e=*--s.top; //栈不为空的时候用e做返回值，删除S的栈顶元素，并返回OKreturn OK;}}int StackTraverse(SqStack &s) //运算符栈的遍历{char *t;t=s.base ;if (s.top==s.base){printf("运算符栈为空!\n"); //栈为空栈的时候返回ERRORreturn ERROR;}while(t!=s.top){printf(" %c",*t); //栈不为空的时候依次取出栈内元素t++;}return ERROR;}（2）数字栈部分：struct SqStackn //定义数栈{int *base; //栈底指针int *top; //栈顶指针int stacksize; //栈的长度};int InitStackn (SqStackn &s) //建立一个空栈S{s.base=(int*)malloc(50*sizeof(int));if(!s.base)exit(OVERFLOW); //存储分配失败s.top=s.base;s.stacksize=50;return OK;}int GetTopn(SqStackn s,int &e) //数栈取栈顶元素{if (s.top==s.base){printf("运算数栈为空!\n"); //栈为空的时候返回ERRORreturn ERROR;}elsee=*(s.top-1); //栈不为空的时候，用e作返回值，返回S的栈顶元素，并返回OKreturn OK;}int Pushn(SqStackn &s,int e) //数栈入栈{if (s.top-s.base >=s.stacksize){printf("运算数栈满!\n"); //栈满的时候，追加5个存储空间s.base=(int*)realloc (s.base,(s.stacksize+5)*sizeof(int) );if(!s.base) exit (OVERFLOW);s.top=s.base+s.stacksize; //插入元素e为新的栈顶元素s.stacksize+=5;}*(s.top)++=e; //栈顶指针变化return OK;}int Popn(SqStackn &s,int &e) //数栈出栈{if (s.top==s.base){printf(" 运算符栈为空!\n"); //栈为空栈的视时候，返回ERRORreturn ERROR;}else{e=*--s.top; //栈不空的时候，则删除S的栈顶元素，用e返回其值，并返回OKreturn OK;}}int StackTraversen(SqStackn &s) //数栈遍历{int *t;t=s.base ;if (s.top==s.base){printf(" 运算数栈为空!\n"); //栈为空栈的时候返回ERRORreturn ERROR;}while(t!=s.top){printf(" %d",*t); //栈不为空的时候依次输出t++;}return ERROR;}五、算法及时间复杂度1、算法：建立两个不同类型的空栈，先把一个‘# ’压入运算符栈。

输入一个算术表达式的字符串（以‘#’结束），从第一个字符依次向后读，把读取的数字放入数字栈，运算符放入运算符栈。

判断新读取的运算符和运算符栈顶得运算符号的优先级，以便确定是运算还是把运算符压入运算符栈。

最后两个‘#’遇到一起则运算结束。

数字栈顶的数字就是要求的结果。

2、时间复杂度：O(n)数据压缩存储栈，其操作主要有：建立栈int Push(SeqStack *S, char x)入栈int Pop(SeqStack *S, char x)出栈。

以上各操作运算的平均时间复杂度为O(n)，其主要时间是耗费在输入操作。

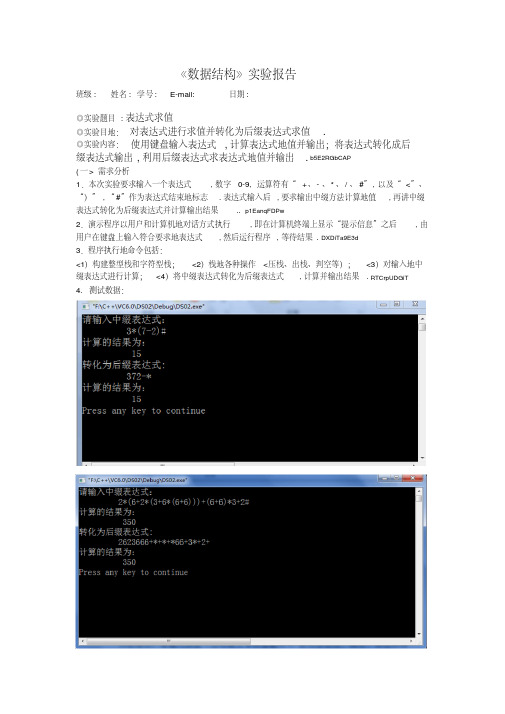
六、测试用例如图所示。

最终结果如图所示：七、源代码/*********************************************************************************************** ***第七题算术表达式求值[问题描述]一个算术表达式是由操作数(operand)、运算符(operator)和界限符(delimiter)组成的。

假设操作数是正整数，运算符只含加减乘除等四种运算符，界限符有左右括号和表达式起始、结束符“#”，如：#（7+15）*（23-28/4）#。

引入表达式起始、结束符是为了方便。

编程利用“算符优先法”求算术表达式的值。

[基本要求]（1）从键盘读入一个合法的算术表达式，输出正确的结果。

（2）显示输入序列和栈的变化过程。

************************************************************************************************ ***/#include <stdio.h>#include <string.h>#include <stdlib.h>#include <math.h>#include <conio.h>#include <ctype.h>#define OK 1#define ERROR 0#define STACK_INIT_SIZE 100//#define STACKINCREMENT 10//========================================================// 以下定义两种栈，分别存放运算符和数字//========================================================//*******************运算符栈部分*************************struct SqStack //定义栈{char *base; //栈底指针char *top; //栈顶指针int stacksize; //栈的长度};int InitStack (SqStack &s) //建立一个空栈S{if (!(s.base = (char *)malloc(50 * sizeof(char))))exit(0);s.top=s.base;s.stacksize=50;return OK;}char GetTop(SqStack s,char &e) //运算符取栈顶元素{if (s.top==s.base) //栈为空的时候返回ERROR{printf("运算符栈为空!\n");return ERROR;}elsee=*(s.top-1); //栈不为空的时候用e做返回值，返回S的栈顶元素，并返回OKreturn OK;}int Push(SqStack &s,char e) //运算符入栈{if (s.top-s.base >= s.stacksize){printf("运算符栈满!\n");s.base=(char*)realloc (s.base,(s.stacksize+5)*sizeof(char) ); //栈满的时候，追加5个存储空间if(!s.base) exit (OVERFLOW);s.top=s.base+s.stacksize;s.stacksize+=5;}*(s.top)++=e; //把e入栈return OK;}int Pop(SqStack &s,char &e) //运算符出栈{if (s.top==s.base) //栈为空栈的时候，返回ERROR{printf("运算符栈为空!\n");return ERROR;}else{e=*--s.top; //栈不为空的时候用e做返回值，删除S的栈顶元素，并返回OKreturn OK;}}int StackTraverse(SqStack &s) //运算符栈的遍历{char *t;t=s.base ;if (s.top==s.base){printf("运算符栈为空!\n"); //栈为空栈的时候返回ERRORreturn ERROR;}while(t!=s.top){printf(" %c",*t); //栈不为空的时候依次取出栈内元素t++;}return ERROR;}//**********************数字栈部分***************************struct SqStackn //定义数栈{int *base; //栈底指针int *top; //栈顶指针int stacksize; //栈的长度};int InitStackn (SqStackn &s) //建立一个空栈S{s.base=(int*)malloc(50*sizeof(int));if(!s.base)exit(OVERFLOW); //存储分配失败s.top=s.base;s.stacksize=50;return OK;}int GetTopn(SqStackn s,int &e) //数栈取栈顶元素{if (s.top==s.base){printf("运算数栈为空!\n"); //栈为空的时候返回ERRORreturn ERROR;}elsee=*(s.top-1); //栈不为空的时候，用e作返回值，返回S的栈顶元素，并返回OKreturn OK;}int Pushn(SqStackn &s,int e) //数栈入栈{if (s.top-s.base >=s.stacksize){printf("运算数栈满!\n"); //栈满的时候，追加5个存储空间s.base=(int*)realloc (s.base,(s.stacksize+5)*sizeof(int) );if(!s.base) exit (OVERFLOW);s.top=s.base+s.stacksize; //插入元素e为新的栈顶元素s.stacksize+=5;}*(s.top)++=e; //栈顶指针变化return OK;}int Popn(SqStackn &s,int &e) //数栈出栈{if (s.top==s.base){printf(" 运算符栈为空!\n"); //栈为空栈的视时候，返回ERRORreturn ERROR;}else{e=*--s.top; //栈不空的时候，则删除S的栈顶元素，用e返回其值，并返回OKreturn OK;}}int StackTraversen(SqStackn &s) //数栈遍历{int *t;t=s.base ;if (s.top==s.base){printf(" 运算数栈为空!\n"); //栈为空栈的时候返回ERRORreturn ERROR;}while(t!=s.top){printf(" %d",*t); //栈不为空的时候依次输出t++;}return ERROR;}//======================================================== // 以下定义函数//======================================================== int Isoperator(char ch) //判断是否为运算符，分别将运算符和数字进入不同的栈{switch (ch){case '+':case '-':case '*':case '/':case '(':case ')':case '#':return 1;default:return 0;}}int Operate(int a, char op, int b) //运算操作{int result;switch(op){case '+':result=a+b;break;case '-':result=a-b;break;case '*':result=a*b;break;case '/':result=a/b;break;}return result;}char Precede(char ch1, char ch2) //运算符优先级的比较{char p;switch(ch1){case '+':case '-':if (ch2=='+'||ch2=='-'||ch2==')'||ch2=='#')p = '>'; //ch1运算符的优先级小于ch2运算符elsep = '<';break;case '*':case '/':if (ch2 == '(')p = '<';elsep = '>';break;case '(':if (ch2 == ')')p = '=';else if (ch2 == '#'){printf(" 表达式错误!运算符不匹配!\n") ;exit(0);}elsep = '<';break ;case ')':if (ch2 == '('){printf(" 表达式错误!运算符不匹配!\n") ;exit(0);}elsep = '>';break ;case '#':if (ch2 == ')'){printf(" 表达式错误!运算符不匹配!\n") ;exit(0);}else if (ch2 == '#')p = '=';elsep='<';break;}return p;}//======================================================== // 以下是求值过程//======================================================== int EvaluateExpression() //参考书p53算法3.4{int a, b, temp, answer;char ch,op,e;char *str;int j = 0;SqStackn OPND; //OPND为运算数字栈SqStack OPTR; //OPTR为运算符栈InitStack(OPTR);Push(OPTR,'#'); //,所以此栈底是'#'，因为运算符栈以'#'作为结束标志InitStackn(OPND);// printf("\n\n按任意键开始求解:\n\n");// ch=getch();printf("\n请输入表达式并以'#'结束:\n");str =(char*)malloc(50*sizeof(char));gets(str);ch=str[j]; //ch是字符型的，而e是整型的整数j++;GetTop(OPTR,e); //e为栈顶元素返回值while (ch!='#' || e!='#'){if (!Isoperator(ch)) //遇到数字,转换成十进制并计算{temp=ch-'0'; //将字符转换为十进制数ch=str[j];j++;while(!Isoperator(ch)){temp=temp*10 + ch-'0'; //将逐个读入运算数的各位转化为十进制数ch=str[j];j++;}Pushn(OPND,temp);}else if (Isoperator(ch)) //判断是否是运算符,不是运算符则进栈switch (Precede(e,ch)){case '<' : Push(OPTR,ch); // 栈顶元素优先权低ch = str[j++];printf("\n\n 运算符栈为：\n"); //输出栈，显示栈的变化StackTraverse(OPTR);printf("\n 运算数栈为：\n");StackTraversen(OPND);break;case '=' : Pop(OPTR,op); // 脱括号并接收下一字符ch = str[j++] ;printf("\n\n 运算符栈为：\n");StackTraverse(OPTR);printf("\n 数栈为：\n");StackTraversen(OPND);break;case '>' : Pop(OPTR,op); //弹出最上面两个，并运算，把结果进栈Popn(OPND,b);Popn(OPND,a);Pushn(OPND,Operate(a,op,b));printf("\n\n 运算符栈为：\n");StackTraverse(OPTR);printf("\n 数栈为：\n");StackTraversen(OPND);}else{printf("您的输入有问题，请检查重新输入!");exit(0);}GetTop(OPTR,e); //取出运算符栈最上面元素是否是'#' } //whileGetTopn(OPND,answer); //已输出。