数据结构实验二——算术表达式求值实验报告
数据结构表达式求值实验报告

竭诚为您提供优质文档/双击可除数据结构表达式求值实验报告篇一:数据结构实验二——算术表达式求值实验报告《数据结构与数据库》实验报告实验题目算术表达式求值学院:化学与材料科学学院专业班级:09级材料科学与工程系pb0920603姓学邮名:李维谷号:pb09206285箱:指导教师:贾伯琪实验时间:20XX年10月10日一、需要分析问题描述:表达式计算是实现程序设计语言的基本问题之一,它的实现是栈的应用的一个典型例子。
设计一个程序,演示通过将数学表达式字符串转化为后缀表达式,并通过后缀表达式结合栈的应用实现对算术表达式进行四则混合运算。
问题分析:在计算机中,算术表达式由常量、变量、运算符和括号组成。
由于不同的运算符具有不同的优先级,又要考虑括号,因此,算术表达式的求值不可能严格地从左到右进行。
因而在程序设计时,借助栈实现。
设置运算符栈(字符型)和运算数栈(浮点型)辅助分析算符优先关系。
在读入表达式的字符序列的同时完成运算符和运算数的识别处理,然后进行运算数的数值转换在进行四则运算。
在运算之后输出正确运算结果,输入表达式后演示在求值中运算数栈内的栈顶数据变化过程,最后得到运算结果。
算法规定:输入形式:一个(:数据结构表达式求值实验报告)算术表达式,由常量、变量、运算符和括号组成(以字符串形式输入)。
为使实验更完善,允许操作数为实数,操作符为(、)、.(表示小数点)、+、-、*、/、^(表示乘方),用#表示结束。
输出形式:演示表达式运算的中间结果和整个表达式的最终结果,以浮点型输出。
程序功能:对实数内的加减乘除乘方运算能正确的运算出结果,并能正确对错误输入和无定义的运算报错,能连续测试多组数据。
测试数据:正确输入:12*(3.6/3+4^2-1)#输出结果:194.4无定义运算:12*(3.6/(2^2-4)+1)#输出结果:表达式出错,除数为0,无意义错误输入:12+s#输出结果:eRRoR!二、概要设计拟采用两种类型的展分别对操作数和操作符进行操作。
数据结构实验报告--表达式求值
void Initstack1(stack1 *s>
{
(*s>->base = (int *>malloc(SIZE * (sizeof(int>>>
。
(*s>->top = (*s>->base
。
(*s>->stacksize = INCREMENT 。
}
int Ifempty2(stack2 *s>
<6)中缀转后缀并计算模块:
( 三 > 详细设计
1.元素类型 , 结点类型和指针类型:
typedef struct{
int stacksize 。 int *base 。
int *top 。
}Sqstack1,*stack1 。
typedef struct{
int stacksize 。
char *base 。
{
if(((a=='*'>||(a=='/'>>&&((b=='+'>||(b=='-'>||(b=='#'>>>
5PCzVD7HxA
return '>'
。
else
return '<'
。
}
<4)运算符操作模块;
int Operate(int a,char b,int c>
{
int t 。
if(b == '+'> t = a + c
{
算术表达式求值实验报告

算术表达式求值实验报告前言算术表达式求值是计算机科学中比较基础的内容,同时也是很实用的技能,因为有时候我们需要用程序来计算一些复杂的数学运算。
在本次实验中,我们将对算术表达式的求值进行深入研究,并实际编写程序来实现这一功能。
实验原理算术表达式通常由数字、运算符和括号组成,我们需要将其转换为计算机能够直接执行的形式。
常见的算术表达式求值方法有两种:1.中缀表达式求值中缀表达式就是我们平时所熟悉的数学表达式,如2+3*4-5/2。
中缀表达式求值需要遵循一定的运算符优先级和括号的影响,可以通过栈来实现。
首先,我们需要将中缀表达式转换为后缀表达式,即将运算符放在数字后面。
具体的转换方法可以使用栈来实现。
遍历中缀表达式,遇到数字就直接输出,遇到运算符就将其与栈顶运算符进行比较,如果优先级高于栈顶运算符,则将其入栈,否则将栈顶运算符弹出并输出,直到遇到优先级小于等于栈顶运算符或者栈顶为空时,将运算符入栈。
最后将栈中的运算符依次弹出并输出即可。
转换为后缀表达式之后,我们可以通过再次遍历后缀表达式来求值。
遇到数字将其入栈,遇到运算符则弹出栈顶两个数字进行运算,并将结果入栈。
遍历完毕后,栈中剩下的数字就是最终结果。
2.前缀表达式求值前缀表达式就是将运算符放在数字前面的表达式,如:- + * 3 4 5 6。
前缀表达式求值与后缀表达式求值类似,不同之处在于需要从右至左遍历表达式,并将运算符与栈顶数字进行操作。
实验步骤在本次实验中,我们将通过 Python 语言来实现算术表达式求值功能。
具体步骤如下:1. 输入待求值的算术表达式。
2. 对算术表达式进行转换,得到后缀表达式或前缀表达式。
3. 遍历后缀表达式或前缀表达式,求出最终结果。
4. 输出结果。
实验结果我们在 Python 中编写了求解算术表达式的程序,以下是一些样例输入和输出:1. 输入:2+3*4 输出:142. 输入:(2+3)*4 输出:203. 输入:-+*3456 输出:-9通过多组测试,我们可以发现程序能够正确地求解各种算术表达式,包括包含括号和负数的表达式。
数据结构实验二——算术表达式求值实验报告

《数据结构与数据库》实验报告实验题目算术表达式求值学院:化学与材料科学学院专业班级:09级材料科学与工程系PB0920603姓名:李维谷学ﻩﻩ号:PB09206285邮ﻩ箱:指导教师:贾伯琪实验时间:2010年10月10日一、需要分析问题描述:表达式计算就是实现程序设计语言得基本问题之一,它得实现就是栈得应用得一个典型例子.设计一个程序,演示通过将数学表达式字符串转化为后缀表达式,并通过后缀表达式结合栈得应用实现对算术表达式进行四则混合运算。
问题分析:在计算机中,算术表达式由常量、变量、运算符与括号组成.由于不同得运算符具有不同得优先级,又要考虑括号,因此,算术表达式得求值不可能严格地从左到右进行。
因而在程序设计时,借助栈实现.设置运算符栈(字符型)与运算数栈(浮点型)辅助分析算符优先关系。
在读入表达式得字符序列得同时完成运算符与运算数得识别处理,然后进行运算数得数值转换在进行四则运算.在运算之后输出正确运算结果,输入表达式后演示在求值中运算数栈内得栈顶数据变化过程,最后得到运算结果。
算法规定:输入形式:一个算术表达式,由常量、变量、运算符与括号组成(以字符串形式输入)。
为使实验更完善,允许操作数为实数,操作符为(、)、、(表示小数点)、+、-、*、/、^(表示乘方),用#表示结束。
输出形式:演示表达式运算得中间结果与整个表达式得最终结果,以浮点型输出。
程序功能:对实数内得加减乘除乘方运算能正确得运算出结果,并能正确对错误输入与无定义得运算报错,能连续测试多组数据。
测试数据:正确输入:12*(3、6/3+4^2—1)#输出结果:194、4无定义运算:12*(3、6/(2^2—4)+1)#输出结果:表达式出错,除数为0,无意义错误输入:12+s#输出结果:ERROR!二、概要设计拟采用两种类型得展分别对操作数与操作符进行操作.程序中将涉及下列两个抽象数据类型:1、设定“操作数”得栈得抽象数据类型定义:ADT SqStack_f{ﻩ数据对象:D={ﻩ数据关系:R1={〈>|,,i=2,…,n}约定端为栈顶,端为栈底。
数据结构表达式求值实验报告

实验报告课程名:数据结构(C语言版)实验名:表达式求值姓名:班级:学号:时间:2014.10.25一实验目的与要求1. 了解栈的应用2. 利用栈进行算术表达式求值二实验内容1.以字符串的形式给出一个算术表达式, 计算出该算术表达式的值。
2.表达式中可能出现”+”, ”−”, ”∗”, ”/”, ”(”, ”)”。
三实验结果与分析分析:r:读入字符t:栈顶字符r( ) # 低优先运算符高优先运算符( 入栈出栈错误入栈入栈) 错误错误错误错误错误t # 入栈错误结束入栈入栈低优先运算符入栈出栈+运算出栈+计算出栈+计算入栈高优先运算符入栈出栈+运算出栈+计算出栈+计算出栈+计算1, 入栈2, 错误3, 出栈4, 出栈+计算5, 结束( ) # 低优先运算符高优先运算符( 1 3 2 1 1) 2 2 2 2 2# 1 2 5 1 1低优先运算符 1 4 4 4 1高优先运算符 1 4 4 4 4此实验可用两个栈和数组来实现,一个操作栈,一个数字栈,两个栈的字符进行优先权比较可得到5种结果。
首先置操作栈为空栈,表达式起始符“#”作为数字栈的栈底元素,依次读入表达式的每个字符,若是操作字符进操作栈,若是数字进数字栈,操作栈和数字栈的栈顶元素比较优先权后进行相应操作,直至结束,最后输出值即可。
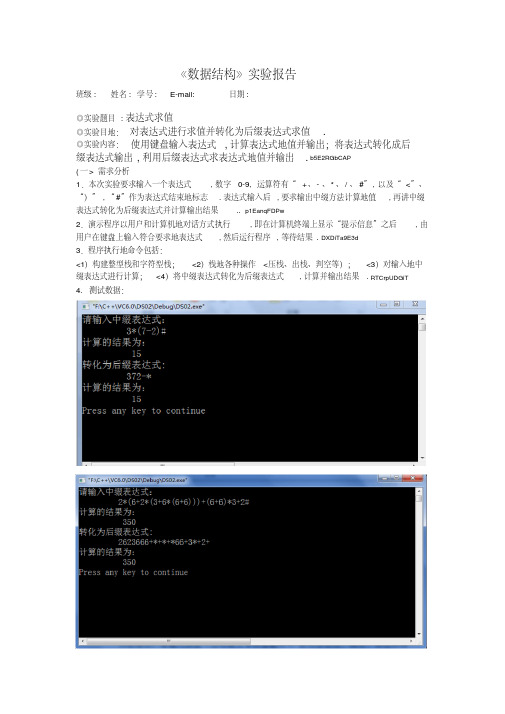
实验程序:#include<stdio.h>#include<stdlib.h>#include<string.h>int change(char c)//字符转换{int j=-1;switch(c){case '(':j=0;break;case ')':j=1;break;case '#':j=2;break;case '+':j=3;break;case '-':j=3;break;case '*':j=4;break;case '/':j=4;break;}return(j);}int compu(int x,int y,char c)//数字计算转换{int j=-1;switch(c){case '+':j=x+y;break;case '-':j=x-y;break;case '*':j=x*y;break;case '/':j=x/y;break;}return(j);}void get(char a[],int num_op,int method[5][5]){int a_length=strlen(a)+1;//表达式的长度int p=0,num_p=0,op_p=0;int *num_s=(int *)malloc((a_length)*sizeof(int));// char *op_s=(char *)malloc((a_length)*sizeof(int));// op_s[op_p]='#';op_p++;//进字符栈int k=-1;//输出结果判断int ox,oy;while(1){char c=a[p];//将表达式中的字符一个一个赋值给cif(c>='0'&&c<='9')//判断是不是数字{num_s[num_p]=c-48;//将Ascll码转换成对应数字num_p++;//进数字栈p++;//代表表达式的位置开始为0指向第一位}else{int t=method[change(op_s[op_p-1])][change(c)];//将5种操作的一种传给tswitch(t){case 1:op_s[op_p]=c;op_p++;p++;break;case 2:k=0;break;case 3:op_p--;p++;break;case 4:ox=num_s[num_p-2];oy=num_s[num_p-1];num_p=num_p-2;num_s[num_p]=compu(ox,oy,op_s[op_p-1]);//将计算的值存入num_s[]num_p++;//入数字栈op_p--;break;case 5:k=1;break;}}if(k>=0)//跳出循环{break;}}switch(k)//0错误,1输出结果{case 0:printf("表达式错误!");break;case 1:printf("%s=%d\n",a,num_s[num_p-1]);break;}}int main(int argc,char *argv[]){ char a[20];puts("请输入个位数的表达式:");gets(a);int num_op=5;//表示操作的种数int method[5][5]={{1,3,2,1,1},{2,2,2,2,2},{1,2,5,1,1},{1,4,4,4,1},{1,4,4,4,4}};//1表示入栈,2表示错误,//3表示出栈,4表示出栈+计算,//5表示结束get(a,num_op,method);return 0;}图1.表达式求值运行结果。
数据结构表达式求值(中缀)实验报告

数据结构表达式求值(中缀)实验报告题目名称表达式求值学号姓名指导教师日期一1. 问题描述:在计算机中,算术表达式由常量、变量、运算符和括号组成。
由于不同的运算符具有不同的优先级,又要考虑括号,因此,算术表达式的求值不可能严格地从左到右进行,在程序设计时,借助栈实现。
2. 表达式求值这个程序,主要利用栈和数组,把运算的先后步骤进行分析并实现简单的运算,以字符列的形式从终端输入语法的正确的、不含变量的整数表达式。
利用已知的算符优先关系,实现对算术四则运算的求值,在求值中运用栈、运算栈、输入字符和主要操作的变化过程。
该程序相当于一个简单的计算机计算程序,只进行简单的加减乘除和带括号的四则运算。
1、基本思想(中缀表达式求值)要把一个表达式翻译成正确求值的一个机器指令序列,或者直接对表达式求值,首先要能够正确解释表达式,要了解算术四则运算的规则即:(1)先乘除后加减;(2)从左到右计算;(3)先括号内,后括号外。
下表定义的运算符之间的关系:b + - * / () # a+ > > < < < > > _ > > < < < > > * > > > > < > > / > > > > < > > ( < < < < < = ) > > > > > > # < < < < < =为了实现运算符有限算法,在程序中使用了两个工作栈。
分别是:运算符栈OPTR,操作数栈OPND.基本思想:(1)首先置操作数栈为空栈,表达式起始符“#”为运算符栈的栈底元素;(2)依次读入表达式中每个字符,若是操作数则进OPND栈,若是运算符则和OPTR栈得栈顶运算符比较优先级后作相应操作。
数据结构实验报告-算术表达式求值

- - 1.前言12.概要设计12.1 数据构造设计12.2 算法设计12.3 ADT描述22.4 功能模块分析23.详细设计33.1 数据存储构造设计33.2主要算法流程图〔或算法伪代码〕44.软件测试75.心得体会8参考文献8附录9- -优质-..1.前言在计算机中,算术表达式由常量、变量、运算符和括号组成。
由于不同的运算符具有不同的优先级,又要考虑括号,因此,算术表达式的求值不可能严格地从左到右进展。
因而在程序设计时,借助栈实现。
算法输入:一个算术表达式,由常量、变量、运算符和括号组成〔以字符串形式输入〕。
为简化,规定操作数只能为正整数,操作符为+、-*、/,用#表示完毕。
算法输出:表达式运算结果。
算法要点:设置运算符栈和运算数栈辅助分析算符优先关系。
在读入表达式的字符序列的同时,完成运算符和运算数的识别处理,以及相应运算。
2.概要设计2.1 数据构造设计任何一个表达式都是由操作符,运算符和界限符组成的。
我们分别用顺序栈来存放表达式的操作数和运算符。
栈是限定于紧仅在表尾进展插入或删除操作的线性表。
顺序栈的存储构造是利用一组连续的存储单元依次存放自栈底到栈顶的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置,base为栈底指针,在顺序栈中,它始终指向栈底,即top=base可作为栈空的标记,每当插入新的栈顶元素时,指针top增1,删除栈顶元素时,指针top减1。
2.2 算法设计为了实现算符优先算法。
可以使用两个工作栈。
一个称为OPTR,用以存放运算符,另一个称做OPND,用以存放操作数或运算结果。
1.首先置操作数栈为空栈,表达式起始符〞#〞为运算符栈的栈底元素;2.依次读入表达式,假设是操作符即进OPND栈,假设是运算符那么和OPTR栈的栈顶运算符比拟优先权后作相应的操作,直至整个表达式求值完毕〔即OPTR栈的栈顶元素和当前读入的字符均为〞. .word.zl.数据构造课程设计第 2 页#〞〕。
数据结构表达式求值完整篇(含实验报告)

&s,SElemType_OPND&e); //出栈
/*
#i nclude "common .h"
#include "Sqstack.h"
#in clude "other.h"
//
void OPTR_I ni tStack(Sqstack_OPTR &s)
3前面的都听简单的,就是 小数编写这块想了很久,
定义了low做判定符号的标志。如果在运算符后输入负号则low=-1(将p入栈时入栈
的是p*low),继续输入ch
总结:
我觉得写的好的地方在于定义了flag,low分别作为小数入栈和负号与减号区别的条
件。第一次写这么长的代码,还有就是将输入的字符再转到小数这段代码可以留着很有 用。开始考虑的大整数想麻烦了,直接用double难度降低了很多
//取操作数的栈顶元素
voidOPTR_Push(Sqstack_OPTR
&s,SElemType_OPTR e);//入栈
voidOPND_Push(Sqstack_OPND
&s,SElemType_OPND e); //入栈
voidOPTR_Pop(Sqstack_OPTR
&s,SEIemType_OPTR&e); //出栈
//栈基本操作的函数声明
void OPTR_lnitStack(Sqstack_OPTR &s);
//运算符栈初始化
void OPBiblioteka D_InitStack(Sqstack_OPND &s);
//操作数栈初始化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数据结构与数据库》实验报告实验题目算术表达式求值学院:化学与材料科学学院专业班级:09级材料科学与工程系PB0920603姓名:李维谷学号:PB09206285邮箱:**************指导教师:贾伯琪实验时间:2010年10月10日一、需要分析问题描述:表达式计算是实现程序设计语言的基本问题之一,它的实现是栈的应用的一个典型例子。
设计一个程序,演示通过将数学表达式字符串转化为后缀表达式,并通过后缀表达式结合栈的应用实现对算术表达式进行四则混合运算。
问题分析:在计算机中,算术表达式由常量、变量、运算符和括号组成。
由于不同的运算符具有不同的优先级,又要考虑括号,因此,算术表达式的求值不可能严格地从左到右进行。
因而在程序设计时,借助栈实现。
设置运算符栈(字符型)和运算数栈(浮点型)辅助分析算符优先关系。
在读入表达式的字符序列的同时完成运算符和运算数的识别处理,然后进行运算数的数值转换在进行四则运算。
在运算之后输出正确运算结果,输入表达式后演示在求值中运算数栈内的栈顶数据变化过程,最后得到运算结果。
算法规定:输入形式:一个算术表达式,由常量、变量、运算符和括号组成(以字符串形式输入)。
为使实验更完善,允许操作数为实数,操作符为(、)、.(表示小数点)、+、-、*、/、^(表示乘方),用#表示结束。
输出形式:演示表达式运算的中间结果和整个表达式的最终结果,以浮点型输出。
程序功能:对实数内的加减乘除乘方运算能正确的运算出结果,并能正确对错误输入和无定义的运算报错,能连续测试多组数据。
测试数据:正确输入:12*(3.6/3+4^2-1)#输出结果:194.4无定义运算:12*(3.6/(2^2-4)+1)# 输出结果:表达式出错,除数为0,无意义 错误输入:12+s# 输出结果:ERROR ! 二、 概要设计拟采用两种类型的展分别对操作数和操作符进行操作。
程序中将涉及下列两个抽象数据类型:1、设定“操作数”的栈的抽象数据类型定义: ADT SqStack_f{数据对象:D={i a },+∈∈N i R a i数据关系:R1={<1,-i i a a >|1-i a ,D a i ∈,i=2,…,n}约定n a 端为栈顶,i a 端为栈底。
基本操作:InitStack_f(&S)操作结果:构造一个空栈S 。
GetTop_f(&S,&e) 初始条件:栈S 已存在。
操作结果:用e 返回S 的栈顶元素。
Push_f(&S ,ch) 初始条件:栈S 已存在。
操作结果:插入元素ch 为新的栈顶元素。
Pop_f(&S,&e)初始条件:栈S 已存在。
操作结果:删除S 的栈顶元素,并以e 返回其值。
}ADT SqStack_f2、设定“操作符”的栈的抽象数据类型定义: ADT SqStack_c{数据对象:D={i a {}},'^'/'''*'''''+∈-+∈N i a i 数据关系:R1={<1,-i i a a >|1-i a ,D a i ∈,i=2,…,n}约定n a 端为栈顶,i a 端为栈底。
基本操作:InitStack_c(&S)操作结果:构造一个空栈S 。
GetTop_c(&S,&e) 初始条件:栈S 已存在。
操作结果:用e 返回S 的栈顶元素。
Push_c(&S ,ch) 初始条件:栈S 已存在。
操作结果:插入元素ch 为新的栈顶元素。
Pop_c(&S,&e) 初始条件:栈S 已存在。
操作结果:删除S 的栈顶元素,并以e 返回其值。
}ADT SqStack_c3、本程序包含六个模块1)主程序模块void main( ){初始化;while(命令==“继续”){接受数据;处理数据;接受命令;}}2)栈模块——实现栈抽象数据类型3)判断运算符优先级模块——判断运算符的优先级别4)后缀表达式转换模块——将中缀表达式转换为后缀表达式,方便操作5)无括号表示式求值运算模块——根据后缀表达式求值,并输出中间和最终结果6)运算结果输出模块——以正确形式输出表达式的值三、详细设计1、主程序中需要的全程量#define TTACK_INIT_SIZE 100 //初始分配最大空间量#define STACKINCREMENT 10 //(默认)增补空间量2、结点类型、指针类型typedef struct{float *base; //存储实型数据元素的一位数组float *top; //栈顶指针int stacksize; //栈数组容量}SqStack_f; //有序存储实型的顺序表类型typedef struct{char *base; //存储字符数据元素的一位数组char *top; //栈顶指针int stacksize; //栈数组容量}SqStack_c; //有序存储字符型的顺序表类型void InitStack_f(SqStack_f *s)void InitStack_f(SqStack_f *s)//构造一个存储实型(字符型)的空栈,预设空间为100,分配失败就退出void GetTop_f(SqStack_f *s,float *e)void GetTop_c(SqStack_c *s,char *e)//若栈s不空,则以e带值返栈顶元素,否则显示错误“ERROR”,并退出程序void Push_f(SqStack_f *s,float e)void Push_c(SqStack_c *s,char e)//在s的栈顶插入新的栈顶元素e,若栈的当前空间已满,则追加存储空间void Pop_f(SqStack_f *s,float *e)//若栈s不空,则删除栈s的栈顶元素,用e带值返回,否则退出程序其中部分操作的伪码算法(由于比较类似,以浮点型的栈为例)void InitStack_f(SqStack_f *s){//构造一个存储实型的空栈,预设空间为100,分配失败就退出s->base=(float *)malloc(TTACK_INIT_SIZE*sizeof(float));if(!s->base)exit(1);s->top=s->base;s->stacksize=TTACK_INIT_SIZE;}void GetTop_f(SqStack_f *s,float *e){//若栈s不空,则以e带值返栈顶元素,否则显示错误“ERROR”,并退出程序if(s->top==s->base){printf("ERROR!\n");exit(1);}*e=*(s->top-1);}{//在s的栈顶插入新的栈顶元素e,若栈的当前空间已满,则追加存储空间if(s->top-s->base>=s->stacksize){s->base=(float*)realloc(s->base,(s->stacksize+STACKINCREMENT)*sizeof(float));if(!s->base){printf("OVERFLOW!\n");exit(1);}s->top=s->base+s->stacksize;s->stacksize+=STACKINCREMENT;}*s->top++=e;}void Pop_f(SqStack_f *s,float *e){//若栈s不空,则删除栈s的栈顶元素,用e带值返回,否则退出程序if(s->top==s->base)exit(1);*e=*--s->top;}3、判断运算符优先级的算法:算符间的优先关系如下:伪码算法:int precede(char Top_char,char s1_char){//栈顶的运算符赋给Top_char,新读入的运算符赋给s1_char。
判断它们的优先级//若栈顶运算符优先级高,则返回1,否则返回0int i,pre[2];char op[2];op[0]=Top_char; //栈顶的运算符赋给op[0]op[1]=s1_char; //新读入的运算符赋给op[1]for(i=0;i<2;i++)switch(op[i]){case'(':case')':pre[i]=0;break; //将括号的优先级设为0case'+':case'-':pre[i]=1;break; //将+ - 运算符的优先级设为1case'*':case'/':pre[i]=2;break; //将* / 运算符的优先级设为2case'^':pre[i]=3;break; //将^ 运算符的优先级设为3}if(pre[0]>=pre[1]) //栈顶元素优先级高返回1return 1;elsereturn 0; //否则返回0}4、中缀表达式转换为后缀表达式的算法:算法过程描述:1)首先将左括号“(”压进栈,作为栈底元素;2)从左而右对算数表达式进行扫描,每次读入一个字符s1[i];3)若遇到数字或小数点,则立即写入s2[i],若遇算数运算符,将“”(空格)写入s2[i];4)遇到左括号“(”则压栈;5)若遇算术运算符,如果它们的优先级比栈顶元素高,则直接进栈,否则弹出栈顶元素输出到s2[i],直到新栈顶元素的优先级比它低,然后将它压栈;6)若遇到右括号“)”,则将栈顶元素输出到s2[i],直到栈顶元素为“(”,然后相互抵消;7)当扫描到“#”符号,表明表达式串已全部输入,将栈中的运算符全部输出到s2[i],并删除栈顶元素。
伪码算法:void Translate(char *s1){ //中缀表达式转换为后缀表达式char s2[80];SqStack_c Optr;int i=0,j=0;cha r t;InitStack_c(&Optr);//初始化一个存储字符型的空栈,便于存储运算符Push_c(&Optr,'(');// 首先将左括号“(”压进栈,作为栈底元素while(s1[i]!='#') //当扫描到的不是“#”,即表达式串没结束时{if(s1[i]>='0' && s1[i]<='9' || s1[i]=='.') //若果是数字或小数点则将其输出给s2[i]{s2[j++]=s1[i];if((s1[i+1]<'0' || s1[i+1]>'9') && s1[i+1]!='.')s2[j++]=' ';}elseswitch(s1[i]) //扫描到的是运算符{case'(':Push_c(&Optr,s1[i]);break;// 遇到左括号“(”则压栈case')':Pop_c(&Optr,&t); //若遇到右括号“)”,则将栈顶元素输出到s2[i]while(t!='(') //直到栈顶元素为“(”,然后相互抵消{s2[j++]=t;Pop_c(&Optr,&t);}break;default:while(GetTop_c(&Optr,&t),precede(t,s1[i])){//遇到算数运算符则比较优先级Pop_c(&Optr,&t);//栈顶元素优先级高,则弹出到s2[i]s2[j++]=t;}Push_c(&Optr,s1[i]);//栈顶元素优先级低,直接压栈}i++;}Pop_c(&Optr,&t);while(t!='(') //表达式串已结束,栈中的运算符全部输出到s2[i],并删除栈顶元素{s2[j++]=t;Pop_c(&Optr,&t);}for(i=0;i<j;i++) //将s2复制给s1s1[i]=s2[i];s1[i]= '#';s1[i+1]='\0';//为了方便打印后缀表达式,在字符串结尾加‘\0’}5、表示式求值运算的算法:算法描述:1)读入无括号的后缀表达式;2)若为数值和小数点则将其联合转换为浮点型后进栈(存放操作数);3)若为运算符,让栈顶元素和次顶元素与次运算符进行相应的运算,运算结果打印并进栈;4)重复2)3)步骤,直到输入为“#”,则此时栈中的结果便是所追求的表达式的值。
