各地区建筑业总产值对建筑业企业利润总额的影响
2018年建筑业发展统计分析

2018年全国建筑业基本情况2018年,在以习近平同志为核心的党中央坚强领导下,建筑业深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大和十九届二中、三中全会精神,改革创新,开拓进取,加快推动建筑业改革发展,建筑业发展质量和效益不断提升。
全国建筑业企业(指具有资质等级的总承包和专业承包建筑业企业,不含劳务分包建筑业企业,下同)完成建筑业总产值235085.53亿元,同比增长9.88%;完成竣工产值120786.22亿元,同比增长3.42%;签订合同总额494409.05亿元,同比增长12.49%,其中新签合同额272854.07亿元,同比增长7.14%;房屋施工面积140.89亿平方米,同比增长6.96%;完成房屋竣工面积41.35亿平方米,同比下降1.33%;实现利润8104亿元,同比增长8.17%。
截至2018年底,全国有施工活动的建筑业企业95400个,同比增长8.34%;从业人数5563.30万人,同比增长0.48%;按建筑业总产值计算的劳动生产率为373187元/人,同比增长7.40%。
(一)建筑业增加值增速仍低于国内生产总值增速,但支柱产业地位依然稳固经初步核算,2018年全年国内生产总值900309亿元,比上年增长6.60%。
全年全社会建筑业实现增加值61808亿元,图1 2009-2018年国内生产总值、建筑业增加值及增速图2 2009-2018年建筑业增加值占国内生产总值比重比上年增长4.50%,增速低于国内生产总值增速2.10个百分点(图1)。
自2009年以来,建筑业增加值占国内生产总值的比例始终保持在6.5%以上。
2018年达到了6.87%的较高点,在2015年、2016年连续两年下降后连续两年出现回升(图2),建筑业国民经济支柱产业的地位稳固。
增长0.48%。
建筑业从业人数占全社会就业人员总数的7.17%,比上年提高0.04个百分点,占比再创新高(图6)。
建筑业在吸纳农村转移人口就业、推进新型城镇化建设和维护社会稳定等方面继续发挥显著作用。
建筑行业经营分析情况

建筑市场稳定行业贡献显著——2015年建筑业生产经营情况分析2015年,面对严峻复杂的国内国际经济形势,我市建设领域抢抓机遇,深挖潜力,全市建筑业运行质量稳步提升,外埠市场竞争力不断提高。
一、建筑业企业总体情况及运行特点(一)入库新增企业略有增加2015年,我市建筑业企业单位数(指纳入一套表统计,具有建筑业资质的施工总承包和专业承包企业、劳务分包企业)达到1021家,比上年净增6家,其中,总承包和专业承包企业867家,净增9家;劳务分包企业154家,减少3家。
(二)建筑规模保持稳步增长1.建筑合同体量继续扩大。
2015年,全市建筑业企业(一套表中的总承包和专业承包建筑业企业,下同)签订合同额为5559.30亿元,同比增长0.4%,其中,当年新签订合同额3079.25亿元,下降3.3%,占全部合同额的55.4%,低于上年比重近6个点。
2.全省首位度稳中有升。
截止到年末,全市建筑业企业完成建筑业总产值3006.60亿元,同比增长4.5%。
占全省的52.8%,比上年提升0.3个百分点,持续保持上升的态势。
从结构上看,建筑工程产值累计完成2603.90亿元,同比增长3.5%,占总产值的86.6%;安装工程产值累计完成251.55亿元,同比增长6.4%,占总产值的8.4%。
从经济类型看,国有及国有控股建筑业企业依然是我市建筑业一支举足轻重的队伍,占全市建筑业企业数五分之一的国有及国有控股建筑业企业完成产值1451.78亿元,占全市总产值的48.3%,同比增长1.4%。
从区域看,瑶海区以建筑业总产值753.57亿元位居第一,包河区、蜀山区分别以657.63亿元和334.61亿元位居二、三位,连续2年位次没有变动;13个县区(市)与上年相比,10涨3跌,其中庐江县以15.4%的增幅居首,高新区和瑶海区分别以15.3%和10.2%位居二、三位,而降幅前3位的分别为巢湖市、长丰县和经开区,分别下降20.1%、5%和1.1%。
第五章-异方差性(作业任务)
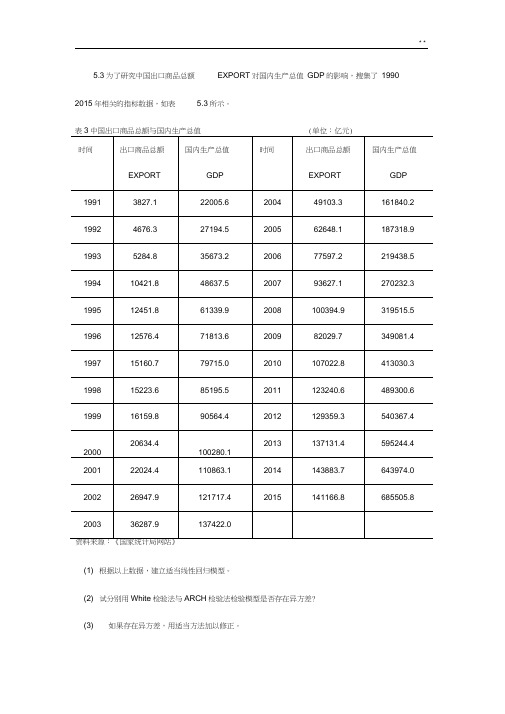
5.3为了研究中国出口商品总额EXPORT对国内生产总值GDP的影响,搜集了1990 2015年相关的指标数据,如表 5.3所示。
(1) 根据以上数据,建立适当线性回归模型。
(2) 试分别用White检验法与ARCH检验法检验模型是否存在异方差?(3) 如果存在异方差,用适当方法加以修正。
解:(1)Dependent Variable: YMethod: Least SquaresDate: 04/18/20 Time: 15:38Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -673.0863 15354.24 -0.0438370.965 4X 4.061131 0.201677 20.136840.000 0R-squared 0.946323 Mean dependent var234690. 8Adjusted R-squared 0.943990 S.D. dependent var210356. 7S.E. of regression 49784.06 Akaike info criterion 24.5454Sum squared resid 5.70E+10 Schwarz criterion 24.64291 Log likelihood -304.8174 Hannan-Quinn criter. 24.57244F-statistic 405.4924 Durbin-Watson stat 0.366228Prob(F-statistic) 0.000000模型回归的结果:AY 673.0863 4.0611X it ( 0.0438 )(20.1368)R20.9463, n 25(2) white:该模型存在异方差Heteroskedasticity Test: WhiteF-statistic 4.493068 Prob. F(2,22) 0.0231Obs*R-squared 7.250127 Prob. Chi-Square(2) 0.0266 Scaled explained SS 8.361541 Prob. Chi-Square(2) 0.0153Test Equation:Dependent Variable: RESIDEMethod: Least SquaresDate: 04/18/20 Time: 17:45Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -1.00E+09 1.43E+09 -0.7003780.491 0XA2 -0.455420 0.420966 -1.081847 0.2910 X 102226.2 60664.19 1.685117 0.1061R-squared 0.290005 Mean dependent var2.28E+0 9Adjusted R-squared 0.225460 S.D. dependent var 3.84E+09S.E. of regression 3.38E+09 Akaike info criterion 46.83295Sum squared resid 2.51E+20 Schwarz criterion 46.97922 Log likelihood -582.4119 Hannan-Quinn criter. 46.87352F-statistic 4.493068 Durbin-Watson stat 0.749886Prob(F-statistic) 0.023110ARCH检验:该模型存在异方差Test Equation:Dependent Variable: RESID A2Method: Least SquaresDate: 04/18/20 Time: 19:55Sample (adjusted): 1992 2015Included observations: 24 after adjustmentsVariableCoefficient Std. Error t-Statistic Prob. C8.66E+08 6.92E+08 1.251684 0.2238RESID A 2(-1) 0.817146 0.1889444.3248020.0003 R-squared0.459511 Mean dependent var 2.37E+09 Adjusted R-squared 0.434944 S.D. dependent var 3.90E+09S.E. of regression 2.93E+09 Akaike info criterion 46.51293 Sum squared resid 1.89E+20 Schwarz criterion 46.61110 Log likelihood -556.1552 Hannan-Quinn criter. 46.53898 F-statistic 18.70391Durbin-Watson stat0.888067Prob(F-statistic)0.000273(3)修正:加权最小二乘法修正却 WF Woricflil-ri UTLECi id tl e^cJ\ i « T t"l t-|<p-r f T 护i ■"i-i ■「■ H 1 < ~HV Prbll 1 T ffM r« 11 BHR 7 F r F -K * J *■ J —厂ilTHL 日芦£臼电*电引 OdiJ 1 0*左(■ 20 3>5r^lucilifl -MI^I TGR 1 Z7Q I S w= — T ,皿”=E Ba^-oa 山口 fE=-UH a P -OE = -口曰 3.2 1 且-口9 I B 之与尸-口口 ti .3-Z2E-DO 出q,峙尸・C 旦( 4.3-1 E-O^3 0 3IE 09 N.HMU O-QI 立o 右匚> - nO4 TDE--W Z.&15^=- DC1 hi-tiE - "IIIJ i. um r ci Q SJ ^F -iii i 旦日二-①口Dependent Variable: Y Method: Least Squares Date: 04/18/20 Time: 20:46 Sample: 1991 2015Included observations: 25 Weighting series: W2Weight type: Inverse variance (average scaling)VariableCoefficientStd. Errort-StatisticProb.C 10781.17 2188.706 4.925821 0.0001 X3.9316060.19200420.476670.0000Weighted StatisticsR-squared0.947998 Mean dependent var 51703.40 Adjusted R-squared 0.945737 S.D. dependent var 11816.72 S.E. of regression 8420.515 Akaike info criterion 20.99135 Sum squared resid1.63E+09Schwarz criterion21.08886「工 P U 『匕 7 日nQ r U J-4m y Q M-n!R-0 Kc D 」a 口 9m 日0: B 吝口 oaooom 口 「1 ;「m =2 Q 工H rKLog likelihood -260.3919 Hannan-Quinn criter. 21.01839F-statistic 419.2938 Durbin-Watson stat 0.539863 Prob(F-statistic) 0.000000 Weighted mean dep. 39406.30 Unweighted StatisticsR-squared 0.944994 Mean dependent var234690. 8Adjusted R-squared 0.942602 S.D. dependent var 210356.7S.E. of regression 50396.82 Sum squared resid 5.84E+1修正后进行white检验:Heteroskedasticity Test: WhiteF-statistic 0.261901 Prob. F(2,22) 0.7720 Obs*R-squared 0.581387 Prob. Chi-Square(2) 0.7477 Scaled explained SS 0.211737 Prob. Chi-Square(2) 0.8995Test Equation:Dependent Variable: WGT_RESID A2Method: Least SquaresDate: 04/18/20 Time: 20:41Sample: 1991 2015Included observations: 25Collinear test regressors dropped from specificationVariable Coefficient Std. Error t-Statistic Prob.C 71441488 22046212 3.2405340.003 8X*WGTA2 -2711.961 5055.773 -0.536409 0.5971 WGTA2 13536351 20714871 0.653461 0.5202R-squared 0.023255 Mean dependent var 65232673 Adjusted R-squared -0.065539 S.D. dependent var 61762160 S.E. of regression 63753972 Akaike info criterion 38.89113Sum squared resid 8.94E+16 Schwarz criterion 39.03739 Log likelihood -483.1391 Hannan-Quinn criter. 38.9317F-statistic 0.261901 Durbin-Watson stat 0.898907Prob(F-statistic) 0.771953修正后的模型为AY 10781.17 3.931606X it (4.925821)(20.47667)R20.9480, n 255.4 表5.4的数据是2011年各地区建筑业总产值(X)和建筑业企业利润总额(Y)。
建筑业产值工作报告

建筑业产值工作报告
1. 总体产值情况,报告会对建筑业在特定时间段内的总产值进行概述,包括总产值的金额、产值的增长率等指标,以便对建筑业的整体发展趋势有一个直观的了解。
2. 不同领域的产值分布,报告会对建筑业内不同领域的产值进行分析,比如建筑工程、房地产开发、建筑材料生产等,以便了解各个领域的发展状况和贡献度。
3. 地区分布情况,报告会对建筑业产值在不同地区的分布情况进行分析,比如各个省市的产值情况,以便了解各地区建筑业发展的差异和特点。
4. 影响产值的因素,报告会分析影响建筑业产值的因素,比如宏观经济政策、市场需求变化、技术创新等,以便为未来发展提出建议和对策。
5. 未来发展展望,报告会对建筑业未来发展的趋势和展望进行预测和分析,包括行业发展的机遇和挑战,以便为相关部门和企业提供决策参考。
综上所述,建筑业产值工作报告是对建筑行业产值情况进行全面分析和总结的重要文件,能够为政府部门、企业和相关机构提供决策参考,促进建筑业持续健康发展。
建筑业企业经营情况分析业情
2 2010 年 年度建筑 筑业企业 业经营情 情况分析 析年 济回升向好势 势头、实现转 转型发展的重 重要一年。
我 我区建筑业 2010 年是巩固经济 企业紧紧抓 抓住这一机遇 遇,进一步开 开拓市场,加 加快发展步伐 伐,主要生产 产经营指标 继续保持平 平稳上升趋势 势,总体呈现 现产值与利润 润同步较快增 增长、劳动生 生产率略有 提高的良性 性发展态势, 为促进全区 区经济平稳健 健康发展发挥 挥了积极作用 用。
一、 总体运行情 情况全区共 共计总承包和 和专业承包资 资质等级的建 建筑业企业 102 家,全年 年累计完成 较上年同期 建筑业总产 产值 149.17 亿元, 同比增 增长 36.7%, 期提高 16.6 个 个百分点, 较前三季度 度提高 20.4 个百分点, 呈现逐季增 增长的发展趋 趋势。
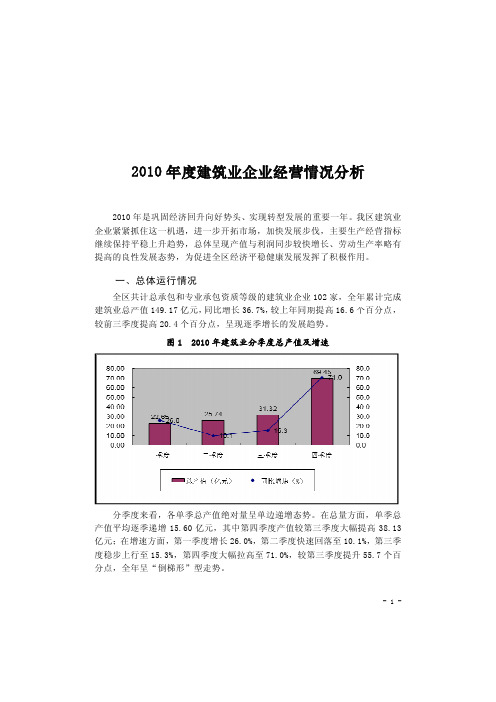
图1 2010 年建 建筑业分季度 度总产值及增 增速分季度 度来看,各单 单季总产值绝 绝对量呈单边 边递增态势。
。
在总量方面 面,单季总 产值平均逐 逐季递增 15.60 亿元,其 其中第四季度 度产值较第三 三季度大幅提 提高 38.13 亿元;在增 增速方面,第 第一季度增长 长 26.0%,第二季度快速 速回落至 10.1%,第三季 度稳步上行 行至 15.3%, 第四季度大 大幅拉高至 71.0%,较第 7 第三季度提升 升 55.7 个百 分点,全年 年呈“倒梯形 形”型走势。
。
- 1 -分行业来看,房屋和土木工程建筑业、建筑安装业、建筑装修业分别完成 产值 131.90 亿元、 5.95 亿元、 10.98 亿元, 同比增长为 34.3%、 68.2%和 52.1%, 三个行业占全部产值比重分别为 88.4%、4.0%和 7.4%,与上年同期相比,比重 呈“两升一降”趋势,其中建筑安装业和建筑装修业比重分别上升 0.8 和 0.7 个百分点,房屋和土木工程建筑业比重下降 1.6 个百分点。
计量经济学第三章案例分析

习题5.4一、模型设定假定各地区建筑业总产值和建筑业企业利润总额之间满足线性约束,则理论模型设定为表1各地区建筑业总产值(X )和建筑业企业利润总额(Y)i i i X Y μββ++=21二、参数估计估计结果为=2.368138+0.034980t=(0.261691) (19.94530)=0.932055 F=397.8152iY ˆiX 2R三、检验模型的异方差(一)goldfeld-quandt检验由图得到残差平方和21i=5739.944,残差平方和22i=23084.48 ,根据goldfeld-quandt检验,F统计量为F===4.0217在α=0.05下,式中α分子、分母的自由度均为10,查F分母表得临界值F0.05(10,10)=2.98,因为F=4.0217>F0.05(10,10)=2.98,所以拒绝原假设,表明模型确实存在异方差(二)White检验根据White检验中辅助函数的构造,则辅助函数为经估计出现White 检验结果,见图从图可以看出,n =20.15100,由White 检验知,查分布表,得临界值(2)=5.9915,同时X 和的t 检验也显著。
比较计算的统计量与临界值,因为n =20.15100>(2)=5.9915,所以拒绝原假设,不拒绝备择假设,表明模型存在异方差。
四、异方差性的修正在运用WLS 法估计中,可以分别选中各种权数做比较,从中则较为理想的权数。
经估计检验用权数1/X t 2的效果最好。
下图为估计结果tt t tv x x +∂+∂+∂=22102σ2R 2χ205.0χ2X 2R 205.0χ可以看出,运用加权最小二乘法消除了预防差性后,参数的t 检验均显著,F 检验也显著,即估计结果为t=(8.303693) (6.569011)=0.976392 DW=1.816022 F=43.15191五.结论这说明个地区建筑业总产值每增加1元,平均来说将增加0.018026元建筑业企业利润总额,而不是引子中得出的需要增加0.37627元建筑业企业利润总额。
庞皓计量经济学第三版课后习题及答案顶配

庞皓计量经济学第三版课后习题及答案顶配庞皓计量经济学第三版课后习题及答案顶配 Last revised by LE LE in 2021第⼆章练习题及参考解答表中是1992年亚洲各国⼈均寿命(Y)、按购买⼒平价计算的⼈均GDP(X1)、成⼈识字率(X2)、⼀岁⼉童疫苗接种率(X3)的数据(1)分别分析各国⼈均寿命与⼈均GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系。
(2)对所建⽴的回归模型进⾏检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国⼈均寿命与⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系:1)⼈均寿命与⼈均 GDP 关系Y i 1 2 X1i u i估计检验结果:2)⼈均寿命与成⼈识字率关系3)⼈均寿命与⼀岁⼉童疫苗接种率关系(2)对所建⽴的多个回归模型进⾏检验由⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命回归结果的参数 t 检验值均明确⼤于其临界值,⽽且从对应的P 值看,均⼩于 ,所以⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命都有显着影响.(3)分析对⽐各个简单线性回归模型⼈均寿命与⼈均 GDP 回归的可决系数为⼈均寿命与成⼈识字率回归的可决系数为⼈均寿命与⼀岁⼉童疫苗接种率的可决系数为相对说来,⼈均寿命由成⼈识字率作出解释的⽐重更⼤⼀些为了研究浙江省财政预算收⼊与全省⽣产总值的关系,由浙江省统计年鉴得到以下数据:的显着性,⽤规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果 2011 年,全省⽣产总值为 32000 亿元,⽐上年增长 %,利⽤计量经济模型对浙江省 2011 年的财政预算收⼊做出点预测和区间预测(3)建⽴浙江省财政预算收⼊对数与全省⽣产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学⽣独⽴完成由12对观测值估计得消费函数为:(1)消费⽀出C的点预测值;(2)在95%的置信概率下消费⽀出C平均值的预测区间。
贵州省人民政府关于建筑业改革的若干规定-黔府[1984]49号
![贵州省人民政府关于建筑业改革的若干规定-黔府[1984]49号](https://img.taocdn.com/s3/m/699b201fe97101f69e3143323968011ca300f7a6.png)
贵州省人民政府关于建筑业改革的若干规定正文:---------------------------------------------------------------------------------------------------------------------------------------------------- 贵州省人民政府关于建筑业改革的若干规定(1984年6月28日黔府〔1984〕49号)建筑业是国民经济的一个重要物质生产部门。
建筑业的经济效益如何,对整个国民经济关系极大。
长期以来,建筑业缺乏独立经营的必要条件,加上我省建筑业本身的素质比较差,经营管理和技术水平都比较落后,因而普遍存在着工期长、消耗高、浪费大、技术进步慢等问题。
为了适应社会主义现代化建设的需要,建筑业必须围绕缩短工期、提高质量、降低消耗、增加盈利等问题加快进行改革。
为此,特作如下规定。
一、改革经营方式,实行招标、投标。
凡是重要工程的设计和施工,都必须实行招标、投标;一般工程也可以由建设单位择优选定设计和施工单位。
省内、省外的国营和集体施工单位,经资质审查合格后,都可以参加投标,以鼓励竞争,防止垄断。
各级城乡建设主管部门,要加强对招标、投标工作的组织领导和管理。
二、积极推行各种投资包干制。
目前要全面推行施工图预算加系数包干和住宅平方米造价包干,并积极创造条件,实行投资包干、工程概算包干、工程造价一次包死,超支国家不补,节约归承建单位。
三、改进分配方式,大力推行百元产值工资含量包干办法。
工资含量和利奖比例,由城乡建设主管部门会同有关部门核定;工资总额进入成本,当年工资节余,由企业自行支配并允许转入下年使用。
实行工期奖和全优奖,做到优质优价。
奖金由建设单位支付。
具体办法,由有关部门制定。
建筑业内部要推行多种形式的经济责任制,打破“大锅饭”。
各建筑公司、工程队、混合小分队和专业班组要层层承包,推行栋号包干、施工队“五费”(即人工费、机械费、材料费、管理费、其他直接费)包干和浮动工资等办法,职工收入高不封顶,低不保基本工资。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、 结论
本案例对各地区建筑业总产值和建筑业企业利润总额之间的关系进行了分析,并对模 型中异方差等问题进行了修正,得出如下结论:建筑业总产值入每增加 1 万元,平均来说 可导致建筑业企业利润总额相应增加,即建筑业总产值与建筑业企业利润总额之间呈正相 关关系,建筑业总产值的增加可以带动建筑业企业的发展。适度增加建筑业总产值可以更 好的发展经济。
计量经济学 期末实验报告
实验名称:各地区建筑业总产值对建 筑业企业利润总额的影响 姓名: 学号: 班级: 指导教师: 时间:
一、 研究的背景
近年来,由于房地产事业的快速发展,同时也带动了建筑业的总产值业的飞速增长, 为了研究各地区建筑业总产值和建筑业企业利润总额之间的关系,预测未来的增长趋势, 需建立计量经济学模型。
表 4. white 检验结果
从表 4 可以看出,nR2=7.962241,由 white 检验知,在α =0.05 下,查χ 2 分布表,得临界 值χ
2 0.05
(2)=5.99147,比较计算的χ 2 统计量与临界值,因为 nR2=7.962241>χ
异方差修正 (1)w1=1/Xt
建筑业总产值(X) 25767692 12219419 16146909 10607041 6811038.3 21000402 15441660 7861403.8 32890450 21517230 21108043 18288148 29995140 6127370 821834 11287118 7383390.8 8758777.8 25241801 70105724 69717052 15169772 21099840 3487908.1 7566795.1 602940.7 11730972 4369038.8 1254431.1 1549486.5 4508313.7
二、 指标选取和数据搜集
从《中国统计年鉴》可以收集到以下数据:
表 1.各地区建筑业总产值和建筑业企业利润总额(单位:万元)
地区 北京 天津 河北 山西 内蒙古 辽宁 福建 江西 山东 河南 湖北 湖南 广东 广西 海南 重庆 吉林 黑龙江 上海 江苏 浙江 安徽 四川 贵州 云南 西藏 陕西 甘肃 青海 宁夏 新疆
建筑业企业利润总额(Y) 960256.4 379211.6 446520.8 194565.9 353362.6 836846.6 375531.9 188502.4 1190084.1 574938.7 698837.4 545655.7 1388554.6 126343.1 14615.7 386177.5 102742 98028.5 794136.5 2368711.7 1887291.7 378252.8 466176 41893.1 266333.1 52895.2 224646.6 152143.1 24468.3 25224.6 68276.6
不拒绝 H0:β 1 =0;因为 t(β 2)=20.82325> t0.025(29)=2.045,所以应拒绝 H0:β 2 =0。 这表明常数项对被解释变量“建筑业企业利润总额”没有显著影响,“建筑业总产值”对 “建筑业企业利润总额”有显著影响。 3.计量经济学检验 (1)异方差检验(white 检验) : 为确定该模型是否存在异方差,用 Eviews 软件对模型进行 White 检验,经估计出现 检验结果如下所示:
80000000 建 筑 业 企 业 利 润 总 额 ( Y ) 70000000 60000000 50000000 40000000 30000000 20000000 10000000 0 0 500000 1000000 1500000 2000000 2500000
建筑业总产值(X)
从散点图可以看出建筑业企业利润总额(Y)与建筑业总产值(X)大体呈现为线性关系, 为分析建筑业企业利润总额随建筑业总产值变动的数量规律性,可以建立如下简单的线性 回归模型: Yt = β
三、 实验过程
(一)模型设定
为了分析各地建筑业企业利润总额与建筑业总产值的关系,选择 2007 年“建筑业企 业利润总额”为被解释变量(用 Y 表示),选择 2007 年“建筑业总产值”为解释变量(用 X)表示。 为分析建筑业企业利润总额(Y)和建筑业总产值(X)的关系,作如下散点图:
表 2.建筑业企业利润总额与建筑业总产值的散点图
表 5.用权数 w1 的结果
(2)W2=1/Xt2
表 6.用权数 w2 的结果
(3)W3=1/sqr(Xt)
表 7.用权数 w3 的结果
经估计检验发现用权数 w3 的效果最好。 表 7 的估计结果如下: Yt = −9038.879 + 0.031133Xt (-0.591165) (17.60107) R2=0.780906,DW=2.033524,F=309.7978 括号中数据为 t 统计量值。 可以看出运用加权最小二乘法消除了异方差性后,参数的 t 检验均显著,F 检验也显 著,并说明建筑业总产值入每增加 1 万元,平均来说可导致建筑业企业利润总额增加 0.031133万元。 (2)自相关检验 经上述异方差检验和修正后,消除异方差。对样本量为 31、一个解释变量的模型、5% 显著水平, 查 DW 统计表可知, dl=1.297, du=1.570, 模型中 du<DW<4-du,模型中没有自相关。
1
+ β 2 Xt + μ
t
其中,β 1 、β 2 为模型参数;μ t 为随机扰动项。 (二)参数估计 利用 Eviews 软件,生成 Y、X 的数据,并采用这些数据对模型进行 OLS 回归,结果如表 3 所示:
表 3.回归结果
可用规范的形式将参数估计和结果写为 Yt = −28992.91 + 0.032345Xt (36196.79) (0.001553) t =(-0.800980) (20.82325) R2=0.937312 (三)模型检验 1. 经济意义检验 所估计的参数β 1 = −28992.91,β 2 = 0.032345 ,这说明建筑业总产值入每增加 1 万元,平均来说可导致建筑业企业利润总额增加0.032345万元。这与理论分析和经验判断 一致。 2 统计意义检验 (1)拟合优度:由表 3 中的数据可以得到 R2=0.937312,这说明模型对样本的拟合很好。 (2)方程显著性(F 检验) :由表 3 知,F 检验的 p 值<0.05,说明回归方程是显著的。 (3) 参数显著性 (t 检验) : 针对 H0: β 1 =0 和 H0: β 2 =0, 由表 3 知, 估计的回归系数β 1的标准 误差和 t 值分别为:SE(β 1)=36196.79,t(β 1)=-0.800980;β 2的标准误差和 t 值 分别为:SE(β 2)= 0.001553,t(β 2)=20.82325。取α =0.05,查 t 分布表得自由度为 n-2=29 的临界值 t0.025(29)=2.045。因为 t(β 1)=-0.800980< t0.025(29)=2.045,所以 F=433.6076 n=31
