ANSYS中的转子动力学计算
ANSYS转子动力学分析
（仅仅适用于线单元） Z
rotation axis: x
B
Y
A
Ф
Whirl Orbit Plots
Print orbit: PRORB
PRINT ORBITS FROM NODAL SOLUTION *****ANSYS VERIFICATION RUN ONLY***** DO NOT USE RESULTS FOR PRODUCTION
多级转子 Campbell图
Campbell Diagram …
y
ω
Elliptical whirl orbit
As frequencies split with increasing spin velocity, ANSYS identifies:
• forward (FW) and backward (BW) whirl • stable / unstable operation • critical speeds (PRCAMP)
OMEGA/CMOMGA Command
• OMEGA: 该命令指定结构在总体迪卡儿系下的转速（角速度）
转动速度可以在下列分析类型中定义：
• Static • Harmonic - Full or mode superposition • Transient - Full or mode superposition
STATIC, MODAL, HARMONIC, TRANSIENT
转子动力学求解
对比项
Stationary Frame
Rotating Frame
单元类型
BEAM4, PIPE16, MASS21, SOLID45, SOLID95, SOLID185, SOLID186, BEAM188, BEAM189.
利用ANSYS进行转子临界转速计算
万方数据第５期张利民等：利用ＡＮＳＹＳ进行转子临界转速计算３５２算例图１ＣＯＭＢＩ２１４单元２．１算例１如图２所示的转子一支承系统，其中转子总长为１．０３ｍ，轴和盘的材料属性如下：杨氏模量Ｅ＝２．０６×１０１１Ｐａ，密度ｐ＝７８００ｋｇ／ｍ３，泊松比移＝０．３。
轴为实心轴，直径Ｄ＝０．０６ｍ；盘的厚度ｈ＝０．０３ｍ；直径Ｄ。
＝０．２ｍ；每个盘上有３６个叶片，叶片厚０．０２２ｍ，宽０．０２ｍ，高０．０４ｍ；假设轴承周向刚度对称并忽略阻尼，刚度为３×１０７Ｎ／ｍ。
模型，确定同一阶振型的正迸动与反进动固有频率‘４１。
由ＡＮＳＹＳ算出的数据绘制一维模型的ＣＡＭＰＢＥＬＬ图如下：＾雹Ｖ馨啜‘围４一维模型的ＣＡＭＰＢＥＬＬ圈根据ＣＡＭＰＢＥＬＬ图可知，前四阶临界转速为：９５Ｈｚ、１５４Ｈｚ、１８６Ｈｚ、３８１Ｈｚ。
由于篇幅原因只给出了第一阶振型和第四阶振型。
图２双支承转子一支承系统图５（ａ）一维模型第一阶振型２．１．Ｉ一雒模型求解法在ＡＮＳＹＳｌ２．０软件中建立该转子一支承系统的一维模型如图３所示。
圈３一维梗型利用有限元方法计算转子临界转速时，转子会出现正进动和反进动。
由于陀螺效应的作用，堕着转子自转角速譬的提亭，辱进动固有频考会Ｉｔｓ（ｂ）一维模型第四阶振型降低，而正进动固有频率将提高。
根据临界转速２．１．２三维模型求解法的定义，应只对正进动固有频率进行分析。
在后在ＡＮＳＹＳｌ２．０中建立的三维模型如图６所万方数据沈阳航空工业学院学报第２７卷刁≮：图６三维模型用ＡＮＳＹＳ建立带叶片的转子支承系统的三维模型时，为了准确地加载弹簧阻尼单元，需要在指定的位置加入硬点。
由于硬点只能加载到面单元和线单元上，所以如果想把硬点加载到转轴中心线上需要用ＡＮＳＹＳ中的Ｄｉｖｉｄｅ命令把三维模型用面切开。
这样就可以在面上创建硬点。
三维模型的ＣＡＭＰＢＥＬＬ图如图７所示：＾蛊Ｖ＊爨图７三维模型的ＣＡＭＰＢＥＬＬ图图８（ｂ）三维模型第四阶振型９９Ｈｚ、１５７Ｈｚ、１９０Ｈｚ、３９０Ｈｚ。
Ansys转子动力学
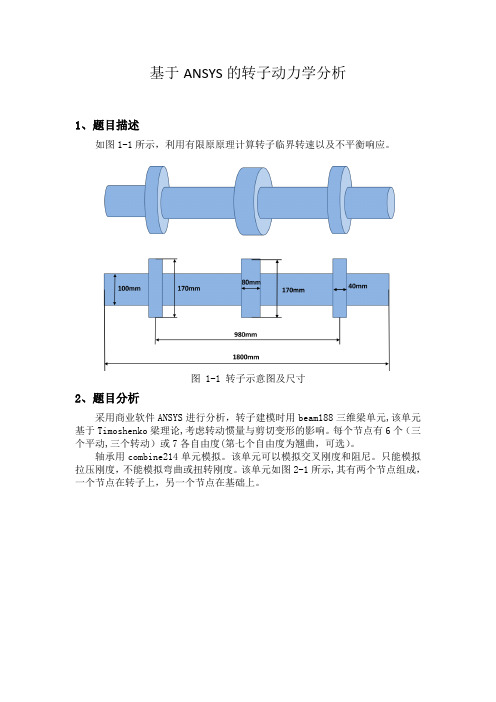
基于ANSYS的转子动力学分析1、题目描述如图1-1所示，利用有限原原理计算转子临界转速以及不平衡响应。
图 1-1 转子示意图及尺寸2、题目分析采用商业软件ANSYS进行分析，转子建模时用beam188三维梁单元,该单元基于Timoshenko梁理论,考虑转动惯量与剪切变形的影响。
每个节点有6个（三个平动,三个转动）或7各自由度(第七个自由度为翘曲，可选）。
轴承用combine214单元模拟。
该单元可以模拟交叉刚度和阻尼。
只能模拟拉压刚度，不能模拟弯曲或扭转刚度。
该单元如图2-1所示,其有两个节点组成，一个节点在转子上，另一个节点在基础上。
图 2-1 combine214单元对于质量圆盘，可以用mass21单元模拟，该单元有6个自由度，可以模拟X ，Y ，Z 三个方向的平动质量以及转动惯性。
3、计算与结果分析 3。
1 转子有限元模型建模时，采用钢的参数，密度取37800/kg m ,弹性模量取112.1110pa ，泊松比取0.3。
轴承刚度与阻尼如表1所示,不考虑交叉刚度与阻尼，且为各项同性。
Kxx Kyy Cxx Cyy 4e7N/m 4e7N/m 4e5N 。
s/m 4e5N 。
s/m将转子划分为93个节点共92个单元。
有限元模型如图3-1所示.图 3—1 转子有限元模型施加约束时，由于不考虑纵向振动与扭转振动，故约束每一节点的纵向与扭转自由度，同时约束轴承的基础节点。
施加约束后的模型如3-2所示。
图 3-2 施加约束后的有限元模型3.1 转子临界转速计算在ANSYS中可以很方便的考虑陀螺力矩的影响.考虑陀螺力矩时，由于陀螺矩阵是反对称矩阵，所以求取特征值时要用特殊的方法。
本文考虑陀螺力矩的影响，分析了在陀螺力矩的影响下,转子涡动频率随工作转速的变化趋势,其Campell图如图3-3所示。
同时给出了转子的前四阶正进动涡动频率与反进动涡动频率以及固有频率。
如表3—2所示。
表 3—2 转子涡动频率随转速的变化Ω(rpm ） 010000 20000 3000040000 1F ω（Hz ） 54。
利用ANSYS进行转子动力特性计算
利用ANSYS进行转子动力特性计算屈文忠江汶清华大学工程力学系，100084[ 摘要 ] 本文利用大型有限元计算软件ANSYS5.5实现转子动力特性的计算。
该计算过程用命令流方式可实现柔性转子系统的临界转速和不平衡响应的计算。
[ 关键词 ] 有限元法；ANSYS软件；转子系统；动力特性转子动力学的理论研究和实验分析在国内外已相当成熟。
发展到今天，现代的计算方法可以分为两大类：传递矩阵法和有限元法。
计算转子临界转速必须能够考虑旋转结构涡动时产生的陀螺效应对转子临界转速的影响，这是转子临界转速计算同其他非旋转结构固有频率计算的差异所在。
大部分通用有限元计算软件不具备计算转子临界转速的功能。
本文利用ANSYS5.5计算了文献1(顾家柳等编著的《转子动力学》)中第68页的例子，命令流文件详细给出了其计算过程。
ANSYS计算转子动力学问题可用单元为BEAM4和PIPE16，其中的实常数设置为Keyoption(7)=1，实常数Spin=转子自转角速度(ω)rad/s。
选取DAMP方法求解特征值。
采用有限元方法计算转子临界转速时，转子会出现正进动和反进动。
由于陀螺效应的作用，随着转子自转角速度的提高，反进动固有频率将降低，而正进动固有频率将提高。
根据临界转速的定义，应只对正进动固有频率（Ωc）进行分析。
在后处理中首先剔除负固有频率，确定同一阶振型的正进动和反进动固有频率。
改变转子自转角速度（ω），计算出新的Ωc，最后画出Ωc～ω曲线。
Ωc～ω曲线与正进动等转速线的交点即为转子的临界转速值。
转子固有频率随转速变化的计算结果如表1所示。
表1 转子固有频率随转速的变化计算结果转速(rad/s) 第一阶正进动(Hz) 第一阶反进动(Hz)1 268.07677 268.0609710 268.14745 267.98942100 268.81721 267.23317200 269.48903 266.29788300 270.09388 265.24944400 270.64005 264.07318500 271.13476 262.75363600 271.58422 261.27522700 271.99383 259.62319800 272.36823 257.78468900 272.71144 255.750131000 273.02694 253.514401100 273.31775 251.077761200 273.58650 248.446281300 273.83547 245.631501400 274.06667 242.649721500 274.28184 239.520661600 274.48253 236.266171700 274.67009 232.908831722 274.70972 232.158651800 274.84573 229.470941900 275.01051 225.973672000 275.16537 222.43656由表1中数据可绘制出转子系统的compell图，如图1所示。
基于ANSYS的磁悬浮轴承转子系统的动力学特性研究
产品设计与应用基于ANS YS的磁悬浮轴承转子系统的动力学特性研究万金贵1,汪希平2,高琪1,张飞1(1.上海第二工业大学实验实训中心,上海201209;2.上海大学机电工程与自动化学院,上海200072)摘要:针对一个实际应用的磁悬浮支承柔性转子系统,进行多组参数条件下的有限元模态分析,分别得到系统的前8阶临界转速与模态振型。
将有限元计算结果与试验结果进行对比分析,验证了有限元分析的正确性。
通过对该磁悬浮转子系统的有限元分析表明:/轴承主导型0的低阶临界转速及振动模态是由轴承控制器各控制通道决定的;而/转子主导型0的高阶临界转速及振动模态符合传统的轴承转子系统动力学特性普遍规律。
关键词:转子系统;磁悬浮轴承;ANSYS;动力学特性;临界转速;模态振型中图分类号:T H133.3;O241.82文献标志码:A文章编号:1000-3762(2010)06-0001-05 R esearch on Dyna m ic Character istics of R otor Syste m Suppor tedby AM B B ased on ANS YS M oda l Ana lysisWAN Ji n-gui1,WANG X i-p i n g2,G AO Q i1,Z HANG Fe i1(1.P racti ca l Center,Shangha i Second P olytechn i c University,Shanghai201209,China;2.School ofM echatron i cs Engi neer i ng and Auto m atio n,Shangha iUn i versity,Shangha i200072,Ch i na)Abstr ac t:The fi n ite e l em ent m o da l analysis of the practical flex i ble rotor system supported by A MB is ca rried out ac2 cordi ng to diff e rent gro ups of para m eters.The first8-order cr iti ca l speeds and m ode shapes are sol ved respecti ve ly.The correctness of t he calculati on resu lts is tested and ver ifi ed by t he exper i m ents.The calculati on resu lts are d iscussed and t he dyna m ic characteristi cs of t he rotor syste m supported byA M B are su mmed up.That i s,the"bear i ng-do m i na2 ted"lo w-order critical speeds and vi brati on m odes are dec i ded by the A MB control channe,l and the"rot or-do m i na2 ted"hi gh-order cr iti ca l speeds and vibratio n m odes a re i n li ne with t he universa l la w of dy na m ics character i sti cs of t he conventi ona l beari ng rotor syste m.K ey word s:rotor syste m;ac ti ve m agne ti c beari ng;ANS YS;dy na m ic character i stics;critica l speed;m o de shape主动磁悬浮轴承(acti v e magnetic bearing, A MB)是利用电磁铁产生可控电磁力将转子悬浮支承的一种新型轴承,由于具有一系列独特的优点而引起人们的广泛关注[1]。
转子动力学基础-ANSYS-APDL和ANSYS-Workbench对比
图6中A代表椭圆的长轴、B代表椭圆的短轴，圆盘1的轴心轨迹是半径为0.797e-4m的圆，圆盘2的轴心轨迹是轨迹为半径0.308e-4m的圆，与理论解一致。
3
3.1
如图所示的电机含有两个转子：内转子和外转子。
内转子是一根实心轴，较长；它的两端通过轴承与机架相连；在两端距离轴承不远的地方装有两个圆盘（图中没有绘制，在有限元分析中圆盘会用质量单元表示），而且右边的圆盘上存在不平衡质量，该不平衡质量产生了不平衡的力（f0= 70e-6kg·m）。
（1）7号节点（内转子上）和12号节点（外转子上）的幅值与频率的关系图。也就是要绘制这两个点的幅频关系曲线。
（2）在某一个给定频率处的转轴轨迹图。
（3）在某一个给定频率处转轴的涡动动画。
注：例子来自ANSYS help中转子动力学——8.7. Example Unbalance Harmonic Analysis。
这是一个有关 的8次代数方程，对于给定的 ，可解出4个正向涡动角速度和4个反向涡动角速度。
绘制涡动角速度随自转角速度变化曲线可得坎贝尔图，令 分别等于± 代入频率方程，即可分别解出在同步正涡动和同步反涡动下的临界转速。
表1临界转速
所谓转子的临界转速通常是指同步正向涡动时的临界转速。对于本算例的两圆盘转子系统，临界转速只有两个，即1158r/min和3183r/min。
在后处理中采用PLVAR命令输出圆盘1和圆盘2节点的总位移变化曲线。
圆盘节点位移随激励频率变化关系
从图2可以看出，曲线在19.2Hz和52.7Hz出现峰值，该两个峰值频率对应同步正进动（涡动）临界转速1152rpm和3162rpm，与模态分析结果相对应。
当频率为19.2Hz时，采用PLORB命令得到转子系统的轴心轨迹图如下。
基于ANSYS经典界面的偏心圆盘启动的转子动力学分析-2
基于ANSYS经典界面的偏心圆盘启动的转子动力学分析－２这是＜基于ANSYS经典界面的偏心圆盘启动的转子动力学分析－１＞的续篇，为方便阅读，重抄题目如下．【问题描述】一个转子如下图所示。
该转子两端简支，在距离下端三分之一处有一个轴承支撑；而在距离上端三分之一处有一个刚性圆盘，该圆盘存在一个偏心质量。
现在该转轴从静止开始转动，经过４秒转速达到５０００ＲＰＭ。
要求对该转子的启动过程进行仿真，考察偏心圆盘所在处的轴位移和弯曲应力随时间变化的过程。
其它已知条件如下：（１）几何参数轴的长度: 0.4 m轴的半径: 0.01 m（２）圆盘的惯性参数:质量= 16.47 kg惯性矩(XX,YY) = 9.47e-2 kg.m2惯性矩(ZZ) = 0.1861 kg.m2偏心质量(0.1g)位于圆盘上，距离轴心的距离为0.15 m .（３）材料参数：弹性模量(E) = 2.0e+11 N/m2泊松比(υ) = 0.3密度= 7800 kg/m3《注》该算例来自于ANSYS APDL转子动力学部分的帮助实例。
【问题分析】１.这是一个瞬态动力学问题。
２.该瞬态动力学问题要考虑科里奥利效应，因此在分析中要打开coriolis开关。
３.使用ＢＥＡＭ１８８建模转子，使用ＭＡＳＳ２１建模圆盘，使用两个一维的弹簧单元ＣＯＭＢＩＮ１４建模轴承，对这两个弹簧设置不同的刚度，以模拟非轴对称的轴承。
４.轴上所有节点限制轴向位移以及围绕轴转动的位移。
轴的两个端点进一步限制住所有平移，而代表轴承与机架连接的ＣＯＭＢＩＮ１４的机架端节点位移全固定。
５.使用数组存储不平衡力的两个分量。
这里要使用一系列中间变量。
具体算法请参见＜基于ANSYS经典界面的偏心圆盘启动的转子动力学分析－１＞。
６.做瞬态动力学分析，在加载时，对节点施加集中力，并把不平衡力数组设置为其参数，从而施加变化的力。
７.使用时间历程后处理器，首先提取所需节点的位移和弯曲应力，然后绘制其图形。
基于ANSYS的转子动力学分析
Ｍｏｄｅｌｉｎｇ
ｌ
引言
旋转机械被广泛地应用于燃气轮机、航空发动机、工业压缩机以及各种电动机等装置
中，研究转子系统的动力学特性对旋转机械设计、制造、故障诊断、延寿等具有重要的意 义。 在进行转子动力学分析时，人们期望建立分析对象的高保真模型，减少计算模型与实际 问题的差异，获得原物理问题的准确结果。长期以来，转子动力特性计算的解析法、传递矩 阵法、基于梁单元的有限元法¨．２１等分析方法，在建立计算模型时均对实际转子系统做出相 当程度的简化，这导致计算模型与实际问题产生较大的差异，并且其分析对象和分析能力有 限，无法对复杂转子结构进行有效的分析；而利用实体单元建模的有限元法则可以对多种复 杂转子结构进行高保真模拟，并考虑各结构间的动力影响，分析计算更加接近实际。 通用有限元程序ＡＮＳＹＳ在其１Ｉ．０版本中推出了转子动力学计算的功能模块，可以对转 子系统进行实体建模，并考虑实体模型在转动状态下产生陀螺力矩时的动力特性。 本文通过对ＡＮＳＹＳ
否
ＡＮＳＹＳ粱单元与实体单元转子动力学分析能力
粱
否
实体 是 是 是 是 小 大 大 是 是
是
３应用实例
（１）验证性算例
对参考文献［５］中的简单转子模型进行计算分析，图ｌ所示为建立的实体模型，转子
模型采用ｓｏｆｉｄ４５单元建立，端部约束所有自由度，中间支撑处约束径向和周向自由度。材
料属性由参考文献［５］给定。
嘲２转于结构州意罔
现代振动与噪声技术（第８卷 图３是本文建立的转子实体有限元模型。对该转子振动特性的讨论可参见参考文献 ６］。
图３转子系统的有限兀模型
４结论
本文对ＡＮＳＹＳ中的实体单元转子动力学分析功能及其理论基础进行了介绍，并对ＡＮ－ ＳＹＳ中基于梁单元和实体单元的转子动力学分析能力进行了对比。本文中的验证性算例说明 了采用实体单元对转于建模计算的准确性和有效性；扩展性算例则说明了实体单元建模在转
ANSYS 中的转子动力学计算
ANSYS 中的转子动力学计算雷先华 安世亚太转子动力学是固体力学的一个重要分支，它主要研究旋转机械的“转子－支承”系统在旋转状态下的振动、平衡和稳定性问题，其主要研究内容有几个方面：临界转速、动力响应、稳定性、动平衡技术和支承设计。
在旋转机械研究设计中，转子动力学的性能分析是极其重要的一个方面。
传统的转子动力学分析采用传递矩阵方法进行，由于将大量的结构信息简化为极为简单的集中质量—梁模型，不能确保模型的完整性和分析的准确度；而有限元在处理转子动力学问题时，可以很好地兼顾模型的完整性和计算的效率，但多年来转子的“陀螺效应”一直是制约转子动力学有限元分析的“瓶颈”问题。
ANSYS 很好地解决了动力特性分析中“陀螺效应”影响的问题，而且陀螺效应的考虑不受计算模型上的限制，使得转子动力学有限元分析变得简单高效。
本文对ANSYS 的转子动力学计算功能进行简要介绍。
1 ANSYS 转子动力学的理论基础ANSYS 转子动力学分析中，两种参考坐标系可供选择：静止坐标系和旋转坐标系。
空间点P 在静止坐标系（其原点在O ′）下的位置矢量为r ′，在旋转坐标系（其原点在O ）下的位置矢量为r 。
在静止坐标系下转子的动力方程为：[][][]{}{}([]){}{}M uC C u K u F gyr +++=&&& []C gyr 为陀螺效应矩阵。
在旋转坐标系下转子的动力方程为：[][][]{}{}([]){}([]){}M u C C u K K u F cor spin r r r+++−=&&& []C cor 为哥氏效应矩阵，[]K spin 为旋转软化效应刚度矩阵。
2 ANSYS 转子动力学的计算功能和新技术ANSYS 转子动力学计算包含如下功能：– 无阻尼临界转速分析– 不平衡响应分析– 阻尼特征值分析– 涡动和稳定性预测 为了分析时计入哥氏效应、陀螺效应和支承的影响，ANSYS 发展了下列新技术单元：SHELL 1814节点有限应变壳单元 PLANE 182二维4节点结构实体单元 PLANE 183二维8节点结构实体单元 SOLID 185三维8节点结构实体单元 SOLID 186三维20节点结构实体单元 SOLID 187三维10节点四面体结构实体单元BEAM 188三维一次有限应变梁单元 BEAM 189 三维二次有限应变梁单元COMBIN214 二维轴承单元（可变刚度和阻尼）ANSYS 考虑陀螺效应时没有计算模型上的限制，故可选择一维（梁、管）、二维（轴对称）和三维复杂计算模型进行分析。
利用ANSYS进行转子临界转速计算
第 5期
张利民等 : 利用 ANSYS 进行 转子临界转速计算
35
模型, 确定同一阶振型的正进动与反进动固有频 率
[ 4]
。由 ANSYS 算 出 的数 据绘 制 一 维模 型 的
CAMPBELL 图如下:
图 1 COM BI 214 单元
2 算例
2 . 1 算例 1 如图 2 所示的转子 - 支承系统 , 其中转子总 长为 1 . 03m, 轴和盘的材料属性如下: 杨氏模量 E = 2 . 06 10 Pa , 密度
7
图 2 双支承转子 - 支承系统
2 . 1 . 1 一维模型求解法 在 ANSYS12. 0 软件中建立该转子 - 支承系 统的一维模型如图 3 所示。
图 3 一维模型
利用有限元方法计算转子临界转速时, 转子 会出现正进动和反进动。由于陀螺效应的作用, 随着转子自转角速度的提高, 反进动固有频率会 降低, 而正进动固有频率将提高。根据临界转速 的定义 , 应只对正进动固有频率进行分析。在后 处理中首先剔除负固有频率, 然后分析各阶模态 2 . 1 . 2 三维模型求解法 在 ANSYS12 . 0 中建立的三维 模型如图 6 所
2010年 10 月 第 27卷 第 5期
沈阳航空工业学院学报 Journa l o f Shenyang Institute of A e ronautica l Eng ineer ing
O ct . 2010 V o.l 27 N o. 5
文章编号 : 1007 1385( 2010) 05 0034 04
作者简介 : 张利民 ( 1985 ) , 男 , 河北廊坊人 , 硕士 研究生 , 主要研 究方向 : 航 空发 动机 强度、 振动 噪声 , E - m ai: l zhang li m in2828@ 163 . com; 王克明 ( 1954 ) , 男 , 辽宁沈阳人 , 教授 , 主要研究方向 : 航空发动机强度、 振动噪声。
利用ANSYS进行转子临界转速计算
算耗用时间短。计算精度较三维模型略差。
１ ２ 三维模 型 ．
三维模 型采 用 Ｓ ＬＤ ８ Ｏ Ｉ１５单元 。Ｓ ＬＤ ８ Ｏ Ｉ１５单
作者简介 ： 张利 民（９ ５一 ， ， １８ ） 男 河北廊坊人 ， 硕士研 究生 ， 主要研 究方向： 航空发 动机 强度 、 动 噪声 ， 振 Ｅ—ｍ ｉ：ｈ ｎ ｍｉ ８ ８ ａｌｚａ￣ｉ ｎ ２ ＠ ２
的平移和绕 ， ， ｌ ｚ轴的转动。点 的质量 和转动 ，
惯量 以实 常数形 式定 义 。 弹簧 阻尼单元 可定 义 为 Ｃ ＭＢ １ 元 ， Ｏ Ｉ ４单 ２ 单
元模 型如 图 １所 示 。Ｃ ＭＢ １ Ｏ Ｉ ４由两 个 节 点 ，‘ ２ 、 ，
进行转子系统动力特性分析需建立简化合理的有 限元模 型 。本文 介 绍 了 两种 有 限元 建 模 方法 ： 一 维模 型法和 三维模 型法 。并用 这两种 方法 对转 子
一
（ ） 轴 作 为 弹性 直 管 单 元 处 理 ， 虑 剪 切 １转 考 形 变 ， 分布 ； 质量 （ ） 盘和 叶片作 为点 单 元 处 理 。点 单 元 的 ２轮 质 量为轮 盘和 叶片 的总质量 ， 点单元 的转 动惯 量
收 稿 日期 ：００—０ ２ ２１ ６— ８
维模 型 的优点 是 ： 对计 算机 配置 要求低 ， 计
２１年 １月 第 ００ 第５ ２ 卷 ０ 期 ７
Ｊｕ ａ ｏ Ｓ ｅｙｎ ｓｔｔ ｏ 院ｏ ａｔａ Ｅ ｇｎｅｉｇ ｏｒ ｌ ｆ ｈｎ沈 阳航 空ｕ 业ｆ ｅ学 报 ｌ ｎｉｅｒ ｎ ａｇＩ ｔ 工 学 ｒｎｕｉ ｎｉ ｅ Ａ ｃ ｎ
０ ｔ Ｏ０ ｃ． ｌ ２
Ｖ０． ７ Ｎｏ ５ １２ ．
临界转速和振型。并把两种模 型的计算结果与用传递矩阵法求得的计算结 果进行 了对 比。通 过
(必看)ANSYS转子动力学计算讨论
关于ansys做转子动力学问题若干思考（百思论坛）最近想学习一下ansys做转子动力学分析,看了点资料,有点自己感想还有一些别的网友的建议,个人认为比较不错的贴了出来一转子动力学插件:转子动力学插件演示版我已经用了基本上图形可以出来,由于版本原因例程和实际的对应有点问题,如果要有时间我可以把我做的过程,贴出来.难点:坎贝尔图我有些不太了解1 2 5 10频率还有一些刚度考虑的随转速在变化,有函数关系例子上提到了用matrix27模拟刚度,而它只用了刚度阻尼单元,好像没有考虑刚度x y 的交叉项,另外因为是演示版,节点有所限制总的来说不错!将来的要做的工作:滑动轴承模拟滚动轴承模拟挤压油膜阻尼器密封转定件接触(碰摩)电磁场耦合自润滑轴承(石墨)有感:各位学习ansys的高手,有没有兴趣自己开发上面单元,这是很有用的工作,我很感兴趣,但有碍于自己知识水平有限,尤其理论水平,有心无力,如果有对此感兴趣的希望一起研究研究;另外对于ansys做转子的动力学的书籍市场上几乎没有,呵呵希望能组织一些人力把这本书完成功在当代利在千秋提示:1 根据本人自己瞎琢磨,以及看论坛的各位高手的留言觉得做模态分析临界转速计算一般用实体单元的少由于不能考虑陀螺力矩shaft:可以采用beam系列模拟pipe系列也行这些能考虑陀螺力矩叶轮叶片:采用mass21模拟,计算转动惯量,质量通过实常数设置刚度阻尼陀螺质量矩阵:都可以采用matrix27模拟,当然也有用弹簧阻尼单元做的, 问题有过考虑油膜的非线性怎么模拟?2. 网友1:目前轴承计算,采用将刚度和阻尼的8个系数,以施加力和力矩的方式解决> 这个我没搞懂,如果那位给个例子3Q网友2: Pip16能考虑陀螺力矩的影响,实体单元没有角自由度因此不能考虑陀螺力矩的影响,如果你的转子没有类似大圆盘的部分或者大的转动部分在轴的接近轴向中心,或者转速不高,就不用考虑陀螺力矩的影响,可以先采用pipe16做一下看随着转速提高,陀螺力矩对固有频率的影响.网友3:可用于陀螺矩阵下列单元可用: Mass21\beam4\pipe16\beam188\beam189上面三个网友的解释,转自:simwe3 实体单元solid45我用过计算临界转速,其他的甚么都对称,计算出来的水平和竖直方向的固有频率差很多,不知道甚么原因,和用pipe16模拟的差很多,我觉得约束形式对临界转速影响很大,对于实体单元来说模拟轴承本身就不容易,所以个人倾向于用pipe16模拟轴,计算精度也不差,我做过实验一阶临界转速和实际转子系统几乎不差多少,二阶由于实验很难观察到所以这个没有对比,但是可以采用捶击法测出转子的各阶固有频率进行对比,这个我也大概试过,二阶还是差点!在simwe上的一篇文章计算转子的临界转速！！！! 计算临界转速/PREP7MP,EX,1,2.1e11MP,NUXY,1,0.3Mp,DENS,1,7850ET,1,COMBIN14ET,2,SOLID45R,1,0.1, , ,*afun,deg ! 设置角度为（度默认为弧度）r1=0.025/2r2=0.240/2l=0.025CYL4,0,0,0,0,r1,20VEXT,all, , ,0,0,l,,,,CSYS,1VGEN,18,all, , , ,20, , ,0CSYS,0VGEN,25,all, , , , ,l, ,0ASEL,NONECYL4,0,0,r1,0,r2,20VEXT,all, , ,0,0,l,,,,CSYS,1VGEN,18,all, , , ,20, , ,0VSEL,S,LOC,X,r1,r2VGEN, ,all, , , , ,10*l, , ,1ALLSEL,ALLNUMMRG,ALL, , , ,LOWNUMCMP,ALLLSEL,S,LOC,X,0,r1LSEL,A,LOC,X,r2LESIZE,all, , ,1, , , , ,0LSEL,INVELESIZE,all,l, , , , , , ,0MSHAPE,0,3DMSHKEY,1VSEL, , , ,allVSWEEP,allCM,rotor,VOLUCM,Erotor,ELEMsaveVSEL,S,LOC,Z,10*l,11*l!*/GODK,P51X, , , ,0,ALL, , , , , ,OMEGA,0,0,0,1CMOMEGA,EROTOR,100,0,0,,,, , , ,0另外希望大家推荐几个不错的论坛,我现在偶尔上上simwe,最近在刚结构注册了一个帐号好像7天以后才可以发言,现在还在等.大家要是看到有ansys做转子方面的文章论坛还有不错的帖子,希望大家跟贴我想学习一下呵呵谢谢大家!ansys10.0已将考虑了陀螺力矩,加上了这部分功能,可惜我为了装转子动力学插件,现在版本改回了8.1,希望用过10.0这个功能的可以讨论一下,那里不明白,那里懂了!如果有对这方面感兴趣的网友,看看这个帖子相当不错/vi ... 2407&highlight=simwe上的一个帖子【讨论】做转子动力学时：如何获得转子临界转速。
ANSYS_中的转子动力学计算
ANSYS 中的转子动力学计算雷先华 安世亚太转子动力学是固体力学的一个重要分支，它主要研究旋转机械的“转子－支承”系统在旋转状态下的振动、平衡和稳定性问题，其主要研究内容有几个方面：临界转速、动力响应、稳定性、动平衡技术和支承设计。
在旋转机械研究设计中，转子动力学的性能分析是极其重要的一个方面。
传统的转子动力学分析采用传递矩阵方法进行，由于将大量的结构信息简化为极为简单的集中质量—梁模型，不能确保模型的完整性和分析的准确度；而有限元在处理转子动力学问题时，可以很好地兼顾模型的完整性和计算的效率，但多年来转子的“陀螺效应”一直是制约转子动力学有限元分析的“瓶颈”问题。
ANSYS 很好地解决了动力特性分析中“陀螺效应”影响的问题，而且陀螺效应的考虑不受计算模型上的限制，使得转子动力学有限元分析变得简单高效。
本文对ANSYS 的转子动力学计算功能进行简要介绍。
1 ANSYS 转子动力学的理论基础ANSYS 转子动力学分析中，两种参考坐标系可供选择：静止坐标系和旋转坐标系。
空间点P 在静止坐标系（其原点在O ′）下的位置矢量为r ′，在旋转坐标系（其原点在O ）下的位置矢量为r 。
在静止坐标系下转子的动力方程为：[][][]{}{}([]){}{}M uC C u K u F gyr +++=&&& []C gyr 为陀螺效应矩阵。
在旋转坐标系下转子的动力方程为：[][][]{}{}([]){}([]){}M u C C u K K u F cor spin r r r+++−=&&& []C cor 为哥氏效应矩阵，[]K spin 为旋转软化效应刚度矩阵。
2 ANSYS 转子动力学的计算功能和新技术ANSYS 转子动力学计算包含如下功能：– 无阻尼临界转速分析– 不平衡响应分析– 阻尼特征值分析– 涡动和稳定性预测 为了分析时计入哥氏效应、陀螺效应和支承的影响，ANSYS 发展了下列新技术单元：SHELL 1814节点有限应变壳单元 PLANE 182二维4节点结构实体单元 PLANE 183二维8节点结构实体单元 SOLID 185三维8节点结构实体单元 SOLID 186三维20节点结构实体单元 SOLID 187三维10节点四面体结构实体单元BEAM 188三维一次有限应变梁单元 BEAM 189 三维二次有限应变梁单元COMBIN214 二维轴承单元（可变刚度和阻尼）考虑陀螺效应时没有计算模型上的限制，故可选择一维（梁、管）、二维（轴对称）和三维复杂计算模型进行分析。
(必看)ANSYS转子动力学计算讨论
关于ansys做转子动力学问题若干思考（百思论坛）最近想学习一下ansys做转子动力学分析,看了点资料,有点自己感想还有一些别的网友的建议,个人认为比较不错的贴了出来一转子动力学插件:转子动力学插件演示版我已经用了基本上图形可以出来,由于版本原因例程和实际的对应有点问题,如果要有时间我可以把我做的过程,贴出来.难点:坎贝尔图我有些不太了解1 2 5 10频率还有一些刚度考虑的随转速在变化,有函数关系例子上提到了用matrix27模拟刚度,而它只用了刚度阻尼单元,好像没有考虑刚度x y 的交叉项,另外因为是演示版,节点有所限制总的来说不错!将来的要做的工作:滑动轴承模拟滚动轴承模拟挤压油膜阻尼器密封转定件接触(碰摩)电磁场耦合自润滑轴承(石墨)有感:各位学习ansys的高手,有没有兴趣自己开发上面单元,这是很有用的工作,我很感兴趣,但有碍于自己知识水平有限,尤其理论水平,有心无力,如果有对此感兴趣的希望一起研究研究;另外对于ansys做转子的动力学的书籍市场上几乎没有,呵呵希望能组织一些人力把这本书完成功在当代利在千秋提示:1 根据本人自己瞎琢磨,以及看论坛的各位高手的留言觉得做模态分析临界转速计算一般用实体单元的少由于不能考虑陀螺力矩shaft:可以采用beam系列模拟pipe系列也行这些能考虑陀螺力矩叶轮叶片:采用mass21模拟,计算转动惯量,质量通过实常数设置刚度阻尼陀螺质量矩阵:都可以采用matrix27模拟,当然也有用弹簧阻尼单元做的, 问题有过考虑油膜的非线性怎么模拟?2. 网友1:目前轴承计算,采用将刚度和阻尼的8个系数,以施加力和力矩的方式解决> 这个我没搞懂,如果那位给个例子3Q网友2: Pip16能考虑陀螺力矩的影响,实体单元没有角自由度因此不能考虑陀螺力矩的影响,如果你的转子没有类似大圆盘的部分或者大的转动部分在轴的接近轴向中心,或者转速不高,就不用考虑陀螺力矩的影响,可以先采用pipe16做一下看随着转速提高,陀螺力矩对固有频率的影响.网友3:可用于陀螺矩阵下列单元可用: Mass21\beam4\pipe16\beam188\beam189上面三个网友的解释,转自:simwe3 实体单元solid45我用过计算临界转速,其他的甚么都对称,计算出来的水平和竖直方向的固有频率差很多,不知道甚么原因,和用pipe16模拟的差很多,我觉得约束形式对临界转速影响很大,对于实体单元来说模拟轴承本身就不容易,所以个人倾向于用pipe16模拟轴,计算精度也不差,我做过实验一阶临界转速和实际转子系统几乎不差多少,二阶由于实验很难观察到所以这个没有对比,但是可以采用捶击法测出转子的各阶固有频率进行对比,这个我也大概试过,二阶还是差点!在simwe上的一篇文章计算转子的临界转速！！！! 计算临界转速/PREP7MP,EX,1,2.1e11MP,NUXY,1,0.3Mp,DENS,1,7850ET,1,COMBIN14ET,2,SOLID45R,1,0.1, , ,*afun,deg ! 设置角度为（度默认为弧度）r1=0.025/2r2=0.240/2l=0.025CYL4,0,0,0,0,r1,20VEXT,all, , ,0,0,l,,,,CSYS,1VGEN,18,all, , , ,20, , ,0CSYS,0VGEN,25,all, , , , ,l, ,0ASEL,NONECYL4,0,0,r1,0,r2,20VEXT,all, , ,0,0,l,,,,CSYS,1VGEN,18,all, , , ,20, , ,0VSEL,S,LOC,X,r1,r2VGEN, ,all, , , , ,10*l, , ,1ALLSEL,ALLNUMMRG,ALL, , , ,LOWNUMCMP,ALLLSEL,S,LOC,X,0,r1LSEL,A,LOC,X,r2LESIZE,all, , ,1, , , , ,0LSEL,INVELESIZE,all,l, , , , , , ,0MSHAPE,0,3DMSHKEY,1VSEL, , , ,allVSWEEP,allCM,rotor,VOLUCM,Erotor,ELEMsaveVSEL,S,LOC,Z,10*l,11*l!*/GODK,P51X, , , ,0,ALL, , , , , ,OMEGA,0,0,0,1CMOMEGA,EROTOR,100,0,0,,,, , , ,0另外希望大家推荐几个不错的论坛,我现在偶尔上上simwe,最近在刚结构注册了一个帐号好像7天以后才可以发言,现在还在等.大家要是看到有ansys做转子方面的文章论坛还有不错的帖子,希望大家跟贴我想学习一下呵呵谢谢大家!ansys10.0已将考虑了陀螺力矩,加上了这部分功能,可惜我为了装转子动力学插件,现在版本改回了8.1,希望用过10.0这个功能的可以讨论一下,那里不明白,那里懂了!如果有对这方面感兴趣的网友,看看这个帖子相当不错/vi ... 2407&highlight=simwe上的一个帖子【讨论】做转子动力学时：如何获得转子临界转速。
基于ANSYS的电机转子的动力学分析
基于ANSYS的电机转子的动力学分析电机转子的动力学分析是电机设计过程中非常重要的一步，它可以帮助工程师优化电机的性能和可靠性。
在进行动力学分析时，通常使用工程仿真软件ANSYS来模拟和分析电机的运动和力学行为。
在进行电机转子的动力学分析时，首先需要确定电机的结构和材料参数。
这包括电机的转子形状、材料特性、叶轮和叶片的结构等。
然后，利用ANSYS软件进行有限元建模，将电机的各个部分进行离散化，确定有限元的节点数和单元类型。
在建立有限元模型时，需要考虑电机的几何形状、质量和惯性分布。
在建立完有限元模型之后，可以利用ANSYS中的动力学分析功能对电机进行力学行为的仿真。
动力学分析可以包括转子的自由振动、受迫振动、失稳分析等。
通过动力学分析，可以了解电机的固有频率、模态形状以及受激励时的响应特性，并根据分析结果进行电机结构参数的优化。
动力学分析还可以帮助工程师评估电机的可靠性和耐久性。
通过对电机在不同工况下的振动、应力、变形等进行分析，可以判断电机在长时间运行过程中是否会出现疲劳破坏、松动等问题。
在动力学分析中还可以考虑电机与周围环境的相互作用，比如电机在高速运转时的气动力、流体力学效应等。
除了动力学分析，ANSYS还可以进行热分析、磁场分析等多种物理场的耦合分析。
通过将转子的动力学分析与热分析、磁场分析等相结合，可以全面评估电机的性能和可靠性。
总之，基于ANSYS的电机转子的动力学分析对于电机设计和性能优化非常重要。
通过动力学分析，可以优化电机的结构参数，提高电机的振动和噪音性能，保证电机的可靠性和耐久性。
同时，动力学分析还可以帮助工程师深入了解电机的机械行为和响应特性，提供有效的设计指导和优化建议。
ansys apdl转子动力学计算例子
ansys apdl转子动力学计算例子ANSYS APDL是一种广泛使用的工程仿真软件，它可以帮助工程师对复杂的机械系统进行建模、分析和优化。
在机械系统中，转子动力学是一个非常重要的部分，因为它对于电力机械和涡轮机械等许多领域的工程应用和设计都有着至关重要的影响。
在本文中，我们将讨论如何使用ANSYS APDL进行转子动力学计算的一些例子。
1. 建立转子动力学模型在进行转子动力学计算之前，我们需要首先建立一个完整的动力学模型。
这个模型应该包括转子、轴承、密封、电机等关键部分。
在ANSYS APDL中，我们可以使用Multiphysics工具进行建模和分析。
Multiphysics工具可以帮助我们将不同的物理场耦合在一起，例如结构、热、电、磁等，并进行模拟计算。
在建模过程中，我们需要考虑到不同的转子部件特性，例如质量、惯性、刚度、阻尼等。
同时，我们还需要考虑到轴承和密封的特性，因为它们对于转子运转的稳定性和寿命有着非常大的影响。
2. 确定运动方程在建立完整的动力学模型之后，我们需要确定运动方程。
这些方程可以描述转子在运转过程中的加速度、速度和位移等变化情况。
在ANSYS APDL中，我们可以使用Modal或Transient 分析进行转子动力学计算。
Modal分析可以帮助我们确定转子在自然频率下的振动特性。
而Transient分析则可以帮助我们模拟转子在运转过程中的动态响应。
3. 执行转子动力学计算当我们确定了转子动力学模型和运动方程之后，我们就可以执行转子动力学计算了。
在ANSYS APDL中，我们可以使用ansys.mechanical.rotorst模块进行转子动力学计算。
ansys.mechanical.rotorst模块可以模拟转子在运转过程中的动态响应，并计算转子的振动、应力和变形等参数。
在执行转子动力学计算之前，我们需要输入各种参数和条件。
例如，我们需要设置转子的转速、工作条件、轴承特性、密封特性等。
基于ANSYS旋转机械模块的转子动力特性分析
应 图中 的临界转 速值 之间 的对 应关 系 。临界 转速 图谱
２１ ０ ２年 第 ４期
冀 成 ， ： 于 ＡＮＳ Ｓ旋 转机 械 模 块 的 转 子 动 力 特 性 分 析 等 基 Ｙ
・３ ・
法 交叉 点 是与 同步 响 应 的 峰值 点 一一 对 应 的 。 同理 ， 其 他类 型 的转子 结构 也得 到 了 以上 结论 。
二 阶 反 进 动
４３ ４
．
一
阶 正进 动
一
阶 临 界转速
一
一
阶反进动
转 速 ／ ｒ・ ｉ 一 （ ｍ ｎ’ ）
图 ４ 偏 置 转 子 Ｃ ｍｐ ｅｌ ａ ｂｌ图
对 于偏 置 、 中 、 居 悬臂 ３种 结 构 的转 子 ， 以悬 臂 转
子 为例对 其 进行 稳 态 不 平 衡 响 应 分 析 ， 图 ７所 示 。 如
２ ０５ ５
２ ０ ０ ４
Ｚ
。
３种结构 的单跨 转 子 有 限元 模 型 ， 利用 梁单 元 、 簧单 弹
元、 质量 点单 元 分 别 对 转 轴 、 动轴 承 、 量 盘 进行 模 滑 质 拟 。通 过 施 加 不 同 转 速 载 荷 ， 到 临 界 转 速 图 谱 得
（ ａ ｂ ｌ图）利 用 ＊Ｇ Ｔ 函数 对 临界 转 速 值 进 行提 Ｃ ｍｐ ｅ ｌ ， Ｅ 取 。分析 结果 表 明 ： 结构 转子 的一 阶临界 转速 较 为 ３种 接近 ； 种 结构 的二 阶转子临界转 速相差 较大 ； ３ 当质 量盘 居中时 ， 临界转 速最 高 ， 随着质 量盘 离对称 中心越 远 ， 临
临界 转速 的计 算 。在 某 种 程 度 上 。转 子 系 统 受 到 的 激 励 载荷 与 转 子 系 统 的 特 性 都 与 转 速 相 关 ， 因此 确 定 转 子
基于ANSYS的轴承-转子系统动力特性研究
ＡＮＳＹＳ
Ｘｉｎｇ—ｊｕｎ
２１００９６，Ｃｈｉｎａ）
９５ ｕｎｉｔ ｉｎ ＡＮＳＹＳ．
（Ｎａｔｉｏｎａｌ
ｅｎｇｉｎｅｅｒｉｎｇ ｒｅｓｅａｒｃｈ ｃｅｎｔｅｒ
Ａｂｓｔｒａｃｔ：Ｔｈｅ ｅｎｔｉｔｙ ｍｏｄｅｌ ｏｆ ｔｈｅ ｂｅａｒｉｎｇ－ｒｏｔｏｒ ｓｙｓｔｅｍ ｉｓ ｅｓｔａｂｌｉｓｈｅｄ ａｎｄ ｍｅｓｈｅｄ ｗｉｔｈ
基于ＡＮＳＹＳ的轴承一转子系统动力特性研究
何新荣，傅行军
（东南大学火电机组振动国家．ｒ－４至研究中心，江苏南京２１００９６）
摘要：在ＡＮＳＹＳ中建立了轴承一转子系统的实体模型，采用Ｓｏｌｉｄｌ８５和Ｓｏｌｉｄ９５单元进行了网格划分，得出了转子系
度对转子系统的动力特性有很大的影响，在进行高速旋转机械动力学设计时，轴承与转子设计必须一起协调 进行，轴承刚度的动态特性不容忽视。 关键词：轴承一转子系统；模态分析；临界转速；支承刚度 中图分类号：ＴＫ２６７
ａ
ｆｉｌｍ．Ｔｈｅ
ｒｅｓｕｌｔｓ ｏｆ ｔｈｅ
ａｎａｌｙｓｉｓ
ｓｈｏｗ ｔｈａｔ ｓｕｐｐｏｒｔ
ｓｔｉｆｆｎｅｓｓ ｈａｖｅ
ｔｏ
ｇｒｅａｔ
ｅｆｆｅｃｔ
ｏｎ
ｄｙｎａｍｉｃ ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ ｏｆ ｔｈｅ ｂｅａｒｉｎｇ－ｒｏｔｏｒ ｓｙｓｔｅｍ．Ｓｏ，ｉｔ ｉｓ ｎｅｃｅｓｓａｒｙ ｔｏ ｄｅｖｏｔｅ ｍｕｃｈ ａｔｔｅｎｔｉｏｎ
系数。 ３．５网格划分
铝合金ＺＬｌ０１，其弹性模量为７Ｅ１０Ｐａ，泊松比０．３２， 密度２６６０ｋｇ／ｍ３。建立的轴承一转子系统实体模型见
图ｌ。 ｛：：＝＝＿………………………‘馔＝ｉ
为了在转子和轴承上具体位置生成节点，先对模 型进行分块然后进行映射网格划分，生成有限元模 型，产生了５３０４４个节点和４８５５４个单元，如图２所
基于ANSYS的电机转子的动力学分析
现代工业上旋转机械单机容量在不断增大，而转子直径不可能随其容量的增大而按比例增大。
高转速轻结构是近代高速旋转机械的发展和设计趋势。
本文使用ansys研究了电机转子动力学问题，得出ansys可以计算转子动力学问题。
1 引言转子动力学的研究，最早可追溯到十九世纪六十年代。
一个多世纪以来，随着大工业的发展，转子系统被广泛地应用于包括燃气轮机、航空发动机、工业压缩机等机械装置中，在电力、航空、机械、化工、纺织等领域中起着非常重要的作用。
因而，转子动力学有着极强的工程应用背景，其相关的研究工作也越来越受到人们的重视。
由于材质的不均匀，制造、加工及安装误差等，转子系统不可避免的存在着质量偏心，同时转子在工作过程中还可能产生热变形以及磨损和介质的姑附等现象，这些因素或多或少都会导致转子不平衡的增大从而使转子的不平衡振动增大。
由过大的不平衡量引起的转子系统的振动是十分有害的，它使机械的效率降低、载荷增加，使一些零部件易于磨损、疲劳而缩短寿命，较大的振动还会恶化操作人员的劳动环境，甚至会导致发生机毁人亡的严重事故。
消除或者减小转子系统的振动首先考虑是对转子进行平衡。
现代工业上旋转机械单机容量在不断增大，而转子直径不可能随其容量的增大而按比例增大。
高转速轻结构是近代高速旋转机械的发展和设计趋势。
转子设计和发展的这种趋势对转子的质量不平衡提出了严格的限制。
这种情况下，转子的动力学变得更加突出和重要。
本文使用ansys研究了某电机转子的动力学问题，为转子动力学设计找到了一个新的途径。
2 模型的建立及计算如图1所示，为电子转子的有限元模型，使用BEAM188单元模拟转子的轴，使用MASS21单元模拟转子，使用单元COMBI214模拟轴承。
图1 电机转子的有限元模型（不显示单元）图2 电机转子的有限元模型（显示单元）图3给出了Beam188 单元的几何简图。
Beam188单元适合于分析从细长到中等粗短的梁结构，该单元基于铁木辛哥梁结构理论，并考虑了剪切变形的影响。
ansys壳单元转子模态计算
一、概述在工程领域，转子是一种常见的机械结构，在旋转机械设备中起着至关重要的作用。
为了确保转子在工作中具有良好的稳定性和可靠性，必须对其进行充分的模态分析和计算。
在此过程中，有限元软件ANSYS是一种常用的工具，可以对转子进行各种模态分析。
二、ANSYS壳单元转子模态计算原理在ANSYS中进行转子模态分析时，通常采用壳单元来建模。
壳单元具有较高的计算精度和效率，可以更好地模拟转子结构的变形和振动情况。
其计算原理如下：1.建立转子几何模型需要对转子的几何形状进行建模。
可以通过ANSYS中的几何建模工具进行建模，也可以直接导入CAD中的转子模型。
在建立模型时，需要考虑转子的轴线、惯性轮廓和叶片形状等因素。
2.网格划分与壳单元建模在建立了几何模型后，需要对其进行网格划分。
通常采用四边形单元或六边形单元进行划分，以保证网格密度的均匀性和合理性。
然后将四边形单元转换为壳单元，以便进行模态分析。
3.加载和约束条件设置在进行模态分析前，需要对转子模型施加适当的加载和约束条件。
加载可以是静载荷、动载荷或者其他外部作用力，约束条件可以是边界条件或轴向约束等。
这些条件的设置对模态计算结果具有重要影响。
4.模态分析计算及结果评价利用ANSYS中的模态分析工具对转子进行模态计算。
在计算完毕后，可以得到转子的各阶固有频率和对应的振动模态。
根据计算结果评价转子的振动稳定性和动力学性能。
三、ANSYS壳单元转子模态计算的优势与其他方法相比，采用ANSYS进行壳单元转子模态计算具有以下优势：1.精度高壳单元可以更好地模拟转子的结构特性，保证模态计算结果的精度和可靠性。
在进行转子模态分析时，可以更好地捕捉转子的振动情况和模态形式。
2.计算高效采用壳单元进行模态计算的过程中，计算效率较高。
ANSYS具有并行计算和优化计算的能力，可以更快速地完成转子模态分析，并节约计算资源。
3.工程应用广泛ANSYS是一种常用的有限元分析软件，广泛应用于工程领域的模态分析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ANSYS 中的转子动力学计算
安世亚太 许明财
转子动力学是固体力学的一个重要分支，它主要研究旋转机械的“转子－支承”系统在旋转状态下的振动、平衡和稳定性问题，其主要研究内容有几个方面：临界转速、动力响应、稳定性、动平衡技术和支承设计。
在旋转机械研究设计中，转子动力学的性能分析是极其重要的一个方面。
旋转机械广泛应用于以下领域: y 涡轮机械 y 能量站 y 机械工具 y 汽车
y 家用器械 y 航空领域 y 船舶推进系统 y 医疗器械 y 计算机设备
传统的转子动力学分析采用传递矩阵方法进行，由于将大量的结构信息简化为极为简单的集中质量—梁模型，不能确保模型的完整性和分析的准确度；而有限元在处理转子动力学问题时，可以很好地兼顾模型的完整性和计算的效率，但多年来转子的“陀螺效应”一直是
制约转子动力学有限元分析的“瓶颈”问题。
ANSYS 很好地解决了动力特性分析中“陀螺效应”影响的问题，而且陀螺效应的考虑不受计算模型上的限制，使得转子动力学有限元分析变得简单高效。
本文对ANSYS 的转子动力学计算功能进行简要介绍。
1 ANSYS 转子动力学的理论基础
ANSYS 转子动力学分析中，两种参考坐标系可供选择：静止坐标系和旋转坐标系。
空间点P 在静止坐标系（其原点在O′）下的位置矢量为r′，在旋转坐标系（其原点在O）下的位置矢量为r。
在静止坐标系下转子的动力方程为：
[][][]{}F {u}K }u ]){gyr [C C (}u
{M =+++&&& 式中:为陀螺效应矩阵
]gyr [C
在旋转坐标系下转子的动力方程为：
[][][]{}F }r ]){u spin [K K (}r
u ]){cor [C C (}r u {M =−+++&&& 式中:为哥氏效应矩阵, 为旋转软化效应刚度矩阵
]cor [C ]spin [K 2 ANSYS 转子动力学的计算功能和新技术
ANSYS 转子动力学计算包含如下功能：
y 无阻尼临界转速分析 y 不平衡响应分析 y 阻尼特征值分析 y 涡动和稳定性预测 典型的应用包括: y 轴的弯曲变形 y 扭转振动 y 转子轴未对准 y 旋转部分的平衡 y 流制振动
为了分析时计入哥氏效应、陀螺效应和支承的影响，ANSYS 发展了下列新技术单元：
SHELL181 4节点有限应变壳单元 PLANE182 二维4节点结构实体单元 PLANE183 二维8节点结构实体单元 SOLID185 三维8节点结构实体单元 SOLID186 三维20节点结构实体单元 SOLID187 三维10节点四面体结构实体单元
BEAM188 三维一次有限应变梁单元 BEAM189 三维二次有限应变梁单元 SOLSH190 三维8节点层合实体-壳单元 COMBIN214
二维轴承单元(可变刚度和阻尼)
ANSYS 考虑陀螺效应时没有计算模型上的限制，故可选择一维（梁、管）、二维（轴对称）和三维复杂计算模型进行分析。
同时，ANSYS 还提供了一系列功能以完善转子动力学的计算，包括：
y CMOMEGA 可以通过组（component CM_NAME）对多个转子指定不同的转速 y CORIOLIS 可以考虑哥氏效应在不同参考坐标系下的影响 y PLCAMP 可绘制坎贝尔图，为临界转速的确定提供了方便 y PRCAMP 可打印固有频率和临界转速 y CAMPB 可绘制预应力结构的坎贝尔图。
y PRORB 可打印出转子涡动幅值
y PLORB 可绘制转子不同截面的涡动轨迹
y SYNCHRO 可以指定激励频率是否与结构速度同步 y 多轴转子
y 正向/反向旋转和不稳定性
3 实例
实例1：梁单元与实体单元比较
coriolis,on
omega,2*62.832,0,0
不同单元结果比较
185单元 188单元
196.42 195.61
First Bending
236.28 235.34
658.52 666.36
Second Bending
698.06 705.42
Torsion 782.58 782.79
1340.9 1385.3
Third Bending
1380.0 1423.5
实例2:圆柱壳模型采用壳单元和实体单元比较
coriolis,on
omega,0,0,314.16,1
不同单元在转速为314.16时的频率值比较
Shell181 Solid185 SolSh190 Solid187 678.48005 681.10140 681.07753 678.23794 758.67024 760.96661 760.94262 757.98816 825.50769 835.28417 835.70065 832.57471 899.35507 908.82694 909.30691 906.02514 1996.7946 2006.0227 2005.9170 1987.4106 2057.3259 2065.6961 2065.5903 2046.7790 2209.1434 2229.2801 2230.0832 2211.4168 2268.7297 2288.0466 2288.8830 2269.8977
3766.5590 3799.1144 3781.9161 3774.9194 3824.0789 3855.8290 3838.7016 3806.0681 3849.0129 3869.5307 3869.3612 3831.3658 3897.0136 3916.1549 3915.9876 3852.2058 4082.9401 4116.1988 4117.2857 4054.2511 4130.9170 4156.9531 4138.1866 4100.4198 4146.2079 4162.8327 4163.9367 4138.8985 4214.0781 4224.4470 4205.7538 4206.3145 实例3:Campbell图表
验证模型图分析结果：Campbell图（FW为正转，BW为反转）
ANSYS与文献[1]计算阻尼自然频率比较
Damped Natural Frequencies(Hz)
F(Hz)
Whirl 0rpm 70,000rpm
ANSYS [1] ANSYS [1] ANSYS [1]
1 BW BW 271.
2 271.1 214.5 213.6
2 FW FW 271.2 271.1 329.8 330.6
3 BW BW 808.8 806.
4 762.4 760.0
4 FW FW 808.8 806.4 844.9 842.6
5 BW BW 1272.0 1273.0 1068.7 1066.5
6 FW FW 1272.0 1273.0 1516.2 1522.0
ANSYS与文献[1]计算临界速度比较
Critical speeds(rpm)
ANSYS [1]
15.494 15.470
17.146 17.159
46.729 46.612
50.114 49.983
64.924 64.752
95.747 96.457
[1] The dynamics of rotor-bearing systems using finite elements, Joumal of Eng. For industry-May 1976
实例4:多轴转子
y自振频率
y不同旋转速度下的临界速度
模型图 一阶模态
内轴Campbell图表及不同旋转速度下的临界速度
外轴Compbell图表及不同旋转速度下的临界速度
实例5:鼓风机轴,转速:10,000rpm
模态分析
模型图 频率及相应模态轨迹
频率结果 稳定性结果
Campbell图表
第一阶FW极限速度
圆盘的不平衡响应
y圆盘偏心距为.002”
y圆盘质量为.0276 lbf-s2/in
y扫频范围为0-10000 rpm
圆盘位移幅值 极限速度轨迹
轴承反作用力
4 结束语
对于旋转机械，转子动力学和整机振动响应是必不可少的研究课题。
传统的传递矩阵分析方法虽然将非常复杂的结构进行了大量简化，使分析变得简单，但同时也不可避免地丢失了大量的细节信息，使模型的完整性变差。
有限元方法能够很好地解决模型的完整性问题，动力缩减技术也使得计算时间大大缩短。
ANSYS 很好地考虑了陀螺效应这一特殊的动力学现象，提供了强大分析工具，使转子动力学和整机振动分析从模型的简化和建立到计算分析变得简单、高效。
在很多的技术领域,由于机械朝着更轻便、更强大、更有效的方向发展,以及容量建设和运行成本的需求,人们越来越感受到转子动力学的重要性。
在应用领域中机械的失效，比如航空发动机、涡轮机组、太空交通工具等的失效，常常会导致巨大的维修费用，更重要的是可能会威胁到人类的生命安全。
ANSYS为许多的工业应用领域提供了完整的转子动力学分析功能：
y可以支持三维实体模型
y可以进行静力、模态、谐响应、瞬态分析
y提供了完善的前/后处理功能。