Ansys-Workbench动力学分析
AnsysWorkbench动力学分析幻灯片

A(i) 描述了系统做第 i 阶主振动时具有的振动形态,称为第 i 阶主振型,或第 i 阶模态。
系统在各个坐标上都将以第 i 阶模态频率 ? 0i 做简谐振动,并且同时通过静平衡位置。
28
? 第三节 模态分析步骤
实例 – 目标: 在这个练习,我们的目标是研究在一定
的约束条件下如图所示的机架的模态,得到其振动特性。
26
? ? ? 2n 0
?
a1
2( n?1) 0
?
?
? an?1
2 0
?
an
?
0
频率方程或特征多项式
解出 n 个值,按升序排列为:
? ? ? 0 ?
2 01
?
2 02
?
?
?
2 0n
? 0i :第 i 阶固有频率
? 01 :基频。
仅取决于系统本身的刚度、质量等物理参数。
? ? ? ? ? 将每一个? 0i 代入方程 ([K] ? 02[M ]) x ? 0
x2 ? x1) (x2 ? x1
)
? ? ?
m1?x?1 m2 ?x?2
? (k1 ? ? k2 x1
k2 )x1 ? (k2
? ?
k2 x2 k3 ) x2
?0 ?0
方程组用矩阵表达为:
?m1
? ?
0
0 m2
?? ?? ??
?x?1 ?x?2
? ? ?
?
?k1 ? k2
? ?
?
k2
? k2
k2 ? k3
50
100
150
200
250
300
Acceleration (cm 2 400
如何简单的区分ANSYS Workbench有限元分析中的静力学与动力学问题

如何简单的区分ANSYS Workbench 有限元分析中的静力学与动力学问题四川 曹文强“力”是一个很神秘的字,是个象形字,形体极像古代的犁形,上部为犁把,下部为耕地的犁头,也形象的解释“力”含义 ,将无形不可见,不可描述的现象充分的表达了出来。
从初中物理我们就学习过,力是物体之间的相互作用,是使物体获得加速度和发生形变的外因,单独就力而言,有三个要素力的大小、方向和作用点。
力学是研究物体的机械运动和平衡规律及其应用的,力学可分为静力学、运动学和动力学三部分。
而今天主要是简单介绍一个静力学与动力学。
首先,静力学与动力学区别是什么?答案很简单,一个是“静”,一个是“动”,动静的含义就是时间的问题。
故,静力学实际是在研究工程结构在静载荷作用下的弹塑性变形和应力状态,以及结构优化问题,其中的静载荷是指不随时间变化的外加载荷,变化较慢的载荷,也可近似地看作静载荷。
当然“静”动力学静力学实际上只是相对而言,严格地说,物体相对于惯性参照系处于静止或作匀速直线运动的状态,即加速度为零的状态,也就是平衡的状态。
对于平衡的状态阐述,牛顿第一运动定律(牛顿第一定律,又称惯性定律、惰性定律)就有一个完整表述:任何物体都要保持匀速直线运动或静止状态,直到外力迫使它改变运动状态为止。
此外,静力学的有五大公理公理一力的平行四边形法则:作用在物体上同一点的两个力,可合成一个合力,合力的作用点仍在该点,其大小和方向由以此两力为边构成的平行四边形的对角线确定,即合力等于分力的矢量和。
公理二二力平衡公理:作用在物体上的两个力,使物体平衡的必要和充分条件是:两个力的大小相等,方向相反,作用线沿同一直线。
公理三加减平衡力系公理:在已知力系上加或减去任意平衡力系,并不改变原力系对刚体的作用。
公理四牛顿第三定律:两物体间的相互作用力,大小相等,方向相反,作用线沿同一直线。
此公理概括了物体间相互作用的关系,表明作用力与反作用力成对出现,并分别作用在不同的物体上。
ANSYSWorkbench在结构瞬态动力学分析中的应用_巨文涛

=
{ un }
2
+
{ un }
Δt ( 6)
其中: α 、δ 为 New mark 积分参数 在时刻控制方程 为了计算下一时刻的位移 u n + 1 , ( 2. 4 ) 为 [ M] C] K] { un + 1 } + [ { un + 1 } + [ { un + 1 } = { Fa } ( 7) 由( 5 ) 和( 6 ) 得 { u n + 1 } = a0 ( { u n + 1 } - { u n } ) - a2 { u n } - a3 { u n } ( 8) { u n + 1 } { u n } + a6 { u n } + a7 { u n + 1 } ( 9) 1 1 1 δ , a = , a = -1 , a4 a1 = 其中 a0 = 2, αΔt 2 αΔt 3 2 α αΔt δ Δt δ a5 = ( - 2) , = -1 , a6 = Δt( 1 - δ) ,a7 = Δtδ 2 α α ( 8 ) 和( 9 ) 得 由( 7 ) 、 M]+ a1[ C] + [ K] M]a0 ( a0[ ) { un + 1 } = { Fa } + [ { u n } + a2 { u n } + a3 { u n } + [ C] ( a1 { u n } + a4 { u n } + a5 ( 10 ) { un } ) 根据以上各式, 速 可以得到 t n + 1 时刻的位移 u n + 1 、 度 u n + 1 和 u n + 1 加速度。 利用式( 5 ) 和( 6 ) 得到的 New mark 求解方法的无 条件稳定必须满足: 1 1 1 1 + δ) 2 , ( 11 ) δ≥ , + δ + α > 0 α≥ ( 4 2 2 2 New mark 参数 1 1 2 ( 12 ) δ = +γ α = ( 1 + γ) , 4 2 其中: γ 为振幅衰减因子 通过观察( 11 ) 和( 12 ) 可以发现无条件稳定也可以 1 1 2 α≥ ( 1 + γ) 且 γ≥0 。因此只要 γ 表述为 δ = + γ, 2 4 ≥0 , 则求解就是稳定的。 2. 2 HHT 算法 HHT 时间积分法由下式给出 在完全瞬态分析中, [ M] { u n + 1 - αm } + [ { u n + 1 - αf } + [ { u n + 1 - αf } = C] K] { Fa n + 1 - αm } 其中 { u n + 1 - αm } = ( 1 - α m ) { u n + 1 } + α m { u n } { u n + 1 - αf } = ( 1 - α f ) { u n + 1 } + α f { u n } { u n + 1 - αf } = ( 1 - α f ) { u n + 1 } + α f { u n } ( 13 )
ansysworkbench瞬态动力学实例

在本文中,我将为您撰写一篇关于ANSYS Workbench瞬态动力学实例的文章。
我们将深入探讨ANSYS Workbench在瞬态动力学仿真方面的应用,从简单到复杂、由浅入深地讨论其原理和实践操作,并共享个人观点和理解。
第一部分:介绍ANSYS Workbench瞬态动力学仿真ANSYS Workbench是一种用于工程仿真的全面评台,包含了结构、流体、热传递、多物理场等多种仿真工具。
瞬态动力学仿真是ANSYS Workbench的重要应用之一,它能够模拟在时间和空间上随机变化的动力学过程,并对结构在外部力作用下的动力响应进行分析。
在瞬态动力学仿真中,ANSYS Workbench可以模拟诸如碰撞、冲击、振动等动态载荷下的结构响应,用于评估零部件的耐久性、振动特性、动态稳定性等重要工程问题。
通过对这些现象的模拟和分析,工程师可以更好地了解结构在实际工况下的性能,进而进行有效的设计优化和改进。
第二部分:实例分析为了更直观地展示ANSYS Workbench瞬态动力学仿真的应用,我们以汽车碰撞仿真为例进行分析。
假设我们需要评估汽车前部结构在碰撞事故中的动态响应,我们可以通过ANSYS Workbench建立汽车前部结构的有限元模型,并对其进行碰撞载荷下的瞬态动力学仿真。
我们需要构建汽车前部结构的有限元模型,包括车身、前保险杠、引擎盖等部件,并设定材料属性、连接方式等。
接下来,我们可以在仿真中引入具体的碰撞载荷,如40km/h车速下的正面碰撞载荷,并进行瞬态动力学仿真分析。
通过仿真结果,我们可以获取汽车前部结构在碰撞中的应力、应变分布,以及变形情况,从而评估其在碰撞事故中的性能表现。
第三部分:个人观点与总结通过以上实例分析,我们可以看到ANSYS Workbench瞬态动力学仿真在工程实践中的重要应用价值。
瞬态动力学仿真不仅能够帮助工程师分析结构在动态载荷下的响应,还可以为设计优化、安全评估等工程问题提供重要参考。
ANSYS workbench联合dyna显示动力学分析
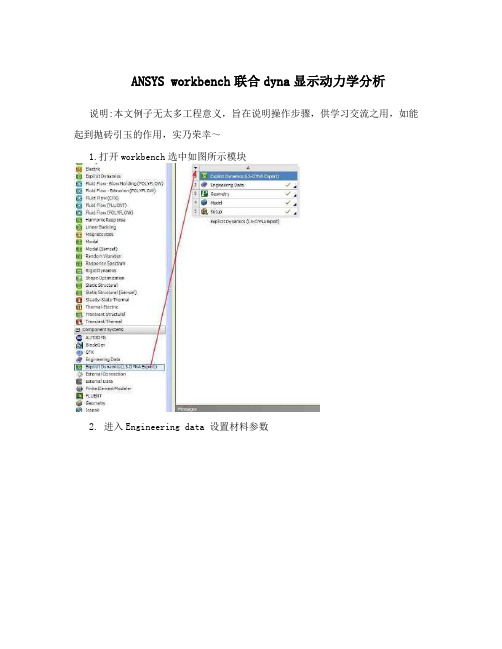
ANSYS workbench联合dyna显示动力学分析说明:本文例子无太多工程意义,旨在说明操作步骤,供学习交流之用,如能起到抛砖引玉的作用,实乃荣幸~1.打开workbench选中如图所示模块2. 进入Engineering data 设置材料参数3. 返回1界面,双击进入model (1)设置材料参数(2)suppress 多余的body4.part 及接触设置5.网格设置及划分6.载荷及边界设置7. 求解设置,求解并保存8.找到K文件,如图所示的文件夹K文件保存在目录(文件名)_files\dp0\SYS\MECH下,如图所示:9.调用ansys-lsdyna求解K文件设置10.通过LS-prepost打开d3plot文件,进行后处理。
如下图:PET/CT示踪剂18F-FDG(氟代脱氧葡萄糖) 氟代脱氧葡萄糖葡萄糖,通常简称为18F-FDG或FDG。
FDG最常用于正电子发射断层扫描(PET)类的医学成像设备:FDG分子之中的氟选用的是属于正电子发射型放射性同位素的氟-18(fluorine-18,F-18,18F,18氟),从而成为18F-FDG(氟-[18F]脱氧葡糖)。
在向病人(患者,病患)体内注射FDG之后,PET扫描仪可以构建出反映FDG 体内分布情况的图像。
接着,核医学医师或放射医师对这些图像加以评估,从而作出关于各种医学健康状况的诊断。
历史二十世纪70年代,美国布鲁克海文国家实验室(Brookhaven National Laboratory)的Tatsuo Ido首先完成了18F-FDG的合成。
1976年8月,宾夕法尼亚大学的Abass Alavi首次将这种化合物施用于两名正常的人类志愿者。
其采用普通核素扫描仪(非PET扫描仪)所获得的脑部图像,表明了FDG在脑部的浓聚(参见下文所示的历史参考文献)。
作用机理与代谢命运作为一种葡萄糖类似物,FDG将为葡萄糖高利用率细胞(high-glucose-using cells)所摄取,如脑、肾脏以及癌细胞。
ANSYS workbench齿轮啮合瞬态动力学分析

ANSYS workbench齿轮啮合瞬态动力学分析齿轮传动是机械系统传动方式中应用最为广泛的一种,今天给介绍一下如何利用workbench实现齿轮啮合的瞬态动力学分析。
有限元分析流程分为3大步、3小步,如下图所示。
今天将以这种方式介绍使用workbench实现齿轮啮合的分析流程。
图1 有限元分析流程一、前处理1.1 几何模型的构建本文几何模型在SolidWorks中创建,并导入workbench中,如图所示图2 齿轮对几何模型1.2 材料定义材料选用结构钢:密度:7850kg/m3,杨氏模量:2.1e11Pa,泊松比:0.31.3 有限元模型的构建有限元模型的构建包括材料赋予、网格划分以及连接关系的构建1.3.1 材料赋予双击瞬态动力学分析流程中的Model,进入Mechanical界面,单击项目树Geometry 下的两个零件,左下角细节框中,Material处指派steel材料1.3.2 网格划分为便于分析及收敛,对网格进行一个简单的控制:首先在左侧项目树Mesh处插入一个method,选中两个齿轮,划分方法为MultiZone;然后插入两个Size,对几个参与啮合的齿面进行尺寸控制,得到了如图所示的网格模型。
图3 网格模型1.3.3 连接关系的构建连接关系包括两部分:接触和运动副,运动副可以实现齿轮的转动,接触可以实现齿轮的传力。
由于workbench会自动创建向邻近位置之间的接触,但默认接触为绑定接触,不符合实际情况,故直接删除,后续手动创建相应接触。
首先在左侧项目树Connections下插入一个Frictional contact,接触面选择其中一个齿轮参与接触的几个齿面,目标面选择另一个齿轮参与接触的几个齿面。
摩擦系数为0.15,Normal Stiffness为1,Update Stiffness为Each iteration,Time Step Controls为Automatic Bisection。
基于ansys workbench齿轮啮合刚度计算及动力学仿真

Keywords:involutetoothprofile;finiteelement;meshingstiffness;geardynamics;quasistaticmethod; contactratio;workbenchsoftware;gearvibration
齿轮是机械装置中的重要零部件,广泛应用 于汽车、航空等领域.啮合刚度是齿轮系统振动的 内部激励源之一,正确地求解啮合刚度以及齿轮 啮合动力学研究对工程实际具有重要意义.
啮合刚度是齿轮动力学分析中的重要参数,而 齿轮副在不同的工况下,实际重合度是不相同的, 齿轮动力学数值仿真时需要啮合刚度有明确的数 学表达式,因此多数学者对啮合刚度进行了曲线拟 合.引用最多的是文献[7]的方法,这些公式中都包 含重合度的因素,若将理论重合度下的啮合刚度公 式代入齿轮动力学方程,将会因为理论重合度与实 际重合度不同,导致动力学分析出现偏差.
第42卷 第2期 2020年 3月
沈 阳 工 业 大 学 学 报 JournalofShenyangUniversityofTechnology
Vol42No2 Mar2020
doi:10.7688/j.issn.1000-1646.2020.02.13
基于 ANSYSworkbench齿轮啮合刚度计算 及动力学仿真
王旭等[1]用材料力学的方法计 算 了 正 常 和 含裂纹齿轮的啮合刚度,并且对有、无裂纹齿轮副 进行了动力学特性分析;万志国等[2]考虑了齿轮 基体变形与齿根圆、基圆不重合的情况,进一步修
收稿日期:2018-03-02. 基金项目:国家自然科学基金项目(51075314);陕西省自然科学基础研究计划项目(2014JM7269). 作者简介:何育民(1968-),男,陕西西安人,副教授,博士,主要从事机械设备状态监测及故障诊断等方面的研究.
WORKBENCH中的动力学分析简介

…求解结果
• 对应于Frequency Finder 分支得ANSYS 命令如下:
– 假如Frequency Finder 分支被选上, 对应于ANTYPE,MODAL 命令 – 定义模态得阶数使用 nmodes 命令, 定义“搜索频率”得最小和最大范围使
用MODOPT,,nmodes,freqb,freqe 命令得freqb 和 freqe,振型被放大通过 MXPAND 命令、 为了节省磁盘空间和计算时间,单元求解选项不能打开,除 非需要得到应力或者应变结果、
影响。 – FE Modeler 用来把Nastran得网格转化到ANSYS中使用。
WORKBENCH中得动力学分析
… ANSYS WORKBENCH概述
Design Simulation ANSYS Workbench
DesignXplorer
DesignModeler
FE Modeler
WORKBENCH中得动力学分析
– 边界条件对于模态分析来说,就是很重要得。因为她们能影响部件得振型和固 有频率、 因此需要仔细考虑模型就是如何被约束得、
– 压缩约束就是非线性得,因此在此分析中将不能被使用、 • 如果存在得话, 压缩约束通常会表现出与无摩擦约束相似、
ANSYS License DesignSpace Entra DesignSpace Professional Structural Mechanical/Multiphysics
们会转化为绑定或者无间隙接触方式来替代并产生作用、
– 假如有间隙存在, 非线性得接触行为将就是自由无约束得(也就就是说, 好像 就是没有接触一样)、 绑定得和无间隙得接触将取决于pinball 区域得大小、
• pinball 区域由缺省值自动产生
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1: 动力学绪论
第一节 动力学分析目的及定义 为什么要对结构进行动力学分析?
土木建筑、地质工程领域
1940年11月7日倒塌—风载
1940年7月1日通车 美国塔科曼悬索大桥
交通运输、航空航天领域
机械、机电领域
什么是结构动力学?
定义:研究结构在动力荷载作用下的动力反应。
目的:动力荷载作用下结构的内力和变形;
4.2: 模态分析
第一节 模态分析的含义
什么是模态分析?
模态分析是用来确定结构的振动特性(固有频率和振型) 的一种技术。 模态分析的好处:
– 使结构设计避免共振或以特定频率进行振动(例如 扬声器);
– 使工程师可以认识到结构对于不同类型的动力载荷 是如何响应的。
建议: 在准备进行其它动力分析之前首先要进行
单地用简谐函数来表示。
FP
t
(3)冲击荷载 荷载的幅值(大小)在很短时间内急剧增大或急剧减小。
FP 冲击荷载
t
FP 突加荷载
t
(4)随机荷载 荷载的幅值变化复杂、难以用解析函数解析表示的荷载。
风荷载 地震作用
25 Wind speed (m/s) 20
15
10
5
0
0
50
100
脉动风
平均风
150
200
fn
n 2
为系统的固有频率,Hz
1 2
T
fn n
为系统的周期,s
2.二自由度无阻尼线性系统
对质量块m1、 m2受力分析, 由Newton第二定律得
mm12xx12 kk13xx12kk22(
x2 x1) (x2 x1)
mm12xx12(kk21x1
k2 )x1 (k2
k2 x2 0 k3)x2 0
第二节 结构动力运动方程
1.单自由度无阻尼线性系统
Newton第二定律
F ma
a x
系统的运动方程
mx kx 0 令
x 02 x 0
02
k m
,则方程变为
无阻尼自由振动解的形式为:
x(t) Acos(nt )
其中A与 由初始条件决定
A为系统的响应的振幅, 为系统的初相位
n
k m
为系统的固有圆频率,弧度/秒
kn1 2mn1 kn2 2mn2 knn 2mnn
2n 0
a 2(n1) 10
an102
an
0
频率方程或特征多项式
解出 n 个值,按升序排列为:
0
2 01
2 02
2 0n
0i :第 i 阶固有频率
机械与动力工程学院 CAD/CAM工程技术研究中心
Ansys Workbench 结构动力学分析
主要内容
4.1: 动力学绪论
4.3: 谐分析
第一节 动力学分析概述 第二节 动力学研究内容 第三节 动力学分析的类型
第一节 谐分析目的 第二节 术语和概念 第三节 谐分析步骤
4.2: 模态分析
第一节 模态分析的含义 第二节 结构动力运动方程 第三节 模态分析步骤
结构 (系统)
输出 (动力荷载)
结构 (系统)
第四类问题:控制问题
输入 (动力荷载)
结构 (系统)
控制系统 (装置、能量)
输出 (动力反应)
输出 (动力反应)
第三节 动力学分析类型
1.动荷载 静荷载:
大小、方向和作用点不随时间变化或变化很 缓慢的荷载。如:结构的自重、雪荷载等。
方程组用矩阵表达为:
m1
0
0 m2
xx12
k1 k2
k2
k2 k2 k3
xx12
0 0
通用表示为:
M x Kx 0
其中:
M 表示质量矩阵
K 表示刚度矩阵
x 表示加速度向量
x 表示位移向量
设方程的解为:
x Asin(0t )
将上式代入微分方程得:
kk2111
m1102 m2102
结构体系
输入
input
质量、刚度 阻尼、约束 频率、振型
动力响应
输出 Output
位移 内力 数值
应力
动位移 加速度 速度 动应力 动力系数
时间函数
第二节 结构动力学研究的内容
第一类问题:反应分析(结构动力计算)
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
第二类问题:参数(或称系统)识别
输入 (动力荷载)
确定结构的动力反应规律。
安全性:确定结构在动力荷载作用下可能产生的最大内力, 作为强度设计的依据; 舒适度:满足舒适度条件(位移、速度和加速度不超过规 范的许可值)。
结构动力体系
静荷载
大小 方向 作用点
结构体系
静力响应
输入 input
刚度、约束 杆件尺寸 截面特性
输出 Output
动荷载
大小 方向 作用点 时间变化
k12 k22
m1202 m2202
•
A1 A2
0 0
A1、 A2 不全为0,则:
k11 m1102 k21 m2102
k12 m1202 0 k22 m2202
02[M ] [K] 0 特征方程
上述方程可求得两个根 01 、02
对于 01 可求得
A11 A21
,
对于 02
可求得
A12 A22
3.多自由度无阻尼线性系统
系统运动方程: M x K x 0 x Rn
方程解为: x Asin(0t )
代入振动方程:[K ] 02[M ] 0
即:
特征方程
k11 2m11 k12 2m12 k1n 2m1n
k21 2m21 k22 2m22 k2n 2m2n 0
动荷载: 大小、方向或作用点随时间变化很快的荷载。
快慢标准: 是否会使结构产生显著的加速度。
显著标准: 质量运动加速度所引起的惯性力与荷载相比 是否可以忽略
问题:你知道有哪些动荷载?
第一章:结构动力学基础
(1)简谐荷载
荷载随时间周期性变化,并可以用简谐函数来表示。
FP
t
(2)一般周期荷载 荷载随时间作周期性变化,是时间t的周期函数,但不能简
t(sec)
250
300
Acceleration (cm/s 2)
400
200
0
-200
t(sec)
0
5
10
15
20
25
30
35
40
45
50
2.动力学分析类型 (1)简谐荷载
谐响应分析
(2)一般周期荷载
谐波分析
(3)冲击荷载 (4)随机荷载
瞬态分析 谱分析
模态分析
3.分析类型的选择原则
(1)如果在相对较长时间内载荷是一个常数,可选择静力 分析,否则为动态分析。 (2)如果动荷载频率小于结构最低阶固有频率的1/3,可进 行静力分析。 (3)载荷对结构刚度的变化可忽略时,可进行线性分析。 (4)载荷引起结构刚度的变化很显著时,或应变超过弹性 范围,或两物体间存在接触,必须进行非线性分析。
