二元合金相图的基本类型和分析
合集下载
第四章__二元合金相图
固溶体的分类
•按溶质原子在溶剂晶格中的位置分：
置换固溶体与间隙固溶体
•按溶质原子在溶剂中的溶解度分：
有限固溶体和无限固溶体
•按溶质原子在固溶体中分布是否有规律分：
无序固溶体和有序固溶体
• 1、置换固溶体 • (substitutional solid solution) • 溶剂原子被溶质原子所置换
杠杆定律
杠杆定律是确定状态图中两相区内两平衡相
的成分和相对重量的重要工具
由杠杆定律可算出合金中平衡两相的相对质
量（即质量分数）
二元合金系，杠杆定律只适用于相图中的两
相区, 且只能在平衡状态下使用。杠杆的两个
端点为给定温度时两相的成分点, 而支点为合
金的成分点。
4、合金的不平衡结晶与树枝状偏析
成的固溶体。
形成条件：溶剂与溶质原子尺寸相近，直径
差别较小，容易形成置换固溶体。
置换固溶体中原子的分布通常是任意的，称
之为无序固溶体。在某些条件下，原子成为 有规则的排列，称为有序固溶体。
固溶体的溶解度
浓度：溶质原子在固溶体中所占的百分比 溶解度：在一定条件下的极限浓度 置换固溶体中，影响溶解度的因素有原子
2、间隙固溶体（interstitial solid solution）
溶质原子溶入溶剂晶格的间隙而形成的固溶体 晶体结构类型
晶格畸变（lattice distortion）
由于溶质原子的介入，原子的排 列规律受到局部的破坏，使晶格 发生扭曲变形。
溶质原子的溶入，使固溶体的晶格发生畸变，变形抗力增 大，金属的强度及硬度升高的现象------固溶强化
T,C 1500 1400 a1 1300 1200 1100 a 1083 1000 Cu L 1455
材料科学基础-8-二元相图(2)
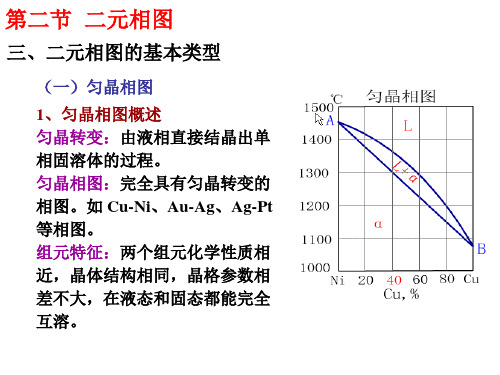
第二节 二元相图
（一）匀晶相图
2、固溶体的平衡凝固
（3）固溶体的结晶规律
c.固溶体的凝固过程与纯金
属一样，也包括形核与长大
两个阶段
e. 平衡凝固得到的固溶体显
微组织和纯金属相同，除了
晶界外，晶粒之间和晶粒内
部的成分却是相同的。
d.合金结晶形核时需要能量
起伏和成分起伏
a. 固溶体的结晶与纯金属不同，它不在
（2）压力加工性：压力加工合金通常是相图上单相固溶体
成分范围内的单相合金或含有少量第二相的合金。
——单相固溶体合金切削加工性能
不够好，而具有两相组织的合金切
削加工性一般比较好。
（4）热处理性：
相图上无固态相变或固溶度变化的
合金不能进行热处理。
孔等缺陷。
——我国20世纪60年代开始研制Pt-Ag合金，但至今无法批量
稳定发展
——国内外通过添加Pd（钯）制成Pt-Pd-Ag三元合金，虽综合
性能不如Pt-Ag合金，但加工性能得以改善。
第二节 二元相图
（三）包晶相图
2、包晶合金的凝固及其平衡组织
（1）ω (Ag)为42.4％的Pt-Ag合金（合金I）
′
% =
× %
第二节 二元相图
1186℃
A
LP+αC ↔ βD
（三）包晶相图
f=2-3+1=0
包晶点
• 1、包晶相图
• 包晶转变：由一个固相与
液相作用生成另一个固相
的过程。
• 包晶相图：两组元在液态
无限互溶，固态下有限互
溶，并发生包晶反应的二
元系相图。
第二节 二元相图
2、包晶合金的凝固及其平衡组织
合金相图
2．Cu-Ni合金的平衡结晶过程如b)图所示。 3．杠杆定理
不同条件下相的成分及其相对量可用杠杆定理求得。
1）确定两平衡相的成分
如图（a）所示，水平线与液相线L的交点 x1 即为相的成分。
2）确定两平衡相的相对量 方法是：
① 设试验合金重量为1，液、固相重量分别为QL、QS ，则 QL+QS =1；
4.2 二元合金相图的基本类型和分析
一、二元匀晶相图
在液态和固态两组元都能无限互溶的相图称为均晶相图。 二元合金系Cu-Ni、Au-Ag、Fe-Cr、Fe-Ni、W-Mo等具有这类相 图。 1．Cu-Ni相图分析
分析：
① 液相线—曲线Al1B ② 固相线—曲线Aa4B ③ 液相区—液相线以上的液相L区域 ④ 固相区—固相线以下的固a相区域 ⑤ 液相线与固相线之间为液、固两相区（L+a） ⑥ A为Cu的熔点（1083℃），B为Ni的熔点（1452℃）。
三、二元包晶相图
二组元在液态无限互溶，在固态有限固溶且发生包晶 反应。如Fe-Fe3C合金（Fe3C----渗碳体）。 1．相图分析 包晶相图组成如图所示。 包晶反应过程如图所示。
2．合金结晶过程 Fe-Fe3C合金结晶过程如图所示。
四、形成稳定化合物的二元合金相图
分析： ① 稳定化合物指熔化前不分解的化合物。 ② 可将稳定化合物看作一个组元，从而把整个相图看成由若
“二元合金相图的基本类型和分析”部分结束！ 请转入：
“铁碳合金相图及应用”
100 %
或 QL x1 Qs x2
3）注意：杠杆定律只能用于两相平衡共存时计算。
4．成分偏析 实际生产条件下为非平衡结晶，因此，先后结晶的部
分成分会不相同。 ① 枝晶偏析（晶内偏析）：先结晶的枝轴与后结晶的枝轴
7-二元合金相图PPT模板
示例 现以Cu-Ni二元合金相图为例进行分析。
如左图所示，A点为Cu的 熔点（1 083℃），B点为Ni的 熔点（1 455℃），该相图上面 一条是液相线，下面一条是固 相线，液相线和固相线把相图 分成三个区域，即液相区L、固 相区α及液固两相区L＋α。
Cu-Ni合金相图及结晶过程示意图
示例 现以Cu-Ni二元合金相图为例进行分析。
金属材料与热处理
合金的结晶过程较为复杂，通常运用合金相图来分析合金的结 晶过程。
相图是表示合金系在平衡条件下，在不同温度、成分下各相 关系的图解，又称为平衡图或状态图。
利用相图，可知各种成分的合金在不同温度的组织状态及一定 温度下发生的结晶和相变，了解不同成分的合金在不同温度下的相 组成及相对含量，了解合金在加热和冷却过程中可能发生的转变。
2.铁碳合金中的相
铁素体
碳溶于α-Fe中形成的间隙固溶 体称为铁素体，用符号F或α表 示。
奥氏体
碳溶于γ-Fe中形成的间隙固溶 体称为奥氏体，用符号A或γ表 示。
铁素体仍保持α-Fe的体心立方 晶格。铁素体中碳的溶解度极小， 室温时约为0.000 8%，在727℃时 碳的溶解度最大，仅为0.021 8%。 铁素体的力学性能与工业纯铁相似， 即塑性、韧性较好，强度、硬度较 低。
45钢室温下的显微组织如下图所示。
亚共析钢结晶过程示意图
如左图所示， F呈白色块状，P 呈层片状，放大倍数不高时呈黑色块 状。所有亚共析钢的室温组织都是F ＋P，只是随碳含量的增加，P越来越 多，F越来越少。
过共析钢
1点以上
1～2点
2～3点
3～4点
过共析钢结晶过程示意图
4点～室温
如上图所示，当温度降到1点时，开始从液相中析出A，降到2点 时液相全部结晶为A。温度降至3点时，开始从A中析出二次渗碳体 （Fe3CⅡ）。温度继续降低，Fe3CⅡ的量不断增多，并呈网状沿奥氏 体晶界分布。剩余A的成分沿ES线变化，冷却至4点时，其中碳的质 量分数达到共析成分，发生共析反应，转变为P。继续冷却，合金组 织不变。
二元相图的基本类型与分析
§4-2二元相图的基本类型与分析一、匀晶相图匀晶相图：组元在液态、固态均能无限互溶所形成的相图。
例如：Cu-Ni Fe-Cr W-Mo相图。
1、点、线、区的意义2、合金K的结晶过程1点以上, 合金为液相L。
1-2之间, 合金发生匀晶反应:L→α,2点以下, 合金全部结晶为α固溶体最终室温组织：单相 固溶体。
3、枝晶偏析固溶体结晶时如果冷却较快, 原子扩散不能充分进行。
先结晶的树枝晶轴含高熔点组元较多, 后结晶的树枝晶枝干含低熔点组元较多。
结果造成在一个晶粒内化学成分的分布不均。
这种现象称为枝晶偏析。
枝晶偏析对材料的机械性能、抗腐蚀性能、工艺性能都不利。
生产上为了消除其影响，常把合金加热到高温(低于固相线100℃左右), 并进行长时间保温, 使原子充分扩散,获得成分均匀的固溶体, 这种处理称为扩散退火。
二、共晶相图共晶相图：两组元在液态下无限溶解，在固态下不能无限溶解，并有共晶转变的相图。
例如：Al-Si Al-Sn Pb-Bi等相图分析：相：α相：Sn溶于Pb中的有限固溶体。
β相：Pb溶于Sn中的有限固溶体。
主要点、线的含义：d点：共晶点cde水平线:共晶反应线cf线:Sn在Pb中的溶解度线(或α相的固溶线)。
合金从高温冷却时,碰到此线，从α相中析出β相。
从固态α相中析出的β相称为β。
IIeg线: Pb在Sn中溶解度线(或β相的固溶线)。
合金从高温冷相。
却时,碰到此线,从β中析出αII1、平衡结晶过程①成分在fc’之间的合金I的平衡结晶过程1点以上：合金为液相L1-2之间：合金发生匀晶反应: L →α,2-3之间：合金全部结晶为α固溶体3点以下：由于Sn 在α中的溶解度沿cf 线降低, 从α中析出βII合金室温组织： α+βII②成分为e 点的合金II 的平衡结晶过程合金冷却到1点温度（T d ）：共晶反应：一种液相在恒温下同时结晶出两种固相的反应叫做共晶反应。
共晶反应条件（d 点的含义）：温度T d = 183℃ 共晶温度液体成分Sn ﹪ = 61.9﹪ 共晶成分共晶反应产物：（αc + βe ）为共晶体；是两相混合物。
二元合金相图(很好很强大)
(ab)、 x1x(ao)的长度。
因此两相的相对重量百分比为：
QL
xx2 x1x2
ob ab
Q
x1x x1x2
ao ab
两相的重量比为：
上式与力学中的杠杆定律完全相似，因此称之为杠 杆定律。即合金在某温度下两平衡相的重量比等于该 温度下与各自相区距离较远的成分线段之比。
在杠杆定律中，杠杆的支点是合金的成分，杠杆的 端点是所求的两平衡相（或两组织组成物）的成分。
④ 过共晶合金结晶过程
与亚共晶合金相似，不同的是
一次相为 ，二次相为Ⅱ 室温组织为Ⅰ+(+)+Ⅱ。
⑶ 组织组成物在相图上的标注
组织组成物是指组成合金显微组织的独立部分。
Ⅰ和Ⅰ, Ⅱ和 Ⅱ,共晶体 (+)都是组
织组成物。 相与相之间的
差别主要在 结构和成分 上。
组织组成物之间的差别主要在形态上。如Ⅰ 、 Ⅱ和 共晶 的结构成分相同，属同一个相，但它们的形
Fe-Fe3C相图
⑷ 三相区的确定：二 元相图中的水平线 是三相区，其三个 相由与该三相区点 接触的三个单相区 的相组成。
常见三相等温水平线上的反应
反应名称 图形特征 共晶反应 包晶反应 共析反应
反应式
说明
L⇄ +
恒温下由一个液相同时 结晶出两个成分结构不 同的新固相。
恒温下由一个液相包着
L + ⇄ 一个固相生成另一个新
铁碳合金相图
共析反应的产物是共析体（铁碳合金中的共析体称珠 光体），也是两相的机械混合物（铁素体+渗碳体)。
与共晶反应不同 的是，共析反应 的母相是固相， 而不是液相。
另外，由于固态 转变过冷度大， 因而共析组织比 共晶组织细。
2.2_二元相图的基本类型
i相图
2.2.2 匀晶相图—学习二元相图的基础
( Binary isomorphous diagrams) •1. 匀晶相图与匀晶转变
•两组元在液态和固态下均可以以任意比例相互溶解，即在固态下形成无限固溶体的 合金相图称为匀晶相图。例如Cu-Ni、Fe-Cr等合金相图均属于此类相图。在这类合 金中，结晶时都是从液相结晶出单相固溶体，这种结晶过程称为匀晶转变。应该指 出，几乎所有的二元合金相图都包含有匀晶转变部分，因此掌握这一类相图是学习 二元合金相图的基础。
用冷却曲线描述K合金的平衡结晶过程，则如图2－8（b）所示。
4.杠杆定律及其应用
图2.9 杠杆定律的证明
•在合金相图中的两相区(如液相和固相)内，若给定某一温度，就能确定在 该温度下两平衡相(如液、固两相)的成分，以及在该温度下两平衡相(如液、 固两相)的相对质量，这就是杠杆定律的内容。 •分析成分为K的Cu-Ni合金，见图2-9 (a)，在tx温度时，液相成分为x1， 固相成分为x2(通过tx温度作一水平线，此水平线与液、固相线的交点即为 L相的成分与α相的成分)。现求在该温度下，已结晶出固溶体α和剩余液相 L的质量分数。
phase
•2.2.3 共晶相图——学习二元相图的关键 ( The eutectic phase
diagram-the key to study two-component phase diagram ) diagram )
•2.2.4 包 晶 相 图 特 征 ( Characteristics of peritectic phase
•2.2.5 具 有 稳 定 化 合 物 相 图 (Phase diagrams with stable
compound) reaction)
2.2.2 匀晶相图—学习二元相图的基础
( Binary isomorphous diagrams) •1. 匀晶相图与匀晶转变
•两组元在液态和固态下均可以以任意比例相互溶解，即在固态下形成无限固溶体的 合金相图称为匀晶相图。例如Cu-Ni、Fe-Cr等合金相图均属于此类相图。在这类合 金中，结晶时都是从液相结晶出单相固溶体，这种结晶过程称为匀晶转变。应该指 出，几乎所有的二元合金相图都包含有匀晶转变部分，因此掌握这一类相图是学习 二元合金相图的基础。
用冷却曲线描述K合金的平衡结晶过程，则如图2－8（b）所示。
4.杠杆定律及其应用
图2.9 杠杆定律的证明
•在合金相图中的两相区(如液相和固相)内，若给定某一温度，就能确定在 该温度下两平衡相(如液、固两相)的成分，以及在该温度下两平衡相(如液、 固两相)的相对质量，这就是杠杆定律的内容。 •分析成分为K的Cu-Ni合金，见图2-9 (a)，在tx温度时，液相成分为x1， 固相成分为x2(通过tx温度作一水平线，此水平线与液、固相线的交点即为 L相的成分与α相的成分)。现求在该温度下，已结晶出固溶体α和剩余液相 L的质量分数。
phase
•2.2.3 共晶相图——学习二元相图的关键 ( The eutectic phase
diagram-the key to study two-component phase diagram ) diagram )
•2.2.4 包 晶 相 图 特 征 ( Characteristics of peritectic phase
•2.2.5 具 有 稳 定 化 合 物 相 图 (Phase diagrams with stable
compound) reaction)
二元合金相图及相变基础知识
3.3
第3章 二元合金相图及相变基础知识
相图的概念
二、 冷却曲线
在液态合金的冷却过程中，可以用热
分析法测定其温度随时间的变化规律，即 冷却曲线。纯金属的冷却曲线上有一个平 台[图3.2(a)、(f)]，说明结晶是在恒温下进 行的。这是因为纯金属在结晶过程中放出 大量的结晶潜热，补偿了向外散失的热量， 达到了热平衡。与纯金属相比，合金结晶 过程中放出的结晶潜热，一般情况下只能 抵消部分散失的热量，结晶是在一定的温 度范围内进行的[图3.2(b)、(c)、(e)]，在冷 却曲线上表现为两个临界点，一个是结晶 开始温度，另一个是结晶终了温度。
以图3.2Pb-Sn合金相图为例，ED线表示Sn在固溶体中的溶解度极限，又 称固溶线，随着温度的降低，Sn在固溶体中的溶解度不断地减少，过剩的Sn 则以固溶体的形式析出，为了区别直接从液相中结晶出的固溶体(称为初生 相)，这种从固溶体中析出的固溶体称为二次相或次生相(用Ⅱ表示)；同 理FG线表示Pb在固溶体中溶解度极 限，随着温度的降低，Pb在固溶体中
2. 两组元液态下完全互溶固态下部分互溶 多数合金尽管在液态下能无限互溶，固态下一个组元在另一组元中却存在
一定的溶解度，它们可以构成共晶相图或包晶相图。 如果当合金组元的含量超出固溶体的溶解度时，合金从液态冷却到某一温
度会同时结晶出两种不同的固相，形成机械混合物，即能发生共晶转变，这类 合金系的相图就称为共晶相图。具有共晶相图的合金系有Pb-Sn、Al-Cu、AlSi等。
LC αP
β 1186℃ D
D点是包晶点。包晶转变终了时，成分为D点的合金组织中原来的L、 相全部转变成相。但成分在PD之间的合金还有相过剩，DC之间的合金 则有L相剩余。
3. 两组元液态完全互溶固态互不溶解 有些合金组元在液态下能够完全互溶，但在固态下彼此互不溶解，这
第3章 二元合金相图及相变基础知识
相图的概念
二、 冷却曲线
在液态合金的冷却过程中，可以用热
分析法测定其温度随时间的变化规律，即 冷却曲线。纯金属的冷却曲线上有一个平 台[图3.2(a)、(f)]，说明结晶是在恒温下进 行的。这是因为纯金属在结晶过程中放出 大量的结晶潜热，补偿了向外散失的热量， 达到了热平衡。与纯金属相比，合金结晶 过程中放出的结晶潜热，一般情况下只能 抵消部分散失的热量，结晶是在一定的温 度范围内进行的[图3.2(b)、(c)、(e)]，在冷 却曲线上表现为两个临界点，一个是结晶 开始温度，另一个是结晶终了温度。
以图3.2Pb-Sn合金相图为例，ED线表示Sn在固溶体中的溶解度极限，又 称固溶线，随着温度的降低，Sn在固溶体中的溶解度不断地减少，过剩的Sn 则以固溶体的形式析出，为了区别直接从液相中结晶出的固溶体(称为初生 相)，这种从固溶体中析出的固溶体称为二次相或次生相(用Ⅱ表示)；同 理FG线表示Pb在固溶体中溶解度极 限，随着温度的降低，Pb在固溶体中
2. 两组元液态下完全互溶固态下部分互溶 多数合金尽管在液态下能无限互溶，固态下一个组元在另一组元中却存在
一定的溶解度，它们可以构成共晶相图或包晶相图。 如果当合金组元的含量超出固溶体的溶解度时，合金从液态冷却到某一温
度会同时结晶出两种不同的固相，形成机械混合物，即能发生共晶转变，这类 合金系的相图就称为共晶相图。具有共晶相图的合金系有Pb-Sn、Al-Cu、AlSi等。
LC αP
β 1186℃ D
D点是包晶点。包晶转变终了时，成分为D点的合金组织中原来的L、 相全部转变成相。但成分在PD之间的合金还有相过剩，DC之间的合金 则有L相剩余。
3. 两组元液态完全互溶固态互不溶解 有些合金组元在液态下能够完全互溶，但在固态下彼此互不溶解，这
二元合金相图
教学内容
1
§4.1 二元合金相图的建立
§4.1.1 名词涵义
组元：组成合金的独立的最基本的单元。一般是 一种元素（如Pb-Sn合金中的Pb和Sn） 或一种稳 定的化合物（如Fe3C） 。
合金系： 由两个或两个以上组元按不同比例配制 成的一系列不同成分的合金（如Pb-Sn系，FeFe3C 系） 。
相图：用来表示合金系中各个合金的结晶过程的 简明图。
成分不均匀 组织不均匀 性能不均匀
富Ni区 富Cu区
18
§4.2.2 共晶相图 1. 相图分析
Pb－Sn合金相图
一定成分的均匀液相， 在一定温度下，从液相 中同时结晶出两种不同 固相的转变称为共晶转 变。所生成的两相混合 物叫共晶体。水平线ced 为共晶反应线。
L
19
共晶相图：两组元液态时彼此无限 互溶，固态下彼此部分固溶，并发 生共晶转变的合金系形成的相图。
Q0
ac
Qa a% ab
Q0
ac
运用杠杆定律时注意，它只适用于相图中的两相 区，并且只能在平衡状态下使用。
杠杆定律的应用： ①确定某一温度下两平衡相的成分； ②确定某一温度下两平衡相的相对量。
16
4. 非平衡结晶与枝晶偏析
实际金属的结晶主要以树枝状长大：这是由于当冷却 速度较大，特别是存在有杂质时，晶体与液体界面的 温度会高于近处液体的温度，形成负温度梯度，且晶 核棱角处的散热条件好，生长快，先形成一次轴，一 次轴又会产生二次轴……，树枝间最后被填充。
α固溶体中Sn 的溶解度极限曲线；
•
dg ， Pb在Sn中溶解度线，或称β相的固溶线；
•
β固溶体中Pb的溶解度极限曲线。
20
④相区： 三个单相区： L、α、β（α、β是有限固溶体）
材料科学基础 4-2二元相图及其类型_OK
后退 下页
nf 的溶解度变化线
●凝固过程：
合金1：L L 合金2 ：L L
21
●不平衡凝固
◆伪共晶
在非共晶成分处获得100%的共晶组 织，只能在非平衡条件下得到。
后退
下页
22
后退
下页
23
◆不平衡共晶
m点以左，n点以右合金不平衡凝固时出现的 共晶组织 。
后退 下24页
◆离异共晶
当初相较多，当发生 共晶反应时，与当初相相 同的一相优先形核，将另 一相推到最后处形成，失 去了共晶形貌，即组织为 离异组织。
上页 下页
25
●包晶相图
后退
下页26
后退
下页27
后退
下页28
1.包晶型反应有何特点？与 共晶反应相比，你能否总结 其规律？
2.分析其冷凝过程，比较平 衡与非平 衡凝固的异同？
下页 30
（4）共析反应：在某一恒温下，一定成分 的固相同时分解成两个成分与结构不同的固 相反应。 （5）包析反应：两个不同成分的固相，在 某一恒温下相互作用生成另一固相的反应。
表5-6是对以上反应类型的总结
上页
下页
31
后退 下页
32
二元相图的分析方法
后退 下页
一、二元相图的一些基本规律
（1）相接触法则：在二元相图中，相邻相区 的相数差为1，点接触除外。 （2）在二元相图中，三相平衡一定是一条水 平线，该向上一定与3个单相区有点接触，其
系中一切具有相同的物理性能与化学性
能的均匀部分，与其它有明显界面分开，
超越界面会有性质突变，否则仍为同一
相。
3
后退 下页
对于合金系统来说，要保持物理性能、 化学性能相同则要满足：成分相同和结 构相同。
第4章+(3)二元合金相图
2.将临界点标 在温度-成分坐 标中的成分垂 线上。
3.将垂线上相 同意义的点连 接起来，并标 上相应的数字 和字母。
大连理工大学经济系0501班 姜珊
8
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
二元相图的建立步骤
4.2二元相图的 基本类型与分析
由凝固开始温度连接起来的相界线称为液相线；
由凝固终结温度连接起来的相界线称为固相线。
(a)Cu-Ni合金的冷却曲线 (b) Cu-Ni 合金相图
大连理工大学经济系0501班 姜珊
9
第4章 二元合金相图
[本章内容]:
4.1二元合金相 4.2.1 二元匀晶相图---相图分析
图的建立
4.2二元相图的 特点：
基本类型与分析 液、固态下均无限互溶。
3
第7章 钢的热处理
3
第8章 钢的合金化
大连理工大学经济系0501班 姜珊
3
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
4.2二元相图的 基本类型与分析
1. 组元
组成合金的最简单、最基本、能够独立存在的 物质。
多数情况下组元是指组成合金的元素。但对于既 不发生分解、又不发生任何反应的化合物也可看 作组元, 如Fe-C合金中的Fe3C，Mg-Si中的Mg2Si。
Cu-Ni合金的平衡组织与枝晶偏析组织
平衡组织
枝晶偏析组织
大连理工大学经济系0501班 姜枝珊 晶偏析组织
19
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
4.2二元相图的 基本类型与分析
4.2.2 二元共晶相图
•当两组元在液态 下完全互溶，在 固态下有限互溶, 并发生共晶反应 时所构成的相图 称作共晶相图。
3.将垂线上相 同意义的点连 接起来，并标 上相应的数字 和字母。
大连理工大学经济系0501班 姜珊
8
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
二元相图的建立步骤
4.2二元相图的 基本类型与分析
由凝固开始温度连接起来的相界线称为液相线；
由凝固终结温度连接起来的相界线称为固相线。
(a)Cu-Ni合金的冷却曲线 (b) Cu-Ni 合金相图
大连理工大学经济系0501班 姜珊
9
第4章 二元合金相图
[本章内容]:
4.1二元合金相 4.2.1 二元匀晶相图---相图分析
图的建立
4.2二元相图的 特点：
基本类型与分析 液、固态下均无限互溶。
3
第7章 钢的热处理
3
第8章 钢的合金化
大连理工大学经济系0501班 姜珊
3
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
4.2二元相图的 基本类型与分析
1. 组元
组成合金的最简单、最基本、能够独立存在的 物质。
多数情况下组元是指组成合金的元素。但对于既 不发生分解、又不发生任何反应的化合物也可看 作组元, 如Fe-C合金中的Fe3C，Mg-Si中的Mg2Si。
Cu-Ni合金的平衡组织与枝晶偏析组织
平衡组织
枝晶偏析组织
大连理工大学经济系0501班 姜枝珊 晶偏析组织
19
第4章 二元合金相图
[本章内容]:
4.1二元合金相 图的建立
4.2二元相图的 基本类型与分析
4.2.2 二元共晶相图
•当两组元在液态 下完全互溶，在 固态下有限互溶, 并发生共晶反应 时所构成的相图 称作共晶相图。
2.2二元相图的基本类型
2.2 二元相图的基本类型
Basic types of two-component phase diagram
一、相图的建立(Setting-up of phase diagram) 相图：平衡状态下，不同成分的合金， 在不同温度下，合金的状态、显微组织 形成规律的图形。 建立：实验法或理论计算法 图2－8 热分析法建立Cu－Ni相图
三、共晶相图（Eutectic diagram）
定义：两组元在液态下无限互溶，在 固态时有限互溶并发生共晶反应（转 变），形成共晶组织的二元相图。 Pb-Sn、 Pb-Sb、 Al-Si、Ag-Cu等 1、相图分析（Pb-Sn为例）
1）特性线与特性点 characteristic lines and points
b）共晶相图
系
Fig.2-18 合金铸造性能与相图的关系
⑴铸造性能与相图的关系
Relationship between Casting Performance and Phase Diagram
液固相线之间的距离越宽，液体流动性越 差，形成枝晶偏析的倾向越大，分散缩孔越 多，铸造性能越差。
即：固溶体溶质含量越多，铸造性能越差。
室温组织:α＋β(αⅡ、βⅡ省略不计) 结晶过程：共晶反应＋二次析出反应
3）亚共晶合金（WSn=19％~61.9% hypoeutectic alloy
L 1 L 183C ( ) 2 Ⅱ ( )
温度/℃
400 327.5
A 300
Ⅲ L
L+α
1
200 α
M 183
E
231.9 B
β+αⅡ+(α+β)
α＋β
F
G
Pb 10 20 30 40 50 60 70 80 90 Sn WSn / %
Basic types of two-component phase diagram
一、相图的建立(Setting-up of phase diagram) 相图：平衡状态下，不同成分的合金， 在不同温度下，合金的状态、显微组织 形成规律的图形。 建立：实验法或理论计算法 图2－8 热分析法建立Cu－Ni相图
三、共晶相图（Eutectic diagram）
定义：两组元在液态下无限互溶，在 固态时有限互溶并发生共晶反应（转 变），形成共晶组织的二元相图。 Pb-Sn、 Pb-Sb、 Al-Si、Ag-Cu等 1、相图分析（Pb-Sn为例）
1）特性线与特性点 characteristic lines and points
b）共晶相图
系
Fig.2-18 合金铸造性能与相图的关系
⑴铸造性能与相图的关系
Relationship between Casting Performance and Phase Diagram
液固相线之间的距离越宽，液体流动性越 差，形成枝晶偏析的倾向越大，分散缩孔越 多，铸造性能越差。
即：固溶体溶质含量越多，铸造性能越差。
室温组织:α＋β(αⅡ、βⅡ省略不计) 结晶过程：共晶反应＋二次析出反应
3）亚共晶合金（WSn=19％~61.9% hypoeutectic alloy
L 1 L 183C ( ) 2 Ⅱ ( )
温度/℃
400 327.5
A 300
Ⅲ L
L+α
1
200 α
M 183
E
231.9 B
β+αⅡ+(α+β)
α＋β
F
G
Pb 10 20 30 40 50 60 70 80 90 Sn WSn / %
第4章第2~3节二元合金相图
3）特征线（5条）
aeb 为液相线；amenb 为固相线； mf、ng — 代表两固溶体ɑ 和β溶 解度曲线； men — 一段水平线又称共晶反应 线，成分在该范围内的合金都将 发生共晶反应。
4）特征区（7个区）
3个单相区： L、ɑ 和β；
3个双相区：（L+ ɑ ）、（L+β） 和（ ɑ +β）；
+βn），称为共析反应，即 γe →（ɑm +βn）
结晶产物为共析体：
呈片层状的特征，但比共 晶体要细密。
3、men为共析反应线：
成分在该范围内的合金都 将发生共析反应。
三、相图与合金性能之间 的关系
（一）合金成分与力学性能之 间关系
（二）合金成分与合金铸造性 能之间关系
（一）合金成分与力学性能和物理性能
温 度 T
时间 t
Cu
20
40
60
80
Ni
wNi%
20%Ni的冷却曲线
温 度 T
时间 t
Cu
20
40
60
80
Ni
wNi%
纯Cu的冷却曲线
温 度 T
时间
Cu t
20
40
60
80
Ni
wNi%
汇总
L L+α
α
温 度 T
Cu
20
40
60
80
Ni
wNi%
二、二元相图的基本类型
及应用
（一）匀晶相图 （二）共晶相图
过共晶合金： 成分位于e-n点之间合金。
共晶反应：
具有一定成分的液体（Le）在 一定温度（共晶温度）下同时结 晶两种成分的固溶体（ɑm +βn） 称为共晶反应，即
二元合金相图的基本类型和分析
3）找出与三相共存水平线点接触的三个单相区，确定三相平衡 转变的性质和反应式。 4）在两相平衡区，可应用杠杆定律求出各相的相对量。 2．相图的应用 ① 相图反映了合金的成分与组成相之间的关系，而组成相的本质 及其相对含量与合金力学性能、物理化学性能密切相关。 ② 相图反映了合金的结晶特性。 ③ 在某种程度上可根据相图来判断合金力学性能、物理化学性能 及合金的铸造性能。如图所示。 ④ 相图也是制定热处理和热变形工艺的重要依据。
2．Cu-Ni合金的平衡结晶过程如b)图所示。 3．杠杆定理 不同条件下相的成分及其相对量可用杠杆定理求得。 1）确定两平衡相的成分 如图（a）所示，水平线与液相线L的交点 2）确定两平衡相的相对量
x1 即为相的成分。
方法是：
① 设试验合金重量为1，液、固相重量分别为QL、QS ，则 QL+QS =1；
三、二元包晶相图
二组元在液态无限互溶，在固态有限固溶且发生包晶 反应。如Fe-Fe3C合金（Fe3C----渗碳体）。 1．相图分析 包晶相图组成如图所示。 包晶反应过程如图所示。 2．合金结晶过程 Fe-Fe3C合金结晶过程如图所示。
四、形成稳定化合物的二元合金相图
分析： ① 稳定化合物指熔化前不分解的化合物。
“二元合金相图的基本类型和分析”部分结束！ 请转入：
“铁碳合金相图及应用”
液相线曲线al1b固相线曲线aa4b液相区液相线以上的液相l区域固相区固相线以下的固a相区域液相线与固相线之间为液固两相区laa为cu的熔点1083b为ni的熔点1452
4.2 二元合金相图的基本类型和分析 一、二元匀晶相图
在液态和固态两组元都能无限互溶的相图称为均晶相图。 二元合金系Cu-Ni、Au-Ag、Fe-Cr、Fe-Ni、W-Mo等具有这类相 图。 1．Cu-Ni相图分析 分析： ① 液相线—曲线Al1B ② 固相线—曲线Aa4B ③ 液相区—液相线以上的液相L区域 ④ 固相区—固相线以下的固a相区域 ⑤ 液相线与固相线之间为液、固两相区（L+a） ⑥ A为Cu的熔点（1083℃），B为Ni的熔点（1452℃）。
第四篇__二元合金相图
形核和晶粒的长大 能量起伏 、结构起伏、成分起伏
固溶体合金在平衡结晶过程中，固相成分 沿固相线变化，液相成分沿液相线变化
α
匀晶转变的特点
➢合金在一定温度范围内结晶； ➢在合金结晶过程中，先结晶出的固相和剩余液
相的成分都与原来合金的成分不同，它们分别 沿着固相线和液相线变化。
➢结论：两相区中，相互处于平衡状态的两个
非常稳定。
它们的合理存在，可有效地提高钢的强度、 热强性、红硬性和耐磨性，是高合金钢和硬 质合金中的重要组成相。
间隙化合物
形成条件：非金属原子半径与金属原子半
径之比大于0.59时，具有复杂结构。如钢中的 Fe3C、Cr23C6、Fe4W2C、Cr7C3、Mn3C等。
特点：具有很高的熔点和硬度, 但比间隙相
第四章 二元合金
内容简介
本章介绍合金相结构和组织的基本概念、 二元合金相图的建立过程和分析相图的基本 方法，以及二元相图与合金性能之间带规律 性的一些关系。
重点掌握合金相结构，并学会分析二元 合金相图。
关于合金的基本概念
➢合金：一种金属元素同另一种或几种元素(k
可以是金属，也可以是非金属), 通过熔化或 其它方法结合在一起所形成的具有金属特性 的物质。
况，包括相的种类和相对量。
➢组织：在显微镜下所观察到的，具有一定大
小、形状和分布的金属内部的微观形貌。
➢在金属或合金中，由于形成的条件不同，各
种相将以不同的数量、形状、大小相互结合， 因此，在显微镜下，可以看到金属或合金具 有各种不同的组织。
➢合金的组织状态：合金在一定条件下，由哪
几个组织组成，以及它们的相对量。
2、间隙固溶体（interstitial solid solution） 溶质原子溶入溶剂晶格的间隙而形成的固溶体
固溶体合金在平衡结晶过程中，固相成分 沿固相线变化，液相成分沿液相线变化
α
匀晶转变的特点
➢合金在一定温度范围内结晶； ➢在合金结晶过程中，先结晶出的固相和剩余液
相的成分都与原来合金的成分不同，它们分别 沿着固相线和液相线变化。
➢结论：两相区中，相互处于平衡状态的两个
非常稳定。
它们的合理存在，可有效地提高钢的强度、 热强性、红硬性和耐磨性，是高合金钢和硬 质合金中的重要组成相。
间隙化合物
形成条件：非金属原子半径与金属原子半
径之比大于0.59时，具有复杂结构。如钢中的 Fe3C、Cr23C6、Fe4W2C、Cr7C3、Mn3C等。
特点：具有很高的熔点和硬度, 但比间隙相
第四章 二元合金
内容简介
本章介绍合金相结构和组织的基本概念、 二元合金相图的建立过程和分析相图的基本 方法，以及二元相图与合金性能之间带规律 性的一些关系。
重点掌握合金相结构，并学会分析二元 合金相图。
关于合金的基本概念
➢合金：一种金属元素同另一种或几种元素(k
可以是金属，也可以是非金属), 通过熔化或 其它方法结合在一起所形成的具有金属特性 的物质。
况，包括相的种类和相对量。
➢组织：在显微镜下所观察到的，具有一定大
小、形状和分布的金属内部的微观形貌。
➢在金属或合金中，由于形成的条件不同，各
种相将以不同的数量、形状、大小相互结合， 因此，在显微镜下，可以看到金属或合金具 有各种不同的组织。
➢合金的组织状态：合金在一定条件下，由哪
几个组织组成，以及它们的相对量。
2、间隙固溶体（interstitial solid solution） 溶质原子溶入溶剂晶格的间隙而形成的固溶体
第2章-二元合金的相图及结晶
2021/4/9
14
二元相图的建立步骤为：[以Cu-Ni合金(白铜)为例] 1. 配制不同成分的合金，测出各合金的冷却曲线，
找出曲线上的临界点（停歇点或转折点）。 2. 将临界点标在温度-成分坐标中的成分垂线上。 3. 将垂线上相同意义的点连接起来，并标上相应的
数字和字母。
相图中，结晶开始点的连线叫液相线。结晶终了点 的连线叫固相线。
液固相线不仅是相区分 界线, 也是结晶时两相的成 分变化线；匀晶转变是变 温转变。
2021/4/9
19
(2) 杠杆定律
处于两相区的合金，不仅由相图可知道（温度一定）两平衡
相的成分，还可用杠杆定律求出两平衡相的相对重量。
现以Cu-Ni合金为例推导杠杆定律：
① 确定两平衡相的成分：设合金成分为x，过x做成 分垂线。在成分垂线相当于
Cu-Ni置换固溶体
Fe-C间隙固溶体
3
固溶体的分类： a、置换固溶体：溶质原子取代溶剂原子的位置，
但整个结构仍然是溶剂的晶体结构。 b、间隙固溶体：溶质原子位于溶剂原子的间隙
位置中。形成间隙固溶体的溶质元素是原子半径较小的 非金属元素，如C、N、B等，而溶剂元素一般是过渡族 元素。形成间隙固溶体的一般规律为r质/r剂<0.59。
a、有限固溶体：在一定的条件下，溶质在固溶体中存在一 极限浓度，如超过此浓度则有其它相形成。
b、无限固溶体：溶质可以任意比例溶入到溶剂中，最高可 达100%。 （只能是置换固溶体）组成元素原子半径、 电化学特性相近，晶格类型相同的置换固溶体，才有可 能形成无限固溶体。
a 、有序固溶体：溶质原子在固溶体中有规律的分布。 （只能是置换固溶体）
属元素，如C、N、B等， 而溶剂元素一般是过渡 族元素。
二元相图的基本类型
0
L
L
1
L
、
L α
α冷
4’ α
却
α
过
k
程
时间→
α——成分沿B4’A变化，先析出含Ni%多；
L——成分沿B1A变化，后析出含Ni%少。
3、杠杆定律及其应用
合金成分x，温度tx xL——液相成分 xα——固相成分 QL——液相重量 Qα——固相重量
温度 →
Ⅰ
L
B
tx
a
A QL
L+α c
b α
Qα
Cu
xL
同时结晶出成分各自固定的两个新固相的 转变过程。
LE 1 8 C 3 MN
相图分析.3
3）特性线与特性点 A——327.5℃，纯Pb的熔点； B——231.9℃；纯Sn的熔点； E——共晶点，WSn=61.9%。
LE 1 8 C 3 MN
相图分析.4
AEB——液相线； AMENB——固相线； MEN——共晶线 ； 成分＞M点合金，在此温度线，均发生共
3）亚共晶合金（WSn=19％~61.9%） L 1L 1 8C 3 () 2 Ⅱ ()
温度/℃
400 327.5
A 300
Ⅲ L
L+α
1
200 α
M 183
E
19
2
61.9
100
α＋βⅡ＋(α＋β)
α+βⅡ
F
α＋β
Pb 10 20 30 40 50 60 70 WSi / %
231.9 B
WSn＜19％的合金
室温组织：α＋βⅡ 二次析出反应： 从单一固溶体相中析出单一新固相的反应。 βⅡ的计算：
βⅡ=F4/FG×100％ 结晶过程： 匀晶反应＋二次析出反应
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4.2 二元合金相图的基本类型和分析 一、二元匀晶相图
在液态和固态两组元都能无限互溶的相图称为均晶相图。 二元合金系Cu-Ni、Au-Ag、Fe-Cr、Fe-Ni、W-Mo等具有这类相 图。 1．Cu-Ni相图分析 分析： ① 液相线—曲线Al1B ② 固相线—曲线Aa4B ③ 液相区—液相线以上的液相L区域 ④ 固相区—固相线以下的固a相区域 ⑤ 液相线与固相线之间为液、固两相区（L+a） ⑥ A为Cu的熔点（1083℃），B为Ni的熔点（1452℃）。
二、二元共晶相图
二组元在液态无限互溶，而在固态仅有限互溶且发 生共晶反应。 以Pb-Sn合金为例。
1．相图分析 ① 相及相区：有α、β、L三种相； 由三个单相区、三个双相区组成相图。 ② AEB为液相线 , ACEDB为固相线。 ③ 共晶线为CED线，称为共晶反应线。
④ 共晶反应 ：浓度为E的L相在共晶反应线时的温度会同时结晶 出两相的混合物，其产物称为共晶组织。即：
3．共析转变 由图分析可知： ① 从固相中同时析出两种不同新相的反应称为共析反应。 ② 共析反应的产物为共析物。 ③ 由于共析反应在固态进行，所以共析组织比共晶组织要细 得多。
六、二元相图的分析与应用
1．二元相图的分析步骤
1）若有稳定化合物，则将其看作一独立组元，把相图分成 几个部分分析。 2）相区接触法则： 二元相图中，相邻相区中的相数只相差一个（点接触 除外）。分析时首先熟悉单相区中的相，再根据相区接触 法则辨别其它相区。
3）找出与三相共存水平线点接触的三个单相区，确定三相平衡 转变的性质和反应式。 4）在两相平衡区，可应用杠杆定律求出各相的相对量。 2．相图的应用 ① 相图反映了合金的成分与组成相之间的关系，而组成相的本质 及其相对含量与合金力学性能、物理化学性能密切相关。 ② 相图反映了合金的结晶特性。 ③ 在某种程度上可根据相图来判断合金力学性能、物理化学性能 及合金的铸造性能。如图所示。 ④ 相图也是制定热处理和热变形工艺的重要依据。
三、二元包晶相图
二组元在液态无限互溶，在固态有限固溶且发生包晶 反应。如Fe-Fe3C合金（Fe3C----渗碳体）。 1．相图分析 包晶相图组成如图所示。 包晶反应过程如图所示。 2．合金结晶过程 Fe-Fe3C合金结晶过程如图所示。
四、形成稳定化合物的二元合金相图
分析： ① 稳定化合物指熔化前不分解的化合物。
2．Cu-Ni合金的平衡结晶过程如b)图所示。 3．杠杆定理 不同条件下相的成分及其相对量可用杠杆定理求得。 1）确定两平衡相的成分 如图（a）所示，水平线与液相线L的交点 2）确定两平衡相的相对量
x1 即为相的成分。
方法是：
① 设试验合金重量为1，液、固相重量分别为QL、QS ，则 QL+QS =1；
② 设液、固相含Ni浓度分别为x1、x2，x为试验合金中的平均 含Ni量(%)，则
QL x1 Qs x2 x
可得:
x2 x QL x2 x1
；
x x1 Qs x2 x1
用图中线段来表示，即为:
xx2 QL 100 % x1 x2
；
Qs
x1 x 100 % x1 x2
Байду номын сангаас
② 可将稳定化合物看作一个组元，从而把整个相图看成由若 干个简单相图所组成。
五、具有固态转变的二元合金相图
1．固态转变主要有： ① 固溶体的脱溶转变； ② 共析转变； ③ 包析转变； ④ 固溶体的同素异晶转变； ⑤ 有序—无序转变等。
2．固溶体的脱溶转变
固溶体因溶解度变化而发生的脱溶转变。如图所示。
所以：
QL xx2 QS x1 x
或
QL x1 Qs x2
3）注意：杠杆定律只能用于两相平衡共存时计算。
4．成分偏析 实际生产条件下为非平衡结晶，因此，先后结晶的部 分成分会不相同。 ① 枝晶偏析（晶内偏析）：先结晶的枝轴与后结晶的枝轴 间成分不同。 ② 区域偏析：由于不平衡冷却造成宏观区域成分不一致。 例如焊接接头中的中心线偏析和层状偏析。 注意：杠杆定律只能用于两相平衡共存时计算。
LE C B
183 。 C
⑤ 固溶线：CF线及DG线分别为α固溶体和β固溶体的固溶线。
2．合金的结晶过程及组织 合金Ⅰ、合金Ⅱ、合金Ⅲ、合金Ⅳ的结晶过程及其组织如 图所示。 分析： ① 相组成 ② 组织组成物 ③ 属这类相图的合金还 有Pb-Sn、Al-Si、AlSn、Al-Cu、Pb-Sb、 Ag-Cu等。
“二元合金相图的基本类型和分析”部分结束！ 请转入：
“铁碳合金相图及应用”
在液态和固态两组元都能无限互溶的相图称为均晶相图。 二元合金系Cu-Ni、Au-Ag、Fe-Cr、Fe-Ni、W-Mo等具有这类相 图。 1．Cu-Ni相图分析 分析： ① 液相线—曲线Al1B ② 固相线—曲线Aa4B ③ 液相区—液相线以上的液相L区域 ④ 固相区—固相线以下的固a相区域 ⑤ 液相线与固相线之间为液、固两相区（L+a） ⑥ A为Cu的熔点（1083℃），B为Ni的熔点（1452℃）。
二、二元共晶相图
二组元在液态无限互溶，而在固态仅有限互溶且发 生共晶反应。 以Pb-Sn合金为例。
1．相图分析 ① 相及相区：有α、β、L三种相； 由三个单相区、三个双相区组成相图。 ② AEB为液相线 , ACEDB为固相线。 ③ 共晶线为CED线，称为共晶反应线。
④ 共晶反应 ：浓度为E的L相在共晶反应线时的温度会同时结晶 出两相的混合物，其产物称为共晶组织。即：
3．共析转变 由图分析可知： ① 从固相中同时析出两种不同新相的反应称为共析反应。 ② 共析反应的产物为共析物。 ③ 由于共析反应在固态进行，所以共析组织比共晶组织要细 得多。
六、二元相图的分析与应用
1．二元相图的分析步骤
1）若有稳定化合物，则将其看作一独立组元，把相图分成 几个部分分析。 2）相区接触法则： 二元相图中，相邻相区中的相数只相差一个（点接触 除外）。分析时首先熟悉单相区中的相，再根据相区接触 法则辨别其它相区。
3）找出与三相共存水平线点接触的三个单相区，确定三相平衡 转变的性质和反应式。 4）在两相平衡区，可应用杠杆定律求出各相的相对量。 2．相图的应用 ① 相图反映了合金的成分与组成相之间的关系，而组成相的本质 及其相对含量与合金力学性能、物理化学性能密切相关。 ② 相图反映了合金的结晶特性。 ③ 在某种程度上可根据相图来判断合金力学性能、物理化学性能 及合金的铸造性能。如图所示。 ④ 相图也是制定热处理和热变形工艺的重要依据。
三、二元包晶相图
二组元在液态无限互溶，在固态有限固溶且发生包晶 反应。如Fe-Fe3C合金（Fe3C----渗碳体）。 1．相图分析 包晶相图组成如图所示。 包晶反应过程如图所示。 2．合金结晶过程 Fe-Fe3C合金结晶过程如图所示。
四、形成稳定化合物的二元合金相图
分析： ① 稳定化合物指熔化前不分解的化合物。
2．Cu-Ni合金的平衡结晶过程如b)图所示。 3．杠杆定理 不同条件下相的成分及其相对量可用杠杆定理求得。 1）确定两平衡相的成分 如图（a）所示，水平线与液相线L的交点 2）确定两平衡相的相对量
x1 即为相的成分。
方法是：
① 设试验合金重量为1，液、固相重量分别为QL、QS ，则 QL+QS =1；
② 设液、固相含Ni浓度分别为x1、x2，x为试验合金中的平均 含Ni量(%)，则
QL x1 Qs x2 x
可得:
x2 x QL x2 x1
；
x x1 Qs x2 x1
用图中线段来表示，即为:
xx2 QL 100 % x1 x2
；
Qs
x1 x 100 % x1 x2
Байду номын сангаас
② 可将稳定化合物看作一个组元，从而把整个相图看成由若 干个简单相图所组成。
五、具有固态转变的二元合金相图
1．固态转变主要有： ① 固溶体的脱溶转变； ② 共析转变； ③ 包析转变； ④ 固溶体的同素异晶转变； ⑤ 有序—无序转变等。
2．固溶体的脱溶转变
固溶体因溶解度变化而发生的脱溶转变。如图所示。
所以：
QL xx2 QS x1 x
或
QL x1 Qs x2
3）注意：杠杆定律只能用于两相平衡共存时计算。
4．成分偏析 实际生产条件下为非平衡结晶，因此，先后结晶的部 分成分会不相同。 ① 枝晶偏析（晶内偏析）：先结晶的枝轴与后结晶的枝轴 间成分不同。 ② 区域偏析：由于不平衡冷却造成宏观区域成分不一致。 例如焊接接头中的中心线偏析和层状偏析。 注意：杠杆定律只能用于两相平衡共存时计算。
LE C B
183 。 C
⑤ 固溶线：CF线及DG线分别为α固溶体和β固溶体的固溶线。
2．合金的结晶过程及组织 合金Ⅰ、合金Ⅱ、合金Ⅲ、合金Ⅳ的结晶过程及其组织如 图所示。 分析： ① 相组成 ② 组织组成物 ③ 属这类相图的合金还 有Pb-Sn、Al-Si、AlSn、Al-Cu、Pb-Sb、 Ag-Cu等。
“二元合金相图的基本类型和分析”部分结束！ 请转入：
“铁碳合金相图及应用”