证书, ssl,CA加密与解密实战例子
信息安全课堂练习

1、如果S盒输入为:123456ABCDEF000100,100011,010001,010110,101010,111100,110111,101111(0,2), (3,1), (1,8), (0,11), (2,5), (2,14),(3,11) ,(3,7)13,8,2,5, 13,11,15,13D825DBFD2、假设DES算法的8个S盒都为S5,R0=FFFFFFFF,k1=555555555555(均为16进制),求F(R0,K1)的值。
答:扩展后的R0和K1异或的结果AAAAAAAAAAAA即1010 1010.......10 0101 2行5列第一圈S盒输出结果DDDDDDDDP盒置换结果BF9DF97B乘法逆元定义:如果gcd( a, b )=1,那么存在a-1,使得a * a-1≡1 mod b,即(a*a-1)mod b =1;存在b-1,使得b * b-1≡1 mod a,即(b*b-1)mod a =1;这里,把a-1称为a模b的乘法逆元,b-1称为b模a的乘法逆元。
欧几里得算法欧几里得算法基于以下定理:gcd( a, b ) = gcd( b, a mod b )算法描述:1、A ←a, B ← b;2、若B = 0, 则返回A = gcd( a, b );3、R = A mod B;4、A ← B;5、B ←R;6、转到2。
3、例求gcd(1180(A), 482(B))解:1180 = 2 * 482 +216482 = 2 * 216 +5050 = 3 * 16 + 216 = 8 * 2 + 0A = 2,B = 0所以,gcd(482,1180) = 24、求7模96的乘法逆元。
答:96 = 13 * 7 + 57 = 1 * 5 + 25 = 2 * 2 + 12 = 1 * 2 + 01 = 5 -2 * ( 7 - 1 * 5) =3 * 5 - 2 * 7= 3 * ( 96 - 13 * 7 ) - 2 * 7= 3 * 96 - 41 * 7= 3 * 96 - 41 * 7 + 96 *7 - 96 *7= (96 - 41)*7 - 4* 967模96的乘法逆元为96 - 41 = 555、求字符串“123456”(ASCII码值31 32 33 34 35 36)的MD5填充消息答:填充消息:消息长48,先填充1位1,然后填充423位0,再用消息长48,即0x00000000 00000030填充,则:M[0] = 31323334 M[1] = 35368000M[2] = 00000000 M[3] = 00000000……M[12]=00000000 M[13]=00000000M[14]=00000000 M[15]=00000030密钥的产生RSA公开密钥密码体制中每个参数的计算:①计算n:用户秘密地选择两个大素数p和q,计算出n pq②计算φ(n):φ(n) (p 1)(q 1)③选择e:从[1, φ(n) 1]中选择一个与φ(n)互素的数e作为公开的加密指数④计算d作为解密指数:用户计算出满足下式的ded 1 mod φ(n) 即:(ed –1) mod φ(n) = 0⑤得出所需要的公开密钥和秘密密钥:秘密密钥(即解密密钥)SK { d, n }p、q、φ(n)和d是秘密的陷门(相互不是独立的),不可泄露RSA加密消息m时(这里假设m是以十进制表示的),首先将消息分成大小合适的数据分组,然后对分组分别进行加密每个分组的大小应该比n小设ci为明文分组mi加密后的密文,则加密公式为ci=mie (mod n)解密时,对每一个密文分组进行如下运算:mi=cid (mod n)(encryption discryption )6、举例RSA的加/解密过程选p=5,q=11,则n= pq = 55,φ(n) = (p−1)(q−1) = 40随机选择e (与φ(n)互素)设e=7d要满足ed 1 mod φ(n)40 = 5 * 7 + 57 = 1 * 5 + 25 = 2 * 2 + 12 = 2 * 1 + 0公开密钥:{7,55}秘密密钥:{23,55}5 = 40 - 5 * 72 = 7 - 1 * 51 = 5 -2 * 21 = 5 -2 * (7 - 1 * 5)= 3 * 5 –2 * 7= 3 *(40 –5 * 7) –2 * 7= 3 * 40 –17 * 7= (40 - 17) * 7 –4 *40所以,d = 23ed = 7 * 23 = 1617、假设需要加密的密文信息c=16,选择e=3,p=5,q=11,试使用RSA算法求明文。
HTTPS原理的证书颁发机构

HTTPS原理的证书颁发机构HTTPS(Hyper Text Transfer Protocol Secure)是一种安全的通信协议,它通过使用SSL/TLS加密技术,为Web通信提供了安全保障。
而证书颁发机构(Certificate Authority,简称CA)是负责颁发和验证SSL证书的机构,它在确保通信安全方面起着至关重要的作用。
一、HTTPS协议简介HTTPS是基于HTTP协议的一种安全协议,它通过使用SSL/TLS协议,对传输的数据进行加密和认证,从而保证了通信过程的安全性。
SSL(Secure Sockets Layer)是Netscape公司在1994年推出的协议,后来逐渐发展为TLS(Transport Layer Security)协议。
TLS是由IETF (Internet Engineering Task Force)组织进行标准化,并取代了SSL协议。
二、SSL/TLS加密原理SSL/TLS协议使用了非对称加密和对称加密相结合的方式,以实现通信数据的机密性和完整性。
1. 非对称加密非对称加密(也称公钥加密)使用了两个密钥,一个是公钥,一个是私钥。
公钥可用于加密数据,私钥用于解密数据。
在HTTPS通信中,服务器拥有一个私钥,而公钥则被放在SSL证书中,可以由客户端获得。
2. 对称加密对称加密(也称为共享密钥加密)使用同一个密钥对数据进行加密和解密。
在HTTPS通信中,一旦建立了安全的通信连接,服务器和客户端之间的数据传输就会使用对称加密算法进行加密和解密。
3. 数字证书数字证书是一种由CA生成的电子文件,用于绑定公钥和实体(通常是网站)。
数字证书中包含了网站的公钥以及其他相关信息,同时还包括CA的签名,以确保证书的可信度。
客户端在与服务器建立HTTPS连接时,会接收到服务器的数字证书,通过验证数字证书的合法性和真实性,来判断是否建立安全的连接。
三、证书颁发机构的职责1. 证书的颁发CA负责颁发SSL证书给申请者,并在证书中绑定网站公钥和相关信息。
SSL-数字签名-数字信封-数字证书
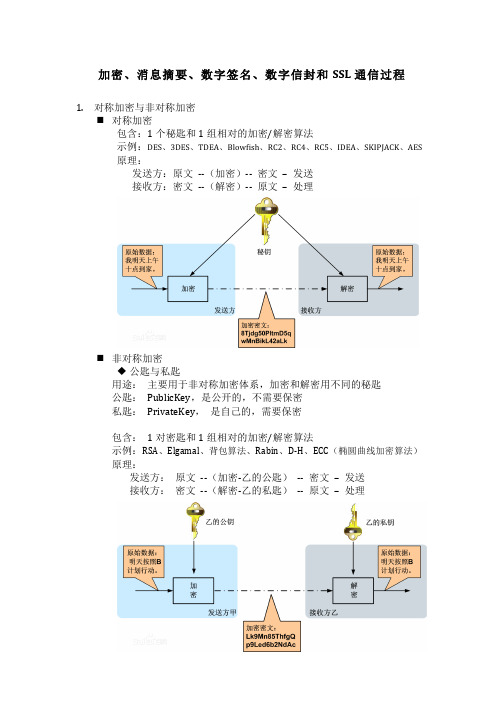
u 公匙与私匙 用途: 主要用于非对称加密体系,加密和解密用不同的秘匙 公匙: PublicKey,是公开的,不需要保密 私匙: PrivateKey, 是自己的,需要保密 包含: 1 对密匙和 1 组相对的加密/解密算法 示例:RSA、Elgamal、背包算法、Rabin、D-‐H、ECC(椭圆曲线加密算法) 原理:
图 4 数字签名示意图 1)Alice 准备了一份合同 M; 2)Alice 用摘要算法计算出该合同 M 的消息摘要 MD; 3)Alice 用自己的私钥对消息摘要 MD 进行加密,该密文 S 就是数字签名; 4)Alice 将合同 M 和合同的数字签名 S,一起传送到给接受者 Bob; 5)Bob 收到 Alice 的合同 M 及合同的数字签名 S; 6)Bob 用 Alice 公钥解密合同签名 S,得到 Alice 计算的合同摘要 MD; 7)Bob 采用相同摘要算法对收到的合同重新计算消息摘要 MD'; 8)Bob 比较 MD 与 MD'是否相等? 9)如结果相等,根据摘要算法的特性表明合同在传输过程中未被篡改。 同时由于非对称加密算法的特性可以断定合同确实是 Alice 发送的,因为用 Alice 公钥能解密成功的数据只有 Alice 用她自己私钥对其进行加密才能产 生,而她的私钥其它人是无法获取的。
继续进行) 证书是否过期,发行服务器证书的 CA 是否可靠,发行者证书的公钥能否正确解开 服务器证书的“发行者的数字签名”,服务器证书上的域名是否和服务器的实际域名 相匹配。 4) 客户端产生一个随机数用于后面通讯的“预主密码”,用服务器公钥对其加密,将其传 给服务器。 u 若服务器要求客户的身份认证(可选),客户端可以建立一个随机数然后对其进行
发送方: 原文 -‐-‐(加密-‐乙的公匙) -‐-‐ 密文 – 发送 接收方: 密文 -‐-‐(解密-‐乙的私匙) -‐-‐ 原文 – 处理
SSL与CA认证应用心得

某项目的业务系统要求在用户使用的过程使用数字证书。
在刚接手这个任务时,我对个中的知识几乎不了解,于是到处搜刮相关资料,网上此类文章甚多,但都比较零散,而且个人认为其中绝大部分未能尽释所疑。
在经历了数天的郁闷及实践以后,终有所悟,作此文以记。
1 对称加密与非对称加密对称加密方法的加密与解密采用相同的密钥,因此任何人只要获得其中的密钥,就可以对密文进行解密。
而非对称加密方法有两个不同密钥,任意一个都可以成为加密密钥,另外一个就是解密密钥,用一个密钥加密的密文必须用另一个密钥才可以解密。
2 公钥与私钥在非对称加密方法的两个密钥中,保管其中一个密钥,禁止泄漏他人,除了密钥拥有者以外,任何人都不知道,此即私钥。
另一个密钥则公之于众,任何人都可以获得,此即公钥。
可知,用私钥加密的密文必须用公钥解密,反之亦然。
3 数字签名数字签名是基于非对称加密方法来实现的。
拥有私钥的一方使用私钥对某一份内容加密后发送给其他人(个体或群休),因为任何人都可以拥有与该私钥对应的公钥,拥有公钥者使用公钥对接收到的密文进行解密,如果能正确解密,则说明此份内容必然是拥有私钥的一方发出。
另一方面,如果拥有公钥的实体希望把一份内容发送给拥有私钥的一方而不希望其它任何人看到,则可以利用该公钥加密此份内容。
因为只有私钥拥有者才可以将密文解密,所以能保证任何其他人无法查看其内容。
4 数字证书数字证书是以数字签名的方式通过第三方权威认证机构有效地进行网上身份认证,以帮助各个实体识别对方身份及表明自身身份的证书,具有防抵赖功能及真实、安全、保密和防篡改的特性。
在此,我们最主要的是需要知道数字证书是一个文件,该文件保存了某个实体(个人、机构或设备等)的信息及该实体所拥有私钥对应的公钥。
5 SSL协议这里主要介绍SSL握手协议以建立安全通信通道的过程。
1) 客户端的浏览器向服务器传送客户端 SSL 协议的版本号,加密算法的种类,产生的随机数,以及其他服务器和客户端之间通讯所需要的各种信息。
HTTPS原理解析及应用实例

HTTPS原理解析及应用实例HTTPS(Hypertext Transfer Protocol Secure)是一种通过加密和身份验证来保护网络通信的安全协议。
它是在HTTP协议基础上添加了SSL/TLS协议,通过使用SSL/TLS协议对数据进行加密,确保数据在传输过程中的安全性。
本文将对HTTPS的原理进行解析,并通过一些应用实例来说明其在实际场景中的应用。
一、HTTPS的原理解析HTTPS的原理主要基于SSL/TLS协议,它通过以下几个步骤来实现数据的安全传输:1. 客户端发起HTTPS请求:当用户在浏览器中输入一个以https://开头的网址时,浏览器会向服务器发送一个HTTPS请求。
2. 服务器发送数字证书:服务器接收到HTTPS请求后,会将自己的数字证书发送给客户端。
数字证书中包含了服务器的公钥。
3. 客户端验证数字证书:客户端收到服务器的数字证书后,会对其进行验证。
验证包括检查证书的合法性、是否过期以及证书颁发机构的可信度等。
4. 客户端生成会话密钥:如果数字证书验证通过,客户端会生成一个随机的会话密钥,并使用服务器的公钥进行加密,然后发送给服务器。
5. 服务器解密会话密钥:服务器收到客户端发送的加密的会话密钥后,使用自己的私钥进行解密,得到会话密钥。
6. 客户端与服务器建立安全连接:客户端和服务器使用会话密钥进行对称加密,保证数据在传输过程中的机密性和完整性。
二、HTTPS的应用实例HTTPS的应用广泛,下面将通过一些实际场景来说明其应用:1. 网络购物:在进行网络购物时,用户需要输入个人敏感信息,如信用卡号码等。
使用HTTPS协议可以保证这些信息在传输过程中的安全性,防止被黑客窃取。
2. 网上银行:网上银行是一个对安全性要求非常高的应用场景,使用HTTPS协议可以保证用户在网上银行操作过程中的安全性,防止被恶意攻击者篡改或窃取信息。
3. 社交媒体:社交媒体平台中,用户会上传和分享大量的个人照片、视频等敏感信息。
secretkey 密钥案例

secretkey 密钥案例SecretKey(密钥)是密码学中的一个重要概念,它用于对消息进行加密和解密。
在这里,我将列举10个与SecretKey密钥相关的案例,以帮助读者更好地理解和应用这一概念。
1. 对称加密算法中的SecretKey对称加密算法是一种使用相同的密钥进行加密和解密的算法。
在这种算法中,密钥被称为SecretKey。
常见的对称加密算法有DES、AES等。
SecretKey在加密和解密过程中起到关键的作用,它必须保密并且只能由通信双方共享。
2. 密钥的生成和管理生成和管理SecretKey是密钥管理的重要环节。
密钥生成需要使用随机数生成器生成足够随机的数据作为密钥。
密钥管理涉及到密钥的存储、传输和更新等方面,必须保证密钥的安全性和可靠性。
3. 密钥的安全传输在通信过程中,密钥的安全传输是非常重要的。
一旦密钥被截获,加密通信就会被窃听和破解。
为了确保密钥的安全传输,可以使用非对称加密算法对密钥进行加密,然后再传输。
4. 密钥的更新和轮换为了保证通信的安全性,密钥的定期更新和轮换是必要的。
密钥的更新可以通过定期生成新的密钥,并将新密钥与旧密钥进行转换。
密钥的轮换可以通过使用多个密钥并定期更换密钥来实现。
5. 密钥的分发和共享在多个通信参与者之间共享密钥是一项复杂的任务。
为了确保密钥的安全性,可以使用密钥分发中心(Key Distribution Center)来分发和管理密钥。
密钥分发中心负责生成密钥、分发密钥并确保密钥的安全性。
6. 密钥的存储和保护密钥的存储和保护是密钥管理的重要环节。
密钥的存储需要使用安全的存储介质,如硬件安全模块(Hardware Security Module)或智能卡等。
密钥的保护包括物理保护和逻辑保护两个方面,物理保护主要是通过控制访问和防止物理攻击来保护密钥,逻辑保护主要是通过加密和访问控制等技术来保护密钥。
7. 密钥的生命周期管理密钥的生命周期管理包括密钥的生成、分发、使用、更新和销毁等过程。
证书解析实例

证书解析实例(最新版)目录1.证书解析的概念和重要性2.证书解析的实例3.证书解析的实际应用4.证书解析的未来发展趋势正文1.证书解析的概念和重要性证书解析,是指对数字证书进行解析,从而获取证书中的信息。
数字证书是网络通信中常用的一种加密方式,可以确保信息传输的安全性。
在网络世界中,数字证书被广泛应用于各种场景,如网站身份验证、电子邮件加密等。
因此,证书解析的重要性不言而喻。
2.证书解析的实例证书解析的实例有很多,下面举一个常见的例子来说明。
假设,有一个网站(如淘宝网),该网站使用数字证书对用户信息进行加密保护。
作为用户,我们可以通过浏览器对网站证书进行解析,从而获取网站的真实身份,确保自己信息的安全。
具体操作如下:首先,打开该网站的安全证书,可以看到证书的详细信息,包括证书的持有者、证书的颁发者、证书的有效期等。
然后,点击证书,可以看到证书的详细信息,包括证书的持有者、证书的颁发者、证书的有效期等。
最后,可以通过证书的颁发者验证证书的真实性,以确保自己信息的安全。
3.证书解析的实际应用证书解析在实际应用中具有广泛的应用,如:(1)网站身份验证:通过证书解析,可以验证网站的真实身份,防止被钓鱼网站欺骗。
(2)电子邮件加密:通过证书解析,可以对电子邮件进行加密,确保邮件内容的安全性。
(3)移动应用安全:通过证书解析,可以确保移动应用的安全性,防止恶意软件的攻击。
4.证书解析的未来发展趋势随着网络技术的不断发展,证书解析也将迎来新的发展机遇。
未来,证书解析技术将会更加成熟,解析速度更快,解析精度更高。
同时,随着量子计算机的研发成功,量子计算机将会对现有的加密技术产生威胁,证书解析技术也将面临新的挑战。
C#使用RSA证书文件加密和解密示例

C#使⽤RSA证书⽂件加密和解密⽰例修改MSDN上的⽰例,使之可以通过RSA证书⽂件加密和解密,中间遇到⼀个⼩问题。
Q:执⾏ExportParameters()⽅法时,回报CryptographicException:该项不适于在指定状态下使⽤(Key not valid for use in specified state)。
A:导⼊带有私钥的证书时,需要使⽤"X509KeyStorageFlags"参数标记"私钥可导出"。
X509Certificate2 prvcrt = new X509Certificate2(@"X:\path\to\CA.pfx", "***password***", X509KeyStorageFlags.Exportable);以下为⽰例程序:View Codeusing System;using System.Collections.Generic;using System.Linq;using System.Text;namespace TeatApp_Crypto{using System;using System.Security.Cryptography;using System.Security.Cryptography.X509Certificates;using System.Text;class RSACSPSample{static void Main(){try{//Create a UnicodeEncoder to convert between byte array and string.UnicodeEncoding ByteConverter = new UnicodeEncoding();//Create byte arrays to hold original, encrypted, and decrypted data.byte[] dataToEncrypt = ByteConverter.GetBytes("Data to Encrypt");byte[] encryptedData;byte[] decryptedData;X509Certificate2 pubcrt = new X509Certificate2(@"X:\path\to\CA.crt");RSACryptoServiceProvider pubkey = (RSACryptoServiceProvider)pubcrt.PublicKey.Key;X509Certificate2 prvcrt = new X509Certificate2(@"X:\path\to\CA.pfx", "***password***", X509KeyStorageFlags.Exportable);RSACryptoServiceProvider prvkey = (RSACryptoServiceProvider)prvcrt.PrivateKey;//Create a new instance of RSACryptoServiceProvider to generate//public and private key data.//using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider())//{//Console.WriteLine(RSA.ToXmlString(false));//Pass the data to ENCRYPT, the public key information//(using RSACryptoServiceProvider.ExportParameters(false),//and a boolean flag specifying no OAEP padding.encryptedData = RSAEncrypt(dataToEncrypt, pubkey.ExportParameters(false), false);Console.WriteLine("Encrypted plaintext: {0}", Convert.ToBase64String(encryptedData));//Pass the data to DECRYPT, the private key information//(using RSACryptoServiceProvider.ExportParameters(true),//and a boolean flag specifying no OAEP padding.decryptedData = RSADecrypt(encryptedData, prvkey.ExportParameters(true), false);//Display the decrypted plaintext to the console.Console.WriteLine("Decrypted plaintext: {0}", ByteConverter.GetString(decryptedData));//}prvkey.Clear();pubkey.Clear();Console.Read();}catch (ArgumentNullException){//Catch this exception in case the encryption did//not succeed.Console.WriteLine("Encryption failed.");}}static public byte[] RSAEncrypt(byte[] DataToEncrypt, RSAParameters RSAKeyInfo, bool DoOAEPPadding){try{byte[] encryptedData;//Create a new instance of RSACryptoServiceProvider.using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider()){//Import the RSA Key information. This only needs//toinclude the public key information.RSA.ImportParameters(RSAKeyInfo);//Encrypt the passed byte array and specify OAEP padding.//OAEP padding is only available on Microsoft Windows XP or//later.encryptedData = RSA.Encrypt(DataToEncrypt, DoOAEPPadding);}return encryptedData;}//Catch and display a CryptographicException//to the console.catch (CryptographicException e){Console.WriteLine(e.Message);return null;}}static public byte[] RSADecrypt(byte[] DataToDecrypt, RSAParameters RSAKeyInfo, bool DoOAEPPadding) {try{byte[] decryptedData;//Create a new instance of RSACryptoServiceProvider.using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider()){//Import the RSA Key information. This needs//to include the private key information.RSA.ImportParameters(RSAKeyInfo);//Decrypt the passed byte array and specify OAEP padding.//OAEP padding is only available on Microsoft Windows XP or//later.decryptedData = RSA.Decrypt(DataToDecrypt, DoOAEPPadding);}return decryptedData;}//Catch and display a CryptographicException//to the console.catch (CryptographicException e){Console.WriteLine(e.ToString());return null;}}}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
加密与解密研究学习编写:laichOpenssl RSA 加密与解密理论RSA是什么:RSA公钥加密算法是1977年由Ron Rivest、Adi Shamirh和LenAdleman在(美国麻省理工学院)开发的。
RSA取名来自开发他们三者的名字。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的所有密码攻击,已被ISO推荐为公钥数据加密标准。
目前该加密方式广泛用于网上银行、数字签名等场合。
RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但那时想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
OpenSSL是什么:众多的密码算法、公钥基础设施标准以及SSL协议,或许这些有趣的功能会让你产生实现所有这些算法和标准的想法。
实践操作以Java为例这是windos7 下Openssl 路径:C:\openssl\binopenssl version -a先来生成私钥:openssl genrsa -out rsa_private_key.pem 1024会在bin 目录下生成rsa_private_key.pem生成的内容:-----BEGIN RSA PRIVATE KEY-----MIICXAIBAAKBgQDbJkpMThepmY82P4wYACp1OB8e8zE66tGfTpfIQu5a/29O8KkQ UklbVgPKh+rNZHFT6srrr0sFEpbIc0CZc75S4aXd58K9+smVcizgijzKC+y47ggf zVBhXHsaEvEcH+IMAW7VKZ4rhdydYUgP+i+XmBTyhXc9cBhR2LoAuS/mDwIDAQAB AoGABKh2sdKDHD7AVYXaQ3RVcrJjrvO6Wyc8l2dDQKVzjYmaYxIodclZ99AHOpnS+tSkuATolUPfk1cGz3HrsJdON0i02E/44U5DY1gVM1YJdJ5Wxwty1Hd57ph96yjycmH1Vl0UMRB4Cmaq0bYzpnmv0Ks1+nvMIacl8sE17RYHxqkCQQDtwkbgDHxb9o2E osy/7qCIapSOFui6sJaMCAgMFDOrhv7DRd3BTebVsKrjwJntty9Mr86UeGr+2Pqk FFIzDcO1AkEA6/aD83YRQs8PYEyef1ztdOrS66KTFpgPd/VufaeNaTJgyM8S2jxCuGavl48OJz+OJckrs4BNJ0JMhHbytn3lMwJAMLJc7+C+y9soyyTJCPqoGKizupKIokwu2Yl/lHHCz3v7zCUQMVpyUAw6RCGbpWuinXNYvWIYkBAC7f5Xg6trDQJBAK4w oWAM/NkQ+gzhAvCKrVDuOR5yOZsoTeMEb7ibBC1wXzpeg1BPxAFU7LM5i/01Ub5bL8OnJ02gB9SR6sMFVTkCQAk0W60+Yn4jaXAtvxy9gMDfAeYoVz30quCZXWitc406 QFhQPj8In5dKF4Ku92BamEyzoj5X7OtTdbYCwEpTAbg=-----END RSA PRIVATE KEY-----根据私钥生成公钥openssl rsa -in rsa_private_key.pem -out rsa_public_key.pem -pubout同样会在bin目录下生成rsa_public_key.pem生成内容:-----BEGIN PUBLIC KEY-----MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDbJkpMThepmY82P4wYACp1OB8e 8zE66tGfTpfIQu5a/29O8KkQUklbVgPKh+rNZHFT6srrr0sFEpbIc0CZc75S4aXd58K9+smVcizgijzKC+y47ggfzVBhXHsaEvEcH+IMAW7VKZ4rhdydYUgP+i+XmBTyhXc9cBhR2LoAuS/mDwIDAQAB-----END PUBLIC KEY-----这时候的私钥还不能直接被使用,需要进行PKCS#8编码:openssl pkcs8 -topk8 -in rsa_private_key.pem -out pkcs8_rsa_private_key.pem -nocryp t同样会在bin目录下生成pkcs8_rsa_private_key.pem生成内容:-----BEGIN PRIVATE KEY-----MIICdgIBADANBgkqhkiG9w0BAQEFAASCAmAwggJcAgEAAoGBANsmSkxOF6mZjzY/jBgAKnU4Hx7zMTrq0Z9Ol8hC7lr/b07wqRBSSVtWA8qH6s1kcVPqyuuvSwUSlshzQJlzvlLhpd3nwr36yZVyLOCKPMoL7LjuCB/NUGFcexoS8Rwf4gwBbtUpniuF3J1hSA/6L5eYFPKFdz1wGFHYugC5L+YPAgMBAAECgYAEqHax0oMcPsBVhdpDdFVysmOu87pbJzyXZ0NApXONiZpjEih1yVn30Ac6mdL61KS4BOiVQ9+TVwbPceuwl043SLTYT/jhTkNjWBUzVgl0nlbHC3LUd3numH3rKPJyYfVWXRQxEHgKZqrRtjOmea/QqzX6e8whpyXywTXtFgfGqQJBAO3CRuAMfFv2jYSizL/uoIhqlI4W6LqwlowICAwUM6uG/sNF3cFN5tWwquPAme23L0yvzpR4av7Y+qQUUjMNw7UCQQDr9oPzdhFCzw9gTJ5/XO106tLropMWmA939W59p41pMmDIzxLaPEK4Zq+Xjw4nP44lySuzgE0nQkyEdvK2 feUzAkAwslzv4L7L2yjLJMkI+qgYqLO6koiiTC7ZiX+UccLPe/vMJRAxWnJQDDpEIZula6Kdc1i9YhiQEALt/leDq2sNAkEArjChYAz82RD6DOEC8IqtUO45HnI5myhN4wRvuJsELXBfOl6DUE/EAVTsszmL/TVRvlsvw6cnTaAH1JHqwwVVOQJACTRbrT5ifiNpcC2/HL2AwN8B5ihXPfSq4JldaK1zjTpAWFA+Pwifl0oXgq73YFqYTLOiPlfs61N1tgLASlMBuA==-----END PRIVATE KEY-----至此,可用的密钥对已经生成好了,私钥使用pkcs8_rsa_private_key.pem,公钥采用rsa_public_key.pem。
补充,第一步生成的私钥文件编码是PKCS#1格式,这种格式Java其实是支持的,只不过多写两行代码而已:1.RSAPrivateKeyStructure asn1PrivKey = new RSAPrivateKeyStructure((ASN1Sequence) ASN1Sequence.fromByteArray(priKeyData));2.RSAPrivateKeySpec rsaPrivKeySpec = new RSAPrivateKeySpec(asn1PrivKey.getModulus(), asn1PrivKey.getPrivateExponent());3.KeyFactory keyFactory= KeyFactory.getInstance("RSA");4.PrivateKey priKey= keyFactory.generatePrivate(rsaPrivKeySpec);代码示例示例2 用JKD生成KEY 进行公私人钥对认证原理所谓的公钥认证,实际上是使用一对加密字符串,一个称为公钥(public key),任何人都可以看到其内容,用于加密;另一个称为密钥(private key),只有拥有者才能看到,用于解密。
通过公钥加密过的密文使用密钥可以轻松解密,但根据公钥来猜测密钥却十分困难。
ssh 的公钥认证就是使用了这一特性。
服务器和客户端都各自拥有自己的公钥和密钥。
为了说明方便,以下将使用这些符号。
Ac 客户端公钥Bc 客户端密钥As 服务器公钥Bs 服务器密钥在认证之前,客户端需要通过某种方法将公钥Ac 登录到服务器上。
认证过程分为两个步骤。
会话密钥(session key)生成客户端请求连接服务器,服务器将As 发送给客户端。
服务器生成会话ID(session id),设为p,发送给客户端。
客户端生成会话密钥(session key),设为q,并计算r = p xor q。
客户端将r 用As 进行加密,结果发送给服务器。
服务器用Bs 进行解密,获得r。
服务器进行r xor p 的运算,获得q。
至此服务器和客户端都知道了会话密钥q,以后的传输都将被q 加密。
认证服务器生成随机数x,并用Ac 加密后生成结果S(x),发送给客户端客户端使用Bc 解密S(x) 得到x客户端计算q + x 的md5 值n(q+x),q为上一步得到的会话密钥服务器计算q + x 的md5 值m(q+x)客户端将n(q+x) 发送给服务器服务器比较m(q+x) 和n(q+x),两者相同则认证成功非对称加密●服务器建立公钥:每一次启动sshd 服务时,该服务会主动去找/etc/ssh/ssh_host*的文件,若系统刚刚安装完成时,由于没有这些公钥,因此sshd 会主动去计算出这些需要的公钥,同时也会计算出服务器自己需要的私钥●客户端主动联机请求:若客户端想要联机到ssh 服务器,则需要使用适当的客户端程序来联机,包括ssh, putty 等客户端程序连接●服务器传送公钥给客户端:接收到客户端的要求后,服务器便将第一个步骤取得的公钥传送给客户端使用(此时应是明码传送,反正公钥本来就是给大家使用的)●客户端记录并比对服务器的公钥数据及随机计算自己的公私钥:若客户端第一次连接到此服务器,则会将服务器的公钥记录到客户端的用户家目录内的~/.ssh/known_hosts 。
若是已经记录过该服务器的公钥,则客户端会去比对此次接收到的与之前的记录是否有差异。
若接受此公钥,则开始计算客户端自己的公私钥●回传客户端的公钥到服务器端:用户将自己的公钥传送给服务器。
此时服务器:具有服务器的私钥与客户端的公钥,而客户端则是:具有服务器的公钥以及客户端自己的私钥,你会看到,在此次联机的服务器与客户端的密钥系统(公钥+私钥)并不一样,所以才称为非对称加密系统。
