2019-2020年中考数学总复习 第2讲 整式及其运算
2020中考数学总复习,整式及其运算+二次函数+直线与圆+平移与旋转
基础诊断
梳理自测，理解记忆
考点突破
分类讲练，以例求法
易错防范
辨析错因，提升考能
基础诊断
返回
1
知识梳理
1.整式：单项式和多项式统称为整式 (1)单项式：由数与字母或字母与字母相乘组成的代数式叫做单项式．
所有字母指数的和叫做单项式的次数，数字因数叫做单项式的系数． (2)多项式：由几个单项式相加组成的代数式叫做多项式．多项式里次
错误答案展示 ①x3·x5＝x3×5＝x15；②x4·x4＝2x4；③(am＋1)2＝a2m＋1；
D.a5÷a2＝a3
分析 根据合并同类项，可判断A错误； 根据同底数幂的乘法底数不变指数相加，可判断B错误； 根据幂的乘方底数不变指数相乘，可判断C错误； 根据同底数幂的除法底数不变指数相减，可判断D正确．
分析
答案
规律方法
规律方法
本题考查了同底数幂的运算法则，熟记法则并根据法则计算是解题关键．
练习1
(2016·苏州)下列运算结果正确的是( D )
A.a＋2b＝3ab
B.3a2－2a2＝1
C.a2·a4＝a8
D.(－a2b)3÷(a3b)2＝－b
分析 利用同底数幂的乘法运算法则以及合并同类项法则、积的乘方 运算法则分别计算得出答案． a＋2b无法计算；3a2－2a2＝a2；a2·a4＝a6；(－a2b)3÷(a3b)2＝－b.
练习4
(2016·邵阳)先化简，再求值：(m－n)2－m(m－2n)，其中m＝ 3 ， n＝ 2 . 解 原式＝m2－2mn＋n2－m2＋2mn＝n2， 当n＝时，原式＝2.
分析
答案
返回
易错防范
返回
易错警示系列 2 幂运算易出现的错误
2019-2020学年(陕西)中考数学总复习 第2讲 整式及其运算教学案.doc
2019-2020学年（陕西）中考数学总复习第2讲整式及其运算教学同类项的概念及合并同类项【例1】若－4x a y＋x2y b＝－3x2y，则a＋b＝__3__．【点评】(1)判断同类项时，看字母和相应字母的指数，与系数无关，也与字母的相关位置无关，两个只含数字的单项式也是同类项；(2)只有同类项才可以合并．1．(1)(2012·毕节)已知12x n －2m y 4与－x 3y 2n 是同类项，则(mn)2010的值为( C ) A ．2010 B ．－2010 C ．1 D ．－1(2)(2014·济宁)化简－5ab ＋4ab 的结果是( D )A ．－1B ．aC ．bD ．－ab整式的混合运算及求值【例2】 (2014·绍兴)先化简，再求值：a(a －3b)＋(a ＋b)2－a(a －b)，其中a ＝1，b ＝－12. 解：原式＝a 2－3ab ＋a 2＋2ab ＋b 2－a 2＋ab ＝a 2＋b 2＝1＋14＝54【点评】 注意多项式乘多项式的运算中要做到不重不漏，应用乘法公式进行简便计算，另外去括号时，要注意符号的变化，最后把所得式子化简，即合并同类项，再代值计算．2．(2012·杭州)化简2[(m －1)m ＋m(m ＋1)][(m －1)m －m(m ＋1)]，若m 是任意整数，请观察化简后的结果，你发现原式表示一个什么数？解：2[(m －1)m ＋m(m ＋1)][(m －1)m －m(m ＋1)]＝2(m 2－m ＋m 2＋m)(m 2－m －m 2－m)＝－8m 3.原式＝(－2m)3，表示3个－2m 相乘，或者说是一个立方数，8的倍数等乘法公式【例3】 (2013·义乌)如图①，从边长为a 的正方形纸片中剪去一个边长为b 的小正方形，再沿着线段AB 剪开，把剪成的两张纸片拼成如图②的等腰梯形．(1)设图①中阴影部分面积为S 1，图②中阴影部分面积为S 2，请直接用含a ，b 的代数式表示S 1和S 2；(2)请写出上述过程所揭示的乘法公式．解：(1)S 1＝a 2－b 2；S 2＝12(2b ＋2a)(a －b)＝(a ＋b)(a －b) (2)(a ＋b)(a －b)＝a 2－b 2【点评】 (1)在利用完全平方公式求值时，通常用到以下几种变形：①a 2＋b 2＝(a ＋b)2－2ab ；②a 2＋b 2＝(a －b)2＋2ab ；③(a＋b)2＝(a－b)2＋4ab；④(a－b)2＝(a＋b)2－4ab.注意公式的变式及整体代入的思想．(2)算式中的局部直接使用乘法公式、简化运算，任何时候都要遵循先化简，再求值的原则．3．(1)整式A与m2－2mn＋n2的和是(m＋n)2，则A＝__4mn__.(2)(2014·广州)已知多项式A＝(x＋2)2＋(1－x)(2＋x)－3.①化简多项式A；②若(x＋1)2＝6，求A的值．解：①A＝(x＋2)2＋(1－x)(2＋x)－3＝x2＋4x＋4＋2－2x＋x－x2－3＝3x＋3②(x＋1)2＝6，则x＋1＝±6，∴A＝3x＋3＝3(x＋1)＝±3 6试题计算①x3·x5；②x4·x4；③(a m＋1)2；④(－2a2·b)2；⑤(m－n)6÷(n－m)3.错解①x3·x5＝x3×5＝x15；②x4·x4＝2x4；③(a m＋1)2＝a2m＋1；④(－2a2·b)2＝－22a4b2；⑤(m－n)6÷(n－m)3＝(m－n)6－3＝(m－n)3.剖析幂的四种运算(同底数幂相乘、幂的乘方、积的乘方、同底数幂相除)是学习整式乘除的基础，对幂运算的性质理解不深刻，记忆不牢固，往往会出现这样或那样的错误．针对具体问题要分清问题所对应的基本形式，以便合理运用法则，对符号的处理，应特别引起重视．正解①x3·x5＝x3＋5＝x8；②x4·x4＝x4＋4＝x8；③(a m＋1)2＝a(m＋1)×2＝a2m＋2；④(－2a2·b)2＝(－2)2a4b2＝4a4b2；⑤(m－n)6÷(n－m)3＝(n－m)6÷(n－m)3＝(n－m)3.。
2019年中考数学专题复习 第二讲整式、因式分解 (共68张PPT)精品物理
答案:1
(3)由题意可知:m=-1,n=0,c=1, ∴原式=(-1)2015+2016×0+12017=0. 答案:0
【答题关键指导】 整体代入法求代数式值的三种方法 (1)直接整体代入求值:如果已知的代数式与要求的代 数式之间都含有相同的式子,只要把已知式子的值直 接代入到要求的式子中,即可得出结果.
(3)(2017·济宁中考)分解因式: ma2+2mab+mb2=____________.
【思路点拨】(1)先提取公因式,再利用平方差公式进 行分解. (2)通过两次提取公因式,来进行因式分解. (3)先提取公因式,再利用完全平方公式进行分解.
【自主解答】 (1)x3-x=x(x2-1)=x(x+1)(x-1). (2)原式=x(x-2)+(x-2)=(x+1)(x-2). (3)原式=m(a2+2ab+b2)=m(a+b)2.
【答题关键指导】 幂的运算的应用 (1)同底数幂的乘除法应用的前提是底数必须相同,若 底数互为相反数时,要应用积的乘方处理好符号问题, 转化成同底数,再应用法则.
(2)同底数幂的乘法、幂的乘方、积的乘方混合运算 的时候要注意三个方面:一是运算顺序,二是正确选择 法则,三是运算符号.
【变式训练】
2.(2017·潍坊中考)下列计算正确的是 ( )
A.a3×a2=a6
B.a3÷a=a3
C.a2+a2=a4
D.(a2)2=a4
【解析】选D.选项A是同底数幂的乘法,结果为a5,故选 项A错误;选项B是同底数幂的除法,结果为a2,故选项B 错误;选项C是合并同类项,结果为2a2,故选项C错误;选 项D是幂的乘方,底数不变,指数相乘,故选项D正确.
中考数学专题复习：第2课 整式及其运算优质课件PPT
【答案】 2
【类题演练 4】 (2018·扬州)计算：(2x＋3)2－(2x＋3)(2x －3)．
【解析】 原式＝4x2＋12x＋9－(4x2－9)＝12x＋18．
1．整式的加减实质就是合并同类项，整式的乘除实质就 是幂的运算．
2．本课主要用到以下三种数学思想方法： (1)数形结合思想： 在列代数式时，常常会遇到一种题型：题中提供一 定的图形，要求通过对图形的观察、探索，提取图 形中反馈的信息，并根据相关的知识列出相应的代 数式，也能用图形来验证整式的乘法和乘法公式．
A．34
B．1
C．23
D．98
【答案】 D
()
题型一 幂的运算
熟记法则，依照法则进行计算.
【典例 1】 有下列运算：①a2·a3＝a6；②(a3)2＝a6；③a5
÷a5＝a；④(ab)3＝a3b3．其中结果正确的个数为 ( )
A．1
B．2
C．3
D．4
【解析】 ①a2·a3＝a5，故本项错误；②(a3)2＝a6，故本 项正确；③a5÷a5＝1，故本项错误；④(ab)3＝a3b3，故本 项正确．故选 B．
注意公式的变形及整体思想的应用．
【典例 3】 (2018·河北)将 9．52 变形正确的是 ( ) A．9．52＝92＋0．52 B．9．52＝(10＋0．5)(10－0．5) C．9．52＝102－2×10×0．5＋0．52 D．9．52＝92＋9×0．5＋0．52
【解析】 9．52＝(10－0．5)2＝102－2×10×0．5＋0．52．
【答案】 C
【类题演练 3】 (2018·乐山)已知实数 a，b 满足 a＋b＝2，
ab＝34，则 a－b＝
()
A．1
中考数学专题训练第2讲整式(知识点梳理)
整式知识点梳理考点01 代数式1.代数式的概念：用运算符号把数和字母连接而成的式子叫作代数式。
单独一个数或一个字母也是代数式.运算符号是指加、减、乘、除、乘方等。
2.代数式的书写规则：（1）含有乘法运算的代数式的书写规则：字母与字母相乘，乘号一般可以省略不写，字母的排列顺序不变.数字与字母相乘，乘号一般也可以省略，但数字一定要写在字母的前面，且当数字是带分数时，必须写成假分数的形式.数字与数字相乘，乘号不能省略.带括号的式子与字母的地位相同。
（2）含有除法运算的代数式的书写规则：当代数式中含有除法运算时，一般不用“÷”，而改用分数线.因为分数线具有括号的作用，所以分数线又称括线。
（3）含有单位名称的代数式的书写规则：若代数式是和或差的形式，如需注明单位，则必须用括号把整个式子括起来后再写单位.若代数式是积或商的形式，则无需加括号，直接在代数式后面写出单位即可。
3.代数式的值（1）代数式的值：一般地，用具体数值代替代数式中的字母，按照代数式中指明的运算计算出的结果，叫作代数式的值。
（2）求代数式的值的步骤：第1步：代入，用具体数值代替代数式里的字母.第2步：计算，按照代数式里指明的运算，计算出结果。
（3）求代数式的值时要注意：一个代数式中的同一个字母，只能用同一个数值去代替.如果代数式里省略了乘号，那么字母用数值代替时要添上乘号，代入负数和分数时要加括号.代入数值时，不能改变原式中的运算符号及数字。
(4)运算时，要注意运算顺序。
（先算乘方，再算乘除，最后算加减，有括号的要求先算括号里面的）考点02 单项式和多项式一、单项式1.单项式的概念：如3、a 、xy 、ab 31-等这些代数式都是数字、字母、数字与字母的积、字母与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式。
2.单项式中不能含有加减法运算，但可以含有除法运算。
3.单项式的系数：单项式中的数字因数叫作这个单项式的系数，确定单项式的系数的注意事项：（1）确定单项式的系数时，最好现将单项式写成数与字母的乘积的形式，在确定系数.（2）圆周率π是常数，单项式中出现π时，应看作系数.（3）当一个单项式的系数是1或-1时，1通常省略不写，负数做系数应包括前面的符号.（4）单项式的系数是带分数时，通常写成假分数。
2024年中考数学总复习专题02整式复习划重点 学霸炼技法
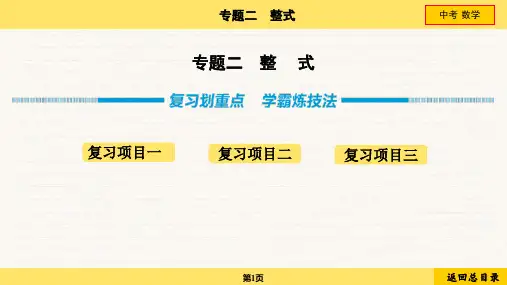
3．x 个单价为 a 元的商品与 y 个单价为 b 元的商品总价为
(_a_x_＋__b_y_)_元．
第11页
返回目录
专题二 整式
中考·数学
考点 2 整式的相关概念 1．单项式： (1)定义：表示数与字母的___积_____的式子叫做单项式，单 独的一个数或一个字母也是单项式． (2)性质：单项式中的____数__字__因__数__叫做这个单项式的系数；
[教材复习] 考点 1 代数式及其求值 1．代数式 用运算符号连接数和字母组成的式子，单独一个数或一个表
示数的字母也叫代数式．
第7页
返回目录
专题二 整式
中考·数学
2．列代数式 把问题中与数量有关的词语，用含有数字、字母和运算符号
的式子表示出来．关键是找出问题中的数量关系及公式，如：
“路程＝速度×时间”“售价＝标价×折扣”等；其次要抓
第4页
返回目录
专题二 整式
中考·数学
◎能推导乘法公式：(a＋b)(a－b)＝a2－b2，(a±b)2＝a2±2ab ＋b2，了解公式的几何背景，并能利用公式进行简单计 算； ◎能用提公因式法、公式法(直接利用公式不超过二次)进行 因式分解(指数是正整数).
Hale Waihona Puke 第5页返回目录专题二 整式
中考·数学
[对接教材]
第16页
返回目录
专题二 整式
中考·数学
考点 3 整式的运算
1．整式的加减
(1)合并同类项：①字母和字母的指数不变；②系数相加减
作为新的系数，如：3x2y＋4x2y＝7x2y.
(2)去括号法则：括号前是“＋”号，去括号时，括号内各项
不变号：a＋(b＋c)＝a____＋____b___＋_____c；
第02讲 代数式、整式与因式分解-2020年中考数学总复习专项讲解(人教版)
【试题精选】 12.(2018 年辽宁大连)因式分解：x2－x＝________________. 答案：x(x－1) 13.(2019 年湖北天门)分解因式：x4－4x2＝_____________. 答案：x2(x＋2)(x－2) 14.(2018 年四川自贡)分解因式：ax2＋2axy＋ay2_________. 答案：a(x＋y)2 15.(2017 年湖南长沙)分解因式：2a2＋4a＋2＝___________. 答案：2(a＋1)2
B.2(a－2)2 C.2(a＋2)(a－2) D.2(a＋2)2
答案：C
4.计算 x·(－x)5÷x2 的结果是__________.
答案：－x4
5.(2018 年浙江嘉兴)分解因式：m2－3m＝_____________.
答案：m(m－3)
代数式
1.(2019 年海南)当 m＝－1 时，代数式 2m＋3 的值是( )
③a5÷a5＝a；④(ab)3＝a3b3，其中结果正确的个数为( )
A.1 个
B.2 个
C.3 个 D.4 个
答案：B
整式运算
6.(2018 年四川成都)下列计算正确的是( )
A.x2＋x2＝x4
B.(x－y)2＝x2－y2
C.(x2y)3＝x6y
D.(－x)2·x3＝x5
答案：D
7.(2017 年江苏徐州)下列各式运算正确的是( )
A.b6÷b3＝b2
B.b3·b3＝b9
C.a2＋a2＝2a2
D.(a3)3＝a6
答案：C
4.(2017 年广东)下列运算正确的是( )
A.a＋2a＝3a2
B.a3·a2＝a5
C.(a4)2＝a6
D.a8÷a2＝a4
人教版九年级下册数学中考综合复习：第2讲《整式及其运算》
第2讲《整式及其运算》要点梳理知识点1：代数式及其求值:1.代数式：用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数和表示数的字母连接起来的式子叫做代数式，代数式不含等号．单独的一个数或一个字母_____(填“是”或“不是”)代数式．2.列代数式：把问题中与数量有关的词语，用含有字母和运算符号的式子表示出来．3.代数式求值：用数值代替代数式里的______，按照代数式中的运算关系计算得出结果． 知识点2：整式3.整式： 统称为整式。
4.同类项：多项式中所含 相同，并且 也相同的项。
如32b a -与32b a 21-；22xy 与2xy 31-同类项。
5.幂的运算法则（m,n 都是整数，a ≠0,b ≠0) 同底数幂相乘幂的乘方 积的乘方 同底数幂相除 am ·an ＝________(am)n ＝________ (ab)n ＝________ am ÷an ＝________1.单项式 概念 表示 或 的 的式子叫做单项式(单独的一个数字或字母也是单项式).如2xm,a ，5,0都是单项式。
系数单项式中的 叫做这个单项式的系数。
次数一个单项式中,所有字母的 叫做这个单项式的次数。
2.多项式 概念 几个单项式的 叫做多项式。
项 多项式中的 叫做多项式的项,不含字母的项叫做 ,如多项式x 3-2y+5的项数是 ,故称为 项式,其中x 3叫做 ，-2y 叫做 ，5叫做 。
次数 一个多项式中, 的项的次数叫做这个多项式的次数,如多项式x3y2+x2y-2y+3的最高次项 的次数是 ,故多项式的次数是 ,此多项式是 。
6．整式乘法7．乘法公式(1)平方差公式：____________________；(2)完全平方公式：__________________．8．整式除法1．法则公式的逆向运用法则公式既可正向运用，也可逆向运用．当直接计算有较大困难时，考虑逆向运用，可起到化难为易的功效．2．整式运算中的整体思想在进行整式运算或求代数式值时，若将注意力和着眼点放在问题的整体结构上，把一些紧密联系的代数式作为一个整体来处理．借助“整体思想”，可以拓宽解题思路，收到事半功倍之效．整体思想最典型的是应用于乘法公式中，公式中的字母a 和b 不仅可以表示单项式，也可以表示多项式，如(x －2y ＋z)(x ＋2y －z)＝[x －(2y －z)][x ＋(2y －z)]＝x 2－(2y －z)2＝x 2－4y 2＋4yz －z 2.3．乘法公式的常用变形：(1)a 2+b 2= ; (2)a 2+b 2= ;(3)(a+b)2= ; (4)(a-b)2= ;(5)a 2+b 2= ; (6)2ab= ; (7)4ab= . 单项式乘以单项式 把系数、同底数幂分别 作为积的 ，只在一个单项式里含有的 ，连同它的 一起作为积的一个 。
2020年中考数学复习专题02 整式及因式分解全面复习系列讲座
1.写答案前,需先写“解:”; 2.按“先化简,再求值”的要求解题, 千万不要把字母的值直接代入原式中 ; 3.化简结果应为最简形式; 4.按整式化简的顺序一步一步化简, 抓住能得分的解题步骤,切勿因跳步 而失分.
中考真题汇编
1．(2019·安徽)计算a3·(－a)的结果是
A．a2
B．－a2
( D)
(2)多项式为四项及以上时,通常需先分组,分组后再利用提公因式法或公式 法进行分解.
考点
因式分解
考点1 考点2 考点3 考点4
因式分解未分解到底 例:a4-1=(a2+1)(a2-1). 错因分析:(a2-1)没有分解! 正解:原式=(a2+1)(a2-1)=(a2+1)(a+1)(a-1).
方法
( C)
)
B
7.[2019·株洲]下列各式中，与 3x2y3 是同类项的是( C )
A．2x5
B．3x3y2
C．－12x2y3
D．－13y5
8．[2019·绵阳]单项式 x－|a－1|y 与 2x b－1y 是同类项，则 ab＝_1_________．
【解析】 由题意知－|a－1|＝ b－1≥0，∴a＝1，b＝1，则 ab＝11＝1. 思维升华 (1)同类项必须符合两个条件：第一，所含字母相同；第二，相同字母 的指数也相同；(2)根据同类项的概念列方程(组)是解此类题的一般方法．
方法
命题角度 4 数式规律
按照以上规律,解决下列问题.
(1)写出第5个等式:
.
(2)写出你猜想的第n个等式(用含n的等式表示
,n为正整数),并证明.
方法
命题角度 4 数式规律
规律探索题的解题方法 规律探索题通常给出一组数字、代数式、等式、不等式或图形, 要求学生通过观察、分析、猜想来探索规律,体现了从特殊到一 般的数学思想. 解题方法: (1)标序号; (2)分析各式或图形中的“变”与“不变”的规律——重点分析“怎样 变”,应结合各式或图形的序号进行前后对比分析; (3)根据各式或图形中的“变”与“不变”写出符合规律的式子. 注意:发现各式或图形与对应序号之间的关系是找出规律的关键.
第2讲 代数式及整式的运算(原卷版) 2020年中考数学优选知识点题型(一领三通)
第2讲 代数式及整式的运算一、考点知识梳理【考点1 代数式定义及列代数式】1.代数式：用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子叫做代数式．2．代数式的值：用数值代替代数式里的字母，按照代数式里的运算关系，计算后所得的结果叫做代数式的值．【考点2 幂的运算】1.同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．a m •a n ＝a m +n （m ，n 是正整数）2.幂的乘方法则：底数不变，指数相乘．（a m ）n ＝a mn （m ，n 是正整数）3.积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘．（ab ）n ＝a n b n （n 是正整数）4.同底数幂的除法法则：底数不变，指数相减．a m ÷a n ＝a m ﹣n （a ≠0，m ，n 是正整数，m ＞n ）【考点3 合并同类项】所含字母相同并且相同字母的指数也分别相同的项叫做同类项．所有的常数项都是同类项.把多项式中同类项合成一项，叫做合并同类项．合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．【考点4 整式的乘法】单项式乘以多项式m(a ＋b)＝am ＋bm多项式乘以多项式(a ＋b)(m ＋n)＝am ＋an ＋bm ＋bn二、考点分析【考点1 代数式定义及列代数式】【解题技巧】(1)在建立数学模型解决问题时，常需先把问题中的一些数量关系用代数式表示出来，也就是列出代数式；(2)列代数式的关键是正确分析数量关系，掌握文字语言(和、差、积、商、乘以、除以等)在数学语言中的含义；(3)注意书写规则：a×b 通常写作a·b 或ab ；1÷a 通常写作1a ；数字通常写在字母前面，如a×3通常写作3a ；带分数一般写成假分数，如115a 通常写作65a. 【例1】（2019.海南中考）当m ＝﹣1时，代数式2m +3的值是（ ）A ．﹣1B ．0C ．1D ．2【一领三通1-1】（2019.云南中考）按一定规律排列的单项式：x 3，﹣x 5，x 7，﹣x 9，x 11，……，第n 个单项式是（ ）A ．（﹣1）n ﹣1x 2n ﹣1B ．（﹣1）n x 2n ﹣1 C ．（﹣1）n ﹣1x 2n +1 D ．（﹣1）n x 2n +1 【一领三通1-2】（2019•台湾）图1的直角柱由2个正三角形底面和3个矩形侧面组成，其中正三角形面积为a ，矩形面积为b ．若将4个图1的直角柱紧密堆叠成图2的直角柱，则图2中直角柱的表面积为何？（ ）A ．4a +2bB ．4a +4bC ．8a +6bD ．8a +12b【一领三通1-3】（2019•台湾）小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面，x 杯饮料，y 份沙拉，则他们点了几份A 餐？（ ）A ．10﹣xB ．10﹣yC ．10﹣x +yD ．10﹣x ﹣y【考点2 幂的运算】【解题技巧】1.在应用同底数幂的乘法法则时，应注意：①底数必须相同，如23与25，（a 2b 2）3与（a 2b 2）4，（x ﹣y ）2与（x ﹣y ）3等；②a 可以是单项式，也可以是多项式；③按照运算性质，只有相乘时才是底数不变，指数相加．2.概括整合：同底数幂的乘法，是学习整式乘除运算的基础，是学好整式运算的关键．在运用时要抓住“同底数”这一关键点，同时注意，有的底数可能并不相同，这时可以适当变形为同底数幂．3.注意：①因式是三个或三个以上积的乘方，法则仍适用；②运用时数字因数的乘方应根据乘方的意义，计算出最后的结果．【例2】（2019•广东中考）下列计算正确的是（）A．b6+b3＝b2B．b3•b3＝b9C．a2+a2＝2a2D．（a3）3＝a6【一领三通2-1】（2019•甘肃中考）计算（﹣2a）2•a4的结果是（）A．﹣4a6B．4a6C．﹣2a6D．﹣4a8【一领三通2-2】（2019•海南中考）下列运算正确的是（）A．a•a2＝a3B．a6÷a2＝a3C．2a2﹣a2＝2D．（3a2）2＝6a4【一领三通2-3】（2019•江苏南京中考）计算（a2b）3的结果是（）A．a2b3B．a5b3C．a6b D．a6b3【一领三通2-4】（2019•山东济南中考模拟）在平面直角坐标系中，任意两点A（a，b），B（c，d），定义一种运算：A*B＝[（3﹣c），]，若A（9，﹣1），且A*B＝（12，﹣2），则点B的坐标是_______．【考点3 合并同类项】【解题技巧】合并同类项时要注意以下三点：（1）要掌握同类项的概念，会辨别同类项，并准确地掌握判断同类项的两条标准：带有相同系数的代数项；字母和字母指数；（2）明确合并同类项的含义是把多项式中的同类项合并成一项，经过合并同类项，式的项数会减少，达到化简多项式的目的；（3）“合并”是指同类项的系数的相加，并把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．（4）只要不再有同类项，就是结果(可能是单项式，也可能是多项式)．【例3】（2019•吉林长春中考）先化简，再求值：（2a+1）2﹣4a（a﹣1），其中a＝．【一领三通3-1】（2019•山东威海中考）下列运算正确的是（）A．（a2）3＝a5B．3a2+a＝3a3C．a5÷a2＝a3（a≠0）D．a（a+1）＝a2+1【一领三通3-2】（2019•辽宁沈阳中考）下列运算正确的是（）A．2m3+3m2＝5m5B．m3÷m2＝mC．m•（m2）3＝m6D．（m﹣n）（n﹣m）＝n2﹣m2【一领三通3-3】（2019•河北石家庄中考模拟）先化简，再求值：（5a2+2a+1）﹣4（3﹣8a+2a2）+（3a2﹣a），其中．【一领三通3-4】（2019•山东青岛中考模拟）化简求值：已知整式2x 2+ax ﹣y +6与整式2bx 2﹣3x +5y ﹣1的差不含x 和x 2项，试求4（a 2+2b 3﹣a 2b ）+3a 2﹣2（4b 3+2a 2b ）的值．【考点4 整式的乘法】【解题技巧】多项式的乘法要注意多项式中每一项不要漏乘，还要注意运算符号，遵循去括号的法则。
中考数学总复习 第2讲 整式及因式分解二次函数(基础讲
第2讲整式及因式分解考标要求考查角度1.明确字母表示数的真实内涵及其规范的书写格式，能用代数式探索有关的规律．2．会用语言文字叙述代数式的意义，同时掌握求代数式的值的方法．3．理解同类项的概念，掌握合并同类项的法则和去括号的法则以及乘法公式，能准确地进行整式的加、减、乘、除、乘方等混合运算．4．能对多项式进行因式分解.整式作为初中数学的基础内容之一，在中考试题中多以填空题和选择题的形式命题，重点考查其基本概念及运算法则，同时也会设计一些新颖的探索与数、式有关的规律性问题.知识梳理一、整式的有关概念1．整式整式是单项式与__________的统称．2．单项式单项式是指由数字或字母的乘积组成的式子；单项式中的________因数叫做单项式的系数；单项式中所有字母指数的____叫做单项式的次数．3．多项式几个单项式的______叫做多项式；多项式中，每一个________叫做多项式的项，其中不含字母的项叫做常数项；多项式中__________项的次数就是这个多项式的次数．二、整数指数幂的运算正整数指数幂的运算法则：a m·a n＝______，(a m)n＝______，(ab)n＝a n b n，a ma n＝a m－n(m，n是正整数)．三、同类项与合并同类项1．同类项所含字母相同，并且相同字母的______也分别相同的项叫做同类项．2．合并同类项把多项式中的同类项合并成一项叫做____________，合并的法则是系数相加，所得的结果作为合并后的______，字母和字母的指数不变．四、求代数式的值1．代数式的值一般地，用数值代替代数式里的字母，按照代数式指明的运算关系计算出的结果就叫做代数式的值．2．求代数式的值的基本步骤(1)代入：一般情况下，先对代数式进行化简，再将数值代入；(2)计算：按代数式指明的运算关系计算出结果．五、整式的运算1．整式的加减(1)整式的加减实质就是合并同类项；(2)整式加减的步骤：有括号，先去括号；有同类项，再合并同类项．注意去括号时，如果括号前面是负号，括号里各项的符号要______．2．整式的乘除(1)整式的乘法．①单项式与单项式相乘：把______、__________分别相乘，作为积的因式，只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．②单项式与多项式相乘：m (a ＋b ＋c )＝ma ＋mb ＋mc ．③多项式与多项式相乘：(m ＋n )(a ＋b )＝ma ＋mb ＋na ＋nB ． (2)整式的除法．①单项式除以单项式：把系数、同底数幂相除，作为商的因式，对于只在被除式里含有的字母，则连同它的______作为商的一个因式．②多项式除以单项式：(a ＋b )÷m ＝a ÷m ＋b ÷m . 3．乘法公式(1)平方差公式：(a ＋b )(a －b )＝a 2－b 2；(2)完全平方公式：(a ±b )2＝a 2±2ab ＋b 2. 六、因式分解1．因式分解的概念把一个多项式化成几个整式的____的形式，叫做多项式的因式分解． 2．因式分解的方法 (1)提公因式法．公因式的确定：第一，确定系数(取各项整数系数的最大公约数)；第二，确定字母或因式底数(取各项的相同字母)；第三，确定字母或因式的指数(取各相同字母的最低次幂)．(2)运用公式法．①运用平方差公式：a 2－b 2＝__________.②运用完全平方公式：a 2±2ab ＋b 2＝________. 3．因式分解的一般步骤一提(提取公因式法)；二套(套公式法)．一直分解到不能分解为止． 自主测试1．(2012福建福州)下列计算正确的是( )A ．a ＋a ＝2aB ．b 3·b 3＝2b 3C ．a 3÷a ＝a 3D ．(a 5)2＝a 72．下列各式中，与x 2y 是同类项的是( )A ．xy 2B ．2xyC ．－x 2yD ．3x 2y 23．(2012四川绵阳)图(1)是一个长为2m ，宽为2n (m ＞n )的长方形，用剪刀沿图中虚线(对称轴)剪开，把它分成四块形状和大小都一样的小长方形，然后按图(2)那样拼成一个正方形，则中间空白部分的面积是( )A ．2mnB ．(m ＋n )2C ．(m －n )2D ．m 2－n 24．(2012四川宜宾)分解因式：3m 2－6mn ＋3n 2＝__________.5．单项式－3π5m 2n 的系数是______，次数是______．考点一、整数指数幂的运算【例1】 (2012湖南郴州)下列计算正确的是( )A ．a 2·a 3＝a 6B ．a ＋a ＝a 2C ．(a 2)3＝a 6D ．a 8÷a 2＝a 4解析：A 项是同底数幂的乘法，a 2·a 3＝a 2＋3＝a 5，故A 项错误；B 项是整式的加减运算，a ＋a ＝2a ，故B 项错误；C 项是幂的乘方，(a 2)3＝a 2×3＝a 6，故C 项正确；D 项是同底数幂的除法，a 8÷a 2＝a 8－2＝a 6，故D 项错误．答案：C方法总结 幂的运算问题除了注意底数不变外，还要弄清幂与幂之间的运算是乘、除还是乘方，以便确定结果的指数是相加、相减还是相乘．触类旁通1下列运算中，正确的是( )A ．x 3·x 2＝x 5B ．x ＋x 2＝x3C ．2x 3÷x 2＝xD ．⎝ ⎛⎭⎪⎫x 23＝x 32考点二、同类项与合并同类项【例2】 单项式－13x a ＋b y a －1与3x 2y 是同类项，则a －b 的值为( )A ．2B ．0C ．－2D ．1解析：本题主要考查了同类项的概念及方程组的解法，由－13x a ＋b y a －1与3x 2y 是同类项，得⎩⎪⎨⎪⎧a ＋b ＝2，a －1＝1，解得⎩⎪⎨⎪⎧a ＝2，b ＝0.所以a －b ＝2－0＝2. 答案：A方法总结 1.同类项必须具备以下两个条件：(1)所含字母相同；(2)相同字母的指数分别相同．二者必须同时具备，缺一不可；2．同类项与项的系数无关，与项中字母的排列顺序无关，如xy 2与－y 2x 也是同类项． 3．根据同类项概念，相同字母的指数相同，列方程(组)是解此类题的一般方法．触类旁通2如果3x 2n －1y m 与－5x m y 3是同类项，则m 和n 的取值是( ) A ．3和－2 B ．－3和2 C ．3和2 D ．－3和－2 考点三、整式的运算【例3】 先化简，再求值：(a ＋b )(a －b )＋(a ＋b )2－2a 2，其中a ＝3，b ＝－13.解：(a ＋b )(a －b )＋(a ＋b )2－2a 2＝a 2－b 2＋a 2＋2ab ＋b 2－2a 2＝2ab ，当a ＝3，b ＝－13时，2ab ＝2×3×⎝ ⎛⎭⎪⎫－13＝－2. 方法总结 整式的乘法法则和除法法则是整式运算的依据，必须在理解的基础上加强记忆，并在运算时灵活运用法则进行计算．使用乘法公式时，要认清公式中a ，b 所表示的两个数及公式的结构特征，注意套用公式．触类旁通3 已知2x －1＝3，求代数式(x －3)2＋2x (3＋x )－7的值． 考点四、因式分解【例4】 (2012湖南常德)分解因式：m 2－n 2＝__________. 答案：(m ＋n )(m －n )方法总结 (1)因式分解时有公因式的要先提取公因式，再考虑是否应用公式法或其他方法继续分解．(2)提取公因式时，若括号内合并的项有公因式，应再次提取；注意符号的变换y －x ＝－(x －y )，(y －x )2＝(x －y )2.(3)应用公式法因式分解时，要牢记平方差公式和完全平方公式及其特点． (4)因式分解要分解到每一个多项式不能分解为止．1．(2012湖南常德)下列运算中，结果正确的是( )A ．a 3·a 4＝a 12B ．a 10÷a 2＝a 5C ．a 2＋a 3＝a 5D ．4a －a ＝3a 2．(2012湖南益阳)下列计算正确的是( )A ．2a ＋3b ＝5abB ．(x ＋2)2＝x 2＋4C ．(ab 3)2＝ab 6D ．(－1)0＝13．(2012湖南湘潭)因式分解：m 2－mn ＝__________.4．(2012湖南益阳)写出一个在实数范围内能用平方差公式分解因式的多项式：__________.5．(2012湖南怀化)当x ＝1，y ＝15时，3x (2x ＋y )－2x (x －y )＝__________.6．(2012湖南株洲)一组数据为：x ，－2x 2,4x 3，－8x 4，…观察其规律，推断第n 个数据应为__________．1．将代数式x 2＋4x －1化成(x ＋p )2＋q 的形式为( )A ．(x －2)2＋3B ．(x ＋2)2－4C ．(x ＋2)2－5D ．(x ＋2)2＋42．如图所示，在边长为a 的正方形中剪去一个边长为b 的小正方形(a ＞b )，把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式( )A ．(a ＋b )2＝a 2＋2ab ＋b 2B ．(a －b )2＝a 2－2ab ＋b 2C ．a 2－b 2＝(a ＋b )(a －b )D ．(a ±b )2＝a 2±2ab ＋b 23．多项式__________与m 2＋m －2的和是m 2－2m .4．若3x m ＋5y 2与x 3y n 的和是单项式，则n m＝__________.5．若m －n ＝2，m ＋n ＝5，则m 2－n 2的值为__________．6．若2x ＝3,4y ＝5，则2x －2y的值为__________．7．给出3个整式：x 2,2x ＋1，x 2－2x .(1)从上面3个整式中，选择你喜欢的两个整式进行加法运算，若结果能因式分解，请将其因式分解；(2)从上面3个整式中，任意选择两个整式进行加法运算，其结果能因式分解的概率是多少？参考答案 【知识梳理】一、1.多项式 2.数字 和 3．和 单项式 次数最高二、a m ＋n a mn三、1.指数 2.合并同类项 系数 五、1.(2)变号2．(1)①系数 同底数幂 (2)①指数 六、1.积2．(2)①(a ＋b )(a －b ) ②(a ±b )2导学必备知识 自主测试1．A a ＋a ＝2a ，A 项正确；b 3·b 3＝b 6，B 项错误；a 3÷a ＝a 2，C 项错误；(a 5)2＝a 10，D 项错误．2．C 只有C 选项中相同字母的指数与x 2y 分别相同．3．C 因为长方形的长为2m ，宽为2n (m ＞n )，则小长方形的长为m ，宽为n ，小正方形的边长为(m －n )，所以面积是(m －n )2.4．3(m －n )2 原式＝3(m 2－2mn ＋n 2)＝3(m －n )2.5．－3π53探究考点方法触类旁通1.A A 项是同底数幂相乘，x 3·x 2＝x3＋2＝x 5，B 项中的两项不是同类项，不能合并，C 项是单项式相除，2x 3÷x 2＝(2÷1)x 3－2＝2x ，D 项⎝ ⎛⎭⎪⎫x 23＝x 323＝x38.触类旁通 2.C 此题考查同类项概念和二元一次方程组的解法，由题意得⎩⎪⎨⎪⎧ 2n －1＝m ，m ＝3，解得⎩⎪⎨⎪⎧m ＝3，n ＝2. 触类旁通3.分析：本题需先把2x －1＝3进行整理，得出x 的值，把代数式进行化简，再把x 的值代入即可求出结果．解：由2x －1＝3得x ＝2，又(x －3)2＋2x (3＋x )－7＝x 2－6x ＋9＋6x ＋2x 2－7＝3x 2＋2，∴当x ＝2时，原式＝14.品鉴经典考题1．D a 3·a 4＝a 7，所以A 项不正确；a 10÷a 2＝a 8，所以B 项不正确；a 2与a 3不是同类项，不能合并，所以C 项不正确；4a －a ＝3a ，D 项正确．2．D 2a 与3b 不能合并，A 项不正确；(x ＋2)2＝x 2＋4x ＋4，B 项不正确；(ab 3)2＝a 2b 6，C 项不正确；由任何一个不等于零的数的零次幂等于1，知D 项正确．3．m (m －n ) m 2－mn ＝m (m －n )．4．答案不唯一，如x 2－1.5．5 3x (2x ＋y )－2x (x －y )＝6x 2＋3xy －2x 2＋2xy ＝4x 2＋5xy .当x ＝1，y ＝15时，原式＝4×12＋5×1×15＝4＋1＝5.6．(－2)n －1x n x 的系数为1＝(－2)1－1，次数为1；－2x 2的系数为－2＝(－2)2－1，次数为2；4x 3的系数为4＝(－2)3－1，次数为3；－8x 4的系数为－8＝(－2)4－1，次数为4；….所以第n 个数据的系数为(－2)n －1，次数为n ，即(－2)n －1x n.研习预测试题1．C x 2＋4x －1＝(x 2＋4x ＋4)－4－1＝(x ＋2)2－5.2．C 因为第一个图是一个大的正方形挖去了一个小的正方形，其面积表达式为a 2－b 2.第二个图是一个梯形，下底为2a ，上底为2b ，高为(a －b )，其面积为12(2a ＋2b )(a －b )＝(a＋b )(a －b )，所以两个图验证了公式：a 2－b 2＝(a ＋b )(a －b )．3．2－3m 由题意得此多项式为(m 2－2m )－(m 2＋m －2)＝m 2－2m －m 2－m ＋2＝2－3m . 4.14 由题意得m ＋5＝3，n ＝2，所以m ＝－2，所以n m ＝2－2＝122＝14. 5．10 m 2－n 2＝(m ＋n )(m －n )＝5×2＝10. 6.35 2x －2y ＝2x ÷22y ＝2x ÷4y ＝3÷5＝35. 7．解：(1)x 2＋(2x ＋1)＝x 2＋2x ＋1＝(x ＋1)2或x 2＋(x 2－2x )＝2x 2－2x ＝2x (x －1)或(2x＋1)＋(x 2－2x )＝2x ＋1＋x 2－2x ＝x 2＋1.(2)由(1)可知，概率为23.。
部编版2020年中考数学总复习 第2讲 整式与因式分解 新版 新人教版
一、知识清单梳理
知识点一：代数式及相关概念
关键点拨及对应举例
1.代数式
（1）代数式：用运算符号 （加、减、乘、除、乘方、开方）把数或表示数的字母连接而成的式子，单独的一个数或一个字母也是代数式．
（2）求代数式的值：用具体数值代替代数式中的字母，计算得出的结果，叫做求代数式的值．
求代数式的 值常运用整 体代入法计算.
例：a－b＝3，则3b－3a＝－9.
2.整式（单项式、多项式）
（1）单项式：表示数字与字母积的代数式，单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数，所有字母的指数和叫做单项式的次数.
（2）多项式：几个单项式的和.多项式 Nhomakorabea的每一项叫做多项式的项，次数最高的项的次数叫做多项式的次数.
(5)多项式÷单项式：①多项式的每一项除以单项式；②商相加．
失分警示：计算多项式乘以多项式时，注意不能漏乘，不能丢项，不能出现变号错.
例：(2a－1)(b＋2)＝2ab＋4a－b－2.
（6） 乘法
公式
平方差公式：(a＋b)(a－b)＝a2－b2.
注意乘法公 式的逆向运用及其变形公式的运用
完全平方公式：(a±b)2＝a2±2ab＋b2.变形公式：
例：－2(3a－2b－1)＝－6a＋4b＋2.
4.幂运算法则
(1)同底数幂的乘法：am·an＝am ＋n；
(2)幂的乘方：(am)n＝amn；
(3)积的乘方：(ab)n＝an·bn；
(4)同底数幂的除法：am÷an＝am－n(a≠0).
其中m,n都在整数
(1)计算时，注意观察，善于运用 它们的逆运算解决问题.例：已知2m+n=2,则3×2m×2n=6.
专题02 整式加减及其运算(6大考点)-2023年中考数学总复习真题探究与变式训练(解析版)
第一部分数与式专题02 整式加减及其运算（6大考点）核心考点一列代数式及代数式求值核心考点二整式的有关概念及运算核心考点三乘法公式的应用核心考点四整式的化简求值核心考点五因式分解核心考点核心考点六规律探索题新题速递核心考点一列代数式及代数式求值例1（2022·贵州六盘水·中考真题）已知，则的值是（）A．4B．8C．16D．12【分析】令，代入已知等式进行计算即可得．【详解】解：观察所求式子与已知等式的关系，令，则，故选：C ．，求代数式的值．”可以这样解：．根据阅读材料，解决问题：若是关于x的一元一次方程的解，则代数式的值是________．【答案】【分析】先根据是关于x的一元一次方程的解，得到，再把所求的代数式变形为，把整体代入即可求值．【详解】解：∵是关于x的一元一次方程的解，∴，∴．故答案为：14，的正方形秧田，，其中不能使用的面积为．(1)用含，的代数式表示中能使用的面积___________；(2)若，，求比多出的使用面积．【答案】(1)(2)50【分析】（1）利用正方形秧田的面积减去不能使用的面积即可得；（2）先求出中能使用的面积为，再求出比多出的使用面积为，利用平方差公式求解即可得．【详解】（1）解：中能使用的面积为，故答案为：．（2）解：中能使用的面积为，则比多出的使用面积为，，，，答：比多出的使用面积为50．【点睛】本题考查了列代数式、平方差公式与图形面积，熟练掌握平方差公式是解题关键．代数式及求值(1)概念：用基本运算符号(加、减、乘、除、乘方、开方等)把数或表示数的字母连接而成的式子叫代数式．单独的一个数或一个字母也是代数式；(2)列代数式：找出数量关系，用表示已知量的字母表示出所求量的过程；(3)代数式求值：把已知字母的值代入代数式中，并按原来的运算顺序计算求值．【变式1】（2022·山东济宁·三模）若是方程的两个根，则的值为（ ）A．9B．8C．7D．5【答案】A【分析】根据一元二次方程根的定义以及根与系数的关系，求解即可．【详解】解：是方程的两个根，则，，∴，，故选：A【点睛】此题考查了一元二次方程根的定义以及根与系数的关系，解题的关键是熟练掌握相关基础知识．【变式2】（2022·甘肃·平凉市第十中学三模）十八世纪伟大的数学家欧拉最先用记号的形式来表示关于的多项式，把等于某数时一的多项式的值用来表示．例如时，多项式的值可以记为，即我们定义．若，则的值为（）A．B．C．D．【答案】C【分析】代入多项式可以得，把整体代入求解即可．【详解】，，得：，，故选：C．【点睛】本题考查求代数式的值，整体代入是解题的关键．【变式3】（2022·浙江丽水·一模）已知，实数m，n满足，．（1）若，则_______；（2）若，则代数式的值是______________．【答案】 7 42或252##252或42【分析】（1）将已知式子因式分解代入得出，然后利用两个完全平方公式之间的关系求解即可；（2）利用（1）中结论得出或，然后分两种情况，将原式化简代入求值即可．【详解】解：（1）∵m+n=3，∴，∴，∴，∴，∵m>n，∴，∴；（2），由（1）得或解得：或当m=5，时，∵，∴，∴m+p=2，∴原式；当，n=5时，∵，∴，∴，∴原式；∴代数式的值为42或252；故答案为：①7；②42或252．【点睛】题目主要考查因式分解的运用，求代数式的值及完全平方公式与平方差公式，熟练掌握运算法则进行变换是解题关键．【变式4】（2022·福建省福州屏东中学模拟预测）已知，，且，则代数式的值是______ ．【答案】【分析】先计算，利用平方差公式求出的值，再把化为完全平方式，代入求值即可．【详解】解：，，．∴．，．．故答案为：．【点睛】本题考查了平方差公式和完全平方式，代数式求值，掌握平方差公式和完全平方式的特点，利用平方差公式求出的值，是解决本题的关键．【变式5】（2022·安徽芜湖·模拟预测）阅读下列材料，完成后面的问题．材料1：如果一个四位数为（表示千位数字为a，百位数字为b，十位数字为c，个位数字为d的四位数，其中a为1～9的自然数，b，c，d为0～9的自然数），我们可以将其表示为：；材料2：把一个自然数（个位不为0）的各位数字从个位到最高位倒序排列，得到一个新的数．我们称该数为原数的兄弟数．如数“123”的兄弟数为“321”．(1)四位数______；（用含x，y的代数式表示）(2)设有一个两位数，它的兄弟数比原数大63，请求出所有可能的数；(3)求证：四位数一定能被101整除．【答案】(1)1000x+10y+505(2)18、29(3)证明过程见详解【分析】（1）依据材料1的方法即可作答；（2）先根据（1）的方法表示出和，在结合题意列出二元一次方程，化简得：，再根据x、y均是1至9的自然数即可求解；（3）利用（1）的方法表示出，依据a为1～9的自然数，b为0～9的自然数，可得10a+b必为整数，即命题得证．(1)根据题意有：，即答案为：；(2)∵，，又∵，∴，∴，∵根据题意有x、y均是1至9的自然数，∴满足要求的x、y的数组有：（1,8）、（2,9），∴可能的数有18和29；(3)证明：∵，∴，∵a为1～9的自然数，b为0～9的自然数，∴10a+b必为整数，∴一定能被101整除，命题得证．【点睛】本题考查了列代数式和求解二元一次方程的整数解的知识，充分理解材料1、2所给的新定义是解答本题的关键．核心考点二整式的有关概念及运算例1（2021·四川绵阳·中考真题）整式的系数是（）A．-3B．3C．D．【答案】A【详解】解：的系数为本题主要考查了单项式的系数，追踪性高等特点，它已被广泛应用于我们的日常生活中，尤其在全球“新冠”疫情防控期间，区区“二维码”已经展现出无穷威力．看似“码码相同”，实则“码码不同”．通常，一个“二维码”由1000个大大小小的黑白小方格组成，其中小方格专门用做纠错码和其他用途的编码，这相当于1000个方格只有200个方格作为数据码．根据相关数学知识，这200个方格可以生成个不同的数据二维码，现有四名网友对的理解如下：YYDS（永远的神）：就是200个2相乘，它是一个非常非常大的数；DDDD（懂的都懂）：等于；JXND（觉醒年代）：的个位数字是6；QGYW（强国有我）：我知道，所以我估计比大．其中对的理解错误的网友是___________（填写网名字母代号）．用，将化为，再与比较，即可判断的乘方的个位数字的规律即可判断的逆用可得，即可判断【详解】是200个2相乘，YYDS，DDDD（懂的都懂）的理解是错误的；，2的乘方的个位数字4个一循环，，的个位数字是，，且，故QGYW（强国有我）的理解是正确的；故答案为：DDDD．【点睛】本题考查了乘方的含义，幂的乘方的逆用等，熟练掌握乘方的含义以及乘方的运算第1个等式：，第2个等式：，第3个等式：，第4个等式：，……按照以上规律．解决下列问题：(1)写出第5个等式：________；(2)写出你猜想的第n个等式（用含n的式子表示），并证明．【答案】(1)(2)，证明见解析【分析】（1）观察第1至第4个等式中相同位置的数的变化规律即可解答；（2）观察相同位置的数变化规律可以得出第n个等式为，利用完全平方公式和平方差公式对等式左右两边变形即可证明．（1）解：观察第1至第4个等式中相同位置数的变化规律，可知第5个等式为：，故答案为：；（2）解：第n个等式为，证明如下：等式左边：，等式右边：，故等式成立．【点睛】本题考查整式规律探索，发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键．整式及有关概念(1)单项式：由数与字母或字母与字母相乘组成的代数式叫做单项式，所有字母指数的和叫做单项式的_次数，单项式中的数字因数叫做单项式的系数．单独的数、字母也是单项式；(2)多项式：由几个单项式组成的代数式叫做多项式，多项式里次数最高项的次数叫多项式的次数，一个多项式中的每个单项式叫做多项式的项，其中不含字母的项叫做常数项；(3)整式：单项式和多项式统称为整式；(4)同类项：多项式中所含字母相同并且相同字母的指数也相同的项，叫做同类项；所有的常数项都是同类项．整式的运算1．同底数幂的乘法法则：（都是正整数）同底数幂相乘，底数不变，指数相加。
2023年中考数学备考学案：第2课时+《数与式》之整式与因式分解
第2课时 整式与因式分解学习目标：1．掌握整式的运算法则和幂的运算性质，准确地进行整式的混合运算；2．理解因式分解的概念，准确地对多项式进行因式分解．学习过程：一、问题唤醒1．用代数式表示：一个两位数，个位上的数字为x ，十位上的数字比个位上的数字小2，则这个两位数是__________．2．单项式2372y x -的系数是_________，次数是_________． 3．下列单项式中，与2ab 是同类项的是（ ）A ．b a 22B ．22a bC ．2abD ．ab 34．直接写出结果：32a a ⋅＝______，37a a ÷＝______，53)(a ＝______，2)(ab ＝______．5．化简：a a 53-＝_________，22(1)m m ＝_________．6．因式分解：x x 22-＝_________，942-x ＝_________，1682++a a ＝_________，26x x ＝_________，2232x x ＝_________．二、问题导学【知识点1】：整式的混合运算例1：化简：(1))5)(1()4(+--+m m m m 225)2()2)(2(2a b a b a b a -++-+）（同质训练：先化简再求值：22)()2)((x y x y x y x -----，其中.1202312023+=-=y x ，【知识点2】：因式分解例2：将下列多项式进行因式分解（1）42-x（2）x x x 9623+-（3）)()(22y x y y x x --- （4）256x x同质训练：将下列多项式进行因式分解（1）122++a a （2）29ab a -（3）3522-+x x （4）222224)(b a b a -+（5）1)(2)(2++-+y x y x （6）)1()2)(1--+-x x x x （【知识点3】：代数式求值问题例3：已知122--a a 的值为0，则4632--a a 的值为_________.同质训练：如果22320190x x --=，那么32220222020x x x ---=_________.【知识点4】：规律题例4：如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数－2所对应的点重合，再让圆沿着数轴按顺时针方向滚动，那么数轴上的数－2017将与圆周上的哪个数字重合（ ）A ．0B ．1C ．2D ．3同质训练：设 321,,a a a 是一列正整数，其中1a 表示第一个数，2a 表示第二个数，依此类推，n a 表示第n 个数(n 是正整数)，已知11=a ，221114）（）（---=+n n n a a a ，则=2022a _________.三、自主小结四、适度作业A 层：1．单项式652y x -的系数是_______，次数是_______． 2．4232a a ⋅＝______，36a a ÷＝______，32)2(a -＝______，222a a +-＝______．3．若6122=-b a ，且31=-b a ，则b a +的值为_______． 4．已知52=m ，则m 32＝_______；m +32＝_______．5．若代数式362++kx x 是一个完全平方式，则k ＝______．6．若222-=-a a ，则a a 4252-+＝_______．7．若084422=+-++b a b a ，则22-⋅b a 的值为______．8．下列运算正确的是（ ） A ．2532a a a =+ B ．224)2(b a b a +=+C ．632a a a =⋅D ．2336()ab a b 9. 把多项式x 2+ax +b 分解因式，得(x +1)(x -3)，则a 、b 的值分别是（ ） A ．a =2，b =3 B ．a =-2，b =-3C ．a =-2，b =3D ．a =2，b =-310．化简：（1）)4)(2)(2(2+-+m m m （2）22)2()2(y x y x +--（3）)1(4)12(2--+a a a （4）)1()2)(2--+-x x x x （．11．因式分解（1）a a 93- （2）ab b a 4)(2-+ （3）181222+-x x（4）32232ab b a b a +- （5）35122+-x x （6）)1()1(2---x x x12．如图，直线l 1与直线l 2所成的角∠B 1OA 1＝30°，过点A 1作A 1B 1⊥l 1交直线l 2于点B 1，OB 1＝2，以A 1B 1为边在△OA 1B 1外侧作等边三角形A 1B 1C 1，再过点C 1作A 2B 2⊥l 1，分别交直线l 1和l 2于A 2，B 2两点，以A 2B 2为边在△OA 2B 2外侧作等边三角形A 2B 2C 2，…按此规律进行下去，则第2022个等边三角形A 2022B 2022C 2022的周长为． B 层：13．已知12322--+=x ax x A ，12-+-=ax x B ，且B A 63+的值与x 无关，则a 的值为________．14．如果代数式5a +3b 的值为﹣4，则代数式2（a +b ）+4（2a +b +2）的值为 ． 15. 如图1是一个长为2a 、宽为2b 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．（1）观察图2，请你直接写出下列三个代数式22(),(),a b a b ab +-之间的等量关系为_______；（2）运用你所得到的公式解答下列问题：①若m ，n 为实数，且2m n +=-，3=-mn ，求m n -的值．①如图3，21,S S ，分别表示边长为p ，q 的正方形的面积，且C B A ，，三点在一条直线上，若62021=+==+q p AB S S ，，求图中阴影部分的面积．图1 图2 图3。
2020数学中考备考-第2讲 整式与因式分解
按一定规律排列的,请利用其中规律,写出第 n 个数 an=
n(n 1) 2 2n1
(用含 n
的式子表示).
思路点拨:观察分母 3,5,9,17,33,…,可知规律为 2n+1;观察分子 1,3,6,10,15,…,可
知规律为 n(n 1) ,即可求解. 2
解析:观察分母 3,5,9,17,33,…, 可知规律为 2n+1,观察分子 1,3,6,10,15,…,
(2)项:多项式中的每个 单项式 叫做多项式的项,其中不含 字母 的项
叫做常数项. (3)次数:多项式里次数最 高 项的次数,叫做这个多项式的次数.
3.整式
单项式 与 多项式 统称整式.
整式的运算
1.同类项 所含 字母 几个 常数
相同,并且相同字母的 项也是同类项.
指数
也相同的项叫做同类项,
2.合并同类项
2
2
(1)整式的混合运算,熟练掌握运算顺序和运算法则是解题的关键,同时注 意运算符号和漏项问题. (2)符合公式的要应用乘法公式去简化运算.
因式分解
[例5] 分解因式: (1)a2(a-b)-4(a-b)= (2)2a3b-4a2b2+2ab3=
(a-b)(a-2)(a+2) ; 2ab(a-b)2 .
解:(x-2)(x+2)-x(x-1) =x2-4-x2+x =x-4, 当x=3时,原式=3-4=-1.
点击进入 实战演练
平方差公式:(a+b)(a-b)= a2-b2 .
完全平方公式:(a±b)2= a2±2ab+b2
.
7.整式的除法 (1)单项式除以单项式:把 系数 与 同底数幂 分别相除作为商的因式,
中考数学 第2讲 代数式及整式的运算(解析版)
第2讲 代数式及整式的运算一、考点知识梳理【考点1 代数式定义及列代数式】1.代数式：用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子叫做代数式． 2．代数式的值：用数值代替代数式里的字母，按照代数式里的运算关系，计算后所得的结果叫做代数式的值．【考点2 幂的运算】同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加． a m •a n ＝a m +n （m ，n 是正整数） 幂的乘方法则：底数不变，指数相乘． （a m ）n ＝a mn （m ，n 是正整数）积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘． （ab ）n ＝a n b n （n 是正整数）同底数幂的除法法则：底数不变，指数相减． a m ÷a n ＝a m ﹣n （a ≠0，m ，n 是正整数，m ＞n ） 【考点3 合并同类项】所含字母相同并且相同字母的指数也分别相同的项叫做同类项．所有的常数项都是同类项. 把多项式中同类项合成一项，叫做合并同类项．合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变． 【考点4 整式的乘法】单项式乘以多项式m(a ＋b)＝am ＋bm多项式乘以多项式(a ＋b)(m ＋n)＝am ＋an ＋bm ＋bn 二、考点分析【考点1 代数式定义及列代数式】【解题技巧】(1)在建立数学模型解决问题时，常需先把问题中的一些数量关系用代数式表示出来，也就是列出代数式；(2)列代数式的关键是正确分析数量关系，掌握文字语言(和、差、积、商、乘以、除以等)在数学语言中的含义；(3)注意书写规则：a×b 通常写作a·b 或ab ；1÷a 通常写作1a；数字通常写在字母前面，如a×3通常写作3a ；带分数一般写成假分数，如115a 通常写作65a.【例1】（2019.海南中考）当m ＝﹣1时，代数式2m +3的值是（ ） A ．﹣1 B ．0 C ．1 D ．2【答案】C ．【分析】将m ＝﹣1代入代数式即可求值；【解答】解：将m ＝﹣1代入2m +3＝2×（﹣1）+3＝1； 故选：C ．【一领三通1-1】（2019.云南中考）按一定规律排列的单项式：x 3，﹣x 5，x 7，﹣x 9，x 11，……，第n 个单项式是（ ） A ．（﹣1）n ﹣1x 2n ﹣1 B ．（﹣1）n x 2n ﹣1 C ．（﹣1）n ﹣1x 2n +1 D ．（﹣1）n x 2n +1【答案】C ．【分析】观察指数规律与符号规律，进行解答便可． 【解答】解：∵x 3＝（﹣1）1﹣1x 2×1+1， ﹣x 5＝（﹣1）2﹣1x 2×2+1， x 7＝（﹣1）3﹣1x 2×3+1， ﹣x 9＝（﹣1）4﹣1x 2×4+1， x 11＝（﹣1）5﹣1x 2×5+1， ……由上可知，第n 个单项式是：（﹣1）n ﹣1x 2n +1， 故选：C ．【一领三通1-2】（2019•台湾）图1的直角柱由2个正三角形底面和3个矩形侧面组成，其中正三角形面积为a ，矩形面积为b ．若将4个图1的直角柱紧密堆叠成图2的直角柱，则图2中直角柱的表面积为何？（ ）A ．4a +2bB ．4a +4bC ．8a +6bD ．8a +12b【答案】C ．【分析】根据已知条件即可得到结论．【解答】解：∵正三角形面积为a，矩形面积为b，∴图2中直角柱的表面积＝2×4a+6b＝8a+6b，故选：C．【一领三通1-3】（2019•台湾）小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为10份意大利面，x杯饮料，y份沙拉，则他们点了几份A餐？（）A．10﹣x B．10﹣y C．10﹣x+y D．10﹣x﹣y【答案】A．【分析】根据点的饮料能确定在B和C餐中点了x份意大利面，由题意可得点A餐10﹣x；【解答】解：x杯饮料则在B和C餐中点了x份意大利面，y份沙拉则在C餐中点了y份意大利面，∴点A餐为10﹣x；故选：A．【考点2 幂的运算】【解题技巧】1.在应用同底数幂的乘法法则时，应注意：①底数必须相同，如23与25，（a2b2）3与（a2b2）4，（x﹣y）2与（x﹣y）3等；②a可以是单项式，也可以是多项式；③按照运算性质，只有相乘时才是底数不变，指数相加．2.概括整合：同底数幂的乘法，是学习整式乘除运算的基础，是学好整式运算的关键．在运用时要抓住“同底数”这一关键点，同时注意，有的底数可能并不相同，这时可以适当变形为同底数幂．3.注意：①因式是三个或三个以上积的乘方，法则仍适用；②运用时数字因数的乘方应根据乘方的意义，计算出最后的结果．【例2】（2019•广东中考）下列计算正确的是（）A．b6+b3＝b2B．b3•b3＝b9C．a2+a2＝2a2D．（a3）3＝a6【答案】C．【分析】直接利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘法运算法则分别化简得出答案．【解答】解：A、b6+b3，无法计算，故此选项错误；B、b3•b3＝b6，故此选项错误；C、a2+a2＝2a2，正确；D、（a3）3＝a9，故此选项错误．故选：B．【一领三通2-1】（2019•甘肃中考）计算（﹣2a）2•a4的结果是（）A．﹣4a6B．4a6C．﹣2a6D．﹣4a8【答案】C．【分析】直接利用积的乘方运算法则化简，再利用同底数幂的乘法运算法则计算得出答案．【解答】解：（﹣2a）2•a4＝4a2•a4＝4a6．故选：B．【一领三通2-2】（2019•海南中考）下列运算正确的是（）A．a•a2＝a3B．a6÷a2＝a3C．2a2﹣a2＝2 D．（3a2）2＝6a4【答案】A．【分析】根据同底数幂乘除法的运算法则，合并同类项法则，幂的乘方与积的乘方法则即可求解；【解答】解：a•a2＝a1+2＝a3，A准确；a6÷a2＝a6﹣2＝a4，B错误；2a2﹣a2＝a2，C错误；（3a2）2＝9a4，D错误；故选：A．【一领三通2-3】（2019•江苏南京中考）计算（a2b）3的结果是（）A．a2b3B．a5b3C．a6b D．a6b3【答案】D．【分析】根据积的乘方法则解答即可．【解答】解：（a2b）3＝（a2）3b3＝a6b3．故选：D．【一领三通2-4】（2019•山东济南中考模拟）在平面直角坐标系中，任意两点A（a，b），B（c，d），定义一种运算：A*B＝[（3﹣c），]，若A（9，﹣1），且A*B＝（12，﹣2），则点B的坐标是______．【答案】（﹣1，8）．【分析】根据新运算公式列出关于c、d的方程组，解方程组即可得c、d的值；进一步得到点B的坐标．【解答】解：根据题意，得，解得：．则点B的坐标为（﹣1，8）．故答案为：（﹣1，8）．【考点3 合并同类项】【解题技巧】合并同类项时要注意以下三点：（1）要掌握同类项的概念，会辨别同类项，并准确地掌握判断同类项的两条标准：带有相同系数的代数项；字母和字母指数；（2）明确合并同类项的含义是把多项式中的同类项合并成一项，经过合并同类项，式的项数会减少，达到化简多项式的目的；（3）“合并”是指同类项的系数的相加，并把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．（4）只要不再有同类项，就是结果(可能是单项式，也可能是多项式)．【例3】（2019•吉林长春中考）先化简，再求值：（2a+1）2﹣4a（a﹣1），其中a＝．【答案】2．【分析】直接利用完全平方公式以及单项式乘以多项式分别化简得出答案．【解答】解：原式＝4a2+4a+1﹣4a2+4a＝8a+1，当a＝时，原式＝8a+1＝2．【一领三通3-1】（2019•山东威海中考）下列运算正确的是（）A．（a2）3＝a5B．3a2+a＝3a3C．a5÷a2＝a3（a≠0）D．a（a+1）＝a2+1【答案】C．【分析】根据合并同类项法则，幂的乘方的性质，单项式与多项式乘法法则，同底数幂的除法的性质对各选项分析判断后利用排除法求解．【解答】解：A、（a2）3＝a6，故本选项错误；B、3a2+a，不是同类项，不能合并，故本选项错误；C、a5÷a2＝a3（a≠0），正确；D、a（a+1）＝a2+a，故本选项错误．故选：C．【一领三通3-2】（2019•辽宁沈阳中考）下列运算正确的是（）A．2m3+3m2＝5m5B．m3÷m2＝mC．m•（m2）3＝m6D．（m﹣n）（n﹣m）＝n2﹣m2【答案】B．【分析】根据合并同类项、幂的乘法除法、幂的乘方、完全平方公式分别计算即可．【解答】解：A.2m3+3m2＝5m5，不是同类项，不能合并，故错误；B．m3÷m2＝m，正确；C．m•（m2）3＝m7，故错误；D．（m﹣n）（n﹣m）＝﹣（m﹣n）2＝﹣n2﹣m2+2mn，故错误．故选：B．【一领三通3-3】（2019•河北石家庄中考模拟）先化简，再求值：（5a2+2a+1）﹣4（3﹣8a+2a2）+（3a2﹣a），其中．【分析】首先去括号，合并同类项，将两代数式化简，然后代入数值求解即可．【解答】解：∵（5a2+2a+1）﹣4（3﹣8a+2a2）+（3a2﹣a）＝5a2+2a+1﹣12+32a﹣8a2+3a2﹣a＝33a﹣11，∴当a＝时，原式＝33a﹣11＝33×﹣11＝0；【一领三通3-4】（2019•山东青岛中考模拟）化简求值：已知整式2x2+ax﹣y+6与整式2bx2﹣3x+5y﹣1的差不含x和x2项，试求4（a2+2b3﹣a2b）+3a2﹣2（4b3+2a2b）的值．【分析】根据两整式的差不含x和x2项，可得差式中x与x2的系数为0，列式求出a、b的值，然后将代数式化简再代值计算．【解答】解：2x2+ax﹣y+6﹣（2bx2﹣3x+5y﹣1）＝2x2+ax﹣y+6﹣2bx2+3x﹣5y+1＝（2﹣2b）x2+（a+3）x﹣6y+7，∵两个整式的差不含x和x2项，∴2﹣2b＝0，a+3＝0，解得a＝﹣3，b＝1，4（a2+2b3﹣a2b）+3a2﹣2（4b3+2a2b）＝4a2+8b3﹣4a2b+3a2﹣8b3﹣4a2b＝7a2﹣8a2b，当a＝﹣3，b＝1时，原式＝7a2﹣8a2b＝7×（﹣3）2﹣8×（﹣3）2×1＝7×9﹣8×9×1＝63﹣72＝﹣9．【考点4 整式的乘法】【解题技巧】多项式的乘法要注意多项式中每一项不要漏乘，还要注意运算符号，遵循去括号的法则。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020年中考数学总复习第2讲整式及其运算一、选择题(每小题6分，共18分)1．(2014·舟山)下列运算正确的是( B)A．2a2＋a＝3a3B．(－a)2÷a＝aC．(－a)3·a2＝－a6D．(2a2)3＝6a62．(2012·安徽)为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为( A)A．2a2B．3a2C．4a2D．5a2解析：四个等腰直角三角形拼在一起成为边长为a的正方形，加上中间一块正方形，所以阴影部分面积为2a23．(2014·毕节)若－2a m b4与5a n＋2b2m＋n可以合并成一项，则m n的值是( D)A．2 B．0 C．－1 D．1二、填空题(每小题6分，共30分)4．(2014·连云港)计算(2x＋1)(x－3)2．5．(2014·凉山)已知x1＝3＋2，x212＋x22＝__10__．6．(2012·长沙)若实数a，b满足|3a－a b的值为__1__．7．(2012·黔东南州)二次三项式x2－kx＋9是一个完全平方式，则k的值是__±6__．解析：∵x2－kx＋9＝x2－kx＋32，∴－kx＝±2×x×3，解得k＝±68．(2014·扬州)设a1，a2，…，a2014是从1，0，－1这三个数中取值的一列数，若a1＋a2＋…＋a2014＝69，(a1＋1)2＋(a2＋1)2＋…＋(a2014＋1)2＝4001，则a1，a2，…，a2014中为0的个数__165__．三、解答题(共52分)9．(10分)计算：(1)(2012·乐山)3(2x2－y2)－2(3y2－2x2)；原式＝6x2－3y2－6y2＋4x2＝10x2－9y2(2)(2014·无锡)(x＋1)(x－1)－(x－2)2.原式＝x2－1－x2＋4x－4＝4x－510．(12分)先化简，再求值：(1)(2012·泉州)(x＋3)2＋(2＋x)(2－x)，其中x＝－2；原式＝x2＋6x＋9＋4－x2＝6x＋13，当x＝－2时，原式＝6×(－2)＋13＝1(2)(2014·衡阳)(a＋b)(a－b)＋b(a＋2b)－b2，其中a＝1，b＝－2.原式＝a2－b2＋ab＋2b2－b2＝a2＋ab；当a＝1，b＝－2时，原式＝12＋1×(－2)＝1－2＝－111．(10分)观察下列算式：①1×3－22＝3－4＝－1，②2×4－32＝8－9＝－1，③3×5－42＝15－16＝－1，④________________________，……(1)请你按以上规律写出第4个算式；(2)把这个规律用含字母的式子表示出来；(3)你认为(2)中所写出的式子一定成立吗？并说明理由．解：(1)4×6－52＝24－25＝－1(2)答案不唯一．如n(n＋2)－(n＋1)2＝－1(3)n(n＋2)－(n＋1)2＝n2＋2n－(n2＋2n＋1)＝n2＋2n－n2－2n－1＝－1.所以一定成立12．(10分)(2012·珠海)观察下列等式：12×231＝132×21，13×341＝143×31，23×352＝253×32，34×473＝374×43，62×286＝682×26，……以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．(1)根据上述各式反映的规律填空，使式子称为“数字对称等式”：①52×____＝____×25；②____×396＝693×____．(2)设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a＋b≤9，写出表示“数字对称等式”一般规律的式子(含a，b)，并证明．解：(1)①∵5＋2＝7，∴左边的三位数是275.右边的三位数是572，∴52×275＝572×25；②∵左边的三位数是396，∴左边的两位数是63，右边的两位数是36，∴63×396＝693×36；故答案为：①275，572；②63，36(2)∵左边两位数的十位数字为a，个位数字为b，∴左边的两位数是10a＋b，三位数是100b＋10(a＋b)＋a，右边的两位数是10b＋a，三位数是100a＋10(a＋b)＋b，∴一般规律的式子为：(10a＋b)×[100b＋10(a＋b)＋a]＝[100a＋10(a＋b)＋b]×(10b＋a)证明：左边＝(10a＋b)×[100b＋10(a＋b)＋a]＝(10a＋b)(100b＋10a＋10b＋a)＝(10a＋b)(110b＋11a)＝11(10a＋b)(10b＋a)，右边＝[100a＋10(a＋b)＋b]×(10b＋a)＝(100a ＋10a ＋10b ＋b )(10b ＋a )＝(110a ＋11b )(10b ＋a )＝11(10a ＋b )(10b ＋a )，∴左边＝右边，故“数字对称等式”一般规律的式子为：(10a ＋b )×[100b ＋10(a ＋b )＋a ]＝[100a ＋10(a ＋b )＋b ]×(10b ＋a )13．(10分)试确定a 和b ，使x 4＋ax 2－bx ＋2能被x 2＋3x ＋2整除．解：由于x 2＋3x ＋2＝(x ＋1)(x ＋2)．因此，设x 4＋ax 2－bx ＋2＝(x ＋1)(x ＋2)·M.当x ＝－1时，即1＋a ＋b ＋2＝0，当x ＝－2时，即16＋4a ＋2b ＋2＝0，∴a ＝－6，b ＝32015年名师预测1．下列运算正确的是( C )A .54·12＝326B .（a 3）2＝a 3C ．(1a ＋1b )2÷(1a 2－1b 2)＝b ＋ab －aD ．(－a)9÷a 3＝(－a)62．已知(m －n)2＝8，(m ＋n)2＝2，则m 2＋n 2＝( C ) A ．10 B ．6 C ．5 D ．32019-2020年中考数学总复习 第30讲 图形的平移一、选择题(每小题6分，共24分)1．(2014·呼和浩特)已知线段CD 是由线段AB 平移得到的，点A(－1，4)的对应点为C(4，7)，则点B(－4，－1)的对应点D 的坐标为( A )A ．(1，2)B ．(2，9)C ．(5，3)D ．(－9，－4)2．(2014·滨州)如图，如果把△ABC 的顶点A 先向下平移3格，再向左平移1格到达A′点，连接A′B，则线段A′B 与线段AC 的关系是( D )A ．垂直B ．相等C ．平分D ．平分且垂直3．(2014·邵阳)某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( D )A ．甲种方案所用铁丝最长B ．乙种方案所用铁丝最长C ．丙种方案所用铁丝最长D ．三种方案所用铁丝一样长4．(2013·滨州)如图，等边△ABC 沿射线BC 向右平移到△DCE 的位置，连接AD ，BD ，则下列结论：①AD＝BC ；②BD，AC 互相平分；③四边形ACED 是菱形．其中正确的个数有( D )A ．0个B ．1个C ．2个D ．3个 二、填空题(每小题7分，共28分) 5．(2014·宜宾)在平面直角坐标系中，将点A(－1，2)向右平移3个单位长度得到点B ，则点B 关于x 轴的对称点C 的坐标是__(2，－2)__．6．(2012·无锡)如图，△ABC 中，∠ACB ＝90°，AB ＝8 cm ，D 是AB 的中点．现将△BCD 沿BA 方向平移1 cm ，得到△EFG，FG 交AC 于点H ，则GH 的长等于__3__ cm .解析：∵△ABC 中，∠ACB ＝90°，AB ＝8 cm ，D 是AB 的中点，∴AD ＝BD ＝CD ＝12AB ＝4cm ；又∵△EFG 由△BCD 沿BA 方向平移1 cm 得到的，∴GH ∥CD ，GD ＝1 cm ，∴GH DC ＝AGAD，即GH 4＝4－14，解得GH ＝3(cm ) 7．如图①，两个等边△ABD，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A′B′D′的位置得到图②，则阴影部分的周长为__2__．解析：∵两个等边△ABD ，△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A′B′D′的位置，∴A ′M ＝A ′N ＝MN ，MO ＝DM ＝DO ，OD ′＝D′E ＝OE ，EG ＝EC ＝GC ，B ′G ＝RG ＝RB′，∴OE ＋OM ＋MN ＋NR ＋GR ＋EG ＝A′D′＋BC ＝1＋1＝28．(2012·广安)如图，把抛物线y ＝12x 2平移得到抛物线m ，抛物线m 经过点A(－6，0)和原点O(0，0)，它的顶点为P ，它的对称轴与抛物线y ＝12x 2交于点Q ，则图中阴影部分的面积为__272__．解析：过点P 作PM⊥y 轴于点M ，设抛物线m 的对称轴交x 轴于点N.∵抛物线平移后经过原点O 和点A (－6，0)，∴平移后的抛物线对称轴为x ＝－3，得出二次函数解析式为y ＝12(x ＋3)2＋h ，将(－6，0)代入得出0＝12(－6＋3)2＋h ，解得h ＝－92，∴点P 的坐标是(3，－92)，根据抛物线的对称性可知，阴影部分的面积等于矩形NPMO 的面积，∴S ＝3×|－92|＝272三、解答题(共48分)9．(12分)(2013·云南)如图，下列网格中，每个小正方形的边长都是1，图中“鱼”的各个顶点都在格点上．(1)把“鱼”向右平移5个单位长度，并画出平移后的图形；(2)写出A，B，C三点平移后的对应点A′，B′，C′的坐标．解：(1)如图所示：(2)结合坐标系可得A′(5，2)，B′(0，6)，C′(1，0)10．(12分)(2014·湘潭)在边长为1的小正方形网格中，△AOB的顶点均在格点上．(1)B点关于y轴的对称点坐标为__(－3，2)__；(2)将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；(3)在(2)的条件下，A1的坐标为__(－2，3)__．解：(2)△A1O1B1如图所示：11．(12分)(2014·珠海)如图，在Rt△ABC中，∠BAC＝90°，AB＝4，AC＝3，线段AB 为半圆O的直径，将Rt△ABC沿射线AB方向平移，使斜边与半圆O相切于点G，得到△DEF，DF与BC交于点H.(1)求BE的长；(2)求Rt △ABC 与△DEF 重叠(阴影)部分的面积．解：(1)连接OG ，如图，∵∠BAC ＝90°，AB ＝4，AC ＝3，∴BC ＝AB 2＋AC 2＝5，∵Rt △ABC 沿射线AB 方向平移，使斜边与半圆O 相切于点G ，得△DEF ，∴AD ＝BE ，DF ＝AC ＝3，EF ＝BC ＝5，∠EDF ＝∠BAC ＝90°，∵EF 与半圆O 相切于点G ，∴OG ⊥EF ，∵AB ＝4，线段AB 为半圆O 的直径，∴OB ＝OG ＝2，∵∠GEO ＝∠DEF ，∴Rt △EOG ∽Rt △EFD ，∴OE EF ＝OG DF ，即OE 5＝23，解得OE ＝103，∴BE ＝OE－OB ＝103－2＝43(2)BD ＝DE －BE ＝4－43＝83.∵DF∥AC ，∴DH AC ＝BD AB ，即DH 3＝834，解得DH ＝2.∴S 阴影＝S △BDH＝12BD·DH ＝12×83×2＝83，即Rt △ABC 与△DEF 重叠(阴影)部分的面积为8312．(12分)(2013·绍兴)如图，矩形ABCD 中，AB ＝6，第1次平移将矩形ABCD 沿AB 的方向向右平移5个单位，得到矩形A 1B 1C 1D 1，第2次平移将矩形A 1B 1C 1D 1沿A 1B 1的方向向右平移5个单位，得到矩形A 2B 2C 2D 2，…，第n 次平移将矩形A n －1B n －1C n －1D n －1沿A n －1B n －1的方向平移5个单位，得到矩形A n B n C n D n (n ＞2)．(1)求AB 1和AB 2的长； (2)若AB n 的长为56，求n.解：(1)∵AB ＝6，第1次平移将矩形ABCD 沿AB 的方向向右平移5个单位，得到矩形A 1B 1C 1D 1，第2次平移将矩形A 1B 1C 1D 1沿A 1B 1的方向向右平移5个单位，得到矩形A 2B 2C 2D 2…∴AA 1＝5，A 1A 2＝5，A 2B 1＝A 1B 1－A 1A 2＝6－5＝1，∴AB 1＝AA 1＋A 1A 2＋A 2B 1＝5＋5＋1＝11，∴AB 2的长为5＋5＋6＝16(2)∵AB 1＝2×5＋1＝11，AB 2＝3×5＋1＝16，∴AB n ＝(n ＋1)×5＋1＝56，解得n ＝10 2015年名师预测1．如图，将△ABC 沿BC 方向平移2 cm 得到△DEF，若△ABC 的周长为16 cm ，则四边形ABFD 的周长为( C )A ．16 cmB ．18 cmC ．20 cmD ．22 cm,第1题图),第2题图)2．如图，将等腰直角△ABC 沿BC 方向平移得到△A 1B 1C 1.若BC ＝32，△ABC 与△A 1B 1C 1重叠部分的面积为2，则BB 1＝．解析：设B 1C ＝2x B 1C边上的高为x ，∴12×x×2x ＝2，解得x ＝2(舍去负值)，∴B 1C ＝22，∴BB 1＝BC －B 1C ＝2。