2012 西南交通大学 大学物理 AII 作业答案 No.7 场的量子性
2012 西南交通大学 大学物理 AII 作业答案 No.3 波的干涉

解:(1) 在 S 2 外侧 C 点,两列波的相位差为:
λ λ 2 所以 S 2 的位相应为: ϕ 2 = 2 kπ + π / 2 , ( k = 0 , ± 1, ± 2 , ⋅ ⋅⋅) ,初相为 ϕ 2 = π / 2
(2) 在 S1 S 2 中垂线上任一点,若产生相消干涉,则
∆ϕ = ϕ 2 − ϕ 1 −
x
) 2 x π 1 或者:将 y1 写成 y1 = A cos ( 2πνt + 2 π x / λ ) = A cos ( 2 π v t + π + 2π − ) λ 2 2 x π x π 反射波为: y 2 = A cos ( 2 π v t − 2π + π ) = A cos [ 2 π v t + − (2π − )] λ 2 λ 2 x π π 合成驻波方程为: y = y1 + y 2 = 2 A cos( 2π − ) cos( 2πvt + ) λ 2 2
解:两相干波在 P 点的相位差为:
是
4π
。
2
∆ϕ = ϕ 2 − ϕ 1 −
2π
λ
( r2 − r1 ) =
2π 21 1 π −0− λ − 3λ ) = − 4π ( λ 4 2
M
• S1 • S2 • C
∆ϕ = 4π
3. S 1 , S 2 为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相 距
解:据驻波形成条件可设另一简谐波的波动方程为:
(SI)
[ C ]
y 2 = 2.0 × 10 − 2 cos[ 2π (
t x + ) + ϕ2 ] 0.02 20
西南交大2012-2013第二学期大学物理AI期末试卷
密封装订线
姓名
学号
密封装订线
t
F
F
F
F
F
t
1(A)
t
2(B)
t
3(C)
t
4(D)
2. 若产生如图所示的自感电动势方向,则通过线圈的电流是:
(A) 恒定向右
(B) 恒定向左
(C) 增大向左
(D) 增大向右
、
k
表示)。
5.(本小题 2 分)一个带电为 Q 的空腔导体,其内部无其他带电体,则电荷将分布于空腔导体的 ___________________(选填:内表面;外表面;导体体内;内表面和外表面)。
学号
密封装订线
班级
密封装订线
第1页共7页
6.(本小题 2 分)在均匀磁场中放置一半径为 R 的半圆形导线,电流强度为 I,导线两端连线与磁感
S
B t
d
S
②
_________________________
④
二、判断题(每小题 2 分,共 16 分。请将表示正确的符号:T,表示错误的符号:F,填入相应 题号后的括号内。填入其它符号和其它位置处答案不得分)
1.( 2.(
3.( 4.( 5.( 6.(
7.( 8.(
)一对大小相同、方向相反的作用力,所做的功也一定相消为零。 )花样滑冰运动员以一只脚为轴旋转,当她两臂收拢时, 则绕轴转动角动量减小,转动角速度
为 l 、截面积为 S,质量为 m 的棒,且这根棒安放在运动方向上,则乙测得此棒的密度为
。
2.(本小题 2 分)有一边长为 a 的正方形平面,在其中垂线上距中心 O 点 1 a 处, 2
No7场的量子性玻尔理论答案
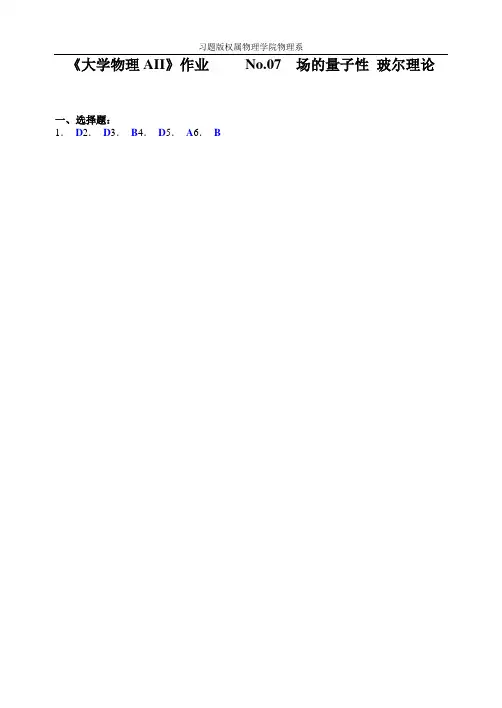
习题版权属物理学院物理系《大学物理AII》作业No.07 场的量子性玻尔理论一、选择题:1.D2.D3.B4.D5.A6.B二、填空题:1.光电效应中,当频率为Hz 10315⨯的单色光照射在逸出功为4.0eV 的金属表面时,金属中逸出的光电子的最大速率为 m ⋅s -1。
(普朗克常量s J 1063.634⋅⨯=-h ,电子质量m e =kg 1011.931-⨯) 解:由爱因斯坦光光电效应方程 2021mv h h +ν=ν可得逸出光电子的最大速率()()()16311915340s m 1072.11011.9106.10.41031063.622----⋅⨯=⨯⨯⨯-⨯⨯⨯⨯=-=mh h v νν2.以波长为207.0=λμm 的紫外光照射金属钯表面产生光电效应,已知钯的红限频率1501021.1⨯=νHz ,则其遏止电压a U = V 。
(普朗克常量s J 1063.634⋅⨯=-h ,基本电荷 19106.1-⨯=e C)解:由爱因斯坦光电效应方程 a U e h h +=0νν可得遏止电压:()V 99.0106.11021.110207.01031063.6191568340≈⨯⎪⎪⎭⎫ ⎝⎛⨯-⨯⨯⨯⨯=ν-λ=---eh c h U a3.如图所示,一频率为ν的入射光子与起始静止的自由电子发生碰撞和散射。
如果散射光子的频率为ν',反冲电子的动量为p ,则在与入射光子平行的方向上的动量守恒定律的分量形式为 。
解:以光子和电子为研究对象,在入射光子运动的方向上:初始动量为 c h h p νλ==0碰撞后动量为 θφνcos cos p ch p +'=' 由守恒定律可得与入射光子平行的方向上动量的分量形式θφννcos cos p ch ch +'=4.康普顿散射中, 当出射光子与入射光子方向成夹角θ = 时, 光子的频率减少得最多;当θ = 时,光子的频率保持不变。
大学物理AII基本概念(选择 填空)附答案

振动一、选择题1.下列运动中,属于简谐振动的是( ) A .单摆的摆动 B .平抛运动 C .斜抛运动 D .地震2.下列关于简谐振动的说法中,错误的是( ) A .简谐振动是振动的最基本形式B .作简谐振动的物体,加速度和位移成反比C .简谐振动的物体,所受合外力方向始终指向平衡位置D .做简谐振动的物体,加速度方向与位移方向相反3.简谐振动的能量,下列说法中正确的是( ) A .简谐振动的动能守恒 B .简谐振动的势能守恒 C .简谐振动的机械能守恒 D .简谐振动角动量守恒4.关于简谐振动,下列说法中正确的是( ) A .同一周期内没有两个完全相同的振动状态 B .质点在平衡位置处,振动的速度为零 C .质点在最大位移处,振动的速度最大 D .质点在最大位移处,动能最大5.关于旋转矢量法,下列说法中错误的是( ) A .矢量A 的绝对值等于振动的振幅B .矢量A 的旋转角速度等于简谐振动的角频率C .矢量A 旋转一周,其端点在x 轴的投影点就作一次全振动D .旋转矢量法描述简谐振动,就是矢量A 本身在作简谐振动6.简谐振动中,速度的相位比位移的相位( )A .超前2π B .落后2π C .超前π D .落后π-7.简谐振动中,加速度和位移的相位关系( ) A .同相 B .反相C .超前2π D .落后2π8.两个同方向同频率的简谐振动合成,若合振动振幅达到最大值,说明( ) A .两分振动同相 B .两分振动反相 C .两分振动相位差为2π D .两分振动相位差为32π9.简谐振动的一个振动周期内( )A .振动速度不相同B .振动位移不相同C .振动相位不相同D .以上都不对二、填空题10.回复力的方向始终指向 。
11.作简谐振动的物体,其加速度和位移成 (正比或反比)而方向 (相同或相反) 。
12.周期是物体完成一次 所需要的时间。
13.频率表示单位时间内发生 的次数。
14.简谐振动中当质点运动到平衡位置时, 最大, 最小。
2012-2013-1-AII期末试卷及参考答案
0 ________________。
型半导体的能带结构图。
E
导带
8、图 4 是
禁带
满带
杂质能级
9、 它在静止时的寿命为 2.5 10 s 。 介子是不稳定的粒子,
8
图4
当 介子以速率 0.8c 相对实验室运动时, 在实验室测得它在 衰变前飞行的距离为 m(c 为真空中的光速)。
3、设谐振子的振幅为 A ,周期为 T ,下列说法正确的是( (A)谐振子从平衡位置运动到最远点所需的最短时间为 T 8 ;
(B)谐振子从平衡位置运动到最远点的一半距离所需最短时间为 T 8 ; (C)谐振子从平衡位置出发经历 T 12 ,运动的位移大小为 A 3 ; (D)谐振子从平衡位置运动到最远点所需的最短时间为 T 4 。
9、 10 ;
2 2 2 10、 。 or or 2 4
(2) 0, 1, 3 条(2 分) ;
a
(3 分) ;
(4)主要区别:主极大的强度、主极大明纹的宽度、相邻两主极大之间的光强分布不 同。 (3 分) 四、 (10 分)选择以下两种方法求解即可: (1)利用薛定谔方程
) (c 表
c ; k 1
(B)
1 k2 c; k
)
(C)
c ; k 1
(D)
k2 1 c。 k
7、以下说法错误的是(
(A)准静态过程和可逆过程都是物理学中的理想过程; (B)气体向真空中绝热自由膨胀的过程可近似看成是准静态过程; (C)在孤立系统中所发生的自然过程总是沿着熵增大的方向进行; (D)孤立系统进行可逆过程时熵不变。
n1 n2 n3
λ e
图3
3、 处于基态的氢原子吸收了 13.056 eV 的能量后跃迁到某一激发态能级, 当它从激发态向下 跃迁时,可能辐射出_______条巴耳末系的谱线。 4、用波长为 的单色光垂直照射到空气劈尖上,从反射光中观察干涉条纹,距棱边 L 处为 暗条纹。现连续增大劈尖角 ,直到该点处再次出现暗条纹为止,由此可知劈尖角的改变量
《大学物理AII》作业 No.08 量子力学基出 参考解答

解: (1)由波函数归一化条件 ( Axe x ) 2 dx
0 2
2 A2 1 ,可得 A 2 3 ; ( 2 ) 3 d ( x ) 0, dx
2
(2)粒子的概率密度 ( x ) 43 x 2 e 2 x (x>=0),令 可得: 43 2 xe x (1 x ) 0 ,即 x (1 x ) 0 。
出, 电子的物质波波长是 10 10 m 数量级,在现有的条件下电子的波动性是可以通 过实验进行检验的, 讨论电子等微观粒子的波动性具有实际意义;但是宏观物体 物质波的波长远远小于 10 10 m 数量级, 无法通过我们所能利用的任何仪器装置来 验证其波动性。 因此谈论宏观物体是否遵从德布罗意关系,是否具有波动性是没 有意义的,宏观物体的波动性可以不用考虑。
处于 n=4 的激发态时,则:在 x=0 到 x=
P 3 1 x dx
2 0 a 4x 4x sin dx 3 sin 2 d 0 a a a 4 a a a 3
1 1 4x 1 8x 1 2 1 8 a sin sin 29.9% 2 2 a 4 a 0 2 3 4 a 3
。
3 。 2
2、计算下列两种情况下的速度不确定量: (1)宏观子弹:m =10 克,v=800m/s, Δx=1cm;
(2)原子中的电子:me=9×10-28 克,ve=108cm/s, Δx=10-8cm 第一种情况下, 如果把普朗克常数视为零结果怎样?第二种情况下呢?根据计算 结果总结出采用量子力学与经典力学处理问题的分界线。
大物AI作业参考解答_No.07 电势 (1)
粒子的荷质比α= 4.78×107 C/kg,已知该粒子沿着二者连线方向以 1.50×107 m/s 的速度
从很远处射向金原子核,则该粒子能到达距离金原子核的最近距离为 4.8×10-14 m。(基
本电荷 e = 1.60×10-19 C,真空介电常量ε0 = 8.85×10-12 C2 N-1 m-2)
α v
金核
答案:当到达最近距离时,粒子的动能完全转变为电势能,即 m v2 / 2 = q U
其中,U = Q / (4πε0 d) , Q = 79 e,q/m = α
1
联立以上关系,得 d = 4.8×10-14 m
4. 图中所示为静电场的等势线图,已知 U1>U2>U3。在图上画出 a、b 两点电场强度的方向,
答案:① 错,球面上各点场强大小相等,但因方向不相同,所以不能说球面上电场均匀。 ② 正确 ③ 错,球面是等势面,电场力做功相等。
三、计算题
1.电荷以相同的面密度σ分布在半径为 10cm 和 20cm 的两个同心球面上。设无限远处电势 为零,球心处的电势为 300V。求 (1) 电荷面密度σ (2) 若要使球心处的电势也为零,外球面上应放掉多少电荷? (真空介电常量ε0 = 8.85×10-12 C2 N-1 m-2)
1、理解静电力做功的特点,理解静电场的保守性; 2、掌握静电场的环路定理; 3、理解电势、电势差的概念,掌握利用场强积分和叠加原理求电势的方法; 4、理解电势梯度的意义,并能利用它求电场强度; 5、掌握点电荷、均匀带电球面、均匀带电球体等典型带电体的电势分布。
-------------------------------------------------------------------------------------------------------------------一、填空题
2012 西南交通大学 大学物理 AII 作业答案 No.5 光的干涉
No.5 光的干涉
一、判断题 [ F ] 1.光程就是光在空间通过的路程。 解:光的在介质中传播的几何路程与介质折射率的乘积定义为等效真空程,又叫光程,见教材 106 页。 [ F ] 2.杨氏双缝干涉是通过分振幅获得相干光的。 解:应为分波面法 [ T ] 3.光从光疏介质入射到光密介质界面反射时,将发生半波损失。在反射面上,反射光将产生 π 的相位突变。 解:教材81页。 [ T ] 4.相干长度就是能够观察到干涉现象的最大光程差。 解:教材123页。 [ T ] 5.薄透镜的物点和像点间是等光程的。 解:教材 96 页。 二、选择题 2.将一个平面波照射在图 a 所示的双缝上,屏上形成了一个干涉图样(图 b)。如果我们将双缝中的其中一 条缝上覆盖一个玻璃板(图 c),因为玻璃中的波长比空气中的波长短,所以从双缝出射的波的相位将不同, 如果相位差是 180 o ,图 b 中的干涉图样将如何变化?
有明纹条件 ∆ = ± kλ ( k = 0,1,2,3,........) 得 x k = ( ± kλ + 3λ ) ⋅ 相邻明纹间距 ∆ x = x k +1 − x k =
Dλ d
3. 如图所示, 牛顿环装置的平凸透镜与平板玻璃间有一小缝隙e0。 现用波长为 λ 的单色光垂直照射,已知平凸透镜的曲率半径为R,求反射光形成的牛顿环的各 暗环半径。
λ
2
,所以材
λ
4n
,当 k=0 时 e 有最小值,故 e min =
λ
4n
= 120nm
第 k+5 级明条纹的间距是 5λ
4. 波长为 λ 的平行单色光垂直照射到劈尖薄膜上,劈尖角为 θ ,劈尖薄膜的折射率为 n,第 k 级明条纹与
2 nθ五条明条纹间距为 L = 5l =
大学物理西南交大作业参考答案
电势、导体与※电介质中的静电场 (参考答案)班级: 学号: 姓名: 成绩: 一 选择题1.真空中一半径为R 的球面均匀带电Q ,在球心O 处有一带电量为q 的点电荷,如图所示,设无穷远处为电势零点,则在球内离球心O 距离为r 的P 点处的电势为:(A )r q04πε; (B ))(041R Qrq +πε; (C )rQq 04πε+; (D ))(041R qQ rq -+πε;参考:电势叠加原理。
[ B ]2.在带电量为-Q 的点电荷A 的静电场中,将另一带电量为q 的点电荷B 从a 点移动到b ,a 、b 两点距离点电荷A 的距离分别为r 1和r 2,如图,则移动过程中电场力做功为:(A ))(210114r r Q --πε; (B ))(21114r r qQ-πε;(C ))(210114r r qQ--πε; (D ))(4120r r qQ --πε。
参考:电场力做功=势能的减小量。
A=W a -W b =q(U a -U b ) 。
[ C ]3N 点,有人(A )电场强度E M <E N ; (B )电势U M <U N ; (C )电势能W M <W N ; (D )电场力的功A >0。
r 2 (-Qbr 1B a(q )[ C ]4.一个未带电的空腔导体球壳内半径为R ,在腔内离球心距离为d (d <R )处,固定一电量为+q 的点电荷,用导线把球壳接地后,再把地线撤去,选无穷远处为电势零点,则球心O 处的点势为: (A )0; (B )d q04πε; (C )-R q04πε; (D ))(1140R dq-πε。
外表面无电荷(可分析)。
虽然内表面电荷分布不均,但到O 点的距离相同,故由电势叠加原理可得。
[ D ]※5.在半径为R 的球的介质球心处有电荷+Q ,在球面上均匀分布电荷-Q ,则在球内外处的电势分别为: (A )内r Qπε4+,外r Q 04πε-; (B )内r Qπε4+,0; 参考:电势叠加原理。
2012春《大学物理AI》段考试卷评讲 (2)
玉林师范学院期中课程考试试卷
(2011——2012学年度第二学期)
命题教师:陈雪星 命题教师所在学院(系):物理科学与工程技术学院 课程名称:大学物理AI 考试专业:应用物理
8、两物体在完全弹性碰撞的过程中,其特点是(1)动量守恒 . (2) 动能守恒 。 解:本题考查对碰撞特点的掌握。
9、变力 F 由A 到B 两位置所作的功W =
解:这是变力作功的定义式。
B
A
F dr
。
10、汽车以匀速 v 沿平直路面前进,车中一人以相对车厢的速
度u 向上掷一质量为m 的小球;若将坐标系选在车上,小球的动能
解:保守力的特点是做功与路径无关,有 F保 dl 0
l
8、( √)动量定理反映了质点运动状态的变化与外力作用的关系。 解: 根据动量定理的物理意义可知,此说法正确。
9、( ×)一个物体的动量改变了,其动能也一定改变。 解: 动量改变,动能不一定变;但动能改变了,其动量一定改变。
6、有一段路面水平的公路,在转弯处轨道半径为R,汽车轮 胎与路面间的摩擦系数为μ,要使汽车不至于发生侧向打滑的事 故,汽车在该处的行驶速率( ③ ) (P49习题2-3) ①不得小于
gR ; ③不得大于 gR ;
②必须等于 gR ④还应由汽车的质量m决定。
N
解:如右图所示,汽车在转弯处,受到地面
的大小( ① )。 (P49习题2-2) ①不为零,但保持不变;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ
, λ=
hc 。 由图可知, 从 n =1
∆E , 能级越高,相邻能级能量差越小,从 n = 4 能级跃迁到 n = 3 能级 ∆E 最小, h
5. 氢原子从能级为-0.85eV的状态跃迁到能级为-3.4eV的状态时, 所发射的光子能量是2.55eV, 它是电子从 n = 4 的能级到 n = 2 的能级的跃迁。 解:光子能量 ε = ∆E = −0.85 − ( −3.4) = 2.55(eV) , 又
= 6.63×10 = 4.66×10
−34 −17
ϕ
2
= 1 + 0.024 = 1.024 (Å)
(2) 由能量守恒定律,反冲电子的动能
hc
λ0
−
hc
λ
8
×3×10 ×(
1 1 − ) −10 1 × 10 1.024 × 10 −10
(J) = 291(eV)
3.试求氢原子线系极限的波数表达式及赖曼系(由各高能激发态跃迁到基态所发射的谱线构成) 、巴耳末 系(由各高能激发态跃迁到 n=2 的定态所发射的谱线构成)、 帕邢系(由各高能激发态跃迁到 n=3 的定态所发 射的谱线构成)的线系极限波数。 (已知:里得伯恒量R = 1.097×10 m-1) 解:由 λ =
解: “全部” 二字太绝对了, 虽然教材169页的那个表中表明巴耳末系是可见光, 但利用 当高激发态n=∞时,辐射光子的波长为364.6nm,并不在可见光波长范围之内。 [ F ] 5.夫兰克-赫兹实验只能证明原子能级的存在,不能测电离电势。
1
λ
= R(
1 1 − 2 ), 2 2 n
解:将夫兰克-赫兹实验装置稍加改进,还可以测得较高激发电势和使原子电离成一价正离子的第一电离 电势。 二、选择题: 1.已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U0 (使电子从金属逸出需作功 eU0 ),则此单色光的波长λ必须满足: [ A ] (A) λ ≤
-19
C)
E k m 4.0 × 10 = = 2.5 (V) 1.6 × 10 −19 e 由光电效应方程 hν = hν 0 + E k m , 得红限频率
−19
ν0 =
hv − E k m c E k m 3 × 108 4 × 10 −19 = − = − = 4.0 × 1014 (Hz) −9 − 34 h 300 × 10 6.63 × 10 λ h
3. 康普顿散射中, 当出射光子与入射光子方向成夹角 θ = __π __ 时, 光子的频率减少得最多; 当 θ = __0__ 时,光子的频率保持不变。 解:由康普顿散射公式Δλ = λ ' -λ = 2λ c sin 2 当 n = 0 时,波长不变,所以频率不变。
θ
2
可知,当θ= π 时,波长增加得最多,所以频率减少得最多;
5.假定氢原子原来是静止的,则氢原子从 n=3 的激发态直接通过辐射跃迁到基态的反冲速度大约为 [ C ] (A) 10m⋅s-1 (B) 100 m⋅s-1 -1 (C) 4 m⋅s (D) 400 m⋅s-1 -27 (已知:氢原子的质量m=1.67×10 kg) 解:从 n = 3 到 n = 1 辐射光子的能量为 hν = E 3 − E1 , 动量大小为 p光 =
O
(A)
U
O
(B)
U
O
(C)
U
O
(D)
U
解:光的强度 I=Nhv, 其中 N 为单位时间通过垂直于光线的单位面积的光子数。保持频率 v 不变,增大光 强 I,则光子数 N 增加,光电子数也随之增加,电流 i 也增加,截止电压与频率有关,因之不变。
3. 在 X 射线散射实验中,若散射光波长是入射光波长的 1.2 倍,则入射光光子能量 ε 0 与散射光光子能量
ε 之比为
B
[
]
(A) 0.8 (C) 1.6
(B) 1.2 (D) 2.0
解:
ε=
hc
λ
,
ε0 λ = =1.2 ε λ0
ε0 =
hc
λ0
, λ = 1.2λ0 ,所以
ε0 λ = = 1 .2 ε λ0
4.氢原子从能量为-0.85eV 的状态跃迁到激发能(从基态到激发态所需的能量)为 10.19eV 的状态时,所发 射的光子的能量为 [ A ] (A) 2.56eV (B) 3.41eV (C) 4.25eV (D) 9.95eV 解:激发态的能量 E n = E1 + ∆E = −1.36 + 10.19 = −3.41(eV) 发射光子的能量为 ε = E n − E = −3.41 − ( −0.85) = 2.56(eV)
三、填空题: 1.当波长为 300nm的光照射在某金属表面时, 光电子的动能范围为 0 ~ 4.0×10-19J。则:此金属的遏止电 压为|Ua| = ___2.5____ V,红限频率为ν 0 = ___4.0×1014____ Hz。 (已知:普郎克常量h = 6.63×10-34J⋅s,基本电荷e =1.6×10 解:遏止电压为|Ua|=
4
= 1.63×10
−7
(m)
2.用波长λ0 = 1 Å的光子做康普顿实验。则: (1)散射角 ϕ = 90 的康普顿散射波长是多少? (2)分配给这个反冲电子的动能有多大?
o
解:(1) 由康普顿散射公式可得散射光波长
λ = λ0 + ∆λ = λ0 + 2λc sin 2
E k = hv0 − hv =
紫外线
+
×B ×
M
× × × E×
−
解:(1)当电子匀速直线地穿过互相垂直的电场和磁场区域时,电子所受的电场力与洛仑磁力大小相等,即
eE = evB
E 5 × 10 3 所以光子的最大速度率 v = = = 106 (m⋅s-1) B 0.005 1 2 hc hc 1 2 (2) 由光电效应方程: hv = hv 0 + mv , = + mv 2 λ λ0 2 1 1 = 可得波长为 λ = 2 1 mv 1 9.11 × 10 −31 × 1012 + + λ0 2hc 2.6 × 10 −7 2 × 6.63 × 10 −34 × 3 × 108
解:教材159页。从粒子完全非弹性碰撞过程中能量转化考虑,金属中的电子可以瞬时全部吸收光子的能 量,不需要能量积累过程,光电效应是瞬时发生的。 [ T ] 3.康普顿散射的入射光可以是可见光。
解:此题如果改为“使得康普顿效应显著,入射光可以是可见光” ,那么结果就应该为[F]。P163页例题3 上面那段话。 “在入射光子能量较低时(如使用可见光或紫外线入射) ,外层电子不能再看做是静止的自由 电子,康普顿散射公式不再适用。这种场合康普顿效应不能出现,只能观察到光电效应。 ” [ F ] 4.氢原子光谱的巴尔末系光谱线全部在可见光范围内。
h
氢原子辐射光子前后动量守恒,有 0 = p光 − p氢 , p氢 = p光 , 所以,反冲速度为 v =
λ
=
hν , c
p氢 m氢
=
hν
c = m氢
− 13.6 × (
1 −1 × 1.6 × 10 −19 ) 2 3 = 3.86 (m⋅s −1 ) 1.67 × 10 − 27 × 3 × 10 8
2.某光电管阴极对于λ = 4910 Å的入射光,发射光电子的遏止电压为 0.71 伏。当入射光的波长为___3.82 ×103 __ Å时,其遏止电压变为 1.43 伏。 (已知:电子电量e = 1.60×10
-19
C。普朗克常量h = 6.63×10-34J⋅s)
2
解:由光电效应方程
⎫ = hν 0 + e U a ⎪ 1 1 ⎪ λ ⎬ → ( − )hc = e(| U a ' | − | U a |) hc λ' λ ′ ⎪ = hν 0 + e U a ⎪ λ′ ⎭ 1 1 λ' = = ′ | − | U a |) 1 e(| U a 1 1.6 × 10 −19 × (1.43 − 0.71) + + λ hc 4.9 × 10 −7 6.63 × 10 −34 × 3 × 108 = 3.82 × 10 3 (Å) hc
En = En =
1 E 1 = −0.85 , n = n2 1 E 1 = −3 .4 , n2
− 13.6 =4 − 0.85 − 13.6 =2 − 3.4
n=
所以从 n = 4 到 n = 2 能级跃迁。
3
四、计算题: 1.如图所示, 某金属M的红限波长λ0 = 260nm (1nm = 10-9m = 10Å)。今 用单色紫外线照射该金属, 发现有光电子放出, 其中速度最大的光电 子可以匀速直线地穿过相互垂直的均匀电场 ( 场强 E = 5 × 10 3 V⋅ m −1 ) 和均匀磁场(磁感应强度为 B = 0.005 T )区域, 求: (1) 光电子的最大速度 v; (2) 单色紫外线的波长 λ 。 (已知:电子质量me = 9.11×10-31kg。普朗克常量h = 6.63×10-34J⋅s)
©物理系_2012_09
《大学物理 AII》作业
No.7 场的量子性 玻尔理论
一、判断题: (用“T”和“F”表示) [ T ] 1.物理学史上的 “紫外灾难”现象出现于黑体辐射的经典理论解释。 解:教材 155 页。 瑞利-金斯公式在长波方面与实验曲线吻合,但在短波方面函数(总辐出度)趋于无穷大。 [ F ] 2.光电效应中光电子的出现,靶材料需要对入射光能量进行累积。
7
~
1
λ
= R(
1 1 − 2 ) (n > k) 2 k n ~
