23框图化简
合集下载
自动控制原理:方框图的化简..

X1 (s) G(s) X (s)
X 2 ( s) X ( s)
X (s)
G (s)
X1 (s) G(s) X (s)
X (s)
G (s)
X1 (s) G(s) X (s)
G (s)
X 2 (s) G(s) X (s)
1 / G ( s)
X 2 ( s) X ( s)
5. 相加点移动的规则
E ( s)
d
1 ( Ls R )
I a (s)
Ed (s) kd (s)
1 ( s ) [ M ( s ) M L ( s )] Js
( s )
kd
Ed (s)
M ( s)
M ( s)
L
1 Js
( s )
M ( s) km I a ( s)
I a (s)
km
X o ( s)
X i ( s)
B( s )
G (s) 1 G (s)
X o ( s)
U a ( s)
例
1 ( Ls R )
I a (s)
km
M ( s)
M L ( s)
1 Js
( s )
Ed (s)
kd
( s ) 为输出时,令 M L (s) 0
I a (s) 1 ( Ls R )
X i ( s) E ( s ) G ( s )
X o ( s)
X i ( s)
B( s )
H (s)
G(s) 1 G( s) H ( s)
X o ( s)
当反馈回路传递函数 H ( s) 1 时,系统为单位反馈 系统。
2.4框图化简及梅逊公式

C(s)
有1组三个互不接触回路: L3 abefij
不存在四个互不接触回路: L4 0
1 L1 L2 L3
k 第k个前向通道的余子式;其值为 中除去与第k个前
向通道接触的回路后的剩余部分;
1 1 L1 L2 L3 ... 1
R(S ) E (S )
G1 G2
C (S )
R(S ) 1 E (S ) G1 C (S ) 1 C (S )
G2
信号流图是由定向线段(支路)将一些节点(变量)连接起来 组成的。支路上的传递函数称为支路增益
[几个术语]:
输入节点(源点):只有输出支路的 节点。如: R,N。
R
1
N 1 E P G Q G1 2
补充例题1
g
h b
R(s ) 1
a
c
d
1
2
3
i
4
5
l
e j6
7f
k
1 C (s )
8
9
m
Байду номын сангаас
补充例题2
R(s )
G1
1 1
G2
C (s )
3) 反馈联接:
R(s ) E (s)
G (s )
C (s )
H (s )
称为闭环传递函数
C ( s) G( s) ( s ) R( s ) 1 G ( s ) H ( s )
H (s)G2 (s)
①
R(s)
G1 ( s)
G2 ( s)
-
G3 ( s)
H ( s)G2 ( s)
第2章(4)传递函数方块图及其化简

G(s) 1 G(s)H (s)
G(s) 1 Gk (s)
B(s)
H(s)
前向通道传递函数、
反馈通道传递函数、
开环传递函数、
正反馈、负反馈;
2.方框图的变换与化简:(1)串、并联的化简; (2)分支点跨过环节的移动规则; (3)相加点的拆并及跨过环节的移动规则; (4)反馈与并联交错的化简
Xo(s)
G1(S)
G2(S)
Xi(s) G1(S) G2(S)
Xo(s)
G(s)
X X
o(s) i(s)
X o(s) X (s)
X (s) Xi(s)
G2
(
s)G1(
s
)
n
G(s) Gi (s) i 1
负载效应问题
i1 R1 i2 R2
G1(s)
1 R1C1s
1
G2 (s)
Xo(s)
C
略
H1
jik 04
16
X (s) 0 求 Xo(s) 。令
Xi2(s)
i1
Xi 1(s)
H3
+
-
-
G1 B +
G2
,
Xi
2(
Xi1(s)处的相加点取消,
H1 变成(-H1)。原图改画成:
s)
Xi 2(s) +
G3
Xo(s)
+
+
-A +
+
-
G3 Xo(s) A +
H2
C
H2
G2
+
-
B G1
复习:
1.微分方程的拉氏算子解法; 2.系统的响应就是微分方程的解 总响应x(t) =零输入响应xZ(t)+零状态响应xs(t)
结构图化简

比较点(或综合点):表示对两
个以上的信号进行加减运算。
u(t),U(s)
u(t) r(t) U(s) R(s)
r(t),R(s)
方框(或环节):表示对信号进 行的数学变换。方框中写入环节 的传递函数。
U(s)
C(s)=U(s)G(s) G(s)
2.4.2 结构图的化简
为了便于系统分析和设计,常常需要对系统的复杂的结构 图作等价变换,或者通过变换使系统结构图简化,求取系 统的总传递函数。因此,结构图变换是控制理论的基本内 容。
Rs
Cs
G1 sG2 s......Gn s
Cs Gn s
5
并联连接的等效变换
传递函数的并联连接, 其等效传递函数为这些 传递函数的和。
Rs
G1s
C1 s Cs
G 2 s C2 s
C1 s G1 s R s,C2 s G2 s R s G s C1 s C2 s G1 s G2 s R s G s G1 s G2 s
输入信号
U(s) 信号线
方框 G(s)
C(s)=U(s)G(s)
输出信号 信号线
信号线:带有箭头的直线,表示信号的流向,在直线旁 标记信号的时间函数或象函数。
引出点(或测量点):表示信号引出或测量的位置。代 表同一个变量作用在不同对象上,而不是理解成输出一 部分!
方框(或环节):表示对信号进行的数学变换。方框中 写入环节的传递函数。
s
sG4 s +G1 s
G2
s
G3
s
G4
s
H1
s
17
谢谢!
18
比较点前后移动
Rs Gs
Cs
Q
Gs Cs
数字逻辑基础卡诺图化简
101
0
110
0
1 2020/8/14 1 1
1
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
111
1
2020/8/14
15
(2)从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填
入1,其余的小方块中填入0。
例4: 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
① 无关项的概念
对应于输入变量的某些取值下,输出函数的值可 以是任意的(随意项、任意项),或者这些输入变量的 取值根本不会(也不允许)出现(约束项),通常把这 些输入变量取值所对应的最小项称为无关项或任意项, 在卡诺图中用符号“×”表示,在标准与或表达式中用 ∑d( )表示。
例:当8421BCD码作为输入变量时,禁止码1010~ 1111这六种状态所对应的最小项就是无关项。
相邻 相邻
② 几何相邻的必须
逻辑相邻:变量的 取值按00、01、11、 10的顺序(循环码 ) 排列 。
图1-11 三变量卡诺图的画法
2020/8/14
12
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”: 上下相邻,左右相 邻,并呈现“循环 相邻”的特性,它 类似于一个封闭的 球面,如同展开了 的世界地图一样。
复习:
真值表--逻辑表达式(化简)--逻辑电路图
例:三变量表决逻辑 Y=? 逻辑图?
2020/8/14
2.3系统的方框图及其简化
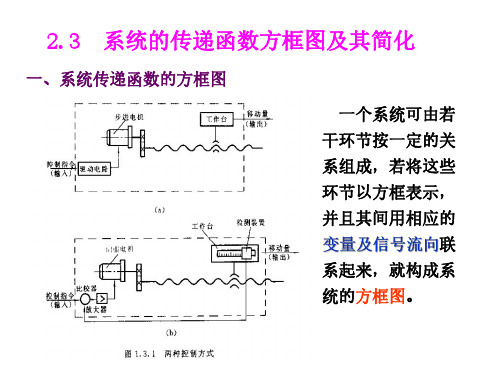
例:求系统传递函数。
Xi(s) + E(+s)
分
+
支
B(s)
点
前
移 Xi(s) + E(+s)
+
B(s)
G1 +
H2
G2
G3
H1
H2G3
G1 +
G2
G3
H1
Xo(s) Xo(s)
Xi(s) + E(+s)
+
B(s)
G1 +
H2G3 G2
H1
Xo(s) G3
Xi(s) + E(+s) G1
+
B(s)
纲也要相同。 相加点可以有多个输入,
但输出是唯一的。
C
A + A-B+C +
B
(3) 分支点
分支点表示同一信号向不同方向的传递。只传递信号, 不传递能量。
在分支点引出的信号不仅量纲相同,而且数值也相 等。
X(s) X(s) X(s)
2、系统方框图的建立步骤
(1) 建立系统(或元件)的
;
(2) 对这些原始微分方程进行
函数无量纲,而且H(s)的量纲是G(s)的量纲的倒数。
小小总结:
前述三种基本连接形式:串联、并联、反馈
G(s)
①两个环 Xi(s)
节相串联
G1(Gs) 1 ( sX)1G(s)2 (Gs)2(s)
Xo(s)
②两个环节 G(s)
相并联
G1(s) Xo1(s)
Xi(s)
G1(s)
G2
+
(s) +_
G2 (s) Xo2(s)
自动控制原理方框图的化简课件

化简过程中的误差分析
误差来源分析
分析化简过程中可能产生的误差来源,如近似处理、线性化等。
误差传递与影响
评估误差对系统性能的影响,了解误差传递的方式和程度。
误差补偿与修正
根据误差分析结果,采取适当的补偿和修正措施,减小误差对系 统性能的影响。
化简后系统的性能分析
稳定性分析
通过化简后系统的传递函数或状态方程,分析系统的 稳定性。
方框图的组成元素
总结词
方框图由输入、输出、转换和反馈四个基本元素组成。
详细描述
方框图由输入、输出、转换和反馈四个基本元素组成。输入是系统接收的信号 或信息,输出是系统输出的信号或信息,转换是系统内部对输入进行处理的过 程,反馈则是系统对输出的反应或调整。
方框图的作用
• 总结词:方框图可以清晰地表示系统的结构、功能和动态特性。
04
方框图化简的注意事项
化简方法的适用性
确定化简方法的适用范围
01
不同的化简方法适用于不同类型和规模的方框图,应先判断所
处理的方框图是否适用。
理解化简方法的原理
02
掌握化简方法的原理和步骤,确保正确应用化简方法。
考虑化简后的系统性能
03
在化简方框图时,应考虑化简对系统性能的影响,如稳定性、
动态响应等。
02
通过化简方框图,可以快速识 别故障传递路径和关键环节, 提高故障诊断的效率和准确性 。
03
化简后的方框图可以作为故障 诊断的参考模型,为故障排除 提供指导和支持。
谢谢观看
• 详细描述:方框图具有多种作用。首先,它可以清晰地表示系统的结构,将复杂的系统分解为若干个简单的组成部分, 便于理解和分析。其次,通过方框图可以明确地表示出系统的功能,即各个组成部分的作用及其相互关系。此外,方框 图还可以表示系统的动态特性,例如信号的传递、处理和反馈过程,有助于揭示系统的动态行为和性能。在自动控制原 理中,方框图是分析和设计控制系统的重要工具之一。通过对方框图的分析,可以了解系统的性能、稳定性、可控性和 可观测性等方面的问题,为控制系统的设计和优化提供依据。
233控制系统方框图的化简及传递函数
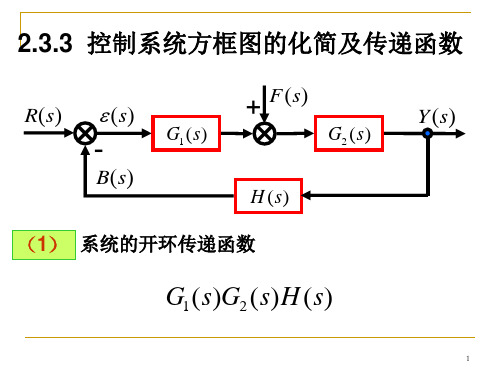
U 2 ( s)
22
两个相加点互相交换移动
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
23
小回路化简
U1 ( s ) A
-
-
1 R1
1 sC1
1 R2C2 s 1
12
结论
下列闭环传递函数
(s)
F ( s)
(s)
F ( s )
具有相同的特征多项式
13
闭环特征多项式:
1 G1 (s)G2 (s) H (s)
14
G1 (s)G2 (s) (s) 1 G1 (s)G2 (s) H (s)
输出对输入 对 比
G2 (s) F ( s) 1 G1 (s)G2 (s) H (s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
35
G3 ( s) G1 ( s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
小回路化简
R( s )
G1 ( s) G3 ( s) G1 ( s)
G1 ( s)G2 ( s) 1 G1 ( s)G2 ( s)
1 G2 ( s)G3 ( s) 1 G1 ( s)G2 ( s)
E (s)
E ( s) 1 G2 (s)G3 (s) R(s) 1 G1 (s)G2 (s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方括号内每一项的符号是这样决定的: 相加点处对反馈信号为相加时取负号; 相加点处对反馈信号为相减时取正号。
注意在应用此公式时,必须要具备以下条件: 1、整个方框图只有一条前向通道。 2、各局部反馈回路间存在公共的传递
公式:
G(s)
G1G2
1 G1R1 G2R2
J1s2
q As
K2
qos
T2s
1 J2s2 fs
qos
经相加点前移和分支点后移即可求出传函。
注意:
1. 绘制物理系统方框图时,要正确 列写微分方程。
2. 要对每个方程消减的中间变量慎 重选取,选择正确,系统的方框 图容易画出。
G1G2G3G4
X (s) o
1 G2G3G5 G3G4G6 G1G2G3G4G7
G(s)
G1G2G3G4
1 G2G3G5 G3G4G6 G1G2G3G4G7
可得公式:(含有多个局部反馈的闭环传递函数)
GB (s)
Xo (s) Xi (s)
前向通道的传递函数之积
1 [每一反馈回路的开环传递函数之积]
2、相加点(比较点)的移动
1)后移:相加点后移,必须在移动支路上 串联所经过传递函数的方框。
2)前移:相加点前移,必须在移动支路上 串联所经过传递函数的倒数的方框。
2.3.2 简化原则(其他一些规则)
1.当相加点之间无其他方框和分支点时, 相加点可以前后交换。
2.对串联的方框,如果中间没有相加点 或分支点,可以前后交换或结合为一个。
(2)
T1s
1
J1s 2
T2 s (2)
q A s
T2s K2qAsqo s
q A s
K2
qo s
(3)
(3)
T2 s
T2 s J2s2qo s fsqo s (4)
T2 s
1
q o s
J2s2 fs
(4)
综合上述图形:
1
K1
T2s
qi(s)
q As
K1
T1(s)
J2s2 fs
1
G2
Xo (s)
R2
实际:
G(s) G1 G2 1 G1R1 1 G2R2
G1G2
1 G1R1 G2R2 G1G2R1R2
因为两局部反馈之间不存在公共的方框。
Xi
G1
R1
G2
Xo
R2
应用公式:
G(s)
G1G2
1 G1R1 G2R2G1
实际:G(s)
1
G1
1 G1R1 G1
1 G1R1
3.相加点为两个以上输入量时,相加 点可以分开,先后相加,结果不变。
4.分支点移动到相加点之前,必须在 移动的分支路上补加上信号,即在 移动分支路上增加相同的相加点。
5.要分清是并联的方框图还是反馈的 方框图,再做相应的处理。
2.3.3 简化过程中的两条原则
(等效原则在具体的传递函数中的体现) (化简后的检验规则)
1
1
1i
A
对J1 J1qA (t) T1(t) T2 (t)
对k2 T2 (t) k2[q A (t) qo (t)]
对J J q(t) fq(t) T (t)
2
2o
o
2
设初始条件为零,由拉氏变换得
T1
s
K1
q i
s
q
A
s
(1)
qi s
T1 s
K1
q A s (1)
J1s2qAs T1sT2 s
G4 (s)
G7 (s)
G6 (s)
消去回路Ⅰ,得
G1 ( s )
G5 (s)
1 G4 (s)
G2 (s)
G3 (s)G4 (s) 1 G3 (s)G4 (s)G6 (s)
G7 (s)
消去回路Ⅱ,得
G1 ( s )
G2G3G4 1 G2G3G5 G3G4G6
G7 (s)
消去回路Ⅲ,得
X i (s)
2.3 方框图的变换
2.3.1 移动规则 2.3.2 简化原则(其他一些规则) 2.3.3 简化过程中的两条原则 2.3.4 方框图的绘制
2.3.1 移动规则
1、分支点的移动
1)前移:分支点前移,必须在移动支路 (分支路)上串联所经过传递函数的方框。
2)后移:分支点后移,必须在移动支路 (分支路)上串联所经过传递函数的倒数 的方框。
T
J
dw d 2q
TJ J dt dt2
例:
qi (t)
k1
J1
k2
J2
f
T1 (t )
q A (t)
T2 (t)
qo (t)
qi (t) —
T1(t),T2 (t) —
qo (t) —
J1,J 2 —
k1, k2 — 扭簧刚度 f — 粘性摩擦系数
解:对每一个元件列方程
对k T (t) k [q (t) q (t)]
1.前向通道中传递函数的乘积必须 保持不变。
2.各反馈回路开环传递函数的乘积 必须保持不变。
例:化简方框图,求系统传递函数。
G1 ( s )
G5 (s)
G2 (s)
G3 (s) G4 (s)
G7 (s)
G6 (s)
解:A点后移,得
G1 ( s )
G5 (s)
G2 (s)
G3 (s)
1 G4 (s)
G2 G2R2
G1G2
(正确)
1 G1R1 G1G2R2
因为两个反馈回路之间 有公共的方框, 所以应用公式是正确的 。
2.3.4 方框图的绘制
对扭转弹簧
q1w1 k q 2w2
T
T
k (q 1
q ) 2
k t
(w 1
w )dt 2
qw f 11
qw 22
T
T
f
(w1
w 2
)
f
(q1 q2 )
qw
