圆锥的体积 圆柱与圆锥PPT精品课件
合集下载
《圆柱和圆锥——圆柱的体积》数学教学PPT课件(3篇)
V=sh
S h
教学新知
教学新知
试一试：一个圆柱形零件，底面半径是5厘米，高是8厘米。 这个零件的体积是多少立方厘米？
V=sh=5²π×8=628（cm³）
教学新知
练一练：
1.计算圆柱的体积。（单位：cm）
V=sh=4²π×8=401.92（cm³） V=sh=3²π×6=169.56（cm³）
V=sh=1.5²π×0.5×2=7.065（m³）
8.两个底面积相等的圆柱，一个高是4.5分米，体积是81立方分米。另 一个高是3分米，它的体积是多少立方分米？
s=V1÷h1=81÷4.5=18（dm²） V2=sh2=18×3=54（m³）
课堂练习
9.把3个高相等、底面半径都是10厘米的圆柱形盒子叠放在 一起，如图 所示，拿走1个盒子，表面积就减少314平方厘米。每个盒子的体积是 多少立方厘米？
个近似的长方体。拼成的长方体的底面积等于圆柱的（底面积）， 高就是圆柱的（ 高 ）。 （2）用字母V表示圆柱的体积，S表示圆柱的底面积，h表示圆柱的高， 圆柱的体积公式可以写成（V=sh）。 （3）一个圆柱的底面积是0.6平方分米，高是3.5分米，体积是（2.1）立 方分米。
课后习题
2.—根木料如图所示，求这根木料的体积。（单位:m)
2.一根圆柱形木料，底面周长是62.8厘米，高是50厘米。这根木料的体 积是多少？
r=C÷2π=62.8÷6.28=10（cm） V=sh=10²π×50=15700（cm³）
教学新知
例一：完成下面的表格。
底面积/m2
高/m
体积/m3
圆 柱
0.6
1.2
0.25
3
0.72 0.75
《圆柱与圆锥——圆锥的体积》数学教学PPT课件(2篇)
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
等底等高
通过实验我知道了：圆柱 的体积等于和它等底等高 的圆锥的体积的 3 倍。
圆柱体的体积是与它等底等高的圆锥体体积的3倍，圆锥体的体积是与 它等底等高的圆柱体体积的三分之一。 那么圆锥体积的计算公式： 圆锥体积=底面积×高×13
V=1/3sh=1/3×3.6×2=2.4（m³） h=2.4÷4÷2=0.3（m）
8.将一个底面直径是20cm，高为10cm的金属圆锥体，全部浸没在直径 是40cm的圆柱形水槽中，水槽水面会升高多少cm?
V=1/3sh=1/3×100×3.14×10=3140/3（cm³） h=V÷s=3140/3÷20²÷3.14=5/6（cm）
2.把一个底面直径是2分米，高是3分米的圆柱体削成一个最大 的圆锥体削去（6.28）立方分米。
3.一个圆柱体和一个圆锥体的底面积和体积分别相等，已知圆 柱体的高6厘米，那么圆锥体的高是 ( 18 )厘米。
课后习题
4.等底等高的圆柱和圆锥的体积相差16立方米，这个圆柱的
体积是（24）立方米，圆锥的体积是（ 8 ）立方米。
装满一车沙，卸后沙堆成—个高是5米的圆锥形，它的底面积是多
少平方米？
V长方体=4×1.5×4=24（m³）
S=V长方体÷h÷1/3=14.4（m²）
2.—堆圆锥形黄沙，底面周长是25.12米，高1.5米，每立方米的黄沙重
1.5吨。这堆沙重多少吨？
V=⅓sh=⅓×（25.12÷6.28）²×3.14×1.5=25.12（m³）
V圆柱=sh=3²×3.14×5=141.3（dm³）
人教版六年级数学下册第三单元《圆柱与圆锥》课件共10个精品课件
柱的底面直径与高的比。
πd＝h d ：h ＝ 1 ：π
课堂总结
通过这节课的学习， 你有什么收获?
义务教育人教版六年级下册
第3单元 圆柱与圆锥 1.圆 柱
第 5 课时 圆柱的体积
复习导入
填空。 圆柱的侧面积＝（ 底面周长×高 ） 圆柱的表面积＝（ 侧面积＋底面积×2 ） 长方体的体积＝（ 长×宽×高 ） 正方体的体积＝（棱长×棱长×棱长）
底面 侧面
圆柱的底面都 是圆，并且大 小一样。
底面 圆柱的侧面是曲面。
哪个圆柱比较高？为什么？
底面 O
侧面 高
底面 O 侧面 高
底面 O
底面
圆柱两个底面之间的距离叫做高， 圆柱有无数条高。
动手操作： 如果把一张长方形的硬纸贴在木棒上，快速转
动木棒，想一想，转出来的是什么形状？
转动起来像一个圆柱。
8cm
要解决这个问题，就
是要计算什么？
10cm
杯子的容积
10cm
杯子的底面积： 杯子的容积：
8cm
3.14×(8÷2)2
50.24×10
＝3.14×42
＝502.4 (cm3 )
＝3.14×16
＝502.4 (mL)
＝50.24 (cm2 )
答：因为502.4大于498，所以杯子能 装下这袋牛奶。
（长方体）
（正方体 ）
（ 圆柱 ）
课堂总结
通过这节课的学习， 你有什么收获?
义务教育人教版六年级下册
第3单元 圆柱与圆锥 1.圆 柱
第 2 课时 圆柱的认识（2）
复习导入
圆柱由哪几部分组成？ 有什么特征？
上、下底面：圆 侧面：曲面
探究新知
圆柱和圆锥的体积
长方体的底面积等于圆柱体的底面积 长方体的高等于圆柱体的高
长方体的体积=长×宽×高 圆柱的体积=底面积×高 V=Sh V=πr ² h
20厘米 25厘米
20)2＝314(cm2) (1)水桶的底面积：3.14×( 2 3 (2)水桶的容积： 314×25＝7850（cm ）
4分米 10分米
把一个棱长是6厘米的正方体木 块，加工成一个最大的圆锥体， 圆锥的体积是多少立方厘米？
0.8米
求各圆柱的 体积。
0.5分米
求下面各圆柱的体积。
1、底面半径3cm，高5cm。 2、底面直径8m，高10m。 3、底面周长25.12dm，高2dm。
圆柱体积＝底面积
高
圆柱体积＝底面积
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝ 底面积
高
高
圆柱体积＝底面积 圆锥体积＝ 底面积
高
高
1 3
圆柱与圆锥的体积之间有什么关系？
等底等高圆锥体积是圆柱体积的三分之一 等底底面周 长31.4米，高15米，这个玻璃罩的容积 是多少立方米？（玻璃厚度忽略不计）
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
高
圆柱体积＝底面积 圆锥体积＝
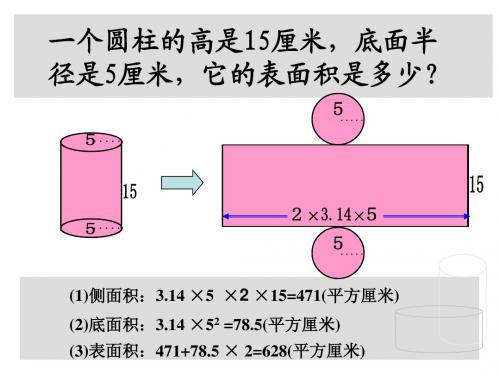
一个圆柱的高是15厘米，底面半 径是5厘米，它的表面积是多少？
苏教版小学六年级下册数学课件 《圆柱的体积》圆柱和圆锥PPT(第3课时)
0.314m³ 中单位
不一致，要将结
果立方 7.把一块长、宽、高分别是5厘d米m改、写3.1为4立dm方、2dm的长
方体铁块，熔铸成
米。
一个底面半径是2dm的圆柱形铁块，这个圆柱形铁块
的高是多少分2米.5？dm
提示：长方体体 积与圆柱体积相
等。
课堂练 习
8.一根圆柱形钢材长2米，截成3段小圆柱后，
试一试：一个圆柱形水杯的容积是1.6升，从里面量， 平方分米。用这个水杯装3/4杯水，水面高多少分米？
先算出3/4杯水的体积是多少。所以：
V=¾×1.6=1.2（l） 高等于体积除以底面积，所以：
h=V÷s=1.2÷1.2=1（dm）
教学新 知
思考： （1）把圆钢竖着拉出水面8厘米，水面下降了4厘米， 能想到一些什么？ （2）全部浸入，水面上升9厘米，你又能想到什么？ 计算出这个圆钢的体积？ （3）这题还可以怎样思考？
试一试：一个圆柱形水池，从里面量，底面直径是8
米，深3.5米。
（1）水池里最多能蓄水多少吨？（1立方米水重1吨）
（2）在水池的底面和四周抹上水泥，抹水泥部分的
（面积1）是V多=少s？h=4²π×3.5=175.84（m³）175.84m³=17 （2）S=2πrh+πr²=2×3.14×4×3.5+3.14×4²=138.
（2）l=4h+4d+15=4（20+30）+15=215cm
教学新 知
练一练：一个用塑料薄膜覆盖的蔬菜大棚，长15米， 横截面是一个半径 2米的（半1）圆搭形建。这个大棚大约要用多少平方米的塑料薄膜？
S=πrh+πr²=3.14×2×15+3.14×2²=106.76（m
圆柱和圆锥的体积
01
02
03
底面形状相同
圆柱和圆锥的底面都是圆 形。
高与底面垂直
圆柱和圆锥的高都与底面 垂直，且都位于底面的中 心。
侧面展开图相似
圆柱和圆锥的侧面展开图 都是长方形或扇形。
圆柱和圆锥的体积关系公式
圆柱体积公式
$V_{cylinder} = pi r^2 h$
圆锥体积公式
$V_{cone} = frac{1}{3} pi r^2 h$
这个公式是由圆的面积公式和高度相 乘得到的。
圆柱体积公式的推导
首先，我们知道圆的面积公式是：A = πr²。 然后，将这个公式乘以高度h，得到圆柱体的体积公式：V = πr²h。
02 圆锥的体积
圆锥体积的定义
圆锥体积是指圆锥所占空间的大小。 圆锥体积可以通过底面积和高来计算。
圆锥体积的公式
圆锥体积的公式为：V = (1/3)πr²h，其中r为底面半径，h为高。
圆柱和圆锥的体积
contents
目录
• 圆柱的体积 • 圆锥的体积 • 圆柱和圆锥的体积关系 • 圆柱和圆锥的体积的应用
01 圆柱的体积
圆柱体积的定义
01
圆柱体积是指圆柱体所占空间的 大小。
02
圆柱体积是高度和底面积的乘积 。
圆柱体积的公式
圆柱体积的公式是：V = πr²h，其中r 是Байду номын сангаас面半径，h是高。
体积关系
$V_{cylinder} = 3V_{cone}$
圆柱和圆锥体积关系的证明
证明方法一：利用几何图形推导
1. 将圆锥的底面平放在桌面上， 使其与桌面紧密接触。
2. 将圆锥的侧面展开成扇形， 并连接扇形的弧边与圆锥的顶点。
苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第3课时)
教学新知
例二：计算圆柱的表面积。（单位：cm）（π取3.14）
S=2π×0.8+2π≈11.304 S=2π×0.5×3.5+2π×0.5²≈12.56
教学新知
例三：一个圆柱形油桶，底面直径是0.6米，高是1米。做这个油桶至少 需要铁皮多少平方米？（得数保留两位小数）
S=2π×0.3×1+2π×0.3²≈2.45（㎡）
能想到一些什么？ （2）全部浸入，水面上升9厘米，你又能想到什么？怎样
计算出这个圆钢的体积？ （3）这题还可以怎样思考？
教学新知
例一：一个圆柱形水桶的容积是80立方分米，里面装了2/5的水。 已知它的底面积是10平方分米，里面水的深度是多少？
【讲解】根据“水桶的容积是80立方分米”和“里 面装了 2/5的水”这两个条件，我们可以求出水桶 内水的体积，然后用水的体积除以水桶底面积得出 水桶内水的深度。 80× =32（立方分米）……水桶内水的体积 32÷10=3.2（分米）……水桶平均剖成两片，其中一片如图所示。（单位：厘米） （1）剖面面积是多少平方厘米？ （2）这片木料的表面积和体积各是多少？
（1）S1=20×12=240（cm²） （2）S2=πrh+πr²+S1=3.14×6×20+3.14×6²+240=792.84（cm²）
V=1/2S3h=1/2×3.14×6²×20=1130.4（cm³）
课后习题
7.把一根长2.4米的圆柱形状的木料锯成4段，表面积增加了 0.18平方米。
这根木料原来的体积是多少立方米？
S=0.18÷6=0.03（m²）
V=sh=0.03×2.4=0.072（m³）
8.一个圆柱高4厘米，底面半径是2厘米。如果将它的底面平均分成若干份，
圆柱圆锥圆台体积和表面积.ppt
1
1
A.4
B.2
3 C. 6
3 D. 4
[答案] D
[解析]
三棱锥B1－ABC的高h＝3，底面积S＝S△ABC＝
3 4
×12＝ 43，
则VB1－ABC＝13Sh＝13×
43×3＝
3 4.
5．若一圆柱与圆锥的高相等，且轴截面面积也相等，那
么圆柱与圆锥的体积之比为( )
A．1
1 B.2
3
3
C. 2
D.4
例题解析
命题方向 多面体与旋转体的面积
【例1】圆台的上、下底面半径分别是10 cm和20 cm，它的侧 面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
命题方向 多面体的体积
[例 2] 长方体相邻三个面的面积分别为 2、3、6 求它的
体积．
[解析] 设长方体的长、宽、高分别为a、b、c则有
据条件得到
1 2
πl2＝2π，解得母线长l＝2,2πr＝πl＝2π，r＝1所以
该圆锥的体积为：V圆锥＝13Sh＝13×
22－12π＝
3 3 π.
[点评] 本题主要考查空间几何体的体积公式和侧面展开 图．审清题意，所求的为体积，不是其他的量，分清图形在 展开前后的变化；其次，对空间几何体的体积公式要记准记 牢，属于中低档题．
[解析]
三棱台ABC－A1B1C1的上、下底面积之比为4:9.连接 A1B、BC1和AC1，把棱台分为三个棱锥B－A1B1C1，C1－ ABC，A1－ABC1.则这三个棱锥体积之比为________．
[答案] 4:9:6
[解析] 如图，设三棱锥B－A1B1C1，C1－ABC，A1－ ABC1体积分别为V1、V2、V3，又设棱台的高为h，上、下底面 积分别为S1、S2.依题意，得
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2）所铺公路的长度 23.55÷10÷0.02
＝2.355÷0.02 ＝117.75（m） 答：能铺117.75m。
四、布置作业
作业：第35页练习六，第7题。 第36页练习六，第8题。
• • • • • •
• • • • • • •
● 一个不注意小事情的人，永远不会成功大事业。──卡耐基 ● 一个能思考的人，才真是一个力量无边的人。──巴尔扎克 ● 一个人的价值，应当看他贡献了什么，而不应当看他取得了什么。 ──爱因斯坦 ● 一个人的价值在于他的才华，而不在他的衣饰。 ──雨果 ● 一个人追求的目标越高，他的才力就发展得越快，对社会就越有 益。──高尔基 ● 生活就像海洋，只有意志坚强的人，才能到达彼岸。──马克思 ● 浪费别人的时间是谋财害命，浪费自己的时间是慢性自杀。──列 宁 ● 哪里有天才，我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 ● 完成工作的方法，是爱惜每一分钟。──达尔文 ● 没有伟大的愿望，就没有伟大的天才。──巴尔扎克 ● 读一切好的书，就是和许多高尚的人说话。──笛卡尔 ● 成功＝艰苦的劳动＋正确的方法＋少谈空话。 ──爱因斯坦
三、知识应用
（二）解决问题
1. 填空 （1）一个圆柱的体积是75.36m³ ,与它等底等高的圆锥的体积是（ 25.12）m³ 。 1 75.36× ＝25.12（m³） 3 （2）一个圆锥的体积是141.3m³ ,与它等底等高的圆柱的体积是（423.9）m³ 。 141.3×3＝423.9（m³ ）
三、知识应用
2. 一个圆柱与一个圆锥的底面积和体积分别相等。 已知圆柱的高是4dm，圆锥的高是多少？
想一想，当一个圆柱与一 个圆锥的底面积和体积分 别相等时，圆锥的高与圆 柱的高又是什么关系呢？
4×3＝12（dm） 答：圆锥的高是12dm 。
三、知识应用
3. 一个圆锥形沙堆，底面积是28.26m2，高是2.5m。用这堆 沙在10m宽的公路上铺2cm厚的路面，能铺多少米？ 2cm＝0.02m （1）沙堆的体积： 转换前后沙子的体积不变，所 1 以铺成的公路路面的体积等于 请你想一想，转换前后沙子 ×28.26×2.5 3 圆锥形沙堆的体积。 的体积是否发生变化？ ＝9.42×2.5 ＝23.55（m³ ）
二、探究新知
工地上有一堆沙子，近似于一个圆锥（如下图）。这堆 沙子的体积大约是多少？如果每立方米沙子重1.5t，这堆沙 子大约重多少吨？（得数保留两位小数。） （1）沙堆底面积： 4 2 3.14 ×（ ）＝3.14×4＝12.56（m2） 2 就要先求出这堆沙的体积， （2）沙堆的体积： 要求出这堆沙子大约重多少吨， 也就是圆锥的体积。 1 ×12.56×1.2＝5.024≈5.02（m³ ） 就要先求什么？ 3 （3）沙堆重： 5.02×1.5＝7.53（t） 答：这堆沙子大约重7.53吨。
圆柱与圆锥
圆锥的体积 （例2、例3）
一、复习旧知
我们已经学会计算圆柱的体积，请你 回忆一下如何计算圆柱的体积？
二、探究新知
你能猜测一下等底、等 高的圆柱和圆锥的体积 圆锥的体积与圆柱的体积有 之间的关系吗？ 没有关系呢？ 圆柱的底面是圆，圆锥的底面也是圆。 如何计算圆锥的体积呢？
Байду номын сангаас
二、探究新知
4m
1.2m
三、知识应用
（一）做一做
1. 一个圆锥形的零件，底面积是19cm2，高是12cm， 这个零件的体积是多少？ 1 ×19 ×12＝76（cm³ ） 3 答：这个零件的体积是76cm³ 。
三、知识应用
（一）做一做
2. 一个用钢铸造成的圆锥形铅锤，底面直径是4cm， 高5cm。每立方厘米钢大约重7.8g。这个铅锤重 多少克？（得数保留整数） （1）铅锤底面积： 4 2 3.14×（ ）＝3.14×4＝12.56（cm2） 2 （2）铅锤的体积： 1 ×12.56×5≈21（cm3） 3 （3）铅锤的质量： 21×7.8≈163（g） 答：这个铅锤大约重163克 。
下面就让我们通过实验， 探究一下圆锥与圆柱体积 之间的关系。
（1）各组准备好等底、等高的圆柱、圆锥形容器。
（2）用倒沙子或水的方法试一试。
二、探究新知
我把圆柱装满水， 再往圆锥里倒。 三次正好装满。 正好倒了三次。
（3）通过实验，你发现圆锥的体积与同它等底、等高的 圆柱的体积之间的关系了吗？ 1 1 V圆锥 ＝ V圆柱 ＝ Sh 3 3