2017-2018湖北省武汉市二中广雅八年级下周练(一)
武汉二中2018年八年级下学期期中考试英语考试试题

武汉市第二初级中学&武汉二中广雅中学2017——2018学年度下学期期中考试八年级英语试卷(考试时间:120分钟满分:120分)听力部分一、听力测试第一节(共5小题,每小题1分,满分5分)听下面5个问题,每个问题后有三个答语,从题中所给的A、B、C三个项选中选出最佳选项,每个问题仅读一遍。
()1. A. Some old books. B. It's Tom's. C. Small and dirty.()2. A. About health. B. Mr Smith. C. In the meeting hall.()3. A. By plane. B. It's beautiful. C. In the USA.()4. A. Wonderful. B. For about 2 hours. C.At 2 this afternoon.()5. A. Very soon. B. With Mr. Black. C. On the wall.第二节(共7小题,每小题1分,满分7分)听下面7段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
每段对话仅读一遍。
()6. When will the woman leave?A. At 7:15.B. At 7:30.C. At 7:45.()7. What are they most probably doing?A. Planning a party.B. Having a party.C. Cleaning the room.()8. What can we learn about the man?A. He sells flowers in winter.B. He likes his flowers a lot.C. He helps the woman plant flowers.()9. Where was Bob yesterday afternoon?A . At home B. At school. C. At the cinema.()10. Who are most probably these two people?A. Husband and wife.B. Teacher and student.C. Boss and secretary.()11. What is the woman looking for?A. Her keys.B. Her handbag.C. Both.()12. Why is Smith so successful?A.He never makes any mistake.B. He can quickly solve problems.C. He is always thinking of others.第三节(共13小题,每小题1分,满分13分)听下面4段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中远出最佳选项,每段对话或独白读两遍。
2018-2019学年湖北省武汉二中广雅中学八年级(下)期中数学模拟试卷(1) 解析版

2018-2019学年湖北省武汉二中广雅中学八年级(下)期中数学模拟试卷(1)一.选择题(共10小题)1.若在实数范围内有意义,则x的取值范围是()A.x>0B.x>3C.x≥3D.x≤32.下列二次根式中的最简二次根式是()A.B.C.D.3.下列计算正确的是()A.2B.C.5D.4.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三条边长是()A.4B.C.4或D.以上都不正确5.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为()A.﹣1B.﹣1C.2D.6.下列命题:①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④在同一个三角形中,等边对等角.其中逆命题成立的个数为()A.1个B.2个C.3个D.4个7.估计的运算结果应在()A.6到7之间B.7到8之间C.8到9之间D.9到10之间8.k、m、n为三整数,若=k,=15,=6,则下列有关于k、m、n的大小关系,何者正确?()A.k<m=n B.m=n<k C.m<n<k D.m<k<n9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④10.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD中点,则=.其中正确的有()A.1个B.2个C.3个D.4个二.填空题(共6小题)11.计算:(1)=;(2)(2)2=;(3)=.12.观察下列等式:①;②;③、…根据上述的规律,写出用n(n为正整数,且n≥2)表示的等式.13.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.14.如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为.15.在△ABC中,AB=15,AC=13,AD为△ABC的高,且AD=12,则S△ABC=.16.如图,∠AOB=30°,点C、D分别在边OA、OB上,且OC=2,OD=4,点M、N 分别在OB、OA上,则CM+MN+ND的最小值是.三.解答题(共8小题)17.计算:18.已知x=+1,y=﹣1,求下列各式的值:(1)x2+2xy+y2,(2)x2﹣y2.19.如图,一根竹子高10尺,折断后竹子的顶端落在离竹子底端3尺处,折断处离地面的高度是多少尺?20.如图,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,且AB=,AD=.(1)请在图中补齐四边形ABCD,并求其面积;(2)判断∠BCD是直角吗?请说明理由;(3)直接写出点C到BD的距离为.21.等腰Rt△ABC中,∠ACB=90°且CA=CB.(1)如图1,若△ECD也是等腰Rt△且CE=CD,△ACB的顶点A在△ECD的斜边DE 上,求证:AE2+AD2=2AC2;(2)如图2,点M是△ACB外一点,CM∥AB,且BM=BA,求的值.22.“武黄城际铁路”是武汉市城市圈内一条连通武汉市和黄石市的快速城际铁路,如图1,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你解决以下问题:(1)求A、C之间的距离;(参考数据≈4.6);(2)若客车的平均速度是60km/h,市内的公共汽车的平均速度为40km/h,城际列车的平均速度为180km/h,为了最短时间到达武昌客运站,应该选择哪种乘车方案?请说明理由.(不计候车时间)(3)“为了安全,请勿超速”.如图2,武黄城际列车通车后,在某直线路段MN限速180千米/小时,为了检测列车是否超速,铁路有关部门在铁路MN旁设立了观测点S,从观测点S测得列车从点P到达点Q行驶了1.5秒钟,已知∠SPN=45°,∠SQN=60°,SQ =200米,此列车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)23.已知△ABC中,AB=AC,∠BAC=2a,∠ADB=a(1)如图1,若a=30°,则线段AD、BD、CD之间的数量关系为;(2)若a=45°①如图2,线段AD、BD、CD满足怎样的数量关系?证明你的结论;②如图3,点E在线段BD上,且∠BAE=45°,AD=5,BD=4,则DE.24.在Rt△ABC中,∠C=90°,AC=BC,O是AB的中点,∠EOF=90°,(1)如图1,点E、F分别在线段AC和线段BC上.试确定EF、AE、BF之间的数量关系,并给出证明.(2)如图2,点E、F分别在线段AC和线段CB的延长线上,且OP平分∠EOF交直线CB于P点,试确定CP、PF、BF之间的数量关系,并加以证明.(3)如图3,在(2)的条件下,连接OC,过P作PM⊥OC于点M,过F作FN⊥OB 于点N,直线PM、FN交于D点,请判断DP、PM、NF之间的数量关系,并证明.参考答案与试题解析一.选择题(共10小题)1.若在实数范围内有意义,则x的取值范围是()A.x>0B.x>3C.x≥3D.x≤3【分析】先根据二次根式有意义的条件得出关于x的不等式,求出x的取值范围即可.【解答】解:∵使在实数范围内有意义,∴x﹣3≥0,解得x≥3.故选:C.2.下列二次根式中的最简二次根式是()A.B.C.D.【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.【解答】解:A、符合最简二次根式的定义,故本选项正确;B、原式=,被开方数含能开得尽方的因数,不是最简二次根式,故本选项错误;C、原式=,被开方数含能开得尽方的因数,不是最简二次根式,故本选项错误;D、被开方数含分母,不是最简二次根式,故本选项错误;故选:A.3.下列计算正确的是()A.2B.C.5D.【分析】利用二次根式的乘法法则对A进行判断;根据二次根式的加减法对B、C进行判断;根据分母有理化对D进行判断.【解答】解:A、原式=6×3=18,所以A选项错误;B、与不能合并,所以B选项错误;C、5与﹣2不能合并,所以C选项错误;D、原式==,所以D选项正确.故选:D.4.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三条边长是()A.4B.C.4或D.以上都不正确【分析】根据勾股定理的逆定理,可设第三条边长为x,如果满足32+52=x2或32+x2=52,即为直角三角形,解出x的值即可解答;【解答】解:设第三条边长为x,∵三角形是直角三角形,∴可得,32+52=x2或32+x2=52,解得,x=或x=4.故选:C.5.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为()A.﹣1B.﹣1C.2D.【分析】首先根据勾股定理计算出AC的长,进而得到AM的长,再根据A点表示﹣1,可得M点表示的数.【解答】解:∵AB=3,AD=1,∴AC==,∵点A为圆心,AC的长为半径作弧交数轴于点M,AM=AC=,∵A点表示﹣1,∴M点表示的数为:﹣1,故选:A.6.下列命题:①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④在同一个三角形中,等边对等角.其中逆命题成立的个数为()A.1个B.2个C.3个D.4个【分析】分别写出命题的逆命题,判断即可.【解答】解:①同旁内角互补,两直线平行,逆命题是:两直线平行,同旁内角互补,正确;②如果两个角是直角,那么它们相等,逆命题是:如果两个角相等,那么他们是直角,不成立;③如果两个实数相等,那么它们的平方相等,逆命题是:如果两数的平方相等,那么这两个数相等,不成立;④在同一个三角形中,等边对等角,逆命题是:在同一个三角形中,相等的角对相等的边,成立.故成立的有2个.故选:B.7.估计的运算结果应在()A.6到7之间B.7到8之间C.8到9之间D.9到10之间【分析】先进行二次根式的运算,然后再进行估算.【解答】解:∵=4+,而4<<5,∴原式运算的结果在8到9之间;故选:C.8.k、m、n为三整数,若=k,=15,=6,则下列有关于k、m、n的大小关系,何者正确?()A.k<m=n B.m=n<k C.m<n<k D.m<k<n【分析】根据二次根式的化简公式得到k,m及n的值,即可作出判断.【解答】解:=3,=15,=6,可得:k=3,m=2,n=5,则m<k<n.故选:D.9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④【分析】由题意,①﹣②可得2xy=45记为③,①+③得到(x+y)2=94由此即可判断.【解答】解:由题意,①﹣②得2xy=45 ③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴(x+y)2=94,∴①②③正确,④错误.故选:B.10.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD中点,则=.其中正确的有()A.1个B.2个C.3个D.4个【分析】①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,易证△ADM≌△ABH,△AHN≌△AMN,得MN=HN,最后根据勾股定理可作判断;②延长CB,截取BI=DE,连接AI,如图,易证△ADE≌△ABI,△AIF≌△AEF,得IF=EF,即DE+BF=EF,成立.③作辅助线,则可证△AFJ为等腰直角三角形,CK=BF=KJ,证明∠JCK=45°,推出四边形BCJK为平行四边形,所以GJ=BC=AD,可证△GJM≌△DAM,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,CF=2a ﹣x,CE=a,由勾股定理可知:3x=2a,则==,成立.【解答】解:①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,∵四边形ABCD是正方形,∴AD=AB,∠ADB=∠ABD=45°,∠BAD=90°,∴∠ABH=45°=∠ADM,在△ADM和△ABM中,∵,∴△ADM≌△ABH(SAS),∴∠DAM=∠BAH,AM=AH,∵∠EAF=45°,∠BAD=90°,∴∠DAM+∠BAN=∠BAH+∠BAN=45°,∴∠MAN=∠HAN=45°,在△AHN和△AMN中,∵,∴△AHN≌△AMN(SAS),∴MN=HN,Rt△BHN中,HN2=BH2+BN2,∴MN2=BN2+DM2,成立.②延长CB,截取BI=DE,连接AI,如图,在△ADE和△ABI中,∵∴△ADE≌△ABI(SAS),同理得△AIF≌△AEF(SAS),∴IF=EF,即DE+BF=EF,成立;③如图,过F作FJ⊥AF交AE的延长线于J,过J作JK⊥BC于K,连接CJ,过J作JG ∥BC交BD于G,∴∠AFJ=∠AFB+∠JFK=90°,∵∠AFB+∠BAF=90°,∴∠BAF=∠JFK,∵∠EAF=45°,∠AFJ=90°,∴△AFJ是等腰直角三角形,在△ABF和△FKJ中,∵,∴△ABF≌△FKJ(SAS),∴AB=FK=BC,BF=KJ,∴CK=BF=KJ,∴∠JCK=45°,∴∠DBC=∠JCK,∴BG∥CJ,∵JG∥BC,∴四边形BCJK为平行四边形,∴GJ=BC=AD,∵AD∥BC∥GJ,∴∠DAM=∠MJK,在△GJM和△DAM中,∵,∴△GJM≌△DAM(AAS),∴AM=MJ,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,∵E为CD中点,∴CD=BC=2a,∴CF=2a﹣x,CE=a,在Rt△EFC中,由勾股定理得:EF2=CE2+CF2∴(a+x)2=a2+(2a﹣x)2解得:3x=2a,则==,成立.故选:D.二.填空题(共6小题)11.计算:(1)=;(2)(2)2=20;(3)=.【分析】(1)直接利用二次根式的性质化简得出答案;(2)直接利用二次根式的性质化简得出答案;(3)直接利用二次根式的性质化简得出答案.【解答】解:(1)==;(2)(2)2=4×()2=4×5=20;(3)===.故答案为:(1);(2)20;(3).12.观察下列等式:①;②;③、…根据上述的规律,写出用n(n为正整数,且n≥2)表示的等式(n≥2且n为整数).【分析】观察可发现整数部分与分子相同,分母为整数的平方减1,据此可解.【解答】解:观察可发现整数部分与分子相同,分母为整数的平方减1,∴用n(n为正整数,且n≥2)表示的等式为:=n.故答案为:=n(n为正整数,且n≥2).13.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.【分析】蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.【解答】解:如图所示,路径一:AB==13;路径二:AB==;路径三:AB==;∵>13>,∴cm为最短路径.14.如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为.【分析】连接AE,根据垂直平分线的性质可得AE=EC,然后在直角△ABE中利用勾股定理即可列方程求得EC的长,然后证明△AOD≌△COE,即可求得.【解答】解:连接AE.∵DE是线段AC的垂直平分线,∴AE=EC.设EC=x,则AE=EC=x,BE=BC﹣EC=12﹣x,∵在直角△ABE中,AE2=AB2+BE2,∴x2=52+(12﹣x)2,解得:x=.即EC=.∵AD∥BC,∴∠D=∠OEC,在△AOD和△COE中,,∴△AOD≌△COE,∴AD=EC=.故答案是:.15.在△ABC中,AB=15,AC=13,AD为△ABC的高,且AD=12,则S△ABC=24或84.【分析】本题应分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的面积求出;(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的面积求出.【解答】解:此题应分两种情况说明:(1)当△ABC为锐角三角形时,在Rt△ABD中,BD==9,在Rt△ACD中,CD==5∴BC=5+9=14∴△ABC的面积为:;(2)当△ABC为钝角三角形时,在Rt△ABD中,BD=9,在Rt△ACD中,CD=5,∴BC=9﹣5=4.∴△ABC的面积为:∴当△ABC为锐角三角形时,△ABC的面积为84;当△ABC为钝角三角形时,△ABC 的面积为24.综上所述,△ABC的面积是84或24.故答案为:84或24.16.如图,∠AOB=30°,点C、D分别在边OA、OB上,且OC=2,OD=4,点M、N 分别在OB、OA上,则CM+MN+ND的最小值是2.【分析】作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接C′D′,与OB、OA分别交于点M、N,连接CM、DN,此时CM+MN+ND=C′M+MN+ND′=C′D′最小,根据勾股定理即可求得CM+MN+ND的最小值.【解答】解:如图,作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接C′D′,与OB、OA分别交于点M、N,连接CM、DN,此时CM+MN+ND=C′M+MN+ND′=C′D′最小,∴CM+MN+ND的最小值是C′D′的长.连接OC′、OD′,由对称性可知:∠C′OB=∠COB=∠COD′=30°,OC′=OC,OC′=OC,∴∠COC′=DOD′=60°,∴△OMC,△ODN为等边三角形,∴∠D′OC′=90°,OC′=2,OD′=4由勾股定理得,C′D′==2.所以CM+MN+ND的最小值是2.故答案为2.三.解答题(共8小题)17.计算:【分析】在二次根式的加减运算中,先对各个二次根式化成最简二次根式,再把同类二次根式合并.【解答】解:原式===14.18.已知x=+1,y=﹣1,求下列各式的值:(1)x2+2xy+y2,(2)x2﹣y2.【分析】(1)根据完全平方公式可以解答本题;(2)根据平方差公式可以解答本题.【解答】解:(1)∵x=+1,y=﹣1,∴x+y=+1+﹣1=2,∴x2+2xy+y2=(x+y)2=(2)2=12;(2)∵x=+1,y=﹣1,∴x+y=+1+﹣1=2,x﹣y==2,x2﹣y2=(x+y)(x﹣y)==4.19.如图,一根竹子高10尺,折断后竹子的顶端落在离竹子底端3尺处,折断处离地面的高度是多少尺?【分析】杆子折断后刚好构成一直角三角形,设杆子折断处离地面的高度是x尺,则斜边为(10﹣x)尺.利用勾股定理解题即可.【解答】解:设杆子折断处离地面x尺,则斜边为(10﹣x)尺,根据勾股定理得:x2+32=(10﹣x)2解得:x=.答:折断处离地面的高度是尺.20.如图,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,且AB=,AD=.(1)请在图中补齐四边形ABCD,并求其面积;(2)判断∠BCD是直角吗?请说明理由;(3)直接写出点C到BD的距离为2.【分析】(1)由AB==、AD==,结合网格与勾股定理可确定点A;(2)求出BC2、CD2、BD2,再利用勾股定理逆定理即可判断;(3)设点C到BD的距离为d,根据S△BCD=BC•CD=BD•d求解可得.【解答】解:(1)如图所示,四边形ABCD即为所求,其面积为5×5﹣×5×1﹣×2×4﹣×1×4﹣×(1+3)×1=14;(2)是,∵BC2=22+42=20,CD2=12+22=5,BD2=32+42=25,∴BC2+CD2=BD2,∴△BCD是直角三角形,且∠BCD=90°,(3)设点C到BD的距离为d,由(2)知,BC=2,CD=,BD=5,根据S△BCD=BC•CD=BD•d,则d===2.故答案为:2.21.等腰Rt△ABC中,∠ACB=90°且CA=CB.(1)如图1,若△ECD也是等腰Rt△且CE=CD,△ACB的顶点A在△ECD的斜边DE 上,求证:AE2+AD2=2AC2;(2)如图2,点M是△ACB外一点,CM∥AB,且BM=BA,求的值.【分析】(1)连结BD,由等腰直角三角形的性质得出∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,得出2AC2=AB2.由SAS 证明△AEC≌△BDC,得出AE=BD,∠E=∠BDC=45°,CE=CD,证出∠BDA=∠BDC+∠ADC=90°,在Rt△ADB中.由勾股定理即可得出结论;(2)过M作MH⊥BC交BC的延长线于H,设AC=BC=a,求得AB=BM=a,根据平行线的性质得到∠HCM=∠ABC=45°,设MH=CH=x,根据勾股定理得到CM=CH=a,于是得到结论.【解答】(1)证明:连接BD,如图所示:∵△ACB与△ECD都是等腰直角三角形,∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,∴2AC2=AB2.∠ECD﹣∠ACD=∠ACB﹣∠ACD,∴∠ACE=∠BCD在△AEC和△BDC中,,∴△AEC≌△BDC(SAS).∴AE=BD,∠E=∠BDC.∴∠BDC=45°,∴∠BDC+∠ADC=90°,即∠ADB=90°.∴AD2+BD2=AB2,∴AD2+AE2=2AC2;(2)过M作MH⊥BC交BC的延长线于H,设AC=BC=a,∵∠ACB=90°,∴AB=BM=a,∵CM∥AB,∴∠HCM=∠ABC=45°,∴MH=CH,设MH=CH=x,∴x2+(x+a)2=()2,解得x=a(负值舍去),∴CM=CH=a,∴==.22.“武黄城际铁路”是武汉市城市圈内一条连通武汉市和黄石市的快速城际铁路,如图1,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你解决以下问题:(1)求A、C之间的距离;(参考数据≈4.6);(2)若客车的平均速度是60km/h,市内的公共汽车的平均速度为40km/h,城际列车的平均速度为180km/h,为了最短时间到达武昌客运站,应该选择哪种乘车方案?请说明理由.(不计候车时间)(3)“为了安全,请勿超速”.如图2,武黄城际列车通车后,在某直线路段MN限速180千米/小时,为了检测列车是否超速,铁路有关部门在铁路MN旁设立了观测点S,从观测点S测得列车从点P到达点Q行驶了1.5秒钟,已知∠SPN=45°,∠SQN=60°,SQ =200米,此列车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)【分析】(1)根据勾股定理解答即可;(2)根据路程与速度的关系得出时间即可;(3)根据三角函数得出PQ,进而判断即可.【解答】解:(1)过点C作AB的垂线,交AB的延长线于E点,∵∠ABC=120°,BC=20,∴BE=10,CE=10,在△ACE中,∵AC2=8100+300,∴AC=20=20×4.6=92km;(2)乘客车需时间t1==1(小时);乘列车需时间t2=+=1(小时);∴选择城际列车.(3)作SH⊥MN于H,如图,∵∠SPN=45°,∠SQN=60°,SQ=200米,∴HS=PH=100,QH=100,∴PQ=100(﹣1)≈73,则速度为m/s<180千米/小时,故为超速.23.已知△ABC中,AB=AC,∠BAC=2a,∠ADB=a(1)如图1,若a=30°,则线段AD、BD、CD之间的数量关系为DC2=DA2+DB2;(2)若a=45°①如图2,线段AD、BD、CD满足怎样的数量关系?证明你的结论;②如图3,点E在线段BD上,且∠BAE=45°,AD=5,BD=4,则DE=.【分析】(1)结论:DC2=DA2+DB2.如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.首先证明△DCM是等边三角形,再证明△ADM是直角三角形即可解决问题.(2)①结论:DC2=DB2+2DA2.如图2中,作AM⊥AD交DB的延长线于M,连接CM.由△DAB≌△MAC,推出BD=CM,∠ADB=∠AMC=45°推出∠DMC=90°,推出DC2=CM2+DM2,由CM=DB,DM=AD,即可证明.②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4﹣x,由AD=AM=5,推出DM=5,BM=DG=5﹣4,在Rt△DEG中,根据DG2+DE2=EG2,列出方程即可解决问题.【解答】解:(1)结论:DC2=DA2+DB2.理由:如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.∵CD=CM,∠DCM=60°,∴△DCM是等边三角形,∴DM=CD=CM,∵∠ADB=30°,∴∠DAB+∠DBA=150°,∵∠MAC=∠DBC,∴∠MAC+∠DAB=∠DBC+∠DAB=∠DBA+∠ABC+∠DAB=150°+60°=210°,∴∠DAM=360°﹣210°﹣60°=90°,∴DM2=DA2+AM2,∵AM=DB,DM=DC,∴DC2=DA2+DB2.故答案为DC2=DA2+DB2.(2)①结论:DC2=DB2+2DA2.理由:如图2中,作AM⊥AD交DB的延长线于M,连接CM.∵∠ADM=45°,∠DAM=90°,∴∠ADM=∠AMD=45°,∴DA=AM,DM=DA,∵∠DAM=∠BAC,∴∠DAB=∠MAC,∵AB=AC,∴△DAB≌△MAC,∴BD=CM,∠ADB=∠AMC=45°∴∠DMC=90°,∴DC2=CM2+DM2,∵CM=DB,DM=AD,∴DC2=DB2+2DA2.②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4﹣x,∵AD=AM=5,∴DM=5,BM=DG=5﹣4,在Rt△DEG中,∵DG2+DE2=EG2,∴(5﹣4)2+x2=(4﹣x)2,解得x=.故答案为=.24.在Rt△ABC中,∠C=90°,AC=BC,O是AB的中点,∠EOF=90°,(1)如图1,点E、F分别在线段AC和线段BC上.试确定EF、AE、BF之间的数量关系,并给出证明.(2)如图2,点E、F分别在线段AC和线段CB的延长线上,且OP平分∠EOF交直线CB于P点,试确定CP、PF、BF之间的数量关系,并加以证明.(3)如图3,在(2)的条件下,连接OC,过P作PM⊥OC于点M,过F作FN⊥OB 于点N,直线PM、FN交于D点,请判断DP、PM、NF之间的数量关系,并证明.【分析】(1)由“ASA”可证△CEO≌△BFO,可得CE=BF,由勾股定理可得结论;(2)连接OC,EP,由“ASA”可证△CEO≌△BFO,可得BF=CE,OE=OF,由“ASA”可证△EOP≌△FOP,可得PE=PF,由勾股定理可得结论;(3)由题意可证△PDF,△BNF均为等腰直角三角形,可得PF=DP,CP=PM,BF=NF,代入(2)的结论可求解.【解答】解:(1)AE2 +BF2 =EF2,理由如下:连接OC,EF,∵∠ACB=90°,AC=BC,点O是AB中点,∴AO=BO=CO,AB⊥CO,∠ACO=∠B=45°,∴∠COB=∠EOF=90°,∴∠EOC=∠FOB,且BO=CO,∠ECO=∠B=45°,∴△CEO≌△BFO(ASA)∴CE=BF,∵AC=BC,∴AE=CF,∵CE2+CF2=EF2,∴AE2 +BF2 =EF2;(2)CP2+BF2=PF2;理由如下:连接OC,EP,∵∠ACB=90°,AC=BC,点O是AB中点,∴AO=BO=CO,AB⊥CO,∠ACO=∠ABC=45°,∴∠COB=∠EOF=90°,∠OCE=∠OBF=135°,∴∠EOC=∠FOB,且BO=CO,∠OCE=∠OBF,∴△CEO≌△BFO(ASA)∴BF=CE,OE=OF,∵OP平分∠EOF,∴∠EOP=∠FOP=45°,且OE=OF,OP=OP,∴△EOP≌△FOP(ASA),∴PF=PE,∴CP2+BF2=CP2+CE2=PE2=PF2;(3)PM2+NF2=DP2.理由如下:∵∠OBC=∠NBF=∠DPF=45°,∴△PDF,△BNF均为等腰直角三角形,∴PF=DP,CP=PM,BF=NF,由(2)可知CP2+BF2=PF2,∴2PM2+2NF2=2DP2,即PM2+NF2=DP2.。
武汉二中八年级下学期语文周清试卷

武汉二中八年级下学期语文周清试卷第一篇:武汉二中八年级下学期语文周清试卷武汉二中八年级下学期语文周清试卷一、(共12分,每小题3分)1、下列词语中加点字的注音或书写无误的一项是()A、差使举箸倏忽面面相觑B、羁绊秕谷愕然寒噤C、惆怅屏避深邃迄今D、陨星怠惰藐小狼奔豕突2、依次填入下列各句横线处的词语,最恰当的一项是()①他用两手攀着上面,两脚再向上______。
②天文学家________,在别的星系上看银河系,也是这样一团扁平漩涡状的星云。
③我们便_________起来,每个都说月亮是属于自己的。
④山尖全白了,给蓝天______上了一道银边。
A、缩猜测争执染B、抬猜想争吵染C、缩猜想争执镶D、抬猜测争吵镶3、下列各句中没有语病的一项是()A、推行有偿使用塑料袋,主要是通过经济手段培养人们尽量减少使用塑料袋,这无疑会对减少白色污染、净化环境产生积极作用。
B、华罗庚除致力于数学研究外,还非常注意培养和提高有志于献身数学科学的青年人,万哲先、王元、陈景润就是其中的杰出代表。
C、通过参加世博会志愿者培训,我萌生了学好外语、为外国友人服务的想法。
D、在汉语语义形成的初期,狗不但和鸡鸭,而且和猪和龙马都是平等的,很受宠爱,它们和龙同属十二生肖之一。
4、将下列语句依次填入文段的空缺处,正确的选项是()你的话语应该是一缕包含早春气息的柔风,_____________;你的表白应该是田野爆裂的豆荚,_____________;你的答辩应该是凭借原则的盾牌,_____________;你的呐喊应该是仰仗正义的力量,_____________。
①迎承谈判桌上的唇枪舌剑;②构思并阐述金色的成熟;③弥合朋友之间人为的小隙;④澎湃青春的热忱和血液。
A、③④①②B、②①③④C、③②①④D、④①③②二、阅读下面的文字,完成5—7题。
人生是立体的①人不仅能创造工具,而且能创造自己。
比如:人生之长、宽、高这三个尺寸,便是我们自己建造起来的。
武汉二中广雅中学2018-2019学年度下学期八年级物理训练卷(一)(word版)
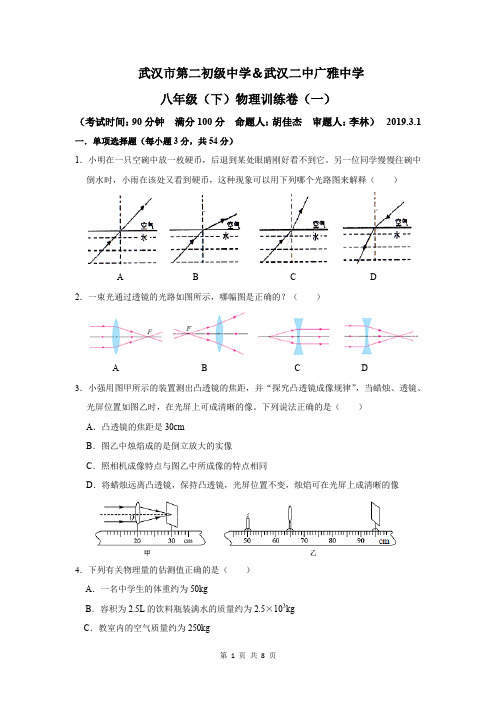
武汉市第二初级中学&武汉二中广雅中学八年级(下)物理训练卷(一)(考试时间:90分钟满分100分命题人:胡佳杰审题人:李林)2019.3.1一.单项选择题(每小题3分,共54分)1.小明在一只空碗中放一枚硬币,后退到某处眼睛刚好看不到它。
另一位同学慢慢往碗中倒水时,小雨在该处又看到硬币,这种现象可以用下列哪个光路图来解释()A B C D2.一束光通过透镜的光路如图所示,哪幅图是正确的?()A B C D3.小强用图甲所示的装置测出凸透镜的焦距,并“探究凸透镜成像规律”,当蜡烛、透镜、光屏位置如图乙时,在光屏上可成清晰的像。
下列说法正确的是()A.凸透镜的焦距是30cmB.图乙中烛焰成的是倒立放大的实像C.照相机成像特点与图乙中所成像的特点相同D.将蜡烛远离凸透镜,保持凸透镜,光屏位置不变,烛焰可在光屏上成清晰的像4.下列有关物理量的估测值正确的是()A.一名中学生的体重约为50kgB.容积为2.5L的饮料瓶装满水的质量约为2.5×103kgC.教室内的空气质量约为250kgD.容量约3.93×1011m3的三峡水库蓄水量约为3.93×1014t5.在“用托盘天平测物体质量”时,某同学用己调节好的天平测物体质量的过程中,通过增、减砝码后,发现指针仍指在分度盘中央刻度线的左边一点,这时他应该()A.把横梁右端的螺母向右旋出一些B.把横梁右端的螺母向左旋进一些C.把天平右盘的砝码减少一些D.向右移动游码6.下表是部分物质的密度,小刚由此提出了对密度的一些看法,正确的是()0℃、1标准大气压下部分物质的密度(kg/m3)水 1.0×103冰0.9×103水银13.6×103干松木0.4×103酒精0.8×103铜8.9×103煤油0.8×103铝 2.7×103A.固态物质的密度一定比液态物质的密度大B.同种物质的密度一定相同C.体积相同的实心铜块和铝块,铜块的质量大D.密度跟物质质量成正比,跟体积成反比7.分别由不同物质a、b、c 组成的三个实心体,它们的体积和质量的关系如图所示,由图可知下列说法正确的是()A.a物质的密度最大B.b物质的密度是1.0×103kg/m3C.c物质的密度是b的两倍D.c的密度与它们的质量、体积有关8.某同学用托盘天平和量筒测量一小石块的密度,图甲是调节天平时的情形,图乙和图丙分别是测量石块质量和体积时的情形,下列说法错误的是()A.甲图中应将平衡螺母向右调,使横梁平衡B.乙图中测石块质量时,天平的读数是44.4gC.由丙图量筒的示数测得石块的体积是20cm3D.计算出石块的密度是2.2×103kg/m39.有些商店还在使用一种案秤,是一种称量质量的工具,如图所示它的工作原理与天平相同,不过两臂长度不等。
2018-2019学年湖北省武汉二中广雅中学八年级(下)期中数学模拟试卷(1) 解析版

2018-2019学年湖北省武汉二中广雅中学八年级(下)期中数学模拟试卷(1)一.选择题(共10小题)1.若在实数范围内有意义,则x的取值范围是()A.x>0B.x>3C.x≥3D.x≤32.下列二次根式中的最简二次根式是()A.B.C.D.3.下列计算正确的是()A.2B.C.5D.4.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三条边长是()A.4B.C.4或D.以上都不正确5.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为()A.﹣1B.﹣1C.2D.6.下列命题:①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④在同一个三角形中,等边对等角.其中逆命题成立的个数为()A.1个B.2个C.3个D.4个7.估计的运算结果应在()A.6到7之间B.7到8之间C.8到9之间D.9到10之间8.k、m、n为三整数,若=k,=15,=6,则下列有关于k、m、n的大小关系,何者正确?()A.k<m=n B.m=n<k C.m<n<k D.m<k<n9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④10.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD中点,则=.其中正确的有()A.1个B.2个C.3个D.4个二.填空题(共6小题)11.计算:(1)=;(2)(2)2=;(3)=.12.观察下列等式:①;②;③、…根据上述的规律,写出用n(n为正整数,且n≥2)表示的等式.13.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.14.如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为.15.在△ABC中,AB=15,AC=13,AD为△ABC的高,且AD=12,则S△ABC=.16.如图,∠AOB=30°,点C、D分别在边OA、OB上,且OC=2,OD=4,点M、N 分别在OB、OA上,则CM+MN+ND的最小值是.三.解答题(共8小题)17.计算:18.已知x=+1,y=﹣1,求下列各式的值:(1)x2+2xy+y2,(2)x2﹣y2.19.如图,一根竹子高10尺,折断后竹子的顶端落在离竹子底端3尺处,折断处离地面的高度是多少尺?20.如图,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,且AB=,AD=.(1)请在图中补齐四边形ABCD,并求其面积;(2)判断∠BCD是直角吗?请说明理由;(3)直接写出点C到BD的距离为.21.等腰Rt△ABC中,∠ACB=90°且CA=CB.(1)如图1,若△ECD也是等腰Rt△且CE=CD,△ACB的顶点A在△ECD的斜边DE 上,求证:AE2+AD2=2AC2;(2)如图2,点M是△ACB外一点,CM∥AB,且BM=BA,求的值.22.“武黄城际铁路”是武汉市城市圈内一条连通武汉市和黄石市的快速城际铁路,如图1,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你解决以下问题:(1)求A、C之间的距离;(参考数据≈4.6);(2)若客车的平均速度是60km/h,市内的公共汽车的平均速度为40km/h,城际列车的平均速度为180km/h,为了最短时间到达武昌客运站,应该选择哪种乘车方案?请说明理由.(不计候车时间)(3)“为了安全,请勿超速”.如图2,武黄城际列车通车后,在某直线路段MN限速180千米/小时,为了检测列车是否超速,铁路有关部门在铁路MN旁设立了观测点S,从观测点S测得列车从点P到达点Q行驶了1.5秒钟,已知∠SPN=45°,∠SQN=60°,SQ =200米,此列车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)23.已知△ABC中,AB=AC,∠BAC=2a,∠ADB=a(1)如图1,若a=30°,则线段AD、BD、CD之间的数量关系为;(2)若a=45°①如图2,线段AD、BD、CD满足怎样的数量关系?证明你的结论;②如图3,点E在线段BD上,且∠BAE=45°,AD=5,BD=4,则DE.24.在Rt△ABC中,∠C=90°,AC=BC,O是AB的中点,∠EOF=90°,(1)如图1,点E、F分别在线段AC和线段BC上.试确定EF、AE、BF之间的数量关系,并给出证明.(2)如图2,点E、F分别在线段AC和线段CB的延长线上,且OP平分∠EOF交直线CB于P点,试确定CP、PF、BF之间的数量关系,并加以证明.(3)如图3,在(2)的条件下,连接OC,过P作PM⊥OC于点M,过F作FN⊥OB 于点N,直线PM、FN交于D点,请判断DP、PM、NF之间的数量关系,并证明.参考答案与试题解析一.选择题(共10小题)1.若在实数范围内有意义,则x的取值范围是()A.x>0B.x>3C.x≥3D.x≤3【分析】先根据二次根式有意义的条件得出关于x的不等式,求出x的取值范围即可.【解答】解:∵使在实数范围内有意义,∴x﹣3≥0,解得x≥3.故选:C.2.下列二次根式中的最简二次根式是()A.B.C.D.【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.【解答】解:A、符合最简二次根式的定义,故本选项正确;B、原式=,被开方数含能开得尽方的因数,不是最简二次根式,故本选项错误;C、原式=,被开方数含能开得尽方的因数,不是最简二次根式,故本选项错误;D、被开方数含分母,不是最简二次根式,故本选项错误;故选:A.3.下列计算正确的是()A.2B.C.5D.【分析】利用二次根式的乘法法则对A进行判断;根据二次根式的加减法对B、C进行判断;根据分母有理化对D进行判断.【解答】解:A、原式=6×3=18,所以A选项错误;B、与不能合并,所以B选项错误;C、5与﹣2不能合并,所以C选项错误;D、原式==,所以D选项正确.故选:D.4.三角形的两边长分别为3和5,要使这个三角形是直角三角形,则第三条边长是()A.4B.C.4或D.以上都不正确【分析】根据勾股定理的逆定理,可设第三条边长为x,如果满足32+52=x2或32+x2=52,即为直角三角形,解出x的值即可解答;【解答】解:设第三条边长为x,∵三角形是直角三角形,∴可得,32+52=x2或32+x2=52,解得,x=或x=4.故选:C.5.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,AC的长为半径作弧交数轴于点M,则点M表示的数为()A.﹣1B.﹣1C.2D.【分析】首先根据勾股定理计算出AC的长,进而得到AM的长,再根据A点表示﹣1,可得M点表示的数.【解答】解:∵AB=3,AD=1,∴AC==,∵点A为圆心,AC的长为半径作弧交数轴于点M,AM=AC=,∵A点表示﹣1,∴M点表示的数为:﹣1,故选:A.6.下列命题:①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④在同一个三角形中,等边对等角.其中逆命题成立的个数为()A.1个B.2个C.3个D.4个【分析】分别写出命题的逆命题,判断即可.【解答】解:①同旁内角互补,两直线平行,逆命题是:两直线平行,同旁内角互补,正确;②如果两个角是直角,那么它们相等,逆命题是:如果两个角相等,那么他们是直角,不成立;③如果两个实数相等,那么它们的平方相等,逆命题是:如果两数的平方相等,那么这两个数相等,不成立;④在同一个三角形中,等边对等角,逆命题是:在同一个三角形中,相等的角对相等的边,成立.故成立的有2个.故选:B.7.估计的运算结果应在()A.6到7之间B.7到8之间C.8到9之间D.9到10之间【分析】先进行二次根式的运算,然后再进行估算.【解答】解:∵=4+,而4<<5,∴原式运算的结果在8到9之间;故选:C.8.k、m、n为三整数,若=k,=15,=6,则下列有关于k、m、n的大小关系,何者正确?()A.k<m=n B.m=n<k C.m<n<k D.m<k<n【分析】根据二次根式的化简公式得到k,m及n的值,即可作出判断.【解答】解:=3,=15,=6,可得:k=3,m=2,n=5,则m<k<n.故选:D.9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是()A.①②B.①②③C.①②④D.①②③④【分析】由题意,①﹣②可得2xy=45记为③,①+③得到(x+y)2=94由此即可判断.【解答】解:由题意,①﹣②得2xy=45 ③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴(x+y)2=94,∴①②③正确,④错误.故选:B.10.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD中点,则=.其中正确的有()A.1个B.2个C.3个D.4个【分析】①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,易证△ADM≌△ABH,△AHN≌△AMN,得MN=HN,最后根据勾股定理可作判断;②延长CB,截取BI=DE,连接AI,如图,易证△ADE≌△ABI,△AIF≌△AEF,得IF=EF,即DE+BF=EF,成立.③作辅助线,则可证△AFJ为等腰直角三角形,CK=BF=KJ,证明∠JCK=45°,推出四边形BCJK为平行四边形,所以GJ=BC=AD,可证△GJM≌△DAM,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,CF=2a ﹣x,CE=a,由勾股定理可知:3x=2a,则==,成立.【解答】解:①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,∵四边形ABCD是正方形,∴AD=AB,∠ADB=∠ABD=45°,∠BAD=90°,∴∠ABH=45°=∠ADM,在△ADM和△ABM中,∵,∴△ADM≌△ABH(SAS),∴∠DAM=∠BAH,AM=AH,∵∠EAF=45°,∠BAD=90°,∴∠DAM+∠BAN=∠BAH+∠BAN=45°,∴∠MAN=∠HAN=45°,在△AHN和△AMN中,∵,∴△AHN≌△AMN(SAS),∴MN=HN,Rt△BHN中,HN2=BH2+BN2,∴MN2=BN2+DM2,成立.②延长CB,截取BI=DE,连接AI,如图,在△ADE和△ABI中,∵∴△ADE≌△ABI(SAS),同理得△AIF≌△AEF(SAS),∴IF=EF,即DE+BF=EF,成立;③如图,过F作FJ⊥AF交AE的延长线于J,过J作JK⊥BC于K,连接CJ,过J作JG ∥BC交BD于G,∴∠AFJ=∠AFB+∠JFK=90°,∵∠AFB+∠BAF=90°,∴∠BAF=∠JFK,∵∠EAF=45°,∠AFJ=90°,∴△AFJ是等腰直角三角形,在△ABF和△FKJ中,∵,∴△ABF≌△FKJ(SAS),∴AB=FK=BC,BF=KJ,∴CK=BF=KJ,∴∠JCK=45°,∴∠DBC=∠JCK,∴BG∥CJ,∵JG∥BC,∴四边形BCJK为平行四边形,∴GJ=BC=AD,∵AD∥BC∥GJ,∴∠DAM=∠MJK,在△GJM和△DAM中,∵,∴△GJM≌△DAM(AAS),∴AM=MJ,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,∵E为CD中点,∴CD=BC=2a,∴CF=2a﹣x,CE=a,在Rt△EFC中,由勾股定理得:EF2=CE2+CF2∴(a+x)2=a2+(2a﹣x)2解得:3x=2a,则==,成立.故选:D.二.填空题(共6小题)11.计算:(1)=;(2)(2)2=20;(3)=.【分析】(1)直接利用二次根式的性质化简得出答案;(2)直接利用二次根式的性质化简得出答案;(3)直接利用二次根式的性质化简得出答案.【解答】解:(1)==;(2)(2)2=4×()2=4×5=20;(3)===.故答案为:(1);(2)20;(3).12.观察下列等式:①;②;③、…根据上述的规律,写出用n(n为正整数,且n≥2)表示的等式(n≥2且n为整数).【分析】观察可发现整数部分与分子相同,分母为整数的平方减1,据此可解.【解答】解:观察可发现整数部分与分子相同,分母为整数的平方减1,∴用n(n为正整数,且n≥2)表示的等式为:=n.故答案为:=n(n为正整数,且n≥2).13.长方体的长、宽、高分别为8cm,4cm,5cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是cm.【分析】蚂蚁有三种爬法,就是把正视和俯视(或正视和侧视,或俯视和侧视)二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.【解答】解:如图所示,路径一:AB==13;路径二:AB==;路径三:AB==;∵>13>,∴cm为最短路径.14.如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为.【分析】连接AE,根据垂直平分线的性质可得AE=EC,然后在直角△ABE中利用勾股定理即可列方程求得EC的长,然后证明△AOD≌△COE,即可求得.【解答】解:连接AE.∵DE是线段AC的垂直平分线,∴AE=EC.设EC=x,则AE=EC=x,BE=BC﹣EC=12﹣x,∵在直角△ABE中,AE2=AB2+BE2,∴x2=52+(12﹣x)2,解得:x=.即EC=.∵AD∥BC,∴∠D=∠OEC,在△AOD和△COE中,,∴△AOD≌△COE,∴AD=EC=.故答案是:.15.在△ABC中,AB=15,AC=13,AD为△ABC的高,且AD=12,则S△ABC=24或84.【分析】本题应分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的面积求出;(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的面积求出.【解答】解:此题应分两种情况说明:(1)当△ABC为锐角三角形时,在Rt△ABD中,BD==9,在Rt△ACD中,CD==5∴BC=5+9=14∴△ABC的面积为:;(2)当△ABC为钝角三角形时,在Rt△ABD中,BD=9,在Rt△ACD中,CD=5,∴BC=9﹣5=4.∴△ABC的面积为:∴当△ABC为锐角三角形时,△ABC的面积为84;当△ABC为钝角三角形时,△ABC 的面积为24.综上所述,△ABC的面积是84或24.故答案为:84或24.16.如图,∠AOB=30°,点C、D分别在边OA、OB上,且OC=2,OD=4,点M、N 分别在OB、OA上,则CM+MN+ND的最小值是2.【分析】作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接C′D′,与OB、OA分别交于点M、N,连接CM、DN,此时CM+MN+ND=C′M+MN+ND′=C′D′最小,根据勾股定理即可求得CM+MN+ND的最小值.【解答】解:如图,作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接C′D′,与OB、OA分别交于点M、N,连接CM、DN,此时CM+MN+ND=C′M+MN+ND′=C′D′最小,∴CM+MN+ND的最小值是C′D′的长.连接OC′、OD′,由对称性可知:∠C′OB=∠COB=∠COD′=30°,OC′=OC,OC′=OC,∴∠COC′=DOD′=60°,∴△OMC,△ODN为等边三角形,∴∠D′OC′=90°,OC′=2,OD′=4由勾股定理得,C′D′==2.所以CM+MN+ND的最小值是2.故答案为2.三.解答题(共8小题)17.计算:【分析】在二次根式的加减运算中,先对各个二次根式化成最简二次根式,再把同类二次根式合并.【解答】解:原式===14.18.已知x=+1,y=﹣1,求下列各式的值:(1)x2+2xy+y2,(2)x2﹣y2.【分析】(1)根据完全平方公式可以解答本题;(2)根据平方差公式可以解答本题.【解答】解:(1)∵x=+1,y=﹣1,∴x+y=+1+﹣1=2,∴x2+2xy+y2=(x+y)2=(2)2=12;(2)∵x=+1,y=﹣1,∴x+y=+1+﹣1=2,x﹣y==2,x2﹣y2=(x+y)(x﹣y)==4.19.如图,一根竹子高10尺,折断后竹子的顶端落在离竹子底端3尺处,折断处离地面的高度是多少尺?【分析】杆子折断后刚好构成一直角三角形,设杆子折断处离地面的高度是x尺,则斜边为(10﹣x)尺.利用勾股定理解题即可.【解答】解:设杆子折断处离地面x尺,则斜边为(10﹣x)尺,根据勾股定理得:x2+32=(10﹣x)2解得:x=.答:折断处离地面的高度是尺.20.如图,每个小正方形的边长为1,四边形ABCD的每个顶点都在格点上,且AB=,AD=.(1)请在图中补齐四边形ABCD,并求其面积;(2)判断∠BCD是直角吗?请说明理由;(3)直接写出点C到BD的距离为2.【分析】(1)由AB==、AD==,结合网格与勾股定理可确定点A;(2)求出BC2、CD2、BD2,再利用勾股定理逆定理即可判断;(3)设点C到BD的距离为d,根据S△BCD=BC•CD=BD•d求解可得.【解答】解:(1)如图所示,四边形ABCD即为所求,其面积为5×5﹣×5×1﹣×2×4﹣×1×4﹣×(1+3)×1=14;(2)是,∵BC2=22+42=20,CD2=12+22=5,BD2=32+42=25,∴BC2+CD2=BD2,∴△BCD是直角三角形,且∠BCD=90°,(3)设点C到BD的距离为d,由(2)知,BC=2,CD=,BD=5,根据S△BCD=BC•CD=BD•d,则d===2.故答案为:2.21.等腰Rt△ABC中,∠ACB=90°且CA=CB.(1)如图1,若△ECD也是等腰Rt△且CE=CD,△ACB的顶点A在△ECD的斜边DE 上,求证:AE2+AD2=2AC2;(2)如图2,点M是△ACB外一点,CM∥AB,且BM=BA,求的值.【分析】(1)连结BD,由等腰直角三角形的性质得出∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,得出2AC2=AB2.由SAS 证明△AEC≌△BDC,得出AE=BD,∠E=∠BDC=45°,CE=CD,证出∠BDA=∠BDC+∠ADC=90°,在Rt△ADB中.由勾股定理即可得出结论;(2)过M作MH⊥BC交BC的延长线于H,设AC=BC=a,求得AB=BM=a,根据平行线的性质得到∠HCM=∠ABC=45°,设MH=CH=x,根据勾股定理得到CM=CH=a,于是得到结论.【解答】(1)证明:连接BD,如图所示:∵△ACB与△ECD都是等腰直角三角形,∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,∴2AC2=AB2.∠ECD﹣∠ACD=∠ACB﹣∠ACD,∴∠ACE=∠BCD在△AEC和△BDC中,,∴△AEC≌△BDC(SAS).∴AE=BD,∠E=∠BDC.∴∠BDC=45°,∴∠BDC+∠ADC=90°,即∠ADB=90°.∴AD2+BD2=AB2,∴AD2+AE2=2AC2;(2)过M作MH⊥BC交BC的延长线于H,设AC=BC=a,∵∠ACB=90°,∴AB=BM=a,∵CM∥AB,∴∠HCM=∠ABC=45°,∴MH=CH,设MH=CH=x,∴x2+(x+a)2=()2,解得x=a(负值舍去),∴CM=CH=a,∴==.22.“武黄城际铁路”是武汉市城市圈内一条连通武汉市和黄石市的快速城际铁路,如图1,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你解决以下问题:(1)求A、C之间的距离;(参考数据≈4.6);(2)若客车的平均速度是60km/h,市内的公共汽车的平均速度为40km/h,城际列车的平均速度为180km/h,为了最短时间到达武昌客运站,应该选择哪种乘车方案?请说明理由.(不计候车时间)(3)“为了安全,请勿超速”.如图2,武黄城际列车通车后,在某直线路段MN限速180千米/小时,为了检测列车是否超速,铁路有关部门在铁路MN旁设立了观测点S,从观测点S测得列车从点P到达点Q行驶了1.5秒钟,已知∠SPN=45°,∠SQN=60°,SQ =200米,此列车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)【分析】(1)根据勾股定理解答即可;(2)根据路程与速度的关系得出时间即可;(3)根据三角函数得出PQ,进而判断即可.【解答】解:(1)过点C作AB的垂线,交AB的延长线于E点,∵∠ABC=120°,BC=20,∴BE=10,CE=10,在△ACE中,∵AC2=8100+300,∴AC=20=20×4.6=92km;(2)乘客车需时间t1==1(小时);乘列车需时间t2=+=1(小时);∴选择城际列车.(3)作SH⊥MN于H,如图,∵∠SPN=45°,∠SQN=60°,SQ=200米,∴HS=PH=100,QH=100,∴PQ=100(﹣1)≈73,则速度为m/s<180千米/小时,故为超速.23.已知△ABC中,AB=AC,∠BAC=2a,∠ADB=a(1)如图1,若a=30°,则线段AD、BD、CD之间的数量关系为DC2=DA2+DB2;(2)若a=45°①如图2,线段AD、BD、CD满足怎样的数量关系?证明你的结论;②如图3,点E在线段BD上,且∠BAE=45°,AD=5,BD=4,则DE=.【分析】(1)结论:DC2=DA2+DB2.如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.首先证明△DCM是等边三角形,再证明△ADM是直角三角形即可解决问题.(2)①结论:DC2=DB2+2DA2.如图2中,作AM⊥AD交DB的延长线于M,连接CM.由△DAB≌△MAC,推出BD=CM,∠ADB=∠AMC=45°推出∠DMC=90°,推出DC2=CM2+DM2,由CM=DB,DM=AD,即可证明.②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4﹣x,由AD=AM=5,推出DM=5,BM=DG=5﹣4,在Rt△DEG中,根据DG2+DE2=EG2,列出方程即可解决问题.【解答】解:(1)结论:DC2=DA2+DB2.理由:如图1中,将△DCB绕点C顺时针旋转60°得到△MAC,连接DM.∵CD=CM,∠DCM=60°,∴△DCM是等边三角形,∴DM=CD=CM,∵∠ADB=30°,∴∠DAB+∠DBA=150°,∵∠MAC=∠DBC,∴∠MAC+∠DAB=∠DBC+∠DAB=∠DBA+∠ABC+∠DAB=150°+60°=210°,∴∠DAM=360°﹣210°﹣60°=90°,∴DM2=DA2+AM2,∵AM=DB,DM=DC,∴DC2=DA2+DB2.故答案为DC2=DA2+DB2.(2)①结论:DC2=DB2+2DA2.理由:如图2中,作AM⊥AD交DB的延长线于M,连接CM.∵∠ADM=45°,∠DAM=90°,∴∠ADM=∠AMD=45°,∴DA=AM,DM=DA,∵∠DAM=∠BAC,∴∠DAB=∠MAC,∵AB=AC,∴△DAB≌△MAC,∴BD=CM,∠ADB=∠AMC=45°∴∠DMC=90°,∴DC2=CM2+DM2,∵CM=DB,DM=AD,∴DC2=DB2+2DA2.②如图3中,在图2的基础上将△AMB绕点A顺时针旋转90°得到△ADG.则△AEG≌△AEB,∠GDE=90°,可得EB=EG,设DE=x.EB=EG=4﹣x,∵AD=AM=5,∴DM=5,BM=DG=5﹣4,在Rt△DEG中,∵DG2+DE2=EG2,∴(5﹣4)2+x2=(4﹣x)2,解得x=.故答案为=.24.在Rt△ABC中,∠C=90°,AC=BC,O是AB的中点,∠EOF=90°,(1)如图1,点E、F分别在线段AC和线段BC上.试确定EF、AE、BF之间的数量关系,并给出证明.(2)如图2,点E、F分别在线段AC和线段CB的延长线上,且OP平分∠EOF交直线CB于P点,试确定CP、PF、BF之间的数量关系,并加以证明.(3)如图3,在(2)的条件下,连接OC,过P作PM⊥OC于点M,过F作FN⊥OB 于点N,直线PM、FN交于D点,请判断DP、PM、NF之间的数量关系,并证明.【分析】(1)由“ASA”可证△CEO≌△BFO,可得CE=BF,由勾股定理可得结论;(2)连接OC,EP,由“ASA”可证△CEO≌△BFO,可得BF=CE,OE=OF,由“ASA”可证△EOP≌△FOP,可得PE=PF,由勾股定理可得结论;(3)由题意可证△PDF,△BNF均为等腰直角三角形,可得PF=DP,CP=PM,BF=NF,代入(2)的结论可求解.【解答】解:(1)AE2 +BF2 =EF2,理由如下:连接OC,EF,∵∠ACB=90°,AC=BC,点O是AB中点,∴AO=BO=CO,AB⊥CO,∠ACO=∠B=45°,∴∠COB=∠EOF=90°,∴∠EOC=∠FOB,且BO=CO,∠ECO=∠B=45°,∴△CEO≌△BFO(ASA)∴CE=BF,∵AC=BC,∴AE=CF,∵CE2+CF2=EF2,∴AE2 +BF2 =EF2;(2)CP2+BF2=PF2;理由如下:连接OC,EP,∵∠ACB=90°,AC=BC,点O是AB中点,∴AO=BO=CO,AB⊥CO,∠ACO=∠ABC=45°,∴∠COB=∠EOF=90°,∠OCE=∠OBF=135°,∴∠EOC=∠FOB,且BO=CO,∠OCE=∠OBF,∴△CEO≌△BFO(ASA)∴BF=CE,OE=OF,∵OP平分∠EOF,∴∠EOP=∠FOP=45°,且OE=OF,OP=OP,∴△EOP≌△FOP(ASA),∴PF=PE,∴CP2+BF2=CP2+CE2=PE2=PF2;(3)PM2+NF2=DP2.理由如下:∵∠OBC=∠NBF=∠DPF=45°,∴△PDF,△BNF均为等腰直角三角形,∴PF=DP,CP=PM,BF=NF,由(2)可知CP2+BF2=PF2,∴2PM2+2NF2=2DP2,即PM2+NF2=DP2.。
武汉二中广雅中学2018-2019学年度第二学期八下数学训练卷(一)

22. (10 分)如图所示,甲、乙两块边长为 a 米(a>1)的正方形田地,甲地修了两条互相乘直的宽为 1 米的通道,乙地正中间修了边长为 1 米的蓄水池,甲乙两田地的剩余地方全部种植小麦,一年后收获小麦 m 千克. (m>0) (1)甲地的小麦种植面积为 平方米,乙地的小麦种植面积为 平方米; (2 分) (2)甲乙两地小麦种植面积较小的是 地; (2 分) (3)若高的单位面积产量是低的单位面积产量的
5.下列等式从左到右的变形,属于因式分解的是( A.x2+2x+1=x(x+2)+1 C.x2+4=(x+2)2 6.若把分式
1 1 1 D. - x 2 + y 2 = ( x + y )( y - x ) 4 2 2
x- y 中 x 和 y 都缩小为原来的一半,那么分式的值( 2x + y
) D.不确定
第 10 题图 9.列车平均提速 v 千米/小时,用相同的时间,列车提速前行驶 S 千米,提速后比提速前多行驶 50 米,设 提速前列车的平均速度为 x 米/小时,下列方程不正确的是( A.
S S + 50 = x x+v
) D.
S S + 50 +v = x x
B.
x S = x + v S + 50
C. x + v =
S + 50 S x
10.如图,△ABC 中,∠ABC=30°,点 D 在△ABC 外,且 BD=2,连 AD、CD,则△ACD 的周长最小值 为( A.1 ) B. 3 C. 2 D. 2 3
二、填空题(每小题 3 分,共 18 分)
1 = ; 12 = ;( 2 5 )2= . 2 12.若 x+m 与 x-2 的乘积之中不含 x 的一次项,则 m=
2018-2019学年湖北省武汉二中广雅中学八年级下学期段测数学试卷 (解析版)
2018-2019学年武汉二中广雅中学八年级第二学期段测数学试卷一、选择题1.有理数3的相反数是()A.﹣3B.﹣C.3D.2.若式子在实数范围内有意义,则x的取值范围是()A.x≤﹣3B.x≥﹣3C.x<﹣3D.x>﹣33.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在0.3,那么估计摸到黄球的概率为()A.0.3B.0.7C.0.4D.0.64.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.5.由几个大小相同的小正方体组成的立体图形的俯视图如图所示,则这个立体图形应是下图中的()A.B.C.D.6.《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是()A.B.C.D.7.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之积为偶数的概率是()A.B.C.D.8.如图是某月的日历表,在此日历表上可以用一个长方形圈出2×2个位置相邻的4个数,若圈出的4个数的和为52,则最大数与最小数的积为()A.153B.272C.128D.1059.如图,△ABE中,点A、B是反比例函数y=(k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S=,DE=2OE,则k的值为()△ABEA.6B.﹣6C.9D.﹣910.如图,在矩形ABCD中,AD=80cm,AB=40cm,半径为8cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD 相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切,此时⊙O移动了()cm.A.56B.72C.56或72D.不存在二、填空题(本大题共6个小题,每小题3分,共18分)11.计算的结果是.12.对于一组统计数据2、7、6、4、3、3,这组数据的中位数是.13.计算﹣的结果是.14.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为.15.平面直角坐标系中,点A(m,n)为抛物线y=ax2﹣(a+1)x﹣2(a>0)上一动点,当0<m≤3时,点A关于x轴的对称点始终在直线y=﹣x+2的上方,则a的取值范围是.16.如图,△ABC中,∠A=90°,点D、E分别在边AB、AC上,=m.若,则m=.三、解答题(共8题,共72分)17.计算:(1)a3•a4•a+(a2)4+(﹣2a4)2(2)28x4y2÷7x3y18.如图,AB∥CD,EF分别交AB,CD于点E、F,∠AEF、∠DFE的平分线分别为EG、FH,求证:EG∥FH.19.中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)请补全条形分布直方图,本次调查一共抽取了名学生;(2)扇形统计图中“1部”所在扇形的圆心角为度;(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?20.如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(﹣2,﹣2)、B(5,﹣3)、C(1,1)都是格点.(1)∠ACB的大小为;(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.把△ABC逆时针旋转,得到△AB1C1,其中点C和点B的对应点分别为点C1和点B1,操作步骤如下:第一步:延长AC到格点B1,使得AB1=AB;第二步:延长BC到格点E,使得CE=CB,连接AE;第三步:取格点F,连接FB1交AE于点C1,则△AB1C1即为所求.请你按步骤完成作图,并直接写出B1、E、F三点的坐标.21.如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD (1)求证:AB与⊙O相切;(2)连接OD,若tan B =,求tan∠ADO.22.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:每件售价(万元)每件成本(万元)每年其他费用(万元)每年最大产销量(件)产品甲6a20200乙201040+0.05x280其中a为常数,且3≤a≤5(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)分别求出产销两种产品的最大年利润;(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.23.如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.(1)求证:AE2=AF•AB;(2)连FG,若BE=2CE,求tan∠AFG;(3)如图2,当tan B=时,CE=FE(请直接写出结果,不需要解答过程).24.已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.(1)求抛物线的解析式;(2)如图1,直线l:y=x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l 翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l 的解析式;(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求的值.参考答案一、选择题(共10小题,每小题3分,共30分)1.有理数3的相反数是()A.﹣3B.﹣C.3D.【分析】依据相反数的定义求解即可.解:3的相反数是﹣3.故选:A.2.若式子在实数范围内有意义,则x的取值范围是()A.x≤﹣3B.x≥﹣3C.x<﹣3D.x>﹣3【分析】根据二次根式的被开方数大于等于0列式进行计算即可得解.解:根据题意得,x+3≥0,解得x≥﹣3.故选:B.3.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在0.3,那么估计摸到黄球的概率为()A.0.3B.0.7C.0.4D.0.6【分析】根据利用频率估计概率得摸到黄球的频率稳定在0.3,进而可估计摸到黄球的概率.解:∵通过大量重复摸球实验后发现,摸到黄球的频率稳定在0.3,∴估计摸到黄球的概率为0.3,故选:A.4.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.解:A、既是轴对称图形,又是中心对称图形,故A正确;B、不是轴对称图形,是中心对称图形,故B错误;C、是轴对称图形,不是中心对称图形,故C错误;D、是轴对称图形,不是中心对称图形,故D错误.故选:A.5.由几个大小相同的小正方体组成的立体图形的俯视图如图所示,则这个立体图形应是下图中的()A.B.C.D.【分析】由俯视图判断出组合的正方体的几何体的列数即可.解:根据给出的俯视图,这个立体图形的左边有2列正方体,右边1列正方体.故选:C.6.《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是()A.B.C.D.【分析】根据题意可得等量关系:人数×8﹣3=物品价值;人数×7+4=物品价值,根据等量关系列出方程组即可.解:设有x人,物品价值y元,由题意得:,故选:C.7.一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、3、4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之积为偶数的概率是()A.B.C.D.【分析】画树状图展示所有16种等可能的结果数,再找出两次抽取的卡片上数字之积为偶数的结果数,然后根据概率公式求解.解:画树状图为:共有16种等可能的结果数,其中两次抽取的卡片上数字之积为偶数的结果数为12,所以两次抽取的卡片上数字之积为偶数的概率==.故选:C.8.如图是某月的日历表,在此日历表上可以用一个长方形圈出2×2个位置相邻的4个数,若圈出的4个数的和为52,则最大数与最小数的积为()A.153B.272C.128D.105【分析】可设正方形框中的第一个数为x,第二个数比x大1,为x+1,第3个数比x大7,为x+7,第4个数比x+7大1,为x+8,再根据四个数的和为52,列出方程求解即可;解:(3)设最小的数为x,依题意有x+x+1+x+7+x+8=52,解得x=9则x+1=10x+7=16x+8=17.∴这四个数为9,10,16,17.∴最大数与最小数的积为9×17=153.故选:A.9.如图,△ABE中,点A、B是反比例函数y=(k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S=,DE=2OE,则k的值为()△ABEA.6B.﹣6C.9D.﹣9【分析】根据题意设A(2a,b),则B(a,2b),E(,0),作BM⊥x轴于M,根据S△ABE=S梯形ABMD+S△BME﹣S△ADE得出﹣ab=,求得ab=﹣3,即可求得k=2ab =﹣6.解:∵点A、B是反比例函数y=(k≠0)图象上的两点,点B恰为线段AC中点,∴设A(2a,b),则B(a,2b),∴k=2ab,∵DE=2OE,∴E(,0),作BM⊥x轴于M,∵S△ABE=S梯形ABMD+S△BME﹣S△ADE,S△ABE=,∴(﹣a)•(b+2b)+(﹣a)•2b﹣(﹣2a)•b=,整理得﹣ab=,解得ab=﹣3,∴k=2ab=﹣6.故选:B.10.如图,在矩形ABCD中,AD=80cm,AB=40cm,半径为8cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD 相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切,此时⊙O移动了()cm.A.56B.72C.56或72D.不存在【分析】根据相同时间内速度的比等于路程的比,可得v1:v2的值,根据相似三角形的性质,可得∠ADB=∠BDP,根据等腰三角形的判定,可得BP与DP的关系,根据勾股定理,可得DP的长,根据有理数的加法,可得P点移动的距离;根据相似三角形的性质,可得EO1的长,分类讨论:当⊙O首次到达⊙O1的位置时,当⊙O在返回途中到达⊙O1位置时,根据v1:v2的值,可得答案.解:存在这种情况,设点P移动速度为v1cm/s,⊙O2移动的速度为v2cm/s,由题意,得==,如图②:设直线OO1与AB交于E点,与CD交于F点,⊙O1与AD相切于G点,若PD与⊙O1相切,切点为H,则O1G=O1H.易得△DO1G≌△DO1H,∴∠ADB=∠BDP.∵BC∥AD,∴∠ADB=∠CBD∴∠BDP=∠CBD,∴BP=DP.设BP=xcm,则DP=xcm,PC=(80﹣x)cm,在Rt△PCD中,由勾股定理,得PC2+CD2=PD2,即(80﹣x)2+402=x2,解得x=50,此时点P移动的距离为40+50=90(cm),∵EF∥AD,∴△BEO1∽△BAD,∴=,即=,EO1=64cm,OO1=56cm.①当⊙O首次到达⊙O1的位置时,⊙O移动的距离为40cm,此时点P与⊙O移动的速度比为==,∵≠,∴此时PD与⊙O1不能相切;②当⊙O在返回途中到达⊙O1位置时,⊙O移动的距离为2(80﹣16)﹣56=72(cm),∴此时点P与⊙O移动的速度比为==,此时PD与⊙O1恰好相切.此时⊙O移动了72cm,故选:B.二、填空题(本大题共6个小题,每小题3分,共18分)11.计算的结果是4.【分析】根据二次根式的性质求出即可.解:=4,故答案为:4.12.对于一组统计数据2、7、6、4、3、3,这组数据的中位数是 3.5.【分析】根据中位数的定义直接解答即可.解:把这些数从小到大排列为2、3、3、4、6、7,则这组数据的中位数是(3+4)÷2=3.5.故答案为:3.5.13.计算﹣的结果是.【分析】根据分式的运算法则即可求出答案.解:原式=+=故答案为:14.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为130°或90°.【分析】根据题意可以求得∠B和∠C的度数,然后根据分类讨论的数学思想即可求得∠ADC的度数.解:∵在△ABC中,AB=AC,∠BAC=100°,∴∠B=∠C=40°,∵点D在BC边上,△ABD为直角三角形,∴当∠BAD=90°时,则∠ADB=50°,∴∠ADC=130°,当∠ADB=90°时,则∠ADC=90°,故答案为:130°或90°.15.平面直角坐标系中,点A(m,n)为抛物线y=ax2﹣(a+1)x﹣2(a>0)上一动点,当0<m≤3时,点A关于x轴的对称点始终在直线y=﹣x+2的上方,则a的取值范围是0<a<1.【分析】求得直线y=﹣x+2,当x=3时的函数值为﹣1,根据题意当x=3时,抛物线的函数值小于1,得到关于a的不等式,解不等式即可求得a的取值范围,解:直线y=﹣x+2中,当x=3时,y=﹣x+2=﹣1,∵A(m,n)关于x轴的对称点始终在直线y=﹣x+2的上方,∴当x=3时,n<1,∴9a﹣3(a+1)﹣2<1,解得a<1,∴a的取值范围是0<a<1,故答案为0<a<1.16.如图,△ABC中,∠A=90°,点D、E分别在边AB、AC上,=m.若,则m=.【分析】作EF⊥BE,CF⊥CE交于点F,易得△ABE∽△CEF,易证四边形BDCF为平行四边形,设BE=2a,CD=BF=3a,可求EF=a,即可求出m的值.解:作EF⊥BE,CF⊥CE交于点F,则∠AEB+∠CEF=90°=∠AEB+∠ABE,∴∠ABE=∠CEF,∵∠A=∠ECF=90°∴△ABE∽△CEF,∴===m,∵=m.∴CF=BD,∵∠A=∠ECF=90°,∴AB∥CF,∴四边形BDCF为平行四边形,设BE=2a,CD=BF=3a,在Rt△BEF中,EF==a,=m,∴=m,∴m=,故答案为.三、解答题(共8题,共72分)17.计算:(1)a3•a4•a+(a2)4+(﹣2a4)2(2)28x4y2÷7x3y【分析】(1)直接利用积的乘方运算法则以及幂的乘方运算法则、同底数幂的乘法运算法则分别化简得出答案;(2)直接利用整式的除法运算法则计算得出答案.解:(1)a3•a4•a+(a2)4+(﹣2a4)2=a8+a8+4a8=6a8;(2)28x4y2÷7x3y=4xy.18.如图,AB∥CD,EF分别交AB,CD于点E、F,∠AEF、∠DFE的平分线分别为EG、FH,求证:EG∥FH.【分析】由AB与CD平行,利用两直线平行,内错角相等得到一对角相等,再由EG 与FH为角平分线,利用角平分线定义及等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.【解答】证明:∵AB∥CD,∴∠AEF=∠EFD(两直线平行,内错角相等).∵EG平分∠AEF,FH平分∠EFD,∴∠GEF=∠AEF,∠HFE=∠EFD(角平分线定义),∴∠GEF=∠HFE,∴EG∥FH(内错角相等,两直线平行).19.中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)请补全条形分布直方图,本次调查一共抽取了40名学生;(2)扇形统计图中“1部”所在扇形的圆心角为126度;(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?【分析】(1)由2部人数及其所占百分比可得总人数,总人数减去0、2、3、4部的人数即可求出1部的人数,从而补全图形;(2)用360°乘以1部人数所占比例可得;(3)用总人数乘以样本中3、4部人数占被调查人数的比例即可得.解:(1)本次调查的总人数为10÷25%=40(人),则“1部”的人数为40﹣(2+10+8+6)=14(人),补全图形如下:故答案为:40;(2)扇形统计图中“1部”所在扇形的圆心角为360°×=126°,故答案为:126;(3)估计至少阅读3部四大古典名著的学生有1000×=350(人).20.如图,在下列10×10的网格中,横、纵坐标均为整点的数叫做格点,例如A(﹣2,﹣2)、B(5,﹣3)、C(1,1)都是格点.(1)∠ACB的大小为90°;(2)要求在下图中仅用无刻度的直尺作图:以A为中心,取旋转角等于∠BAC.把△ABC逆时针旋转,得到△AB1C1,其中点C和点B的对应点分别为点C1和点B1,操作步骤如下:第一步:延长AC到格点B1,使得AB1=AB;第二步:延长BC到格点E,使得CE=CB,连接AE;第三步:取格点F,连接FB1交AE于点C1,则△AB1C1即为所求.请你按步骤完成作图,并直接写出B1、E、F三点的坐标.【分析】(1)利用CA和CB为网格的对角线可判断∠ACB的度数;(2)利用勾股定理得到AB1=AB=5,则利用网格特点可确定B1点的位置,利用∠EAC=∠BAC且AE=AB可确定E点位置,要得到B1C1⊥AE,利用网格特点取F点使B1F⊥AE.解:(1)∠ACB=90°,故答案为90°;(2)如图所示,△AB1C1即为所求.其中B1(3,3);E(﹣3,5),F(﹣4,2).21.如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD(1)求证:AB与⊙O相切;(2)连接OD,若tan B=,求tan∠ADO.【分析】(1)设线段AD与⊙O交于E,连接CE,根据圆周角定理得到CE⊥AD,求得∠ACE=∠DAB,于是得到结论;(2)根据切线的性质得到∠CAB=90°,延长CE交AB于M,则CM为AD的垂直平分线,连接DM,根据全等三角形的性质得到∠CDM=∠CAB=90°,设AM=MD=3a,DB=4a,MB=5a,得到AB=8a,AC=6a,设EN=k,得到AE=DE=2k,CE=4k,过O作ON⊥AD于N,根据三角形的中位线定理得到ON=CE=2k,AN=AE=k,于是得到结论.【解答】(1)证明:设线段AD与⊙O交于E,连接CE,∵AC为⊙O的直径,∴CE⊥AD,∵AC=CD,∴∠ACD=2∠ACE,∵∠ACB=2∠BAD,∴∠ACE=∠DAB,∵∠CAE=90°,∴∠CAE+∠DAB=90,∴∠CAB=90°,∴AB与⊙O相切;(2)解:∵AB与⊙O相切,∴∠CAB=90°,延长CE交AB于M,则CM为AD的垂直平分线,连接DM,∴DM=AM,∵AC=CD,CM=CM,∴△ACM≌△DCM(SSS),∴∠CDM=∠CAB=90°,∴∠BDM=90°,∵tan B =,∴设AM=MD=3a,DB=4a,MB=5a,AB=8a,AC=6a,∴tan∠ACM=tan∠EAM =,∴CE=2AE,AE=2EM,设EN=k,∴AE=DE=2k,CE=4k,过O作ON⊥AD于N,∴ON∥CE,∴ON =CE=2k,AN =AE=k,∴DN=3AN=3k,∴tan∠ADO ==.22.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:产每件售价(万元)每件成本(万元)每年其他费用(万元)每年最大产销量(件)品甲6a20200乙201040+0.05x280其中a为常数,且3≤a≤5(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)分别求出产销两种产品的最大年利润;(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.【分析】(1)根据利润=销售数量×每件的利润即可解决问题.(2)根据一次函数的增减性,二次函数的增减性即可解决问题.(3)根据题意分三种情形分别求解即可:①(1180﹣200a)=440,②(1180﹣200a)>440,③(1180﹣200a)<440.解:(1)y1=(6﹣a)x﹣20,(0<x≤200)y2=10x﹣40﹣0.05x2=﹣0.05x2+10x﹣40.(0<x≤80).(2)对于y1=(6﹣a)x﹣20,∵6﹣a>0,∴x=200时,y1的值最大=(1180﹣200a)万元.对于y2=﹣0.05(x﹣100)2+460,∵0<x≤80,∴x=80时,y2最大值=440万元.(3)①1180﹣200a=440,解得a=3.7,②1180﹣200a>440,解得a<3.7,③1180﹣200a<440,解得a>3.7,∵3≤a≤5,∴当a=3.7时,生产甲乙两种产品的利润相同.当3≤a<3.7时,生产甲产品利润比较高.当3.7<a≤5时,生产乙产品利润比较高.23.如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.(1)求证:AE2=AF•AB;(2)连FG,若BE=2CE,求tan∠AFG;(3)如图2,当tan B=时,CE=FE(请直接写出结果,不需要解答过程).【分析】(1)根据等腰三角形的性质、同角的余角相等得到∠AEF=∠B,证明△AEF ∽△ABE,根据相似三角形的性质证明结论;(2)设CE=a,则BE=2a,证明△AEC∽△BAC,得到AC=a,求出∠AFG=60°,得到答案;(3)设BE=a,CE=EF=b,证明△AEC∽△BAC,得到AC=,证明△BEF ∽△BCA,求出a、b的关系,根据正切的定义解答即可.【解答】(1)证明:∵GC=GE,∴∠GCE=∠GEC,∵CD⊥AB,∴∠DCE+∠B=90°,∵EF⊥BC,∴∠GEC+∠AEF=90°,∴∠AEF=∠B,又∠EAF=∠BAE,∴△AEF∽△ABE,∴=,∴AE2=AF•AB;(2)设CE=a,则BE=2a,∵∠DCB+∠B=90°,∠CAB+∠B=90°,∴∠DCB=∠CAB,∵∠GCE=∠GEC,∴∠CAB=∠GEC,又∠ACE=∠BCA=90°,∴△AEC∽△BAC,∴=,即=,解得,AC=a,∴∠CAE=∠BAE=∠AEF=30°,∴FA=FE,∵∠GAC=∠GCA=30°,∴GA=GC,∵GC=GE,∴GA=GE,又FA=FE,∴∠AFG=60°,∴tan∠AFG=;(3)设BE=a,CE=EF=b,∵△AEC∽△BAC,∴=,即=,解得,AC2=b(a+b),∴AC=,∵EF∥AC,∴△BEF∽△BCA,∴=,即=,整理得,b2+ab﹣a2=0,则()2+﹣1=0,解得,=,∴tan B==,故答案为:.24.已知抛物线y=ax2﹣2ax﹣3a与y轴交于C点,交x轴于A、B,且OB=OC.(1)求抛物线的解析式;(2)如图1,直线l:y=x+b(b<0)交x轴于M,交y轴于N.将△MON沿直线l 翻折,得到△MPN,点O的对应点为P.若O的对应点P恰好落在抛物线上,求直线l 的解析式;(3)如图2,将原抛物线向左平移1个单位,向下平移t个单位,得到新抛物线C1.若直线y=m与新抛物线C1交于P、Q两点,点M是新抛物线C1上一动点,连接PM,并将直线PM沿y=m翻折交新抛物线C1于N,过Q作QT∥y轴,交MN于点T,求的值.【分析】(1)OB=OC=3a,故点B(3a,0),将点B的坐标代入y=ax2﹣2ax﹣3a,即可求解;(2)求出点P的坐标(﹣b,b),将点P的坐标代入抛物线表达式,即可求解;(3)计算x P+x M=k,同理可得:x P+x N=﹣k,而x T=x Q=﹣x P,而TH∥MG,故,即==1.解:(1)∵c=﹣3a,∴OB=OC=3a,故点B(3a,0),将点B的坐标代入y=ax2﹣2ax﹣3a并解得:a=1或﹣(舍去﹣),故抛物线的表达式为:y=x2﹣2x﹣3;(2)连接OP,交MN于点K,则OP⊥MN,则直线OP的表达式为:y=﹣2x,而直线MN的表达式为:y=x+b,联立上述两个表达式并解得:x=﹣b,则点K(﹣b,b),∵点K是OP的中点,由中点公式得:点P的坐标为(﹣b,b),将点P的坐标代入抛物线表达式得:(﹣b)2﹣2(﹣b)﹣3=b,解得:b=﹣(不合题意值已舍去);故直线l的表达式为:y=x﹣;(3)平移后抛物线的表达式C1:y=x2﹣4﹣t①,设直线PM的表达式为:y=kx+c②;则PN的表达式为:y=﹣kx+d,联立①②并整理得:x2﹣kx﹣(4+t+c)=0,∴x P+x M=k,同理可得:x P+x N=﹣k,而x T=x Q=﹣x P,如图2,过点N作x轴的平行线交过点M与y轴的平行线于点G,延长TQ交NG于点H,∴TH∥MG,故,即==1.。
武汉二中广雅中学2014——2015年八(下)数学周练(1)
武汉二中广雅中学八年级(下)数学周练(1)命题人:李兴凯 总分:120分 时间:90分钟一、选择题(3′×12=36′)1.在式子5a ,35a +,1π,31x y +,35x y+中,是分式的个数有( )A .5个B .4个C .3个D .2个 2.如果分式22+-a a 的值为0,则a 的值是( )A . 2±B .2C . 2-D .以上都不对 3.如果把分式xyx y+中的x 和y 都扩大3倍,那么分式的值( ) A .扩大3倍 B .不变 C .缩小3倍 D .缩小6倍 4.下列运算中,正确的是( ) A .()120-=- B .()221=-- C .22414a a =- D .231a a a =÷5.反比例函数的表达式为22)1(--=mx m y , 则m 为( ).A.1B.±1C.0D.-1 6.下列四个点,在反比例函数6y x=图象上的是( ) A .(1,6-) B .(2,4) C .(3,2-) D .(6-,1-)7.若分式方程231x x -=1m x -有增根,则m 的值为( )A .1B .-1C .3D .-3 8.若点(x 1,y 1)(x 2,y 2)(x 3,y 3)都是反比例函数xy 1-=的图象上的点,并且 x 1<0<x 2<x 3,则下列各式中正确的是( )A 、y 1<y 2<y 3B 、y 2<y 3<y 1C 、y 3<y 2<y 1D 、y 1<y 3<y 2 9.直角坐标系中,点A ,点B 的坐标分别为(-4,0),(0,3),则坐标原点O 到线段AB 的距离为( )A.2B.2.4C.5D.610.如图,已知矩形ABCD 沿着直线BD 折叠,使点C 落在C /处,BC /交AD 于E,AD=8,AB=4,则DE 的长为( )A. 3 B . 4; C .5; D .611.如图,一次函数与反比例函数的图像相交于A 、B 两点,则图 中使反比例函数的值小于一次函数的值的x 的取值范围是( )A 、x <-1B 、x >2C 、-1<x <0,或x >2D 、x <-1,或0<x <212.在直角梯形ABCD 中,AD BC ∥,90ABC AB BC E ∠==°,,为AB 边上一点,15BCE ∠=°,且AE AD =.连接DE 交对角线AC 于H ,连接BH .下列结论: ①ACD ACE △≌△; ②CDE △为等边三角形;③CH CB =;④CH BH= 其中结论正确的是( ) A .只有①② B .只有①②④ C .只有③④ D .①②③④ 二、填空题. (3′×4=12′)13.请写出一个图象与直线y=x 没有交点的反比例函数解析式 .14.在△ABC 中,A B =15,A C =13,BC 边上的高A D =12,则△ABC 的面积为 .15. 已知2310a a ++=,则221a a += .16.如图,直线y x b =-+与x 轴交于点C ,与反比例函数y =的图象相交于点A 、B ,若2210OC OA -=,则k = .三、解答与证明. (72′) 17.解方程(本题6分)114112=---+x x x 18.(本题6分)先化简,再求值:211122x x x -⎛⎫-÷⎪++⎝⎭,其中2x =. 19.(本题6分)小王开着私家车到某市接朋友,他家到该市的路程为300千米,其车速与每千米的耗油量之间的关系如下表所示:(1)认真分析表中的数据,试写出y 和x 之间的函数关系式;(3分) (2)若该车油箱最大容积为35升,小王把油箱加满油后出发,接到朋友后迅速返回,如果他保持60千米/小时的速度匀速行驶,问油箱中的油是否够用?请说明理由。
武汉二中广雅中学2017-2018学年度八年级(下)物理训练卷(一)(无答案)
武汉市第二初级中学&武汉二中广雅中学八年级(下)物理训练卷(一)可能用到的物理量:g=10N/kg一、选择题(每小题3分,满分45分,每小题只有一个答案符合题意)1.如图所示,四个力中的一个与其他三个力所产生的作用效果不同的是()A.球拍对乒B.斧头对木C.手对弹簧D.瓶对海乓球的力柴的力的拉力绵的力2.下列体育项目中的一些现象,不能用“力的作用是相互的”来解释的是()A.跳水运动员踩踏跳饭.身体向上跳起B.铅球运动员投出铅球后,身体随着向前倾倒C.滑冰运动员用力推墙身体离墙而去D.游泳运动员向后划水,身体前进3.如图所示,四旋翼无人机下方用细线悬挂一个重物,不考虑空气阻力,则无人机在空中()A.悬停时,重物受到的重力与它对细线的拉力是一对平衡力B.加速上升时,细线对重物的拉力等于重物所受到的重力C.匀速下降时,重物所受的重力大于细线对重物的拉力D.水平匀速飞行时,悬挂重物的细线会偏离竖直方向4.如图所示,一根弹簧,一端固定在竖直墙上,在弹性奶度内用手水平拉伸弹簧的另一端,下列有关“弹簧形变产生的力”的描述正确的是()A.手对弹簧的拉力B.墙对弹簧的拉力C.弹簧对手的拉力D.以上说法都不正确5.如图是汽车拉力赛途经的一段“S”形水平弯道,为了更安全,现场观众应站的位置是图中()A.甲、丁B.甲、乙C.丙、丁D.乙、丙6.如图所示,在竖直平面内用轻质细线悬挂一个小球,将小球拉至A点,使细线处于拉直状态,由静止开始释放小球,不计摩擦,小球可在A、B两点间来回摆动.小球摆到B 点时,细线恰好断开,则小球将()A.在B点保持静止B.沿BE方向运动C.沿BC方向运动D.沿BD方向运动7.乐乐同学随父母去看杂技表演,如图所示,是他看到杂技演员小强将小丽高高举起时的情景,下列说法正确的是()A.小强受到的重力与地面对小强的支持力是一对平衡力B.小丽对小强的压力与小强对小丽的支持力是一对平衡力C.小强受到的重力与地面对小强的支持力是一对相互作用力D.小丽受到的重力与小强对小丽的支持力是一对平衡力8.物理课上,老师演示了如图所示的实验,木块竖立在小车上,随小车一起以相同的速度向右作匀速直线运动.不考虑空气阻力,下列分析正确的是()A.小车的运动速度增大,则它的惯性和动能也随之增大B.小车受到阻力突然停止运动时,那么木块将向右倾倒C.木块随小车一起作匀速直线运动时,木块不受摩擦力D.木块对小车的压力与小车对木块的支持力是一对平衡力9.在同一水平面上,两个完全相同的木块P、Q分别在水平力F1、F2、F3和F4的作用下,以不同的放置方式和运动速度一起向右做匀速直线运动,如图甲、乙、丙、丁所示,则下列关系式正确的是()A.2F1=F2=2F3=F4B.2F1=2F2=F3=F4C.4F1=2F2=2F3=F4D.F1=F2=F3=F410.如图所示,小华将弹簧测力计一端固定,另一端钩住长方体木块A,木块下面是一长木板,实验时拉着长木板沿水平地面向左运动,读出弹簧测力计示数即可测出木块A 所受摩擦力大小.在木板运动的过程中,以下说法正确的是()A.木块A所受摩擦力的方向向左B.木块A相对于地面是运动的C.拉动速度变大时,弹簧测力计示数变大D.木块A受到的是静摩擦力11.踢毽子是一项有益的体育活动,毽子踢出后竖直上升又竖直下落的中,均受到空气阻力的作用,若毽子上升和下落过程中受到的合力大小分别为F1、F2,则F1 、F2的大小关系正确的是()A.F1 > F2B.F1 < F2C.F1 = F2D.无法确定12.如图所示,放在M、N两水平桌面上的P、Q物体,分别在F P=5N、F Q=3N 的水平拉力作用下做匀速直线运动,可以确定()A.桌面M 一定比桌面N 粗糙PB.P的质量一定大于Q 的质量C.P的速度一定大于Q 的速度D.P受到的摩擦力一定大于Q 受到的摩擦力13.如图所示,一个木块在光滑水平面上以v0的速度做匀速直线运动,冲上粗糙斜面后最终静止在A点。
武汉二中广雅中学2017~2018学年度下学期八年级数学试卷4
武汉二中广雅中学2017~2018学年度下学期八年级数学试卷4一、选择题(共10小题,每小题3分,共30分)1.函数x y -=2中自变量x 的取值范围是( )A .x <2B .x ≥2C .x ≤2D .x ≠22.下列函数中,( )是一次函数A .y =kx +1B .44+-=x y C .y =-x 2+1 D .x y 1-= 3.下列命题中,不正确的是( ).A .平行四边形的对角线互相平分B .矩形的对角线互相垂直且平分C .菱形的对角线互相垂直且平分D .正方形的对角线相等且互相垂直平分4.一次函数y =kx +b 的图像经过第一、三、四象限,则( ) A .k >0,b >0 B .k >0,b <0 C .k <0,b >0D .k <0,b <0 5.一根竹子高9尺,折断后竹子顶端落在离竹子底端3尺处,折断处离地面的高度是( )尺 A .5B .4.5C .4D .3 6.已知A (x 1,y 1)、B (x 2,y 2)是一次函数y =-x +1的图象上的点.当x 1<x 2时,y 1、y 2的大小关系为( )A .y 1<y 2B .y 1>y 2C .y 1=y 2D .以上结论都有可能 7.将直线y =-3x 向右平移2个单位,再向上平移1个单位得到直线解析式为( )A .y =-3x -5B .y =-3x +5C .y =-3x +7D .y =-3x -78.如图,菱形ABCD 中,∠ABC =60°,AC 、BD 交于点O ,EF 过点O 且EF ⊥BC ,交BC 、AD分别于点E 、F ,连接BF .若BF =73,则菱形的周长为( )A .324B .24C .316D .169.如图,在平面直角坐标系中,直线l :y =x -1与x 轴交于点A 1,依次作正方形A 1B 1C 1O 、正方形A 2B 2C 2C 1、……、正方形A n B n C n C n ﹣1,使得点A 1、A 2、A 3、……在直线l 上,点C 1、C 2、C 3、……在y轴正半轴上,则点B 18的坐标是( ) A .(216,217-1)B .(217,218-1)C .(216,217+1)D .(217,218+1)10.边长为23的正方形ABCD 中,点E 、F 是对角线AC 、BD 上的两点,AF 、BE 的延长线交于点M .若∠M =45°,BE =10,则DF =( )A .25B .23C .210 D .2 二、填空题(本大题共6个小题,每小题3分,共18分) 11.化简:59=___________ 12.一次函数y =-2x -5与x 轴交于点__________,不经过第___________象限,y 随x 的增大而__________13.如图,将平行四边形ABCD 沿对角线BD 折叠,使点A 落在点A '处.若∠1=∠2=50°,则∠A '为___________14.函数y =kx 和y =ax +b 的图象如图所示,则不等式kx ≥ax +b 的解集为___________15.一号探测气球从海拔10千米处出发,与此同时,二号探测气球从海拔30千米处出发.两只气球所在位置的海拔y (千米)与上升时间x (分)的函数图象如图所示.在上升40分时,两只气球位于同一高度,则这个高度是___________千米16.如图,平面直角坐标系中,直线y =x +4与坐标轴分别交于点A 、B ,点C 在线段OB 上运动,连接AC ,以AC 为边在AC 右侧作正方形ACDE ,点F 为AO 的中点,连接FD ,则FD 的取值范围是_________________三、解答题(共8题,共72分)17.(本题8分)计算:(1)54580+- (2) 22)6324(÷-18.(本题8分)如图,矩形ABCD 的对角线AC 、BD 相交于点O ,且DE ∥AC ,CE ∥BD ,求证:四边形OCED 是菱形19.(本题8分)点P (x ,y )在第一象限,且x +y =10,点A 的坐标为(6,0),设△OP A 的面积为S(1) 用含x 的式子表示S ,并写出x 的取值范围(2) 当点P 的横坐标为5时,△OP A 的面积为多少?20.(本题8分)如图,△ABC三个顶点的坐标分别为A(-4,-2)、B(-1,-1)、C(-1,-4)(1) 画出△ABC关于y轴对称的图形△A1B1C1(2) 在x轴上作出一点P,使P A+PC1的值最小(保留作图痕迹),此时点P的坐标___________21.(本题8分)如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG(1) 求证:四边形DEFG是平行四边形(2) 如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长22.(2017·咸宁中考)(本题10分)某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件.工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y (件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件(1) 第24天的日销售量是__________件,日销售利润是__________元(2) 求y与x之间的函数关系式,并写出x的取值范围(3) 试问销售期间,日销售最大利润是多少元?23.(本题10分)正方形ABCD 中,P 是对角线AC 上的一个动点(点P 与A 、C 不重合),连接BP ,将BP 绕点B 顺时针旋转90°到BQ ,连接QP ,QP 与BC 交于点E(1) 如图1,连接CQ ,求证:△ABP ≌△CBQ(2) 如图2,若QP 延长线与AD 交于点F ,求证:PF =QE(3) 若△CEQ 为等腰三角形,则PFPE =__________(请直接写出结果)24.(本题12分)已知:直线y =x +b 分别与x 轴负半轴、y 轴正半轴交于点A 、B(1) 如图1,若直线AB 过P (1,3),求S △AOB(2) 如图2,点B 关于x 轴的对称点为B ′,将线段AB ′沿x 轴正半轴移动到MN ,直线MN 交直线AB 于点E ,直线BN 交x 轴于点F ,求AFNE 的值 (3) 如图3,在(1)的条件下,在x 轴上是否存在一点Q ,使得∠PQO =∠APO ,若存在请求出Q 点坐标;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018二中八下周练(一)二、单项选择26. --_________? -----I have a stomachache.A. What can I do for youB. What’s the matter with youC. What’s wrong to youD. What’s the wrong with you27. –Jimmy, could you please take out the rubbish? --______________.A. That sounds interestingB. Of course, I’ll do it at onceC. Sorry, I couldn’tD. My pleasure28. –Let’s ______ a time to meet. I miss you so much ! ----How about this Sunday?A. look upB. give upC. fix upD. put up29.— Many teenagers show (an) ________ in the game of King Glory now.--I agree, but they can’t be lost in the game.A. controlB. interestC. feelingD. experience30. –Do you know that Coco won the Oscar for Best Animated Feature Film?--Yeah, the news ________ my spirit a lot.A. grewB. addedC. roseD. raised31. –You hurt my feelings by doing that. –I’m sorry I hurt you. I didn’t _______ to.A. wantB. decideC. meanD. plan32. –Look at the dark clouds in the sky up!--Hurry up! Dark clouds are often _______ of the heavy rain.A. symbolB. signC. signalD. message33. –This cup of coffee is too ________ for me to drink.--Maybe you should add some water of milk.A. heavyB. excitedC. strongD. light34. –What happened to Mary? She is so scared.--She saw a terrible car accident just now. Her voice ________ as she told us about it.A. cutB. troubledC. hurtD. broke35. –What would you like, tea or coffee ? -- ________, thanks. I’d like a cup of water.A. NeitherB. EitherC. EachD. None36. –How does Jim go to school?--He ________ to school in his father’s car, but now he _________ to school.A. is used to go, is used to walkingB. used to go, is used to walk.C. is used to walking, used to walkD. used to go, is used to walking37. –Why were you so excited just now?--I_________ going on a journey to Sanya for summer vacation.A. imaginedB. noticedC. trainedD. risked38. –What’s the trouble with Judy?--Her legs ________and she fell down because of a long walk.A. put outB. broke outC. try outD. gave out39. –Look! Mario is standing ________ there. I want to cheer him up.--I think you don’t need to. Just leave him ________. Mayb e he needs some quiet time now.A. lonely; lonelyB. lonely; aloneC. alone; aloneD. alone, lonely40. –As a monitor, don’t turn a ________ eye to some students’ bad behavior in the class.--I can’t agree more.A. closeB. blindC. deafD. lonely三、完形填空Most people need to hear those “three little words”-I love you.Once in a while, they hear them just in time.I ____41___ Connie the day she was sent to the hospital, where I worked as a woman volunteer.Her husband, Bill, stood ____42___ nearby as she was transferred to the hospital bed.Although Connie was in the final stages of her fight against cancer, she was ____43___.As we became familiar(熟悉), she said how frustrating(沮丧) it was to be married 32 years to a man who often called her “a silly woman”. She looked out of the window at the trees in the courtyard. “I’d give anything if he’d say I love you, it’s just not in his ___44____.”Bill visited Connie every day.In the beginning, he sat next to the bed ___45___ she watched the soaps.Later, when she began sleeping more, he paced up and down the hallway outside her room.Soon, when she no longer watched television and had fewer ___46___ moments, I began spending more of my ___47___ time with Bill.One day, over coffee I got him on the ___48___ of women and how we need romance in our lives. “Do you tell Connie you love her?”I asked(knowing his answer), and he looked at me as if I was ___49___.“I don't have to,”he said.“She knows I do!”“I'm sure she knows,”I said, “but she needs to hear what she has ___50___ to you all the years.”We walked back to Connie's room.Bill ___51___ inside, and I left to visit another patient.The date was February 12.Two days later when Bill saw me, he allowed himself to come into my __52____ for a long time.His face was ___53___ with tears.Finally, he leaned back against the wall and ___54___ a deep breath.“I have to say something,”he said.“I have to say how good I feel about telling her.”He stopped to ___55___ his nose.“This morning I told her how much I loved her…and loved being married to her.You should have seen her smile!”41. A. looked B. met C. watched D. saw42. A. nervously B. carefully C. happily D. carelessly43. A. excited B. upset C. cheerful D. mad44. A. eyes B. heart C. brain D. nature45. A. when B. while C. before D. where46. A. sleepy B. reading C. waking D. standing47. A. difficult B. lonely C. happy D. volunteer48. A. subject B. idea C. lesson D. event49. A. crazy B. bored C. surprised D. ill50. A. loved B. meant C. given D. done51. A. disappeared B. appeared C. fell D. ran52. A. hands B. arms C. face D. feet53. A. red B. black C. wet D. felt54. A. held B. took C. lost D. felt55. A. wash B. keep C. run D. blow四.阅读理解A56. The above material is probably .A. a photo of a western woman C. an advertisementB. an article about a sofa bed D. an announcement57. The sofa bed is sold by a(n) company.A.ChineseB. BritishC. AmericanD. Canadian58. The sofa bed in the material mostly deals with the problem of _______.A. PriceB. styleC. materialD. space59. ‘convert’ in the material means .A. sellB. changeC. produceD. show60. It’s clear the if you buy the kind of sofa bed .A. you’ll have a lower priceB. you need to call on 21 storesC. you’ll have to go to experts for adviceD. you must be a member of Futon companyBThis is my story. It is the beginning of the second semester and a new year in eighth grade. I was over at my best friend Christina’s house. Yet again, she was listening to her favorite CD-Dream Street. When I got to her room she turned down her music and we talked about it. She said that she was the best DS fan ever. I said they’re OK and I like the music. Then she went on to say that I wasn’t a “true” fan, so I left her house and walked home. The next day I found a note in my locker(衣物柜). It was from Christina. It said, “I do not consider you as one of my friends. You are a liar.”After that dreadful day it got worse. I didn’t smile, or even talk to my other friends. I completely shut myself off from the world. I just didn’t understand what went wrong. Finally after a few days, some of my friends got together and came to me. They tried their best to comfort me and make me smile.The time that I realized something very important was that night. After several sleepless nights, I suddenly realized that I was loved, and I had other friends, I could get over it. Quickly, I turned on my light and started writing a letter to each of my friends. I wrote about the good times and how much I cared about them. I told what was happening to me, why I was so upset, and I thanked each of them for helpingme. The next day I gave my friends the letters. When they finished reading them, they thanked me and gave me a big hug. I realized that I needed to be strong and how friends could help with your problems and help you heal.61. From the reading we know _______.A. Christina is a good studentB. the writer and Christina are still good friendsC. the writer did something wrong to her friendsD. the writer learned a good lesson from the experience62. Which of the following is closest to the word “liar”?A. Honest peopleB. Foolish peopleC. Dishonest peopleD. Shy people63. How old is the writer most probably?A. 8-10B. 12-14C. 16-18D. Over 2064. Which of the following is TRUE according to the passage?A. Friends should learn from each other.B. The writer gets on well with other students.C. Good friends should have similar hobby.D. The writer had a fight with Christina.65. The best title for the reading is ______.A. Trouble in FriendshipB. Break off FriendshipC. The lost FriendshipD. True FriendshipCOn Sundays my father always wore that gray apron(围裙). After breakfast when he always announced: "Go ahead everyone. I'll wash the dishes!" For the next hour Dad did the dishes, singing songs like I Had a Hat When I Came In.I suppose it was strange for a boy's father to wear an apron. It was the last Sunday in August. My father seemed happy as we walked home from the supermarket together."Tommy," he said, "There comes a time in every boy's life when he must take on responsibilities(责任). Starting today, I want you to do the dishes on Sunday morning so your mother and I can read the newspaper.""Wash the dishes!?""Anything wrong with taking over the dishes, son?"I started to say something about a man's job or woman's work, but I knew quickly that myprotests(抗议) would be of no use.I didn't taste a bit of breakfast that morning. Dad seemed excited as he talked about a soccer game on TV and didn’t notice me at all.Suddenly, everything grew quiet. My sister began to clear the table. My brother was eating thelast of the egg from his plate. And then my father said to my mother, "Let's go and read the paper, dear."So this was what my life had come. I could learn Latin well, I could be good at playing baseball, I could d anything, but I could never do those dishes. There was nothing left but to refuse.My father came back into the kitchen, and in his right hand was the old apron."I want you to have this, Tommy. It'll keep your clothes from getting wet." And before I couldsay a word, he had put the thing on me. "Thanks, Son."I looked down at the apron. It had seen better days. I could see my dad reaching for the dishes. Soon I was singing about I Had a Hat When I Came In. The words came out of nowhere. And I knew the kind of man I wanted to be.66.We can learn the father regarded doing housework as a person’s ________.A. unacceptableB. impossibleC. uselessD. boring68. When the writer was in the kitchen, the father came back to _______.A. show him how to do the washesB. talk with himB. check his work D. put the apron on him69. The result of the story probably is that _________.A. the writer still thought doing dishes was not his jobB. the writer did nothing but to refuseC. the writer accepted his father’s idea and did as his father had doneD. the writer wasn’t pleased to do as his father asked at last70. The reading is mainly about _________.A. the education of family responsibilityB. a united and happy familyC. a story of the father and his sonD. a lesson of doing dishes五、词与短语选择填空(本题共10分,每小题1分)71. But to his _______, they all agreed to go with him.72. _______ Mr. Wang and the passengers, the man was saved by the doctors in time.73. I think I sat in the same way for too long _______ moving.74. A lot of old people are _______.75. V olunteering here is a dream ________ for me.76. This group was set up to help _______ people.77. After six months of _______ with a dog at Animal Helpers, I was able to bring him home.78. I get such a strong feeling of _______ when I see the animals get better.79. We should listen to them and _______ them. 80. We can't _______ making a plan until tomorrow.71 surprise 72. Thanks to 73. without 74. lonely 75. come true76. disabled 77. training 78. satisfaction 79. care for 80. put off六、阅读填词Ever since I was a child, my mouth has caused me trouble. I’m not a bad person; I have a hard time l 81 when to keep my mouth closed.My mom has told me again and again, "Robert, your constant bad words are hurting me. If you continue to be this rude, you will get into big t 82 ."One day in English class I began working on my homework until I heard a classmate talking behind me. It was Nathaniel, talking to himself as u 83 .I said ever so nicely, "Nathaniel, would you be quiet?" Nathaniel continued talking to himself. I quickly shouted "Nathaniel, shut up!"For the next five minutes, we t 84 hurtful words back and forth at each other."At least I don’t have an ugly lazy eye like you!" I cried out.I knew this would upset him deep inside. It would hurt his f 85 and shut him up.What I said filled himwith anger. He tried to r 86 over my seat and grab me as he shouted, "That’s it! That’s it!"I was s 87 at his reaction, I sat back in my seat. Later on, we were taken to the teacher’s office.There, Mr. Black, our English teacher, asked us what m 88 most to us and made us discuss it. It wasn’t until then that I finally found that when I hurt someone physically, the wounds finally heal(痊愈) e 89 . but when I hurt someone with my words, sometimes the pain never goes away.At the end of discussion, I said sorry to Tom.When I went back to my room, I spent some time praying(祈祷). I began to consider how often what I said hurt others. But I believe that as I keep asking God to help me, he’ll tell me when to keep my mouth closed and it’ll make a big d 90 to my life.81.l_______82.t________83.u_______84.t________85.f________86.r_______87.s________ 88.m_______ 89.e________ 90.d________81 learning 82 trouble 83 usual 84 threw 85 feelings86 reach 87 surprised 88 mattered 89 easily 90 difference七、书面表达(本小题15分)1. Jenny在一家动物医院当志愿者。
