各种数学符号及读法汇总
数学符号读法大全
常用数学符号的读法格式如下：大写字母/小写字母/英文/标音/音标的中文读法/字母所代表的意思1 Α α alpha a：lf 阿尔法角度;系数2 Β βbeta bet 贝塔磁通系数；角度；系数3 Γ γ gamma ga:m 伽马电导系数(小写）4 Δ δ delta delt 德尔塔变动；密度；屈光度5 Ε ε epsilon ep`silon 伊普西龙对数之基数6 Ζ ζ zeta zat 截塔系数；方位角；阻抗;相对粘度;原子序数7 Ηη eta eit 艾塔磁滞系数；效率（小写）8 Θ θ thet θit 西塔温度；相位角9 Ι ι iot aiot 约塔微小,一点儿10 Κ κ kappa kap 卡帕介质常数11 ∧λlambda lambd 兰布达波长(小写）；体积12 Μμ mu mju 缪磁导系数；微(千分之一）；放大因数(小写）13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西离散型随机变量15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派圆周率=圆周÷直径=3.141617 Ρ ρ rho rou 肉电阻系数（小写）18 ∑ σ sigma`sigma西格马总和（大写)，表面密度；跨导（小写）19 Ττ tau tau 套时间常数20 Υ υ upsilon jup`silon 宇普西龙位移21 Φ φphi fai 佛爱磁通；角22 Χχ chi phai 西23 Ψ ψ psi psai 普西角速;介质电通量（静电力线）；角24 Ω ω omega o`miga 欧米伽欧姆(大写）；角速(小写）；角。
数学符号及读法大全(详细)
1数学符号及读法大全符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin yacos x y，余弦函数反函数在x处的值，即 x = cos yatan x y，正切函数反函数在x处的值，即 x = tan yacot x y，余切函数反函数在x处的值，即 x = cot yasec x y，正割函数反函数在x处的值，即 x = sec yacsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
下边界值写在其下部，上边界值写在其上部。
如j从1到100 的和可以表示成：。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积2 符号含义θvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
常用数学符号大全(注音及注解)
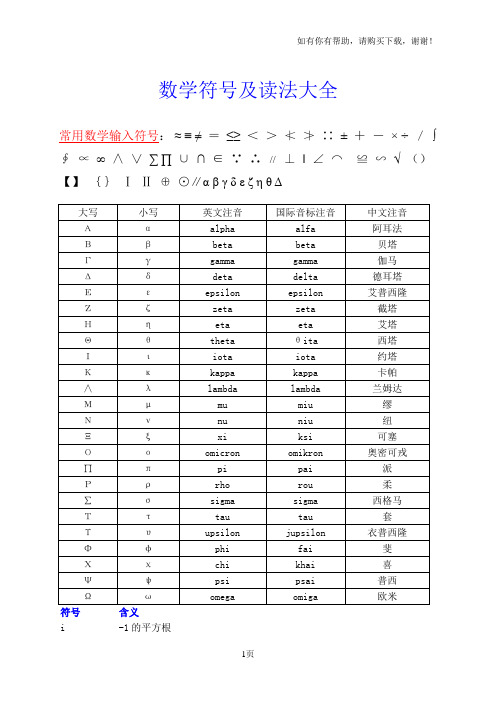
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－× ÷／∫∮∝∞∧∨∑∏∪∩∈∵∴//⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e x a^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
下边界值写在其下部，上边界值写在其上部。
如j从1到100 的和可以表示成：。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积θvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
数学符号及读法大全(详细)
数学符号及读法大全符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin yacos x y，余弦函数反函数在x处的值，即 x = cos yatan x y，正切函数反函数在x处的值，即 x = tan yacot x y，余切函数反函数在x处的值，即 x = cot yasec x y，正割函数反函数在x处的值，即 x = sec yacsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
下边界值写在其下部，上边界值写在其上部。
如j从1到100 的和可以表示成：。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积符号含义θvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
各种数学符号及读法大全
各种数学符号及读法大全数学是一门充满符号的科学，这些符号就像一种特殊的语言，帮助我们更简洁、准确地表达数学概念和进行运算。
下面就为大家介绍一些常见的数学符号及其读法。
一、基本运算符号1、加号（＋）：读作“加”，例如“2 ＋3”读作“二加三”。
2、减号（－）：读作“减”，比如“5 2”读作“五减二”。
3、乘号（×）：读作“乘”，像“4 × 5”读作“四乘五”。
在数学中，有时也会用“·”表示乘号，例如“3·2”，同样读作“三乘二”。
4、除号（÷）：读作“除以”，例如“6 ÷ 3”读作“六除以三”。
二、比较符号1、等于号（＝）：读作“等于”，比如“2 ＋ 3 ＝5”读作“二加三等于五”。
2、大于号（＞）：读作“大于”，例如“5 ＞3”读作“五大于三”。
3、小于号（＜）：读作“小于”，像“2 ＜4”读作“二小于四”。
4、大于等于号（≥）：读作“大于等于”，比如“x ≥ 5”读作“x 大于等于五”。
5、小于等于号（≤）：读作“小于等于”，例如“y ≤ 8”读作“y 小于等于八”。
三、括号1、小括号（）：通常读作“括号”，例如“（2 ＋ 3）× 4”读作“括号二加三括号乘四”。
2、中括号：读作“中括号”，像“ 5 （3 1）÷ 2”读作“中括号五减去括号三减一括号除以二”。
3、大括号｛｝：读作“大括号”，比如“｛ 2, 4, 6, 8 ｝”读作“大括号二，四，六，八”。
四、分数符号1、分数线（—）：例如“3/5”，读作“五分之三”。
分子在前，分母在后。
2、带分数：由整数部分和分数部分组成，例如“2 又1/3”，读作“二又三分之一”。
五、指数符号1、平方（²）：例如“5²”，读作“五的平方”。
2、立方（³）：像“2³”，读作“二的立方”。
3、多次方：比如“4 的 5 次方”写作“4^5”，读作“四的五次方”。
数学符号及读法大全
数学符号及读法大全一、基本符号及读法1. 加号（+）：读作“加”或“正”。
例如，2 + 3 读作“二加三”或“二正三”。
2. 减号（）：读作“减”或“负”。
例如，5 2 读作“五减二”或“五负二”。
3. 乘号（×）：读作“乘”。
例如，4 × 6 读作“四乘六”。
4. 除号（÷）：读作“除以”。
例如，8 ÷ 2 读作“八除以二”。
5. 等号（=）：读作“等于”。
例如，3 + 4 = 7 读作“三加四等于七”。
6. 不等号（≠）：读作“不等于”。
例如，5 ≠ 6 读作“五不等于六”。
7. 大于号（>）：读作“大于”。
例如，7 > 5 读作“七大于五”。
8. 小于号（<）：读作“小于”。
例如，3 < 8 读作“三小于八”。
9. 大于等于号（≥）：读作“大于等于”。
例如，x ≥ 5 读作“x大于等于五”。
10. 小于等于号（≤）：读作“小于等于”。
例如，y ≤ 10 读作“y小于等于十”。
二、指数与对数符号及读法1. 指数符号（^）：读作“的幂”。
例如，2^3 读作“二的三次幂”。
2. 对数符号（log）：读作“以为底的对数”。
例如，log₂8 读作“以二为底八的对数”。
三、集合符号及读法1. 属于符号（∈）：读作“属于”。
例如，3 ∈ {1, 2, 3} 读作“三属于集合{一、二、三}”。
2. 不属于符号（∉）：读作“不属于”。
例如，4 ∉ {1, 2, 3} 读作“四不属于集合{一、二、三}”。
3. 空集符号（∅）：读作“空集”。
例如，∅表示一个不包含任何元素的集合。
四、几何符号及读法1. 直线符号（→）：读作“直线”。
例如，AB → 表示直线AB。
2. 射线符号（⇀）：读作“射线”。
例如，AC ⇀表示射线AC。
3. 线段符号（|）：读作“线段”。
例如，BC | 表示线段BC。
4. 角符号（∠）：读作“角”。
例如，∠ABC 表示角ABC。
各种数学符号及读法大全
各种数学符号及读法大全数学是一门重要而有用的学科，它研究自然界中各种事物之间的数量、结构、变化以及空间关系等数量知识。
在数学中，为了简化语言表达，数学家们引用了大量的符号来表达和记载不同的含义，这类符号可以分为两类：一类是数学符号，这些符号仅用于表达数学思想，它们常常只会出现在数学课本里；另一类是数学符号的读法，它们是把不同的数学符号用文字来表达的语言，比如两个音节的读法，一般用来口头表达数学思想。
首先，让我们介绍一些常见的数学符号：1.号（+）：表示相加，它把两个或多个数字连在一起。
如a+b=c。
2.号（-）：表示减法，它把两个或多个数字的差值计算出来。
如a-b=c。
3. 乘号（×）：表示乘法，它把两个或多个数字相乘。
如a×b=c。
4.号（÷）：表示除法，它把一个数除以另一个数。
如a÷b=c。
5.号（=）：表示等于，它可以把两个或多个数字或表达式相等。
6.于号（：表示小于，它表示一个数字或表达式是另一个数字或表达式的小值。
7.于号（>）：表示大于，它表示一个数字或表达式是另一个数字或表达式的大值。
8.号（（））：表示括号，它可以把表达式分开，或者可以把表达式的优先级置高。
9.略号（…）：表示省略，它可以用来表示一个序列中的其余部分。
10.方根号（√）：表示平方根，它是一个数的平方根。
11.数线（-）：表示分数线，它是用来把分数的分子和分母分开的线。
12.分号（％）：表示百分号，它是一种表示百分比的符号。
13.和符号（Σ）：表示求和，它是把一系列值加起来求和的符号。
14.限符号（lim）：表示极限，它是用来表示函数的极限的符号。
15.件符号（∶）：表示条件，它是用来表示一个条件的符号。
16.度符号（∠）：把一个角分成两条对边，这两条对边连接在一起形成一个角度。
其次，我们介绍一些常见的数学符号的读法：1.号（+）：读作“加”。
2.号（-）：读作“减”。
常见数学符号的读法
一、常见数学符号的读法:α(阿而法)、β( 贝塔)、γ(伽马）、δ（德尔塔）、ε（艾普西龙）、ζ（截塔）、η（艾塔）、θ（西塔）、ι（约塔）、κ（卡帕）、λ（兰姆达）、μ（米尤）、ν（纽）、ξ（可系）、ο（奥密克戎）、π（派）、ρ （若）、σ （西格马）、τ （套）、υ （英文或拉丁字母）、φ（斐）、χ（喜）、ψ（普西））、ω（欧米伽）二、数字符号更全面：1. Α α alpha ,/ a:lf /,阿尔法角度；系数2.Β β beta ,/bet/, 贝塔磁通系数；角度；系数3. Γ γ gamma ,/ga:m/, 伽马电导系数（小写）4. Δ δ delta ,/delt/, 德尔塔变动；密度；屈光度5 .Ε ε epsilon ,/ep`silon /,伊普西龙对数之基数6 .Ζ ζ zeta,/ zat/, 截塔系数；方位角；阻抗；相对粘度；原子序数7 .Η η eta ,/eit /,艾塔磁滞系数；效率（小写）8. Θ θ thet,/ θit, 西塔温度；相位角9 .Ι ι iot ,/aiot/, 约塔微小，一点儿10 .Κ κ kappa ,/kap/, 卡帕介质常数11 .∧ λ lambda lambd 兰布达波长（小写）；体积12.. Μ μ mu ,/mju /,缪磁导系数；微（千分之一）；放大因数（小写）13 .Ν ν nu ,/nju /,纽磁阻系数14.Ξ ξ xi,/ksi/, 克西15.Ο ο omicron omik`ron 奥密克戎16.∏ π pi ,/pai /,派圆周率=圆周÷直径=3.141617 .Ρ ρ rho,/ rou /,肉电阻系数（小写）17.∑ σ sigma ,/sigma /,西格马总和（大写），表面密度；跨导（小写）19.Τ τ tau ,/tau /,套时间常数20.Υ υ upsilon ,/jup`silon /,宇普西龙位移21.Φ φ phi,/fai /,佛爱磁通；角22.Χ χ chi,/phai/,西23.Ψ ψ psi ,/psai/, 普西角速；介质电通量（静电力线）；角24.Ω ω omega ,/o`miga /,欧米伽欧姆（大写）；角速（小写）；角三、希腊字母读法Αα：阿尔法Alpha Ββ：贝塔BetaΓγ：伽玛Gamma Δδ：德尔塔 Delte Εε：艾普西龙 Epsilon ζ ：捷塔 Zeta Ζη：依塔 Eta Θθ：西塔 Theta Ιι：艾欧塔 Iota Κκ：喀帕Kappa ∧λ：拉姆达LambdaΜμ：缪Mu Νν：拗 NuΞξ：克西 Xi Οο：欧麦克轮 Omicron ∏π：派 Pi Ρρ：柔 Rho ∑σ：西格玛 Sigma Ττ：套 Tau Υυ：宇普西龙 Upsilon Φφ：fai Phi Χχ：器 Chi Ψψ：普赛 Psi Ωω：欧米伽 Omega。
数学符号及读法大全
数学符号及读法大全常用数学输入符号：≈ ≡ ≠ ＝≤≥ ＜＞≮ ≯ ∷ ± ＋－× ÷ ／∫ ∮ ∝ ∞ ∧ ∨ ∑ ∏ ∪ ∩ ∈ ∵ ∴ ⊥ ‖ ∠ ⌒≌ ∽ √（）【】｛｝Ⅰ Ⅱ ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数； b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
(完整版)数学符号及读法大全
数学符号大全数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-：minus（negative负的）*：multiplied by÷：divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥：greater than or equal to∞：infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b： a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞：approches infinityx2:x squarex3:x cube√￣x:the square root of x3√￣x:the cube root of x3‰：three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号（理科符号）——运算符号1.基本符号：＋－ × ÷（／）2.分数号：／3.正负号：±4.相似全等：∽≌5.因为所以：∵∴6.判断类：＝≠＜≮（不小于）＞≯（不大于）7.集合类：∈（属于）∪（并集）∩（交集）8.求和符号：∑9.n次方符号：¹（一次方） ²（平方） ³（立方）⁴（4次方）ⁿ（n次方）10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":￢12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:｜21.弧:⌒22.圆:⊙11.或与非的"非":￢12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:｜21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。
数学符号及读法大全
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin yacos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
高中数学符号读法大全及意义
高中数学符号读法大全及意义一、基本数学符号1. +：加号，表示加法运算。
2. -：减号，表示减法运算。
3. ×：乘号，表示乘法运算。
4. ÷：除号，表示除法运算。
5. =：等于号，表示相等关系。
6. ≠：不等号，表示不相等关系。
7. <：小于号，表示小于关系。
8. >：大于号，表示大于关系。
9. ≤：小于等于号，表示小于等于关系。
10. ≥：大于等于号，表示大于等于关系。
二、集合符号1. ∈：属于，表示一个元素属于某个集合。
2. ∉：不属于，表示一个元素不属于某个集合。
3. ∪：并集，表示所有在某一个以上的集合中出现的元素的新集合。
4. ∩：交集，表示属于所有给定集合的元素的新集合。
5. ⊆：包含关系（子集），表示一个集合包含于另一个集合。
6. ⊇：包含关系（超集），表示一个集合包含另一个集合。
7. ∅：空集，表示没有任何元素的集合。
三、数学函数符号1. f(x)：函数符号，表示自变量为x时，函数的值。
2. g(x)：函数符号，表示自变量为x时，函数的值。
3. h(x)：函数符号，表示自变量为x时，函数的值。
4. lim：极限符号，表示函数在逼近某个数值时的极限。
5. sin：正弦函数符号，表示角度的正弦值。
6. cos：余弦函数符号，表示角度的余弦值。
7. tan：正切函数符号，表示角度的正切值。
8. log：对数函数符号，表示以某个底数为底的对数函数。
四、微积分符号1. dy/dx：导数符号，表示某个函数在某点的导数。
2. ∫：积分符号，表示函数在某个区间上的积分值。
3. dx：微分符号，表示微分变量。
4. Δx：增量符号，表示微分变量的增量。
五、几何图形符号1. ∆ABC：三角形符号，表示三条边分别为AB、BC和CA的三角形。
2. △DEF：三角形符号，表示三条边分别为DE、EF和FD的三角形。
3. ∠：角符号，表示两条射线之间的角度。
4. ⊥：垂直符号，表示两条直线垂直。
各种数学符号及读法大全
各种数学符号及读法大全常用数学输入符号：≈≡ ≠≤≥ V > < > : : ± +—×÷∕∫ 0X∞ ∧∨∑∏U∩∈••••••丄Il ∠c^s√()【】{} I π®龙格罗伊公式输入符号≈≡≠ ≤≥V > V：：±+ 一×÷∕ ∫OC∞∧∨∑∏U ∩ ∈T ••丄∠ c Θ也s √ 数学符号(理科符号)一一运算符号1.基本符号：+ —× ÷ ( ∕ )3.正负号：±4.相似全等：S 也5.因为所以：6.判断类：=≠ V <（不小于）> >不大于）集）7.集合类：∈（属于）U （并集）∩（交8.求和符号：∑9. n 次方符号：1（一次方）2（平方）3（立方）?（4 次方）?（n 次方）10. 下角标:? ?? ? （如:A?B?C?D?）11. 或与非的"非":「12. 导数符号（备注符号）：‘〃13. 度：°C14. 任意：?15. 推出号：?16. 等价号：?17. 包含被包含：? ? ? ?18. 导数：∫?19. 箭头类:/ / ∖∖↑J? ? ↑J→J20. 绝对值：I21. 弧：C22. 圆：O23. 平均数-，ba 拔数学符号不好打，复制一下吧1 几何符号丄/∕∠-O≡B△2 代数符号X ∧∨∫≠ ≤≥≈∞× ÷ √ ±4 集合符号∪ ∩∈&; §ΓΔ ΘΛΞΟ ΠΣΦIn IV5 特殊符号 ∑ ∏ （圆周率）6 推理符号 |a| ∩ ∪ ≠ ≡ ± ≥//∧∨①②③⑤⑥⑦ ⑧⑨βγδ εζηθ κλμνξο π ρτυii iii iv V Vi血 ixX∟∠I // ∧ ∨ ∩ ∪∫: ：：S ≈B =≠≡≤≥W仝< > ? O 丄C指数0123：o123符号意义∞无穷大PI 圆周率|x| 函数的绝对值∪集合并∩集合交≥大于等于≤小于等于≡恒等于或同余ln(x) 自然对数lg(x) 以2 为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 取整函数x mod y 求余数{x} 小数部分x - floor(x)∫ f(x) δx 不定积分∫ [a:b]f(x) δa到b的定积分[P] P为真等于1否则等于O∑[1 ≤k ≤n]f对n进行求和，可以拓广至很多情况如：∑[n is prime][n < 1O]f(n)∑∑[1 ≤i ≤j ≤n]n^2lim f(x) (x->?) 求极限f(z) f 关于z 的m 阶导函数C(n:m) 组合数，n 中取mP(n:m) 排列数m|n m 整除nm⊥ n m 与n 互质#A 集合A 中的元素个数ceil(x) 取整函数a ∈A a 属于集合A#A 集合A 中的元素个数。
(完整版)数学符号及读法大全,推荐文档
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷ ± ＋－× ÷ ／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa阿耳法Ββbeta beta贝塔Γγgamma gamma伽马Δδdeta delta德耳塔Εεepsilon epsilon艾普西隆Ζζzeta zeta截塔Ηηeta eta艾塔Θθthetaθita西塔Ιιiota iota约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μμmu miu缪Ννnu niu纽Ξξxi ksi可塞Οοomicron omikron奥密可戎∏πpi pai派Ρρrho rou柔∑σsigma sigma西格马Ττtau tau套Υυupsilon jupsilon衣普西隆Φφphi fai斐Χχchi khai喜Ψψpsi psai普西Ωωomega omiga欧米符号含义i-1的平方根f(x)函数f在自变量x处的值sin(x)在自变量x处的正弦函数值exp(x)在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax同a^xlogba以b为底a的对数；blogba = acos x在自变量x处余弦函数的值tan x其值等于sin x/cos xcot x余切函数的值或cos x/sin xsec x正割含数的值，其值等于1/cos xcsc x余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin yacos x y，余弦函数反函数在x处的值，即x = cos yatan x y，正切函数反函数在x处的值，即x = tan yacot x y，余切函数反函数在x处的值，即x = cot yasec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值Σ表示求和，通常是某项指数。
数学符号及读法大全
数学符号及读法大全第一部分：基本数学符号1. 加号 (+)读作：加2. 减号 ()读作：减3. 乘号(×)读作：乘4. 除号(÷)读作：除5. 等号 (=)读作：等于6. 不等号(≠)读作：不等于7. 大于号 (>)读作：大于8. 小于号 (<)读作：小于9. 大于等于号(≥)读作：大于等于10. 小于等于号(≤)读作：小于等于467. 静谧之海468. 翱翔天际469. 晨曦微光470. 暮色温柔471. 琴瑟和鸣472. 碧波荡漾473. 风轻云淡474. 星河滚烫475. 雨后初晴476. 月下独酌477. 寂静之声478. 花前月下479. 时光荏苒480. 笑忘书481. 梦开始的地方482. 时光旅行者483. 漫步星河484. 风起云涌485. 雨落花飞4. 月影斑驳487. 晨光熹微488. 暮色苍茫489. 静谧之夜490. 翱翔天际491. 晨曦微光492. 暮色温柔493. 琴瑟和鸣494. 碧波荡漾495. 风轻云淡496. 星河滚烫497. 雨后初晴498. 月下独酌499. 寂静之声500. 花前月下501. 时光荏苒502. 笑忘书503. 梦开始的地方504. 时光旅行者505. 漫步星河506. 风起云涌507. 雨落花飞508. 月影斑驳509. 晨光熹微510. 暮色苍茫511. 静谧之夜512. 翱翔天际513. 晨曦微光514. 暮色温柔515. 琴瑟和鸣516. 碧波荡漾517. 风轻云淡518. 星河滚烫519. 雨后初晴520. 月下独酌521. 寂静之声522. 花前月下523. 时光荏苒524. 笑忘书525. 梦开始的地方526. 时光旅行者527. 漫步星河528. 风起云涌529. 雨落花飞530. 月影斑驳531. 晨光熹微532. 暮色苍茫533. 静谧之夜534. 翱翔天际535. 晨曦微光536. 暮色温柔537. 琴瑟和鸣538. 碧波荡漾539. 风轻云淡540. 星河滚烫541. 雨后初晴542. 月下独酌543. 寂静之声544. 花前月下545. 时光荏苒546. 笑忘书547. 梦开始的地方548. 时光旅行者549. 漫步星河550. 风起云涌551. 雨落花飞552. 月影斑驳553. 晨光熹微554. 暮色苍茫555. 静谧之夜556. 翱翔天际557. 晨曦微光558. 暮色温柔559. 琴瑟和鸣560. 碧波荡漾561. 风轻云淡562. 星河滚烫563. 雨后初晴565. 寂静之声566. 花前月下567. 时光荏苒568. 笑忘书569. 梦开始的地方570. 时光旅行者571. 漫步星河572. 风起云涌573. 雨落花飞574. 月影斑驳575. 晨光熹微576. 暮色苍茫577. 静谧之夜578. 翱翔天际579. 晨曦微光580. 暮色温柔581. 琴瑟和鸣582. 碧波荡漾583. 风轻云淡584. 星河滚烫585. 雨后初晴5. 月下独酌587. 寂静之声589. 时光荏苒590. 笑忘书591. 梦开始的地方592. 时光旅行者593. 漫步星河594. 风起云涌595. 雨落花飞596. 月影斑驳597. 晨光熹微598. 暮色苍茫599. 静谧之夜600. 翱翔天际601. 晨曦微光602. 暮色温柔603. 琴瑟和鸣604. 碧波荡漾605. 风轻云淡606. 星河滚烫607. 雨后初晴608. 月下独酌609. 寂静之声610. 花前月下611. 时光荏苒612. 笑忘书613. 梦开始的地方614. 时光旅行者615. 漫步星河616. 风起云涌617. 雨落花飞618. 月影斑驳619. 晨光熹微620. 暮色苍茫621. 静谧之夜622. 翱翔天际623. 晨曦微光624. 暮色温柔625. 琴瑟和鸣626. 碧波荡漾627. 风轻云淡628. 星河滚烫629. 雨后初晴630. 月下独酌631. 寂静之声632. 花前月下633. 时光荏苒634. 笑忘书635. 梦开始的地方636. 时光旅行者637. 漫步星河638. 风起云涌639. 雨落花飞640. 月影斑驳641. 晨光熹微642. 暮色苍茫643. 静谧之夜644. 翱翔天际645. 晨曦微光646. 暮色温柔647. 琴瑟和鸣648. 碧波荡漾649. 风轻云淡650. 星河滚烫651. 雨后初晴652. 月下独酌653. 寂静之声654. 花前月下655. 时光荏苒656. 笑忘书657. 梦开始的地方658. 时光旅行者659. 漫步星河660. 风起云涌661. 雨落花飞662. 月影斑驳663. 晨光熹微664. 暮色苍茫665. 静谧之夜666. 翱翔天际667. 晨曦微光668. 暮色温柔669. 琴瑟和鸣670. 碧波荡漾671. 风轻云淡672. 星河滚烫673. 雨后初晴674. 月下独酌675. 寂静之声676. 花前月下677. 时光荏苒678. 笑忘书679. 梦开始的地方680. 时光旅行者681. 漫步星河682. 风起云涌683. 雨落花飞684. 月影斑驳685. 晨光熹微6. 暮色苍茫687. 静谧之夜688. 翱翔天际689. 晨曦微光690. 暮色温柔691. 琴瑟和鸣692. 碧波荡漾693. 风轻云淡694. 星河滚烫695. 雨后初晴696. 月下独酌697. 寂静之声698. 花前月下699. 时光荏苒700. 笑忘书701. 梦开始的地方702. 时光旅行者703. 漫步星河704. 风起云涌705. 雨落花飞706. 月影斑驳707. 晨光熹微708. 暮色苍茫709. 静谧之夜710. 翱翔天际711. 晨曦微光712. 暮色温柔713. 琴瑟和鸣714. 碧波荡漾715. 风轻云淡716. 星河滚烫717. 雨后初晴718. 月下独酌719. 寂静之声720. 花前月下721. 时光荏苒722. 笑忘书723. 梦开始的地方724. 时光旅行者725. 漫步星河726. 风起云涌727. 雨落花飞728. 月影斑驳729. 晨光熹微730. 暮色苍茫731. 静谧之夜732. 翱翔天际733. 晨曦微光734. 暮色温柔735. 琴瑟和鸣736. 碧波荡漾737. 风轻云淡738. 星河滚烫739. 雨后初晴740. 月下独酌741. 寂静之声742. 花前月下743. 时光荏苒744. 笑忘书745. 梦开始的地方746. 时光旅行者747. 漫步星河748. 风起云涌749. 雨落花飞750. 月影斑驳751. 晨光熹微752. 暮色苍茫753. 静谧之夜754. 翱翔天际755. 晨曦微光756. 暮色温柔757. 琴瑟和鸣758. 碧波荡漾759. 风轻云淡760. 星河滚烫761. 雨后初晴762. 月下独酌763. 寂静之声764. 花前月下765. 时光荏苒766. 笑忘书767. 梦开始的地方768. 时光旅行者769. 漫步星河770. 风起云涌771. 雨落花飞772. 月影斑驳773. 晨光熹微774. 暮色苍茫775. 静谧之夜776. 翱翔天际777. 晨曦微光778. 暮色温柔779. 琴瑟和鸣780. 碧波荡漾781. 风轻云淡782. 星河滚烫783. 雨后初晴784. 月下独酌785. 寂静之声7. 花前月下787. 时光荏苒788. 笑忘书789. 梦开始的地方790. 时光旅行者791. 漫步星河792. 风起云涌793. 雨落花飞794. 月影斑驳795. 晨光熹微796. 暮色苍茫797. 静谧之夜798. 翱翔天际799. 晨曦微光800. 暮色温柔801. 琴瑟和鸣802. 碧波荡漾803. 风轻云淡804. 星河滚烫805. 雨后初晴806. 月下独酌807. 寂静之声808. 花前月下809. 时光荏苒810. 笑忘书811. 梦开始的地方812. 时光旅行者813. 漫步星河814. 风起云涌815. 雨落花飞816. 月影斑驳817. 晨光熹微818. 暮色苍茫819. 静谧之夜820. 翱翔天际821. 晨曦微光822. 暮色温柔823. 琴瑟和鸣824. 碧波荡漾825. 风轻云淡826. 星河滚烫827. 雨后初晴829. 寂静之声830. 花前月下831. 时光荏苒832. 笑忘书833. 梦开始的地方834. 时光旅行者835. 漫步星河836. 风起云涌837. 雨落花飞838. 月影斑驳839. 晨光熹微840. 暮色苍茫841. 静谧之夜842. 翱翔天际843. 晨曦微光844. 暮色温柔845. 琴瑟和鸣846. 碧波荡漾847. 风轻云淡848. 星河滚烫849. 雨后初晴850. 月下独酌851. 寂静之声853. 时光荏苒854. 笑忘书855. 梦开始的地方856. 时光旅行者857. 漫步星河858. 风起云涌859. 雨落花飞0. 月影斑驳1. 晨光熹微2. 暮色苍茫3. 静谧之夜4. 翱翔天际5. 晨曦微光6. 暮色温柔7. 琴瑟和鸣8. 碧波荡漾9. 风轻云淡870. 星河滚烫871. 雨后初晴872. 月下独酌873. 寂静之声874. 花前月下875. 时光荏苒876. 笑忘书877. 梦开始的地方878. 时光旅行者879. 漫步星河880. 风起云涌881. 雨落花飞882. 月影斑驳883. 晨光熹微884. 暮色苍茫885. 静谧之夜8. 翱翔天际887. 晨曦微光888. 暮色温柔889. 琴瑟和鸣890. 碧波荡漾891. 风轻云淡892. 星河滚烫893. 雨后初晴894. 月下独酌895. 寂静之声896. 花前月下897. 时光荏苒898. 笑忘书899. 梦开始的地方900. 时光旅行者901. 漫步星河902. 风起云涌903. 雨落花飞904. 月影斑驳905. 晨光熹微906. 暮色苍茫907. 静谧之夜908. 翱翔天际909. 晨曦微光910. 暮色温柔911. 琴瑟和鸣912913. 紫藤花下914. 雪域之鹰915. 翠竹清风916. 风华正茂917. 水墨青花918. 晨曦暮雪919. 琴韵墨香920. 梦里江南921. 花影轻舞922. 时光流转923. 笑忘江湖924. 梦开始的地方925. 时光旅行者926. 漫步星河927. 风起云涌928. 雨落花飞929. 月影斑驳930. 晨光熹微931. 暮色苍茫932. 静谧之夜933. 翱翔天际934. 晨曦微光935. 暮色温柔936. 琴瑟和鸣937. 碧波荡漾938. 风轻云淡939. 星河滚烫940. 雨后初晴941. 月下独酌942. 寂静之声943. 花前月下944. 时光荏苒945. 笑忘书946. 梦开始的地方947. 时光旅行者948. 漫步星河949. 风起云涌950. 雨落花飞951. 月影斑驳952. 晨光熹微953. 暮色苍茫954. 静谧之夜955. 翱翔天际956. 晨曦微光957. 暮色温柔958. 琴瑟和鸣959. 碧波荡漾960. 风轻云淡961. 星河滚烫962. 雨后初晴963. 月下独酌964. 寂静之声965. 花前月下966. 时光荏苒967. 笑忘书968. 梦开始的地方969. 时光旅行者970. 漫步星河971. 风起云涌972. 雨落花飞973. 月影斑驳974. 晨光熹微975. 暮色苍茫976. 静谧之夜977. 翱翔天际978. 晨曦微光979. 暮色温柔980. 琴瑟和鸣981. 碧波荡漾982. 风轻云淡983. 星河滚烫984. 雨后初晴985. 月下独酌9. 寂静之声987. 花前月下988. 时光荏苒989. 笑忘书990. 梦开始的地方991. 时光旅行者992. 漫步星河993. 风起云涌994. 雨落花飞995. 月影斑驳996. 晨光熹微997. 暮色苍茫998. 静谧之夜999. 翱翔天际1000. 晨曦微光。
数学符号及读法大全
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot yasec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
数学符号及读法大全
数学符号及读法大全数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√ （）【】｛｝ⅠⅡ⊕⊙∥α β γ δ ε ζ公式输入符号≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+: plus(positive正的)-：minus（negative负的）*：multiplied by÷：divided by=: be equal to≈: be approximately equal to(): round brackets(parenthess)[]: square brackets{}: braces∵: because∴: therefore≤: less than or equal to≥：greater than or equal to∞：infinityLOGnX: logx to the base nxn: the nth power of xf(x): the function of xdx: diffrencial of xx+y: x plus y(a+b): bracket a plus b bracket closeda=b: a equals ba≠b：a isn't equalto ba>b : a is greater than ba>>b: a is much greater than ba≥b: ais greater than or equal to bx→∞：approches infinityx2: x squarex3: x cube√￣x: the squareroot of x3√￣x: the cube root of x3‰：three peimilln∑i=1xi: the summation of x where x goes from1to n n∏i=1xi: the product of x sub i where igoesfrom 1to n ∫ab: integral betweens a and b数学符号（理科符号）——运算符号1.基本符号：＋－× ÷（／）2.分数号：／3.正负号：±4.相似全等：∽≌5.因为所以：∵∴6.判断类：＝≠ ＜≮（不小于）＞≯（不大于）7.集合类：∈（属于）∪（并集）∩（交集）8.求和符号：∑9.n次方符号：¹（一次方）²（平方）³（立方）⁴（4次方）ⁿ（n次方）10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":￢12.导数符号(备注符号):′ 〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫ ∬19.箭头类:↗↙↖↘↑ ↓ ↔ ↕ ↑ ↓ → ←20.绝对值:｜21.弧:⌒22.圆:⊙11.或与非的"非":￢12.导数符号(备注符号):′ 〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫ ∬19.箭头类:↗↙↖↘↑ ↓ ↔ ↕ ↑ ↓ → ←20.绝对值:｜21.弧:⌒22.圆:⊙α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ωΑ Β Γ Δ Ε Ζ Η Θ Ι Κ ∧Μ Ν Ξ Ο ∏ Ρ ∑ Τ Υ Φ Χ Ψ Ωа б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ъы ь э ю яА Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю ЯΔ。
数学符号及读法大全
数学符号及读法大全数学，这门古老而精深的学科，以其独特的语言和符号系统，描绘出世界的规律与秩序。
在这门科学中，符号与标记如同密码，维系着数学世界的沟通与交流。
下面，我们将一起探索这些数学符号的读法及意义。
1、阿拉伯数字：这是我们日常生活中最为熟悉的数学符号。
从1到9，这些数字在数学中有着广泛的应用。
它们的读法与我们的日常用语基本一致，例如：1读作“一”，2读作“二”，以此类推。
2、十进制位值制：在数学中，我们用逗号或短横线将数字分隔开，表示其十进制位值。
例如，123表示为“一百二十三”。
3、小数：小数点左边的数字表示整数部分，右边的数字表示小数部分。
例如，1.23读作“一点二三”。
4、百分数：百分数是一种方便的表示比率的方式。
例如，50%读作“百分之五十”。
5、加号与减号：加号（+）表示增加或合并，减号（-）表示减少或排除。
例如，1+2读作“一加上二”，2-1读作“二减去一”。
6、乘号与除号：乘号（×）表示相乘，除号（÷）表示相除。
例如，2×3读作“二乘以三”，4÷2读作“二除以四”。
7等于号：等于号（=）表示两个数量相等或等价。
例如，2=2读作“二等于二”。
8、大于号与小于号：大于号（>）表示左边的数大于右边的数，小于号（<）表示左边的数小于右边的数。
例如，3>2读作“三大于二”，2<3读作“二小于三”。
9等价符号：等价符号（≌）表示两个形状、大小完全相同的图形或物体。
例如，△ABC≌△DEF读作“三角形ABC全等于三角形DEF”。
10、不等号：不等号（≠）表示两个数量不相等或不等价。
例如，2≠3读作“二不等于三”。
11、约等于号：约等于号（≈）表示两个数量近似相等。
例如，π≈3.14读作“π约等于三点一四”。
12、根号：根号（√）表示一个数的算术平方根。
例如，√4读作“根号四”。
13、对称轴：对称轴（l）表示一个图形关于某一条直线对称。
数学符号及其读法大全很实用
一些数学符号的读音电工电子2009-09-09 07:53:10 阅读1604 评论3 字号：大中小1 Ααalpha a:lf 阿尔法角度；系数2 Ββbeta bet 贝塔磁通系数；角度；系数3 Γγgamma ga:m 伽马电导系数（小写）4 Δδdelta delt 德尔塔变动；密度；屈光度5 Εεepsilon ep`silon 伊普西龙对数之基数6 Ζζzeta zat 截塔系数；方位角；阻抗；相对粘度；原子序数7 Ηηeta eit 艾塔磁滞系数；效率（小写）8 Θθthet θit西塔温度；相位角9 Ιιiot aiot 约塔微小，一点儿10 Κκkappa kap 卡帕介质常数11 ∧λlambda lambd 兰布达波长（小写）；体积12 Μμmu mju 缪磁导系数；微（千分之一）；放大因数（小写）13 Ννnu nju 纽磁阻系数14 Ξξxi ksi 克西15 Οοomicron omik`ron 奥密克戎16 ∏πpi pai 派圆周率=圆周÷直径=3.141617 Ρρrho rou 肉电阻系数（小写）18 ∑σsigma `sigma 西格马总和（大写），表面密度；跨导（小写）19 Ττtau tau 套时间常数20 Υυupsilon jup`silon 宇普西龙位移21 Φφphi fai 佛爱磁通；角22 Χχchi phai 西23 Ψψpsi psai 普西角速；介质电通量（静电力线）；角24 Ωωomega o`miga 欧米伽欧姆（大写）；角速（小写）；角希腊字母读法Αα：阿尔法AlphaΒβ：贝塔BetaΓγ：伽玛GammaΔδ：德尔塔DelteΕε：艾普西龙Epsilonζ:捷塔ZetaΖη：依塔EtaΘθ：西塔ThetaΙι：艾欧塔IotaΚκ：喀帕Kappa∧λ：拉姆达LambdaΜμ：缪MuΝν：拗NuΞξ：克西XiΟο：欧麦克轮Omicron∏π：派PiΡρ：柔Rho∑σ：西格玛SigmaΤτ：套TauΥυ：宇普西龙UpsilonΦφ：fai PhiΧχ：器ChiΨψ：普赛PsiΩω：欧米伽Omega希腊字母怎么打打开Office文档之后，在你需要输入希腊字母的时候，先将输入法切换为英文状态，然后同时按下三个键Ctrl+Shift+Q ，工具栏上的“字体”就会发生变化此刻，你再对照下表输入a,b,c……即可得到您想要的希腊字母。
常用数学符号大全(注音及注解)
数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≦≧∷±＋－× ÷／∫∬∝∞∡∢∑∏∪∩∈∮∭//≩‖∟≪≌∽√（）【】｛｝ⅠⅡ⊕≨∠αβγδεδεζΓi -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同 a^xlog b a 以b为底a的对数； b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yζ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。
下边界值写在其下部，上边界值写在其上部。
如j从1到100 的和可以表示成：。
这表示1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积ζvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式u w在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
18.导数:∫∬
19.箭头类:↗ ↙ ↖ ↘ ↑ ↓↔↕↑ ↓ → ←
20.绝对值:｜
21.弧:⌒
22.圆:⊙
23.平均数-，ba拔
英文注音
国际音标注音
中文注音
Α
α
alpha
alfa
阿耳法
Β
β
beta
beta
贝塔
Γ
γ
gamma
gamma
伽马
Δ
δ
deta
delta
德耳塔
Ε
ε
epsilon
epsilon
艾普西隆
Ζ
ζ
zeta
zeta
截塔
Η
η
eta
eta
艾塔
Θ
θ
theta
θita
西塔
Ι
ι
iota
iota
约塔
Κ
κ
kappa
kappa
卡帕
∧
7.集合类：∈（属于） ∪（并集） ∩（交集）
8.求和符号：∑
9.n次方符号：¹（一次方） ²（平方） ³（立方）⁴（4次方）ⁿ（n次方）
10.下角标:₁₂₃₄(如:A₁B₂C₃D₄)
11.或与非的"非":￢
12.导数符号(备注符号):′ 〃
13.度:° ℃
14.任意:∀
15.推出号:⇒
16.等价号:⇔
λ
lambda
lambda
兰姆达缪
Ν
ν
nu
niu
纽
Ξ
ξ
xi
ksi
可塞
Ο
ο
omicron
omikron
奥密可戎
∏
π
pi
pai
派
Ρ
ρ
rho
rou
柔
∑
σ
sigma
sigma
西格马
Τ
τ
tau
tau
套
Υ
υ
upsilon
jupsilon
衣普西隆
Φ
φ
phi
fai
斐
Χ
χ
chi
khai
喜
Ψ
ψ
psi
psai
普西
Ω
ω
omega
omiga
欧米
公式输入符号
≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√
数学符号（理科符号）——运算符号
1.基本符号：＋ － × ÷（／）
2.分数号：／
3.正负号：±
4.相似全等：∽ ≌
5.因为所以：∵ ∴
6.判断类：＝ ≠ ＜ ≮（不小于） ＞ ≯（不大于）
各种数学符号及读法大全
时间：2012-12-03
字体：小中大
常用数学输入符号： ≈ ≡ ≠ ＝ ≤≥ ＜ ＞ ≮ ≯ ∷ ± ＋ － × ÷ ／ ∫ ∮ ∝ ∞ ∧ ∨ ∑ ∏ ∪ ∩ ∈ ∵ ∴ ⊥ ‖ ∠ ⌒ ≌ ∽ √ （） 【】｛｝ Ⅰ Ⅱ ⊕ ⊙∥α β γ δ ε ζ η θ Δ
大写
小写