中考数学压轴题解题策略:线段和差最值的存在性问题
一次函数综合—线段和差、存在性问题解析
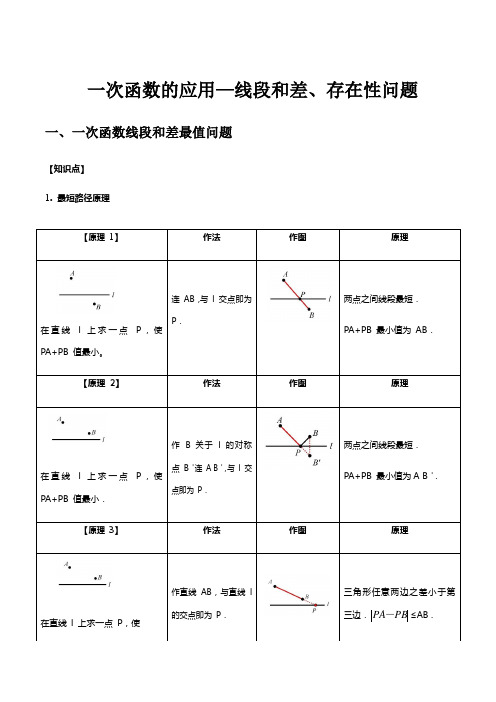
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P,使PA+PB 值最小。
连AB,与l 交点即为P.两点之间线段最短.PA+PB 最小值为AB.【原理2】作法作图原理在直线l 上求一点P,使PA+PB 值最小.作 B 关于l 的对称点B'连A B',与l 交点即为P.两点之间线段最短.PA+PB 最小值为A B'.【原理3】作法作图原理在直线l 上求一点P,使作直线AB,与直线l的交点即为P.三角形任意两边之差小于第三边.≤AB .PBPA-(1)求线段和最小时动点坐标或直线解析式; (2)求三角形周长最小值;(3)求线段差最大时点的坐标或直线解析式。
3. 口诀:“和小异,差大同”(一)一次函数线段和最小值问题【例题讲解】★★☆例题1.在平面直角坐标系xOy 中,y 轴上有一点P ,它到点(4,3)A ,(3,1)B 的距离之和最小,则点P 的坐标是( ) A .(0,0)B .4(0,)7C .5(0,)7D .4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ,使的值最大 .作 B 关于 l 的对称点 B '作直线 A B ',与 l 交点即为 P .三角形任意两边之差小于第三边.≤A B ' .PB PA -PB PA -PB PA -【解析】解:作A 关于y 轴的对称点C ,连接BC 交y 轴于P ,则此时AP PB +最小,即此时点P 到点A 和点B 的距离之和最小,(4,3)A ,(4,3)C ∴-,设直线CB 的解析式是y kx b =+,把C 、B 的坐标代入得:3413k bk b =-+⎧⎨-=+⎩,解得:47k =-,57b =,4577y x ∴=-+,把0x =代入得:57y =, 即P 的坐标是5(0,)7,故选:C .【备注】本题考查了轴对称-最短路线问题,一次函数的解析式,坐标与图形性质等知识点,关键是能画出P 的位置,题目比较典型,是一道比较好的题目.★★☆练习1.如图,在平面直角坐标系中,已知点(2,3)A ,点(2,1)B -,在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是 .【答案】(1,0)-【解析】解:作A 关于x 轴的对称点C ,连接BC 交x 轴于P ,则此时AP BP +最小,A 点的坐标为(2,3),B 点的坐标为(2,1)-,(2,3)C ∴-,设直线BC 的解析式是:y kx b =+,把B 、C 的坐标代入得:2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩.即直线BC 的解析式是1y x =--,当0y =时,10x --=,解得:1x =-,P ∴点的坐标是(1,0)-.故答案为:(1,0)-.【备注】本题考查了一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,轴对称-最短路线问题的应用,关键是能找出P 点,题目具有一定的代表性,难度适中.★★☆练习2.如图,直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点,以线段AB 为边在第一象限内作正方形ABCD .若点P 为x 轴上的一个动点,求当PC PD +的长最小时点P 的坐标.【答案】详见解析【解析】解:直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点,则点A 、B 的坐标分别为:(0,3),(4,0),如图所示,过点C 作CH x ⊥轴交于点H ,90ABO BAO ∠+∠=︒,90ABO CBH ∠+∠=︒,CBH BAO ∴∠=∠,又90AOB CHB ∠=∠=︒,AB BC =,()AOB BHC AAS ∴∆≅∆,4CH OB ∴==,3HB OA ==,故点(7,4)C ,同理可得点(3,7)D ,确定点C 关于x 轴的对称点(7,4)C '-,连接C D '交x 轴于点P ,则此时PC PD +的长最小,将点C '、D 的坐标代入一次函数表达式并解得: 直线CD 的表达式为:116144y x =-+, 当0y =时,6111x =,故点61P,0).(11【备注】本题考查的是一次函数上坐标点的特征,涉及到点的对称性、正方形性质等,本题的难点在于:通过证明三角形全等,确定点C、D的坐标.★★☆例题2.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,3OB=,D为边OB的中点,若E为x轴上的一个动点,当CDE∆的周长最小时,求点E OA=,4的坐标()A.(3,0)-B.(1,0)C.(0,0)D.(3,0)【答案】B【解析】解:如图,作点D关于x轴的对称点D',连接CD'与x轴交于点E,连接DE.若在边OA上任取点E'与点E不重合,连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+,可知CDE∆的周长最小.OB=,D为边OB的中点,42∴=,OD∴,(0,2)D在矩形OACB 中,3OA =,4OB =,D 为OB 的中点,3BC ∴=,2D O DO '==,6D B '=,//OE BC ,Rt ∴△D OE Rt '∽△D BC ',∴OE D OBC D B '=' 即236OE = 1OE =,∴点E 的坐标为(1,0)故选:B .【备注】此题主要考查轴对称--最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是三角形两边之和大于第三边.★★☆练习1.如图,在平面直角坐标系中,点A 、B 的坐标分别为(1,4)和(3,0),点C 是y 轴上的一个动点,连接AC 、BC ,当ABC ∆的周长最小值时,ABC ∆的面积为 .【答案】3【解析】解:如图,作点A 关于y 轴的对称点A ',连接A B '交y 轴于点C ',此时ABC ∆'的周长最小,设直线A B ' 的解析式为y kx b =+,(1,4)A '-,(3,0)B ,∴430k b k b -+=⎧⎨+=⎩,1k ∴=-,3b =,∴直线A B ' 的解析式为3y x =-+,当0x =时,3y =,(0,3)C ∴',ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=.所以ABC ∆'的面积为3.故答案为:3.【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积,解决本题的关键是掌握轴对称的性质.★★☆练习2.如图,在平面直角坐标系中,直线122y x =+与x 轴、y 轴分别交于A 、B 两点,以AB 为边 在第二象限内作正方形ABCD .(1)求点A 、B 的坐标,并求边AB 的长;(2)求点C 和点D 的坐标;(3)在x 轴上找一点M ,使MDB ∆的周长最小,请求出M 点的坐标,并直接写出MDB ∆的周长最小值.【答案】详见解析【解析】解: (1)对于直线122y x =+, 令0x =,得到2y =;令0y =,得到4x =-,(4,0)A ∴-,(0,2)B ,即4OA =,2OB =, 则224225AB =+=;(2)过D 作DE x ⊥轴,过C 作CF y ⊥轴,四边形ABCD 为正方形,AB BC AD ∴==,90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒,90FBC ABO ∠+∠=︒,90ABO BAO ∠+∠=︒,90DAE BAO ∠+∠=︒,FBC OAB EDA ∴∠=∠=∠,()DEA AOB BFC AAS ∴∆≅∆≅∆,2AE OB CF ∴===,4DE OA FB ===,即426OE OA AE =+=+=,246OF OB BF =+=+=,则(6,4)D -,(2,6)C -;(3)如图所示,连接BD ,找出B 关于y 轴的对称点B ',连接DB ',交x 轴于点M ,此时BM MD DM MB DB +=+'='最小,即BDM ∆周长最小,(0,2)B ,(0,2)B ∴'-,设直线DB '解析式为y kx b =+,把(6,4)D -,(0,2)B '-代入得:642k b b -+=⎧⎨=-⎩,解得:1k =-,2b =-,∴直线DB '解析式为2y x =--,令0y =,得到2x =-,则M 坐标为(2,0)-, 此时MDB ∆的周长为21062+.【备注】本题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,坐标与图形性质,勾 股定理,全等三角形的判定与性质,正方形的性质,对称性质,以及一次函数与坐标轴的交点,熟练掌握 性质及定理是解本题的关键(二)一次函数线段差最大值问题【例题讲解】★★☆例题1.已知,如图点(1,1)A ,(2,3)B -,点P 为x 轴上一点,当||PA PB -最大时,点P的坐标为( )A .1(,0)2B .5(,0)4C .1(,0)2-D .(1,0)【答案】A【解析】解:作A 关于x 轴对称点C ,连接BC 并延长交x 轴于点P , (1,1)A ,C ∴的坐标为(1,1)-,连接BC ,设直线BC 的解析式为:y kx b =+,∴123k b k b +=-⎧⎨+=-⎩, 解得:21k b =-⎧⎨=⎩, ∴直线BC 的解析式为:21y x =-+, 当0y =时,12x =, ∴点P 的坐标为:1(2,0),当B ,C ,P 不共线时,根据三角形三边的关系可得:||||PA PB PC PB BC -=-<,∴此时||||PA PB PC PB BC -=-=取得最大值.故选:A .【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系.此题难度较大,解题的关键是找到P 点,注意数形结合思想与方程思想的应用.★★☆练习1.平面直角坐标系中,已知(4,3)A 、(2,1)B ,x 轴上有一点P ,要使PA PB -最大,则P 点坐 标为【答案】(1,0)【解析】解:(4,3)A 、(2,1)B ,x 轴上有一点P ,||PA PB AB ∴-,∴当A ,B ,P 三点共线时,PA PB -最大值等于AB 长,此时,设直线AB 的解析式为y kx b =+,把(4,3)A 、(2,1)B 代入,可得3412k b k b =+⎧⎨=+⎩, 解得11k b =⎧⎨=-⎩, ∴直线AB 的解析式为1y x =-,令0y =,则1x =,P ∴点坐标为(1,0),故答案为:(1,0). 【备注】本题主要考查了坐标与图形性质,利用待定系数法求得直线AB 的解析式是解决问题的关键. ★★☆练习2.如图,在平面直角坐标系中,点A 的坐标为(0,4),点B 的坐标为(6,0),点P 在一次函数1322y x =+的图象上运动,则PB PA -的最大值为( )A .2B .233C .4D .143【答案】C【解析】解:如图,作点A 关于直线1322y x =+的对称点K ,连接AK 交直线于H ,连接PK .AK PH ⊥,(0,4)A ,∴直线AK 的解析式为24y x =-+,由132224y x y x ⎧=+⎪⎨⎪=-+⎩,解得12x y =⎧⎨=⎩, (1H ∴,20,AH KH =,(2,0)K ∴.PB PA PB PK KB ∴-=-,∴当点P 在BK 的延长线上时,P B P K BK '-'=的值最大,最大值为624-=,故选:C .【备注】本题考查一次函数图象上的点的特征、轴对称等知识,解题的关键是学会利用对称解决最值问题 属于中考常考题型.【题型知识点总结】一次函数最短路径问题注意事项:1. 根据“和小异,差大同”判断是否需要作对称;2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。
初中数学几何线段及线段和、差的最值问题探析

初中数学几何线段及线段和、差的最值问题探析一、一般处理方法常用定理两点之间,线段最短垂线段最短三角形三边关系PA+PB最小,需转化,使点在线异侧|PA-PB|最大,需转化,使点在线同侧具体例题分析类型一利用两点之间线段最短1.立体图形平面展开图求最短路径例1.有一圆柱体如图,高4cm,底面半径5cm,A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行的最短距离。
试题分析:此题为常规题型,碰到立体图形中的最短路径问题把它展开成平面图形再利用两点之间线段求解即可。
解:AB =,BC为底面周长的一半即BC =πAC = ==答:蚂蚁爬行的最短距离为cm。
2.通过作轴对称求距离之和的最小值例2:如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周长是试题分析:此题出现一个定点两条定直线,所以我们是通过这个定点分别关于这两条直线作对称点,再根据三角形三边关系,最终转为两点之间线段最短来处理。
解:设∠POA=θ,则∠POB=30°﹣θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形. 联盟∵OA是PE的垂直平分线,∴EQ=QP;同理,OB是PF的垂直平分线,∴FR=RP,∴△PQR的周长=EF.∵OE=OF=OP=10,且∠EOF=∠EOP+∠POF=2θ+2=60°,∴△EOF是正三角形,∴EF=10,即在保持OP=10的条件下△PQR的最小周长为10.故选A.3.利用平移求线段和的最小值例3:荆州护城河在CC’处直角转弯,河宽相等,从A 处到达B处,需经过两座桥DD’、EE’,护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到B点路径最短?试题分析:由于含有固定线段“桥”,导致不能将ADD’E’EB通过轴对称直接转化为线段,需要构造平行四边形将AD、BE平移至D’F、E’G,即可得到桥所在位置解:作AF⊥CD,且AF=河宽,作BG⊥CE,且BG=河宽,连接GF,与河岸相交于E’、D’,作DD’、EE’即为桥证明:由做法可知,AF∥DD’,AF=DD’,则四边形AFDD’为平行四边形于是AD=FD’同理,BE=GE’由两点之间线段最短可知,GF最小即当桥建于如图所示位置时,ADD’E’EB最短二、利用垂线段最短求最值1.通过转移点,转化为一个定点到一条定直线的距离的最小值例1:如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是C. D.试题分析:此题,两条线段涉及到三个点,其中B为定点,另外两个点均为动点,但通过角平分线这个条件可以把BM转化成关于线段AD对称的线段EM. 从而把两条线段之和的最值转化为点E到直线AB的最短距离。
专题9线段和差最值的存在性问题(教师)
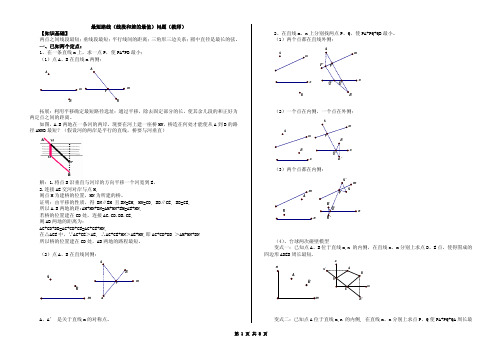
最短路线(线段和差的最值)问题(教师) 【知识基础】 两点之间线段最短; 垂线段最短; 平行线间的距离; 三角形三边关系; 圆中直径是最长的弦。
一、已知两个定点: 1、在一条直线 m 上,求一点 P,使 PA+PB 最小; (1)点 A、B 在直线 m 两侧:A2、在直线 m、n 上分别找两点 P、Q,使 PA+PQ+QB 最小。
(1)两个点都在直线外侧:AAmm PAnP'Q'Q Bnm BP BmB拓展:利用平移确定最短路径选址:通过平移,除去固定部分的长,使其余几段的和正好为 两定点之间的距离。
如图,A.B 两地在一条河的两岸,现要在河上建一座桥 MN,桥造在何处才能使从 A 到 B 的路 径 AMNB 最短?(假设河的两岸是平行的直线,桥要与河垂直)(2)一个点在内侧,一个点在外侧:A mA mPB Q n B'B n(3)两个点都在内侧: 解:1.将点 B 沿垂直与河岸的方向平移一个河宽到 E, 2.连接 AE 交河对岸与点 M, 则点 M 为建桥的位置,MN 为所建的桥。
证明:由平移的性质,得 BN∥EM 且 BN=EM, MN=CD, BD∥CE, BD=CE, 所以 A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在 CD 处,连接 AC.CD.DB.CE, 则 AB 两地的距离为: AC+CD+DB=AC+CD+CE=AC+CE+MN, 在△ACE 中,∵AC+CE>AE, ∴AC+CE+MN>AE+MN,即 AC+CD+DB >AM+MN+BN 所以桥的位置建在 CD 处,AB 两地的路程最短。
(2)点 A、B 在直线同侧:AA'm Am AP BB nQ B'n(4) 、台球两次碰壁模型 变式一:已知点 A、B 位于直线 m,n 的内侧,在直线 n、m 分别上求点 D、E 点,使得围成的 四边形 ADEB 周长最短.nnAPB mA'A B D E m B'A BB mA'mA、A’ 是关于直线 m 的对称点。
中考复习之 线段和差最值问题

线段和(差)最值问题引例:如图,有一圆形透明玻璃容器,高15cm,底面周长为24cm,在容器内壁柜上边缘4cm 的 A 处,停着一只小飞虫,一只蜘蛛从容器底部外向上爬了3cm 的 B 处时( B 处与 A 处恰好相对),发现了小飞虫,问蜘蛛怎样爬去吃小飞虫最近?它至少要爬多少路?(厚度忽略不计).Ⅰ.专题精讲:最值问题是一类综合性较强的问题,而线段和(差)问题,要归归于几何模型:(1 )归于“两点之间的连线中,线段最短”凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.(2 )归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.Ⅱ.典型例题剖析 :一.归入“两点之间的连线中,线段最短”BⅠ .“饮马”几何模型:A条件:如下左图, A、B 是直线 l 同旁的两个定点.问题:在直线l 上确定一点 P,使 PA+ PB 的值最小.l模型应用:1.如图,正方形ABCD 的边长为 2,E 为 AB 的中点, P 是 AC 上一动点.则PB+PE 的最小值是.2.如图,⊙ O 的半径为 2,点 A、B、C 在⊙ O 上, OA⊥ OB,∠ AOC=60 °, P 是 OB 上一动点,则 PA+PC 的最小值是.3.如图,在锐角△ ABC 中, AB= 42,∠ BAC= 45°,∠ BAC 的平分线交 BC 于点 D, M、 N 分别是 AD 和 AB 上的动点,则BM+MN 的最小值是.第1题第2题第3题第4题4.如图,在直角梯形ABCD 中,∠ ABC= 90°, AD ∥BC,AD = 4, AB= 5,BC= 6,点 P 是 AB 上一个动点,当PC+ PD 的和最小时,PB 的长为 __________.5.如图,等腰梯形ABCD 中, AB= AD = CD= 1,∠ ABC= 60°,P 是上底,下底中点 EF 直线上6.如图, MN 是半径为 1 的⊙ O 的直径,点 A 在⊙ O 上,∠ AMN = 30°,B 为 AN 弧的中点, P 是直径 MN 上一动点,则PA+ PB 的最小值为.第 5 题第 6 题第 7 题7.已知 A(- 2, 3), B(3, 1), P 点在 x 轴上,若 PA+ PB 长度最小,则最小值为.8.已知:如图所示,抛物线y=- x2+ bx+ c 与 x 轴的两个交点分别为A(1,0), B(3, 0).( 1)求抛物线的解析式;( 2)设点 P 在该抛物线上滑动,且满足条件S△PAB= 1 的点 P有几个?并求出所有点P 的坐标;( 3)设抛物线交 y 轴于点 C,问该抛物线对称轴上是否存在点M ,使得△ MAC 的周长最小?若存在,求出点 M 的坐标;若不存在,请说明理由.Ⅱ.台球两次碰壁模型已知点 A 位于直线m,n 的内侧,在直线m、 n 分别上求点P、Q 点,使 PA+PQ+QA 周长最短 .变式:已知点 A、B 位于直线 m,n 的内侧,在直线 m、 n 分别上求点 D、 E 点,使得围成的四边形ADEB 周长最短 .模型应用:2.如图,已知平面直角坐标系, A, B 两点的坐标分别为 A(2 ,- 3), B(4,- 1)设 M,N 分别为 x 轴和 y 轴上的动点,请问:是否存在这样的点M(m,0), N(0,n),使四边形ABMN 的周长最短?若存在,请求出m=______,n = ______(不必写解答过程);若不存在,请说明理由.中考赏析:1 .著名的恩施大峡谷( A)和世界级自然保护区星斗山( B)位于笔直的沪渝高速公路X 同侧, AB=50km 、B 到直线 X 的距离分别为 10km 和 40km ,要在沪渝高速公路旁修建一服务区P,向 A、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图( AP 与直线X 垂直,垂足为P), P 到 A、 B 的距离之和 S1= PA+ PB,图( 2)是方案二的示意图(点 A 关于直线 X 的对称点是 A',连接 BA'交直线 X 于点 P),P 到 A、B 的距离之和 S2=PA+ PB.(1)求 S1、S2,并比较它们的大小;(2)请你说明 S2= PA+ PB 的值为最小;( 3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线 Y 的距离为 30km,请你在 X 旁和 Y 旁各修建一服务区 P、 Q,使 P、 A、B、 Q 组成的四边形的周长最小.并求出这个最小值.3218x+ 3 和 y 轴的交点为A,M 为2.如图,抛物线 y= x -55OA 的中点,若有一动点 P,自 M 点处出发,沿直线运动到 x轴上的某点(设为点 E),再沿直线运动到该抛物线对称轴上的某点(设为点 F),最后又沿直线运动到点 A,求使点 P 运动的总路程最短的点 E,点 F 的坐标,并求出这个最短路程的长.Ⅲ.已知A、B 是两个定点,P、Q 在直线m 上要求P、Q 两点,使得( 1)点 A、 B 在直线 m 两侧:是直线 m 上的两个动点,P 在 Q 的左侧,且 PQ 间长度恒定 , PA+PQ+QB 的值最小. (原理用平移知识解 )( 2)点 A、 B 在直线 m 同侧:实战演练:1.如图,已知平面直角坐标系,A, B 两点的坐标分别为A(2 ,- 3), B(4,- 1)若 C(a,0) ,D (a+3,0) 是 x 轴上的两个动点,则当 a = ______时,四边形ABDC 的周长最短.2.如图,在平面直角坐标系中,矩形OACB 的顶点 O 在坐标原点,顶点A、B 分别在x 轴、 y 轴的正半轴上,OA=3,OB=4, D 为边 OB 的中点 .( 1)若 E 为边 OA 上的一个动点,当△CDE 的周长最小时,求点 E 的坐标;( 2)若 E、F 为边 OA 上的两个动点,且 EF= 2,当四边形 CDEF 的周长最小时,求点 E、F 的坐标 .3.如图,已知在平面直角坐标系 xOy 中,直角梯形 OABC 的边 OA 在 y 轴的正半轴上, OC 在 x 轴的正半轴上, OA=AB=2,OC=3,过点 B 作 BD⊥ BC,交 OA 于点 D.将∠ DBC 绕点 B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点 E 和 F.( 1)求经过A、 B、 C 三点的抛物线的解析式;( 2)当 BE 经过( 1)中抛物线的顶点时,求CF 的长;( 3)在抛物线的对称轴上取两点P、 Q(点 Q 在点 P 的上方),且 PQ=1,要使四边形BCPQ 的周长最小,求出P、 Q 两点的坐标.4.如图,已知点 A(- 4, 8)和点 B( 2, n)在抛物线y=ax 2 上.( 1)求 a 的值及点 B 关于 x 轴对称点 P 的坐标,并在x 轴上找一点 Q,使得 AQ+ QB 最短,求出点 Q 的坐标;( 2)平移抛物线y= ax2,记平移后点 A 的对应点为 A′,点 B 的对应点为 B′,点 C(- 2, 0)和点 D (- 4, 0)是 x 轴上的两个定点.① 当抛物线向左平移到某个位置时,′′A C+ CB 最短,求此时抛物线的函数解析式;②当抛物线向左或向右平移时,是否存在某个位置,使四边形′′A B CD 的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.yA8642BD C- 4- 2 O24x- 2- 4二.求两线段差的最大值问题(运用三角形两边之差小于第三边)几何模型:在一条直线m 上,求一点P,使 PA-PB 的差最大;( 1)点 A、 B 在直线 m 同侧:(2)点A、B在直线m异侧:模型应用:12-x+2的顶点为 A,与 y 轴交于点 B.1. 如图,抛物线y=- x4(1)求点 A、点 B 的坐标;(2)若点 P 是 x 轴上任意一点,求证:PA- PB≤ AB;(3)当 PA- PB 最大时,求点P的坐标 .2. 如图,已知直线 y=1x+1 与y轴交于点 A,y2与 x 轴交于点 D ,抛物线 y=1x 2+ bx+ c 与直线交于A、E 两E 2( 1)求该抛物线的解析式;( 3)在抛物线的对称轴上找一点M,使 | AM - MC| 的值最大,求出点M 的坐标.3.如图,直线y=-3x+ 2 与 x 轴交于点C,与 y 轴交于点B,点 A 为 y 轴正半轴上的一点,⊙A 经过点 B 和点 O,直线 BC 交⊙A 于点 D.( 1)求点 D 的坐标;( 2)过 O,C,D 三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段 PO 与 PD 之差的值最大?若存在,请求出这个最大值和点P 的坐标.若不存在,请说明理由.4.已知:如图,把矩形 OCBA 放置于直角坐标系中, OC=3, BC= 2,取 AB 的中点 M,连接MC ,把△ MBC 沿 x 轴的负方向平移OC 的长度后得到△DAO .( 1)试直接写出点 D 的坐标;( 2)已知点 B 与点 D 在经过原点的抛物线上,点P 在第一象限内的该抛物线上移动,过点P 作 PQ⊥ x 轴于点 Q,连接 OP.若以 O、P、Q 为顶点的三角形与△ DAO 相似,试求出点 P 的坐标;( 3)试问在( 2)抛物线的对称轴上是否存在一点T,使得|TO- TB|的值最大?若存在,则求出。
线段和差的最值问题解题策略

当Q运动到E时,PQ+QA最小
CB 32 32 3 2
小结
E? F!
09北京25 设G为y轴上一点,点P从 点M出发,先沿y轴到达 G点,再沿GA到达A点. P点在y轴上运动的速度 是它在直线GA上运动速 度的2倍.
试确定G点的位置,使P点按照上述要求到达A点所用的时间 最短.(要求:简述确定G点位置的方法,但不要求证明)
09内江27
对于动点Q(1,n),求PQ+QB的最小值 .
第一步 寻找、构造几何模型
要求PQ+QB的最小值?
经典模型:牛喝水!
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA ! 当Q运动到E时,PQ+QA最小
AP 32 32 3 2
第二步 计算——勾股定理
把PQ+QB转化为PQ+QA !
第一步 寻找、构造几何模型
08福州22
要求四边形MNFE 的周长最小?
把三条线段转移到同 一条直线上就好了!
第二步 计算——勾股定理
E' F ' 3 4 5
2 2
EF 1 2 5
2 2
因此四边形 MNFE的周经典模型:台球两次碰壁问题
经验储存:没有经验,难有思路
09济南24
已知在对抛物线的称轴上存在一点P,使得△PBC的周长 最小,请求出点P的坐标 .
第一步 寻找、构造几何模型
要求△PBC的周长最小? 只要PB+PC最小就好了!
经典模型:牛喝水!
第二步 计算——勾股定理
把PB+PC转化为PA+PC !
当P运动到H时,PA+PC最小
中考几何中“线段和的最值”问题的教学策略

中考几何中“线段和的最值”问题的教学策略一、问题产生的背景在初四总复习中,我们在教学中发现有一类求线段和差极值的题目,学生常常找不到解题的突破口,教学难度及学生掌握难度较大。
如:(中考数学选)如图,已知直线y =21x +1与y 轴交于点A ,与x 轴交于点D ,抛物线y =21x2+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).(1)求该抛物线的解析式;(3)-MC |的值最大,求出点问题的第三问常令许多同学甚至是优等生的同学都瞠目结舌。
综观近几年的数学中考题,此类题频频出现在选择、填空、综合题中。
通过平日测试来看,此类题的失分很高,应该引起我们的重视。
二、造成学生对问题困惑的原因我们一起研究分析后,发现几何极值问题在教课书虽然没有专题讲解,但却给出了它的模型。
学生对几何极值模型的陌生,及教师在复习时对教材例习题的拓展延伸程度不够,是导致学生对这类问题困惑的根本原因。
课本中的例题与习题,都是通过筛选的题目的精华,在解题的思路和方法上具有典型性和代表性,在由知识转化为能力的过程中具有示范性和启发性.它们的解题方法和结论本身都具有广泛迁移的可能.现实教学过程中,教师对教材例题、习题开发的意识不强,在备课中不能对例题、习题进行深层次的挖掘、拓展、再创造,在授课时也往往出现一笔带过、草草了事的教学现状,根本没有很好的利用例题、习题的所潜在的价值,而教材例题、习题的开发能促使学生的学习方式由“重结论轻过程”向“过程与结果”并重的方向发展,使学生挖掘隐含问题的本质属性,从而达到“做一题,通一类,会一片”的解题境界.正如数学教育家波利亚指出的:“一个有责任性的教师穷于应付繁琐的数学内容和过量的题目,还不如适当选择某些有意义但有不太复杂的题目去帮助学生发掘题目的各个方面,在指导学生的解题过程中,提高他们的才智和解题能力.三、问题前后知识的联系:课本题目再现:鲁教版七年级教材第一册第一章第三节第轴对称的性质15页试一试:如图所示,要在公路帝修建一个蔬菜收购站,由蔬菜基地A,B向收购站运送蔬菜,收购站应建在什么地方,才能使从A,B到它的距离之各最短?本题涉及的知识不是一个简单的轴对称变换,其变化过程实际是求一类几何极值的过程,此题模式是求几何几何的典型模式。
几何图形中线段和差最值问题

中考数学压轴题解题策略几何图形中线段和差最值问题的解题策略两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A 与PB 的差的最大值就是AB ,此时点P 在AB 的延长线上,即P ′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1 图2 图31.如图,在锐角ABC △中,45AB BAC =∠=°,BAC ∠的平分线交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是___________ .2.如图,菱形ABCD 的两条对角线分别长6和8,点P 是对角线AC 上的一个动点,点M 、N 分别是边AB 、BC 的中点,则PM +PN 的最小值是_____________.3、如图,已知正方形ABCD 的边长为8,F 是DA 上一点,且FA=2,点P 是BD 上一动点,则 AP+PF 的最小值为 .4、如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD+PE 的和最小,则其最小值为A B CD N M (第1题第2题图 D A B C P M N5.如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.6.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙B和⊙A上的动点,求PE+PF的最小值.7.如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=3,M是AD边的中点,N 是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C 长度的最小值是.8.如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF 沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的小值是()A.B.6 C.D.49.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C. 则A′C长度的最小值是 .10.如图,矩形ABCD中,AB=2,BC=3,以A为圆心,1为半径画圆,E是⊙A上一动点,P 是BC上的一动点,则PE+PD的最小值是.11.如图,∠MON=90°,矩形ABCD 的顶点A 、B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为____12.如图,已知A (0, 2)、B (6, 4)、E (a , 0)、F (a +1, 0),求a 为何值时,四边形ABEF 周长最小?请说明理由.13. 如图,△ABC 中,∠ACB =90°,AC =2,BC =1.点A 、C 分别在x 轴和y 轴的正半轴上,当点A 在x 轴上运动时,点C 也随之在y 轴上运动.在整个运动过程中,求点B 到原点的最大距离.14. 如图,已知A (-2,0)、B (4, 0)、(D -.设F 为线段BD 上一点(不含端点),连结AF ,一动点M 从点A 出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止.当点F 的坐标是多少时,点M 在整个运动过程中用时最少?15.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8.点E 是BC 边上的点,连结AE ,过点E 作AE 的垂线交AB 边于点F ,求AF 的最小值.16.如图,抛物线21442y x x =-+与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程.17.如图,在△ABC 中,∠ABC =90°,AB =6,BC =8,O 为AC 的中点,过O 作OE⊥OF ,OE ,OF 分别交射线AB ,BC 于E ,F ,连接EF ,则EF 长度的最小值为_______.18.如图,在Rt AOB ∆中,OA OB ==,⊙O 的半径为1,点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线长PQ 的最小值为 .O B F E A19、在三角形ABC中,AB=AC=2,∠ABC=30°,点M,N分别在边AB,AC上,将三角形AMN沿MN 翻折,点A落到点A’处,则线段BA’长度的最小值是ANMA'B C20.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是.。
线段和差的最值问题解题策略课件

高阶练习题
总结词
挑战综合应用
详细描述
高阶练习题难度较高,需要综合运用线段和 差最值问题的多种解题策略,挑战解题者的 思维深度和广度,培养综合应用能力。
06 问题拓展与思考
相关问题链接
线段和差与面积关系
探讨线段和差与面积的最值问题,如何通过线段和差来求解面积 的最值。
线段和差与其他几何量关系
研究线段和差与周长、体积等其他几何量的最值问题之间的联系。
生产制造中的应用
探讨线段和差最值问题在生产制造、工艺设计和 优化中的实际应用,如何提高生产效率和降低成 本。
THANKS
02 解题策略
代数法
通过代数运算,将问题转化为函数最值问题,利用求导或不 等式性质求解。
代数法是解决线段和差最值问题的基本方法之一。首先,将 问题中的线段长度表示为变量,然后通过代数运算,将问题 转化为一个函数最值问题。接下来,利用求导或不等式性质 ,找到函数的最值点,从而得到线段和差的最值。
几何法
详细描述
解决这类问题需要理解线段的性质和 几何定理,如勾股定理、三角形的三 边关系等。通过这些定理可以推导出 线段和差的最值条件,从而找到解决 问题的关键点。
三角形中的线段和差问题
总结词
三角形中的线段和差问题涉及到三角 形的边长和角度,需要结合三角形的 性质进行求解。
详细描述
解决这类问题需要掌握三角形的边角 关系,如正弦定理、余弦定理等。通 过这些定理可以推导出线段和差与角 度之间的关系,从而找到最值条件。
将参数方程转换为普通方程,便 于计算和比较线段长度。
05 练习题与解析
基础练习题
总结词
掌握基础概念
详细描述
基础练习题主要涉及线段和差最值问题的基本概念和简单应用,适合初学者通过练习理解和掌握基本 解题方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线段和差最值的存在性问题解题策略
专题攻略
两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).
三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).
两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA 与PB 的差的最大值就是AB ,此时点P 在AB 的延长线上,即P ′. 解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.
图1 图2 图3
例题解析
例❶ 如图1-1,抛物线y =x 2
-2x -3与x 轴交于A 、B 两点,与y 轴交于点C ,点P 是抛物线对称轴上的一个动点,如果△PAC 的周长最小,求点P 的坐标.
图1-1
【解析】如图1-2,把抛物线的对称轴当作河流,点A 与点B 对称,连结BC ,那么在△PBC 中,PB +PC 总是大于BC 的.如图1-3,当点P 落在BC 上时,PB +PC 最小,因此PA +PC 最小,△PAC 的周长也最小.
由y =x 2
-2x -3,可知OB =OC =3,OD =1.所以DB =DP =2,因此P (1,-2).
图1-2 图1-3
例❷如图,抛物线21442
y x x =-+与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程.
图2-1
【解析】如图2-2,按照“台球两次碰壁”的模型,作点A 关于抛物线的对称轴对称的点A ′,作点B 关于x 轴对称的点B ′,连结A ′B ′与x 轴交于点M ,与抛物线的对称轴交于点N .
在Rt △AA ′B ′中,AA ′=8,AB ′=6,所以A ′B ′=10,即点G 走过的最短路程为10.根据相似比
可以计算得到OM =83,MH =43
,NH =1.所以M (83, 0),N (4, 1).
图2-2
例❸ 如图3-1,抛物线248293
y x x =-++与y 轴交于点A ,顶点为B .点P 是x 轴上的一个动点,求线段PA 与PB 中较长的线段减去较短的线段的差的最小值与最大值,并求出相应的点P 的坐标.
图3-1
【解析】题目读起来像绕口令,其实就是求|PA -PB |的最小值与最大值.
由抛物线的解析式可以得到A (0, 2),B (3, 6).设P (x , 0).
绝对值|PA -PB |的最小值当然是0了,此时PA =PB ,点P 在AB 的垂直平分线上(如图3-2).解方
程x 2+22=(x -3)2+62
,得416x =.此时P 41(,0)6
. 在△PAB 中,根据两边之差小于第三边,那么|PA -PB |总是小于AB 了.如图3-3,当点P 在BA 的延
长线上时,|PA -PB |取得最大值,最大值AB =5.此时P 3(,0)2-.
图3-2 图3-3
例❹如图4-1,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,求PK+QK的最小值.
图4-1
【解析】如图4-2,点Q关于直线BD的对称点为Q′,在△KPQ′中,PK+QK总是大于PQ′的.如图4-3,当点K落在PQ′上时,PK+QK的最小值为PQ′.如图4-4,PQ′的最小值为Q′H,Q′H就是菱形ABCD的高,Q′H=3.
这道题目应用了两个典型的最值结论:两点之间,线段最短;垂线段最短.
图4-2 图4-3 图4-4
例❺如图5-1,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙B和⊙A上的动点,求PE+PF的最小值.
图5-1
【解析】E、F、P三个点都不确定,怎么办?BE=1,AF=2是确定的,那么我们可以求PB+PA-3的最小值,先求PB+PA的最小值(如图5-2).
如图5-3,PB+PA的最小值为AB′,AB′=6.所以PE+PF的最小值等于3.
图5-2 图5-3
例❻如图6-1,已知A(0, 2)、B(6, 4)、E(a, 0)、F(a+1, 0),求a为何值时,四边形ABEF周长最小?请说明理由.
图6-1
【解析】在四边形ABEF 中,AB 、EF 为定值,求AE +BF 的最小值,先把这两条线段经过平移,使得两条线段有公共端点.
如图6-2,将线段BF 向左平移两个单位,得到线段ME .
如图6-3,作点A 关于x 轴的对称点A ′,MA ′与x 轴的交点E ,满足AE +ME 最小.
由△A ′OE ∽△BHF ,得'OE HF OA HB =.解方程6(2)24a a -+=,得43
a =.
图6-2 图6-3
例❼ 如图7-1,△ABC 中,∠ACB =90°,AC =2,BC =1.点A 、C 分别在x 轴和y 轴的正半轴上,当点A 在x 轴上运动时,点C 也随之在y 轴上运动.在整个运动过程中,求点B 到原点的最大距离.
图7-1
【解析】如果把OB 放在某一个三角形中,这个三角形的另外两条边的大小是确定的,那么根据两边之和大于第三边,可知第三边OB 的最大值就是另两边的和.
显然△OBC 是不符合条件的,因为OC 边的大小不确定.
如图7-2,如果选AC 的中点D ,那么BD 、OD 都是定值,OD =1,BD =2.
在△OBD 中,总是有OB <OD +BD .
如图7-3,当点D 落在OB 上时,OB 最大,最大值为21+.
图7-2 图7-3
例❽如图8-1,已知A(-2,0)、B(4, 0)、(5,33)
D-.设F为线段BD上一点(不含端点),连结AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止.当点F的坐标是多少时,点M在整个运动过程中用时最少?
图8-1
【解析】点B(4, 0)、(5,33)
D-的坐标隐含了∠DBA=30°,不由得让我们联想到30°角所对的直角边等于斜边的一半.
如果把动点M在两条线段上的速度统一起来,问题就转化了.
如图8-2,在Rt△DEF中,FD=2FE.如果点M沿线段FD以每秒2个单位的速度运动到点D时,那么点M沿线段FE以每秒1个单位的速度正好运动到点E.因此当AF+FE最小时,点M用时最少.如图8-3,当AE⊥DE时,AF+FE最小,此时F(2,23)
-.
图8-2 图8-3
例❾如图9-1,在Rt△ABC中,∠C=90°,AC=6,BC=8.点E是BC边上的点,连结AE,过点E 作AE的垂线交AB边于点F,求AF的最小值.
图9-1
【解析】如图9-2,设AF的中点为D,那么DA=DE=DF.所以AF的最小值取决于DE的最小值.
如图9-3,当DE⊥BC时,DE最小.设DA=DE=m,此时DB=5
3 m.
由AB=DA+DB,得
5
10
3
m m
+=.解得
15
4
m=.此时AF=
15
2
2
m=.图9-2 图9-3
例❿ 如图10-1,已知点P 是抛物线214y x =上的一个点,点D 、E 的坐标分别为(0, 1)、(1, 2),连结PD 、PE ,求PD +PE 的最小值.
图10-1
【解析】点P 不在一条笔直的河流上,没有办法套用“牛喝水”的模型.
设P 21(,
)4x x ,那么PD 2=2222211(1)(1)44
x x x +-=+.所以PD =2114x +. 如图10-2,2114
x +的几何意义可以理解为抛物线上的动点P 到直线y =-1的距离PH .所以PD =PH .因此PD +PE 就转化为PH +PE . 如图10-3,当P 、E 、H 三点共线,即PH ⊥x 轴时,PH +PE 的最小值为3.
高中数学会学到,抛物线是到定点的距离等于到定直线的距离的点的集合,在中考数学压轴题里, 如果要用到这个性质,最好铺垫一个小题,求证PD =PH .
图10-2 图10-3。
